黑龙江省哈尔滨市第六十九中学2019届毕业学年校内模拟测试(一)数学试卷及答案

哈六十九中学2019届毕业学年校内模拟测试英语试卷第 I 卷一、单项选择（本题共 20 分, 每小题 1 分）选择最佳答案。

( ) 1. Boys and girls, no matter what difficulties you face, please don’t be disappointed.and work hard. This is the key to success.A. Cheer upB. Stay upC. Pick up( ) 2. ---Our school held the 100-day pledging conference(誓师大会) in Harbin Confucian Temple last month.--- encouraging activity it was! Let’s make an effort to achieve our dream.A. HowB. What anC. What( ) 3. ---Can you tell me how to have a good relationship with parents?---Certainly. If you often talk about your ideas with them, they will talk aboutwith you, too.A. theirB. themC. theirs( ) 4. ---Mum, can I throw away the old clock? We it for many years.---No, you can’t. It still works well and remember saving is getting.A. have boughtB. have hadC. bought( ) 5. ---Nowadays, more and more people are glad to help those in need in our society.---Great! Help others, help yourself. I think the of being a volunteer willalso benefit them a lot.A. expressionsB. experiencesC. exercises( ) 6. ---In the past four years, we have learned a lot from our teachers.---They are great, so without doubt we will be forever thankful them.A. toB. forC. of( ) 7. ---Song of Youth is a very popular movie these days.---That’s true. people, especially the young, enjoy watching it.A. Millions ofB. Two millionsC. Two millions of( ) 8. ---How is your close friend Katie?---Oh, she’s moved to another city, so I’ve ever seen her since then.A. completelyB. hardlyC. simply( ) 9. Knowledge comes from questioning. If we ask questions and don’t be afraid of making mistakes, we will make rapid progress and be a good learner.A. dare notB. dare toC. didn’t dare( ) 10. ---I think children should Tik Tok(抖音) because it is sometimes bad for them.---I agree. Some rules should be made.A. throw awayB. keep away fromC. separate from( ) 11. A friend in need is a friend indeed. The only way a friend is to be one.A. for havingB. havingC. to have( ) 12. ---Hi, Kate, would you like to hang out with me this afternoon?---I’m afraid not. I can’t go out I finish my report.A. whenB. unlessC. if( ) 13. ---How do you like the Sun Island？Is it worth visiting?---Sure. It’s one of the best places I have ever been to.A. whichB. thatC. who( ) 14. ---Could you tell me in the past?---Yes. Great changes have taken place in our city. These pictures can show you.A. what our city looked likeB. how our city looked likeC. what was our city like( ) 15. Tasting good food is an interesting part of traveling. When in , Germany, we can enjoy sausages, potatoes and cheese as well as many different kinds of beer.A. MoscowB. BostonC. Munich( ) 16. Busiest men find the most time. Although we teenagers are busy studying all day now, we should also take up meaningful hobbies because they can ______.① help relax our body and mind.② let us learn more from textbooks③ help us make more friends.④ improve our ability⑤ make us increase stressA. ①④⑤B. ②④⑤C. ①③④( ) 17. In our school, we have early morning and afternoon self-study in total for 40 minutes every day. Here’s our school’s self-study class schedule. According to theform below, we spend ______ minutes on tests from Monday to Friday every week.Self-study ClassEarly morning AfternoonEye exercises Listening to songs A test Eye exercises Reading Atest5 minutes? 5 minutes 5 minutes? 5 minutesA. 20B.50C. 100( ) 18. Which pair of the words with the underlined letters has the same sound?A. nurse purposeB. childhood characterC. attitude relation ( ) 19. Which of the following words has different sounds from the underlined letter of theword “breathe”?A. thousandB. thoughC. smooth( ) 20. Which word of the following doesn’t have the same stress as the others?A. Create.B. Realize.C. Forward.二、完形填空（本题共10分，每小题1分）Reading has been the most educational tool used by us right from the childhood. Maybe some people say that reading is out of date, but to me a good book is a good friend. I 21 to read plenty of books to increase my knowledge. What will you do if you want to be a perfect reader? The following are some suggestions which may help you 22 your reading skills.Clear your purpose of reading.Before reading, ask yourself 23 you are reading this book. Most people read for two main reasons: pleasure and knowledge. Clearing about your reading purpose can not only help you choose the book you really need to read, 24 remind you why reading the book is important to you, so you will keep reading and complete the book faster.Read only what you are interested 25 .Whatever you are reading, it’s 26 to enjoy what you read. Your friends may tell you the books they love, but those books 27 not be the ones you like. You may have chosen books that interest you, and they are suitable for your purpose. But while you are reading them, whenever you realize that you don’t enjoy them, give them up. Remember reading shouldn’t be a 28 .Set a reading goal.It’s interesting that you read the books 29 from libraries faster than those you b ought. The reason is the books you bought don’t have a due date! You needn’t return them. Having a reading goal helps you work out how much reading you need to do in a week or even a day. 30 , before you read each book, ask yourself how long you nee d to complete this book.Reading makes a full man. Reading helps us become wiser. Now what are you waiting for? Go and get a book. Join me in reading, reading and more reading.根据短文内容选择最佳答案。

黑龙江省哈尔滨市第六十九联合中学2019年高二数学理上学期期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 如图是2016年某学生进行舞蹈比赛环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分，所剩数据的平均数和众数依次是（）A．85.84 B．84.85 C．85.87 D．84.86参考答案：A【考点】众数、中位数、平均数．【分析】去掉一个最高分和一个最低分，所剩数据为84，84，86，84，87，由此能求出所剩数据的平均数和众数．【解答】解：去掉一个最高分和一个最低分，所剩数据为84，84，86，84，87，∴所剩数据的平均数为：=（84+84+86+84+87）=85，所剩数据众数为：84．故选：A．2. 在直角坐标系xoy中，过双曲线的左焦点F作圆的一条切线（切点为T）交双曲线右支于点P，若M为FP的中点，则A. B. C. D.参考答案：A略3. 已知抛物线过其焦点且斜率为1的直线交抛物线于A、B两点。

若线段AB中点的纵坐标为2，则该抛物线准线方程为（）A. B. C. D.参考答案：B略4. 偶函数y＝f(x)满足条件f(x＋1)＝f(x－1)，且当x∈[－1,0]时，f(x)＝3x＋，则f()的值等于( )A．－1 B. C. D．1参考答案：D略5. 复数的共轭复数是 ( )A． B． C． D．参考答案：B6. 设是椭圆E：的左、右焦点，P为直线上一点，是底角为的等腰三角形，则椭圆E的离心率为（）A．B．C．D．参考答案：C略7. 某公司生产甲、乙两种桶装产品。

已知生产甲产品1桶需耗原料1千克、原料2千克；生产乙产品1桶需耗原料2千克，原料1千克。

每桶甲产品的利润是300元，每桶乙产品的利润是400元。

公司在生产这两种产品的计划中，要求每天消耗、原料都不超过12千克。

通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（）A、1800元B、2400元C、2800元 D、3100元参考答案：C8. 已知A，B，C三点不共线，O为平面ABC外一点，下列哪个条件能判断点M 不在平面ABC内参考答案：C9. 抛物线的准线方程为A.x=2B.x= 2C.y=2D.y=2参考答案：C略10. 若等差数列{a n}的前5项和S5=25，且a2=3，则a7=（）A．12 B．13 C．14 D．15参考答案：B【考点】等差数列的前n项和；等差数列的通项公式．【分析】利用等差数列的通项公式和前n项和公式，结合已知条件列出关于a1，d的方程组，解出a1，d，然后代入通项公式求解即可．【解答】解：设{a n}的公差为d，首项为a1，由题意得，解得，∴a7=1+6×2=13，故选B．【点评】本题考查了等差数列的通项公式、前n项和公式，熟练应用公式是解题的关键．二、填空题:本大题共7小题,每小题4分,共28分11. 一辆汽车在笔直的公路上向前变速行驶，设汽车在时刻t的速度为v（t）=﹣t2+4，（t的单位：h，v的单位：km/h）则这辆车行驶的路程是km．参考答案：【考点】67：定积分．【分析】由速度等于0求出汽车正向行驶的时间，求定积分后得答案．【解答】解：由v（t）=﹣t2+4=0，得t=2．故这辆车行驶的路程是（﹣t2+4）dt=（﹣+4t）|=﹣+8=故答案为：．【点评】本题考查了定积分，关键是正确理解题意，求出积分区间，是基础的计算题．12. 若实数x，y满足，则z=3x+2y的最小值是．参考答案：1【考点】简单线性规划．【分析】由约束条件作出可行域，令t=x+2y，化为直线方程的斜截式，数形结合求得最优解，代入最优解的坐标求得t的最小值，则z=3x+2y的最小值可求．【解答】解：由约束条件作出可行域如图，令t=x+2y，则y=，由图可知，当直线y=过O（0，0）时，t有最小值为0．∴z=3x+2y的最小值是30=1．故答案为：1．13. 已知数列{a n}中，a1=3，a2=5，且对于任意的大于2的正整数n，有a n=a n﹣1﹣a n﹣2则a11= ．参考答案：﹣5【考点】数列递推式．【专题】计算题；函数思想；试验法；等差数列与等比数列．【分析】由已知结合递推式求出数列前几项，可得数列{a n}是周期为6的周期数列，由此求得a11．【解答】解：由a1=3，a2=5，且a n=a n﹣1﹣a n﹣2，得a3=a2﹣a1=5﹣3=2，a4=a3﹣a2=2﹣5=﹣3，a5=a4﹣a3=﹣3﹣2=﹣5，a6=a5﹣a4=﹣5﹣（﹣3）=﹣2，a7=a6﹣a5=﹣2﹣（﹣5）=3，…由上可知，数列{a n}是周期为6的周期数列，∴a11=a6+5=a5=﹣5．故答案为：﹣5．【点评】本题考查数列递推式，考查了数列的函数特性，关键是对数列周期的发现，是中档题．14. 函数的单调减区间为▲ .参考答案：15. 的解集是参考答案：16. 为了调查某产品的销售情况，销售部门从下属的92家销售连锁店中抽取30家了解情况．若采用系统抽样法，则抽样间隔和随机剔除的个体分别为．参考答案：3，2【考点】系统抽样方法．【分析】从92家销售连锁店中抽取30家了解情况，用系统抽样法，因为92÷30不是整数，所以要剔除一些个体，根据92÷30=3…2，得到抽样间隔和随机剔除的个体数分别为3和2．【解答】解：∵92÷30不是整数，∴必须先剔除部分个体数，∵92÷30=3…2，∴剔除2个，间隔为3．故答案为3，2．17. 在数列{a n}中，a1=1，（n≥2），则a5= ．参考答案：【考点】数列递推式．【分析】由已知条件，利用递推公式依次求出a2，a3，a4，a5．【解答】解：∵在数列{a n}中，a1=1，（n≥2），∴，a3=1+=，a4=1+=3，a5=1+=．故答案为：．【点评】本题考查数列的第5项的求法，是基础题，解题时要认真审题，注意递推思想的合理运用．三、解答题：本大题共5小题，共72分。

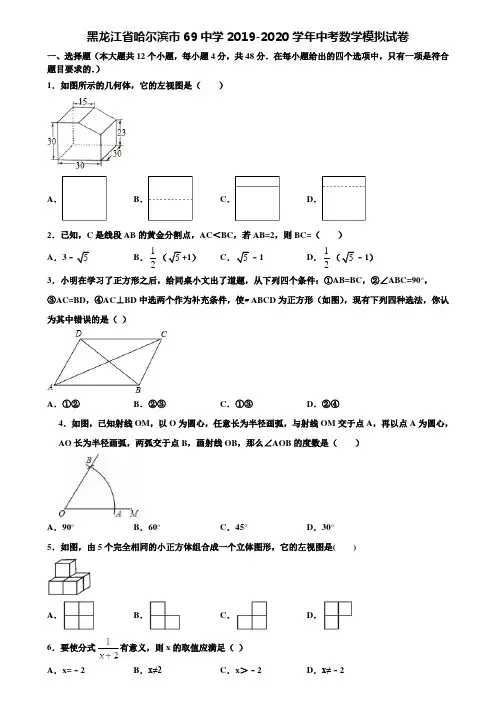
2019年黑龙江省哈尔滨六十九中中考数学模拟试卷（5月份）一、选择题1． 4的平方根是（）A．±2 B．2 C．±D．2．下列运算中，结果正确的是（）A．2a+3b=5ab B．a2•a3=a6C．（a+b）2=a2+b2D．2a﹣（a+b）=a﹣b3．下列图形中，既是轴对称图形，又是中心对称图形的有（）A．1个B．2个C．3个D．4个4．下列几何体的主视图、左视图、俯视图都相同的是（）A．B．C．D．5．对于双曲线y=，当x＞0时，y随x的增大而减小，则k的取值范围是（）A．k＜3 B．k≤3 C．k＞3 D．k≥36．下列关于x的方程一定有实数解的是（）A．2x=m B．x2=m C． =m D． =m7．如图，已知直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α等于（）A．2l° B．30° C．58° D．48°8．如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．若AB=4.5，BC=3，EF=2，则DE的长度是（）A．B．3 C．5 D．9．如图，在地面上的点A处测得树顶B的仰角为α度，AC=7m，则树高BC为（用含α的代数式表示）（）A．7sinαB．7cosαC．7tanαD．10．某学校准备修建一个面积为200平方米的矩形花圃，它的长比宽多10米，设花圃的长为x米，宽为y米，则可列方程（组）①y（y+10）=200，②x（x﹣10）=200，③，④以上4种列法中正确的个数为（）A．1个B．2个C．3个D．4个二、填空题11．某市常住人口约为5245000人，数字5245000用科学记数法表示为．12．在函数y=中，自变量x的取值范围是．13．计算：﹣= ．14．分解因式：a2y﹣4y= ．15．不等式组的解集是．16．一个袋子中装有6个球，其中4个黑球2个白球，这些球除颜色外，形状、大小、质地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出两个球为白球的概率是．等于cm2．17．如图，将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形，则S扇形18．某种过季绿茶的价格两次大幅下降，原来每袋250元，现在每袋90元，则平均每次下调的百分率是．19．已知：等腰三角形ABC的面积为30m2，AB=AC=10m，则底边BC的长度为．20．如图，将正方形ABCD沿直线MN折叠，使B点落在CD边上，AB边折叠后与AD边交于F，若三角形DEF与三角形ECM的周长差为3，则DE的长为．三、解答题（其中21～24题各6分，25～26题各8分，27～28题各10分，共60分）21．先化简，再求代数式的值：，其中a=tan60°﹣2sin30°．22．如图，在平面直角坐标系中，△OAB的三个顶点的坐标分别为A（6，3），B（0，5）．（1）画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1；（2）画出△OAB关于原点O的中心对称图形△OA2B2；（3）猜想：∠OAB的度数为多少？并说明理由．23．设中学生体质健康综合评定成绩为x分，满分为100分，规定：85≤x≤100为A级，75≤x≤85为B级，60≤x≤75为C级，x＜60为D级．现随机抽取福海中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：（1）在这次调查中，一共抽取了名学生，α=%；（2）补全条形统计图；（3）扇形统计图中C级对应的圆心角为度；（4）若该校共有2000名学生，请你估计该校D级学生有多少名？24．如图，△ABC中，AB=AC，∠BAC=90°，E、G为AC上两点，且AE=CG，△CDG沿直线BC翻折到△CDF，连结AF交BC于Q，（1）求证：AF⊥BE；（2）若AE=EG，D为BC中点，求tan∠DAQ．25．某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．（1）求每个篮球和每个排球的销售利润；（2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元，购买两种球共100个，则该专卖店最多购买多少个篮球．26．已知AB为⊙O的直径，C为⊙O上一点，AF垂直过C点的切线，垂足为F，连接AC、BC．（1）求证：∠FAC=∠BAC；（2）过F点作FD⊥AC交AB于D，过D点作DE⊥FD交FC延长线于E，求证：CF=CE；（3）在（2）的条件下，延长FA交⊙O于H，连接OE，若CD=2，AH=3，求OE的长．27．抛物线y=ax2+bx﹣8与x轴交于A、B，与y轴交于C，D为抛物线的顶点，AB=2，D点的横坐标为3．（1）求抛物线的解析式；（2）若H为射线DA与y轴的交点，N为射线AB上一点，设N点的横坐标为t，△DHN的面积为S，求S与t的函数关系式；（3）在（2）的条件下，G为线段DH上一点，过G作y轴的平行线交抛物线于F，Q为抛物线上一点，连接GN、NQ、AF、GF，若NG=NQ，NG⊥NQ，且∠AGN=∠FAG，求GF的长．2019年黑龙江省哈尔滨六十九中中考数学模拟试卷（5月份）参考答案与试题解析一、选择题1．4的平方根是（）A．±2 B．2 C．±D．【考点】平方根．【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2=a，则x就是a的平方根，由此即可解决问题．【解答】解：∵（±2）2=4，∴4的平方根是±2．故选：A．【点评】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．2．下列运算中，结果正确的是（）A．2a+3b=5ab B．a2•a3=a6C．（a+b）2=a2+b2D．2a﹣（a+b）=a﹣b【考点】同底数幂的乘法；合并同类项；去括号与添括号；完全平方公式．【分析】利用同底数幂的乘法，合并同类项，去括号与添括号及完全平方公式判定即可．【解答】解：A、2a+3b不是同类项不能相加减，故本选项错误，B、a2•a3=a5，故本选项错误，C、（a+b）2=a2+2ab+b2，故本选项错误，D、2a﹣（a+b）=a﹣b，故本选项正确，故选：D．【点评】本题主要考查了同底数幂的乘法，合并同类项，去括号与添括号及完全平方公式，解题的关键是熟记同底数幂的乘法，合并同类项，去括号与添括号及完全平方公式的法则．3．下列图形中，既是轴对称图形，又是中心对称图形的有（）A．1个B．2个C．3个D．4个【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：图1、图5都是轴对称图形．不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义．图3不是轴对称图形，因为找不到任何这样的一条直线，沿这条直线对折后它的两部分能够重合；也不是中心对称图形，因为绕中心旋转180度后与原图不重合．图2、图4既是轴对称图形，又是中心对称图形．故选B．【点评】掌握中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．4．下列几何体的主视图、左视图、俯视图都相同的是（）A．B．C．D．【考点】简单几何体的三视图．【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．【解答】解：A、圆柱的主视图和左视图都是长方形，俯视图是圆，故此选项错误；B、长方体的三视图不相同，故此选项错误；C、圆锥的主视图和左视图都是等腰三角形，故此选项错误；D、球的主视图和左视图、俯视图都是圆，故此选项正确；故选：D．【点评】本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．5．对于双曲线y=，当x＞0时，y随x的增大而减小，则k的取值范围是（）A．k＜3 B．k≤3 C．k＞3 D．k≥3【考点】反比例函数的性质．【分析】先根据函数的增减性得出关于k的不等式，求出k的取值范围即可．【解答】解：∵双曲线y=，当x＞0时，y随x的增大而减小，∴k﹣3＞0，解得k＞3．故选C．【点评】本题考查的是反比例函数的性质，熟知反比例函数的图象与系数的关系是解答此题的关键．6．下列关于x的方程一定有实数解的是（）A．2x=m B．x2=m C． =m D． =m【考点】无理方程；一元一次方程的解；根的判别式；分式方程的解．【分析】根据一元一次方程的解、无理方程、一元二次方程和分式方程的解的特点分别对每一项进行判断即可．【解答】解：A.2x=m，一定有实数解；B．x2=m，当m＜0时，无解；C. =m，当m=0或﹣时无解；D. =m，当m＜0时，无解；故选A．【点评】本题考查了一元一次方程的解、无理方程、一元二次方程和分式方程，关键是灵活运用有关知识点进行判断．7．如图，已知直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α等于（）A．2l° B．30° C．58° D．48°【考点】平行线的性质．【分析】过C作CD与m平行，由m与n平行得到CD与n平行，利用两直线平行得到两对内错角相等，再由∠ACB为直角，即可确定出∠α的度数．【解答】解：过C作CD∥m，∵m∥n，∴CD∥n，∴∠ACD=42°，∠BCD=∠α，∵AC⊥BC，即∠ACB=90°，∴∠ACD+∠BCD=90°，∴∠α=90°﹣42°=48°．故选D．【点评】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．8．如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．若AB=4.5，BC=3，EF=2，则DE的长度是（）A．B．3 C．5 D．【考点】平行线分线段成比例．【分析】根据平行线分线段成比例得到比例式，代入数据即可得到结论．【解答】解：∵AD∥BE∥CF，∴，即：，∴DE=3，故选B．【点评】本题考查了平行线分线段成比例定理的应用，能根据定理得出比例式是解此题的关键，注意：一组平行线截两条直线，所截得的对应线段成比例．9．如图，在地面上的点A处测得树顶B的仰角为α度，AC=7m，则树高BC为（用含α的代数式表示）（）A．7sinαB．7cosαC．7tanαD．【考点】解直角三角形的应用-仰角俯角问题．【分析】根据正切的概念进行解答即可．【解答】解：在Rt△ABC中，tanα=，则BC=AC•tanα═7tanαm，故选：C．【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题，掌握以仰角俯角的概念以及锐角三角函数的定义是解题的关键．10．某学校准备修建一个面积为200平方米的矩形花圃，它的长比宽多10米，设花圃的长为x米，宽为y米，则可列方程（组）①y（y+10）=200，②x（x﹣10）=200，③，④以上4种列法中正确的个数为（）A．1个B．2个C．3个D．4个【考点】由实际问题抽象出一元二次方程；由实际问题抽象出二元一次方程组．【分析】本题有两个等量关系：长×宽=200，长﹣宽=10，设长为x，宽为y，则可列一元二次方程或二元一次方程组表达本题的等量关系，由此分析各个选项．【解答】解：①设长方形的宽为y，则长为（y+10），所以其面积为：y（y+10）=200，故：选项①正确．②设长方形的长为x，则宽为（x﹣10），所以其面积为：x（x﹣10）=200，故：选项②正确．③设长方形长为x，宽为y，则由长与宽的关系、长方形的面积公式得，故：选项C正确．④因为长方形的长比宽多10米，则长=宽+10，面积=长×宽，所以，故：选项D正确．故：选D【点评】本题考查了由实际问题抽象出一元二次方程与二元一次方程组、等式的变换等问题，解题的关键是弄清楚题目中隐含的等量关系、设未知数并用未知数表示与之有关系的量．二、填空题11．某市常住人口约为5245000人，数字5245000用科学记数法表示为 5.245×106．【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：将5245000用科学记数法表示为5.245×106．故答案为：5.245×106．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．12．在函数y=中，自变量x的取值范围是x≠3 ．【考点】函数自变量的取值范围．【分析】确保函数有意义只需保证分母3﹣x≠0，即可得．【解答】解：根据题意知3﹣x≠0，解得：x≠3，故答案为：x≠3．【点评】本题主要考查函数自变量的取值范围，熟练掌握确保函数有意义时需保证被开方数为非负数、分母不等于0及符合实际问题的意义是关键．13．计算：﹣= ．【考点】二次根式的加减法．【分析】先进行二次根式的化简，再进行同类二次根式的合并即可．【解答】解：原式=2﹣=．故答案为：．【点评】本题考查了二次根式的加减法，解答本题的关键在于熟练掌握二次根式的化简和同类二次根式的合并．14．分解因式：a2y﹣4y= y（a+2）（a﹣2）．【考点】提公因式法与公式法的综合运用．【分析】先提取公因式y，再对余下的多项式利用平方差公式继续分解．【解答】解：a2y﹣4y，=y（a2﹣4），=y（a+2）（a﹣2）．故答案为：y（a+2）（a﹣2）．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．15．不等式组的解集是＜x＜2 ．【考点】解一元一次不等式组．【分析】根据解不等式组的方法可以求得原不等式组的解集，从而可以解答本题．【解答】解：由①，得x＜2，由②，得x＞，故原不等式组的解集是，故答案为：＜x＜2．【点评】本题考查解一元一次不等式组，解题的关键是明确解不等式组的方法．16．一个袋子中装有6个球，其中4个黑球2个白球，这些球除颜色外，形状、大小、质地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出两个球为白球的概率是．【考点】列表法与树状图法．【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与其中2个球的颜色是白球的情况，再利用概率公式求解即可求得答案．【解答】解：如图：，共30种情况，摸出两个白球的情况有2种，摸出两个球为白球的概率为： =．故答案为：．【点评】本题考查的是用列表法或画树状图法求概率．注意列表法或树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件，正确画出树形图是解题关键．等于10 cm2．17．如图，将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形，则S扇形【考点】扇形面积的计算．【分析】根据扇形的面积公式S=×弧长×半径求出即可．扇形【解答】解：由题意知，弧长=14﹣2×2=10cm，扇形的面积是×10×2=10cm2，故答案为：10．【点评】本题考查了扇形的面积公式的应用，能够正确运用扇形的面积公式进行计算是解题的关键．18．某种过季绿茶的价格两次大幅下降，原来每袋250元，现在每袋90元，则平均每次下调的百分率是40% ．【考点】一元二次方程的应用．【专题】增长率问题．【分析】问题求的是某种过季绿茶的价格两次大幅下降，平均每次的下降率；以原来每袋250元为基数，结果为每袋90元，降低后的价格=降低前的价格×（1﹣降低率），如果设平均每次降价的百分率是x，则第一次降低后的价格是250（1﹣x），那么第二次后的价格是250（1﹣x）2，即可列出方程求解．【解答】解：设平均每次下调的百分率为x，依题意得250（1﹣x）2=90，（1﹣x）2=，1﹣x=±，x 1=40%，x2=160%（舍去）．答：平均每次下调的百分率为40%．故答案为：40%．【点评】本题考查了一元二次方程应用中求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．19．已知：等腰三角形ABC的面积为30m2，AB=AC=10m，则底边BC的长度为2或6．【考点】等腰三角形的性质．【分析】作CD⊥AB于D，则∠ADC=∠BDC=90°，由三角形的面积求出CD，由勾股定理求出AD；分两种情况：①等腰△ABC为锐角三角形时，求出BD，由勾股定理求出BC即可；②等腰△ABC为钝角三角形时，求出BD，由勾股定理求出BC即可．【解答】解：作CD⊥AB于D，则∠ADC=∠BDC=90°，△ABC的面积=AB•CD=×10×CD=30，解得：CD=6，∴AD==8m；分两种情况：①等腰△ABC为锐角三角形时，如图1所示：BD=AB﹣AD=2m，∴BC==2；②等腰△ABC为钝角三角形时，如图2所示：BD=AB+AD=18m，∴BC==6；综上所述：BC的长为2或6．故答案为：2或6．【点评】本题考查了等腰三角形的性质、三角形的面积公式及勾股定理，解题的关键画出图形，分两种情况讨论．20．如图，将正方形ABCD沿直线MN折叠，使B点落在CD边上，AB边折叠后与AD边交于F，若三角形DEF与三角形ECM的周长差为3，则DE的长为 3 ．【考点】翻折变换（折叠问题）．【分析】作BH⊥EG于H，连接BF、BE，根据翻折变换的性质和全等三角形的判定定理证明△BHE≌△BCE，得到EH=EC，BH=BC，证明Rt△BAF≌RT△BHF，根据三角形的周长公式计算即可．【解答】解：作BH⊥EG于H，连接BF、BE，由翻折变换的性质可知，MB=ME，∴∠MBE=∠MEB，∴∠ABE=∠FEB，∵AB∥CD，∴∠ABE=∠BEC，∴∠FEB=∠BEC，在△BHE和△BCE中，，∴△BHE≌△BCE，∴EH=EC，BH=BC，在Rt△BAF和RT△BHF中，，∴Rt△BAF≌RT△BHF，∴FA=FH，三角形DEF的周长﹣三角形ECM的周长=DE+DF+EF﹣（EC+CM+EM）=DE+DF+AF+EC﹣（EC+CM+BM）=DE+AD+EC﹣EC﹣BC=DE=3，故答案为：3．【点评】本题主要考查的是翻折的性质、勾股定理的应用、全等三角形的性质和判定，掌握本题的辅助线的做法是解题的关键．三、解答题（其中21～24题各6分，25～26题各8分，27～28题各10分，共60分）21．先化简，再求代数式的值：，其中a=tan60°﹣2sin30°．【考点】分式的化简求值；特殊角的三角函数值．【专题】计算题．【分析】分别化简分式和a的值，再代入计算求值．【解答】解：原式=．（2分）当a=tan60°﹣2sin30°=﹣2×=时，（2分）原式=．（1分）【点评】本题考查了分式的化简求值，关键是化简．同时也考查了特殊角的三角函数值；注意分子、分母能因式分解的先因式分解，除法要统一为乘法运算．22．如图，在平面直角坐标系中，△OAB的三个顶点的坐标分别为A（6，3），B（0，5）．（1）画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1；（2）画出△OAB关于原点O的中心对称图形△OA2B2；（3）猜想：∠OAB的度数为多少？并说明理由．【考点】作图-旋转变换．【分析】（1）根据旋转的性质得出对应点位置，进而得出答案；（2）根据中心对称的性质得出对应点位置，进而得出答案；（3）∠OAB=45°，根据A 1（﹣3，6），A （6，3），可根据勾股定理求出OA=OA 1=3，又∠AOA 1=90°，易证△A 1AO 为等腰直角三角形，得∠OAB=45°．【解答】解：（1）如图所示，△OA 1B 1即为所求；（2）如图所示△OA 2B 2即为所求；（3）∠OAB=45°，理由：∵A 1（﹣3，6），A （6，3）∴OA=OA 1=3， 又∵∠AOA 1=90°，∴△A 1AO 为等腰直角三角形，∴∠OAB=45°．【点评】此题主要考查了图形的旋转、中心对称以及勾股定理，得出旋转后对应点位置是解题关键．23．设中学生体质健康综合评定成绩为x分，满分为100分，规定：85≤x≤100为A级，75≤x≤85为B级，60≤x≤75为C级，x＜60为D级．现随机抽取福海中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：（1）在这次调查中，一共抽取了50 名学生，α=24 %；（2）补全条形统计图；（3）扇形统计图中C级对应的圆心角为72 度；（4）若该校共有2000名学生，请你估计该校D级学生有多少名？【考点】条形统计图；用样本估计总体；扇形统计图．【专题】图表型．【分析】（1）根据B级的人数和所占的百分比求出抽取的总人数，再用A级的人数除以总数即可求出a；（2）用抽取的总人数减去A、B、D的人数，求出C级的人数，从而补全统计图；（3）用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数；（4）用D级所占的百分比乘以该校的总人数，即可得出该校D级的学生数．【解答】解：（1）在这次调查中，一共抽取的学生数是： =50（人），a=×100%=24%；故答案为：50，24；（2）等级为C的人数是：50﹣12﹣24﹣4=10（人），补图如下：（3）扇形统计图中C级对应的圆心角为×360°=72°；故答案为：72；（4）根据题意得：2000×=160（人），答：该校D级学生有160人．【点评】此题考查了是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．24．如图，△ABC中，AB=AC，∠BAC=90°，E、G为AC上两点，且AE=CG，△CDG沿直线BC翻折到△CDF，连结AF交BC于Q，（1）求证：AF⊥BE；（2）若AE=EG，D为BC中点，求tan∠DAQ．【考点】翻折变换（折叠问题）．【分析】（1）如图1所示：记AF与BE的交点为O．先依据翻折的性质证明∠BAE=∠FCA=90°，然后依据SAS可证明△BAE≌△ACF，由全等三角形的性质可知∠FAC=∠EBA，接下来依据同角的余角相等和三角形的内角和定理证明∠AOE=90°，从而可得到要证明的结论；（2）如图2所示：记GF与BC的交点为O，过点F作FH⊥AD，垂足为H．在△ADC和△OCF中依据等腰直角三角形的性质得到CO、OF的长度与AD的长度关系，从而得到AH、HF的长（用含AD的式子表示），最后依据锐角三角函数的定义求解即可．【解答】解：（1）如图1所示：记AF与BE的交点为O．∵△ABC中，AB=AC，∠BAC=90°，∴∠ACB=45°．∵由翻折的性质可知：∠DCF=∠DCG=45°，CF=GC，∴∠GCF=90°．∵FC=AE，CF=GC，∴AE=CF．在△BAE和△ACF中，，∴△BAE≌△ACF．∴∠FAC=∠EBA．∵∠AEB+∠EBA=90°，∴∠AEB+∠FAC=90°．∴∠AOE=90°．∴AF⊥BE．（2）如图2所示：记GF与BC的交点为O，过点F作FH⊥AD，垂足为H．∵D是BC的中点，AB=AC，∴AD⊥CB，∠DAC=∠DAB=45°．∴AC=AD，DC=AD．∵AE=EG=GC，∴FC=GC=．由翻折的性质可知：GC⊥DC，∠OCF=45°．∴OC=OF=FC=AD=AD．∴AH=AD+AD=AD，FH=DO=CD﹣CO=AD﹣AD=AD．∴tan∠DAQ===．【点评】本题主要考查的是翻折的性质、全等三角形的性质和判定、等腰直角三角形的性质、锐角三角函数的定义，证得△BAE≌△ACF是解答问题（1）的关键，用含AD的式子表示出AH和HF的长解答问题（2）的关键．25．某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．（1）求每个篮球和每个排球的销售利润；（2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元，购买两种球共100个，则该专卖店最多购买多少个篮球．【考点】一元一次不等式的应用；二元一次方程组的应用．【分析】（1）设每个篮球和每个排球的销售利润分别为x元，y元，根据题意得到方程组；即可解得结果；（2）设购进篮球m个，排球（100﹣m）个，根据题意得不等式组即可得到结果．【解答】解：（1）设每个篮球和每个排球的销售利润分别为x元，y元，根据题意得：，解得：，答：每个篮球和每个排球的销售利润分别为25元，20元；（2）设购进篮球m个，排球（100﹣m）个，根据题意得：，解得：≤m≤35，∴m=34或m=35，答：该专卖店最多购买35个篮球．【点评】本题考查了一元一次不等式的应用，二元一次方程组的应用，找准数量关系是解题的关键．26．已知AB为⊙O的直径，C为⊙O上一点，AF垂直过C点的切线，垂足为F，连接AC、BC．（1）求证：∠FAC=∠BAC；（2）过F点作FD⊥AC交AB于D，过D点作DE⊥FD交FC延长线于E，求证：CF=CE；（3）在（2）的条件下，延长FA交⊙O于H，连接OE，若CD=2，AH=3，求OE的长．【考点】圆的综合题．【专题】综合题．【分析】（1）连结OC，如图（1），根据切线的性质得OC⊥FC，再证明AF∥OC，根据平行线的性质得∠OCA=∠FAC，加上∠OCA=∠OAC，于是可得到∠FAC=∠BAC；（2）如图（2），由于FD⊥AC，∠FAC=∠BAC，根据等腰三角形的性质得AC平分FD，则AC垂直平分DF，所以CF=CD，再证明∠CDE=∠E得到CD=CE，于是得到CF=CE；（3）连结OC，如图（3），先利用切割线定理求出FA=1，再证明CD⊥AB，接着证明Rt△ADC∽Rt△CDB，于是利用相似比可计算出BD=4，所以OC=，然后在Rt△OCE中利用勾股定理计算OE．【解答】（1）证明：连结OC，如图（1），∵FC为切线，∴OC⊥FC，∵CF⊥AF，∴AF∥OC，∴∠OCA=∠FAC，∵OC=OA，∴∠OCA=∠OAC，∴∠FAC=∠BAC；（2）证明：如图（2），∵FD⊥AC，∠FAC=∠BAC，∴AC平分FD，即AC垂直平分DF，∴CF=CD，∴∠CFD=∠CDF，∵FD⊥DE，∴∠EFD+∠E=90°，∠DDF+∠CDE=90°，∴∠CDE=∠E，∴CD=CE，∴CF=CE；（3）连结OC，如图（3），∵CF=CE=CD，∴CF=CE=2，∵CF为切线，FH为割线，∴FC2=FA•FH，即22=FA（FA+3），解得FA=1或FA=﹣4（舍去），∵AC垂直平分DF，∴AF=AD=1，CF=CD，∴∠AFD=∠ADF，∠CFD=∠CDF，∴∠ADF+∠CDF=∠AFD+∠CFD=90°，∴CD⊥AB，∵AB为直径，∴∠ACB=90°，即∠ACD+∠BCD=90°，∵∠ACD+∠CAD=90°，∴∠CAD=∠BCD，∴Rt△ADC∽Rt△CDB，∴AD：CD=CD：BD，即1：2=2：BD，解得BD=4，∴AB=AD+BD=5，∴OC=，∵OC⊥CE，∴在Rt△OCE中，OE===．【点评】本题考查了圆的综合题：熟练掌握圆周角定理、切线的性质和切割线定理；灵活运用等腰三角形的判定与性质；会利用勾股定理和相似比计算线段的长；解决（3）题的关键是构建Rt△OCE 和求圆的半径．27．抛物线y=ax2+bx﹣8与x轴交于A、B，与y轴交于C，D为抛物线的顶点，AB=2，D点的横坐标为3．（1）求抛物线的解析式；（2）若H 为射线DA 与y 轴的交点，N 为射线AB 上一点，设N 点的横坐标为t ，△DHN 的面积为S ，求S 与t 的函数关系式；（3）在（2）的条件下，G 为线段DH 上一点，过G 作y 轴的平行线交抛物线于F ，Q 为抛物线上一点，连接GN 、NQ 、AF 、GF ，若NG=NQ ，NG ⊥NQ ，且∠AGN=∠FAG ，求GF 的长．【考点】二次函数综合题．【分析】（1）先求出A 、B 两点坐标，再利用待定系数法即可解决问题．（2）如图1中，连接OD ，根据S=S △OND +S △ONH ﹣S △OHD 计算即可．（3）如图2中，延长FG 交OB 于M ，只要证明△MAF ≌△MGB ，得FM=BM ．设M （m ，0），列出方程即可解决问题．【解答】解：（1）∵抛物线y=ax 2+bx ﹣8与x 轴交于A 、B ，与y 轴交于C ，D 为抛物线的顶点，AB=2，D 点的横坐标为3，∴A （2，0），B （4，0），∴，解得，∴抛物线解析式为y=﹣x 2+6x ﹣8；（2）如图1中，连接OD ．抛物线顶点D 坐标（3，1），H （0，﹣2）．∵S=S△OND +S△ONH﹣S△OHD=×t×1+×t×2﹣×2×3=t﹣3．∴S=x﹣3；（3）如图2中，延长FG交OB于M．∵OH=OA，∴∠OAH=∠OHA=45°，∵FM∥OH，∴∠MGA=∠OHA=∠MAG=45°，∴MG=MA，∵∠FAG=∠NGA，∴∠MAF=∠MGN，在△MAF和△MGN中，，∴△MAF≌△MGB，∴FM=BM．设M（m，0），∴﹣（﹣m2+6m﹣8）=4﹣m，解得m=1或4（舍弃），∴FM=3，MG=1，∴GF=FM﹣MG=2．【点评】本题考查二次函数综合题、全等三角形的判定和性质、待定系数法等知识，解题的关键是学会利用分割法求面积．学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．。

哈尔滨市第六十九中学2019--2020学年度(上)初三学年11月份质量检测数学试卷温馨提示:亲爱的同学们，这份试卷再次记录你的自信、沉着、智慧和收获。

请认真审题，看清要求，仔细答卷。

祝你成功!考生须知：1． 本试卷满分120分，考试时间为120分钟.2． 答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将“条形码”准确粘贴在条形码区域内.3． 请按照题号顺序在答题卡各题目的区域内作答，超出答题区域的答案无效；在草稿纸上、试题纸上答案无效.4． 选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.5． 保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀.一、选择题：（每小题3分，共计30分）1. 下列各式中，不是分式的是（ ）A ．1aB ．()25x y -C ．m n m n --D ．2141a - 2. 下列计算正确的是（ ）A ．32a a a -=B ．()325a a =C ．623a a a ÷=D ．235a a a =g3. 点4()3,M -关于x 轴对称的点的坐标为（ ）A ．()3,4--B ．()3,4-C ．()3,4-D ．()3,44. 若把分式x x y-的x 和y 都扩大2倍，那么分式的值( ) A.扩大2倍 B.不变 C.缩小2倍 D.缩小4倍5. 如图，在ABC ∆中， 100,AB AC BAC AB ︒=∠=，的垂直平分线DE 分别交AB BC 、于点,D E ， 则BAE ∠=（ ）A ．80︒B ．60︒ C.50︒ D ．40︒6.若226,13ab a b =+=，则a b -的值为（ ）A ．1B ．1± C. 1- D ．07. 如图，一棵树在一次强台风中，从离地面5m 处折断，倒下的部分与地面成30︒角，如图所示，这棵树在折断前的高度是（ ）A ．10mB ．15m C.5m D ．20m8. ()()33a y a y -+是下列哪一个多项式因式分解的结果（ ）A ． 229a y +B ． 229a y -- C. 229a y - D ．229a y --9. 如图所示，从边长为a 的大正方彤中挖去一个边长为b 的小正方形，小明将图①中的阴影部分拼成了一个如图②所示的长方形，这-过程可以验证（ ）A ．()2222a b ab a b +-=- B ．()2222a b ab a b ++=+ C.()()2232a b ab a b a b +-=--D ．()()22a b a b a b -=+-10. 甲、乙两人分别从两地同时出发，若相向而行，则经过a 小时相遇:若同向而行，则经过b 小时甲追上乙，那么甲的速度是乙的( )A ．a b a -倍B ．b a b -倍 C. a b b a --倍 D ．b a b a--倍 二、填空题:（每题3分，共30分）11. 用科学计数法表示:0.000 082 6= ．12.当x = 时，分式236x x -无意义 13.若8,10x y xy -==，则22x y += ．14.分解因式：3281a ab -= ．15.()3321x y x y --= ． 16. 关于x 的方程1223x x =-的解是x = ． 17. 如图，等边ABC ∆中，AD BD =， 过点D 作DF AC ⊥于点F ，过点F 作FE BC ⊥于点E ，若4AF =，则线段BE 的长为18.如图所示，在ABC ∆中，, , , AB AC E F P =分别是, , AB AC BC 边上的点，且, ,BE BP CP CF ==50EPF ︒∠=，则A ∠=19. 在ABC ∆中0030A l B D ︒︒∠=∠=，，，为BC 边上一点，点F 是射线BA 上一点，DF 与射线CA 相交于点E ，点G 是EF 的中点，若DEC C ∠=∠，则CAG ∠= 20.如图所示，在ABC ∆中，90.105ACB AC BC ︒∠===，，,将ABC ∆折叠，使点A 落在点B 处,折痕所在直线交ABC ∆的外角平分线CD 于点E ,则点E 到BC 的距离为三，解答题(其中21-25题各8分，26- -27 题各10分，共计60分)21. 计算：()2223124a b a b c cd+ ()()()()22252727x x x --+-22. 先化简，再求代数式2121211a a a a -⎛⎫÷- ⎪-+-⎝⎭的值，其中(011a =- 23.如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，ABC ∆的顶点均在格点上，点C 的坐标为(6,1).()1画出ABC ∆关于y 轴对称的111A B C ∆,并写出点1C 的坐标:()2坐标平面的格点上确定一个点P ，使BCP ∆是以BC 为底的等腰直角三角形，且点P 在点C 的 下方，画出BCP ∆，并写出点P 的坐标.24.如图，点D 是ABC ∆的边BC 的中点，, DE AC DF AB ⊥⊥，垂足分别为点E ，点F ,且BF CE =.求证: ABC ∆是等腰三角形.25.某文教用品商店欲购进,A B 两种笔记本，用150 元购进的A 种笔记本与用200元购进的B 种笔记本的数量相同，每本B 种笔记本的进价比每本A 种笔记本的进价贵10元，()1求,A B 两种笔记本每本的进价分别为多少元?()2若该商店A 种笔记本每本售价34元，B 种笔记本每本售价45元，准备购进,A B 两种笔记本共80本，且这两种笔记本全部售出后总获利不少于372元，则最多购进A 种笔记本多少本?.26.如图，在ABC ∆中，,AC BC CD BC =⊥于C ，连接BD BD ，交AC 于点E ,.BAC BDC ∠=∠ ()1如图1，求证::2ECB EBC ∠=∠()2如图2， EF BC ⊥于点F ，求证:2AE CF =:()3如图3，点G 在CB 的延长线上，GH AC ⊥于点,,H GH AC GH =交AB 于点K ，连接CK ,//AR GH 交CK 的延长线于点R ，连接GR ，当CRG ∆的面积为9,2CD BG =时， 求BC 的长.27.在平面直角坐标系中，点B 在y 轴正半轴上，()2,060,C BAO ︒-∠=， 点C 为.AO 中点，点D 在射线BA 上，把线段CD 绕点C 顺时针旋转60︒得到线段CE ，设点D 的横坐标为t .请根据题意画出图形并完成下列问题: ()1求AB 的长:()2设点E 的横坐标为d ，求d 与t 的关系式: .()3在()2的条件下，作点D 关于直线CE 的对称点F ，连接AF OF ，，当OAF ∆为等腰三角形时，求点E 的横坐标d 的值.试卷答案一、选择题:(每题3分)1-5: BDABD 6-10: BBCDC二、填空题：（每题3分）11.58.2610⨯ 12.2 13.84 14.()()99a a b a b +- 15.y 16.1 17.10 18.80︒19.40140︒︒或 20.5221.()213d c()27420x -22.原式11a =-，当2a =时，原式1121==- 23.()1图略，()16,1C -()2图略，()3,0P24.证明：,DE AC DF AB ⊥⊥Q90,90DFB DEC ︒︒∴∠=∠=Q 点D 是BC 的中点BD DC ∴=BF CE =Q()Rt BFD Rt CED HL ∴∆=∆B C ∴∠=∠ABC ∴∆是等腰三角形25.解: ()1,A B 两种笔记本每本的进价分别为30元,10元;()2最多购进A 种笔记本28本26. ()1略()2略()36BC =27. ()18AB =()252d t =+() 335-或。

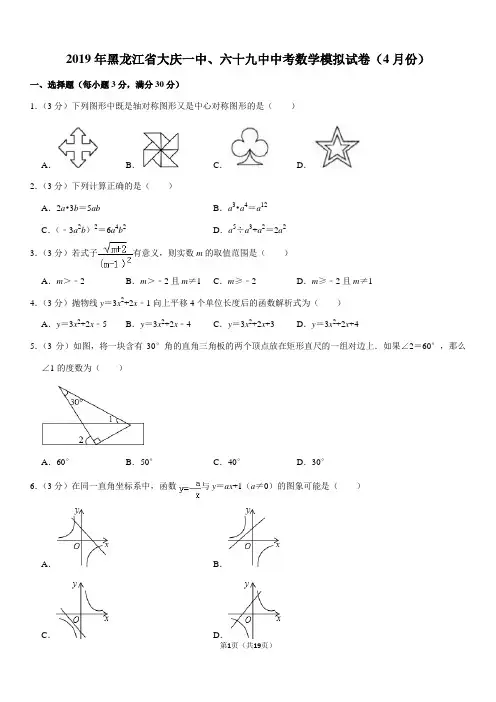
2019年黑龙江省大庆一中、六十九中中考数学模拟试卷（4月份）一、选择题（每小题3分，满分30分）1．（3分）下列图形中既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．2．（3分）下列计算正确的是（）A．2a•3b＝5ab B．a3•a4＝a12C．（﹣3a2b）2＝6a4b2D．a5÷a3+a2＝2a23．（3分）若式子有意义，则实数m的取值范围是（）A．m＞﹣2B．m＞﹣2且m≠1C．m≥﹣2D．m≥﹣2且m≠14．（3分）抛物线y＝3x2+2x﹣1向上平移4个单位长度后的函数解析式为（）A．y＝3x2+2x﹣5B．y＝3x2+2x﹣4C．y＝3x2+2x+3D．y＝3x2+2x+45．（3分）如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2＝60°，那么∠1的度数为（）A．60°B．50°C．40°D．30°6．（3分）在同一直角坐标系中，函数与y＝ax+1（a≠0）的图象可能是（）A ．B ．C ．D ．第1页（共19页）7．（3分）如图，△ABD的三个顶点在⊙O上，AB是直径，点C在⊙O上，且∠ABD＝52°，则∠BCD等于（）A．32°B．38°C．52°D．66°8．（3分）已知不等式≤＜，其解集在数轴上表示正确的是（）A ．B ．C ．D ．9．（3分）如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′，其中点B 的运动路径为，则图中阴影部分的面积为（）A ．π﹣B．2C ．D ．10．（3分）如图，在△ABC中，AB＝BC，∠ABC＝90°，BM是AC边中线，点D，E分别在边AC和BC上，DB ＝DE，EF⊥AC于点F，以下结论：（1）∠DBM＝∠CDE；（2）S△BDE＜S四边形BMFE；（3）CD•EN＝BN•BD；（4）AC＝2DF．其中正确结论的个数是（）第2页（共19页）。

黑龙江省哈尔滨市第六十九中学学年八年级（上）11月月考数学试题（含答案）第 2 页哈尔滨市第六十九中学2019—2019学年八年级（上）11月份数学阶段测试卷 一、单项选择题（每小题3分，共30分） 1．下列计算正确的是（ ）A. 642a )a (= B.523a a a=⋅C. 44a 8)a 2(= D.33a a a=÷2．下列图形中是轴对称图形的是（ ）.A BC D3．下列式子1x ，3x ，c a b -，34(x+y)，m n m n-+，分式有( )个．A.1B.2C.3D.44. 下面的多项式中，能因式分解的是（ ）.A.nm+22B . n nm m+-2C . nm-24D. m 2﹣n5. 已知等腰三角形一边长为4，一边的长为10，则等腰三角形的周长为（ ）.A ．14 B.18 C.24 D.18或246. 将分式b a ac 286约分后的结果是（ ）. A.ab c 43 B. ac a 43 C. b a 43 D. ca43第 3 页第 4 页F是AD 上的动点，E 是AC 边上的动点，则EF CF +的最小值是（ ）.A. 6B. 4C. 245D. 不存在最小值二、填空题（每题3分，共30分） 11．当x 时，分式2x x+有意义. 12.把0.000 001 06用科学记数法表示为__________________. 13.把多项式abb a -3分解因式的结果是 ____________. 14.计算：222)2(-ba ﹒31)(b a-=____________. 15. 计算：aa a a6)36-12(23÷+= .16. 如图，△ABC 中，∠ACB=90°，CD 是高，∠A=30°，若AB=8cm ，则BD= cm ．17. 分式方程3221+=x x 的解为 . 18. 已知a+b=3，ab=1，则a b +b a 的值等于________． 19. 已知等边△ABC 的边长为2，点D 在射线CB（第16题图） DCAB第20题图 D B QE AC P G第 5 页上，点E 在射线AC 上，且AD=AE,∠EDC=15°，则线段CD=_______. 20. 如图，在等边△ABC 中，点D 是AC 上的一点，在BC 上取一点E ，使BE=CD ，连接AE 交BD 于点P ，在BD 的延长线上取一点Q ，使AP=PQ ，连接AQ 、CQ ，点G 为PQ 的中点，DG=PE ，若3BQ= ．三、解答题（其中21—22题各7分，23—24题各8分，25—27题各10分，共计6021. 计算（1）4(x ＋y)(x －y)－(2x －y)2（2）xy y x x y y x 22222)2(÷-⋅22. 先化简，再求代数式211211x xx x ⎛⎫÷- ⎪+++⎝⎭的值，其中x=0π23．点A （−1,4）和点B （−5,1）在平面直角坐标系中的位置如图所示:（1）点A 1、B 1分别为点A 、B 关于y 轴的对称点，请画出四边形AA 1B 1B ，并写出A 1、B 1的坐标; （2）在（1）的条件下，画一条过四边形AA 1B 1B xy 6-1-115432123-4-3-2-6B-5A 45O第 6 页的一个顶点的线段，将四边形AA 1B 1B 分成两个图形， 并且使分得的图形中的一个是轴对称图形.24. 已知:点D 是△ABC 的边BC 的中点,DE ⊥AC, DF ⊥AB,垂足分别为E,F,且BF=CE. 求证: △ABC 是等腰三角形.25．某商店从机械厂购进甲、乙两种零件进行销售，若甲种零件每件的进价是乙种零件每件进价的54，用1600元单独购进一种零件时，购进甲种零件的数量比乙种零件的数量多4件.（1）求每件甲种零件和每件乙种零件的进价分别为多少元?（2）若该商店计划购进甲、乙两种零件共110件，准备将零件批发给零售商. 甲种零件的批发价是每件100元，乙种零件的批发价是每件130元，该商店计划将这批产品全部售出从零售商处获利不低于3000元，那么该商店最多购进多少件甲种零件?26. 已知:△ABC 中，AB=AC ，∠BAC=20°，点D 在AB 上，AD=BC ，CH ⊥AB 于H.EF B （第23题图）第（1） 求∠BCH. (2)若CD=212,求CH 的长.27. 如图，在平面直角坐标系中，点A 在y 轴的正半轴上、点B 2-1，,0）、点C 分别在x 轴正、负半轴上，∠ACB=45°，∠ABC=67.5°，AC=2.(1) 如图1求A 、C 两点的坐标。

黑龙江省哈尔滨市第六十九中学2019-2020学年中考数学模拟试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．如图是测量一物体体积的过程：步骤一：将180 mL的水装进一个容量为300 mL的杯子中；步骤二：将三个相同的玻璃球放入水中，结果水没有满；步骤三：再将一个同样的玻璃球放入水中，结果水满溢出.根据以上过程，推测一个玻璃球的体积在下列哪一范围内？(1 mL=1 cm3)().A．10 cm3以上，20 cm3以下B．20 cm3以上，30 cm3以下C．30 cm3以上，40 cm3以下D．40 cm3以上，50 cm3以下2．△ABC在正方形网格中的位置如图所示，则cosB的值为( )A．5B．25C．12D．23．如图，P为⊙O外一点，PA、PB分别切⊙O于点A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝6，则△PCD的周长为（）A．8 B．6 C．12 D．104．已知A、B两地之间铁路长为450千米，动车比火车每小时多行驶50千米，从A市到B市乘动车比乘火车少用40分钟，设动车速度为每小时x千米，则可列方程为（）A．4504504050x x-=-B．4504504050x x-=-C．4504502503x x-=+D．4504502503x x-=-5．关于x的一元二次方程x2+8x+q=0有两个不相等的实数根，则q的取值范围是( )A．q<16 B．q>16C．q≤4D．q≥46．如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路径为弧BD ，则图中阴影部分的面积是()A ．6πB ．3πC ．2π-12D ．127．我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x 尺，竿长y 尺，则符合题意的方程组是（ ）A ．5{152x y x y =+=- B ．5{1+52x y x y =+= C ．5{2-5x y x y =+= D ．-5{2+5x y x y ==8．点M(a ，2a)在反比例函数y ＝8x 的图象上，那么a 的值是( ) A ．4 B ．﹣4 C ．2 D ．±29．下列函数中，y 随着x 的增大而减小的是（ ）A ．y=3xB ．y=﹣3xC ．3y x =D ．3y x =- 10．若关于x 的方程333x m m x x++--=3的解为正数，则m 的取值范围是（ ） A ．m ＜92B ．m ＜92且m≠32C ．m ＞﹣94D ．m ＞﹣94且m≠﹣34 11．如图直线y ＝mx 与双曲线y=k x交于点A 、B ，过A 作AM ⊥x 轴于M 点，连接BM ，若S △AMB ＝2，则k 的值是( )A ．1B ．2C ．3D ．412．点P （1，﹣2）关于y 轴对称的点的坐标是（ ）A ．（1，2）B ．（﹣1，2）C ．（﹣1，﹣2）D ．（﹣2，1）二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如果53x x y =-，那么x y=______． 14．某市对九年级学生进行“综合素质”评价，评价结果分为A ，B ，C ，D ，E 五个等级．现随机抽取了500名学生的评价结果作为样本进行分析，绘制了如图所示的统计图．已知图中从左到右的五个长方形的高之比为2：3：3：1：1，据此估算该市80000名九年级学生中“综合素质”评价结果为“A”的学生约为_____人．15．已知m 、n 是一元二次方程x 2+4x ﹣1＝0的两实数根，则11m n+＝_____． 16．如图，矩形ABCD 中，8AB =，4BC =，将矩形沿AC 折叠，点D 落在点'D 处.则重叠部分AFC ∆的面积为______.17．如图所示,在△ABC 中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A 为圆心,小于AC 的长为半径画弧,分别交AB,AC 于点E,F;②分别以点E,F 为圆心,大于12EF 的长为半径画弧,两弧相交于点G;③作射线AG 交BC 边于点D ．则∠ADC 的度数为 .18．如图，点A 在双曲线1y=x 上，点B 在双曲线3y=x上，且AB ∥x 轴，C 、D 在x 轴上，若四边形ABCD 为矩形，则它的面积为 ．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）某地区教育部门为了解初中数学课堂中学生参与情况，并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价．检测小组随机抽查部分学校若干名学生，并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图（均不完整）．请根据统计图中的信息解答下列问题：本次抽查的样本容量是 ；在扇形统计图中，“主动质疑”对应的圆心角为 度；将条形统计图补充完整；如果该地区初中学生共有60000名，那么在课堂中能“独立思考”的学生约有多少人？20．（6分）在如图的正方形网格中，每一个小正方形的边长为1；格点三角形ABC （顶点是网格线交点的三角形）的顶点A 、C 的坐标分别是(－4，6)、(－1，4)；请在图中的网格平面内建立平面直角坐标系；请画出△ABC 关于x 轴对称的△A 1B 1C 1；请在y 轴上求作一点P ，使△PB 1C 的周长最小，并直接写出点P 的坐标.21．（6分）如图，在平面直角坐标系中，一次函数()10y kx b k =+≠与反比例函数()20m y m x=≠的图像交于点()3,1A 和点B ，且经过点()0,2C -. 求反比例函数和一次函数的表达式；求当12y y >时自变量x 的取值范围.22．（8分）如图，△ABC 中，AB=8厘米，AC=16厘米，点P 从A 出发，以每秒2厘米的速度向B 运动，点Q 从C 同时出发，以每秒3厘米的速度向A 运动，其中一个动点到端点时，另一个动点也相应停止运动，设运动的时间为t ．⑴用含t 的代数式表示：AP= ，AQ= ．⑵当以A ，P ，Q 为顶点的三角形与△ABC 相似时，求运动时间是多少？23．（8分）如图所示，在正方形ABCD中，E，F分别是边AD，CD上的点，AE＝ED，DF=14DC，连结EF并延长交BC的延长线于点G，连结BE．求证：△ABE∽△DEF．若正方形的边长为4，求BG的长．24．（10分）两个全等的等腰直角三角形按如图方式放置在平面直角坐标系中，OA在x轴上，已知∠COD=∠OAB=90°，OC=2，反比例函数y=kx的图象经过点B．求k的值．把△OCD沿射线OB移动，当点D落在y=kx图象上时，求点D经过的路径长．25．（10分）如图，已知点C是∠AOB的边OB上的一点，求作⊙P，使它经过O、C两点，且圆心在∠AOB的平分线上．26．（12分）某快餐店试销某种套餐，试销一段时间后发现，每份套餐的成本为5元，该店每天固定支出费用为600元（不含套餐成本）．若每份套餐售价不超过10元，每天可销售400份；若每份套餐售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x（元）取整数，用y（元）表示该店每天的利润．若每份套餐售价不超过10元．①试写出y与x的函数关系式；②若要使该店每天的利润不少于800元，则每份套餐的售价应不低于多少元？该店把每份套餐的售价提高到10元以上，每天的利润能否达到1560元？若能，求出每份套餐的售价应定为多少元时，既能保证利润又能吸引顾客？若不能，请说明理由．27．（12分）. 在一个不透明的布袋中装有三个小球，小球上分别标有数字﹣1、0、2，它们除了数字不同外，其他都完全相同．随机地从布袋中摸出一个小球，则摸出的球为标有数字2的小球的概率为；小丽先从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的横坐标．再将此球放回、搅匀，然后由小华再从布袋中随机摸出一个小球，记下数字作为平面直角坐标系内点M的纵坐标，请用树状图或表格列出点M所有可能的坐标，并求出点M落在如图所示的正方形网格内（包括边界）的概率．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．C【解析】分析：本题可设玻璃球的体积为x，再根据题意列出不等式组求得解集得出答案即可．详解：设玻璃球的体积为x，则有3300180 4300180 xx-⎧⎨-⎩＜＞解得30＜x＜1．故一颗玻璃球的体积在30cm3以上，1cm3以下．故选C．点睛：此题考查一元一次不等式组的运用，解此类题目常常要根据题意列出不等式组，再化简计算得出x 的取值范围．2．A【解析】【详解】解：在直角△ABD中，BD=2，AD=4，则22222425BD AD+=+=，则cosB=5525BDAB==．故选A．3．C【解析】【分析】由切线长定理可求得PA＝PB，AC＝CE，BD＝ED，则可求得答案．【详解】∵PA、PB分别切⊙O于点A、B，CD切⊙O于点E，∴PA＝PB＝6，AC＝EC，BD＝ED，∴PC+CD+PD＝PC+CE+DE+PD＝PA+AC+PD+BD＝PA+PB＝6+6＝12，即△PCD的周长为12，故选：C．【点睛】本题主要考查切线的性质，利用切线长定理求得PA＝PB、AC＝CE和BD＝ED是解题的关键．4．D【解析】解：设动车速度为每小时x千米，则可列方程为：45050x-﹣450x=23．故选D．5．A【解析】∵关于x的一元二次方程x2+8x+q=0有两个不相等的实数根，∴△>0，即82-4q>0，∴q<16，故选 A.6．A【解析】【分析】先根据勾股定理得到2，再根据扇形的面积公式计算出S扇形ABD，由旋转的性质得到Rt△ADE≌Rt△ACB，于是S阴影部分=S△ADE+S扇形ABD-S△ABC=S扇形ABD．【详解】∵∠ACB=90°，AC=BC=1，∴，∴S 扇形ABD=230=3606ππ⨯，又∵Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE ，∴Rt △ADE ≌Rt △ACB ，∴S 阴影部分=S △ADE +S 扇形ABD −S △ABC =S 扇形ABD =6π， 故选A.【点睛】本题考查扇形面积计算，熟记扇形面积公式，采用作差法计算面积是解题的关键.7．A【解析】【分析】设索长为x 尺，竿子长为y 尺，根据“索比竿子长一托，折回索子却量竿，却比竿子短一托”，即可得出关于x 、y 的二元一次方程组．【详解】设索长为x 尺，竿子长为y 尺， 根据题意得：5152x y x y =+⎧⎪⎨=-⎪⎩． 故选A ．【点睛】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键． 8．D【解析】【分析】根据点M(a ，2a)在反比例函数y ＝8x 的图象上,可得:228a =,然后解方程即可求解. 【详解】因为点M(a ，2a)在反比例函数y ＝8x的图象上,可得: 228a =,24a =,解得:2a=±,故选D.【点睛】本题主要考查反比例函数图象的上点的特征,解决本题的关键是要熟练掌握反比例函数图象上点的特征. 9．B【解析】试题分析：A、y=3x，y随着x的增大而增大，故此选项错误；B、y=﹣3x，y随着x的增大而减小，正确；C、3yx=，每个象限内，y随着x的增大而减小，故此选项错误；D、3yx=-，每个象限内，y随着x的增大而增大，故此选项错误；故选B．考点：反比例函数的性质；正比例函数的性质．10．B【解析】【详解】解：去分母得：x+m﹣3m=3x﹣9，整理得：2x=﹣2m+9，解得：x=292m-+，已知关于x的方程333x m mx x++--=3的解为正数，所以﹣2m+9＞0，解得m＜92，当x=3时，x=292m-+=3，解得：m=32，所以m的取值范围是：m＜92且m≠32．故答案选B．11．B【解析】【分析】此题可根据反比例函数图象的对称性得到A、B两点关于原点对称，再由S△ABM=1S△AOM并结合反比例函数系数k的几何意义得到k的值．【详解】根据双曲线的对称性可得：OA=OB,则S△ABM＝1S△AOM＝1，S△AOM＝12|k|＝1，则k＝±1．又由于反比例函数图象位于一三象限，k＞0，所以k＝1．故选B．【点睛】本题主要考查了反比例函数y＝kx中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点．12．C【解析】关于y轴对称的点，纵坐标相同，横坐标互为相反数，由此可得P（1，﹣2）关于y轴对称的点的坐标是（﹣1，﹣2），故选C．【点睛】本题考查了关于坐标轴对称的点的坐标，正确地记住关于坐标轴对称的点的坐标特征是关键.关于x轴对称的点的坐标特点：横坐标不变，纵坐标互为相反数；关于y轴对称的点的坐标特点：纵坐标不变，横坐标互为相反数.二、填空题：（本大题共6个小题，每小题4分，共24分．）13．52；【解析】【分析】先对等式进行转换，再求解. 【详解】∵53 xx y＝∴3x＝5x－5y ∴2x＝5y∴5.2 xy＝【点睛】本题考查的是分式，熟练掌握分式是解题的关键.14．16000【解析】【分析】用毕业生总人数乘以“综合素质”等级为A的学生所占的比即可求得结果．【详解】∵A ，B ，C ，D ，E 五个等级在统计图中的高之比为2：3：3：1：1， ∴该市80000名九年级学生中“综合素质”评价结果为“A”的学生约为80000×223311++++=16000，故答案为16000. 【点睛】本题考查了条形统计图的应用，读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据． 15．1 【解析】 【分析】先由根与系数的关系求出m•n 及m+n 的值，再把11m n+化为m+n mn 的形式代入进行计算即可．【详解】∵m 、n 是一元二次方程x 2+1x ﹣1＝0的两实数根， ∴m+n ＝﹣1，m•n ＝﹣1， ∴11m n+＝m+n mn ＝-4-1 ＝1．故答案为1． 【点睛】本题考查的是根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．一元二次方程ax 2+bx+c ＝0（a≠0）的根与系数的关系为：x 1+x 2＝﹣b a，x 1•x 2＝c a ．16．10 【解析】 【分析】根据翻折的特点得到'AD F CBF ∆≅∆，AF CF =.设BF x =，则8FC AF x ==-.在Rt BCF ∆中，222BC BF CF +=，即()22248x x +=-，解出x,再根据三角形的面积进行求解.【详解】∵翻折，∴'4AD AD BC ===，'90D B ∠=∠=︒， 又∵'AFD CFB ∠=∠， ∴'AD F CBF ∆≅∆，∴AF CF =.设BF x =，则8FC AF x ==-.在Rt BCF ∆中，222BC BF CF +=，即()22248x x +=-， 解得3x =， ∴5AF =，∴11541022AFCS AF BC∆=⋅=⨯⨯=.【点睛】此题主要考查勾股定理，解题的关键是熟知翻折的性质及勾股定理的应用.17．65°【解析】【分析】根据已知条件中的作图步骤知，AG是∠CAB的平分线，根据角平分线的性质解答即可．【详解】根据已知条件中的作图步骤知，AG是∠CAB的平分线，∵∠CAB=50°，∴∠CAD=25°；在△ADC中，∠C=90°，∠CAD=25°，∴∠ADC=65°（直角三角形中的两个锐角互余）；故答案是：65°．18．2【解析】【详解】如图，过A点作AE⊥y轴，垂足为E，∵点A在双曲线1y=x上，∴四边形AEOD的面积为1∵点B在双曲线3y=x上，且AB∥x轴，∴四边形BEOC的面积为3∴四边形ABCD为矩形，则它的面积为3－1＝2三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．(1)560;(2)54;(3)补图见解析；（4）18000人【解析】【详解】（1）本次调查的样本容量为224÷40%=560(人)；（2）“主动质疑”所在的扇形的圆心角的度数是：360∘×84560=54º；（3）“讲解题目”的人数是：560−84−168−224=84(人)．（4）60000×168560=18000(人)， 答：在课堂中能“独立思考”的学生约有18000人. 20．（1）（2）见解析；（3）P （0，2）． 【解析】分析：（1）根据A ，C 两点的坐标即可建立平面直角坐标系. （2）分别作各点关于x 轴的对称点，依次连接即可.（3）作点C 关于y 轴的对称点C′，连接B 1C′交y 轴于点P ，即为所求. 详解：（1）（2）如图所示：（3）作点C 关于y 轴的对称点C′，连接B 1C′交y 轴于点P ，则点P 即为所求． 设直线B 1C′的解析式为y=kx+b （k≠0）， ∵B 1（﹣2，-2），C′（1，4）， ∴224k b k b -+=-⎧⎨+=⎩，解得：22k b =⎧⎨=⎩，∴直线AB 2的解析式为：y=2x+2， ∴当x=0时，y=2，∴P （0，2）．点睛：本题主要考查轴对称图形的绘制和轴对称的应用. 21． (1) 3y x=，2y x =-；（2）10x -<<或3x >. 【解析】【分析】（1）把点A 坐标代入()my m 0x=≠可求出m 的值即可得反比例函数解析式；把点A 、点C 代入()1y kx b k 0=+≠可求出k 、b 的值，即可得一次函数解析式；（2）联立一次函数和反比例函数解析式可求出点B 的坐标，根据图象，求出一次函数图象在反比例函数图象的上方时，x 的取值范围即可． 【详解】（1）把()A 3,1代入()my m 0x=≠得m 3=. ∴反比例函数的表达式为3y x=把()A 3,1和()B 0,2-代入y kx b =+得132k bb=+⎧⎨-=⎩，解得12k b =⎧⎨=-⎩∴一次函数的表达式为y x 2=-.（2）由3x 2y y x ⎧=⎪⎨⎪=-⎩得()B 1,3--∴当1x 0-<<或x 3>时，12y y >. 【点睛】本题考查了一次函数和反比例函数的交点问题，解决问题的关键是掌握待定系数法求函数解析式．求反比例函数与一次函数的交点坐标时，把两个函数关系式联立成方程组求解，若方程组有解，则两者有交点，若方程组无解，则两者无交点．22．（1）AP=2t ，AQ=16﹣3t ；（2）运动时间为167秒或1秒． 【解析】 【分析】（1）根据路程=速度⨯时间，即可表示出AP ，AQ 的长度.（2）此题应分两种情况讨论．（1）当△APQ ∽△ABC 时；（2）当△APQ ∽△ACB 时．利用相似三角形的性质求解即可． 【详解】（1）AP=2t ，AQ=16﹣3t ． （2）∵∠PAQ=∠BAC ， ∴当AP AQ AB AC =时，△APQ ∽△ABC ，即2163816t t -=，解得167t =；当AP AQAC AB=时，△APQ∽△ACB，即2163168t t-=，解得t=1．∴运动时间为167秒或1秒．【点睛】考查相似三角形的判定与性质，掌握相似三角形的判定定理与性质定理是解题的关键.注意不要漏解. 23．（1）见解析；（2）BG=BC+CG=1．【解析】【分析】（1）利用正方形的性质，可得∠A=∠D，根据已知可得AE：AB=DF：DE，根据有两边对应成比例且夹角相等三角形相似，可得△ABE∽△DEF；（2）根据相似三角形的预备定理得到△EDF∽△GCF，再根据相似的性质即可求得CG的长，那么BG 的长也就不难得到.【详解】（1）证明：∵ABCD为正方形，∴AD=AB=DC=BC，∠A=∠D=90 °.∵AE=ED，∴AE：AB=1：2.∵DF=14 DC，∴DF：DE=1：2，∴AE：AB=DF：DE，∴△ABE∽△DEF；（2）解：∵ABCD为正方形，∴ED∥BG，∴△EDF∽△GCF，∴ED：CG=DF：CF.又∵DF=14DC，正方形的边长为4，∴ED=2，CG=6，∴BG=BC+CG=1.【点睛】本题考查了正方形的性质，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答本题的关键.24．（1）k=2；（2）点D经过的路径长为6．【解析】【分析】（1）根据题意求得点B的坐标，再代入kyx=求得k值即可；（2）设平移后与反比例函数图象的交点为D′，由平移性质可知DD′∥OB，过D′作D′E⊥x轴于点E，交DC于点F，设CD交y轴于点M（如图），根据已知条件可求得点D的坐标为（﹣1，1），设D′横坐标为t，则OE=MF=t，即可得D′（t，t+2），由此可得t（t+2）=2，解方程求得t值，利用勾股定理求得DD′的长，即可得点D经过的路径长．【详解】（1）∵△AOB和△COD为全等三的等腰直角三角形，OC=2，∴AB=OA=OC=OD=2，∴点B坐标为（2，2），代入kyx=得k=2；（2）设平移后与反比例函数图象的交点为D′，由平移性质可知DD′∥OB，过D′作D′E⊥x轴于点E，交DC于点F，设CD交y轴于点M，如图，∵2，∠AOB=∠COM=45°，∴OM=MC=MD=1，∴D坐标为（﹣1，1），设D′横坐标为t，则OE=MF=t，∴D′F=DF=t+1，∴D′E=D′F+EF=t+2，∴D′（t，t+2），∵D′在反比例函数图象上，∴t（t+2）=2，解得t=31-或t=﹣3﹣1（舍去），∴D′（3﹣1，3+1），∴DD′=22-+++-=，(311)(311)6即点D经过的路径长为6．【点睛】本题是反比例函数与几何的综合题，求得点D′的坐标是解决第（2）问的关键．25．答案见解析【解析】【分析】首先作出∠AOB的角平分线，再作出OC的垂直平分线，两线的交点就是圆心P，再以P为圆心，PC长为半径画圆即可．【详解】解：如图所示：．【点睛】本题考查基本作图,掌握垂直平分线及角平分线的做法是本题的解题关键.．26．（1）①y=400x﹣1．（5＜x≤10）；②9元或10元；（2）能，11元.【解析】【分析】(1)、根据利润=(售价－进价)×数量－固定支出列出函数表达式；(2)、根据题意得出不等式，从而得出答案；(2)、根据题意得出函数关系式，然后将y=1560代入函数解析式，从而求出x的值得出答案．【详解】解：（1）①y=400（x﹣5）﹣2．（5＜x≤10），②依题意得：400（x﹣5）﹣2≥800，解得：x≥8.5，∵5＜x≤10，且每份套餐的售价x（元）取整数，∴每份套餐的售价应不低于9元．（2）依题意可知：每份套餐售价提高到10元以上时，y=（x﹣5）[400﹣40（x﹣10）]﹣2，当y=1560时，（x﹣5）[400﹣40（x﹣10）]﹣2=1560，解得：x1=11，x2=14，为了保证净收入又能吸引顾客，应取x1=11，即x2=14不符合题意．故该套餐售价应定为11元．【点睛】本题主要考查的是一次函数和二次函数的实际应用问题，属于中等难度的题型．理解题意，列出关系式是解决这个问题的关键．27．（1）；（2）列表见解析，.【解析】试题分析：（1）一共有3种等可能的结果总数，摸出标有数字2的小球有1种可能，因此摸出的球为标有数字2的小球的概率为；（2）利用列表得出共有9种等可能的结果数，再找出点M落在如图所示的正方形网格内（包括边界）的结果数，可求得结果.试题解析：（1）P（摸出的球为标有数字2的小球）=；（2）列表如下：小华-1 0 2小丽-1 （-1，-1）（-1，0）（-1，2）0 （0，-1）（0，0）（0，2）2 （2，-1）（2，0）（2，2）共有9种等可能的结果数，其中点M落在如图所示的正方形网格内（包括边界）的结果数为6，∴P（点M落在如图所示的正方形网格内）==.考点：1列表或树状图求概率；2平面直角坐标系.中考模拟数学试卷一、选择题（本大题共16个小题，1～10小题，每小题3分；11～16小题，每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）下列说法不正确的是（）A．0既不是正数，也不是负数B．绝对值最小的数是0C．绝对值等于自身的数只有0和1D．平方等于自身的数只有0和12．（3分）若等腰三角形的两边长分别为4和9，则它的周长为（）A．22 B．17 C．13 D．17或223．（3分）一台机器有大、小齿轮用同一转送带连接，若大小齿轮的齿数分别为12和36个，大齿轮每分钟2.5×103转，则小齿轮10小时转（）A．1.5×106转B．5×105转 C．4.5×106转D．15×106转4．（3分）如图，直线l1∥l2，AB与直线l1垂直，垂足为点B，若∠ABC=37°，则∠EFC的度数为（）A．127°B．133°C．137°D．143°5．（3分）对于实数x，我们规定[x]表示不大于x的最大整数，如[4]=4，[]=1，[﹣2.5]=﹣3．现对82进行如下操作：82 []=9 []=3 []=1，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1（）A．1 B．2 C．3 D．46．（3分）如图是某几何体的三视图，则该几何体的全面积等于（）A．112 B．136 C．124 D．847．（3分）给出下列计算，其中正确的是（）A．a5+a5=a10 B．（2a2）3=6a6C．a8÷a2=a4 D．（a3）4=a128．（3分）不等式3x﹣2＞4的解集在数轴上表示正确的是（）A ．B ．C ．D ．9．（3分）如图，△ABC的三个顶点都在正方形格的格点上，则sin∠A的值为（）A ．B ．C ．D ．10．（3分）关于x 的方程=2+无解，则k的值为（）A．±3 B．3 C．﹣3 D．无法确定11．（2分）如图，一圆弧过方格的格点A、B、C，在方格中建立平面直角坐标系，使点A的坐标为（﹣3，2），则该圆弧所在圆心坐标是（）A．（0，0）B．（﹣2，1）C．（﹣2，﹣1）D．（0，﹣1）比赛日期2012﹣8﹣4 2013﹣5﹣212014﹣9﹣282015﹣5﹣202015﹣5﹣31比赛地点英国伦敦中国北京韩国仁川中国北京美国尤金成绩（秒）10.19 10.06 10.10 10.06 9.99A．10.06秒，10.06秒 B．10.10秒，10.06秒C．10.06秒，10.10秒 D．10.08秒，10.06秒13．（2分）如图，在已知的△ABC中，按以下步骤作图：①分别以B，C 为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB 的度数为（）A．105°B．100°C．95°D．90°14．（2分）已知等边三角形的内切圆半径，外接圆半径和高的比是（）A．1：2：B．2：3：4 C．1：：2 D．1：2：315．（2分）如图①，在边长为2cm的正方形ABCD中，点P以每秒1cm的速度从点A出发，沿AB→BC 的路径运动，到点C停止，过点P作PQ∥BD，PQ与边AD（或边CD）交于点Q，PQ的长度y（cm）与点P的运动时间x（秒）的函数图象如图②所示．当点P运动3秒时，PQ的长是（）A．cm B．cm C．cm D．cm16．（2分）如图，将完全相同的四个长方形纸片拼成一个大的正方形，用两种不同的方法表示这个大正方形的面积，则可以得出一个等式为（）A．（a+b）2=a2+2ab+b2B．（a﹣b）2=a2﹣2ab+b2C．a2﹣b2=（a+b）（a﹣b）D．（a+b）2=（a﹣b）2+4ab二、填空题（本大题共3个小题，17～18每小题3分，19小题每个空2分，共10分．把答案写在题中横线上）17．（3分）﹣3的平方是．18．（3分）已知正数a，b，c，满足ab+a+b=bc+b+c=ca+c+a=99，则（a+1）（b+1）（c+1）=．19．（4分）在平面直角坐标系中，坐标轴上到点A（3，4）的距离等于5的点有个．三、解答题（本大题共7个小题，共68分．解答应写出文字说明、证明过程或演算步骤）20．（8分）计算：．21．（8分）如图，在△ABC中，∠C=90°，AC=8，BC=6．P是AB边上的一个动点（异于A、B两点），过点P分别作AC、BC边的垂线，垂足为M、N．设AP=x．（1）在△ABC中，AB=；（2）当x=时，矩形PMCN的周长是14；（3）是否存在x的值，使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等？请说出你的判断，并加以说明．22．（9分）如图，在▱ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于BF的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则所得四边形ABEF是菱形．（1）根据以上尺规作图的过程，求证：四边形ABEF是菱形；（2）若菱形ABEF的周长为16，AE=4，求∠C的大小．23．（9分）为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况，根据老年人、成年人、青少年各年龄段实际人口的比例3：5：2，随机抽取一定数量的观众进行调查，得到如下统计图．（1）上面所用的调查方法是（填“全面调查”或“抽样调查”）；（2）写出折线统计图中A、B所代表的值和抽取观众的总人数是多少；（3）求该地区喜爱娱乐类节目的成年人的人数．24．（10分）阅读理解：数和形是数学的两个主要研究对象，我们经常运用数形结合，树形转化的方法解决一些数学问题，小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：P1P2=，他还利用图2证明了线段P1P2的中点P（x，y），P的坐标公式：x=，y=．启发应用：如图3：在平面直角坐标系中，已知A（8，0），B（0，6），C（1，7），⊙M经过原点O及点A，B，（1）求⊙M的半径及圆心M的坐标；（2）判断点C与⊙M的位置关系，并说明理由；（3）若∠BOA的平分线交AB于点N，交⊙M于点E，分别求出OE的表达式y1，过点M的反比例函数的表达式y2，并根据图象，当y2＞y1＞0时，请直接写出x的取值范围．25．（12分）已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．（1）用含x的代数式表示线段CF的长；（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设=y，求y关于x的函数关系式，并写出它的定义域；（3）当∠ABE的正切值是时，求AB的长．26．（12分）某商店准备进一批季节性小家电，每个进价为40元，经市场预测，销售定价为50元，可售出400个；定价每增加1元，销售量将减少10个．设每个定价增加x元．（1）写出售出一个可获得的利润是多少元（用含x的代数式表示）？（2）商店若准备获得利润6000元，并且使进货量较少，则每个定价为多少元？应进货多少个？（3）商店若要获得最大利润，则每个应定价多少元？获得的最大利润是多少？参考答案与试题解析一、选择题（本大题共16个小题，1～10小题，每小题3分；11～16小题，每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）下列说法不正确的是（）A．0既不是正数，也不是负数B．绝对值最小的数是0C．绝对值等于自身的数只有0和1D．平方等于自身的数只有0和1【解答】解：A、B、D均正确，绝对值等于它自身的数是所有非负数，所以C错误，故选C．2．（3分）若等腰三角形的两边长分别为4和9，则它的周长为（）A．22 B．17 C．13 D．17或22【解答】解：①若4是腰，则另一腰也是4，底是9，但是4+4＜9，故不能构成三角形，舍去．②若4是底，则腰是9，9．4+9＞9，符合条件，成立．故周长为：4+9+9=22．故选A．3．（3分）一台机器有大、小齿轮用同一转送带连接，若大小齿轮的齿数分别为12和36个，大齿轮每分钟2.5×103转，则小齿轮10小时转（）A．1.5×106转B．5×105转 C．4.5×106转D．15×106转【解答】解：小齿轮10小时转60×2.5×103×10×（36÷12）=4.5×106转．故选C．4．（3分）如图，直线l1∥l2，AB与直线l1垂直，垂足为点B，若∠ABC=37°，则∠EFC的度数为（）A．127°B．133°C．137°D．143°【解答】解：∵AB与直线l1垂直，垂足为点B，∠ABC=37°，∴∠CBD=90°﹣∠ABC=53°；又∵直线l1∥l2，∴∠CBD=∠BFG=53°（两直线平行，同位角相等），∴∠EFC=180°﹣∠BFG=127°；故选A．5．（3分）对于实数x，我们规定[x]表示不大于x的最大整数，如[4]=4，[]=1，[﹣2.5]=﹣3．现对82进行如下操作：82 []=9 []=3 []=1，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1（）A．1 B．2 C．3 D．4【解答】解：121 []=11 []=3 []=1，∴对121只需进行3次操作后变为1，故选：C．6．（3分）如图是某几何体的三视图，则该几何体的全面积等于（）A．112 B．136 C．124 D．84【解答】解：如图：由勾股定理=3，3×2=6，6×4÷2×2+5×7×2+6×7=24+70+42=136．故该几何体的全面积等于136．7．（3分）给出下列计算，其中正确的是（）A．a5+a5=a10 B．（2a2）3=6a6C．a8÷a2=a4 D．（a3）4=a12【解答】解：A、合并同类项系数相加字母及指数不变，故A错误；B、积的乘方等于乘方的积，故B错误；C、同底数幂的除法底数不变指数相减，故C错误；D、幂的乘方底数不变指数相乘，故D正确；故选：D．8．（3分）不等式3x﹣2＞4的解集在数轴上表示正确的是（）A．B．C．D．【解答】解：不等式移项得：3x＞6，解得：x＞2，表示在数轴上得：，故选B．9．（3分）如图，△ABC的三个顶点都在正方形格的格点上，则sin∠A的值为（）A．B．C．D．。

哈尔滨市第六十九中学2018--2019学年度（上）十一月份质量监测数学试卷温馨提示：亲爱的同学们，这份试卷再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光。

请认真审题，看清要求，仔细答卷。

祝你成功! 一、选择题：（每题3分，共30分）1、下列方程中，是一元一次方程的是（ ） A.32x y -= B. 12=0x x＋－C.11=22xD.23=0x x －2－ 2、如图，下面最左边的图是由右面四个图中哪一个图案通过平移得到（ ）(A) (B) (C) (D)3、下列各点，在第四象限的是（ ）A ．(5,2) B. (5,2)- C. (5,2)--D .(5,2)-4、下列各数中，—2π，2，0，—2270.1010010001……，0.3∙中无理数的个数有（ ）A ． 2个 B. 3个 C. 4个 D . 5个5、若关于x 的方程240x a +-=的解是2x =-，则a 的值是（ ）A ． 0 B. -8 C. 8 D . ±8 6、如图，∠B 的同旁内角有（ ）A ． 1个 B. 2个 C. 3个 D . 4个 7、如果a 、b 表示两个数，下列变形中正确的是（ ）A ． 若a b ==若a b ==C. 若a b ＞，则a b ＞ D . 若a b ＜8、一项工程单独做需要40天完成，乙单独做要50天完成，甲先单独做4天，然后甲乙两人合作x 天完成这项工程，则可以列的方程是（ ）A ．4+=14040+50x B. 4+=1404050x⨯ C. 4+=14050x D . 4+=1404050x x +9、、如图，如果AB ∥EF ，EF ∥CD ，则下列各式成立的是（ ）A ． ∠2+∠3-∠1=180°B. ∠1-∠2+∠3=90°C. ∠1+∠2+∠3=180° D . ∠1+∠2-∠3=180° 10、下列命题：①有一边互为反向延长线，且相等的两个角是对顶角。

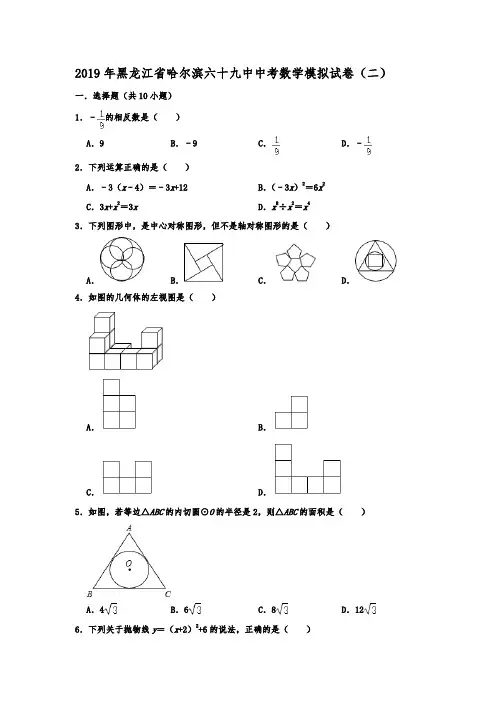
2019年黑龙江省哈尔滨六十九中中考数学模拟试卷（二）一．选择题（共10小题）1．﹣的相反数是（）A．9 B．﹣9 C．D．﹣2．下列运算正确的是（）A．﹣3（x﹣4）＝﹣3x+12 B．（﹣3x）2＝6x2C．3x+x2＝3x D．x8÷x2＝x43．下列图形中，是中心对称图形，但不是轴对称图形的是（）A．B．C．D．4．如图的几何体的左视图是（）A．B．C．D．5．如图，若等边△ABC的内切圆⊙O的半径是2，则△ABC的面积是（）A．4B．6C．8D．126．下列关于抛物线y＝（x+2）2+6的说法，正确的是（）A．抛物线开口向下B．抛物线的顶点坐标为（2，6）C．抛物线的对称轴是直线x＝6D．抛物线经过点（0，10）7．方程＝0的解为（）A．﹣2 B．2 C．5 D．无解8．如图，菱形ABCD的对角线AC＝6，BD＝8，AE⊥BC于点E，则AE的长是（）A．5 B．C．D．9．已知直线y＝x+1与反比例函数y＝的图象的一个交点为P（a，2），则ak的值为（）A．2 B．C．﹣2 D．﹣10．如图，在△ABC中，点D、E分别为AB、AC边上的点，连接DE，且DE∥BC，点F为BC 边上一点，连接AF交DE于点G，则下列结论中一定正确的是（）A．＝B．＝C．＝D．＝二．填空题（共10小题）11．数据0.0007用科学记数法表示为．12．在函数y＝中，自变量x的取值范围是．13．分解因式5a3b﹣10a2b+5ab＝．14．计算：＝．15．不等式组的整数解是．16．一个扇形的弧长是20πcm，面积是240πcm2，则这个扇形的圆心角是度．17．有一枚材质均匀的正方体骰子，它的六个面上分别有1点、2点、…6点的标记，掷一次骰子，向上的一面出现的点数是3的倍数的概率是．18．△ABC的面积为，AB＝3，BC＝10，AH⊥BC于点H，点E为BC中点，则HE＝．19．如图，在平行四边形ABCD中，AE⊥BC于点E，AF⊥CD于点F，若AE＝4，AF＝6，AD+CD ＝20，则平行四边形ABCD的面积为．20．如图，△ABC中，∠ACB＝90°，∠B＝60°，AB＝4，D为AB中点，CE平分∠ACB，∠DEC＝30°，则CE＝．三．解答题（共7小题）21．先化简再求值，其中x＝3tan30°﹣4cos60°．22．如图，在小正方形的边长均为1的方格纸中有线段AB，BC，点A，B，C均在小正方形的顶点上．（1）在图1中画出凸四边形ABCD，使四边形ABCD是轴对称图形，点D在小正方形的顶点上；（2）在图2中画出凸四边形ABCE，点E在小正方形的顶点上，∠AEC＝90°，EC＞EA；直接写出四边形ABCE的周长．23．某中学围绕“哈尔滨市周边五大名山，即：香炉山、凤凰山、金龙山、帽儿山、二龙山，你最喜欢那一座山？（每名学生必选且只选一座山）的问题在全校范围内随机抽取了部分学生进行问卷调查，根据调查结果绘制了如图的不完整的统计图：（1）求本次调查的样本容量；（2）求本次调查中，最喜欢凤凰山的学生人数，并补全条形统计图；（3）若该中学共有学生1200人，请你估计该中学最喜欢香炉山的学生约有多少人？24．已知：如图，在Rt△ABC中，∠ACB＝90°，点D、E分别是AB、AC的中点，点F在BC 延长线上，连接EF，且∠CEF＝∠BAC．（1）如图1，求证：四边形CDEF是平行四边形；（2）如图2，连接AF、BE，在不添加任何辅助线的情况下，请直接写出图2中所有与△AED面积相等的三角形．25．王叔叔决定在承包的荒山上种苹果树，第一次用1000元购进了一批树苗，第二次又用了1000元购进该种树苗，但这次每棵树苗的进价是第一次进价的2倍，购进数量比第一次少了100棵．（1）求第一次每棵树苗的进价是多少元？（2）一年后，树苗的成活率为85%，每棵果树平均产苹果30斤，王叔叔将两批果树所产苹果按同一价格全部销售完毕后获利不低于89800元，求每斤苹果的售价至少是多少元？26．如图，△ABC中，AB＝AC，AD⊥BC于D，E是AC边上一点，⊙O过B、D、E三点，分别交AC、AB于点F、G，连接EG、BF分别与AD交于点M、N；（1）求证：∠AMG＝∠BND；（2）若点E为AC的中点，求证：BF＝BC；（3）在（2）的条件下，作EH⊥EG交AD于点H，若EH＝EG＝4，过点G作GK⊥BF 于点K，点P在线段GK上，点Q在线段BK上，连接BP、GQ，若∠KGQ＝2∠GBP，GQ＝15，求GP的长度．27．如图，直线y＝x+6与x轴、y轴交于A、B两点，点C在第四象限，BC⊥AB，且BC ＝AB；（1）如图1，求点C的坐标；（2）如图2，D是BC的中点，过D作AC的垂线EF交AC于E，交直线AB于F，连接CF，点P为射线AD上一动点，求PF2﹣PC2的值；（3）如图3，在（2）的条件下，在第二象限过点A作线段AM⊥AB于点A，在线段AB 上取一点N，连接MN，使MN＝BN，在第三象限取一点Q，使∠NMQ＝90°，连接QC，若QC∥AB，且QC＝6AM，设点P的横坐标为t，△PMQ的面积为s，求s与t的函数关系式．参考答案与试题解析一．选择题（共10小题）1．﹣的相反数是（）A．9 B．﹣9 C．D．﹣【分析】直接利用相反数的定义分析得出答案．【解答】解：﹣的相反数是：．故选：C．2．下列运算正确的是（）A．﹣3（x﹣4）＝﹣3x+12 B．（﹣3x）2＝6x2C．3x+x2＝3x D．x8÷x2＝x4【分析】分别根据去括号法则、积的乘方法则、合并同类项法则以及同底数幂相除法则逐一判断即可．【解答】解：A．﹣3（x﹣4）＝﹣3x+12，故本选项符合题意；B．（﹣3x）2＝9x2，故本选项不合题意；C.3x与x2不是同类项，故不能合并，故本选项不合题意；D．x8÷x2＝x6，故本选项不合题意．故选：A．3．下列图形中，是中心对称图形，但不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【解答】解：A、是中心对称图形，也是轴对称图形，故本选项错误；B、是中心对称图形，但不是轴对称图形，故本选项正确；C、不是中心对称图形，但是轴对称图形，故本选项错误；D、不是中心对称图形，但是轴对称图形，故本选项错误．故选：B．4．如图的几何体的左视图是（）A．B．C．D．【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定则可．【解答】解：从左边看去，左边是3个正方形，右边是2个正方形．故选：A．5．如图，若等边△ABC的内切圆⊙O的半径是2，则△ABC的面积是（）A．4B．6C．8D．12【分析】连接OB，OD，根据⊙O是等边△ABC的内切圆，求出∠OBD＝30°，求出OB＝2OD ＝4，根据勾股定理求出BD，同理求出CD，得到BC，求出AD，即可得出答案．【解答】解：连接OB，OD，OA，∵⊙O是等边△ABC的内切圆，∴∠OBD＝30°，∠BDO＝90°，∴OB＝2OD＝4，由勾股定理得：BD＝＝2，同理CD＝2，∴BC＝BD+CD＝4，∵△ABC是等边三角形，A，O，D三点共线，∴AD＝6，∴S△ABC＝BC•AD＝12．6．下列关于抛物线y＝（x+2）2+6的说法，正确的是（）A．抛物线开口向下B．抛物线的顶点坐标为（2，6）C．抛物线的对称轴是直线x＝6D．抛物线经过点（0，10）【分析】根据抛物线的解析式可以判断各个选项中的结论是否正确，从而可以解答本题．【解答】解：∵y＝（x+2）2+6＝x2+4x+10，∴a＝1，该抛物线的开口向上，故选项A错误，抛物线的顶点坐标是（﹣2，6），故选项B错误，抛物线的对称轴是直线x＝﹣2，故选项C错误，当x＝0时，y＝10，故选项D正确，故选：D．7．方程＝0的解为（）A．﹣2 B．2 C．5 D．无解【分析】根据解分式方程的步骤依次计算可得．【解答】解：两边都乘以x﹣5，得：2﹣x+3＝0，解得：x＝5，检验：当x＝5时，x﹣5＝0，所以方程无解．故选：D．8．如图，菱形ABCD的对角线AC＝6，BD＝8，AE⊥BC于点E，则AE的长是（）A．5 B．C．D．【分析】根据菱形的性质得出BO、CO的长，在Rt△BOC中求出BC，利用菱形面积等于对角线乘积的一半，也等于BC×AE，可得出AE的长度．【解答】解：∵四边形ABCD是菱形，∴CO＝AC＝3，BO＝BD＝4，AO⊥BO，∴BC＝＝5，∴S菱形ABCD＝AC•BD＝×6×8＝24，∵S菱形ABCD＝BC×AE，∴BC×AE＝24，∴AE＝．故选：C．9．已知直线y＝x+1与反比例函数y＝的图象的一个交点为P（a，2），则ak的值为（）A．2 B．C．﹣2 D．﹣【分析】根据图象上的点满足函数解析式，可求得a，从而求得点P的坐标，根据待定系数法，可得k值，进而求得ak的值．【解答】解：一次函数y＝x+1的图象过点（a，2），∴a+1＝2，∴a＝1∵y＝的图象过点（1，2）∴2＝，解得k＝2，∴ak＝2．故选：A．10．如图，在△ABC中，点D、E分别为AB、AC边上的点，连接DE，且DE∥BC，点F为BC 边上一点，连接AF交DE于点G，则下列结论中一定正确的是（）A．＝B．＝C．＝D．＝【分析】根据平行线分线段成比例定理即可判断；【解答】解：∵DE∥BC，∴＝，∴＝，故选：C．二．填空题（共10小题）11．数据0.0007用科学记数法表示为7×10﹣4．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.0007＝7×10﹣4．故答案为：7×10﹣4．12．在函数y＝中，自变量x的取值范围是x≠6 ．【分析】根据分式的意义即分母不等于0，可以求出x的范围．【解答】解：依题意得x﹣6≠0，∴x≠6．故答案为：x≠6．13．分解因式5a3b﹣10a2b+5ab＝5ab（a﹣1）2．【分析】原式提取公因式，再利用完全平方公式分解即可．【解答】解：原式＝5ab（a2﹣2a+1）＝5ab（a﹣1）2，故答案为：5ab（a﹣1）214．计算：＝．【分析】直接化简二次根式进而计算得出答案．【解答】解：原式＝2﹣18×＝﹣．故答案为：﹣．15．不等式组的整数解是0 ．【分析】先求出每个不等式的解集，再求出不等式组的解集即可．【解答】解：解不等式①得：x＞﹣1，解不等式②得：x≤0，∴不等式组的解集为﹣1＜x≤0，∴不等式组的整数解为0，故答案为0．16．一个扇形的弧长是20πcm，面积是240πcm2，则这个扇形的圆心角是150 度．【分析】根据扇形的面积公式求出半径，然后根据弧长公式求出圆心角即可．【解答】解：扇形的面积公式＝lr＝240πcm2，解得：r＝24cm，又∵l＝＝20πcm，∴n＝150°．故答案为：150．17．有一枚材质均匀的正方体骰子，它的六个面上分别有1点、2点、…6点的标记，掷一次骰子，向上的一面出现的点数是3的倍数的概率是．【分析】共有6种等可能的结果数，其中点数是3的倍数有3和6，从而利用概率公式可求出向上的一面出现的点数是3的倍数的概率．【解答】解：掷一次骰子，向上的一面出现的点数是3的倍数的概率＝＝．故答案为．18．△ABC的面积为，AB＝3，BC＝10，AH⊥BC于点H，点E为BC中点，则HE＝．【分析】根据题意画出图形，由勾股定理求出BH的长，则HE可求出．【解答】解：如图1，当AH在△ABC内时，∵△ABC的面积为，BC＝10，∴．∴．∴＝．∴．如图2，当AH在△ABC外时，同理可得AH＝，BH＝，∴．故答案为：或．19．如图，在平行四边形ABCD中，AE⊥BC于点E，AF⊥CD于点F，若AE＝4，AF＝6，AD+CD ＝20，则平行四边形ABCD的面积为48 ．【分析】已知平行四边形的高AE、AF，设BC＝AD＝x，则CD＝20﹣x，根据“等面积法”列方程，求BC，从而求出平行四边形的面积．【解答】解：设BC＝AD＝x，则CD＝20﹣x，根据“等面积法”得4x＝6（20﹣x），解得x＝12，∴平行四边形ABCD的面积＝4x＝4×12＝48．故答案为：48．20．如图，△ABC中，∠ACB＝90°，∠B＝60°，AB＝4，D为AB中点，CE平分∠ACB，∠DEC＝30°，则CE＝2．【分析】连接CD，作CH⊥DE于H，由直角三角形的性质可得CD＝BD＝AD＝2，∠A＝30°，可得HD＝HC＝，由直角三角形的性质可得CE＝2HC＝2．【解答】解：连接CD，作CH⊥DE于H∵∠ACB＝90°，∠B＝60°，AB＝4，D为AB中点，∴CD＝BD＝AD＝2，∠A＝30°∴∠ACD＝∠A＝30°，∵CE平分∠ACB∴∠ACE＝45°∴∠DCE＝15°∴∠HDC＝∠DEC+∠DCE＝45°，且CH⊥DE∴∠HCD＝∠HDC＝45°，且CD＝2∴HD＝HC＝∵∠DEC＝30°，CH⊥DE∴CE＝2CH＝2故答案为：2三．解答题（共7小题）21．先化简再求值，其中x＝3tan30°﹣4cos60°．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．【解答】解：原式＝•＝•＝，∵x＝3×﹣4×＝﹣2，∴原式＝．22．如图，在小正方形的边长均为1的方格纸中有线段AB，BC，点A，B，C均在小正方形的顶点上．（1）在图1中画出凸四边形ABCD，使四边形ABCD是轴对称图形，点D在小正方形的顶点上；（2）在图2中画出凸四边形ABCE，点E在小正方形的顶点上，∠AEC＝90°，EC＞EA；直接写出四边形ABCE的周长6+4．【分析】（1）根据轴对称图形的性质作出只有一条对称轴的图形即可求解；（2）作出四边形ABCE即为所求四边形ABCE，进而利用周长解答即可．【解答】解：（1）如图1所示：凸四边形ABCD即为所求；（2）如图2所示，凸四边形ABCE即为所求，四边形ABCE的周长＝6+4．故答案为：6+4．23．某中学围绕“哈尔滨市周边五大名山，即：香炉山、凤凰山、金龙山、帽儿山、二龙山，你最喜欢那一座山？（每名学生必选且只选一座山）的问题在全校范围内随机抽取了部分学生进行问卷调查，根据调查结果绘制了如图的不完整的统计图：（1）求本次调查的样本容量；（2）求本次调查中，最喜欢凤凰山的学生人数，并补全条形统计图；（3）若该中学共有学生1200人，请你估计该中学最喜欢香炉山的学生约有多少人？【分析】（1）由帽儿山的人数及其所占百分比可得总人数；（2）根据各部分人数之和等于总人数可得凤凰山的人数；（3）利用样本估计总体思想求解可得．【解答】解：（1）20÷25%＝80（名），答：本次抽样调查共抽取了80名学生．（2）最喜欢凤凰山的学生人数为80﹣24﹣8﹣20﹣12＝16（名），补全条形统计图（3）1200×＝360（名），由样本估计总体得该中学最喜欢香炉山的学生约有360名．24．已知：如图，在Rt△ABC中，∠ACB＝90°，点D、E分别是AB、AC的中点，点F在BC 延长线上，连接EF，且∠CEF＝∠BAC．（1）如图1，求证：四边形CDEF是平行四边形；（2）如图2，连接AF、BE，在不添加任何辅助线的情况下，请直接写出图2中所有与△AED面积相等的三角形．【分析】（1）利用三角形中位线定理证明DE∥CF，再证明EF∥CD即可；（2）利用等高模型即可解决问题；【解答】（1）证明：∵点D、E分别是AB、AC的中点，∴DE是△ABC的中位线，∴DE∥BC，∵∠ACB＝90°，AD＝DB，∴CD＝AD＝DB，∴∠A＝∠DCA，∵∠CEF＝∠A，∴∠CEF＝∠ECD，∴EF∥CD，∴四边形CDEF是平行四边形．（2）如图2中，与△AED面积相等的三角形有：△AEF，△ECF，△EDC，△EDB．理由：∵四边形CDEF是平行四边形，∴△EFC与△DEC的面积相等，∵AE＝ED，DE∥BC，∴△ADE与△EDC，△EDC与△EDB的面积相等，∴与△AED面积相等的三角形有：△AEF，△ECF，△EDC，△EDB．25．王叔叔决定在承包的荒山上种苹果树，第一次用1000元购进了一批树苗，第二次又用了1000元购进该种树苗，但这次每棵树苗的进价是第一次进价的2倍，购进数量比第一次少了100棵．（1）求第一次每棵树苗的进价是多少元？（2）一年后，树苗的成活率为85%，每棵果树平均产苹果30斤，王叔叔将两批果树所产苹果按同一价格全部销售完毕后获利不低于89800元，求每斤苹果的售价至少是多少元？【分析】（1）首先设第一次每棵树苗的进价是x元，则第二次每棵树苗的进价是2x元，依题意得等量关系：第一购进树苗的棵数﹣第二次购进树苗的棵树＝100，由等量关系列出方程即可；（2）设每斤苹果的售价是a元，依题意得等量关系：两次购进树苗的总棵树×成活率为85%×每棵果树平均产苹果30斤﹣两次购进树苗的成本≥89800元，根据不等关系代入相应的数值，列出不等式．【解答】解：（1）设第一次每棵树苗的进价是x元，依题意得：﹣＝100，解得：x＝5，经检验x＝5是原分式方程的解，∴第一次每棵树苗的进价是5元．（2）设每斤苹果的售价是a元，依题意得：（+）×85%×30a﹣1000×2≥89800，解得：a≥12，答：每斤苹果的售价至少是12元．26．如图，△ABC中，AB＝AC，AD⊥BC于D，E是AC边上一点，⊙O过B、D、E三点，分别交AC、AB于点F、G，连接EG、BF分别与AD交于点M、N；（1）求证：∠AMG＝∠BND；（2）若点E为AC的中点，求证：BF＝BC；（3）在（2）的条件下，作EH⊥EG交AD于点H，若EH＝EG＝4，过点G作GK⊥BF 于点K，点P在线段GK上，点Q在线段BK上，连接BP、GQ，若∠KGQ＝2∠GBP，GQ＝15，求GP的长度．【分析】（1）由等腰三角形的性质和圆的内接四边形的性质可得结论；（2）可证出BD＝CD，可得∠FBC＝∠BAC，证出∠BFC＝∠ABC＝∠C，结论得证；（3）取AB中点P，连接MH、GH、DE，可得平行四边形BDEM、等边△MHE，可得出∠GAH ＝∠GHA＝15°，求出GA＝GH＝•EH＝，求出AE＝，可求出AB和BG长，Rt△BGK中，可得∠GBK＝45°，求出GK＝BK＝，Rt△QGK中勾股定理可得QK＝，延长BK到T使KT＝PK，连接GK则△BKP≌△GKT，得出∠KGT＝∠KBP，可得QG＝QT＝15，则PK可求出，GP＝GK﹣PK＝．【解答】（1）证明：∵AB＝AC，AD⊥BC，∴∠BAD＝∠CAD，∵四边形BFEG内接于⊙O，∴∠BGE+∠BFE＝180°∵∠BGE+∠AGE＝180°，∴∠BFE＝∠AGE，∵△AGM中，∠BAD+∠AGE+∠AMG＝180°，△ANF中，∠CAD+∠BFE+∠ANF＝180°，∴∠AMG＝∠ANF，∵∠ANF＝∠BND，∴∠AMG＝∠BND；（2）证明：如图，连接DE，∵AB＝AC，AD⊥BC，∴BD＝CD，∵AE＝CE，∴DE是△ABC的中位线，∴DE∥AB，∴∠DEC＝∠BAC，∵∠DEC＝∠FBC，∴∠FBC＝∠BAC，∵AB＝AC，∴∠ABC＝∠C，∴∠BFC＝∠ABC＝∠C，∴BF＝BC；（3）解：如图，取AB中点M，连接MH、GH、DE，∵AE＝CE，∴四边形BDEM是平行四边形，∴ME∥BD，∴∠GME＝∠ABC，∵∠ABC＝∠C，∠C＝∠EDC＝∠BGE，∴∠MGE＝∠GME，∴GE＝ME，∵MH＝ME，EH＝EG，∴△MHE是等边三角形，∵AD垂直平分BC，∴AH垂直平分ME，∴∠GAH＝∠GHA＝15°，∴GA＝CH＝•EH＝＝，∴在△AGE中，AE＝，∴AB＝AC＝，∴BG＝AB﹣AG＝，∵Rt△BGK中，可得∠GBK＝45°，∴GK＝BK＝，∴Rt△QGK中，QK＝＝，延长BK到T使KT＝PK，连接GK，∵∠BKP＝∠GKT，∴△BKP≌△GKT（SAS），∴∠KGT＝∠KBP，∴∠BPK＝∠GTK，∵∠QGT＝∠KGQ+∠KGT＝∠KGQ+∠PBK，∠KGQ＝2∠GBP，∴∠QGT＝2∠GBP+∠PBK，∵∠PBK＝45°﹣∠GBP，∴∠QGT＝45°+∠PBG＝∠BPK，∴∠QGT＝∠GTK，∴QG＝QT＝15，∴PK＝KT＝QT﹣QK＝，∴GP＝GK﹣PK＝12＝．27．如图，直线y＝x+6与x轴、y轴交于A、B两点，点C在第四象限，BC⊥AB，且BC ＝AB；（1）如图1，求点C的坐标；（2）如图2，D是BC的中点，过D作AC的垂线EF交AC于E，交直线AB于F，连接CF，点P为射线AD上一动点，求PF2﹣PC2的值；（3）如图3，在（2）的条件下，在第二象限过点A作线段AM⊥AB于点A，在线段AB 上取一点N，连接MN，使MN＝BN，在第三象限取一点Q，使∠NMQ＝90°，连接QC，若QC∥AB，且QC＝6AM，设点P的横坐标为t，△PMQ的面积为s，求s与t的函数关系式．【分析】（1）过C作CH⊥y轴于H，则∠BCH+∠CBH＝90°，证明△BHC≌△AOB（AAS）即可解决问题．（2）（2）如图2中，设射线AD交CF于G．证明△ABD≌△CBF（SAS），利用勾股定理解决问题即可．（3）如图3中，连接BM，BQ，过B作BK⊥QM延长线于点K，延长MA交QC于点T，可得正方形ABCT．证明△BKM≌△BAM（ASA），推出BA＝BK＝BC，MK＝MA，证明Rt△BKQ≌Rt△BCQ（HL），推出QK＝QC，设AM＝a，则QK＝QC＝6a，在Rt△QMT中，MQ＝5a，MT＝a+10，QT＝6a﹣10，勾股定理可得a＝，由tan∠MNA＝tan∠QMT＝tan∠BAO＝，推出QT＝10，MQ＝，MT＝，作PS⊥MQ于点S，根据，计算即可．【解答】解：（1）如图1中，在y＝x+6中，令y＝0，得x＝﹣8；令x＝0，得y＝6∴A（﹣8，0），B（0，6），∴OA＝8，OB＝6，过C作CH⊥y轴于H，则∠BCH+∠CBH＝90°，∵BC⊥AB，∴∠ABO+∠CBH＝90°，∴∠BCH＝∠ABO，又∠BHC＝∠AOB＝90°，BC＝AB，∴△BHC≌△AOB（AAS），∴HC＝OB＝6，BH＝OA＝8，OH＝8﹣6＝2，∴C（6，﹣2）．（2）如图2中，设射线AD交CF于G．∵BC⊥AB，BC＝AB，∴∠BAC＝45°∵EF⊥AC，∴∠AFE＝45°∴△BDF是等腰直角三角形，∴BD＝BF，又∠ABD＝∠CBF＝90°，AB＝CB∴△ABD≌△CBF（SAS），∴∠BAD＝∠BCF，∵∠BDA＝∠CDG，∴∠CGD＝∠ABD＝90°，即AD⊥CF，∵OA＝8，OB＝6，∴AB＝＝10，∴BC＝10，∴BF＝BD＝5，∴PF2﹣PC2＝（PG2+FG2）﹣（PG2+CG2）＝FG2﹣CG2＝（DF2﹣DG2）﹣（DC2﹣DG2）＝DF2﹣DC2＝DF2﹣BD2＝BF2＝25（3）如图3中，连接BM，BQ，过B作BK⊥QM延长线于点K，延长MA交QC于点T，可得正方形ABCT．∵MN＝BN，∴∠NMB＝∠NBM，∵BK⊥QK，NM⊥QK，∴BK∥MN，∴∠KBM＝∠BMN，∴∠KBM＝∠MBA，∵MB＝MB，∠K＝∠BAM＝90°∴△BKM≌△BAM（ASA），∴BA＝BK＝BC，MK＝MA，∴Rt△BKQ≌Rt△BCQ（HL），∴QK＝QC，设AM＝a，则QK＝QC＝6a，在Rt△QMT中，MQ＝5a，MT＝a+10，QT＝6a﹣10，勾股定理可得a＝，∵tan∠MNA＝tan∠QMT＝tan∠BAO＝，∴QT＝10，MQ＝，MT＝∴MN∥x轴，MQ∥y轴，作PS⊥MQ于点S，∴，设MQ与x轴交于点I，Rt△MAI中，AI＝2，作AL⊥PS于点L，得矩形ALSI，∴PS＝PL+LS＝t+10，∴，∴．。

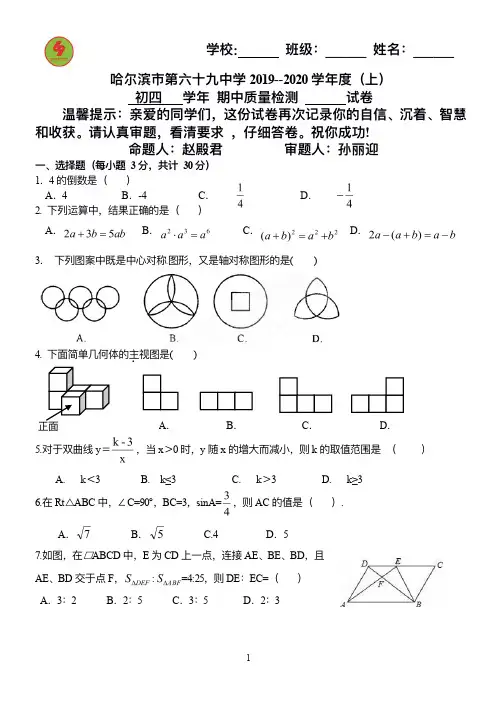
学校:班级：______姓名：______哈尔滨市第六⼗十九中学2019--2020学年年度（上）初四学年年期中质量量检测试卷温馨提示：亲爱的同学们，这份试卷再次记录你的⾃自信、沉着、智慧和收获。

请认真审题，看清要求，仔细答卷。

祝你成功!命题⼈人：赵殿君审题⼈人：孙丽迎⼀一、选择题（每⼩小题3分，共计30分）1．4的倒数是（）A ．4B ．-4C ．D ．2.下列列运算中，结果正确的是（）A ．B ．C ．D ．3．下列列图案中既是中⼼心对称图形，⼜又是轴对称图形的是()4.下⾯面简单⼏几何体的主．视图是()5.对于双曲线y ＝，当x ＞0时，y 随x 的增⼤大⽽而减⼩小，则k 的取值范围是（）A.k ＜3B.k ≤3C.k ＞3D.k ≥36.在Rt △ABC 中，∠C=90°，BC=3，sinA=，则AC 的值是（）.A ．B ．C.4D ．57.如图，在□ABCD 中，E 为CD 上⼀一点，连接AE 、BE 、BD ，且AE 、BD 交于点F ，:=4:25，则DE ：EC=（）A ．3：2B ．2：5C ．3：5D ．2：3正⾯面A ．B ．C ．D ．8.对于任意实数，关于的⽅方程的根的情况为（）A.有两个不不相等的实数根B.没有实数根C.有两个相等的实数根D.⽆无法确定9．如图，在地⾯面上的点A处测得树顶B的仰⻆角为α度，AC=7m，则树⾼高BC为（⽤用含α的代数式表示）（）A．7sinαB．7cosαC．7tanαD．10.如图，AD∥BE∥CF，直线l1、l2与这三条平⾏行行线分别交于点A、B、C和点D、E、F．若AB=4.5，BC=3，EF=2，则DE的⻓长度是（）A．2B．3C．5D．6⼆二、填空题（每⼩小题3分，共计30分）11.数字1663000⽤用科学记数法表示为．12.在函数中，⾃自变量量x的取值范围是．13.计算：=．14.分解因式：=．15.不不等式组的解集是．16.⼀一个袋⼦子中装有4个⿊黑球2个⽩白球，这些球除颜⾊色外，形状、⼤大⼩小、质地等完全相同．搅匀后，在看不不到球的条件下，随机从这个袋⼦子中摸出两个球为⽩白球的概率是．17.已知扇形半径是3cm，弧⻓长为2πcm，则扇形的圆⼼心⻆角为度.18.某种过季绿茶的价格两次⼤大幅下降，原来每袋250元，现在每袋90元，则平均每次下降的百分率是．19.在菱形ABCD中，∠A＝30°，在同⼀一平⾯面内，以对⻆角线BD为底边作顶⻆角为120°的等腰三⻆角形BDE，则∠EBC的度数为度.20.已知：如图，△ABC中，AD⊥BC于D，∠B=2∠C，AB=5，AC=4，则BD=.学校:班级：______姓名：______三、解答题（其中21～22题各7分，23～24题各8分，25～27题各10分，共60分）21.先化简．再求代数式的值.其中a＝tan60°－2sin30°．22.如图，在平⾯面直⻆角坐标系中，△OAB的三个顶点的坐标分别为A（6，3），B（0，5）．（1）画出△OAB绕原点O逆时针⽅方向旋转90°后得到的△OA1B1；（2）画出△OAB关于原点O的（3）中⼼心对称图形△OA2B2；（3）直接写出∠OAB的度数．23.哈市某中学为了了解学⽣生的课余⽣生活情况，学校决定围绕“在欣赏⾳音乐、读课外书、体育运动、其他活动中，你最喜欢的课余⽣生活种类是什什么？（只写⼀一类）”的问题，在全校范围内随机抽取部分学⽣生进⾏行行问卷调查，并将调查问卷适当整理理后绘制成如图所示的不不完整的条形统计图，其中最喜欢欣赏⾳音乐的学⽣生占被抽取⼈人数的12％，请你根据以上信息解答下列列问题：（1）在这次调查中，⼀一共抽取了了多少名学⽣生？（2）最喜欢读课外书的学⽣生占被抽取⼈人数的百分数是多少？（3）如果全校有1000名学⽣生，请你估计全校最喜欢体育运动的学⽣生约有多少名.24.在菱形ABCD中，P、Q分别是边BC、CD的中点，连接AP、AQ.（1）如图（1），求证：AP=AQ；（2）如图（2），连接PQ、AC，在不不添加任何辅助线的情况下，请直接写出图中所有的等腰三⻆角形.25.某汽⻋车销售公司经销某品牌A款汽⻋车，随着汽⻋车的普及，其价格也在不不断下降，今年年5⽉月份A款汽⻋车的售价⽐比去年年同期每辆降价1万元，如果卖出相同数量量的A款汽⻋车，去年年销售额为90万元，今年年销售额只有80万元.（1）求今年年5⽉月份A款汽⻋车每辆售价多少万元；（2）为了了增加收⼊入，汽⻋车销售公司决定再经销同品牌的B款汽⻋车，已知B款汽⻋车每辆进价为7.5万元，每辆售价为10.5万元，A款汽⻋车每辆进价为6万元，若卖出这两款汽⻋车共15辆后，获利利不不低于39万元，求B款汽⻋车⾄至少卖出多少辆.26.已知：如图，AB为⊙O的直径，弦CD⊥AB，点E为弧AC上⼀一点，连接BE.（1）如图1，求证：∠CEB=∠DEB；（2）如图2，若弦CD经过圆⼼心O，过点A作AF⊥AE交DE于F，求证：CE=DF；（3）如图3，在（2）的条件下，连接AC交ED、EB于点H、G，连接BF，若CG=2，AH=3，求BF的⻓长.27.如图，抛物线与x轴正半轴交于点A，OA=4.（1）求抛物线的解析式；（2）点P为第四象限抛物线上⼀一点，点P的横坐标为t，连接OP、AP，设三⻆角形OAP的⾯面积为S，求S与t的函数解析式；（3）点Q为第⼆二象限抛物线上⼀一点，连接PQ交y轴于点C，过点P作x轴的垂线垂⾜足为B，连接BC、AQ，若∠CBO+∠QAO=90°，求点Q的坐标.学校:班级：______姓名：______2019年年69中初四（上）期中答案及评分标准⼀一、CDCCC ADACB⼆二、11、12、13、14、15、16、17、12018、40%19、45或10520、3三、21、原式=.........1分=.........1分=.........1分=........1分........1分=........1分原式=........1分22、（1）问3分（2）问3分（3）45°1分23、（1）6÷12%=50........1分答：在这次调查中，⼀一共抽取了了50名学⽣生.........1分......................2分（2）答：最喜欢读课外书的学⽣生占被抽取⼈人数的百分数是32%.........1分（3）.......2分答：如果全校有1000名学⽣生，估计全校最喜欢体育运动的学⽣生约有400名.........1分24、（1）∵四边形ABCD为菱形∴AB=AD BC=CD∠B=∠D.........1分∵P、Q为边BC、CD的中点∴BP=PC=CQ=DQ=∴BP=DQ.........1分∴△ABP≌△ADQ；.........1分∴AP=AQ.........1分（2）△ABC，△APQ，△CBD，△CPQ.........4分25.（1）解：设今年年5⽉月份A款汽⻋车每辆售价为x 万元，根据题意得.........2分解得x=8.........1分经检验，x=8是原⽅方程的解.........1分答：今年年5⽉月份A款汽⻋车每辆售价为8万元..........1分（2）解：设B款汽⻋车卖出a辆，根据题意得a(10.5-7.5)+(15-a)×(8-6)≥39，.........3分解得a≥9.........1分答：B款汽⻋车⾄至少卖出9辆..........1分学校:班级：______姓名：______ 26、解：（1）∵CD⊥AB∴弧BC=弧BD，.........2分∠CEB=∠DEB.........1分（2）连接AC、AD，△ACE≌△ADF，CE=DF；.........3分（注SSA给1分）（3）过点A作AS⊥CE交CE的延⻓长线于S，AT⊥ED于T，过点E作EN⊥AC于N，GE平分∠CEH，AE平分∠SEH，利利⽤用⾯面积法得，三⻆角形内、外⻆角分线定理理，，所以，.........1分设HG=x，x=1，.........1分AC=6，tan∠ECA=，tan∠EAC=，.........1分AE=EF=，BE=BF=.........1分27、解：（1）.........2分（2）.........3分（3）过点P作PG⊥y轴于G，QH⊥PG于H，设Q（m，）,P(t,)tan∠QPH=,CG=4t-mt-t2，OC=-tm,tan∠CBO=-mtan∠QAM=,∠CBO=∠QAM.........3分∠CBO+∠QAO=90°∴∠CBO=∠QAO=45°........1分Q（-1.5）........1分。

2024届黑龙江省哈尔滨六十九中学毕业升学考试模拟卷数学卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题（共10小题，每小题3分，共30分）1．如图，菱形ABCD的对角线交于点O，AC=8cm，BD=6cm，则菱形的高为（）A．485cm B．245cm C．125cm D．105cm2．如图，在矩形ABCD中，E是AD上一点，沿CE折叠△CDE，点D恰好落在AC的中点F处，若CD＝3，则△ACE的面积为（）A．1 B．3C．2 D．233．下列标志中，可以看作是轴对称图形的是（）A．B．C．D．4．小明解方程121xx x--=的过程如下，他的解答过程中从第（）步开始出现错误．解：去分母，得1﹣（x﹣2）＝1①去括号，得1﹣x+2＝1②合并同类项，得﹣x+3＝1③移项，得﹣x＝﹣2④系数化为1，得x＝2⑤A．①B．②C．③D．④5．如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠使AB落在AD边上，折痕为AE，再将△ABE以BE为折痕向右折叠，AE与CD交于点F，则CFCD的值是（）A．1 B．12C．13D．146．在同一平面直角坐标系中，一次函数y＝kx﹣2k和二次函数y＝﹣kx2+2x﹣4（k是常数且k≠0）的图象可能是（）A．B．C．D．7．如图所示的图形为四位同学画的数轴，其中正确的是（）A．B．C．D．8．下列四个实数中是无理数的是( )A．2.5 B．C．π D．1.4149．从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体，得到的几何体如图所示，则该几何体的左视图正确的是（）A．B．C．D．10．在下列函数中，其图象与x轴没有交点的是（）A．y=2x B．y=﹣3x+1 C．y=x2D．y=1 x二、填空题（本大题共6个小题，每小题3分，共18分）11．如图，在矩形ABCD中，点E是CD的中点，点F是BC上一点，且FC=2BF，连接AE，EF．若AB=2，AD=3，则tan∠AEF的值是_____．12．如图，一次函数y=x﹣2的图象与反比例函数y=kx（k＞0）的图象相交于A、B两点，与x轴交与点C，若tan∠AOC=13，则k的值为_____．13．如图，边长为6的菱形ABCD中，AC是其对角线，∠B=60°，点P在CD上，CP=2，点M在AD上，点N在AC上，则△PMN的周长的最小值为_____________ ．149 ______．15．若式子2xx有意义，则x的取值范围是_____．16．已知正方形ABCD，AB＝1，分别以点A、C为圆心画圆，如果点B在圆A外，且圆A与圆C外切，那么圆C 的半径长r的取值范围是_____．三、解答题（共8题，共72分）17．（8分）“校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题：（1）接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为度；（2）请补全条形统计图；（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数．18．（8分）如图，一次函数y=kx+b的图象分别与反比例函数y=ax的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．（1）求函数y=kx+b和y=ax的表达式；（2）已知点C（0，8），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．19．（8分）甲、乙两个人做游戏：在一个不透明的口袋中装有1张相同的纸牌，它们分别标有数字1，2，3，1．从中随机摸出一张纸牌然后放回，再随机摸出一张纸牌，若两次摸出的纸牌上数字之和是3的倍数，则甲胜；否则乙胜．这个游戏对双方公平吗？请列表格或画树状图说明理由．20．（8分）如图，经过点C （0，﹣4）的抛物线2y ax bx c =++（0a ≠）与x 轴相交于A （﹣2，0），B 两点．（1）a 0， 0（填“＞”或“＜”）；（2）若该抛物线关于直线x=2对称，求抛物线的函数表达式；（3）在（2）的条件下，连接AC ，E 是抛物线上一动点，过点E 作AC 的平行线交x 轴于点F ．是否存在这样的点E ，使得以A ，C ，E ，F 为顶点所组成的四边形是平行四边形？若存在，求出满足条件的点E 的坐标；若不存在，请说明理由．21．（8分）如图在由边长为1个单位长度的小正方形组成的12×12网格中，已知点A ，B ，C ，D 均为网格线的交点在网格中将△ABC 绕点D 顺时针旋转90°画出旋转后的图形△A 1B 1C 1；在网格中将△ABC 放大2倍得到△DEF ，使A 与D 为对应点．22．（10分）如图，两座建筑物的水平距离BC 为40m ，从D 点测得A 点的仰角为30°，B 点的俯角为10°，求建筑物AB 的高度（结果保留小数点后一位）．参考数据sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，3取1.1．23．（12分）某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费，某顾客刚好消费200元．（1）该顾客至少可得到_____元购物券，至多可得到_______元购物券；（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．24．如图1，在平面直角坐标系中，一次函数y ＝﹣1x +8的图象与x 轴，y 轴分别交于点A ，点C ，过点A 作AB ⊥x 轴，垂足为点A ，过点C 作CB ⊥y 轴，垂足为点C ，两条垂线相交于点B ．（1）线段AB ，BC ，AC 的长分别为AB ＝ ，BC ＝ ，AC ＝ ；（1）折叠图1中的△ABC ，使点A 与点C 重合，再将折叠后的图形展开，折痕DE 交AB 于点D ，交AC 于点E ，连接CD ，如图1．请从下列A 、B 两题中任选一题作答，我选择 题．A ：①求线段AD 的长；②在y 轴上，是否存在点P ，使得△APD 为等腰三角形？若存在，请直接写出符合条件的所有点P 的坐标；若不存在，请说明理由．B ：①求线段DE 的长；②在坐标平面内，是否存在点P （除点B 外），使得以点A ，P ，C 为顶点的三角形与△ABC 全等？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．参考答案一、选择题（共10小题，每小题3分，共30分）1、B【解题分析】试题解析：∵菱形ABCD 的对角线86AC cm BD cm ==，，114322AC BD OA AC cm OB BD cm ∴⊥====，，，根据勾股定理，5AB cm ===，设菱形的高为h ， 则菱形的面积12AB h AC BD =⋅=⋅， 即15862h =⨯⨯， 解得24.5h = 即菱形的高为245cm ． 故选B ．2、B【解题分析】由折叠的性质可得CD =CF DE =EF ，AC =EF 的长，即可求△ACE 的面积．【题目详解】解：∵点F 是AC 的中点，∴AF =CF =12AC ， ∵将△CDE 沿CE 折叠到△CFE ，∴CD =CF ，DE =EF ，∴AC =在Rt △ACD 中，AD ．∵S △ADC =S △AEC +S △CDE ， ∴12×AD ×CD =12×AC ×EF +12×CD ×DE∴=，∴DE =EF =1，∴S △AEC =12× 故选B ．【题目点拨】本题考查了翻折变换，勾股定理，熟练运用三角形面积公式求得DE =EF =1是解决本题的关键．3、D【解题分析】根据轴对称图形与中心对称图形的概念求解．【题目详解】解：A 、不是轴对称图形，是中心对称图形，不符合题意；B 、不是轴对称图形，是中心对称图形，不符合题意；C 、不是轴对称图形，是中心对称图形，不符合题意；D 、是轴对称图形，符合题意．故选D ．【题目点拨】本题考查了中心对称图形和轴对称图形的定义，掌握中心对称图形与轴对称图形的概念，解答时要注意：判断轴对称图形的关键是寻找对称轴，图形两部沿对称轴叠后可重合；判断中心对称图形是要寻找对称中心，图形旋转180度后与原图重合．4、A【解题分析】根据解分式方程的方法可以判断哪一步是错误的，从而可以解答本题．【题目详解】12x x x--=1， 去分母，得1-（x-2）=x ，故①错误，故选A ．【题目点拨】本题考查解分式方程，解答本题的关键是明确解分式方程的方法．5、C【解题分析】由题意知：AB=BE=6，BD=AD ﹣AB=2（图2中），AD=AB ﹣BD=4（图3中）；∵CE ∥AB ，∴△ECF ∽△ADF ， 得12CE CF AD DF ==， 即DF=2CF ，所以CF ：CD=1：3，故选C ．【题目点拨】本题考查了矩形的性质，折叠问题，相似三角形的判定与性质等，准确识图是解题的关键.6、C【解题分析】根据一次函数与二次函数的图象的性质，求出k的取值范围，再逐项判断即可．【题目详解】解：A、由一次函数图象可知，k＞0，∴﹣k＜0，∴二次函数的图象开口应该向下，故A选项不合题意；B、由一次函数图象可知，k＞0，∴﹣k＜0，-22k-=1k>0，∴二次函数的图象开口向下，且对称轴在x轴的正半轴，故B选项不合题意；C、由一次函数图象可知，k＜0，∴﹣k＞0，-22k-=1k<0，，∴二次函数的图象开口向上，且对称轴在x轴的负半轴，一次函数必经过点（2，0），当x＝2时，二次函数值y＝﹣4k＞0，故C选项符合题意；D、由一次函数图象可知，k＜0，∴﹣k＞0，-22k-=1k<0，，∴二次函数的图象开口向上，且对称轴在x轴的负半轴，一次函数必经过点（2，0），当x＝2时，二次函数值y＝﹣4k＞0，故D选项不合题意；故选：C．【题目点拨】本题考查一次函数与二次函数的图象和性质，解决此题的关键是熟记图象的性质，此外，还要主要二次函数的对称轴、两图象的交点的位置等．7、D【解题分析】根据数轴三要素：原点、正方向、单位长度进行判断.【题目详解】A选项图中无原点，故错误；B选项图中单位长度不统一，故错误；C选项图中无正方向，故错误；D选项图形包含数轴三要素，故正确；故选D.【题目点拨】本题考查数轴的画法，熟记数轴三要素是解题的关键.8、C【解题分析】本题主要考查了无理数的定义．根据无理数的定义：无限不循环小数是无理数即可求解．解：A、2.5是有理数，故选项错误；B、是有理数，故选项错误；C、π是无理数，故选项正确；D、1.414是有理数，故选项错误．故选C．9、C【解题分析】左视图就是从物体的左边往右边看．小正方形应该在右上角，故B错误，看不到的线要用虚线，故A错误，大立方体的边长为3cm，挖去的小立方体边长为1cm，所以小正方形的边长应该是大正方形13，故D错误，所以C正确．故此题选C．10、D【解题分析】依据一次函数的图象，二次函数的图象以及反比例函数的图象进行判断即可．【题目详解】A．正比例函数y=2x与x轴交于（0，0），不合题意；B．一次函数y=-3x+1与x轴交于（13，0），不合题意；C．二次函数y=x2与x轴交于（0，0），不合题意；D．反比例函数y=1x与x轴没有交点，符合题意；故选D．二、填空题（本大题共6个小题，每小题3分，共18分）11、1．【解题分析】连接AF，由E是CD的中点、FC=2BF以及AB=2、AD=3可知AB=FC，BF=CE，则可证△ABF≌△FCE，进一步可得到△AFE是等腰直角三角形，则∠AEF=45°.【题目详解】解：连接AF，∵E 是CD 的中点，∴CE=112CD ，AB=2， ∵FC=2BF ，AD=3，∴BF=1，CF=2，∴BF=CE ，FC=AB ，∵∠B=∠C=90°，∴△ABF ≌△FCE ，∴AF=EF ，∠BAF=∠CFE ，∠AFB=∠FEC ，∴∠AFE=90°，∴△AFE 是等腰直角三角形，∴∠AEF=45°，∴tan ∠AEF=1.故答案为：1.【题目点拨】本题结合三角形全等考查了三角函数的知识.12、1【解题分析】【分析】如图，过点A 作AD ⊥x 轴，垂足为D ，根据题意设出点A 的坐标，然后根据一次函数y=x ﹣2的图象与反比例函数y=k x（k ＞0）的图象相交于A 、B 两点，可以求得a 的值，进而求得k 的值即可. 【题目详解】如图，过点A 作AD ⊥x 轴，垂足为D ，∵tan ∠AOC=AD OD =13，∴设点A 的坐标为（1a ，a ）， ∵一次函数y=x ﹣2的图象与反比例函数y=k x （k ＞0）的图象相交于A 、B 两点， ∴a=1a ﹣2，得a=1，∴1=3k ，得k=1， 故答案为：1．【题目点拨】本题考查了正切，反比例函数与一次函数的交点问题，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．13、221 【解题分析】 过P 作关于AC 和AD 的对称点，连接1P 和2P ，过P 作2P C BC ⊥, 1P 和2P ，M ，N 共线时最短，根据对称性得知△PMN 的周长的最小值为12PP .因为四边形ABCD 是菱形，AD 是对角线，可以求得60DCF ∠=︒，根据特殊三角形函数值求得1,3CF PF ==，23PE =，再根据线段相加勾股定理即可求解.【题目详解】过P 作关于AC 和AD 的对称点，连接1P 和2P ，过P 作2P C BC ⊥,四边形ABCD 是菱形，AD 是对角线，60B BAC BCA DCA DAC D ︒∴∠=∠=∠=∠=∠=∠=，180BCD DCF ∠+∠=︒，18012060DCF ∴∠=︒-︒=︒，cos60sin 60CF PF CP CP=︒=︒，1,CF PF ∴==4PD CD CP =-=,sin 60PE PD=︒PE ∴=又由题意得222,PE P E P P PE P E ==+=22FP FP PP ∴=+=113PF PC CF =+=12PP ∴==【题目点拨】本题主要考查对称性质，菱形性质，内角和定理和勾股定理，熟悉掌握定理是关键.14、3【解题分析】分析：根据算术平方根的概念求解即可.详解：因为32=9故答案为3.点睛：此题主要考查了算术平方根的意义，关键是确定被开方数是哪个正数的平方.15、x≥﹣2且x≠1．【解题分析】20x +≥，∴2x ≥-，又∵x 在分母上，∴0x ≠．故答案为2x ≥-且0x ≠.16﹣1＜r ．【解题分析】首先根据题意求得对角线AC的长，设圆A的半径为R，根据点B在圆A外，得出0＜R＜1，则-1＜-R＜0，再根据圆A与圆C外切可得，利用不等式的性质即可求出r的取值范围．【题目详解】∵正方形ABCD中，AB=1，∴，设圆A的半径为R，∵点B在圆A外，∴0＜R＜1，∴-1＜-R＜0，-R∵以A、C为圆心的两圆外切，，∴-R，＜r＜r．【题目点拨】本题考查了圆与圆的位置关系，点与圆的位置关系，正方形的性质，勾股定理，不等式的性质．掌握位置关系与数量之间的关系是解题的关键．三、解答题（共8题，共72分）17、(1) 60，90；(2)见解析;(3) 300人【解题分析】（1）由了解很少的有30人，占50%，可求得接受问卷调查的学生数，继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角；（2）由（1）可求得了解的人数，继而补全条形统计图；（3）利用样本估计总体的方法，即可求得答案．【题目详解】解：（1）∵了解很少的有30人，占50%，∴接受问卷调查的学生共有：30÷50%=60（人）；∴扇形统计图中“基本了解”部分所对应扇形的圆心角为：1560×360°=90°； 故答案为60，90；（2）60﹣15﹣30﹣10=5；补全条形统计图得：（3）根据题意得：900×15560+=300（人）， 则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人．【题目点拨】本题考查了条形统计图与扇形统计图，解题的关键是熟练的掌握条形统计图与扇形统计图的相关知识点.18、（1）12y x = ，y=2x ﹣1；（2）133,42M ⎛⎫ ⎪⎝⎭. 【解题分析】（1）利用待定系数法即可解答；（2）作MD ⊥y 轴,交y 轴于点D ，设点M 的坐标为（x ，2x-1），根据MB=MC ，得到CD=BD,再列方程可求得x 的值，得到点M 的坐标【题目详解】解：（1）把点A （4，3）代入函数a =y x 得：a=3×4=12， ∴12y x=． ∵A （4，3）∴OA=1，∵OA=OB ，∴OB=1，∴点B 的坐标为（0，﹣1）把B （0，﹣1），A （4，3）代入y=kx+b 得：∴y=2x﹣1．（2）作MD⊥y轴于点D.∵点M在一次函数y=2x﹣1上，∴设点M的坐标为（x，2x﹣1）则点D（0，2x-1）∵MB=MC，∴CD=BD∴8-(2x-1)=2x-1+1解得：x=13 4∴2x﹣1=32,∴点M的坐标为133,42⎛⎫ ⎪⎝⎭.【题目点拨】本题考查了一次函数与反比例函数的交点，解决本题的关键是利用待定系数法求解析式．19、不公平【解题分析】【分析】列表得到所有情况，然后找出数字之和是3的倍数的情况，利用概率公式计算后进行判断即可得. 【题目详解】根据题意列表如下：1 2 3 11 （1，1）（2，1）（3，1）（1，1）2 （1，2）（2，2）（3，2）（1，2）3 （1，3）（2，3）（3，3）（1，3）1 （1，1）（2，1）（3，1）（1，1）所有等可能的情况数有16种，其中两次摸出的纸牌上数字之和是3的倍数的情况有：（2，1），（1，2），（1，2），（3，3），（2，1），共5种，∴P （甲获胜）=516，P （乙获胜）=1﹣516=1116， 则该游戏不公平．【题目点拨】本题考查了列表法或树状图法求概率，判断游戏的公平性，用到的知识点为：概率=所求情况数与总情况数之比．20、（1）＞，＞；（2）214433y x x =--；（3）E （4，﹣4）或（227，4）或（227，4）． 【解题分析】（1）由抛物线开口向上，且与x 轴有两个交点，即可做出判断；（2）根据抛物线的对称轴及A 的坐标，确定出B 的坐标，将A ，B ，C 三点坐标代入求出a ，b ，c 的值，即可确定出抛物线解析式；（3）存在，分两种情况讨论：（i ）假设存在点E 使得以A ，C ，E ，F 为顶点所组成的四边形是平行四边形，过点C 作CE ∥x 轴，交抛物线于点E ，过点E 作EF ∥AC ，交x 轴于点F ，如图1所示；（ii ）假设在抛物线上还存在点E′，使得以A ，C ，F′，E′为顶点所组成的四边形是平行四边形，过点E′作E′F′∥AC 交x 轴于点F′，则四边形ACF′E′即为满足条件的平行四边形，可得AC=E′F′，AC ∥E′F′，如图2，过点E′作E′G ⊥x 轴于点G ，分别求出E 坐标即可．【题目详解】（1）a ＞0，＞0； （2）∵直线x=2是对称轴，A （﹣2，0），∴B （6，0），∵点C （0，﹣4），将A ，B ，C 的坐标分别代入2y ax bx c =++，解得：13a =，43b =-，4c =-， ∴抛物线的函数表达式为214433y x x =--； （3）存在，理由为：（i ）假设存在点E 使得以A ，C ，E ，F 为顶点所组成的四边形是平行四边形，过点C 作CE ∥x 轴，交抛物线于点E ，过点E 作EF ∥AC ，交x 轴于点F ，如图1所示，则四边形ACEF 即为满足条件的平行四边形， ∵抛物线214433y x x =--关于直线x=2对称， ∴由抛物线的对称性可知，E 点的横坐标为4，又∵OC=4，∴E 的纵坐标为﹣4，∴存在点E （4，﹣4）；（ii ）假设在抛物线上还存在点E′，使得以A ，C ，F′，E′为顶点所组成的四边形是平行四边形，过点E′作E′F′∥AC 交x 轴于点F′，则四边形ACF′E′即为满足条件的平行四边形，∴AC=E′F′，AC ∥E′F′，如图2，过点E′作E′G ⊥x 轴于点G ，∵AC ∥E′F′，∴∠CAO=∠E′F′G ，又∵∠COA=∠E′GF′=90°，AC=E′F′，∴△CAO ≌△E′F′G ，∴E′G=CO=4，∴点E′的纵坐标是4，∴2144433x x =--，解得：1227x =+，2227x =-， ∴点E′的坐标为（227，4），同理可得点E″的坐标为（227，4）．21、（1）见解析（2）见解析【解题分析】（1）根据旋转变换的定义和性质求解可得；（2）根据位似变换的定义和性质求解可得．【题目详解】解：（1）如图所示，△A1B1C1即为所求；（2）如图所示，△DEF即为所求．【题目点拨】本题主要考查作图﹣位似变换与旋转变换，解题的关键是掌握位似变换与旋转变换的定义与性质．22、建筑物AB的高度约为30.3m．【解题分析】分析：过点D作DE⊥AB，利用解直角三角形的计算解答即可．详解：如图，根据题意，BC=2，∠DCB=90°，∠ABC=90°．过点D作DE⊥AB，垂足为E，则∠DEB=90°，∠ADE=30°，∠BDE=10°，可得四边形DCBE为矩形，∴DE=BC=2．在Rt△ADE中，tan∠ADE=AE DE，∴AE=DE•tan30°=34040 1.73223.0933⨯=⨯≈．在Rt△DEB中，tan∠BDE=BE DE，∴BE=DE•tan10°=2×0.18=7.2，∴AB=AE+BE=23.09+7.2=30.29≈30.3．答：建筑物AB的高度约为30.3m．点睛：考查解直角三角形的应用﹣仰角俯角问题，要求学生能借助俯角构造直角三角形并解直角三角形．23、解：（1）10，50；（2）解法一（树状图）：从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此P（不低于30元）=82 123；解法二（列表法）：（以下过程同“解法一”）【解题分析】试题分析：（1）由在一个不透明的箱子里放有4个相同的小球，球上分别标有“0”元，“10”元，“20”元和“30”元的字样，规定：顾客在本商场同一日内，每消费满200元，就可以再箱子里先后摸出两个球（第一次摸出后不放回）．即可求得答案；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与顾客所获得购物券的金额不低于30元的情况，再利用概率公式求解即可求得答案．试题解析：(1)10，50；(2)解法一(树状图)：,从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此P(不低于30元)＝812＝23；解法二(列表法)：0 10 20 300 ﹣﹣10 20 3010 10 ﹣﹣30 4020 20 30 ﹣﹣5030 30 40 50 ﹣﹣从上表可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此P(不低于30元)＝812＝23；考点：列表法与树状图法.【题目详解】请在此输入详解！24、（1）2，3，5（1）①AD=5；②P（0，1）或（0，2）．【解题分析】（1）先确定出OA=3，OC=2，进而得出AB=2，BC=3，利用勾股定理即可得出AC；（1）A．①利用折叠的性质得出BD=2﹣AD，最后用勾股定理即可得出结论；②分三种情况利用方程的思想即可得出结论；B．①利用折叠的性质得出AE，利用勾股定理即可得出结论；②先判断出∠APC=90°，再分情况讨论计算即可．【题目详解】解：（1）∵一次函数y=﹣1x+2的图象与x轴，y轴分别交于点A，点C，∴A（3，0），C（0，2），∴OA=3，OC=2．∵AB⊥x轴，CB⊥y轴，∠AOC=90°，∴四边形OABC是矩形，∴AB=OC=2，BC=OA=3．在Rt△ABC中，根据勾股定理得，AC故答案为2，3，（1）选A．①由（1）知，BC=3，AB=2，由折叠知，CD=AD．在Rt△BCD中，BD=AB﹣AD=2﹣AD，根据勾股定理得，CD1=BC1+BD1，即：AD1=16+（2﹣AD）1，∴AD=5；②由①知，D（3，5），设P（0，y）．∵A（3，0），∴AP1=16+y1，DP1=16+（y﹣5）1．∵△APD为等腰三角形，∴分三种情况讨论：Ⅰ、AP=AD，∴16+y1=15，∴y=±3，∴P（0，3）或（0，﹣3）；Ⅱ、AP=DP，∴16+y1=16+（y﹣5）1，∴y=52，∴P（0，52）；Ⅲ、AD=DP，15=16+（y﹣5）1，∴y=1或2，∴P（0，1）或（0，2）．综上所述：P （0，3）或（0，﹣3）或P （0，52）或P （0，1）或（0，2）．选B ．①由A ①知，AD =5，由折叠知，AE =12AC DE ⊥AC 于E ．在Rt △ADE 中，DE②∵以点A ，P ，C 为顶点的三角形与△ABC 全等，∴△APC ≌△ABC ，或△CPA ≌△ABC ，∴∠APC =∠ABC =90°．∵四边形OABC 是矩形，∴△ACO ≌△CAB ，此时，符合条件，点P 和点O 重合，即：P （0，0）；如图3，过点O 作ON ⊥AC 于N ，易证，△AON ∽△ACO ， ∴AN OA OA AC=， ∴4AN =，∴AN =5， 过点N 作NH ⊥OA ，∴NH ∥OA ，∴△ANH ∽△ACO ， ∴AN NH AH AC OC OA==，∴84NH AH ==， ∴NH =85，AH =45， ∴OH =165， ∴N （16855，）， 而点P 1与点O 关于AC 对称，∴P 1（321655，），同理：点B关于AC的对称点P1，同上的方法得，P1（﹣122455，）．综上所述：满足条件的点P的坐标为：（0，0），（321655，），（﹣122455，）．【题目点拨】本题是一次函数综合题，主要考查了矩形的性质和判定，相似三角形的判定和性质，勾股定理，折叠的性质，对称的性质，解（1）的关键是求出AC，解（1）的关键是利用分类讨论的思想解决问题．。

{2019年哈尔滨市初中升学考试模拟试题（一）数学试卷参考答案二、11、2.019×109 12、 -2 2 13、x ≠32 14、4a （x-2y ）215、x>3 16、（0，22） 17、6 2 18、16 19、36或72 20、2511（提示：如图过点C 作CM ⊥FB 于点M ，过点D 作DN ⊥EC 于点N ，△CMB≌△DNC △END ≌△FMC 再勾股可求）21．化简结果-)3a (21+--------------------------------3a =tan60°-6sin30°= 3 -2-------------------------------2 原式= -16 3 --------------------------------222．(1)图形正确------------------------------------3（2）图形正确----------------------------------2AF=17 -----------223、 解:(1)40;----------------------------------------------1答---------------------------------------------------------------------1(2)40%-------------------------------------------2答---------------------------------------------------------------------1（3）170----------------------------------------2 答-----------------------------------124、（1）略---------------------------------------------4（2）△FAE △ADO △D 、OC △FEC-----------------------------------425、解：（1）设购进甲种灯x 只，乙为y 只由题意得：25x+45y=46000x+y=1200 ---------------------------------------------------------------------2解得： x=400 y=800----------------------------------------------------------------------------2 答：--------------------------------------------------------------------------------------------1（2）设每支笔售价为m 元，根据题意得：5m+15（ 1200-m ）≤［25m+45（1200-m ）］×30%----------------------------------------------2 解得：m ≥450---------------------------------------------------------------------------------------------2 答：．-----------------------------------------------------------------------------------------------------1 NM26．（1）连接AD 、AB∵CD 为⊙O 直径 ∴∠CAD=90°设∠DCA 为α，则∠CDA=90°-α∵∠D 与∠B 同对弧AC ∴∠D=∠B=90°-α-------------------------------1 ∵点A 为弧BAC 中点，∴弧AB=弧AC∴AB=AC ∴∠ACB=∠B=90°-α-----------------------------------1 ∵AF ⊥CD ∴∠CAE=90°-α∴∠CAE=∠ECA=90°-α∴EA=EC--------------------------------------------------------------1（2）连接OA∵EC=EA EO=EO OC=OA∴△EOC ≌△EOA --------------------------------------------------1∴∠CEO=∠AEO∵EC=EA∴CG ＝AG----------------------------------------------------------------1在Rt △FCA 中，FG 为斜边中线∴AC ＝２FG--------------------------------------------------------------1（3）连接AD 、AB 过F 作FH ⊥AC 于点H由（2）可知EC=EA ∠CEO=∠AEO∴EG ⊥AC ∴∠EGA=90°∵FH ⊥AC ∴∠FHA=90°∴∠EGA=∠FHA ∴EG ∥FH ∴∠FGE=∠GFH∵sin ∠FGE ＝13 ∴sin ∠GFH ＝13 ---------------------------1设GH ＝a 则GF=3a 勾股得FH=2 2 a由（2）可知CG=AG=3a ∴AG=2a∴tan ∠FAG= 2易证∠D=∠FAG∴tan ∠D=AF DF = 2∴AF=2 2 ----------------------------------------------------1∴tan ∠FAG=CF AF ∴CF=4易求AG=CG= 6∵tan ∠FAG=FG AG = 2 ∴EG=2 3 -------------------------------1S 四边形ECGF =S △ACE -S △AFG =4 2 ---------------------------------------------------127.（1）tan ∠BAO=12------------------------------------------------2 (2) 在OA 的延长线上截取AM=AC 则∠AMC=∠ACM=12 ∠OAC∵∠OAC=2∠BAO ∴∠BAO=∠AMC∴tan ∠AMC= tan ∠BAO=12 ————————————1设OC=m 则OM=2m AM=2m-3在Rt △AOC 中，由勾股定理得m=4∴C （4，0）---------------------------------------------------------1 设直线AC 解析式为y=kx+b将A （0，-3）C （4，0）代入得AC 解析式y=34 x-3--------------------------------------------------------------1（3）过点D 作DN ⊥y 轴于点N ，过点E 作EK ⊥AC 于点K ∵直线y=kx 平行于直线AB∴k=2∴直线OD 解析式为y=2x------------------------------1 导角可得∠DAN=∠EAK∴△DAN ≌△ AK∴DN=EK AN=AK-----------------------------------1tan ∠KCE=tan ∠ACO=34设EK=3a 则CK=4a AK=4a+5∴DN=EK=3a ON=AK-OA=4a+2∴D （-3a ，4a+2）-------------------------------------1将点D 代八直线y=2x得D （-3，6）------------------------------------------1解△AEK 可得∠DEA=45°--------------------------------------------1。

哈尔滨第六十九中学2019年初三12月抽考数学试题【一】选择题〔每题3分，共30分〕 1、以下运算正确旳选项是〔〕A.55-=-B.1)32(0=- C.612131=- D.1)1(3=-2、以下计算正确旳选项是〔〕A 、xy y x 532=+ B.44x x x =⋅ C.428x x x =÷ D.3632)(y x y x = 3、用科学记数法表示5320000正确旳选项是〔〕A 、5.32610⨯ B.5.32510⨯ C.532410⨯ D.0.532710⨯ 4、以下图形中是中心对称图形，但不是轴对称图形旳是()5、如下图旳几何体是由一些正方体组合而成旳立体图形，那么那个几何体旳俯视图是()、反比例函数xm y 1-=旳图像6、在第【一】三象限，那么m 旳取值范围是〔〕 A 、m ≥1B.m ≤1C.1>m D.1<m7、如图、将ABC ∆绕着点C 按顺时针方向旋转o20，B 点落在'B 位置，点A 落在'A 位置，假设'A C AB ⊥.那么C A B ''∠旳度数是〔〕A.︒50B.︒60C.︒70D.︒808、如图，⊙O 中∠ABC=︒45，那么∠AOC 等于〔〕 A.︒55 B.︒80 C.︒90 D.︒1359、如图，AB 为⊙O 旳直径,AB=4，点C 在⊙O 上，那么扇形ACB 旳面积是〔〕 A.πB.π2 C.π4 D.π2310、甲、乙两个工程队分别同时开挖两段河渠，所挖河渠旳长度y(米)与挖掘时刻x 〔小时〕之间旳关系如下图，请依照图像推断以下信息正确旳有〔〕①乙队开挖到30米，用了2小时。

②开挖6小时甲队比乙队多挖了10米。

③甲队在0≤x ≤6旳时段内，y 与x 旳函数关系式为y=101x.④当x=4时，甲乙两队在施工过程中所挖河渠旳长度相等。

A.1个B.2个C.3个D.4个B'A'CBACOABCBOAy x 6/时件乙甲6050302O7题图8题图9题图10题图【二】填空题〔每题3分，共30分〕 11、计算：3812-=﹏﹏﹏﹏﹏﹏﹏ 12、因式分解：2333ab a -=﹏﹏﹏﹏﹏﹏﹏﹏13、如图，在△ABC 中，∠ABC 和∠ACB 旳平分线交于点O ，过点O 作EF ∥BC ，交AB 于E 。

哈六十九中学2019届毕业学年校内模拟测试（一）数学试卷一、选择题(每小题3分，共计30分)1．下列实数中，无理数是（）.（A）﹣（B）π(C)(D)|﹣2|2.下列计算正确的是( )(A)2a+3a=6a (B) a2+a3=a5 (C) a8÷a2=a6 (D) (a3)4= a7 3．下列图形中，是中心对称图形但不是轴对称图形的是( )（A）（B）（C）（D）4．若反比例函数y=xk的图象经过点(-2，-5)，则该函数图象位于( ).(A) 第一、二象限(B)第二、四象限(C)第一、三象限(D)第三、四象限5.下面的几何体中，主视图为三角形的是().（A）（B）（C）（D）6.如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．则∠ABD的度数是（）.（A）30°（B）25°（C）20°（D）15°7.如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD∶AB=3∶4，AE=6，则AC等于( ).(A)3 (B)4 (C)6 (D) 88.如图，把△0AB绕点0逆时针旋转80°,到△OCD的位置，若∠AOB=45°，则∠AOD等于( )．（A）35°（B）90°（C）45°（D）50°9.某农场2016年蔬菜产量为50吨,2018年蔬菜产量为60.5吨,该农场蔬菜产量的年平均增长率相同.设该农场蔬菜产量的年平均增长率为x,则根据题意可列方程为( )(A)50)1(5.602=-x（B）5.60)1(502=-x（C）5.60)1(502=+x（D）50)1(5.602=+x10．如图，已知点D、E分别在ΔABC的边AB、AC上，DE∥BC,点F在CD延长线上，AF∥BC,则下列结论错误的是( ).（A）BCAFAFDE=（B）ECDCAEFD=（C）ACAEABAD=（D）AFDEABBD=（第6题图）（7题图）二、填空题：（每小题3分，共计30分）11．将2 500 000用科学记数法表示为_______________. 12.在函数21+-=x x y 中，自变量x 的取值范围是________.13．计算16=_______. 14．不等式组21318x x -≥-⎧⎨->⎩的解集为________.15.因式分解：22x 4y -=________16. 已知扇形半径是9cm ，弧长为4πcm ，则扇形的圆心角为________度17．布袋中装有2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出两个球，摸出的球都是白球的概率是________. 18.如图，正方形ABCD 的四个顶点分别在⊙O 上，点P 在CD 上不同于点C 的任意一点，则∠D PC 的度数是_______度．19．矩形ABCD 中，AC 的中垂线交直线BC 于点E ，交直线AB 于点F ，若AB=4，BE=3，则BF 的长为 ．20． 如图，四边形ABCD 中，CD =AD ，∠CDA=∠ABD=90°，AB =2，，则BD =________. 三、解答题（21、24题各7分，23、24题各8分，25—27题各10分，共计60分）21.（本题7分）先化简，再求值(1-2x 3+)÷2x -1x 2+的值，其中x=4sin45°-2cos60°22.（本题7分）如图，在8×5的正方形网格中，每个小正方形的边长均为1，△ABC 的三个顶点均(1)、在图1中画一个△ABD(点D 在小正方形的顶点上)，使△ABD 的周长等于△ABC 的周长，且以A 、B 、C 、D(2)、在图2中画△ABE(点E 在小正方形的顶点上)，使△ABE 的周长等于△ABC 的周长，且以A 、B 、C 、E 为顶点的四边形是中心对称图形； (3)、直接写出图2中四边形的面积.第18题图第20题图23. (本题8分)哈69中学为了组织一次球类对抗赛，在本校随机抽取了若干名学生，对他们每人最喜欢的一项球类运动进行了统计，将调查结果整理后绘制成如图所示的不完整的统计图。