Planck和Rayleigh-Jeans黑体辐射公式的推导
- 格式:doc
- 大小:144.50 KB
- 文档页数:5
所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态: 处于某一温度 T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
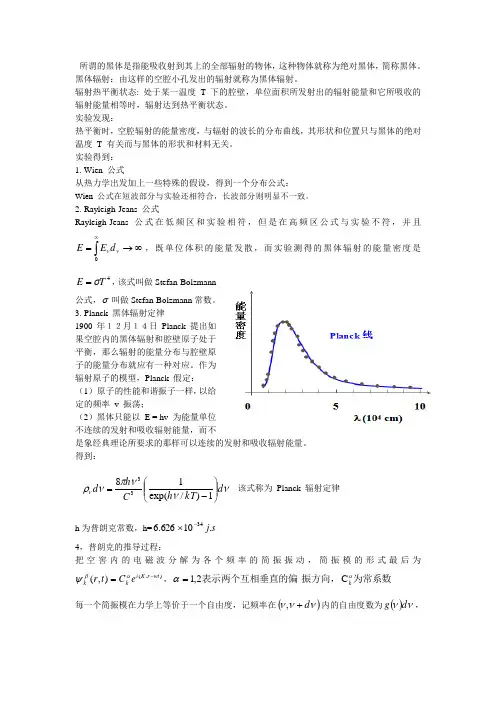
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度 T 有关而与黑体的形状和材料无关。
实验得到: 1. Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定: (1)原子的性能和谐振子一样,以给定的频率 v 振荡;(2)黑体只能以 E = hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为 Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g ,则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。
普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态:处于某一温度T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
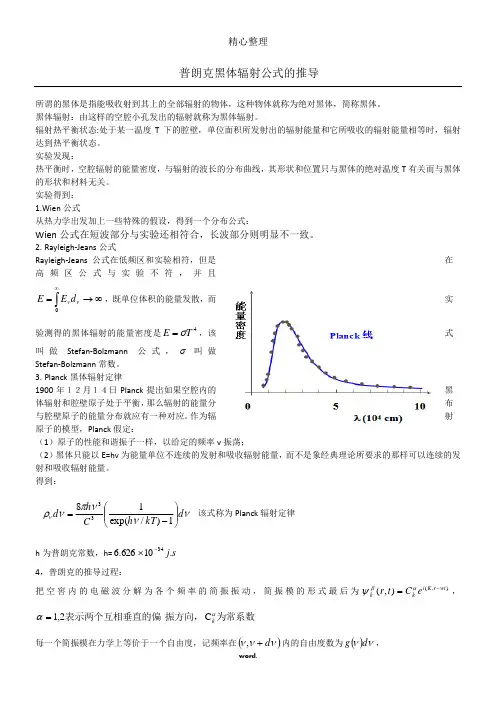
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。
实验得到: 1.Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann 公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率v 振荡; (2)黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g ,则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。
欢迎阅读普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态:处于某一温度T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
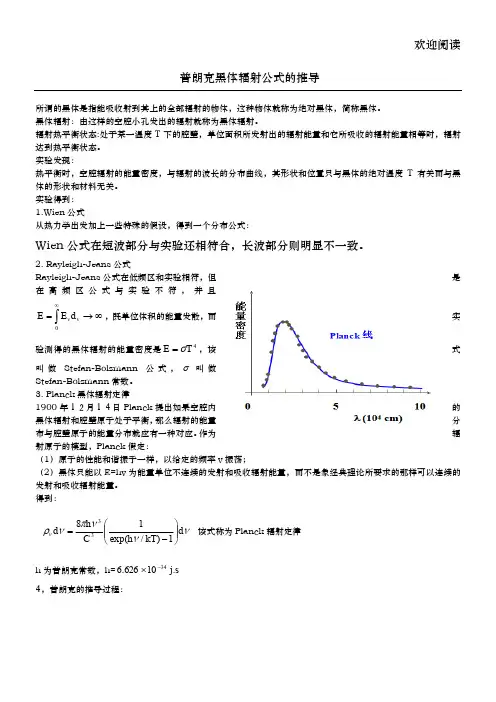
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。
实验得到: 1.Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann 公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率v 振荡;(2)黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g , 则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。

普朗克和瑞利-金斯黑体辐射公式的推导1 引言马克斯·普朗克于1900年建立了黑体辐射定律的公式,并于1901年发表。
其目的是改进由威廉·维恩提出的维恩近似(至于描述黑体辐射的另一公式:由瑞利勋爵和金斯爵士提出的瑞利-金斯定律,其建立时间要稍晚于普朗克定律。
由此可见瑞利-金斯公式所导致的“紫外灾难”并不是普朗克建立黑体辐射定律的动机)。
维恩近似在短波范围内和实验数据相当符合,但在长波范围内偏差较大;而瑞利-金斯公式则正好相反。
普朗克得到的公式则在全波段范围内都和实验结果符合得相当好。
在推导过程中,普朗克考虑将电磁场的能量按照物质中带电振子的不同振动模式分布。
得到普朗克公式的前提假设是这些振子的能量只能取某些基本能量单位的整数倍,这些基本能量单位只与电磁波的频率有关,并且和频率成正比。
这即是普朗克的能量量子化假说,这一假说的提出比爱因斯坦为解释光电效应而提出的光子概念还要至少早五年。
然而普朗克并没有像爱因斯坦那样假设电磁波本身即是具有分立能量的量子化的波束,他认为这种量子化只不过是对于处在封闭区域所形成的腔(也就是构成物质的原子)内的微小振子而言的,用半经典的语言来说就是束缚态必然导出量子化。
普朗克没能为这一量子化假设给出更多的物理解释,他只是相信这是一种数学上的推导手段,从而能够使理论和经验上的实验数据在全波段范围内符合。
不过最终普朗克的量子化假说和爱因斯坦的光子假说都成为了量子力学的基石。
2 公式推导2.1 普朗克公式和瑞利-金斯公式的推导黑体是指在任何温度下,对于各种波长的电磁辐射的吸收系数恒等于1的物体。
黑体辐射的能量是由电磁场的本征振动引起的,为简化推导过程,在此将黑体简化为边长为L 的正方形谐振腔。
则腔内的电磁场满足亥姆霍兹方程: 2222u+k u 0 (k )ωμε∇== (1) 用分离变量法,令u(x,y,z)X(x)Y(y)Z(z)=则(1)式可分解为三个方程:222222222000x y z d X k X dx d Y k Y dyd Z k Z dz⎧+=⎪⎪⎪+=⎨⎪⎪+=⎪⎩ 其中2222x y zk k k ωμε++= 得(1)式的驻波解为:112233(,,)(cos sin )(cos sin )(cos sin )x x y y z z u x y z c k x d k x c k y d k y c k z d k z =+++由在x=0,x=L,y=0,y=L,z=0,z=L 上的边界条件0n E n∂=∂及0D E ⋅=可得:123cos sin sin sin cos sin sin sin cos x x y z y x y z z x y z E A k x k y k z E A k x k y k zE A k x k y k z⎧=⎪=⎨⎪=⎩ x x k n L π=,y y k n L π=,z z k n L π= ,,0,1,2,x y z n n n= (其中1A ,2A ,3A 满足关系1230x y z k A k A k A ++=)则j k (j 表示第j 个本征态)的绝对值为: 2222222()()()j x y z j k n n n n L Lππ=++= 换成第j 个本征态的频率得:222()2j j c n Lν= 当j L λ>>时,j λ和j ν可视为连续变化,不必取分立值,即有: 222()2c n Lν= (2) (2)式表明在整数n 空间一组整数,,x y z n n n 即对应一个本征模的频率。

瑞恩-金斯黑体辐射公式的推导摘要:一、引言二、瑞恩-金斯黑体辐射公式的基本原理1.普朗克辐射定律2.斯特藩-玻尔兹曼定律3.瑞恩-金斯公式与黑体辐射的关系三、瑞恩-金斯黑体辐射公式的推导过程1.瑞恩公式2.金斯公式3.合并推导四、公式应用与实例1.黑体辐射强度计算2.实际应用场景五、结论与展望正文:一、引言瑞恩-金斯黑体辐射公式是描述黑体辐射强度与温度、波长之间关系的重要公式。
它是由英国物理学家瑞恩(Ryan)和金斯(Jeans)在20世纪初独立发现的。
本文将简要介绍瑞恩-金斯黑体辐射公式的基本原理,并详细推导公式,最后探讨其在实际应用场景中的作用。
二、瑞恩-金斯黑体辐射公式的基本原理1.普朗克辐射定律普朗克辐射定律指出,物体发出的辐射强度与物体的温度成正比,与波长成反比。
公式表示为:I = ελ^(-5/2),其中I为辐射强度,ε为黑体辐射系数,λ为波长。
2.斯特藩-玻尔兹曼定律斯特藩-玻尔兹曼定律描述了一个物体发出的总辐射功率与物体的温度、表面积和表面辐射率的关系。
公式表示为:P = εσAλ^(-4),其中P为辐射功率,σ为斯特藩-玻尔兹曼常数,A为物体表面积,ε为黑体辐射系数,λ为波长。
3.瑞恩-金斯公式与黑体辐射的关系瑞恩和金斯分别对斯特藩-玻尔兹曼定律进行了修正,得到了瑞恩公式和金斯公式。
瑞恩公式为:I = ελ^(-1) * (1 - 2λ/πd)^(-2),金斯公式为:I =ελ^(-1) * (1 - 2λ/πd)^(-2) * e^(-βλ),其中d为黑体厚度,β为黑体辐射衰减系数。
三、瑞恩-金斯黑体辐射公式的推导过程1.瑞恩公式瑞恩公式是对斯特藩-玻尔兹曼定律的修正,考虑了黑体内部辐射的叠加效应。
通过对斯特藩-玻尔兹曼定律进行修正,得到了瑞恩公式。
2.金斯公式金斯公式是在瑞恩公式的基础上,引入了黑体辐射衰减系数β。
通过对瑞恩公式进行修正,得到了金斯公式。
3.合并推导将瑞恩公式和金斯公式进行合并,可以得到一个更加通用的黑体辐射公式。

黑体辐射定律的基本理论及公式推导1.引言所谓黑体,就是对什么光都吸收而无反射也无透射的物体。
黑体在现实中是不存在的,就像质点,刚体,电偶极子等物理概念一样是一个理想化的物理模型。
物理上可以用如图1所示的装置来模拟黑体。
耐火材料做成的物体内部挖空一部分区域,并且在物体一个面开一个非常的小孔,一旦光线射进小孔后,在空腔内壁经过多次吸收和反射,几乎完全被吸收掉,再跑出小孔的几率特别小,因此可以把空腔的小孔视为黑体的表面。
定义吸收本领(,)v T 为在频率附近,单位频率间隔内被物体吸收的辐射通量与照射在该物体上的辐射通量之比,则黑体的吸收本领(,)1v T 。
由于任何一个物体,当它的温度恒定时,它辐射的电磁波和吸收的电磁波达到平衡。
定义物体的辐射本领(,)R v T 为一个温度T 下物体单位表面积在单位时间内发射、频率在vv dv 内单位频率间隔的辐射能。
波长表示辐射本领R(λ,T)和频率表示的辐射本领(,)R v T 之间的关系为2(,)(,)/R T cR v T ,物体的辐射本领(,)R v T 和吸收本领(,)v T 及辐射场的谱能量密度之比为一普适常数,即1859年提出的基尔霍夫定律。
图 1-1 黑体的模拟(,)(,)(,)4R v T c Fv T v T (1-1)上式中c 为真空中的光速,该常数F 被证明等于(,)/4c v T 。
对黑体而言有(,)1v T ,黑体的辐射本领0(,)R v T 为0(,)(,)/4R v T Fc v T (1-2)(1-2)式意味着黑体的辐射本领(,)R v T 就等于基尔霍夫定律里面的普适常量。
因此黑体辐射的研究对于任何物体的热辐射规律具有重大的意义,其物理价值是不言而喻的。
2 普朗克黑体辐射定律公式及其推导2.1 普朗克公式普朗克假说:黑体是由带电的线性谐振子所组成,这些谐振子能量不能连续变化,只能取一些分立的值,这些分立值是最小能量的整数倍,即000,,2,3,,n,称为谐振子的能级。

黑体辐射能量密度公式推导无数的实验事实已经确定了热辐射是电磁波。
当电磁场与物体大道平衡时,电磁场的辐射能量完全由温度确定,而能量在各个频率的分布也完全确定。
我们只考虑电磁场的能量,不考虑电磁场与物体如何交换能量而达到平衡。
事实上,不论物体与电磁场交换能量的机制如何,达到平衡时电磁场的能量分布是完全确定的。
我们考虑电磁场处在一个空窖内,保持能量不变,因之能量不能穿过空窖的边界而辐射出去。
假如边界是由完全的导体做成的,则电场强度必与边界垂直。
根据波印廷(Poynting)定理,通过单位面积在单位时间内辐射的能量为(用高斯单位制),(1)其中c是光速,E和H是电场强度和磁场强度。
假如电磁场强度垂直于边界,则由公式(1)可以看出,能量辐射的方向将与边界平行而不能流出边界。
为了解决辐射能量分布于各个频率的问题,我们首先讨论如何把电磁波分解为各个频率的振动,这称为简正振动方式。
这种分解可以通过分离变数法解波动方程而求得。
在真空中麦克斯韦的电磁场方程组为(2)对于最后一个方程运用算符,注意下列恒等式,其中A为一任意矢量,得, (3) 再利用(2)中第一和第二两方程,化得, (4) 对于中第二方程运用算符,经过同上面一样的运算,得,(5)这两个方程(4)和(5)是波动微分方程,没一个都是矢量方程,包含有三个标量方程,共有六个方程。
这六个方程的形式全是一样的,即,(6)其中φ可以是E x, E y, E z, H x, H y, H z六个量中的任意一个。
为了可以用分离变数法解波动方程(6),我们假设辐射所存在的空窖的边界是由下列三对平面构成的:.空窖的体积是. (7)晋斯(Jeans)把(6)式中φ和的初值(即在t = 0时的值)用三重傅里叶级数展开,因而所得到的解分为各种频率的驻波形式。
我们现在讲把晋斯的证明稍加改变,用分离变数法求(6)式的解,并且不用电磁场强度而用矢势。
用矢势的好处是演算的过程可以简化一些。

Planck 和Rayleigh-Jeans 黑体辐射公式的推导 Made by 0310340 陶波 0310351郑启飞 0310337盛海翔 黑体是指在任何温度下,对于各种波长的电磁辐射的吸收系数恒等于1的物体黑体辐射的能量是由电磁场的本征振动引起的,为简化 推导过程,在此将黑体简化为边长为L 的正方形谐振腔。
如 图示:则腔内的电磁场满足亥姆霍兹方程:V 2u+k 2u = 0 (k 2 = ar用分离变量法,令 u(x,y,z) = X(x)Y(y)Z(z)则(1)式可分解为三个方程:d2Z 、dz 2 其中 疋+X+k 血得(i )式的驻波解为:d 2Xdx 2 + k ;X=O(1) + k ;Z =Ou{x. y. z) = (q cos k x x + d} sin k x x)(c2 cos k y y + d2 sin k y y) •(c3 cos k z z + d3 sin k z z)8E由在x=0,x=L,y=0,y=L,z=0,z=L 上的边界条件。
及D・E = 0可得:E x = A cos k x xsin k y y sin k z z< E y =爲sin geos k y y sin k z zE z= sin k x x sin k y cos k z zTC z 71k y =~n y , k z = —W z 力竹代=0 丄Z(其中A, 4,人满足关系任4 +心堆+=。
)则勺(j表示第j个本征态)的绝对值为:换成第j个本征态的频率得:当L»2.时,人和匕可视为连续变化,不必取分立值,即有:(2)(2)式表明在整数n空间一组整数g代即对应一个本征模的频率。
因此,频率区间V内的本征模数,在数值上等空间内数值半径由n^n+兀范围内球壳体积的(V 为腔的体积) 又因为每一个频率为V 的单色平面波还存在着两个独立的 相互垂直的偏振态,则频率间隔“内的本征模数为: dN(v) = ^^v 2dvc设^(T,v)表示温度为T,频率为V 的本征振动的平均能 量,P (T, V )为相应的能量密度,则振动频率在V 到v + dv 之间的能量为:0—1 7V p ⑴ v)dv = g(T, v)dN(v) = v 2£(T. v)dv 本征振动是简谐振动,由三维谐振子的能量本征值:3E n =(n + ^)hv (n =0, b 2…)系统处于热平衡状态时,处于各本征能量的谐振子分布遵从 麦克斯韦-波尔兹曼分布律:E即:N®xexp(—»)八分之一,即: dN(v) = 47rn 2p(T,v)dv = ^-v 2£(T^dv c (3)E工& exp(-芹) g(T\ v)=」 -F-所以: 工exp(-昱) V kT若令0冷,Z = ”exp(—0巴) 则⑷式可改写为:曲占3Z =工 exp(-0 E n ) =工 exp[-0 (n + -)hv] n n /3 =exp(——Zn/)工 exp (—〃 0/n/) 2 n3 exp(- —/zv)l_exp(_0/nz)贾T )/) =—丄必=—世—2亠科十 代入(3)式得:p(T 、v)dv =冬 V 2£(T. v)dv ='兀''vc此即为Planck 黑体辐射公式。

普朗克黑体辐射公式的详细推导普朗克假设黑体辐射是由一系列离散的微观振动体产生的,这些振动体能够吸收和释放以能量量子(hf)为单位的能量。
当这些振动体处于平衡状态时,设振动体的能量分布函数为Ψ(ε),其中ε表示振动体的能量。
考虑单位体积和单位能量范围内的振动体数目,记为N(ε)dε,其中N表示单位体积内振动体的总数。
根据统计力学的理论,N(ε)dε可表达为波尔兹曼分布,即:N(ε)dε = g(ε)exp(-ε/kBT)dε其中,g(ε)表示在特定能量范围内的能量态的数目,exp(-ε/kBT)是由玻尔兹曼因子得到,k是玻尔兹曼常数,T是温度。
由于辐射的能量不连续,因此,可以将单位体积和单位频率范围内的振动体数目表示为N(v)dv,其中v表示频率,dv表示频率范围。
考虑到能量和频率之间的关系,有ε = hv,其中h是普朗克常数。
根据可加性和幂次原理,能量态的数目g(ε)应满足:g(ε)dε=4π(2m/h^2)^(3/2)ε^(1/2)dε其中,m是振动体的质量。
将ε和dε用v和dv表示,并对能量态的数目函数进行简化得到:g(v)dv = (8πv^2/c^3)dv其中,c是光速。
由于单位体积和单位能量范围内的振动体数目与单位体积和单位频率范围内的振动体数目之间有关系:N(ε)dε = N(v)dv将上述得出的g(ε)和g(v)带入上式,并整理可得:N(v) = (8πv^2/c^3)exp(-hv/kBT)dv可以将上式转化为单位面积、单位时间、单位频率范围内的能量密度u(v):u(v) = N(v)hv代入上式并进行整理,得到:u(v) = (8πhv^3/c^3)exp(-hv/kBT)dv利用频率和波长的关系,即v=c/λ,可以将上式转化为以波长表示的能量密度:u(λ) = (8πhc/λ^5)exp(-hc/λkBT)dλ这就是普朗克黑体辐射公式的最终形式。
通过对普朗克黑体辐射公式的推导,我们可以看出,普朗克假设了黑体辐射的能量是以能量量子为单位的离散量,这个假设是量子力学发展的重要先导。

黑体辐射的普朗克公式推导普朗克公式描述了黑体辐射的能量分布。
为了推导普朗克公式,我们可以按照以下步骤进行。
首先,我们考虑一个处于热平衡状态的黑体辐射腔室。
由于电磁波是由光子组成的,我们可以将其视为一种粒子,具有能量E和频率ν的量子。
根据量子理论,光子的能量与其频率之间存在关系:E = hν,其中h是普朗克常数。
接下来,我们考虑在辐射腔室中的光子数目与能量之间的关系。
根据统计物理学中的玻尔兹曼分布定律,光子数目n与能量E之间满足以下关系:n(E) = (1 / (exp(E / (kT)) - 1)在这里,k是玻尔兹曼常数,T是绝对温度。
该公式描述了光子在不同能量级上的分布情况。
为了得到黑体辐射的能量分布,我们需要计算每个能量级上光子的平均能量。
因此,我们可以使用平均能量公式:<E> = Σ(n * E) / Σn其中,Σ表示对所有能量级求和。
我们将这个表达式应用到光子数目公式中,得到:<E> = Σ((E / (exp(E / (kT)) - 1)) / Σ(1 / (exp(E / (kT)) - 1))接下来,我们将求和转化为积分,以便对能量连续变化的情况进行处理。
通过引入积分变量x = E / (kT),我们可以将上述表达式重写为:<E> = ∫((x^3 / (exp(x) - 1)) / ∫(x^2 / (exp(x) - 1))这就是普朗克公式的推导过程。
最后,我们可以根据上述公式计算不同温度下黑体辐射的能量分布。
需要注意的是,上述推导过程涉及了一些复杂的数学运算和近似方法,包括积分转换、级数展开等。
因此,要完整地推导出普朗克公式需要更详细的数学推导。

普朗克黑体辐射公式的详细推导辐射是物体由于内部热运动而产生的电磁波。
普朗克假设黑体辐射是由许多振动的谐振子(即电磁振子)组成的,每个谐振子只能具有离散能量值。
普朗克假设这些能量是量子化的,即能量E只能取整数倍的基本能量hν,其中ν为辐射频率。
设一个振子的能量为E,频率为ν,则E=hν。
普朗克认为振子的能量只能取整数倍的基本能量hν,因此振子的能量只能是离散的。
假设在单位时间内,频率在ν到ν+dν范围内,能量在E到E+dE范围内的谐振子数为n(E,ν)。
则单位体积内频率在ν到ν+dν范围内,能量在E到E+dE范围内的谐振子数为:n(E,ν)dEdν为了求解n(E,ν),我们需要引入玻尔兹曼分布和玻尔兹曼常数k。
在热平衡状态下,系统中具有能量E的状况数(即相同的谐振子数)为:W(E)=n(E,ν)*e^(-E/kT)其中,T为系统的温度,n(E,ν)为单位体积内频率在ν到ν+dν范围内,能量在E到E+dE范围内的谐振子数。
根据统计物理学的理论,系统的熵S与状况数W的关系为:dS = k * ln W(E)将W(E)代入上式并对E求微分,我们可以得到:dS = k * [ d(n(E,ν)) - (E/kT) * dn(E,ν) ]根据熵的最大化原理,熵是关于能量的单调递增函数,即dS>=0,即有:d(n(E,ν)) - (E/kT) * dn(E,ν) >= 0 (式1)我们将式1两边对E积分,可得:∫(d(n(E,ν)) - (E/kT) * dn(E,ν)) = ∫0到E dn(E,ν) (式2)其中,积分区间为0到E。
对式2进行变换,得到:n(E,ν) - (∫0到E (E/kT) * dn(E,ν)) = ∫0到E dn(E,ν)整理后,我们可以得到:n(E,ν)=[∫0到E(1/e^(E/kT))]*n(E,ν)令x=E/(kT),则式子变为:n(E,ν)=[∫0到x(1/e^x)]*n(E,ν)通过计算可知,上式的积分结果为:∫0到x(1/e^x)=1-(1+x)e^(-x)将该结果代入n(E,ν)的表达式中,我们可以得到:n(E,ν)=(1-(1+x)e^(-x))*n(E,ν)(式3)进一步简化,我们可以得到:n(E,ν)=(1-(1+E/(kT))e^(-E/(kT)))*n(E,ν)(式4)根据统计物理学的经验公式,单位体积频率为ν到ν+dν范围内,能量为E到E+dE范围内的谐振子数n(E,ν)与能量E的关系为:n(E,ν)=C*E^3*1/(e^(E/(kT))-1)(式5)其中,C为常数。
普朗克黑体辐射公式的推导所谓的黑体是指能吸收射到其上的全部辐射的物体,这种物体就称为绝对黑体,简称黑体。
黑体辐射:由这样的空腔小孔发出的辐射就称为黑体辐射。
辐射热平衡状态:处于某一温度T 下的腔壁,单位面积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与黑体的绝对温度T 有关而与黑体的形状和材料无关。
实验得到: 1.Wien 公式从热力学出发加上一些特殊的假设,得到一个分布公式:Wien 公式在短波部分与实验还相符合,长波部分则明显不一致。
2. Rayleigh-Jeans 公式Rayleigh-Jeans 公式在低频区和实验相符,但是在高频区公式与实验不符,并且∞→=⎰∞v v d E E ,既单位体积的能量发散,而实验测得的黑体辐射的能量密度是4T E σ=,该式叫做Stefan-Bolzmann 公式,σ叫做Stefan-Bolzmann 常数。
3. Planck 黑体辐射定律1900年12月14日Planck 提出如果空腔内的黑体辐射和腔壁原子处于平衡,那么辐射的能量分布与腔壁原子的能量分布就应有一种对应。
作为辐射原子的模型,Planck 假定:(1)原子的性能和谐振子一样,以给定的频率v 振荡; (2)黑体只能以E=hv 为能量单位不连续的发射和吸收辐射能量,而不是象经典理论所要求的那样可以连续的发射和吸收辐射能量。
得到:νννπνρνd kT h C h d ⎪⎪⎭⎫ ⎝⎛-=1)/exp(1833该式称为Planck 辐射定律 h 为普朗克常数,h=s j .10626.634-⨯4,普朗克的推导过程:把空窖内的电磁波分解为各个频率的简振振动,简振模的形式最后为).(),(wt r K i k k e C t r -=αβψ,为常系数振方向,表示两个互相垂直的偏ααk C 2,1=每一个简振模在力学上等价于一个自由度,记频率在()νννd +,内的自由度数为()ννd g ,则(0,v )范围内的总自由度数G(v)与g(v)的关系为()()ννννd g G ⎰=0。
普朗克公式推导瑞利金斯公式引言当人们研究物质的辐射现象时,发现黑体辐射的能量分布并不符合经典物理学的预期。
为了解释这一现象,德国物理学家马克斯·普朗克于1900年提出了普朗克公式。
普朗克公式解释了黑体辐射的能量分布,并奠定了量子理论的基础。
瑞利金斯公式则是由英国物理学家雷利和金斯利在1905年提出的,它用于描述物质微粒经过散射后的能量分布。
本文将从普朗克公式出发,推导瑞利金斯公式。
普朗克公式普朗克公式可以用来描述在特定温度下黑体辐射的能量密度分布。
该公式的表达式为:E(λ,T) = (2hc²/λ⁵) / (exp(hc/λkT) - 1)其中,E(λ,T)表示黑体辐射在波长为λ时的能量密度,T表示温度,h为普朗克常数,c为光速,k为波尔兹曼常数。
瑞利金斯公式瑞利金斯公式用于描述散射后的光的能量分布。
该公式的表达式为:I(θ) = I₀(cos(θ))²其中,I(θ)表示经过散射后的光的强度分布。
θ表示散射光与初始光的夹角。
从普朗克公式到瑞利金斯公式的推导过程为了推导瑞利金斯公式,我们需要从普朗克公式出发。
我们以散射光的波长为λ’,初始光的波长为λ,散射角为θ,初始光的能量密度为E(λ,T)。
我们要求出经过散射后的光的能量密度E’(λ’,T’)。
首先,考虑散射光在单位面积上的散射体积。
我们设单位时间内单位面积上散射出去的光子数为dN,其表达式为:dN = σnI(θ)dAdt其中,σ表示散射截面面积,n表示单位体积内散射颗粒数目,I(θ)表示初始光的强度分布,dA表示单位面积,dt表示时间间隔。
根据瑞利金斯公式的描述,散射后的光的强度分布与θ有关,可以用I(θ)表示。
因此,我们可以将上式改写为:dN = σnI(θ)dΩdt其中,dΩ表示立体角元素。
根据光学中的基本关系,散射角θ和波长λ’与初始光的波长λ之间存在关系:cos(θ) = (λ - λ’)/λ则我们可以将散射光的波长λ’表示为:λ’ = (λ - cos(θ)λ)接下来,我们要求出散射光的能量密度。
普朗克黑体辐射公式推导普朗克黑体辐射公式是描述黑体辐射谱的一个重要公式,由德国物理学家马克斯·普朗克于公元1900年推导得出。
这个公式在量子力学的起源和发展中起到了重要的作用,被称为“普朗克的奇迹”。
下面我们将对普朗克黑体辐射公式进行推导。
首先,我们需要了解什么是黑体辐射。
黑体是指一个能将所有传入它的辐射吸收完全,并能以最大限度地辐射出来的理想物体。
黑体辐射谱指的是黑体在不同波长上辐射的强度分布特性。
普朗克的推导基于两个假设。
第一,电磁辐射是由许多具有不同能量的微观振动子组成的。
第二,这些微观振动子的能量是量子化的,即只能取离散的特定值。
根据热力学理论,一个谐振子在频率ω上分布的能量是由玻尔兹曼分布给出的:n(ω) = (1 / (exp(ħω / kT) - 1)其中n(ω)是单位体积中在频率ω上的振动子数,ħ是普朗克常量除以2π,k是玻尔兹曼常量,T是温度。
一个谐振子的能量为ħω,所以单位体积中在频率ω上的能量分布就是n(ω)乘以该能量:E(ω)=ħω*n(ω)现在我们将微观振动子的能量与频率进行积分,得到所有振动子的能量。
积分的范围从零到无穷大,对于每一个能量级别ΔE,能量能取的频率范围是(ΔE-ΔE+δΔE),其中δΔE是能量级别间的间隔。
我们有:E(ΔE)=∫(ΔE-ΔE+δΔE)E(ω)dω代入E(ω)的表达式:E(ΔE)=∫(ΔE-ΔE+δΔE)ħω*n(ω)dω然后将n(ω)的表达式代入:E(ΔE) = ∫(ΔE-ΔE+δΔE) ħω * (1 / (exp(ħω / kT) - 1)) dω接下来,我们通过变换积分变量,将积分变为更简洁的形式。
令x=ħω/(kT),代入上式:E(ΔE) = (kT)^4 / (ħ^3 c^2) ∫(ΔE-ΔE+δΔE) x^3 / (exp(x) - 1) dx右边的积分是一个标准的积分,可以通过数值计算或查表得到。
下面我们将这个积分表示为一个函数f(x)。
黑体辐射力计算公式普朗克辐射定律(Planck)则给出了黑体辐射的具体谱分布,在一定温度下,单位面积的黑体在单位时间、单位立体角内和单位波长间隔内辐射出的能量为B(λ,T)=2hc2 /λ5 ·1/exp(hc/λRT)-1B(λ,T)—黑体的光谱辐射亮度(W,m-2 ,Sr-1 ,μm-1 ) λ—辐射波长(μm)T—黑体绝对温度(K、T=t+273k)C—光速(2.998×108 m·s-1 )h—普朗克常数,6.626×10-34 J·SK—波尔兹曼常数(Bolfzmann),1.380×10-23 J·K-1 基本物理常数由图2.2可以看出:①在一定温度下,黑体的谱辐射亮度存在一个极值,这个极值的位置与温度有关,这就是维恩位移定律(Wien)λm T=2.898×103 (μm·K)λm —最大黑体谱辐射亮度处的波长(μm)T—黑体的绝对温度(K)根据维恩定律,我们可以估算,当T~6000K时,λm ~0.48μm(绿色)。
这就是太阳辐射中大致的最大谱辐射亮度处。
当T~300K,λm~9.6μm,这就是地球物体辐射中大致最大谱辐射亮度处。
②在任一波长处,高温黑体的谱辐射亮度绝对大于低温黑体的谱辐射亮度,不论这个波长是否是光谱最大辐射亮度处。
如果把B(λ,T)对所有的波长积分,同时也对各个辐射方向积分,那么可得到斯特番—波耳兹曼定律(Stefan-Boltzmann),绝对温度为T的黑体单位面积在单位时间内向空间各方向辐射出的总能量为B(T)B(T)=δT4 (W·m-2 )δ为Stefan-Boltzmann常数, 等于5.67×10-8 W·m-2 ·K-4 但现实世界不存在这种理想的黑体,那么用什么来刻画这种差异呢?对任一波长,定义发射率为该波长的一个微小波长间隔内,真实物体的辐射能量与同温下的黑体的辐射能量之比。
普朗克黑体辐射公式推导步骤1:假设黑体内的辐射能量由一系列处于不同能级上的振子所组成。
考虑到振子的能量是量子化的,那么每个振子只能具有离散的能量,即E = nhv,其中E为能量,n为量子数,v为辐射频率,h为普朗克常数。
步骤2:设想黑体内的振子可以具有不同的能量量子数n,表示各个振子能量的分布情况。
我们假设振子的能量量子数n符合玻尔兹曼分布,即n能级的占有数为exp(-E_n / kT),其中E_n为n能级的能量,k为玻尔兹曼常数,T为黑体的温度。
步骤3:进一步假设振子的能量量子数n的平均值为,每个振子的能量为E = nhv,则黑体的总能量可以表示为U = ∑(nE) = ∑(nhvexp(-E_n / kT))。
在这里,∑代表对所有能级进行求和。
步骤4:将能量量子数n的平均值表示为,并代入总能量公式。
整理得:U = ∑((nvexp(-E_n / kT))hv步骤5:通过积分,将对所有可能的能级n进行求和替换为对能量E的积分。
利用代换关系dn = dE / hv,将求和替换为积分。
同样,将E_n也替换为E。
U = ∫(Eexp(-E / kT)) / (hv) * dE步骤6:对积分进行推导求解,得到:U = (kT)^4 / (h^3c^2) * ∫(E^3 / (exp(E / kT) - 1)) * dE这就是普朗克黑体辐射公式的具体形式,其中c为光速。
该公式描述了黑体辐射频谱与温度之间的依赖关系,表征了能量密度与频率的分布规律。
简单总结一下,普朗克黑体辐射公式的推导基于能量量子化和能级分布的假设。
通过对振子能量的分布以及总能量的计算,得到了描述黑体辐射的具体公式。
这个公式的重要性在于引入了能量的量子化概念,为后来量子力学的发展奠定了基础。
Planck 和Rayleigh-Jeans 黑体辐射公式的推导
Made by 0310340 陶波
0310351 郑启飞 0310337 盛海翔
黑体是指在任何温度下,对于各种波长的电磁辐射的吸收系数恒等于1的物体
黑体辐射的能量是由电磁场的本征振动引起的,为简化推导过程,在此将黑体简化为边长为L 的正方形谐振腔。
如图示
:
则腔内的电磁场满足亥姆霍兹方程:
2222u+k u 0 (k )ωμε∇== (1)
用分离变量法,令u(x,y,z)X(x)Y(y)Z(z)= 则(1)式可分解为三个方程: 22
2
22
222200
0x y z d X k X dx d Y k Y dy
d Z
k Z dz
⎧+=⎪⎪⎪+=⎨⎪⎪+=⎪⎩ 其中 2222x y z
k k k ωμε++= 得(1)式的驻波解为:
112233(,,)(cos sin )(cos sin )(cos sin )
x x y y z z u x y z c k x d k x c k y d k y c k z d k z =++⋅+由在x=0,x=L,y=0,y=L,z=0,z=L 上的边界条件0n
E n
∂=∂及0D E ⋅=可得:
123cos sin sin sin cos sin sin sin cos x x y z y x y z z x y z E A k x k y k z E A k x k y k z
E A k x k y k z
⎧=⎪
=⎨⎪
=⎩ x x k n L π
=
,
y y k n L
π
=,
z z k n L
π
= ,,0,1,2,x y z n n n =
(其中1A ,2A ,3A 满足关系1230x y z k A k A k A ++=)
则j k
(j 表示第j 个本征态)的绝对值为:
22222
22()()()j x y z j k n n n n L L
ππ=++=
换成第j 个本征态的频率得:222
()2j
j c n L
ν=
当j L λ>>时,j λ和j ν可视为连续变化,不必取分立值,即有:
2
22
()2c n L
ν= (2)
(2)式表明在整数n 空间一组整数,,x y z n n n 即对应一个本征模的频率。
因此,频率区间ν 内的本征模数,在数值上等于整数n 空间内数值半径由n n n →+ 范围内球壳体积的
八分之一,即:
2322314()44()L dN n n
V B c c
π
νππνννν=⋅==⋅⋅ (V 为腔的体积)
又因为每一个频率为ν的单色平面波还存在着两个独立的相互垂直的偏振态,则频率间隔ν 内的本征模数为:
2
38()V dN d c
πννν=
设(,)T εν表示温度为T ,频率为
ν的本征振动的平均能
量,(,)T ρν为相应的能量密度,则振动频率在ν到d νν
+之间的能量为:
2
38(,)(,)()(,)V V T d T dN T d c
πρννενννενν==
2
38(,)(,)T d T d c
πρνννενν= (3)
本征振动是简谐振动,由三维谐振子的能量本征值:
3
()2
n E n h ν=+ (n=0,1,2…)
系统处于热平衡状态时,处于各本征能量的谐振子分布遵从麦克斯韦-波尔兹曼分布律: 即:exp()n
n
E E N kT
∝-
所以:exp()(,)exp()n
n n
n n
E E kT T E kT εν-=
-∑∑ (4) 若令1
kT β=,
exp()n
n
Z E β=-∑
则(4)式可改写为:1(,)dZ
T Z d ενβ=-
由
3
exp()exp[()]
23
exp()exp()
23exp()
21exp()
n n n
n
Z E n h h n h h h ββννβννβν=-=-+=---=
--∑∑∑
所以:1(,)exp()1dZ h T h Z d kT
ν
εννβ=-=-
代入(3)式得:
3
23388(,)(,)exp()1h T d T d d c c kT
ππνρνννεννν
ν==-
此即为Planck 黑体辐射公式。
若按经典理论,由热力学与统计物理的能量均分定理可知平
均能量为:
(,)
T kT εν=
则:
22
33
88
(,)(,)
T d T d kT d
c c
ππ
ρνννενννν
==
此即为Rayleigh-Jeans黑体辐射公式。
两公式的曲线与实验曲线的符合情况如图
:。