小学几何之蝴蝶定理

小学几何之蝴蝶定理在小学几何的奇妙世界里，有一个充满趣味和智慧的定理，那就是蝴蝶定理。

它就像一把神奇的钥匙，能帮助我们解开许多几何谜题。

蝴蝶定理的名字听起来是不是很有趣？就好像一只美丽的蝴蝶在几何图形中翩翩起舞。

那到底什么是蝴蝶定理呢？让我们一起来揭开它神秘的面纱。

想象一下有一个四边形，它的两条对角线相交于一点。

在这个四边形中，相对的两个三角形的面积之间存在着一种特殊的关系，这就是蝴蝶定理所描述的内容。

比如说，我们有一个四边形 ABCD，对角线 AC 和 BD 相交于点 O。

那么根据蝴蝶定理，三角形 AOB 和三角形 DOC 的面积之积等于三角形 AOD 和三角形 BOC 的面积之积。

可能你会觉得有点抽象，那我们通过一个具体的例子来感受一下。

假设四边形 ABCD 是一个平行四边形，AB 平行于 CD，AD 平行于BC。

AC 和 BD 相交于点 O。

因为平行四边形的对边相等且平行，所以三角形 ABC 和三角形 ADC 的面积相等。

又因为三角形 AOB 和三角形BOC 分别以 AO 和 OC 为底边时，它们的高相同，所以三角形 AOB 和三角形 BOC 的面积之比就等于 AO 与 OC 的长度之比。

同样的道理，三角形 AOD 和三角形 DOC 的面积之比也等于 AO 与OC 的长度之比。

这就意味着三角形 AOB 和三角形 BOC 的面积之积等于三角形 AOD 和三角形 DOC 的面积之积，这正是蝴蝶定理的体现。

蝴蝶定理在解决一些几何问题时非常有用。

比如，当我们已知四边形中某些部分的面积，要求其他部分的面积时，就可以运用蝴蝶定理来找到答案。

再比如，如果我们知道了两个三角形的面积关系，以及对角线的交点位置，也可以通过蝴蝶定理求出整个四边形的面积。

那小朋友们在学习蝴蝶定理的时候，可能会遇到一些困难。

这是很正常的，因为几何需要我们有一定的空间想象力和逻辑思维能力。

不过别担心，我们可以通过多做一些练习题，多画一些图形来帮助自己理解。

小学几何之蝴蝶定理在小学几何的奇妙世界里，有一个充满趣味和智慧的定理——蝴蝶定理。

它就像一把神奇的钥匙，能帮助我们轻松解开许多几何难题。

那什么是蝴蝶定理呢？咱们先来看一个简单的图形。

想象有一个四边形，它的两条对角线相交于一点。

然后，分别从这个交点向四边形的四条边作垂线。

这时，你会发现一个有趣的现象：在两条对角线上相对的两个三角形的面积乘积相等。

比如说，有一个四边形 ABCD，对角线 AC 和 BD 相交于点 O，过点 O 分别作 AB、BC、CD、DA 的垂线，垂足分别为 E、F、G、H。

那么，三角形 AOB 和三角形 COD 的面积乘积就等于三角形 AOD 和三角形 BOC 的面积乘积。

这就是蝴蝶定理的基本内容。

可能有的小朋友会问了，为什么会有这样神奇的定理呢？咱们来试着证明一下。

假设三角形 AOB 的面积为 S₁，三角形 BOC 的面积为 S₂，三角形COD 的面积为 S₃，三角形 AOD 的面积为 S₄。

因为三角形的面积等于底乘以高除以 2，而三角形 AOB 和三角形BOC 都以 BO 为底边，它们的高分别是 AE 和 CF。

所以，S₁/S₂＝（AE×BO/2) ／（CF×BO/2) ＝ AE/CF。

同理，三角形 AOD 和三角形 COD 都以 DO 为底边，它们的高分别是 AH 和 CG。

所以，S₄/S₃＝（AH×DO/2) ／（CG×DO/2) ＝AH/CG。

又因为三角形 AEO 和三角形 CGO 相似（因为对顶角相等，直角相等），所以 AE/CF ＝ AH/CG。

从而得出 S₁×S₃＝ S₂×S₄，这就证明了蝴蝶定理。

蝴蝶定理在解决实际问题中可有大用处啦！比如，有一道这样的题目：在一个四边形中，两条对角线相交，其中一条对角线被交点分成 3 厘米和 5 厘米两段，另一条对角线被交点分成 2 厘米和 4 厘米两段。

求这个四边形中相对的两个三角形的面积比。

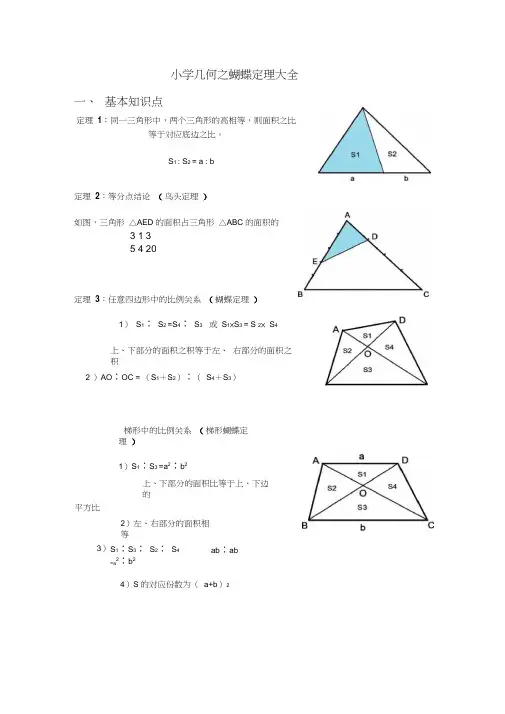
小学几何之蝴蝶定理大全一、基本知识点定理1：同一三角形中，两个三角形的高相等，则面积之比等于对应底边之比。

定理2：等分点结论（鸟头定理）如图，三角形△AED 的面积占三角形△ABC 的面积的3 1 35 4 20定理3：任意四边形中的比例关系（蝴蝶定理）1）S1∶S2 =S4∶S3 或S1×S3 = S 2× S4上、下部分的面积之积等于左、右部分的面积之积2 ）AO∶OC = （S1＋S2）∶（S4＋S3）梯形中的比例关系（梯形蝴蝶定理）1）S1∶S3 =a2∶b2上、下部分的面积比等于上、下边的平方比2）左、右部分的面积相等3）S1∶S3∶S2∶S4=a 2∶b2ab∶abS1 : S2 = a : b4）S 的对应份数为（a+b）2定理 4：相似三角形性质2) S 1 ∶S 2 = a 2 ∶A 2定理 5：燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ ECS △ BGA ∶ S △BGC = S △ AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例 1、如图， AD DB ， AE EF FC ，已知阴影部分面积为 5 平方厘米， 多少平方厘米？1) BCHABC 的面积是例2、有一个三角形ABC 的面积为1，如图，且AD 1 AB，21ABC中，，D为BC的中点， E 为AB上的一点，且BE= AB,已知四边3形EDCA的面积是35 ，求三角形ABC的面积.例4、例 1 如图，ABCD 是直角梯形，求阴影部分的面积和。

（单位：厘米）例5、两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？（单位：平方厘米）例6、如下图，图中BO=2DO，阴影部分的面积是 4 平方厘米，求梯形ABCD的面积是多少平B三角形DEF 的面积.BE 1BC ，31CF CA ，求4例3、如图，在三角形方厘米？例7、（小数报竞赛活动试题）如图，某公园的外轮廓是四边形ABCD ，被对角线AC、BD 分成四个部分，△AOB 面积为1平方千米，△BOC 面积为2平方千米，△COD 的面积为 3 平方千米，公园陆地的面积是 6.92 平方千米，求人工湖的面积是多少平方千米？例8、如图：在梯形ABCD 中，三角形AOD 的面积为9 平方厘米，25 平方厘米，求梯形ABCD 的面积。

小学奥数几何篇五大模型蝴蝶定理一、蝴蝶定理的定义与公式蝴蝶定理是小学奥数几何篇中的一个重要模型，它描述了在等腰三角形中，一条平行于底边的线段将底边平分，并且这条线段与等腰三角形的两腰相交于同一点时，该线段的中点与等腰三角形的顶点、底边的中点以及两腰上的交点形成一个等腰三角形。

蝴蝶定理的公式如下：设等腰三角形ABC中，AB=AC，底边BC的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，则AG=BG=CG。

二、蝴蝶定理的应用1. 在等腰三角形中求边长：通过蝴蝶定理，可以快速求出等腰三角形中未知边的长度。

例如，已知等腰三角形ABC中，AB=AC，底边BC 的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，求AG的长度。

解答：根据蝴蝶定理，AG=BG=CG，又因为AB=AC，所以AG=AB/2=a。

2. 在等腰三角形中求角度：通过蝴蝶定理，可以求出等腰三角形中未知角的度数。

例如，已知等腰三角形ABC中，AB=AC，底边BC的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，求∠AGB的度数。

解答：由于AG=BG=CG，所以△AGB是等边三角形，∠AGB=60°。

3. 在等腰三角形中求面积：通过蝴蝶定理，可以求出等腰三角形中未知部分的面积。

例如，已知等腰三角形ABC中，AB=AC，底边BC的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，求△AGB的面积。

解答：由于△AGB是等边三角形，所以△AGB的面积=（a^2 √3）/ 4。

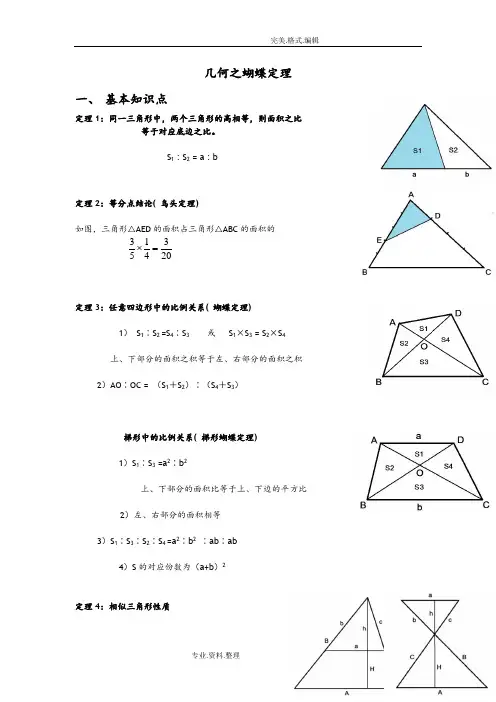
几何之蝴蝶定理一、 基本知识点定理1：同一三角形中，两个三角形的高相等，则面积之比 等于对应底边之比。

S 1 : S 2 = a : b定理2：等分点结论( 鸟头定理)如图，三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3：任意四边形中的比例关系( 蝴蝶定理)1） S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2）AO ∶OC = （S 1＋S 2）∶（S 4＋S 3）梯形中的比例关系( 梯形蝴蝶定理)1）S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2）左、右部分的面积相等3）S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4）S 的对应份数为（a+b ）2定理4：相似三角形性质CBEFDA1）Hh C c B b A a ===2） S 1 ∶S 2 = a 2 ∶A 2定理5：燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC 的面积是多少平方厘米？例2、有一个三角形ABC 的面积为1，如图，且12AD AB =，13BE BC =，14CF CA =，求三角形DEF 的面积.例3、如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积.例4、例1 如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）例5、两条对角线把梯形ABCD分割成四个三角形。

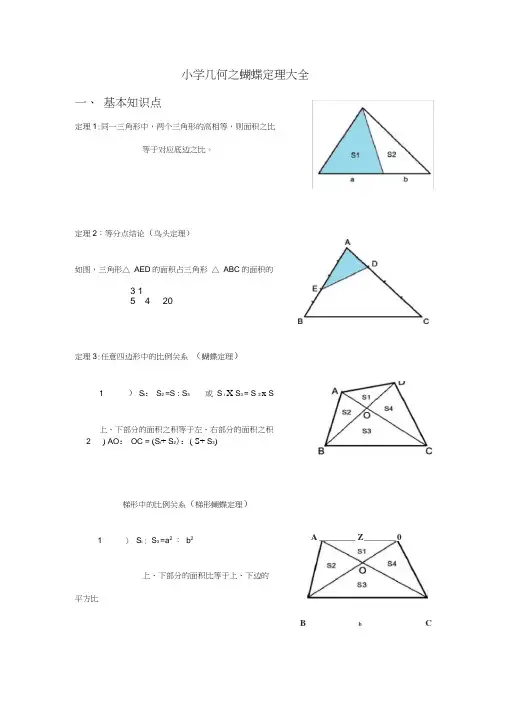
小学几何之蝴蝶定理大全一、基本知识点定理1:同一三角形中，两个三角形的高相等，则面积之比等于对应底边之比。

定理2：等分点结论（鸟头定理）如图，三角形△ AED的面积占三角形△ ABC的面积的3 15 4 20定理3:任意四边形中的比例关系（蝴蝶定理）1 ）S i：S2 =S : S3 或S i X S3 = S 2 x S上、下部分的面积之积等于左、右部分的面积之积2 ) AO： OC = (S i+ S2)：( S+ S3)梯形中的比例关系（梯形蝴蝶定理）A ________ Z_______ 01 ）S i : S3 =a2：b2上、下部分的面积比等于上、下边的平方比B b C2）左、右部分的面积相等2 23 ) S : S B : S2: S4 =a : b : ab : ab）S的对应份数为（a+b）定理4:相似三角形性质a b _c _hA B C H2 22 ) S i : S = a : A定理5:燕尾定理S △ ABG : S △ AGC = S △ BGE : S △ GEC = BE : ECS△BGA :S △ BGC=:S △AGF :S △GFC :=AF:FCS△AGC :S △ BCG=:S △ADG :S △DGB :=AD:DB二、例题分析例1、如图，AD DB , AE EF FC，已知阴影部分面积为5平方厘米, 多少平方厘米ABC的面积是例2、有一个三角形ABC的面积为1，如图，且AD - AB，BE21CF CA，求4三角形DEF的面积.例3、如图，在三角形ABC中，，D为BC的中点，E为AB上的一点，且1丄AB,已知四边形EDCA勺面积是35,求三角形ABC的面积.（单位：厘米）例4、例1如图，ABCD是直角梯形，求阴影部分的面积和。

例5、两条对角线把梯形 ABCD 分割成四个三角形。

已知两个三角形的面积（如图所示） ，求另两个三角形的面积各是多少（单位：平方厘米）例6、如下图，图中 B0=2DO 阴影部分的面积是 4平方厘米，求梯形 ABCD 勺面积是多少平 方厘米例7、（小数报竞赛活动试题）如图，某公园的外轮廓是四边形ABCD 被对角线 AC BD 分成四个部分，△ AOB 面积为1平方千米，△ BOC 面积为2平方千米，△ COD 勺面积为3平方千米，公园陆地的面积例8、如图：在梯形 ABCD 中,三角形 AOD 的面积为9平方厘米,平方厘米，求梯形 ABCD 勺面积。

小学奥数几何篇五大模型蝴蝶定理(附答案)在小学奥数的几何部分，蝴蝶定理是一个非常有用的工具，它可以帮助我们解决一些复杂的几何问题。

蝴蝶定理主要描述了在四边形中，当两条对角线互相垂直时，四边形被分成四个小三角形，而这四个小三角形的面积之间存在一定的关系。

蝴蝶定理的内容如下：设四边形ABCD中，AC和BD是互相垂直的对角线，交于点O。

设四个小三角形的面积分别为S1、S2、S3、S4。

那么，蝴蝶定理可以表述为：S1 + S2 = S3 + S4。

这个定理听起来可能有些抽象，但实际上它的应用非常广泛。

我们可以通过蝴蝶定理来解决一些看似复杂的问题。

下面，我将通过一些例子来展示蝴蝶定理的应用。

例1：在四边形ABCD中，AC和BD是互相垂直的对角线，且AC =8cm，BD = 6cm。

如果三角形ABC的面积是24cm²，那么三角形ADC的面积是多少？解答：根据蝴蝶定理，我们有S1 + S2 = S3 + S4。

由于三角形ABC的面积是24cm²，所以S1 = 24cm²。

又因为AC = 8cm，BD = 6cm，我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 8cm6cm = 24cm²。

因此，三角形ADC的面积也是24cm²。

例2：在四边形ABCD中，AC和BD是互相垂直的对角线，且AC = 10cm，BD = 5cm。

如果三角形ABC的面积是20cm²，那么三角形ADC的面积是多少？解答：同样地，根据蝴蝶定理，我们有S1 + S2 = S3 + S4。

由于三角形ABC的面积是20cm²，所以S1 = 20cm²。

又因为AC = 10cm，BD = 5cm，我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 10cm 5cm = 25cm²。

因此，三角形ADC的面积是25cm²。

小学几何之蝴蝶定理 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】CFE ADBCBEFDA几何之蝴蝶定理一、 基本知识点定理1：同一三角形中，两个三角形的高相等，则面积之比 等于对应底边之比。

S 1 : S 2 = a : b 定理2：等分点结论( 鸟头定理)如图，三角形△AED 的面积占三角形△ABC 的面积的 定理3：任意四边形中的比例关系( 蝴蝶定理)1） S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积 2）AO ∶OC = （S 1＋S 2）∶（S 4＋S 3）梯形中的比例关系( 梯形蝴蝶定理) 1）S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2）左、右部分的面积相等3）S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab 4）S 的对应份数为（a+b ）2 定理4：相似三角形性质1） HhC c B b A a ===2） S 1 ∶S 2 = a 2 ∶A 2 定理5：燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶EC S △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FC S △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC 的面积是多少平方厘米？例2、有一个三角形ABC 的面积为1，如图，且12AD AB =，13BE BC =，14CF CA =，求三角形DEF 的面积.例3、如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积.例4、例1 如图，ABCD 是直角梯形，求阴影部分的面积和。

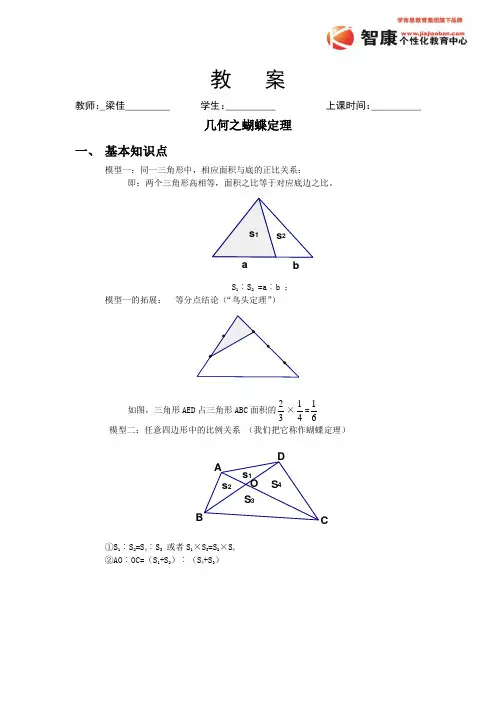
小学几何之蝴蝶定理大全小学几何之蝴蝶定理大全一、基本知识点定理1：同一三角形中，两个三角形的高相等，则面积之比等于对应底边之比。

定理2：等分点结论（鸟头定理）在△ABC中，D为BC的中点，连接AD并延长交EF于点G，则有：frac{S_{\triangle AEG}}{S_{\triangleBGC}}=\frac{AD}{BC}$frac{S_{\triangle AFG}}{S_{\triangle BGC}}=\frac{AB-AD}{BC}$定理3：任意四边形中的比例关系（蝴蝶定理）1）上、下部分的面积之积等于左、右部分的面积之积：或 $S_1\times S_3=S_2\times S_4$2）AO∶OC=（S1＋S2）∶（S4＋S3）梯形中的比例关系（梯形蝴蝶定理）1）上、下部分的面积比等于上、下边的平方比：2）左、右部分的面积相等3）$4）S的对应份数为（a+b）2定理4：相似三角形性质1）$\frac{a}{A}=\frac{b}{B}=\frac{c}{C}=\frac{h}{H}$ 2）$\frac{S_1}{S_2}=\frac{a^2}{A^2}$定理5：燕尾定理S_{\triangle ABG}:S_{\triangle AGC}=S_{\triangle BGE}:S_{\triangle GEC}=S_{\triangle BGA}:S_{\triangle BGC}=S_{\triangle AGF}:S_{\triangle GFC}=S_{\triangle AGC}:S_{\triangle BCG}=S_{\triangle ADG}:S_{\triangle DGB}=二、例题分析例1、如图，AD=DB，AE=EF=FC，已知阴影部分面积为5平方厘米，求ABC的面积。

删除明显有问题的例题）例4、如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）例5、两条对角线把梯形ABCD分割成四个三角形。

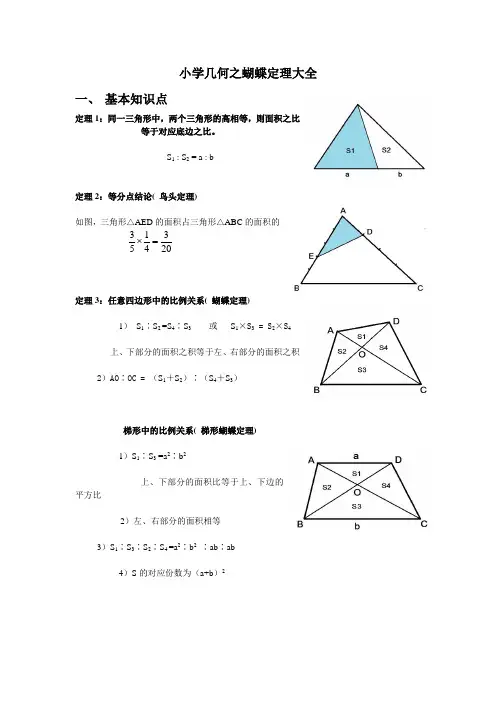
小学几何之蝴蝶定理大全一、 基本知识点定理1：同一三角形中，两个三角形的高相等，则面积之比 等于对应底边之比。

S 1 : S 2 = a : b定理2：等分点结论( 鸟头定理)如图，三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3：任意四边形中的比例关系( 蝴蝶定理)1） S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2）AO ∶OC = （S 1＋S 2）∶（S 4＋S 3）梯形中的比例关系( 梯形蝴蝶定理)1）S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2）左、右部分的面积相等3）S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4）S 的对应份数为（a+b ）2定理4：相似三角形性质1）HhC c B b A a ===2） S 1 ∶S 2 = a 2 ∶A 2定理5：燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC 的面积是多少平方厘米？CFEADBC B EFD A例2、有一个三角形ABC的面积为1，如图，且12AD AB=，13BE BC=，14CF CA=，求三角形DEF的面积.例3、如图，在三角形ABC中，，D为BC的中点，E为AB上的一点，且BE=13AB,已知四边形EDCA的面积是35，求三角形ABC的面积.例4、例1 如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）例5、两条对角线把梯形ABCD分割成四个三角形。

数学中的蝴蝶定理是一个关于圆的射影几何定理，其表述如下：设M为圆内弦PQ的中点，过M作弦AB和CD。

设AD和BC各相交PQ于点X和Y，则M是XY的中点。

该定理有多种证明方法，以下是其中一种常用的证明方法：
利用相似三角形证明：
首先，作过M的两个弦AB和CD，分别交PQ于X和Y。

接着，作圆心O关于PQ的垂线MO，分别交AD、BC于点E和F。

由于角EMO和角FMO都是直角，所以三角形EMO与三角形FMO相似。

根据相似三角形的性质，我们有：
MX/ME = MY/MF
MX/MY = ME/MF
由于ME和MF分别是AD和BC的中线，所以ME/MF = AE/CF。

由于AE和CF平行于PQ，根据平行线的性质，我们知道MX/MY = AE/CF。

由于AE和CF分别是AD和BC的两条弦，所以AE/CF = AD/BC。

从而得到：
MX/MY = AD/BC
这就是蝴蝶定理的证明。

CFEF几何之蝴蝶定理一、 基本知识点定理1：同一三角形中，两个三角形的高相等，则面积之比 等于对应底边之比。

S 1 : S 2 = a : b 定理2：等分点结论( 鸟头定理)如图，三角形△AED 的面积占三角形△ABC 的面积的 定理3：任意四边形中的比例关系( 蝴蝶定理)1） S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4 上、下部分的面积之积等于左、右部分的面积之积 2）AO ∶OC = （S 1＋S 2）∶（S 4＋S 3） 梯形中的比例关系( 梯形蝴蝶定理) 1）S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2）左、右部分的面积相等3）S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab 4）S 的对应份数为（a+b ）2 定理4：相似三角形性质 1）HhC c B b A a === 2） S 1 ∶S 2 = a 2 ∶A 2 定理5：燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶EC S △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FC S △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC 的面积是多少平方厘米？例2、有一个三角形ABC 的面积为1，如图，且AD 13BE BC =，14CF CA =，求三角形DEF 的面积.AB 上的一点，且BE=13AB,例3、如图，在三角形ABC 中，，D 为BC 的中点，E 已知四边形EDCA 的面积是35，求三角形ABC 的面积.例4、例1 如图，ABCD 是直角梯形，求阴影部分的面积和。

（单位：厘米）例5、两条对角线把梯形ABCD 分割成四个三角形。

小学蝴蝶定理公式蝴蝶定理公式是数学运算中相当重要的一条公式，尤其是在小学数学课堂教学当中，它经常被老师们用来让学生来推导和运算，这条公式又称为勾股定理，如果你想更好地理解它，那么你有必要先了解它背后的原理以及运用它所推导出的其他结论。

蝴蝶定理公式也叫做勾股定理，它是希腊数学家勾股在公元前三世纪创立的，它的形式如下：a +b = c这里的a、b、c分别表示三条直线的长度，它们构成一个三角形和一个直角三角形，并且这三条直线也都是直角三角形的边。

这条公式显示了在直角三角形内，任意直角三角形的两个直角边的平方之和，等于它们直角角的那条斜边的平方。

由蝴蝶定理公式，可以得出以下几个重要的结论：（1）直角三角形面积公式：S = 1/2 a b在一个直角三角形中，a 为直角边，b 为斜边，则其面积 S 为 a b乘积的一半。

（2）关于直角三角形的等值定理：如果在一个直角三角形中，其中任意一条直角边的平方与其他两条边的乘积相等，则这三条边是等值边。

（3）角度定理：在一个直角三角形中，a 为直角边，b 为斜边，则直角角的弧度为 arctan（b/a）。

从上述可以得出，蝴蝶定理公式的应用非常广泛，它不仅能够用于直角三角形的计算，还可以用于圆的面积计算，还可以用于其他三角形，正多边形的计算。

此外，蝴蝶定理公式还可以用于几何学中的其他计算，比如说求点到直线的距离、求曲线的长度等。

蝴蝶定理公式对小学数学课堂教学非常重要，它有助于学生学习数学和理解数学原理，并且可以更好地理解更深层次的数学问题。

上述每条蝴蝶定理公式都有其独特的特性，能够更好地帮助学生了解其中所有的数学概念和原理，从而实现知识与实践的结合。

在小学课堂教学当中，老师们可以通过蝴蝶定理公式的运用，让学生从实际的例子出发，学习数学的推理能力，让学生更好地理解其中的数学原理，并让他们掌握蝴蝶定理公式的应用，以便他们能够在今后的数学学习中更好地运用。

小学几何之蝴蝶定理大全一、基本知识点定理1:同一三角形中，两个三角形的高相等，则面积之比S i : S2 = a : ba b等于对应底边之比。

定理2:等分点结论(鸟头定理)如图，三角形△AED的面积占三角形△ ABC的面积的20定理3:任意四边形中的比例关系(蝴蝶定理)1) S i : S2 =S4 : S3 或S i X S3 = S2X S4上、下部分的面积之积等于左、右部分的面积之积2 ) AO： OC = (S i+ S2)：( S4+ S3)梯形中的比例关系(梯形蝴蝶定理)1) S i : S3 =a2: b2上、下部分的面积比等于上、下边的平方比2) 左、右部分的面积相等B b C3) S i : S3 : S2 : S4 =a2: b2: ab : ab4) S的对应份数为(a+b) 2定理4:相似三角形性质2) S i : S 2 = a 2 : A 2定理5:燕尾定理S AABG:S A AGC : =S A BGE : :S A GEC =BE : ECS A BGA : :S A BGC : =S A AGF :S A GFC =AF : FC S A AGC : :S A BCG : =S A ADG:S A DGB=AD :DB二、例题分析例1、如图，AD DB , AE EF FC ，已知阴影部分面积为 5平方厘米, 多少平方厘米？ABC 的面积是例2、有一个三角形 ABC 的面积为1，如图，且AD - AB , BE21例3、如图，在三角形 ABC 中，，D 为BC 的中点，E 为AB 上的一点，且 BE=—AB,已知四边3例4、例1如图，ABCD 是直角梯形，求阴影部分的面积和。

（单位：厘米）例5、两条对角线把梯形 ABCD 分割成四个三角形。

已知两个三角形的面积（如图所示） 另两个三角形的面积各是多少？（单位：平方厘米）例6、如下图，图中 BO=2DO 阴影部分的面积是 4平方厘米，求梯形 ABCD 勺面积是多少平三角形DEF 的面积.-BC , CF3-CA ，求 4形EDCA 勺面积是35,求三角形 ABC 的面积.，求B方厘米?例7、（小数报竞赛活动试题）如图，某公园的外轮廓是四边形ABCD ,被对角线AC、BD分成四个部分，△ AOB 面积为1平方千米，△ BOC面积为2平方千米，△ COD的面积为3平方千米，公园陆地的面积是6.92平方千米，求人工湖的面积是多少平方千米？例8、如图：在梯形ABCD中，三角形AOD的面积为9平方厘米25平方厘米，求梯形ABCD的面积。