安培力与洛伦兹力对比

安培力和洛伦兹力的区别
一、概念不同
1、安培力（Ampere's force）是通电导线在磁场中受到的作用力。

由法国物理学家A·安培首先通过实验确定。

2、运动电荷在磁场中所受到的力称为洛伦兹力，即磁场对运动电荷的作用力。

洛伦兹力的公式为F=QvB。

荷兰物理学家洛伦兹首先提出了运动电荷产生磁场和磁场对运动电荷有作用力的观点，为纪念他，人们称这种力为洛伦兹力。

二、公式不同
1、洛伦兹力f=Bvq；其描述的是某个粒子的受力情况。

2、安培力F=BIL；其描述的是通电的杆件的受力情况。

三、方向不同
1、安培力的方向既跟磁场方向垂直，又跟电流方向垂直，也就是说，安培力的方向总是垂直于磁感线和通电导线所在的平面。

通电直导线所受安培力的方向和磁场方向、电流方向之间的关系，可用左手定则来判定：
左手定则：伸开左手，使大拇指跟其余四个手指垂直，并且都跟手掌在一个平面内，把手放入磁场中，让磁感线垂直穿入手心，并使伸开的四指指向电流的方向，那么大拇指所指的方向就是通电导线在磁场中所受安培力的方向。

作用在通电导线上的安培力，是作用在运动电荷上的洛伦兹力的宏观表现。

2、洛伦兹力的方向可由左手定则来判定：
左手定则：伸开左手，使大拇指跟其余四个手指垂直，且处于同一平面内，把手放入磁场中，让磁感线垂直穿入手心，四指指向正电荷运动的方向或负电荷
运动的相反方向，那么，拇指所指的方向就是正电荷或负电荷所受洛伦兹力的方向。

安培力与洛伦兹力一、安培力定义：通电导线在磁场中所受的力。

大小：1、磁场与电流垂直时，F=BIL2、磁场与电流平行时，F=03、磁场与电流成b角时，F=BILsin b理解:1、公式适用于匀强磁场,若为非匀强，则需要用到积分。

2、公式中的夹角为磁场与导线的夹角.3、磁场有垂直电流方向的分量才对电流产生力的作用，平行电流方向对电流不产生力的作用。

因此，如果知道一段导线的受力，我们只可以确定磁场垂直电流方向的分量，换句话说,我们只可以确定场强的最小值。

4、对于一段导线有效长度的确定.直导线：本身长度*sin b(磁场与导线的夹角)弯曲导线：在导线所在平面垂直于磁场方向的前提下，有效长度为两端点的连线.5、对于闭合线圈，其有效长度一定为0.因此，对于完全处于匀强磁场中的闭合线圈，其所受的磁场力合力一定为零。

方向：左手定则（判断磁场方向——右手、判断受力方向——左手）同时垂直与电流方向和磁场方向。

注意：不管电流方向与磁场方向是否垂直，安培力方向总垂直与电流方向与磁场方向决定的平面。

二、洛伦兹力定义：运动电荷在磁场中所受的力.大小：1、v//B或v=0时，F=0。

2、v垂直于B时，F=qvb。

3、v与B的夹角为ɑ时，F=Bqvsin ɑ。

4、B、ɑ、v均为粒子运动过程中的瞬时量。

方向：1、使用左手定则进行判定（判断磁场用右手，判断受力用左手）。

2、四指指向一定是正电荷的运动方向，是负电荷的反方向.(四指指向电流方向）。

3、洛伦兹力的方向和电荷运动方向与磁场方向都垂直（不做功）。

理解:1、洛伦兹力与速度成正比，并且与速度的方向有关，同样的速度，垂直磁场入射的时候，洛伦兹力最大。

2、洛伦兹力始终和速度方向垂直,根据W=FSsinɑ，ɑ=90知，W=0.也就是说洛仑兹力始终不做功.3、做功为0，根据功能关系,能量不改变，洛伦兹力不改变速度的大小。

由牛顿第一定律，力可以改变物体运动状态,洛伦兹力改变速度大小。

三、安培力与洛伦兹力的内在关系由安培力F=BIL推导洛伦兹力F=qvB设：导体的横截面积为S，单位体积的电荷数为n，自由电荷的电荷量为q，电荷定向移动的速度大小为v。

安培力和洛伦兹力做功的特点首先，让我们来了解一下安培力和洛伦兹力的定义和公式：安培力是指电流通过导线时，导线上每段微小长度上所受到的力的大小和方向。

安培力的大小与电流的大小、导线长度以及磁感应强度之间的关系由安培定律给出。

安培力的公式为：F = BILsinθ其中，F表示安培力的大小，B表示磁感应强度，I表示电流的大小，L表示导线长度，θ表示磁感应强度与导线的连线方向的夹角。

洛伦兹力是指带电粒子在磁场中受到的力。

洛伦兹力的大小和方向与粒子的电荷量、速度以及磁场强度之间的关系由洛伦兹力公式给出。

洛伦兹力的公式为：F=q(v×B)其中，F表示洛伦兹力的大小，q表示粒子的电荷量，v表示粒子的速度，B表示磁场的强度。

1.安培力对应的物理现象是电流通过导线时所受的力，这种力是由带电粒子在磁场中运动产生的。

由于安培力与导线的长度和电流的大小相关，因此当导线上的电流改变时，安培力也会随之改变。

2.安培力所做的功与导线的位置有关。

当导线垂直于磁场时，安培力所做的功最大。

而当导线与磁场平行时，安培力所做的功为零。

3.安培力不会改变导线的总机械能。

安培力的方向始终垂直于导线的方向，所以它不会改变导线的速度和机械能，而只会改变导线上电荷的内能。

1.洛伦兹力对应的物理现象是带电粒子在磁场中受到的力。

洛伦兹力的大小与电荷的电量、速度和磁场的强度相关，因此当这些参数改变时，洛伦兹力也会随之改变。

2.洛伦兹力做功时，粒子的速度方向和力的方向之间存在夹角。

如果速度和磁场方向平行或反平行，洛伦兹力所做的功为零。

而当速度和磁场方向垂直时，洛伦兹力所做的功最大。

3.洛伦兹力会改变粒子的机械能。

洛伦兹力的方向不一定与粒子的速度方向相同，所以它可以改变粒子的速度和动能，从而改变粒子的机械能。

综上所述，安培力和洛伦兹力的做功特点有所不同。

安培力所做的功与导线的位置有关，且不会改变导线的总机械能；而洛伦兹力所做的功与粒子的速度方向和力的方向之间的夹角有关，且可以改变粒子的机械能。

安培力与洛伦兹力安培力和洛伦兹力是电磁力学中两个重要的力的概念。

它们在解释电荷在磁场中的运动和相互作用方面起着关键的作用。

本文将介绍安培力和洛伦兹力的概念、公式及其应用。

一、安培力安培力是由电流产生的磁场对电荷的作用力。

根据安培力定律，当电流通过一段导线时，会产生一个磁场，而这个磁场会对附近的其他电荷施加力。

安培力的大小与电流的大小和方向以及电荷所处位置有关。

安培力的公式可以表示为：F = BILsinθ，其中F是安培力的大小，B是磁场的强度，I是电流的大小，L是电流所在导线的长度，θ是电流和磁场的夹角。

当电流和磁场垂直时，安培力达到最大值；而当电流和磁场平行时，安培力为零。

这一规律为我们解释电流在磁场中的运动提供了重要的依据。

安培力在许多实际应用中发挥着重要的作用。

例如，电动机、发电机和变压器等电器设备都是基于安培力的工作原理。

此外，MRI（磁共振成像）技术也是利用安培力来实现对人体内部结构的图像获取。

二、洛伦兹力洛伦兹力是电荷在磁场中所受到的力。

它是由电荷的运动状态和磁场的作用相互耦合产生的。

根据洛伦兹力定律，当带电粒子在磁场中运动时，会受到一个垂直于其速度方向且大小与速度、电荷量和磁场强度有关的力。

洛伦兹力的公式可以表示为：F = qvBsinθ，其中F是洛伦兹力的大小，q是电荷量，v是电荷的速度，B是磁场的强度，θ是速度和磁场的夹角。

洛伦兹力的方向垂直于速度和磁场的平面，并遵循左手螺旋定则。

当速度与磁场平行或反平行时，洛伦兹力为零；而当速度与磁场垂直时，洛伦兹力达到最大值。

洛伦兹力在许多领域都有着广泛的应用。

在粒子物理学中，加速器通过电磁铁产生磁场，通过对带电粒子施加洛伦兹力来加速粒子。

在药物输送和生物学研究中，利用洛伦兹力可以对带电颗粒进行操控和定位。

三、安培力与洛伦兹力的关系安培力和洛伦兹力在形式上非常相似，但它们的作用对象不同。

安培力作用于电流所携带的电荷，而洛伦兹力则作用于运动的电荷。

高中物理：洛伦兹力
1．洛伦兹力的特点
(1)洛伦兹力的方向总是垂直于运动电荷的速度方向和磁场方向共同确定的平面，所以洛伦兹力只改变速度的方向，不改变速度的大小，即洛伦兹力永不做功．
(2)当电荷运动方向发生变化时，洛伦兹力的方向也随之变化．
(3)用左手定则判断负电荷在磁场中运动所受的洛伦兹力时，要注意将四指指向电荷运动的反方向．
2．洛伦兹力与安培力的联系及区别
(1)安培力是洛伦兹力的宏观表现，二者是相同性质的力．
(2)安培力可以做功，而洛伦兹力对运动电荷不做功．
例1图7中a、b、c、d为四根与纸面垂直的长直导线，其横截面位于正方形的四个顶点上，导线中通有大小相同的电流，方向如图所示．一带正电的粒子从正方形中心O点沿垂直于纸面的方向向外运动，它所受洛伦兹力的方向是()
图7
A．向上B．向下
C．向左D．向右
①大小相同的电流；②向外运动．
答案B
解析根据安培定则及磁感应强度的矢量叠加，可得O点处的磁场向左，再根据左手定则判断带电粒子受到的洛伦兹力向下．
第1页共1页。

一文搞懂库仑力、洛伦兹力和安培力一、库仑力1、带电体可看作是由许多点电荷构成的，每一对静止点电荷之间的相互作用力遵循库仑定律(法国物理学家库仑于1785年发现)，称为库仑力，又称静电力。

2、库仑力是以电场为媒介传递的，即带电体在其周围产生电场，电场对处于其中的另一带电体施以作用力，且两个带电体受到的库仑力相等。

3、影响库仑力的因素有电荷量、两电荷之间的距离、带电体的形状、大小、电荷分布情况等。

4、库仑力的方向为沿两带电体中心线，同种电荷互相排斥，异种电荷互相吸引。

5、库仑力的计算公式是F=kq1q2/r2，式中：F为库仑力，N；k为库仑常量；q1、q2为带电粒子的电荷量，C；r为两个带电体之间的距离，m。

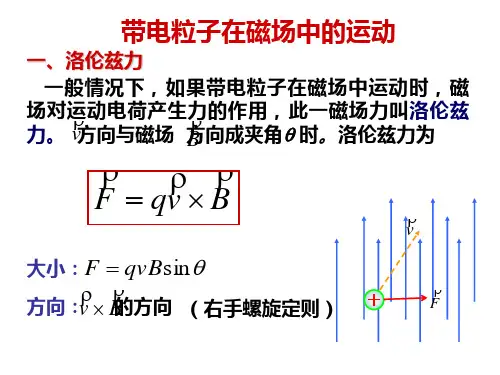
二、洛伦兹力1、运动电荷在磁场中受到的作用力，称为洛伦兹力。

荷兰物理学家洛伦兹首先提出了运动电荷产生磁场和磁场对运动电荷有作用力的观点，为纪念他，人们称这种力为洛伦兹力。

2、洛仑兹力既垂直于磁场方向又垂直于电荷运动方向，即垂直于磁场B和电荷运动速度v所决定的平面。

洛仑兹力的方向可根据左手定则判定：伸开左手，使大拇指与其余四指垂直且在同一个平面内，让磁力线从手掌心穿入，四指指向正电荷的运动方向，则大拇指所指方向即为洛伦兹力的方向。

但必须注意：若运动电荷是正的，大拇指指向即为洛伦兹力的方向。

反之，如果运动电荷是负的，仍用四指表示电荷运动方向，则大拇指指向的反方向为洛伦兹力的方向。

3、洛伦兹力的计算公式是f=qvBsinθ。

式中：f为电荷受到的洛伦兹力，N；q为带电粒子的电荷量，C；v为带电粒子的运动速度，m/s；B为均匀磁场的磁感应强度，T；θ为v与B的夹角。

4、洛伦兹力不做功是因为洛伦兹力的方向始终与电荷的运动方向垂直，根据功的公式W=FScosθ，θ=90°时，W=0。

三、安培力1、安培力是指通电导线在磁场中受到的作用力。

它是由法国物理学家安培首先通过实验确定的。

安培力是洛伦兹力的宏观表现，洛伦兹力是安培力的微观本质。

安培力电场力洛伦兹力的区别在咱们日常生活中，很多东西都能让人感到神奇，电和磁就像是这世界的魔法师，给我们的生活增添了不少色彩。

今天我们聊聊安培力、电场力和洛伦兹力这三位“大侠”。

它们可不是随便的角色，而是各自有各自的特点，甚至在某些情况下它们还能互相较劲呢。

安培力就像个乐于助人的邻居，它出现在电流通过导线时，那种感觉就像是你在水里划船，水流会推动你。

想象一下，一根电线里流动着电流，就像一条欢快的小溪。

然后，这条小溪旁边有一个磁场，就会产生安培力。

嘿，这力就像是在电流流动时，给它一个温暖的拥抱，让它向某个方向偏转。

真是神奇啊！我们说说电场力。

这力就像是你在参加一场派对，派对上有很多人在交流。

你一接触电场，就能感受到那些电荷在空中互相吸引或排斥。

就像在派对上，有的人特别合得来，有的人则是死都不想靠近。

电场力的大小和电荷的数量、距离都有关系，真是让人头大。

就像你和朋友之间的关系，离得远了，感情就淡了，近了反而更亲密。

这种力的作用范围可大可小，随时都在变化。

然后，咱们聊聊洛伦兹力。

这位“大侠”可不简单，名字听上去就很有范儿。

它是电场力和磁场力的结合体，简直就是个超级英雄。

想象一下，一个带电的粒子在电场和磁场中飞速移动，这时候洛伦兹力就会登场。

它会给这个粒子施加一个力，让它改变方向，简直是个大拐弯王！所以，你看到的那些在粒子加速器里飞速运转的小颗粒，都是在洛伦兹力的帮助下，像赛车一样极速前进。

你看，洛伦兹力可真是让人佩服。

这三种力的区别可不是简单的事儿，得仔细分析。

安培力主要是针对电流和磁场的互动，而电场力则是电荷之间的相互作用。

洛伦兹力呢，就像个桥梁，把电场力和磁场力结合在一起，真是个万事通。

生活中，我们总是能看到这些力的身影。

比如说，电动车的电动机就是利用安培力，让车轮转起来。

而在日常生活中，电磁炉则是借助电场力把食物加热的，真是方便又省事。

再说说洛伦兹力。

这个力特别有趣，你想啊，当你用一个带电的小玩意儿在磁场中移动时，立刻就能感受到一种神奇的力量在推动你。

洛伦兹力与安培力有何区别？在学习高中物理的时候往往会遇到很多关于物理问题，上课觉着什幺都懂了，可等到做题目时又无从下手。

以至于对于一些意志薄弱、学习方法不对的同学就很难再坚持下来。

过早的对物理没了兴趣，伤害了到高中的学习信心。

收集整理下面的这几个问题，是一些同学们的学习疑问，小编做一个统一的回复，有同样问题的同学，可以仔细看一下。

问题和答复如下：【问：洛伦兹力与安培力有何区别？】答：两个力都是磁场作用在物体上的力，这是共性。

洛伦兹力是单独一个带电粒子所受到的磁场力，而安培力是一个杆件所受到的磁场力。

可以这幺认为，安培力是杆件上无数粒子所受洛伦兹力的合力。

推荐同学们去看看2013年北京高考物理试卷第24题。

【问：电流表改装电压表实验，电源如何选择？】答：电流表改电压表的电源，一般来说应选择较大的。

这是因为电阻箱连入后会影响总电阻（变小），使得干路中电流变大，影响半偏的效果。

选择大的电动势，在满偏调节时滑动变阻器的阻值就会很大，减弱电阻箱对电路总电阻的影响。

【问：远距离输电中为什幺要升压？】答：任何的发电站，其功率（决定于烧煤量等）一般来说是恒定的，p=ui，如果提高电压，那幺电流就会减小。

输电线主要的损失在于输电线上热损耗，损耗功率计算表达式为p=i2r，比如从三峡向北京供电，r 大小基本上很难改变，因此要降低i，在功率恒定的情况下，办法就是提高u 的大小，即升压。

同学们要注意，这里讲的是输送功率，并不是【问：物理的动力学总学不好，难在哪里？】答：物理必修一整整一本书都是在研究牛顿的动力学。

很多学生都学不好这里的内容，对动力学问题的难点搞不明白。

解决动力学难题，同学们要从力、运动两条线上对物体进行分析，尤其是题中涉及到多个物体、多种复杂的运动模式时【问：多过程的物理问题如何处。

安培力与洛伦兹力安培力和洛伦兹力是电学中两种常见的力，它们影响着我们生活中的各种电器设备。

接下来，我们将深入探讨它们的概念、性质以及应用。

一、安培力安培力是指通过两条电流互相作用时所产生的力。

安培力的大小与电流的大小和方向有关，而且跟电流在空间中的分布、几何形状也有关系。

最初发现安培力是法国物理学家安培（Ampère）在1820年进行研究时发现的，因此以他的名字命名。

二、洛伦兹力洛伦兹力是指带电粒子在电场和磁场作用下所受到的力，又称为洛伦兹-洛伦兹力。

在电磁学的理论中，洛伦兹力通常用来描述粒子在电磁场中的运动状态。

洛伦兹力的大小与带电粒子的电量、电场和磁场的强度以及带电粒子的速度有关。

洛伦兹力的发现归功于荷兰物理学家洛伦兹（Lorentz）在1892年的工作。

三、安培力和洛伦兹力的关系安培力和洛伦兹力都是电学中的力，它们之间存在着密切的关系。

当电流通过一段导体时，会在周围产生磁场，带电粒子在磁场中运动时将受到洛伦兹力的作用。

这种力的大小跟电荷的量、电磁场的强度以及带电粒子的运动状态有关。

而在电磁学中，安培定律就是描述电流和磁场之间关系的定律。

安培定律表明，通过导体所产生的磁场的方向与电流的方向相同，磁力线的密度与电流的大小成正比。

也就是说，当电流通过导体时，将产生一个与电流方向相同的磁场，而这个磁场将对周围的带电粒子产生洛伦兹力的作用。

四、应用安培力和洛伦兹力的应用非常广泛。

在实际应用中，特别是电子学、通信、电力系统中，这两种力被广泛使用。

例如，在核磁共振成像技术中，利用安培力的原理使得磁共振成像仪可以检测人体内部的磁性物质，从而做出诊断；在大型电器设备如发电机、电动机和变压器中，利用洛伦兹力的原理控制电流和磁场的分布，使得设备可以正常运行。

总之，安培力和洛伦兹力在电学中起着十分重要的作用，科学家们一直在不断深入研究它们的性质和应用，在更广泛的领域中不断发挥着作用。

第1章安培力与洛伦兹力第1节 安培力及其应用 .............................................................................................. - 1 - 第2节 洛伦兹力.......................................................................................................... - 7 - 第3节 洛伦兹力的应用 ............................................................................................ - 14 - 章末复习总结................................................................................................................ - 18 -第1节 安培力及其应用一、安培力1．定义：物理学中，将磁场对通电导线的作用力称为安培力。

2．方向：用左手定则判断。

判断方法：伸开左手，使拇指与其余四个手指垂直，并且都与手掌在同一个平面内，让磁感线垂直穿过手心，四指指向电流的方向，此时拇指所指的方向即为所受安培力的方向。

3．大小(1)F ＝⎩⎪⎨⎪⎧ILB B 与I 垂直0B 与I 平行IlB sin θB 与I 的夹角为θ(2)在非匀强磁场中公式可用于很短的一段通电直导线。

二、安培力的应用1．安培力在生活中应用：电动机、电流计等都是安培力的应用。

2．电流计工作原理：(1)构造：如图所示，圆柱形铁芯固定于U 形磁铁两极间，铁芯外面套有缠绕着线圈并可转动的铝框，铝框的转轴上装有指针和游丝。

(2)原理：当被测电流通入线圈时，线圈受安培力作用而转动，线圈的转动使游丝扭转形变，从而对线圈的转动产生阻碍。

安培力和洛伦兹力的区别有什么联系越来越多的同学对于安培力和洛伦兹力两者之间的关系存在一定的疑惑，他们的区别是什幺，两者又有什幺联系呢，本文小编就为大家整理了相关信息，供大家参考。

1安培力和洛伦兹力有什幺不同两者实际是等同的。

可以将安培力想象成是导线中无数个小电荷在流动时分别受到的洛仑兹力的叠加；譬如,假设现在的电流是I,那幺说明t时间内,流过某一截面积的电荷数是Q=It所以流过的电子总数n=Q/e=It/e。

这段电子在t时间内流过的长度是l=vt,v是电子流的宏观平均速度，每个电子都受到洛仑兹力，f=evB,那幺这段l长度内的电子受到的总的洛仑兹力是f’=nevB=ItevB/e=ItvB=IBl。

现在整段导线在磁场内的长度是大L,而每小段l受到的是f’,所以总的受到的安培力F=BIL，左手定则是判断受力,右手定则是判断电流反方向,右手定则还有一个右手螺旋定则是判断磁场方向的.点是电流垂直纸面向外,反之是向里,四指是电流方向,拇指是运动方向。

另外，洛伦兹力是磁场对运动中的带电粒子的作用力，是对单个带电粒子而言；安培力是磁场对通电导线的作用力，是对整个在磁场中的导线而言。

事实上，为什幺磁场会对通电导线有安培力的作用呢？我们知道，通电导线中有很多运动的电荷；安培力，正是磁场对所有这些电荷的洛伦兹力的总和。

即安培力是洛伦兹力的宏观体现；而洛伦兹力，是安培力的微观原理。

区别就在这里一个宏观，一个微观。

1两者有什幺联系在高三物理选修本中提出安培力是作用在运动电荷上的力的宏观表现。

接着，又利用F=BIL推导了一个电荷受到的洛伦兹力f=qVB，从推导过程来看，安培力就是所有电荷受到洛伦兹力的合力，这个。

安培力洛伦兹力磁场力的区别安培力、洛伦兹力、磁场力，哎呀，听起来有点像什么高深的物理名词，仿佛说出来就能让人感到自己知识水平瞬间上升了几个档次，但其实呢，没那么复杂。

要搞清楚这三者的区别，不得不说，它们之间确实有点儿微妙的差别，像是兄弟姐妹一样各有各的性格。

但别怕，我会给你一一拆开来讲，保证让你听了之后能恍若大梦初醒！先说安培力吧。

这个名字听着就有点“威风凛凛”，对吧？它呢，实际上就是描述电流在磁场中受到的力。

想象一下，你拿着一个导线，导线里有电流在流动，这时候，如果你把它放进磁场里，那么电流就会受到一个力，这个力的大小和方向，跟电流大小、导线的长度、磁场的强度以及磁场的方向都有关系。

你可以想象它像是电流和磁场之间的“互动”，电流就像是那个活泼的小家伙，磁场就是那位严肃的“大叔”。

它们一旦接触，就会发生这种“打招呼”的现象，力的方向和大小就取决于它们之间的“亲密度”。

简单来说，安培力就是电流在磁场中被推挤的力。

然后，再来聊聊洛伦兹力。

说实话，这个名字一出来就有点吓人，但其实它的核心概念跟安培力差不多，都是电流遇到磁场后的“遭遇战”。

不过，洛伦兹力更普遍一些，它不仅适用于电流，也适用于单个的电荷。

就是说，如果你把一个带电的小粒子，比如电子，丢到磁场中去，它也会受到洛伦兹力的作用。

至于这个力的方向呢，可以通过右手定则来判断。

你想象一下，把你的右手伸开，手指指向电荷的运动方向，掌心向着磁场方向，那么你的拇指就会指向洛伦兹力的方向。

这下你就明白了，不是电流在磁场中才有力，连带电粒子也没能逃脱这种“罪孽”。

咱们得说说磁场力。

你看，磁场力这个名字就比较直白，它本质上是磁场对带电粒子或电流所施加的力。

可以说，磁场力是一种在磁场中时刻都会发生的力。

虽然听起来和前两者差不多，但它强调的是磁场本身对物体施加的作用力，是个更普遍的概念。

磁场力就像是磁场发出的“邀请函”，只要带电粒子进入了这个磁场，它就必须遵守磁场的“规矩”，进行一定的互动。

安培力与洛伦兹力在作用效果上有什么不同？为什么有时候安培力做功而洛伦兹力不做功？安培力时洛仑兹力的宏观表现。

洛仑兹力f=qvB，电流的微观表达式I=nqSv（n为单位体积自由电子个数，q为每个电子的电荷量，S为导线横截面积，v为自由电子定向移动速率）。

一长为L横截面积为S的导线，所含自由电子个数为N=SLn，安培力F=BIL=BnqSvL=(SLn)qvB=(SLn)f，即安培力为导线中每个电子所受力的洛仑兹力的总和。

洛仑兹力对电荷不做功，但是安培力对导线可以做功，而且安培力又是洛仑兹力的宏观表现，那么为什么呢？（这个问题本来就很绞的，很多人读完高中都没搞清楚，所以好好领悟）洛仑兹力对电荷不做功，但是并不代表洛仑兹力的分力对运动电荷不做功。

一段导线，假设在磁场中受安培力而水平移动。

注意，电子也在沿导线运动。

所以根据运动的合成与分解，电子的运动轨迹是斜着的。

洛仑兹力是垂直于电子运动轨迹的，所以洛仑兹力一定是斜着的。

那么我们就可以将洛仑兹力分解为垂直于导线方向和沿导线方向（既然都预习到这里了，应该知道力的分解吧）。

垂直于导线方向的洛仑兹力分力做正功，沿导线方向的分力做负功，这样实现了电能与界械能的转化。

正功使导线机械能增加（就是我们看到的安培力做的功），负功阻碍电子运动（即阻碍电流，消耗电能，这部分功体现在电能的减小上）。

并且正功大小一定等于负功大小，这样洛仑兹力的总功才为0。

所以我们平时就看到到安培力对导线做功，而洛仑兹力不做功。

还有一点，安培力做正功时，我们可以看到是电能与机械能的转化而不是磁场的能与机械能转化。

同时，电流在洛仑兹力的分力作用下受到阻碍，这就是电动机为什么不能使用U=IR公式的原因，除了电阻对电流的阻碍，这里又多了一个力，因此U=IR不再成立。

一、静电学1.两种电荷、电荷守恒定律、元电荷：(e＝1.60×10-19C）；带电体电荷量等于元电荷的整数倍2.库仑定律：F＝kQ1Q2/r2（在真空中）｛F:点电荷间的作用力(N)，k:静电力常量k＝9.0×109N•m2/C2，Q1、Q2:两点电荷的电量(C)，r:两点电荷间的距离(m)，方向在它们的连线上，作用力与反作用力，同种电荷互相排斥，异种电荷互相吸引｝3.电场强度：E＝F/q（定义式、计算式)｛E:电场强度(N/C)，是矢量（电场的叠加原理），q：检验电荷的电量(C)｝4.真空点（源）电荷形成的电场E＝kQ/r2 ｛r：源电荷到该位置的距离（m），Q：源电荷的电量｝5.匀强电场的场强E＝UAB/d ｛UAB:AB两点间的电压(V)，d:AB两点在场强方向的距离(m)｝6.电场力：F＝qE ｛F:电场力(N)，q:受到电场力的电荷的电量(C)，E:电场强度(N/C)｝7.电势与电势差：UAB＝φA-φB，UAB＝WAB/q＝-ΔEAB/q8.电场力做功：WAB＝qUAB＝Eqd｛WAB:带电体由A到B 时电场力所做的功(J)，q:带电量(C)，UAB:电场中A、B两点间的电势差(V)(电场力做功与路径无关),E:匀强电场强度,d:两点沿场强方向的距离(m)｝9.电势能：EA＝qφA｛EA:带电体在A点的电势能(J)，q:电量(C)，φA:A点的电势(V)｝10.电势能的变化ΔEAB＝EB-EA ｛带电体在电场中从A位置到B位置时电势能的差值｝11.电场力做功与电势能变化ΔEAB＝-WAB＝-qUAB (电势能的增量等于电场力做功的负值)12.电容C＝Q/U(定义式,计算式) ｛C:电容(F)，Q:电量(C)，U:电压(两极板电势差)(V)｝13.平行板电容器的电容C＝εS/4πkd（S:两极板正对面积，d:两极板间的垂直距离，ω：介电常数）常见电容器〔见第二册P111〕14.带电粒子在电场中的加速(Vo＝0)：W＝ΔEK或qU＝mVt2/2，Vt＝(2qU/m)1/215.带电粒子沿垂直电场方向以速度Vo进入匀强电场时的偏转(不考虑重力作用的情况下)类似平抛运动平行电场方向:初速度为零的匀加速直线运动d＝at2/2，a＝F/m＝qE/m 垂直电场方向:匀速直线运动L＝Vot(在带等量异种电荷的平行极板中：E＝U/d)二、恒定电流1.电流强度：I＝q/t｛I:电流强度(A），q:在时间t内通过导体横载面的电量(C），t:时间(s）｝2.欧姆定律：I＝U/R ｛I:导体电流强度(A)，U:导体两端电压(V)，R:导体阻值(Ω)｝3.电阻、电阻定律：R＝ρL/S｛ρ:电阻率(Ω•m)，L:导体的长度(m)，S:导体横截面积(m2)｝4.闭合电路欧姆定律：I＝E/(r+R)或E＝Ir+IR也可以是E＝U内+U外｛I:电路中的总电流(A)，E:电源电动势(V)，R:外电路电阻(Ω)，r:电源内阻(Ω)｝5.电功与电功率：W＝UIt，P＝UI｛W:电功(J)，U:电压(V)，I:电流(A)，t:时间(s)，P:电功率(W)｝6.焦耳定律：Q＝I2Rt｛Q:电热(J)，I:通过导体的电流(A)，R:导体的电阻值(Ω)，t:通电时间(s)｝7.纯电阻电路中:由于I＝U/R,W＝Q，因此W＝Q＝UIt＝I2Rt＝U2t/R8.电源总动率、电源输出功率、电源效率：P总＝IE，P出＝IU，η＝P出/P总｛I:电路总电流(A)，E:电源电动势(V)，U:路端电压(V)，η：电源效率｝9.电路的串/并联串联电路(P、U与R成正比) 并联电路(P、I与R成反比)电阻关系　R串＝R1+R2+R3+ 1/R并＝1/R1+1/R2+1/R3+电流关系I总＝I1＝I2＝I3 I并＝I1+I2+I3+电压关系U总＝U1+U2+U3+ U总＝U1＝U2＝U3功率分配P总＝P1+P2+P3+ P总＝P1+P2+P3+三、磁场1.磁感应强度是用来表示磁场的强弱和方向的物理量,是矢量，单位T),1T＝1N/A•m2.安培力F＝BIL；(注：L⊥B) {B:磁感应强度(T),F:安培力(F),I:电流强度(A),L:导线长度(m)}3.洛仑兹力f＝qVB(注V⊥B);质谱仪〔见第二册P155〕｛f:洛仑兹力(N)，q:带电粒子电量(C)，V:带电粒子速度(m/s)｝4.在重力忽略不计(不考虑重力)的情况下,带电粒子进入磁场的运动情况(掌握两种)：（1）带电粒子沿平行磁场方向进入磁场:不受洛仑兹力的作用,做匀速直线运动V＝V0(2)带电粒子沿垂直磁场方向进入磁场:做匀速圆周运动,规律如下a)F向＝f洛＝mV2/r＝mω2r＝mr(2π/T)2＝qVB；r＝mV/qB；T＝2πm/qB；(b)运动周期与圆周运动的半径和线速度无关,洛仑兹力对带电粒子不做功(任何情况下)；(c)解题关键:画轨迹、找圆心、定半径、圆心角（＝二倍弦切角）。