高鸿业《西方经济学(微观部分)》(第6版)课后习题详解(博弈论初步)【圣才出品】
- 格式:pdf
- 大小:461.71 KB
- 文档页数:9

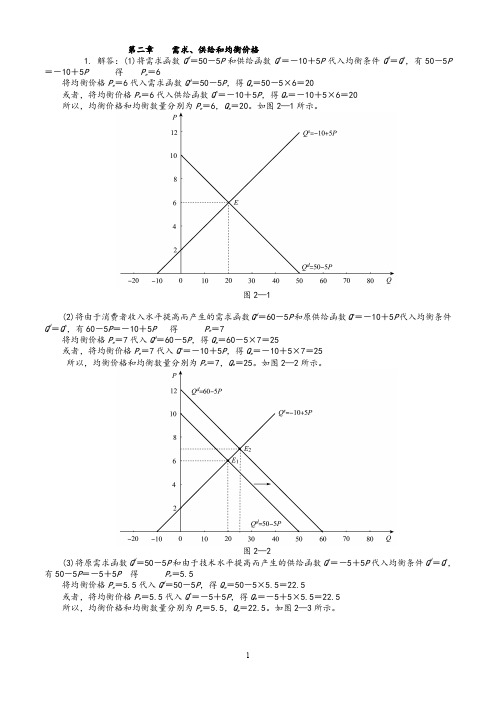
第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P 和供给函数Q s=-10+5P 代入均衡条件Q d=Q s,有50-5P =-10+5P 得 P e =6将均衡价格P e =6代入需求函数Q d=50-5P ,得Q e =50-5×6=20或者,将均衡价格P e =6代入供给函数Q s=-10+5P ,得Q e =-10+5×6=20 所以,均衡价格和均衡数量分别为P e =6,Q e =20。
如图2—1所示。
图2—1 (2)将由于消费者收入水平提高而产生的需求函数Q d =60-5P 和原供给函数Q s =-10+5P 代入均衡条件Q d=Q s,有60-5P =-10+5P 得 P e =7将均衡价格P e =7代入Q d=60-5P ,得Q e =60-5×7=25或者,将均衡价格P e =7代入Q s=-10+5P ,得Q e =-10+5×7=25 所以,均衡价格和均衡数量分别为P e =7,Q e =25。
如图2—2所示。
图2—2(3)将原需求函数Q d =50-5P 和由于技术水平提高而产生的供给函数Q s =-5+5P 代入均衡条件Q d =Q s,有50-5P =-5+5P 得 P e =5.5将均衡价格P e =5.5代入Q d=50-5P ,得Q e =50-5×5.5=22.5或者,将均衡价格P e =5.5代入Q s=-5+5P ,得Q e =-5+5×5.5=22.5 所以,均衡价格和均衡数量分别为P e =5.5,Q e =22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E 就是一个体现了静态分析特征的点。


第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5。
5将均衡价格P e=5。
5代入Q d=50-5P,得Q e=50-5×5。
5=22。
5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5。
5=22.5所以,均衡价格和均衡数量分别为P e=5。
5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E 就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s =-10+5P 和需求函数Q d =50-5P 表示,均衡点E 具有的特征是:均衡价格P e =6,且当P e =6时,有Q d =Q s =Q e =20;同时,均衡数量Q e =20,且当Q e =20时,有P d =P s =P e =6。

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P =-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E 就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s =-10+5P 和需求函数Q d=50-5P 表示,均衡点E 具有的特征是:均衡价格P e =6,且当P e =6时,有Q d =Q s=Q e =20;同时,均衡数量Q e =20,且当Q e =20时,有P d =P s =P e =6。

高鸿业《西方经济学(微观部分)》(第6版)课后习题详解第8章生产要素价格的决定1.说明生产要素理论在微观经济学中的地位。
答:微观经济学的核心是价格决定理论,包括产品价格的决定和生产要素价格的决定以及产品和生产要素价格的同时决定——即一般均衡问题。
从商品的角度来看,微观经济学可以分为两个部分,即关于“产品”的理论和关于“要素”的理论。
前者讨论产品的价格和数量的决定,后者讨论要素的价格和数量的决定。
产品的理论和要素的理论是相互联系的。
特别是,产品理论离不开要素理论,否则就不完全。
这是因为:首先,产品理论在讨论产品的需求曲线时,假定了消费者的收入水平为既定,但并未说明收入水平是如何决定的;其次,在推导产品的供给曲线时,假定了生产要素的价格为既定,但并未说明要素的价格是如何决定的。
这两点都与要素理论有关。
因此,要素理论可以看成是产品理论的自然的延伸和发展。
在经济学中,生产要素的决定理论是分配理论的重要理论基础。
生产要素分为三大类:土地、劳动和资本。
这三种生产要素的价格分别是地租、工资和利息。
三种要素的均衡价格一旦被决定,其均衡数量也就决定了,每种要素的价格与数量的乘积即为要素所有者的收入。
所以,要素价格决定理论也是经济学中的收入分配理论。
产品理论通常被看成是“价值”理论,要素理论通常被看成是“分配”理论。
产品理论加上要素理论,或者说,价值理论加上分配理论,构成了整个微观经济学的一个相对完整的体系。
2.试述完全竞争厂商的要素使用原则。
答:厂商在使用要素时同样遵循利润最大化原则,即要求使用要素的“边际成本”和“边际收益”相等。
在一般情况下,厂商使用要素的边际收益是“边际收益产品”(要素的边际产品和产品的边际收益的乘积),边际成本是“边际要素成本”。
因此,一般厂商使用要素的原则是:边际收益产品等于边际要素成本。
在完全竞争条件下,边际收益产品等于“边际产品价值”(要素的边际产品和产品价格的乘积),而边际要素成本等于“要素价格”。
第二章需求、供给和均衡价格1。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P =-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2-2所示.图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5。
5代入Q d=50-5P,得Q e=50-5×5。
5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5。
5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22。
5。
如图2-3所示.图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征.也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E 就是一个体现了静态分析特征的点.它是在给定的供求力量的相互作用下达到的一个均衡点.在此,给定的供求力量分别用给定的供给函数Q s =-10+5P 和需求函数Q d =50-5P 表示,均衡点E 具有的特征是:均衡价格P e =6,且当P e =6时,有Q d =Q s =Q e =20;同时,均衡数量Q e =20,且当Q e=20时,有P d =P s =P e =6。
高鸿业《西方经济学(微观部分)》(第6版)课后习题附带答案详解(完整版)引言《西方经济学(微观部分)》是高鸿业教授编写的一本经济学教材,该教材旨在介绍西方经济学的基本概念和理论,以及微观经济学的相关内容。
本文档为该教材的课后习题的答案详解,共计1200字。
第一章供需和市场机制1.1 供给和需求1.1.1 习题1.解答:供给和需求是市场经济中最基本的两个概念。
供给表示所有卖方愿意在一定价格下出售的商品或劳务的数量。
需求表示在一定价格下,所有买方愿意购买的商品或劳务的数量。
供给和需求关系紧密,是市场价格形成的基础。
备注:在这道习题中,要求解答供给和需求的概念以及它们之间的关系。
可以简单明了地解释供给和需求的含义,以及它们在市场价格形成中的作用。
2.解答:需求曲线表示在一定价格下,市场上所有买方愿意购买的商品或劳务的数量。
需求曲线通常呈现负斜率,即价格上升时,需求量下降;价格下降时,需求量增加。
这是因为随着价格的上升,购买商品或劳务的成本增加,一部分买方愿意放弃购买;价格下降时,购买商品或劳务的成本减少,买方的购买欲望增加。
备注:这道习题要求解答需求曲线的含义以及变化规律。
在解答中,可以提到需求曲线的负斜率,以及价格对需求量的影响。
3.解答:供给曲线表示在一定价格下,市场上所有卖方愿意出售的商品或劳务的数量。
供给曲线通常呈现正斜率,即价格上升时,供给量增加;价格下降时,供给量减少。
这是因为随着价格的上升,出售商品或劳务的利润增加,卖方愿意增加供给;价格下降时,利润减少,卖方愿意减少供给。
备注:这道习题要求解答供给曲线的含义以及变化规律。
在解答中,可以提到供给曲线的正斜率,以及价格对供给量的影响。
1.1.2 答案1.答案:供给和需求是市场经济中最基本的两个概念。
供给表示所有卖方愿意在一定价格下出售的商品或劳务的数量。
需求表示在一定价格下,所有买方愿意购买的商品或劳务的数量。
供给和需求关系紧密,是市场价格形成的基础。
第10章博弈论初步一、名词解释1.占优策略均衡(中央财经大学2011、2018研;兰州大学2014研)答:占优策略是指无论其他参与人采取什么策略,该参与人的最优策略都是唯一的策略。
如表10-1所示,通过对支付矩阵的分析可以看出,如果A、B两厂商都是理性的,则这个博弈的结果是两厂商都做广告,即不管一个厂商如何决定,另外一个厂商都会选择做广告。
占优策略均衡是指占有策略达到均衡时的状态。
表10-1广告博弈的支付矩阵2.纳什均衡(华中科技大学2002研;中国海洋大学2002研;东北大学2003研;武汉大学2003、2007研;北京大学2004研;北京师范大学2005、2014研;中南大学2005研;东华大学2006研;东北财经大学2007研;中央财经大学2007、2015研;财政部财政科学研究所2008研;华南师范大学2011研;北京理工大学2013研;厦门大学2013研;中南大学2016研;大连理工大学2018研;东北财经大学2018研;东南大学2018研;东北大学2018研;中南财经政法大学2007、2009、2015、2019研)答:纳什均衡是指由约翰·纳什提出每一个博弈者都确信,在给定竞争对手策略的情况下,他选择了最好的策略的策略组合。
此时,给定其他人的战略,任何个人都没有积极性去选择其他战略,从而没有人有积极性去打破这个均衡。
3.混合策略(东北大学2007研;华中科技大学2008研)答:混合策略是指在博弈中,博弈方的决策内容不是确定性的具体的策略,而是以某种概率选择不同的策略。
混合策略情况下的决策原则有以下两个:①博弈参与者互相不让对方知道或猜到自己的选择,因而必须在决策时利用随机性来选择策略,避免任何有规律性的选择。
②博弈参与者选择每种策略的概率一定要恰好使对方无机可乘,即让对方无法通过有针对性倾向的某一种策略而在博弈中占上风。
4.以牙还牙策略(东北财经大学2012研)答:以牙还牙策略的内容是:所有的成员一开始是合作的。
第二章需求、供给和均衡价格1. 解答:(1)将需求函数Qd=50-5P和供给函数Qs=-10+5P代入均衡条件Qd=Qs,有50-5P=-10+5P 得 Pe=6将均衡价格Pe=6代入需求函数Qd=50-5P,得Qe=50-5×6=20 或者,将均衡价格Pe=6代入供给函数Qs=-10+5P,得Qe=-10+5×6=20所以,均衡价格和均衡数量分别为Pe=6,Qe=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Qd=60-5P和原供给函数Qs=-10+5P代入均衡条件Qd=Qs,有60-5P=-10+5P 得Pe=7 将均衡价格Pe=7代入Qd=60-5P,得Qe=60-5×7=25或者,将均衡价格Pe=7代入Qs=-10+5P,得Qe=-10+5×7=25所以,均衡价格和均衡数量分别为Pe=7,Qe=25。
如图2—2所示。
图2—2(3)将原需求函数Qd=50-5P和由于技术水平提高而产生的供给函数Qs=-5+5P代入均衡条件Qd=Qs,有50-5P=-5+5P 得Pe=5.5将均衡价格Pe=5.5代入Qd=50-5P,得Qe=50-5×5.5=22.5 或者,将均衡价格Pe=5.5代入Qs=-5+5P,得Qe=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为Pe=5.5,Qe=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Qs=-10+5P和需求函数Qd=50-5P表示,均衡点E具有的特征是:均衡价格Pe=6,且当Pe =6时,有Qd=Qs=Qe=20;同时,均衡数量Qe=20,且当Qe=20时,有Pd=Ps=Pe=6。
第10章博弈论初步
1.什么是纳什均衡?纳什均衡一定是最优的吗?
答:(1)纳什均衡指的是参与人的这样一种策略组合,在该策略组合上,任何参与人单独改变策略都不会得到好处。
即如果在一个策略组合中,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。
(2)纳什均衡不一定是最优的。
因为每个人从自己理性出发所做出的选择在社会看来可能就不是最优的,存在如“囚徒困境”之类的情况。
2.在只有两个参与人且每个参与人都只有两个策略可供选择的情况下,纯策略的纳什均衡最多可有几个?为什么?
答:在只有两个参与人且每个参与人都只有两个策略可供选择的情况下,纯策略的纳什均衡最多可以有四个。
分析如下:
在只有两个参与人且每个参与人都只有两个策略可供选择的情况下,纳什均衡仅仅要求每个人在对方不改变策略的前提下自己也不改变策略,即参与人是消极应对的。
所以,可能存在四个纯策略的纳什均衡,一个一般的例子如表10-1所示。
表10-1 参与人A、B的支付矩阵
表10-4中,若满足1121a a =、1222a a =、1112b b =和2122b b =,则该博弈矩阵存在四个纯
策略纳什均衡(1111,a b )、(2222,a b )、(1212,a b )和(2121,a b )。
3.在只有两个参与人且每个参与人都只有两个策略可供选择的情况下,纯策略的纳什均衡可能有三个。
试举一例说明。
答:一个一般的例子如表10-2所示。
表10-2中,若满足1121a a =、1222a a =、1112b b =、
2122b b >,则该博弈矩阵存在三个纯策略纳什均衡(11a ,11b )
、(21a ,21b )和(12a ,12b )。
表10-2 参与人A 、B 的支付矩阵
4.在只有两个参与人且每个参与人都只有两个策略可供选择的情况下,如何找到所有的纯策略纳什均衡?
答:在只有两个参与人且每个参与人都只有两个策略可供选择的情况下,可以用“条件策略下划线法”找到所有的纯策略纳什均衡。
分析如下:
例如,对于甲乙两个厂商,对于是否合作的选择。
首先,是用下划线来表示甲厂商的条件策略。
例如,当乙厂商选择合作时,甲厂商的条件策略得出方法如下,比较甲选择合作和非合作时甲的利益的大小,哪个数字大就在该数字下画一条横线;同理,当乙厂商选择不合作时,甲比较选择合作和非合作时甲的利益的大小,哪个数字大就在该数字下画一条横线。
其次,用下划线来表示乙厂商的条件策略。
道理是一样的,只不过是乙比较合作与非合作的收益,在收益大的数字下划横线。
最后,确定博弈的均衡。
一旦把甲厂商和乙厂商的所有条件策略都用下划线方法表示出来以后,确定博弈均衡的任务就变得非常简单——只要找到在两个数字之下都画线的单元格即可。
与这些单元格相对应的策略组合就是所要求的均衡策略组合。
5.设有A、B两个参与人。
对于参与人A的每一个策略,参与人B的条件策略有无可能不止一个?试举一例说明。
答:对于参与人A的每一个策略,参与人B的条件策略有可能不止一个。
当两种选择数值相同时,参与人B的条件策略就有两个,如表10-3所示。
表10-3 参与人A、B的支付矩阵
当A选择不合作策略时,B的两种选择是一样的,所以就有两个条件策略。
6.如果无论其他人选择什么策略,某个参与人都只选择某个策略,则该策略就是该参与人的绝对优势策略(简称优势策略)。
试举一例说明某个参与人具有某个优势策略的情况。
答:如表10-4所示,无论参与人A选择合作还是不合作,参与人B都选择合作,因为>。
32
>,54
表10-4 参与人A、B的支付矩阵
7.混合策略博弈与纯策略博弈有什么不同?
答:两个决策者原来的“非此即彼”策略称之为“纯策略”,而若赋予这些纯策略一些概率向量则称之为“混合策略”。
纯策略博弈不涉及任何概率,是一定会做出的选择,或者可以认为纯策略是混合策略博弈中概率为1的特殊情况,即选择该种策略的概率为1,选择其他任何纯策略的概率为0。
混合策略博弈要考虑具体决策人选择每个概率的大小,从而再作出判断。
8.条件混合策略与条件策略有什么不同?
答:把一决策人在另一决策人选择某种策略下的最优策略称为该决策人的条件优势策略(或相对优势策略),简称条件策略,把与该决策人的这一条件策略相联系的策略组合称为该决策人的条件优势策略组合(或相对优势策略组合),简称条件策略组合。
条件策略不同于条件策略组合。
前者是参与人在给定条件下(如其他参与人已经做出选择时)的相对优势策略,后者则是包括参与人的条件策略以及这些条件在内的相对优势策略组合。
9.混合策略纳什均衡与纯策略纳什均衡有什么不同?
答:在博弈中,博弈方只作出一种特定的选择,并且始终坚持这一选择,这样的肯定性策略又称纯策略。
与之相对应的,只能按一定概率分布选择几种不同的行动的策略称之为混合策略。
混合策略纳什均衡与纯策略纳什均衡的差异集中体现在:混合策略纳什均衡是在一定的概率条件下得出的均衡,是和概率紧密相关的,会随着概率数值的变化而发生变化,而纯策略纳什均衡和概率无关,是一定会发生的。
另外,就一个具体的博弈支付矩阵而言,可能不存在纯策略纳什均衡,但一定存在混合策略纳什均衡。
也就是说,混合策略纳什均衡总是存在的。
10.设某个纯策略博弈的纳什均衡不存在。
试问:相应的混合策略博弈的纳什均衡会存在吗?试举一例说明。
答:某个纯策略博弈的纳什均衡不存在,相应的混合策略博弈的纳什均衡会存在。
举例说明如下:在社会福利博弈中,参与人是政府和一个流浪汉,前者有两个策略:救济或不救济,后者也有两个策略:寻找工作或游荡。
政府想帮助流浪汉,但前提是后者必须试图寻找工作,否则将不给予救济;而流浪汉只有在得不到政府救济时才会寻找工作。
双方的博弈支付矩阵如表10-5所示。
表10-5 社会福利博弈
如表10-5所示,通过对支付矩阵的分析可以看出,这个博弈不存在纯策略博弈的纳什均衡。
但是,相应的混合策略博弈的纳什均衡存在。
通过计算可知,在混合策略纳什均衡下,政府以0.5的概率选择救济,以0.5的概率选择不救济;同时,流浪汉以0.2的概率选择寻找工作,以0.8的概率选择继续游荡。
11.设某个纯策略博弈的纳什均衡是有限的。
试问:相应的混合策略博弈的纳什均衡会是无限的吗?试举一例说明。
答:某个纯策略博弈的纳什均衡是有限的,相应的混合策略博弈的纳什均衡可能会是无限的。
表10-6 存在有限的纯策略均衡时的混合策略均衡
如表10-6所示,显然可见,该博弈有两个纯策略纳什均衡,即(上,左)和(上,右)。
但是,该博弈有无限个混合策略纳什均衡。
比如说,当甲选“上”时,乙以任意概率q(01
≤≤)
q
选择“左”,1q-的概率选择“右”,显然这就是相应的混合策略博弈的纳什均衡,均衡数为无限个。
12.在完全信息动态博弈中,纳什均衡与逆向归纳策略有什么不同?
答:在完全信息动态博弈中,可能存在多个纳什均衡的情况。
在多个纳什均衡中,有些可能并不合理,这就需要通过对纳什均衡进行“精炼”,即采用“逆向归纳法”来进行求解。
通过采用“逆向归纳法”求解可以发现,得出的逆向归纳策略总是纳什均衡。
但是,纳什均衡并不一定也是逆向归纳策略。
这是纳什均衡与逆向归纳策略两者之间的关系,也是两者的区别所在。
简言之,在存在多重纳什均衡时,逆向归纳法就是对纳什均衡的精炼。
13.在下面的博弈树中,确定纳什均衡和逆向归纳策略。