由X射线衍射获得的液体径向分布函数
- 格式:pdf
- 大小:298.13 KB
- 文档页数:8




三、径向分布函数法中心分子第一层:第一配位圈 第二层:第二配位圈 . . .短程有序,远程无序1、 基本概念,基本定义首先定义一个新的函数---n 重相关函数 为当系统的位能E N = 0 ,则系统内分子是独立的,由分布函数公式可得到:g(r)r因此对于分子相互独立的系统,,对于分子间有相互作用的系统,相当于对分子独立性的校正,亦即表示了分子的相关性,因而称之为相关函数。
相关函数中,最重要的是二重相关函数g(2),它可由X射线衍射实验和计算机分子模拟的机器实验结果获得,由式子可知表示如下上式即二重相关函数与位形积分的关系。
对于由球星对称分子构成的液体,仅取决于分子1和2的距离,即可写成g(r),所以就有故上式中的分子相对函数g(r)就是分子的径向分布函数。
因,即第一个分子是任意分布的。
由于液体分子间存在相互作用,第二个分子不可能任意分布,而构成相对于中心分子的局部密度,相应的二重分布函数为将上式代入到中得到所以径向分布函数g(r)的物理意义可解释为:在一个中心分子周围距离为r处,分子的局部密度相对于本体密度的比值。
从径向分布函数g(r)可以计算液体的配位数:实际上N为中心分子周围分子的总数,而为距中心分子r处在r + dr壳层内的分子数目。
若将上式积分到第一配位圈的距离L处,即可得到配位数N(L)为N(L)实际上也是围绕中心分子,半径为r=L的球体内的分子数。
如图已知:r1,r2…rN 代表坐标系原点,指向分子1,2,… N 的向量,体系分子1,分子2分别出现在r1处的体系元 的几率为:称双重标明分布函数;:泛指(任意分子分布在r1, r2处的概率):双重分布函数()()()NkT r r u N kT q u K KNTr id d de d d d e Q N N ττττττϕϕϕ............121/...21/1⎰⎰⎰⎰=-*===2τd ()()()KN kT r r r u d d d d e d d r r P N ϕττττττ213/,...,21212]......[,21⎰⎰-=()()()KN kTr r u d d e r r P N ϕττ⎰⎰-=......,3/...2121()()21212,ττd d r r P()()212,r r ρ()()()()()()()2122212212,,1,r r PNr r P N N r r ≈-=ρxy所以: (几率归一化性质)N 重分布函数:(n 重标明分布函数)(n 重分布函数)数密度径向分布函数定义由式子得到,与一指定分子相距r 处,分子局部密度与平均数密度之比;的定义:()()()()()221212212121,1,NN N d d r r d d r r P V≈-==⎰⎰⎰⎰ττρττ()()()KN n r r r u N n d d e r r r P N ϕττ⎰⎰+-=.........,1,...,2121()()()()()()n n n n r r P n N N M r r ,...1...1,...11+--=ρ()()V r P 111=()()11111==⎰⎰V d d r P ττ()()V Nr n =1ρzr 1xr 2d τ1 d τ2yr 12 ()()ρρr r g =()()()()()()()1221212..,21r g P P r r r r =ρ()12r g ()()()()r g V N r g V N V N r (2)12122⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=ρ所以:最简单的: 2、热力学的计算(用径向分布函数计算)由正则系统配分函数为 从而得到系统的能量为E式中第一项为体系的平均动能,第二项为体系的平均位能。

结构化学复习题(2009.12)一、填空题:(1)使波函数与其复共轭之乘积在全部空间区域内的积分值等于1,这个过程称为波函数的 。
(2)在量子力学中,用 来描述微观粒子运动状态。
(3)动量分量p z 对应的量子力学算符是 。
(4)3p 电子轨道角动量的大小可以表示为 。
(5)在线性变分法中,对两个原子形成化学键起关键作用的积分是 。
(6)波函数必须满足单值性、 、连续性。
(7)将电子和原子核的运动分开处理的近似称为 近似。
(8)电子云径向公布函数D(r)的定义式是 。
(9)电子波函数的值在空间相等的点所构成的空间曲面称为 。
(10)直线型分子对称轴的轴次为 。
(11)一个Cn 对称轴可以生成 个独立的对称操作。
(12)在F 2的分子轨道中(包含内层电子),3σg 的能量 1πu 的能量。
(13)CH 3Br 分子所属的点群为 。
(14)CH 2Cl 2分子所属的点群是 。
(15)原子轨道杂化后,轨道的极大值主要分布在 方向上。
(16)在sp n杂化轨道k ks s kp p c c ψφφ=+中,表示s 轨道成份的量是 。
(17)在第k 个杂化轨道Ψ k 中,某种轨道的总成份αi 与该种轨道的组合系数c i 的关系是 。
(18)HCl 所属的分子点群是 。
(19)在BF 3分子中形成大π键时,B 原子提供的电子数是 。
(20)八面体配位场中中心离子的t 2g 轨道是 三个轨道。
(21)CO 32-基团中所形成的大π键m n π是 。
(22)配位体的群轨道与中心原子相对应的原子轨道的 相同。
(23)在O h 场中,分裂后的每个t 2g 轨道的能量降低了 Dq 。
(24)自然界中存在的晶体空间点阵结构型式只能有 种。
(25)将对称性高、含有阵点数目尽可能少的平行六面体单位称为 。
(26)密置层为ABABAB 式的最密堆积方式是 密堆积。
(27)晶体结构中周期性重复着的内容称为 。
(28)金属原子等径圆球最密堆积中,球的配位数是 。

液体径向分布函数液体径向分布函数是描述液体分子在空间中分布的一种重要统计量,广泛应用于材料科学、化学、物理等学科中的研究。
本文将具体介绍液体径向分布函数的定义、计算方法、物理意义以及应用。
液体中分子间相互作用很强,其分子间的距离分布是非均匀的,径向分布函数是刻画液体分子间距离分布的重要工具。
液体径向分布函数的定义为:在液体内,离分子中心距离为r的微元体积内有分子的平均数目与离分子中心距离为r的微元体积的比值。
即:$g(r)=\frac{1}{4\pi r^2 \rho}\frac{\sum_i \sum_{j\neq i}\delta(r-|r_i-r_j|)}{\sum_i 1}$ (1)其中,$\rho$为液体的密度,$r_i$为第i个分子的位置矢量。
从上式中可以看出,径向分布函数是一个距离的函数,表示距离为r的体积内所含分子数量与密度的比值,也称为“分子配位数”。
液体径向分布函数是通过计算在不同距离r上的微元体积内所含有的分子对数目,然后除以微元体积和粒子密度来得到的。
一般的,液体径向分布函数的计算方法分为以下两类:1.实验测定法:在实验中,可以通过X射线、中子散射等手段测定液体分子间的相互距离,进而得到径向分布函数。
2.计算机模拟方法:通过分子动力学模拟、分子动态学模拟等计算机模拟方法,可以计算出液体分子间的相互作用力,进而求解径向分布函数。
1.反映液体的壁效应:液体分子在固体表面附近的密度较大,径向分布函数可以反映出这种局部的密度变化,表征了液-固界面的结构。
2.描述分子自相似性:一般情况下,径向分布函数乘以体积元以后,是可以归一化的。
对于相同的液体,其径向分布函数在不同温度下呈现出自相似的特征,这表明液体在不同温度下具有相似的结构特征。
3.计算液体的热力学性质:液体径向分布函数是计算液体结构中间相互作用势能、压力、自由能等热力学性质的重要参数。
液体径向分布函数在化学、物理、材料科学等学科中应用广泛,主要应用包括以下几个方面:1.计算物质的相变和物性: 液体径向分布函数可以用于计算物质的相变和物性,如密度、粘度、热容等。


由X 射线衍射获得的液体径向分布函数房春晖,房艳,杨波,雷亚川(中国科学院青海盐湖研究所,陕西西安710043)摘要:主要介绍单原子液体、同核分子液体、杂核分子液体和水溶液电子径向分布函数、原子径向分布函数和分子径向分布函数的定义,简明阐述了气体、液体和晶体,尤其是二维晶体的径向分布函数的物理意义和几何意义。
关键词:径向分布函数;液体结构;水溶液中国分类号:O722 文献标识码:A 文章编号:1008-858X (2002)02-0061-080 前言液体结构一直是理论基础研究的重要领域。
其结构的复杂性和多样性不仅包含丰富的理论内涵,而且具有广泛的应用前景。
液体及其相变在技术上和工业上的巨大应用潜力和液体结构丰富新颖的物理图象,已引起人们日益广泛的重视[1,2]。
例如过饱和溶液介乎于平衡溶液和水合晶体熔盐之间,过饱和度是结晶过程的推动力,母液结构是晶体生长的关键环节,液体的结构直接关系到目前一些前沿难题的攻关,人们期望从分子和离子相互作用的根本上揭示环境科学、盐湖化学、生命和信息科学领域的本质问题。
例如NO 2、S O 2酸雨形成过程中,小水滴的成核机理;大气圈平衡、水圈平衡、生物圈新陈代谢平衡和矿物圈平衡中温室气体二氧化碳及其相关的碳酸盐与水分子的相互作用;普遍存在于生物体中的水和电解质的作用机制,如厌氯作物中硫酸盐与水的相互作用;盐湖开发利用中所涉及的化学相变机制和控制规律等。
随着地球上最重要液体———水战略资源问题日益严峻,液体结构研究将是新世纪化学发展的重要方向之一。
液体径向分布函数描述被研究液体的电子密度、原子密度或分子密度的空间校正关系。
与晶体物质相比较,液体的结构特征更难于直接准确测量和表征。
近年来,随着衍射实验技术和理论计算方法所取得的巨大进步,不仅能够精确有效地测量溶液中各种距离和方向上的原子间相互作用信息,而且能够通过建立几何模型来处理这些具有统计特征的信息,最终实现对溶液中溶剂化离子、溶剂分隔离子对、溶剂共享离子对、接触离子对、以及衍射实验能够测量到的离子簇的原子核间距、配位数和配位几何构型作出离子、分子水平的定量描述。

X射线衍射分析原理及应用一、X射线衍射分析的原理X射线衍射的基本原理是当X射线入射到晶体表面时,由于晶体具有定向排列的原子或离子,X射线与晶体中的电子发生相互作用并散射,形成不同方向上的干涉条纹,通过测量和分析这些干涉条纹的位置和强度可以推断出晶体的结构特征。
具体来说,X射线衍射分析的原理可以归纳为以下几个方面:1. 布拉格法则:当入射角θ和出射角θ'满足布拉格方程nλ = 2d·sinθ,即入射的X射线与晶体晶面的倾角和衍射角满足特定的关系时,会发生衍射。
2.动态散射:在晶体中,入射的X射线会与晶格中的电子发生相互作用,散射成各个方向上的次级波,波的振动方向垂直于入射方向。
3.干涉:次级波在不同晶面的散射电子之间发生干涉,产生特定的干涉条纹。
4.衍射图样:干涉条纹的位置和形状与晶体的晶胞结构、晶面间距以及晶体取向有关,通过测量和分析衍射图样可以确定这些信息。
二、X射线衍射分析的应用1.晶体结构分析:通过在不同角度下测量样品的X射线衍射图样,可以推断出材料的晶体结构,包括晶胞参数、晶面间距、原子位置等信息。
这对于理解材料的物理、化学以及电子结构等性质非常重要。
2.晶体取向分析:X射线衍射分析可以用来确定晶体中不同晶向的取向分布,即晶体中晶面的取向。
这对于材料工艺和性能的控制具有重要意义,例如金属的冷轧、挤压等过程中,晶体的取向对材料的力学性能有很大影响。
3.晶体缺陷分析:晶体中存在着各种缺陷,如位错、晶界、析出相等。
通过观察和分析X射线衍射图样中的峰形和峰宽等信息,可以确定晶体的缺陷类型和含量,进而了解材料的机械、电学以及热学性质。
4.应力分析:在材料的变形过程中,晶体中会引入应力场。
应力会引起晶格的畸变,从而导致X射线衍射图样的形状和位置发生变化。
通过分析这些变化可以得到材料中的应力分布和大小,对于材料的力学性能的评估和优化具有重要意义。
总之,X射线衍射分析是一种非常重要的材料表征方法,可以提供丰富的关于晶体结构、晶胞参数、晶体取向以及晶体缺陷等信息。

试验与研究NiTi非晶薄膜的径向分布函数及结构分析展西国,单连君,姜训勇,张 建(天津理工大学材料科学与工程学院,天津300191)摘 要:径向分布函数(RDF)是描述非晶态材料结构的重要工具,一般是通过对衍射强度的解析计算得到的。
RAD程序是根据非晶材料X射线衍射数据计算其径向分布函数的集成程序。
介绍了该程序的结构和应用方法,并采用RAD程序计算了采用磁控溅射法制备不同成分Ni Ti合金的径向分布函数,利用径向分布函数计算了非晶微结构参数。
结果表明非晶薄膜中钛含量不同影响了非晶微结构参数。
关键词:非晶薄膜;Ni Ti;径向分布函数;软件中图分类号:TB43;TB383 文献标识码:A 文章编号:100124012(2008)0520223203RADIAL DISTRIBU TION FU NC TION AND T H E STRU C TU R EANAL YSIS O F HOU S Ni Ti FIL MZHAN Xi2guo,SHAN Lian2jun,JIANG Xun2yong,ZHANG Jian (Department of Materials Science and Engineering,Tianjin University of Technology,Tianjin300191,China)Abstract:Radial distribution f unction(RDF)is a important tool to demostrate the microstructure of noncystalline solid.It is usually get f rom analysising the diff raction intesity of noncrystalline solid.RAD is a integrated programe to calcualted RDF f rom diffraction data.The main part of programe and the main step were introduced.The radial distribution f unction of Ni Ti film with different composition were calculated by RAD.The microstructure parameter of amorphous film was obtained from the analysis of the radial distribution f unction.The result show that microstructure parameter of amorphous Ni Ti was influence by the content of Ti.K eyw ords:Amorphous film;Ni Ti;Radial distribution function;Software 非晶态结构中原子排列呈现长程无序、短程有序的特点。
Python径向分布函数一、概述径向分布函数(Radial Distribution Function,简称RDF)是用来描述粒子在空间中的分布情况的一种函数。
在物理、化学和材料科学等领域中,径向分布函数是一种常用的工具,可以用来研究原子、分子或离子之间的相互作用、结构和动力学等问题。
在Python中,我们可以使用不同的方法和库来计算和绘制径向分布函数。
本文将介绍如何用Python编写径向分布函数的代码,并给出一些实例来帮助读者更好地理解和应用径向分布函数。
二、计算径向分布函数的方法计算径向分布函数的方法有很多种,其中比较常用的方法有直接计算法、快速傅里叶变换法和分子动力学模拟法等。
下面将分别介绍这三种方法的原理和应用。
2.1 直接计算法直接计算法是最简单和直接的方法,它基于统计学原理,通过计算在一定距离范围内的粒子对的数量来估计径向分布函数。
具体步骤如下:1.将空间划分为一系列的小体积元,通常是立方体或球体。
2.对于每个小体积元,计算其中粒子对的数量。
3.根据粒子对的数量和小体积元的体积,计算径向分布函数的值。
直接计算法的优点是简单易懂,计算速度比较快。
但是它也有一些局限性,比如需要将空间离散化,对于连续分布的粒子系统不适用。
2.2 快速傅里叶变换法快速傅里叶变换法(Fast Fourier Transform,简称FFT)是一种基于傅里叶变换的计算径向分布函数的方法。
它的基本思想是将径向分布函数转化为频率域上的信号,然后利用快速傅里叶变换算法进行计算。
具体步骤如下:1.将粒子的坐标数据转化为径向距离数据。
2.对径向距离数据进行快速傅里叶变换,得到频域上的信号。
3.根据频域上的信号,计算径向分布函数的值。
快速傅里叶变换法的优点是计算速度非常快,尤其适用于大规模的粒子系统。
但是它也有一些限制,比如需要将粒子的坐标数据转化为径向距离数据,对于非球对称的粒子系统不适用。
2.3 分子动力学模拟法分子动力学模拟法是一种基于分子动力学模拟的计算径向分布函数的方法。
化工过程中模型的建立与计算姓名:田保华化工过程中模型的建立与计算1. 概述过程的状态监控或过程的在线监测都需要建立合适的数学模型。
化工过程的数学模型主要有三大类方法,即机理模型,统计模型和混合模型。
描述过程的方程组由过程机理出发,经推导得到,并且由实验验证,这样建立起来的模型就是机理模型。
机理模型方法需要凭借可靠的规律及经验知识来建立原始微分方程式,这些规律和经验知识必须被表达为一般的形式。
机理模型是对实际过程直接的数学描述,是过程本质的反映,因此结果可以外推。
数学模型也可以根据实验装置、中型或者大型工业装置的实测数据,通过数据的回归分析得到的纯经验的数学关系式,这就是统计模型。
统计模型和过程机理无关,是根据实验从输出和输入变量之间的关系,经分析整理得到的。
它只是在实验范围内才是有效的,因而不宜外推或者以较大幅度外推。
由于实验条件的限制,统计模型的局限性很大,所以总是希望尽可能建立机理模型。
对于化工过程来说,由于经验模型受到实际条件的限制,应用范围有限,机理模型求解又十分困难,这样就产生了第三种数学模型,即混合模型。
混合模型是对实际过程进行抽象概括和合理简化,然后对简化的物理模型加以数学描述,混合模型主要是设法回避过程中一些不确定的和复杂的因素,代之以一些统计的结果和一定的当量关系,它是半经验半理论性质的。
在化工过程的数学模拟中,混合模型是应用最广的一种模型。
例如,混合模型用于粉仓中粉体流动数学模型分析等等。
近年来,人们将人工神经网络方法用于化工建模,并取得较好的效果。
化工过程中数学建模的建立一般是基于流体的性质。
流体的热力学性质主要是从状态方程(EOS)得到。
至今,文献报道的EOS已有一百五十种之多,有的从理论分析得到的、有的从实验数据分析归纳而来、还有一些是理论分析和实验数据相结合推出来。
比较经典的EOS有VDW方程,R-K方程,Soave方程,CS方程,33参数的MBWR方程。
这些经验、半经验的EOS只能在一定的温度和密度范围内对于某些流体适应,应用的范围比较窄,理论基础不强[34]。
水的径向分布函数
水的径向分布函数是描述水分子在水中分布情况的一种函数。
它是研究水分子在水中运动和相互作用的重要工具。
径向分布函数是指在一个半径为r的球内,离一个水分子最近的其他水分子数目与理想气体状态下的数目比值。
因此,径向分布函数可以用来描述水分子之间的相互作用。
在理想气体状态下,径向分布函数为1,因为每个分子之间相互独立,没有任何相互作用。
但是,在实际的液体中,水分子之间存在着相互作用,这些相互作用可以通过径向分布函数来描述。
通过实验和计算,我们可以得到水的径向分布函数,从而了解水分子之间的相互作用。
水的径向分布函数与温度、压力、溶质浓度等因素有关。
在一定温度下,随着压力的增加,径向分布函数会发生变化。
当压力足够大时,径向分布函数会发生明显的变化,这是因为压力能够改变水分子之间的相互作用。
此外,在加入溶质后,水的径向分布函数也会发生变化。
这是因为溶质与水分子之间存在着相互作用,从而影响了水分子之间的相互作用。
通过研究径向分布函数,我们可以了解水分子在液态中的运动和相互作用。
这对于研究水的物理化学性质以及液态水在生物学、化学等领域中的应用具有重要意义。
例如,在生物学领域中,了解水分子之间的相互作用可以帮助我们更好地理解生物
大分子的结构和功能。
在化学领域中,了解水分子之间的相互作用可以帮助我们更好地设计和合成新型材料。
总之,水的径向分布函数是描述水分子在液态中相互作用的重要工具。
通过研究径向分布函数,我们可以了解水分子之间的相互作用,并在生物学、化学等领域中应用这些知识。
§1 逸度和逸度系数Fugacity and FugacityCoefficient§1.1 逸度和逸度系数的定义及物理意义§1.2 纯气体的逸度计算§1.3 纯液体逸度§1.4 混合物中组分逸度§1.5 混合物的逸度与其组分逸度§1.6 压力和温度对逸度的影响i i sat isati V ii x P Py γϕϕ=ˆLiVif f =汽液平衡时L i V i μμ=isat ii x p Py ⋅=§1 逸度和逸度系数f :逸度逸度系数理想气体、理想溶液活度系数非理想气体、溶液二.逸度和逸度系数的物理意义1、对于纯物质,理想气体f=Pi是“校正压力”或“有 对于纯物质,真实气体fi效压力”表示真实气体与理想气体的偏差。
Φi2、物质在任何状态下都有逃逸该状态的趋势,逸度表示分子的逃逸趋势,相间的传递推动力。
fi•如在一定T下,液相的水分子有逃入气相的趋势,同时,气相的水分子有逃入液相的趋势。
当两个趋势相等时,气液相两相达到了平衡。
§1.2 纯气体的逸度系数计算§1.2.1 由 PVT 数据计算逸度系数§1.2.2 由 H、S 数据计算逸度系数§1.2.3 由状态方程计算逸度系数§1.2.4 由对应态原理计算逸度系数应用中,首先求逸度系数,再计算逸度。
所以,逸度系数的计算很重要,有以下方法:ii P f ϕ=①普遍化压缩因子法)1()0()lg()lg()lg(ϕωϕϕ+=10ZZ Z ω+=利用对应状态原理的思想iP r r P T ϕϕϕω−→−−−−−−−−→−--10153~123.53.,,解法:图,图ωϕϕϕ)(10=P.55 例3-8P=P s=4246Pa abCP=1MPaP=10MPaT=T cT=313.15K V=V sl=1.808x10-5m3 mol-1VP存在三种f和φ—纯组分、混合物、混合物中的i组分。
由X 射线衍射获得的液体径向分布函数房春晖,房艳,杨波,雷亚川(中国科学院青海盐湖研究所,陕西西安710043)摘要:主要介绍单原子液体、同核分子液体、杂核分子液体和水溶液电子径向分布函数、原子径向分布函数和分子径向分布函数的定义,简明阐述了气体、液体和晶体,尤其是二维晶体的径向分布函数的物理意义和几何意义。
关键词:径向分布函数;液体结构;水溶液中国分类号:O722 文献标识码:A 文章编号:1008-858X (2002)02-0061-080 前言液体结构一直是理论基础研究的重要领域。
其结构的复杂性和多样性不仅包含丰富的理论内涵,而且具有广泛的应用前景。
液体及其相变在技术上和工业上的巨大应用潜力和液体结构丰富新颖的物理图象,已引起人们日益广泛的重视[1,2]。
例如过饱和溶液介乎于平衡溶液和水合晶体熔盐之间,过饱和度是结晶过程的推动力,母液结构是晶体生长的关键环节,液体的结构直接关系到目前一些前沿难题的攻关,人们期望从分子和离子相互作用的根本上揭示环境科学、盐湖化学、生命和信息科学领域的本质问题。
例如NO 2、S O 2酸雨形成过程中,小水滴的成核机理;大气圈平衡、水圈平衡、生物圈新陈代谢平衡和矿物圈平衡中温室气体二氧化碳及其相关的碳酸盐与水分子的相互作用;普遍存在于生物体中的水和电解质的作用机制,如厌氯作物中硫酸盐与水的相互作用;盐湖开发利用中所涉及的化学相变机制和控制规律等。
随着地球上最重要液体———水战略资源问题日益严峻,液体结构研究将是新世纪化学发展的重要方向之一。
液体径向分布函数描述被研究液体的电子密度、原子密度或分子密度的空间校正关系。
与晶体物质相比较,液体的结构特征更难于直接准确测量和表征。
近年来,随着衍射实验技术和理论计算方法所取得的巨大进步,不仅能够精确有效地测量溶液中各种距离和方向上的原子间相互作用信息,而且能够通过建立几何模型来处理这些具有统计特征的信息,最终实现对溶液中溶剂化离子、溶剂分隔离子对、溶剂共享离子对、接触离子对、以及衍射实验能够测量到的离子簇的原子核间距、配位数和配位几何构型作出离子、分子水平的定量描述。
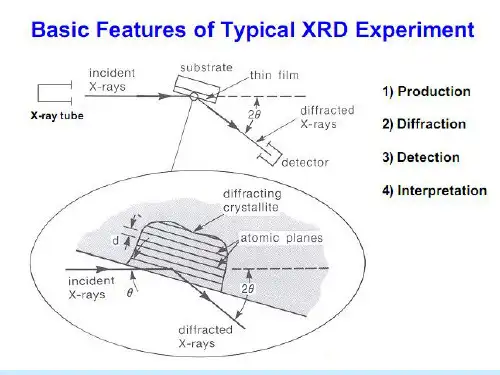
X 射线衍射法是直接获得液体短程有序结构信息的重要实验方法。
与ND 、EX AFS 、ARPEFS 、X AFS 、X ANES 等实验方法比较,实验成本低廉,一般不依赖于大型同步辐射装置。
与MD 、MC 、M M 、MD +M M 、ab Initio 等计算方法比较,是实验事实的直接测量,而没有任何虚拟性。
研究液体结构,一般采用θ/θ型液体X 射线衍射仪。
然而国内外普通实验室一般配备θ/2θ型衍射仪,而不配备θ/θ型衍射仪。
在没有θ/θ型衍射仪的情况下,我们另辟溪径,打收稿日期:2002-01-25作者简介:房春晖(1957-),男,研究员,主要从事溶液结构研究。
第10卷 第2期2002年 6月 盐湖研究JOURNA L OF S A LT LAKE RESE ARCH V ol.10 N o.2Jun. 2002破旧框架,发展了液体结构X射线衍射研究的数据处理方法,建立了用专门测定固体特别是晶体结构的θ/2θ型衍射仪精确测定液体结构的新实验方法,建议了阐述液体衍射曲线和液体结构函数的经验黄金规则,前文我们进行了较为详尽的报道[3-11]。
本文目的是由浅入深,阐述径向分布函数及其物理意义和几何意义。
1 结构函数和傅里叶变换通常由实验测定的衍射强度I,既包含与液体结构有关的局域干涉部分,也包含整体无序散射粒子散射强度累加(即原子的独立散射)和其它与结构无关部分(非等同粒子的贡献项)。
溶液局域干涉引起的短程有序部分,用i(s)函数表示,称之为结构函数。
径向分布函数首先由衍射实验数据进行i(s)函数的计算;然后对包含着大量结构相关信息,但不能直接给出结构参数的结构函数进行傅立叶变换,获得径向分布函数。
后者能直观、准确地给出峰位、峰形和峰宽,而且分别具有明确的物理意义。
然而这种直截了当的数学处理方法,实际上包含着许多技巧和技术上的困难。
因此,下面就此类问题由简单的单原子液体到多原子体系作一详细叙述。
1.1 单原子液体常见的单原子液体,如惰性元素液体、液态汞、高温液态合金等。
从单原子液体获得的相干散射幅射,可用方程[12]来描述。
[I(s)-N f2(s)]/(NZ)=∫∞o4πr2[ρ(r)-ρm-ρo(r)]sin(sr)/(sr)dr(1)式中:I(s)是对零角散射较正后的相干散射强度;N是标度因子,转换实验强度到电子单位的系数;Z是原子序数;f2(s)为相干原子散射因子;ρ(r)是电子对密度;ρm为液体平均电子密度;ρo(r)是同一原子内的电子对密度。
方程(1)可被变换为4πr2[ρ(r)-ρm-ρo(r)]=2r/π∫∞o s[I(r)-N f2(s)]/(NZ)sin(sr)ds(2)物理量4πr2[ρ(r)-ρo)]dr是距离为r,厚度为dr的球壳内的电子数目,不包括同一原子内电子对的贡献项。
4πr2[ρ(r)-ρo(r)]被称为电子径向分布函数(ERDF)。
g E=4πr2ρm+2r/π∫∞o s[I(s)-N f2(s)]/(NZ)sin(sr)ds(3)式中,电子径向分布函数的单位是e2/nm。
对单原子液体,方程(3)还可用原子中心密度函数表示为[I(s)-N f2(S)]/[N f2(S)]=∫∞o4πr2[ρa(r)-ρma][sin(sr)]/(sr)dr(4)ρa(r)是对在r=0时奇异点校正的距离为r 的原子中心密度。
ρma为平均原子密度。
sin (sr)/(sr)项的物理意义,是指原子核间距离为r 的平均散射振幅。
由傅里叶变换,得原子径向分布函数ARDF。
g A=4πr2ρa(r) =4πr2ρma(r)+(2r)/π∫∞o s[I(s)-N f2(s)]/ [N f2(s)]sin(sr)ds(5)原子径向分布函数g A与径向分布函数g (r)有关g(r)=[ρa(r)]/ρa=g A/(4πr2ρma)(6)将方程(5)代入方程(6),得g(r)=1+1/(2πr2ρma)∫∞o s[I(s)-N f2(s)]/[N f2(s)]sin(sr)ds(7)方程(3)和(5)与实验I(s)的应用,包括很多逼近方法,甚至对最简单的体系,如液He。
下面阐述数据处理的一些问题。
1.1.1 自由原子散射因子相干的自由原子散射因子f2(s)被应用在F ourier积分方程中,影响函数核的计算,在进行F ourier变换之前,不相干原子散射I inc(s)必须被计算,并从实验强度中减去,以获得I(s)。
f2 (s)和I inc(s)计算值的精度与用于计算原子散射因子的电子波函数的精度有关。
原子波函数的精确表达式,可能包括电子校正。
这样,仅对最轻的元素,表达式才有用。
最好的未校正波函数(随精度的量级降低)如下:a.相对论Hartree-F ock波函数(RHF);自洽场近似,相对论相互作用项,精确计算的交换项;b.Hartree-F ock波函数(HF);自洽场近似,非相对论相互作用项,精确计算的交换项;c.Dirac-Slater波26 盐湖研究 第10卷函数(DS);自洽场近似,相对论相互作用项,精确计算的交换项;d.Hartree-F ock-Slater波函数(HFS);自洽场近似,非相对论相互作用项,近似计算交换项;e.Hartree波函数;无交换项,自洽场近似,非相对论相互作用项;f.Thomas-Ferri-Dirac统计模型,非相对论校正项,无交换项。
对原子序数≤40的原子,相对论效应是完全可以忽略的。
因此对轻元素,RHF波函数与HF波函数是等效的。
DS和HFS也是等效的,但稍微不如BHF和HF波函数。
对f2(s)和I inc(s)计算,H波函数和TFD是非常差的。
大约在1958年,对轻元素的计算,HF散射是有用的。
从1958年以后,波函数的改善不再影响I (s)的计算。
自由原子的散射因子和不相干散射因子,,直接引用《X射线晶体学国际表》[13]。
在更精细工作中,有必要考虑计算原子散射因子的异常散射校正,实数校正部分用△f′表示,虚数校正部分用△f″表示f=f o+△f′+△f″(8)应该强调指出,由于电子波函数的瞬时性,时间变化的畸变性,原子散射因子不同于自由原子散射因子;尤其是对于分子来说,用自由原子散射因子来计算,这种假设是一种不十分精确的逼近方法。
对于环形分子如苯,进行分子中心校正也是必要的。
C om pton散射可参考Cromer[14,15]和C om pton[16]的工作。
1.1.2 标度衍射强度数值大小一般与仪器的类型,测定条件等因素有关。
这些因素主要是:光源额定功率、施加电压、施加电流、狭缝大小、扫描速率、扫描方式等。
标度因子N,可用下述两种方法确定。
a.积分法当r趋向0时,g(r)趋向0,积分方程为∫∞o s2[I(s)-N f2(s)]/[N f2(s)]ds=-2π2ρa(9)因此,可以确定标度因子N。
b.高角法在大s值下,相干散射强度逼近“无结构”的自由原子散射强度。
I(s)=N f2(s)(10)用对比高s的实验I(s)和N f2(s),确定标度因子。
从理论上讲,这两种方法都应该得出同一数值,也是检验数据的内部一致性的好方法。
但在实际的实验中,两种标度技术强调数据的不同区域,从属于不同的误差类型。
我们曾用两种技术的组合确定了几种多原子离子水溶液体系的标度因子。
具体的作法是,用两种技术的反复对比试探,直到两个标度因子N趋于一致。
两个方法当中,由于积分法用全套衍射数确定标度因子,因此可能更精确一些。
1.1.3 F ourier积分的截断效应在g E和g(r)计算公式中,积分的上限s=∞,下限为s=0。
实际上,由于常见的测角仪的最大散射角(145°)的限制,散射向量只有最大值,而没有无穷大。
如果使用M okα辐射,s= 1618nm-1,对铜靶,s=717nm-1。
因此,电子径向分布函数和原子径向分布函数为g E=4πr2ρm+2r/π∫S minS maxs[I(s)-N f2(s)]/(N z sin(sr)ds(11)g A=4πr2ρma+2r/π∫S minS maxs[I(s)-N f2(s)/[N f2(s)]sin(sr)dr(12)用透射法可在0°测定,而反射法则不能。
正由于积分上限并非无穷大,因而在径向分布函数上出现所谓“乱真波纹”,也有人称之为“幽灵峰”。
乱真波纹的出现,对径向分布函数具有以假乱真的影响。
特别是在低r下,径向分布函数出现非零值。
因此,乱真峰必须除去。
较通用的除去乱真峰的方法,有三种:a.对方程(11)和(12),检查S max的变化对合成分布函数的影响;b.对方程(11)和(12)中F ourier积分的核心部分,乘以一个称为“修饰函数”。