数列的函数特性习题(含答案)

1.2 数列的函数特性课后训练巩固提升1.已知数列{a n}的通项公式是a n=n-1n+1,那么这个数列是( ).A.递增数列B.递减数列C.常数列D.以上都不是a n+1-a n=nn+2−n-1n+1=n2+n-(n2+n-2)(n+1)(n+2)=2(n+1)(n+2)>0,∴a n+1>a n,∴{a n}是递增数列.2.给出下列说法:①已知数列{a n},a n=1n(n+2)(n∈N+),那么1120是这个数列的第10项,且最大项为第一项;②数列{a n}:√2,√5,2√2,√11,…的一个通项公式是a n=√3n-1;③已知数列{a n},a n=kn-5,且a8=11,则a17=29;④已知a n+1=a n+3,则数列{a n}是递增数列.其中正确的有( ).A.4个B.3个C.2个D.1个,令a n=1n(n+2)=1120⇒n=10(n=-12舍去),易知最大项为第一项.①正确.对于②,数列{a n}:√2,√5,2√2,√11,…即为√2,√5,√8,√11,…,亦为√3×1-1,√3×2-1,√3×3-1,√3×4-1,…,故a n=√3n-1.②正确.对于③,a n=kn-5,且a8=11⇒k=2⇒a n=2n-5⇒a17=29.③正确.对于④,由a n+1-a n=3>0,易知④正确.3.对任意的a1∈(0,1),由关系式a n+1=f(a n)得到的数列{a n}满足a n+1>a n(n∈N+),则函数y=f(x)的图象是( ).a n+1=f(a n)得到的数列{a n}满足a n+1>a n,即该函数y=f(x)的图象上任一点(x,y)都满足y>x,结合图象,只有A满足,故选A.4.(多选题)对于数列{a n},若存在正整数k(k≥2),使得a k>a k-1,a k>a k+1,则称a k是数列{a n}的“峰值”,k是数列{a n}的“峰值点”.在数列{a n}中,若-9|,下面哪些数不能作为数列{a n}的“峰值点”().a n=|n+8nA.2B.3C.6D.12a n =|n +8n-9|,所以a 1=0,a 2=3,a 3=103,a 4=3,a 5=125,a 6=53,a 7=67,a 11=3011,a 12=113,a 13=6013,只有a 3>a 2,a 3>a 4,所以“3”是“峰值点”,其他选项不是.故选ACD.5.已知数列{a n },a n =a n +m(a>0,n ∈N +),满足a 1=2,a 2=4,则{a n }是 数列.(填“递增”或“递减”){a 1=a +m =2,a 2=a 2+m =4,∴{m =0,a =2,或{m =3,a =-1(舍去).∴a n =2n , ∴{a n }是递增数列.6.已知数列{a n },a n =n 2-kn(n ∈N +),且{a n }为递增数列,则k 的取值范围是 .n+1-a n =(n+1)2-k(n+1)-n 2+kn=2n+1-k,又{a n }为递增数列,故应有a n+1-a n >0,即2n+1-k>0恒成立,分离参数得k<2n+1,故只需k<3即可.∞,3)7.已知数列{a n }的通项a n ,画出数列的图象.(1)a n =(-1)n ×2; (2)a n =2n-4; (3)a n =(12)n -1.,(1)(2)(3)(第7题) 8.已知数列{a n },a n =1+1a+2(n -1)(n ∈N +,a ∈R,且a≠0).(1)若a=-7,求数列{a n }中的最大项和最小项的值; (2)若对任意的n ∈N +,都有a n ≤a 6成立,求a 的取值范围.∵a=-7,∴a n =1+12n -9(n ∈N +).结合函数f(x)=1+12x -9的单调性,可知1>a 1>a 2>a 3>a 4,a 5>a 6>a 7>…>a n >1(n ∈N +). ∴数列{a n }中的最大项为a 5=2,最小项为a 4=0.(2)a n=1+1a+2(n-1)=1+12n-2-a2,由对任意的n∈N+,都有a n≤a6成立,(1)∵a=-7,∴a n=1+(n∈N+).结合函数f(x)=1+的单调性,可知1>a1>a2>a3>a4,a5>a6>a7>?>a n>1(n∈N+).∴数列{a n}中的最大项为a5=2,最小项为a4=0.(2)a n=1+=1+,由对任意的n∈N+,都有a n≤a6成立,结合函数f(x)=1+的单调性,可知5<<6,即-10<a<-8,故a的取值范围为(-10,-8).。

1.2 数列的函数特性双基达标限时20分钟1．已知a n ＝3n －2，则数列{a n }的图像是( )．A ．一条直线B ．一条抛物线C ．一个圆D ．一群孤立的点解析 ∵a n ＝3n －2，n ∈N ＋，∴数列{a n }的图像是一群孤立的点． 答案 D2．在数列{a n }中，a n ＝n ，则{a n }是 ( )．A ．递增数列B ．递减数列C ．常数列D ．以上都不是解析 ∵a n ＋1－a n ＝(n ＋1)－n ＝1>0，∴数列{a n }是递增数列．答案 A 3．在递减数列{a n }中，a n ＝kn(k 为常数)，则实数k 的取值范围是( )．A ．RB ．(0，＋∞)C ．(－∞，0)D ．(－∞，0]解析 ∵{a n }是递减数列，∴a n ＋1－a n ＝k(n ＋1)－kn ＝k<0.答案 C4．若数列{a n }为递减数列，则{a n }的通项公式可能为________(填写序号)． ①a n ＝－2n ＋1； ②a n ＝－n 2＋3n ＋1；③a n ＝12n ； ④a n ＝(－1)n . 解析 可以通过画函数的图像一一判断．②有增有减，④是摆动数列． 答案 ①③5．数列{－2n 2＋9n ＋3}的最大项是第________项，最大项为________．解析 由已知a n ＝－2n 2＋9n ＋3＝－2⎝⎛⎭⎫n －942＋1058.∵n ∈N ＋，故当n ＝2时，a n 取到最大 值13.答案 2 136．已知数列{a n }是递减数列，且a n ＝(m 2－2m)(n 3－2n)，求实数m 的取值范围． 解 ∵数列为递减数列，∴a n ＋1<a n ，∴a n ＋1－a n ＝(m 2－2m)[(n ＋1)3－2(n ＋1)－n 3＋2n]＝(m 2－2m)(3n 2＋3n －1)<0.∵n ∈N ＋，∴3n 2＋3n －1＝3⎝⎛⎭⎫n ＋122－74≥5>0， ∴m 2－2m<0，解得0<m<2.故实数m 的取值范围为0<m<2.综合提高(限时25分钟)7．已知a n ＝32n －11(n ∈N ＋)，记数列{a n }的前n 项和为S n ，则使S n >0的n 的最小值为 ( )．A ．10B ．11C ．12D ．13 解析 ∵－a 1＝a 10，－a 2＝a 9，－a 3＝a 8，－a 4＝a 7，－a 5＝a 6，∴S 11>0，则当n≥11时， S n >0，故n 最小为11.答案 B8．函数f(x)定义如下表，数列{x n }满足x 0＝5，且对任意的自然数均有x n ＋1＝f(x n )，则x 2 011＝( ).A.1 解析 ∵x 0＝5，x 1＝f(x 0)＝f(5)＝2，x 2＝f(x 1)＝f(2)＝1，x 3＝f(x 2)＝f(1)＝5，x 4＝f(x 3)＝f(5)＝2，…，∴x n 的值周期出现，且周期T ＝3，则x 2 011＝x 670×3＋1＝x 1＝2. 答案 B9．已知数列{a n }满足a 1>0，a n ＋1a n ＝12(n ∈N ＋)，则数列{a n }是________数列(填“递增”或“递减”)． 解析 由已知a 1>0，a n ＋1＝12a n (n ∈N ＋)，得a n >0(n ∈N ＋)．又a n ＋1－a n ＝12a n －a n ＝－12a n <0， 所以{a n }是递减数列． 答案 递减10．已知数列{a n }的通项公式是a n ＝an bn ＋1，其中a ，b 均为正常数，那么a n ＋1与a n 的大小关系是________．解析 ∵a n ＋1－a n ＝＋＋＋1－an bn ＋1＝ a＋＋＋>0.∴a n ＋1－a n >0，即a n ＋1>a n . 答案 a n ＋1>a n11．已知数列{a n }的通项公式为a n ＝n 2－5n ＋4.(1)数列中有多少项是负数？(2)n 为何值时，a n 有最小值？并求出最小值． 解 (1)由n 2－5n ＋4<0，解得1<n<4. 因为n ∈N ＋，故n ＝2,3，所以该数列中有两项是负数．(2)因为a n ＝n 2－5n ＋4＝⎝⎛⎭⎫n －522－94，可知对称轴方程为n ＝52＝2.5.又n ∈N ＋，故n ＝2或3时，a n 有最小值，其最小值为22－5×2＋4＝－2.12．(创新拓展)已知函数f(x)＝2x －2－x ，数列{a n }满足f(log 2a n )＝－2n. (1)求数列{a n }的通项公式；(2)证明数列{a n }是递减数列．(1)解 ∵f(x)＝2x －2－x ，f(log 2a n )＝－2n ， ∴2log 2a n －2－log 2a n ＝－2n ，a n －1a n＝－2n ， ∴a n 2＋2na n －1＝0，解得a n ＝－n±n 2＋1. ∵a n >0，∴a n ＝n 2＋1－n ，n ∈N ＋.(2)证明 a n ＋1a n ＝＋2＋1－＋n 2＋1－n ＝n 2＋1＋n＋2＋1＋＋<1. ∵a n >0，∴a n ＋1<a n ，∴数列{a n }是递减数列．。

《数列的函数特性》基础练习1.已知数列{a n }满足a n +1-a n -3=0，则数列{a n }是（ ）A.递增数列B.递减数列C.常数列D.不能确定2.设a n =-n 2+10n +11，则数列{a n }的最大项为（ ）A.5B.11C.10或11D.363.数列｛a n ｝中，a 1=0，以后各项由公式a 1·a 2·a 3·…·a n ＝n 2给出，则a 3+a 5等于（ ） A. 925 B. 1625 C. 1661 D. 1531 4.已知数列{a n }的通项公式a n =lg1536-(n -1)lg2，则使得a n <0成立的最小正整数n 的值为（ ）A.11B.13C.15D.125.已知数列{a n }中，a 1=1,a 2=3，a n =a n -1+21n a (n ≥3)，则a 5=（ ） A. 1255 B. 313 C.4D.5 6.在数列{a n }中，a 1=1,a n ·a n -1=a n -1+(-1) n (n ≥2)，则53a a 的值是（ ）A. 21B. 32C. 43D. 54 7.已知S k 表示数列的前k 项和，且S k +S k +1=a k +1 (k ∈N +)，那么此数列是（ ）A.递增数列B.递减数列C.常数列D.摆动数列8.已知数列{a n }的通项公式为a n =（43）n -1［（43）n -1-1］，则关于a n 的最大项，最小项叙述正确的是（ ）A.最大项为a 1,最小项为a 3B.最大项为a 1,最小项不存在C.最大项不存在，最小项为a 3D.最大项为a 1，最小项为a 4二、填空题9.已知数列{a n }的通项公式a n =n 2-4n -12（n ∈N +），则（1）这个数列的第四项是（2）65是这个数列的第（3）这个数列从第 项起以后各项为正数.10.已知数列{a n }的通项a n =c nb na (a 、b 、c 都是正实数)，则a n 与a n +1的大小关系是 .11.已知｛a n ｝是递增数列，且对任意的自然数n (n ≥1)，都有a n =n 2+λn 恒成立，则实数λ的取值范围为 .12.若数列{a n }的通项公式为a n =-2n 2+13n ，关于该数列，有以下四种说法：(1)该数列有无限多个正数项；(2)该数列有无限多个负数项；(3)该数列的最大项就是函数f(x )=-2x 2+13x 的最大值；(4)-70是该数列中的一项.其中正确的说法有 .（把所有正确的序号都填上）三、解答题13.已知数列1，2，37，25，513，…. （1）写出这个数列的一个通项公式a n ;（2）判断数列｛a n ｝的增减性.。

基础巩固已知数列{}是递增数列，则当∈＋时，有( )．＋≥．＋≤．＋＞．＋＜已知数列{}的图像是上升的，则{}是( )．递增数列．递减数列．常数列．以上均有可能＝－＋(为常数)，数列{}是递减数列，则有 ( )．＞．＜．≠．∈＝－，则数列{}的图像是( )．一条直线．一条抛物线．一个圆．一群孤立的点求数列{－＋＋}中的最大项．是否是数列{－＋＋}中的一项？综合过关若数列{}的通项公式为＝－＋(∈＋)，画出它在轴上方的图像，并根据图像求出的最大值，并在同一坐标系中画出函数()＝－＋的图像，根据图像求出()的最大值．若用函数来求＝－＋的最大值，应如何处理．已知数列{}的通项公式是＝(∈＋)，求数列{}中的最大项．能力提升一辆邮车每天从地往地运送邮件，沿途(包括、)共有站，从地出发时，装上发往后面站的邮件各一个，到达后面各站后卸下前面各站发往该站的一个邮件，同时装上该站发往下面各站的邮件各一个，试写出邮车在各站装卸完毕后剩余邮件个数所成的数列，画出该数列的图像，并判断该数列的增减性．参考答案答案：答案：答案：答案：分析：由通项公式可以看出：是的二次函数，求二次函数的最值可采用配方法，此时要注意其中自变量为正整数．解：由已知＝－＋＋＝－(－)＋，由于为正整数，故当取时，取到最大值为.∴数列{－＋＋}的最大项为＝.解：令－＋＋＝，解得＝或＝.由于∈＋，则方程－＋＋＝无正整数解，所以不是数列{－＋＋}中的一项．分析：由＝()可知，的图像应该为函数＝()图像上横坐标为正整数的点．求{}的最大值既可用图像来解决，也可用函数的相关知识解决．解：由－＋＞，可得＜＜.又因为∈＋，所以＝、、、、、，分别代入通项公式，可得＝，＝，＝，＝，＝，＝，图像如图所示，为个点．最大值为.函数()＝－＋的图像如图所示(图中曲线)．()＝－＋＝－(－)＋，当＝时，()＝.因为＜＜，且离较近，所以最大值＝.解：令()＝(∈＋)．设＜＜≤，∈＋，∈＋，则()－()＝－＝＝.又＜＜≤，∈＋，∈＋，则－＜，－＞，(＋)(＋)＞.所以＜.所以()＜()．所以当≤时，()是增函数．同理可证，当＞时，()是减函数，所以当＝时，()取最大值()＝，即{}中的最大项为＝.解：将、之间所有站按序编号，通过计算，上面各站剩余邮件数依次排成数列：。

1.2 数列的函数特性课时过关·能力提升1.在数列{x n }中,若x 1=1,x n+1=1x n +1−1,则x 2019等于( )A.-1B.−12 C.12 D.1x 1=1代入x n+1=1xn+1−1,得x 2=−12,再将x 2代入x n+1=1xn +1−1,得x 3=1,则数列{x n }的周期为2,x 2 019=x 1=1.2.已知数列{a n }满足a n ={(3-a )n -3,n ≤7,a n -6,n >7,且{an}是递增数列,则实数a 的取值范围是( )A .(94,3) B.[94,3) C.(1,3)D.(2,3){3-a >0,a >1,(3-a )×7-3<a 8-6,解得2<a<3.3.已知数列{a n }满足a 1=1,a 2=1,a n+2=(1+sin 2nπ2)an +4cos 2nπ2,则a9,a10的大小关系为( ) A.a 9>a 10 B.a 9=a 10C.a 9<a 10D.大小关系不确定n 为奇数时,a 3=2a 1=2,a 5=2a 3=22,a 7=2a 5=23,a 9=2a 7=24; 当n 为偶数时,a 4=a 2+4=5,a 6=a 4+4=9,a 8=a 6+4=13,a 10=a 8+4=17. 所以a 9<a 10.故选C .4.已知函数y=f(x)的图像,且对任意a n∈(0,1),由关系式a n+1=f(a n)得到的数列{a n}满足a n+1>a n(n∈N+),则该函数的图像可能是()A B C Da n+1>a n可知数列{a n}为递增数列.又由a n+1=f(a n)>a n可知当x∈(0,1)时,y=f(x)的图像在直线y=x的上方.5.已知a n=√79n-√80∈N+),则在数列{a n}的前50项中最小项和最大项分别是()A.a1,a50B.a1,a8C.a8,a9D.a9,a50a n=√79n-√80=√80)√80-√79)n-√80=1+√80-√79n-√80所以当n=9时√80-√79n-√80,且√80-√79n-√80,从而a9最大;当n=8时√80-√79n-√80,√80-√79n-√80,从而a8最小,故选C.6.已知数列{a n}满足a n={n2-2016n,n≤2015,2a n-1,n≥2016,则a2016=_________________.2 016=2a2 015=2×(2 0152-2 016×2 015)=-4 030.4 0307.我们可以利用数列{a n}的递推公式a n={n,n为奇数,a n2,n为偶数(n∈N+),求出这个数列各项的值,使得这个数列中的每一项都是奇数,则a24+a25=.研究发现,该数列中的奇数都会重复出现,则第8个5是该数列的第项.24+a25=a12+25=a6+25=a3+25=3+25=28.5=a5=a10=a20=a40=a80=a160=a320=a640.6408.若数列{n (n +4)(23)n}的最大项是第k 项,则k =_____________.k 项,则有 {k (k +4)(23)k≥(k +1)(k +5)(23)k+1,k (k +4)(23)k ≥(k -1)(k +3)(23)k -1,即{k 2≥10,k 2-2k -9≤0.由k ∈N +,可得k=4.★9.如图所示,互不相同的点A 1,A 2,…,A n ,…和B 1,B 2,…,B n …分别在角O 的两条边上,所有A n B n (n ∈N +)相互平行,且所有梯形A n B n B n+1A n+1的面积均相等,设OA n =a n ,若a 1=1,a 2=2,则数列{a n }的通项公式是 .OA n =x (n ≥3),OB 1=y ,∠A 1OB 1=θ,记S △OA 1B 1=12×1×ysin θ=S , 则S △OA 2B 2=12×2×2ysin θ=4S ,S △OA 3B 3=4S +(4S −S)=7S, ……S △OA n B n =12x ·xy sin θ=(3n-2)S , ∴S △OA n B n S △OA 2B 2=12×x×xysinθ12×2×2ysinθ=(3n -2)S 4S,∴x 24=3n -24,∴x =√3n -2,即a n =√3n -2(n ≥3), 经验证知a n =√3n -2(n ∈N +).n =√3n -2 10.已知a n =9n ·(n+1)10n(n ∈N +),则{a n }中有没有最大项?如果有,求出最大项;如果没有,请说明理由.a n 最大(n ≥2),则{a n ≥a n -1,a n ≥a n+1,即{9n ·(n+1)10n≥9n -1·n10n -1,9n ·(n+1)10≥9n+1·(n+2)10,解得8≤n ≤9.因为n ∈N +,所以n=8或n=9, 故数列{a n }的最大项为a 8=a 9=99108. ★11.已知函数f (x )=1-2x x+1(x ≥1),构造数列a n =f (n )(n ∈N +).(1)求证:a n >-2.(2)数列{a n }是递增数列还是递减数列?为什么?a n =1-2n n+1=3-2(n+1)n+1=3n+1−2.∵n ∈N +,∴3n+1>0,∴a n =3n+1−2>−2..理由如下:由(1)知,a n =3n+1−2.∵a n+1-a n =3n+2−3n+1=3n+3-3n -6(n+1)(n+2)=-3(n+1)(n+2)<0, ∴a n+1<a n ,∴数列{a n }是递减数列.。

, [学生用书单独成册])[A.基础达标]1．已知a n ＋1－a n －3＝0，则数列{a n }是( )A ．递增数列B ．递减数列C ．常数列D ．不能确定解析：选A.因为a n ＋1－a n ＝3>0，故数列{a n }是递增数列．2．已知数列{a n }的通项公式为a n ＝n n ＋1，则这个数列是( ) A ．递增数列 B ．递减数列C ．常数列D ．摆动数列解析：选A.因为a n ＋1－a n ＝n ＋1n ＋2－n n ＋1＝（n ＋1）2－n （n ＋2）（n ＋1）（n ＋2）＝1（n ＋1）（n ＋2）>0.故选A.3．数列{a n }中，a n ＝－2n 2＋29n ＋3，则此数列最大项的值是( )A ．109B ．10818C ．108D ．107解析：选C.a n ＝－2n 2＋29n ＋3＝－2(n 2－292n )＋3＝－2·(n －294)2＋3＋2928，当n ＝7时，a n 最大且等于108，故选C.4．已知数列{a n }满足a n ＝n －1n a n －1(n ≥2)，则数列{a n }为( ) A ．递增数列 B ．递减数列C ．常数列D ．以上都有可能解析：选D.若a 1>0，则a n ＜a n －1(n ≥2)，{a n }为递减数列；若a 1＝0，则a n ＝0(n ∈N ＋)，{a n }为常数列；若a 1＜0，则a n ＞a n －1(n ≥2)，{a n }为递增数列，故选D.5．已知数列{a n }的通项公式是a n ＝n －1n ＋1，则a n 与a n ＋1间的大小关系是( ) A ．a n >a n ＋1 B ．a n <a n ＋1C ．a n ＝a n ＋1D ．不能确定解析：选B.因为a n ＋1－a n ＝n n ＋2－n －1n ＋1＝ n （n ＋1）－（n －1）（n ＋2）（n ＋2）（n ＋1）＝n 2＋n －（n 2＋n －2）（n ＋2）（n ＋1）＝2（n ＋2）（n ＋1）>0，所以a n <a n ＋1，选B. 6．已知下列数列：①2 010，2 014，2 018，2 022；②0，12，23，…，n －1n，…； ③1，12，14，…，12n －1，…；④1，－23，35，…，（－1）n －1·n 2n －1，…； ⑤6，6，6，6，6，6.其中，有穷数列是________，无穷数列是________，递增数列是______，递减数列是______，常数列是________，摆动数列是______．(将符合条件的数列的序号填在横线上)解析：①是有穷递增数列；②是无穷递增数列；③是无穷递减数列；④是摆动数列，也是无穷数列；⑤是常数列，也是有穷数列．答案：①⑤ ②③④ ①② ③ ⑤ ④7．已知数列{a n }的通项公式a n ＝n 2－4n －12(n ∈N ＋)，则这个数列从第________项起各项为正数．解析：令a n ＝n 2－4n －12>0，解得n >6或n <－2(舍去)．故从第7项起各项为正数． 答案：78．已知数列{a n }为单调递增数列，通项公式为a n ＝n ＋λn ，则λ的取值范围是________． 解析：由于数列{a n }为单调递增数列，a n ＝n ＋λn ，所以a n ＋1－a n ＝[(n ＋1)＋λn ＋1]－(n ＋λn )＝1－λn （n ＋1）＞0，即λ＜n (n ＋1)(n ∈N ＋)，所以λ＜2. 答案：(－∞，2)9．已知函数f (x )＝x －x 2＋1，数列{a n }满足a n ＝f (n )(n ∈N ＋)，试判断数列{a n }的增减性．解：因为a n ＋1－a n ＝(n ＋1)－（n ＋1）2＋1－(n －n 2＋1)＝1－[（n ＋1）2＋1－n 2＋1]＝1－2n ＋1（n ＋1）2＋1＋n 2＋1＞1－2n ＋1（n ＋1）＋n ＝0，所以a n ＋1＞a n .所以数列{a n }是递增数列．10．已知数列{a n }的通项公式为a n ＝n 2－5n ＋4，(1)数列中有多少项为负数？(2)n 为何值时，a n 有最小值？并求此最小值．解：(1)由n 2－5n ＋4<0得1<n <4，n ∈N ＋，所以n ＝2或3.所以数列中有2项为负数．(2)因为a n ＝n 2－5n ＋4＝⎝⎛⎭⎫n －522－94， 又因为n ∈N ＋，所以n ＝2或3时，a n 有最小值－2.[B.能力提升]1．一给定函数y ＝f (x )的图像在下列各图中，并且对任意a n ∈(0，1)，由关系式a n ＋1＝f (a n )得到的数列{a n }满足a n ＋1>a n (n ∈N ＋)，则该函数的图像是( )解析：选A.由a n ＋1＝f (a n )，a n ＋1>a n 知f (a n )>a n .可以知道x ∈(0，1)时f (x )>x ，即f (x )的图像在y ＝x 图像的上方，由选项中所给的图像可以看出，A 符合条件．2．已知数列{a n }的通项公式a n ＝an bn ＋1(a ，b 为正常数)，那么a n 与a n ＋1的关系是( ) A ．a n >a n ＋1 B ．a n <a n ＋1C ．a n ＝a n ＋1D ．以上都不对解析：选B.考虑函数y ＝ax bx ＋1＝a b （bx ＋1）－a b bx ＋1＝a b ＋－a b bx ＋1＝a b ＋－a b 2x ＋1b， 其图像可由y ＝－a b 2x 先向左平移1b 个单位长度，再向上平移a b个单位长度得到，如图．由图像不难得知y ＝ax bx ＋1在[1，＋∞)上单调递增，所以a n ＝an bn ＋1的值随n 的变大而变大．所以数列{a n }是递增数列，即a n <a n ＋1，故选B.3．已知数列{a n }的通项公式a n ＝n －96n －98，n ∈N ＋，则数列{a n }的最大项为________，最小项为________．解析：将数列{a n }的通项公式变形为a n ＝1＋98－96n －98，考察函数f (x )＝1＋98－96x －98，画出图像(图略)，数列{a n }的图像即为曲线上横坐标为正整数的孤立的点，易知n ＝10时，a n 取得最大值，为10－9610－98；n ＝9时，a n 取得最小值，为9－969－98. 所以，数列{a n }中最大项为a 10＝10－9610－98，最小项为a 9＝9－969－98. 答案：10－9610－98 9－969－984．已知通项公式为a n ＝(m 2－2m )(n 3－2n )的数列是递减数列，则实数m 的取值范围为____________．解析：因为数列{a n }为递减数列，所以a n ＋1<a n .所以a n ＋1－a n ＝(m 2－2m )[(n ＋1)3－2(n ＋1)－n 3＋2n ]＝(m 2－2m )(3n 2＋3n －1)<0. 因为n ∈N ＋，所以3n 2＋3n －1＝3⎝⎛⎭⎫n ＋122－74≥5>0. 所以m 2－2m <0，解得0<m <2.故m ∈(0，2)．答案：(0，2)5．已知数列{a n }的通项公式为a n ＝(n ＋2)⎝⎛⎭⎫910n ，试问n 取何值时，a n 取最大值？试求出a n 的最大值．解：因为a n ＋1a n ＝（n ＋3）⎝⎛⎭⎫910n ＋1（n ＋2）⎝⎛⎭⎫910n ＝9（n ＋3）10（n ＋2）＝910＋910·1n ＋2，由a n ＋1a n ＝1，解得n ＝7，则当n ＝7时，a 8a 7＝1，即a 7＝a 8. 当n <7时，a n ＋1a n>1，即a n ＋1>a n . 当n ≥8时，a n ＋1a n<1，即a n ＋1<a n . 则当n ＝7或n ＝8时，a n 取最大值，最大值为a 7＝a 8＝98107. 6．设f (x )＝log 2x －log x 4(0<x <1)，又知数列{a n }的通项a n 满足f (2a n )＝2n .(1)求数列{a n }的通项公式；(2)试判断数列{a n }的增减性．解：(1)因为f (x )＝log 2x －log x 4(0<x <1)，f (2 a n )＝2n ，所以log 22a n －log 2 a n 4＝2n ，由换底公式，得log 22 a n －log 24log 22a n＝2n ， 即a n －2a n ＝2n ， 所以a 2n －2na n －2＝0，所以a n ＝n ±n 2＋2.①由0<x <1，有0<2an <1，所以a n <0.②由①②得a n ＝n －n 2＋2，此即为数列{a n }的通项公式．(2)a n ＋1a n ＝（n ＋1）－（n ＋1）2＋2n －n 2＋2＝n ＋n 2＋2（n ＋1）＋（n ＋1）2＋2<1， 因为a n <0，所以a n ＋1>a n ，所以数列{a n }是递增数列．。

数列的概念及函数特征测试题A 组一．填空题(本大题共8小题，每小题5分，共40分) 1.数列1,1,1,1,1--，的通项公式的是 。

1. 1(1)n n a +=- 或{11n n a n =-，为奇数，为偶数。

提示：写成两种形式都对，a n 不能省掉。

2. ,52,21,32,1的一个通项公式是 。

2. 2;1n a n =+提示：若把12换成24，同时首项1换成22，规律就明显了。

其一个通项应该为：2;1n a n =+3.在某报《自测健康状况》的报道中，自测血压结果与相应年龄的统计数据如下表. 观察表中数据的特点，用适当的数填入表中空白（ ）内.年龄（岁）30 35 40 45 50 55 60 65收缩压（水银柱 毫米） 110 115 120 125 130 135 （ ）145 舒张压（水银柱 毫米） 70 73 75 78 80 83 （ ）883.140,85。

提示：观察上表规律，收缩压每次增加5，舒张压相应增加3或2，且是间隔出现的，故应填140,85。

4．已知数列{}n a ，1()(2)n a n N n n +=∈+，那么1120是这个数列的第 项.4.10.提示：令1(2)n a n n =+=1120，即n 2+2n-120=0,解得n=10.5.已知数列{a n }的图像是函数1y x=图像上，当x 取正整数时的点列，则其通项公式为 。

5. a n =1n .提示：数列{a n }对应的点列为(n,a n ),即有a n =1n。

6.已知数列{}n a ，22103n a n n =-+，它的最小项是 。

6.2或3项。

提示：22103n a n n =-+=2（n-52）2-192.故当n=2或3时，a n 最小。

7. 已知数列{}n a 满足12a =-，1221n n na a a +=+-，则4a = .7. 25-。

提示：222212a ⨯-=++（）=23，322326213a ⨯=+=-，12622165n a +⨯=+=--。

基础巩固1已知数列{a n}是递增数列，则当n∈N＋时，有()A．a n＋1≥a n B．a n＋1≤a nC．a n＋1＞a n D．a n＋1＜a n2已知数列{a n}的图像是上升的，则{a n}是()A．递增数列B．递减数列C．常数列D．以上均有可能3a n＝－n＋b(b为常数)，数列{a n}是递减数列，则有()A．b＞0 B．b＜0C．b≠0 D．b∈R4a n＝3n－2，则数列{a n}的图像是()A．一条直线B．一条抛物线C．一个圆D．一群孤立的点5求数列{－2n2＋9n＋3}中的最大项．63是否是数列{－2n2＋9n＋3}中的一项？综合过关7若数列{a n}的通项公式为a n＝－2n2＋13n(n∈N＋)，画出它在x轴上方的图像，并根据图像求出a n的最大值，并在同一坐标系中画出函数f(x)＝－2x2＋13x的图像，根据图像求出f(x)的最大值．若用函数来求a n＝－2n2＋13n的最大值，应如何处理．8已知数列{a n}的通项公式是a n＝nn2＋196(n∈N＋)，求数列{a n}中的最大项．能力提升9一辆邮车每天从A地往B地运送邮件，沿途(包括A、B)共有8站，从A地出发时，装上发往后面7站的邮件各一个，到达后面各站后卸下前面各站发往该站的一个邮件，同时装上该站发往下面各站的邮件各一个，试写出邮车在各站装卸完毕后剩余邮件个数所成的数列，画出该数列的图像，并判断该数列的增减性．参考答案1答案：C2答案：A3答案：D4答案：D5分析：由通项公式可以看出：a n 是n 的二次函数，求二次函数的最值可采用配方法，此时要注意其中自变量n 为正整数．解：由已知a n ＝－2n 2＋9n ＋3＝－2(n －94)2＋1058，由于n 为正整数，故当n 取2时，a n 取到最大值为13. ∴数列{－2n 2＋9n ＋3}的最大项为a 2＝13. 6解：令－2n 2＋9n ＋3＝3， 解得n ＝0或n ＝92.由于n ∈N ＋，则方程－2n 2＋9n ＋3＝3无正整数解， 所以3不是数列{－2n 2＋9n ＋3}中的一项．7分析：由a n ＝f (n )可知，a n 的图像应该为函数y ＝f (x )图像上横坐标为正整数的点．求{a n }的最大值既可用图像来解决，也可用函数的相关知识解决．解：由－2n 2＋13n ＞0，可得0＜n ＜132.又因为n ∈N ＋，所以n ＝1、2、3、4、5、6，分别代入通项公式，可得a 1＝11，a 2＝18，a 3＝21，a 4＝20，a 5＝15，a 6＝6，图像如图所示，为6个点．最大值为21.函数f (x )＝－2x 2＋13x 的图像如图所示(图中曲线)． f (x )＝－2x 2＋13x ＝－2(x －134)2＋1698，当x ＝134时，f (x )max ＝1698.因为3＜134＜4，且314离3较近，所以最大值a 3＝21.8解：令f (n )＝nn 2＋196(n ∈N ＋)．设0＜n 1＜n 2≤14，n 1∈N ＋，n 2∈N ＋， 则f (n 1)－f (n 2)＝n 1n 21＋196－n 2n 22＋196＝n 1(n 22＋196)－n 2(n 21＋196)(n 21＋196)(n 22＋196) ＝(n 1n 2－196)(n 2－n 1)(n 21＋196)(n 22＋196). 又0＜n 1＜n 2≤14，n 1∈N ＋，n 2∈N ＋，则n 1n 2－196＜0，n 2－n 1＞0，(n 21＋196)(n 22＋196)＞0.所以(n 1n 2－196)(n 2－n 1)(n 21＋196)(n 22＋196)＜0.所以f (n 1)＜f (n 2)．所以当n ≤14时，f (n )是增函数． 同理可证，当n ＞14时，f (n )是减函数， 所以当n ＝14时，f (n )取最大值f (14)＝128，即{a n }中的最大项为a 14＝128.9解：将A 、B 之间所有站按序1,2,3,4,5,6,7,8编号，通过计算，上面各站剩余邮件数依次排成数列：7,12,15,16,15,12,7,0. 填写下表当n＝1时，a n＋1－a n＝a2－a1＝5＞0，当n＝6时，a n＋1－a n＝a7－a6＝－5＜0，∴{a n}为摆动数列．。

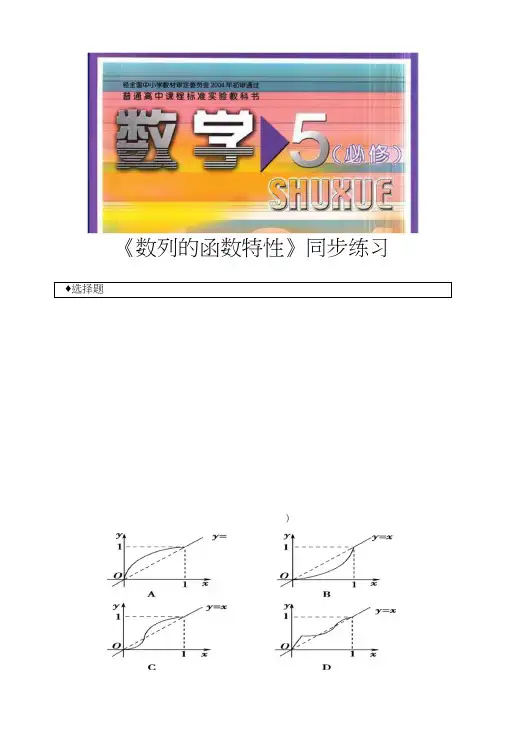
《数列的函数特性》同步练习♦选择题(3-«)x-3,x< 75.设函数/(%)= < >7 ，数列｛如满足a n =J(n), «eN+,且数列｛给｝是递增数列，则实数。

的取值范围是() A. (1,3)B. (2, 3)D ・(1,2)♦填空题6. 数列｛©｝的通项公式是禺=/一7并+50,则数列中的最小项是 __________7. 若数列｛心+ 4)(彳)”｝中的最大项是第比项，则A __________8. 数列｛如｝满足a n =n 2+kn + 2,若不等式冷曲4亘成立，则实数£的取值范围是 ___________ 9. 已知数列｛给｝的通项公式为a ti =n~2\n+20o(1) -60是否是该数列中的项，若是，求岀项数；该数列中有小于0的项吗？共有多少项?(2) /7为何值时，禺有最小值？并求出最小值。

10. 已知函数沧)=2*—2匕数列｛“｝满足Xlog 2^)=-2/?⑴求数列｛如的通项公式；⑵证明数列｛加是递减数列。

1.已知数列｛乩｝的通项公式是為一〃+1,则这个数列是（）A.递增数列B.递减数列C.常数列D.摆动数列2.设外=一/+10卄11,则数列｛给｝屮第几项最大（） A.第6项B.第7项C.第6项或第7项D.第5项 3.已知给=3n —2,则数列｛如的图像是（) A. 一条直线B. —条抛物线C. 一个圆D. 一群孤立的点 4. 一给定函数y=fd ）的图像在下列图中， 并且对任意a ｛ e （0, 1）,由关系式a“+[=7（如）得到的数列仏｝满足如+1＞如,则该函数的图像是（ C.答案与解析1.【解析】数列｛禺｝的通项公式是川+2 川+1+1 〔I 1 1 —1V 77 GN-^,・*. a n+\<a nf aft=^= n+\ = 1 +^H? ^+, _^=^+2_^+T=r^+即数列｛如为递减数列。

高中数学数列的函数特性专题练习题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 数列{−2n 2+29n +3}中最大项是（ ） A.107 B.108 C.10813D.1092. 数列{a n }的通项公式为a n =n 2+1，则a 5的值为（ ） A.5 B.10 C.17 D.263. 数列1，3，7，15，…的通项公式a n 等于（ ） A.2n B.2n +1 C.2n −1 D.2n−14. 下列函数中，对任意a 1∈(0, 1)，由关系式a n+1=f(a n )得到的数列{a n }满足a n+1>a n ，n ∈N +．则该函数是（ ） A.f(x)=x 2 B.f(x)=√x C.f(x)=sin x D.f(x)=cos x5. 已知21=2，22=4，23=8，…，则22012个位上的数字为（ ） A.2 B.4 C.6 D.86. 数列{a n }定义如下：a 1=1，当n ≥2时，a n ={1+a n 2(n 为偶数)1a n−1(n 为奇数)，若a n =85，则n的值等于（ ） A.20 B.28 C.30 D.407. 已知数列的前n 项和，若，恒成立，则实数的最大值是( )A.3B.4C.5D.68. 如果一个数列的各项都是实数，且从第二项开始，每一项与它前一项的平方差是相同的常数，则称该数列为等方差数列，这个常数叫做这个数列的公方差．设正项数列{a n }是首项为2，公方差为2的等方差数列，则第31项为（ ） A.4 B.√62 C.8 D.629. 定义m ⊕n =n m (m >0, n >0)，已知数列{a n }满足a n =n⊕33⊕n(n ∈N ∗)，若对任意正整数n ，都有a n ≥a n 0(n 0∈N ∗)，则a n 0的值为（ ） A.3 B.98C.1D.8910. 设等差数列的公差为，若，则“”是“为递减数列”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件11. 数列{b n }各项均为正数，若b 3=1，b n 2=b n+12，b n =________．12. 已知数列a n ={a n−4，n >4(2−a4)n −a 2，n ≤4(N ∈N ∗)为单调递增数列，则实数a 的取值范围是________．13. 数列{a n }的前n 项和为S n ，S n =3n −2，n ∈N ∗，则a n =________．14. 数列1，−1，1，−1，1…，的通项公式的是________．15. 设数列{a n }的前n 项和为S n ，若S n =n(n +1)(n ∈N ∗)．则a n =________．16. 数列{a n }，通项公式a n =√6n−√98∈N ∗)，则该数列中最大项的序数n =________．17. 已知数列{a n }中，a n =n 2+λn ，且a n 是递增数列，求实数λ的取值范围________．18. 已知数列{a n }中，a n =nn 2+156，则a n 的最大值为________．19. 数列(a n }的通项公式a n =n+2n ，若a 1⋅a 2⋅a 3•…•a n >36成立．则n 的最小值为________．20. 已知点A n (n, a n )为函数y =√x 2+1图象上的点，B n (n, b n )为函数y =x 图象上的点，其中n∈N∗，设c n=a n−b n，则c n与c n+1的大小关系为________.21. 已知数列{a n}的前n项和s n=n+1n+2，则a3=________．22. 已知数列{a n}的前n项和为S n=n2+2n−1，求数列{a n}的通项公式．23. 已知函数f(x)=2x−2−x，数列{a n}满足f(log2a n)=−2n．（1）求数列{a n}的通项公式；（2）求证：数列{a n}是递减数列．24. 设等差数列{a n}满足S6=24，a10=−9．（1）求{a n}的通项公式；（2）求{a n}的前n项和S n及使得S n最大的序号n的值．25. 已知函数f(x)=log2a x(a>0,a≠12)，（1）若f(x1x2...x2015)=8，求f(x12)+f(x22)+...+f(x20152)的值．（2）若x∈(−1, 0)时，求g(x)=f(x+1)>0，求a的取值范围．26. 已知“−1.32，−13，34，−15，…”，求通项．27. 等差数列a1=−40，a3=−30，①求通项公式a n；②若前n项的和为S n，求S n的最小值及此时的n值．28. 数列{a n}中，已知S n=n+1n，求{a n}的通项公式．29. 在数列{a n}中，a n=n3−λn，若数列{a n}为递增数列，求实数λ的取值范围．30. 已知数列{b n}的通项为b n=na n(a>0)，问{b n}是否存在最大项？证明你的结论．31. 已知数列{a n }的通项公式为a n =n 2+λn ，当n ∈N ∗，a n ≤a n+1，求λ的最小值．32. 在数列{a n }中，a n =(n −7)(12)n (n ∈N ∗)，求数列{a n }的最大项．33. 观察规律猜想下列数列的通顶公式： （1）0，1，0，1，0，1…（2）0.9，0.99，0.999，0.9999，…（3）1，3，6，10，15，21，…34. 根据下面4个数列的通项公式，分别作出它们的图象： （1）a n =−n4；（2）b n =2n 3；（3）c n =2n+1n ；（4）d n =(−1)n n ．35. 已知数列{a n }的通项公式为a n =(34)n−1[(34)n−1−1](n ∈N +)．求（1）求数列{a n }中的最大项及其值；（2）求数列{a n }中的最小项及其值．36. 假设数列{a n }各项均不相等，将数列从小到大重新排序后相应的项数构成的新数列成为数列{a n }的排序数列，例如：数列a 2<a 3<a 1，满足则排序数列为2，3，1． (1)写出2，4，3，1的排序数列；(2)求证：数列{a n }的排序数列为等差数列的充要条件是数列{a n }为单调数列．37. 已知数列{a n}的通项公式a n=2．n2+n（1）求a8、a10．是不是它的项？若是，为第几项？（2）问：110)n−1，n∈N∗，如何求数列{a n}中的最大项，最小项38. 已知数列{a n}满足a n=n•(910是多少？39. 如果一个数列从第2项开始，每一项与它的前一项的和等于同一个常数，那么这个数列就叫做等和数列．已知等和数列{a n}的第一项为2，公和为7，求这个数列的通项公式a n．40. 已知等差数列{a n}满足：a1=8，公差d=−2．（1）求数列{a n}的通项公式；（2）记S n为数列{a n}的前n项和，求S n的最大值．参考答案与试题解析高中数学数列的函数特性专题练习题含答案一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】B【考点】数列的函数特性【解析】由题意，a n=−2n2+29n+3看成二次函数，离对称轴越近，值越大．【解答】解：∵a n=−2n2+29n+3=−2(n−294)2+10818，又∵294=714且n∈N+，∴当n=7时，a n最大，最大值为a7=108．故选B．2.【答案】D【考点】数列的函数特性【解析】利用数列的通项公式求解．【解答】解：∵为a n=n2+1，∴a5=52+1=26．故选：D．3.【答案】C【考点】数列的函数特性【解析】分别求出a2−a1，a3−a2，a4−a3，结果构成等比数列，进而推断数列{a n−a n−1}是首相为2，公比为2的等比数列，进而各项相加可得答案．【解答】解：a2−a1=21，a3−a2=22，a4−a3=23，…依此类推可得a n−a n−1=2n−1∴a2−a1+a3−a2+a4−a3…+a n−a n−1=a n−a1=21+22+23+⋯+2n−1=2n−2∴a n−a1=2n−2，a n=2n−1故选C．4.【答案】B【考点】数列的函数特性【解析】由关系式a n+1=f(a n)得到的数列{a n}满足a n+1>a n(n∈N∗)，根据点与直线之间的位置关系，我们不难得到，f(x)的图象在y=x上方．逐一分析不难得到正确的答案．【解答】解：∵a n+1=f(a n)，∴点(a n, a n+1)在函数y=f(x)的图象上，又a n+1>a n，∴点(a n, a n+1)(n∈N∗)始终在直线y=x的上方．对于B:f(x)=√x，其图象在y=x上方．故选B．5.【答案】C【考点】数列的函数特性【解析】分析可得4个数字为一循环，求出2012里面有几个4，还余几，再根据余数判断．【解答】解：∵21=2，个位数字是2，22=4，个位数字是4，23=8，个位数字是8，24= 16，个位数字是6，25=32，个位数字是2；…4个数字为一循环，求出2012里面有几个4，还余几，再根据余数判断．∵2012÷4=503；没有余数，说明22012的个位数字是6．故选C．6.【答案】C【考点】数列的函数特性【解析】由题意可得，a n2=35，再根据条件求出数列的前若干项，求出项为35的序号，从而求得n的值．【解答】解：由题意可得，当n为偶数时，a n>1；当n为奇数时，0<a n≤1．再由a n=85=1+a n2，∴a n2=35．再由条件可得 a 2=2，a 3=12，a 4=3，a 5=13，a 6=32，a 7=23，a 8=4，a 9=14，a 10=43，a 11=34，a 12=52，a 13=25，a 14=53，a 15=35， 故n2=15，n =30，故选C ． 7.【答案】 C【考点】数列的函数特性 【解析】先由S n 求出a n ，根据λa n ≤4+S n 得到λ≤4+S 2a n，求出4+S 2a n的最小值，即可得出结果【解答】因为数列{a n }的前n 项和S n =2n−1−2当n ≥2时，a n =S n −S n−1=(2n+1−2)−(2n −2)=2n 当n =1时，a 1=S 1=22−2=2满足上式， 所以a n =2n (n ∈N ast )又¬n ∈N ast λa n ≤4+S 2n 恒成立，所以加n ∈N +,λ≤4+S 2a n恒成立；令b n =4+S 2n a n=4+22n−1−22n=22n+1+22n=2n−1+22n则b n+1−b n =(2n−2+22n+1)−(2n−1+22n )=2n−1−12n >0对任意n ∈N ast ，显然都成立，所以b n =2n+1+22n单调递增，因此(b n )min =b 1=22+22=5，即4+S n a n的最小值为5所以λ≤5，即实数？的最大值是5．故选：C 8. 【答案】 C【考点】数列的函数特性 【解析】首先，根据题意，得到a n 2−a （n−1）2=2，然后，利用累加法求解其通项公式，然后，求解第31项． 【解答】解：根据题意，得 a 22−a 12=2， a 32−a 22=2， a 42−a 32=2a52−a42=2，…a n2−a（n−1）2=2，∴a n2−a12=2(n−1)∴a n2=a12+2(n−1)=2n+2∴a n=√2n+2，∴a31=√2×31+2=8，故选：C．9.【答案】C【考点】数列的函数特性【解析】由题意可得：a n=n⊕33⊕n =3nn，a n+1a n=3(1−1n+1)3=f(n)，可知：f(n)关于n单调递增，经过假设可得：a1>a2>a3<a4<a5<…，即可得出．【解答】解：由题意可得：a n=n⊕33⊕n =3nn3，a n+1 a n =3n+1(n+1)3×n33n=3(1−1n+1)3=f(n)，则f(n)关于n单调递增，n=1时，f(1)=38<1；n=2时，f(2)=89<1；n≥3时，f(n)>1．∴a1>a2>a3<a4<a5<…，∴n0=3时，满足：对任意正整数n，都有a n≥a n(n0∈N∗)，a n0=3n33=1．故选：C．10.【答案】C【考点】数列的函数特性【解析】利用指数函数的单调性、数列增减性的定义以及等差数列的定义判断即可．【解答】充分性：若d<0，则a n−1−a n=d<0，即a n+1<a n24−z，即b n+1<b n所以，数列{b n}为递减数列，充分性成立；必要性：若{b n}为递减数列，则b n+1<b n，即241n∴a n+1<a n，贝a n+1−a n=d< 0必要性成立．因此，0”是“{b n}为递减数列”的充要条件．故选：C．二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】 1【考点】数列的函数特性 【解析】由b n 2=b n+12，可得b n+1=±b n ，利用数列{b n }各项均为正数，b 3=1，即可得出结论． 【解答】解：∵ b n 2=b n+12， ∴ b n+1=±b n ，∵ 数列{b n }各项均为正数，b 3=1， ∴ b n =1， 故答案为：1． 12.【答案】 (2, 8) 【考点】数列的函数特性 【解析】利用分段函数的单调性，列出不等式组求实数a 的取值范围． 【解答】解：因为数列a n ={a n−4，n >4(2−a4)n −a 2，n ≤4(N ∈N ∗)为单调递增数列，所以：{a >12−a4>0(2−a 4)×4−a 2<a解不等{a >1a <8a <−4，或a >2 即2<a <8 故答案为：(2, 8) 13. 【答案】 {1,n =1⋅【考点】数列的函数特性 【解析】 利用公式a n ={S 1，n =1S n −S n−1，n ≥2求解．【解答】解：∵ 数列{a n }的前n 项和为S n ，S n =3n −2，n ∈N ∗， ∴ a 1=S 1=3−2=1，a n =S n −S n−1=(3n −2)−(3n−1−2) =23⋅3n ．当n=1时，23⋅3n=2≠a1，∴a n={1,n=1⋅．故答案为：{1,n=1⋅．14.【答案】a n=(−1)n+1【考点】数列的函数特性【解析】数列1，−1，1，−1，1…，奇数项为+1，偶数项为−1．即可得到数列的一个通项公式．【解答】解：数列1，−1，1，−1，1…，奇数项为+1，偶数项为−1．因此数列的一个通项公式是a n=(−1)n+1．故答案为：a n=(−1)n+1．15.【答案】2n【考点】数列的函数特性【解析】利用公式a n={S1，n=1S n−S n−1，n≥2求解．【解答】解：∵数列{a n}的前n项和为S n，S n=n(n+1)(n∈N∗)，∴a1=S1=1×(1+1)=2，a n=S n−S n−1=[n(n+1)]−[(n−1)n]=2n．当n=1时，2n=2=a1，∴a n=2n．故答案为：2n．16.【答案】10【考点】数列的函数特性【解析】当n≤9时，a n=1√98−√9698−n <1，且{a n}单调递减；当n≥10时，a n=1+√98−√96n−98>1，且{a n}单调递减，即可得出．【解答】解：a n=√96n−√98=√98+√98−√96n−√98=1+√98−√96n−√98．①当n≤9时，a n=1√98−√96√98−n <1，且{a n}单调递减，故a1=√961−√98<1最大；②当n≥10时，a n=1+√98−√96n−√98>1，且{a n}单调递减，故a10=√9610−√98>1最大．综上可知：该数列中最大项的序数n=10．故答案为：10．17.【答案】(−3, +∞)【考点】数列的函数特性【解析】根据所给的数列的项，写出数列的第n+1项，根据数列是一个递增数列，把所给的两项做差，得到不等式，根据恒成立得到结果．【解答】解：∵a n=n2+λn，∴a n+1=(n+1)2+λ(n+1)∵a n是递增数列，∴(n+1)2+λ(n+1)−n2−λn>0即2n+1+λ>0∴λ>−2n−1∵对于任意正整数都成立，∴λ>−3故答案为：(−3, +∞)18.【答案】0.04【考点】数列的函数特性【解析】a n=nn2+156=1n+156n≤2156=439，由此能求出a n的最大值．【解答】解：a n=nn2+156=1n+156n≤2√156=4√39，当x=156x，即x=2√39时，等式成立，12<2√39<13，所以最大值为n=12或13时出现，n=12时，a n=nn2+156=0.04n=13时，a n=nn2+156=0.04所以当n=12和13时，取最大值0.04．故答案为：0.04．19.【答案】7【考点】数列的函数特性【解析】首先，利用已知条件，进行展开，然后，求解关于n的不等式，确定其最小值．【解答】解：∵a1⋅a2⋅a3•…•a n=31×42×53×64×...×nn−2×n+1n−1×n+2n=12(n+1)(n+2)>36，∴(n+1)(n+2)>72，∴n≥7，∴n的最小值为7．股答案为：7．20.【答案】c n+1<c n【考点】数列的函数特性【解析】此题暂无解析【解答】解：由条件得c n=a n−b n=√n2+1−n=2，∴c n随n的增大而减小，∴c n+1<c n.故答案为：c n+1<c n．三、解答题（本题共计 20 小题，每题 10 分，共计200分）21.【答案】120【考点】数列的函数特性【解析】由数列{a n}的前n项和s n=n+1n+2，利用a3=S3−S2即可得出．【解答】解：∵数列{a n}的前n项和s n=n+1n+2，∴a3=S3−S2=3+13+2−2+12+2=45−34=120．故答案为：120．22.【答案】解：由题意得，S n=n2+2n−1，当n=1时，a1=S1=2，当n≥2时，a n=S n−S n−1=n2+2n−1−[(n−1)2+2(n−1)−1]=2n+1．此时当n=1时不成立．∴数列的通项公式为a n={2,n=12n+1,n≥2．【考点】数列的函数特性【解析】根据S n=n2+2n−1求出a1的值，利用a n=S n−S n−1求出当n>1时a n的表达式，然后验证a1的值，表示出a n．【解答】解：由题意得，S n=n2+2n−1，当n=1时，a1=S1=2，当n≥2时，a n=S n−S n−1=n2+2n−1−[(n−1)2+2(n−1)−1]=2n+1．此时当n=1时不成立．∴数列的通项公式为a n={2,n=12n+1,n≥2．23.【答案】（1）解：∵函数f(x)=2x−2−x，数列{a n}满足f(log2a n)=−2n．∴2log2a n−2−log2a n=−2n，∴a n−1a n=−2n，又a n>0，解得a n=√n2+1−n．（2）证明：∵a n=2，√n2+1+n随着n的增大而增大且大于0，∴数列{a n}是递减数列．【考点】数列的函数特性数列的概念及简单表示法【解析】（1）由于函数f(x)=2x−2−x，数列{a n}满足f(log2a n)=−2n．代入利用对数的运算性质可得a n−1a n=−2n，又a n>0，解出即可．（2）由（1）可得a n=2，即可证明其单调性．【解答】（1）解：∵ 函数f(x)=2x −2−x ，数列{a n }满足f(log 2a n )=−2n ． ∴ 2log 2a n −2−log 2a n =−2n ， ∴ a n −1a n=−2n ，又a n >0，解得a n =√n 2+1−n ． （2）证明：∵ a n =√n 2+1+n，2+1+n 随着n 的增大而增大且大于0，∴ 数列{a n }是递减数列． 24.【答案】 解：（1）设等差数列{a n }的公差为d ， 则S 6=6a 1+6×52d =24，a 10=a 1+9d =−9．解得a 1=9，d =−2，∴ 数列{a n }的通项公式为a n =11−2n ； （2）由（1）知S n =na 1+n(n−1)2×d =10n −n 2配方可得S n =−(n −5)2+25，∴ 由二次函数的性质可得当n =5时，S n 取得最大值． 【考点】等差数列的前n 项和 数列的函数特性【解析】（1）设等差数列{a n }的公差为d ，由已知可得a 1和d 的方程组，解方程组可得通项公式； （2）由（1）可得S n ，由二次函数的性质可得答案． 【解答】 解：（1）设等差数列{a n }的公差为d ， 则S 6=6a 1+6×52d =24，a 10=a 1+9d =−9．解得a 1=9，d =−2，∴ 数列{a n }的通项公式为a n =11−2n ； （2）由（1）知S n =na 1+n(n−1)2×d =10n −n 2配方可得S n =−(n −5)2+25，∴ 由二次函数的性质可得当n =5时，S n 取得最大值． 25.【答案】 解：（1）若f(x 1x 2...x 2015)=8，即有log 2a (x 1x 2...x 2015)=8，即x 1x 2...x 2015=(2a)8，则f(x 12)+f(x 22)+...+f(x 20152)=log 2a x 12+log 2a x 22+...+log 2a x 20152 =log 2a (x 1x 2...x 2015)2=log 2a (2a)16=16；（2）g(x)=f(x +1)>0，即为log 2a (x +1)>0， 由x ∈(−1, 0)，可得x +1∈(0, 1)，则0<2a <1，解得0<a <12．即有a 的取值范围是(0, 12)． 【考点】 数列的求和 数列的函数特性【解析】（1）运用对数的运算法则，计算化简即可得到所求值；（2）由题意可得log 2a (x +1)>0，由x 的范围，结合对数函数的性质，即可得到a 的范围．【解答】 解：（1）若f(x 1x 2...x 2015)=8，即有log 2a (x 1x 2...x 2015)=8，即x 1x 2...x 2015=(2a)8，则f(x 12)+f(x 22)+...+f(x 20152)=log 2a x 12+log 2a x 22+...+log 2a x 20152 =log 2a (x 1x 2...x 2015)2=log 2a (2a)16=16；（2）g(x)=f(x +1)>0，即为log 2a (x +1)>0， 由x ∈(−1, 0)，可得x +1∈(0, 1)， 则0<2a <1，解得0<a <12． 即有a 的取值范围是(0, 12)． 26. 【答案】解：由−1，32，−13，34，−15，…，可知：奇数项为a n =(−1)n ×1n，偶数项为a n =3n．因此通项公式为a n ={3n，n 为偶数˙．【考点】数列的概念及简单表示法 数列的函数特性 【解析】由−1，32，−13，34，−15，…，可知：奇数项为a n =(−1)n ×1n ，偶数项为a n =3n ．即可得出． 【解答】解：由−1，32，−13，34，−15，…，可知：奇数项为a n =(−1)n ×1n ，偶数项为a n =3n ． 因此通项公式为a n ={3n ，n 为偶数˙． 27.【答案】解：①∵等差数列的a1=−40，a3=−30，∴d=a3−a13−1=−30+402=5．∴a n=−40+5(n−1)=5n−45；②由a n=5n−45≤0，解得：n≤9．∴数列{a n}的前8项小于0，第9项等于0．∴数列{a n}的前8项和前9项的和相等最小，等于8×(−40)+8×7×52=−180．【考点】等差数列的前n项和数列的函数特性【解析】①由已知求得等差数列的首项，直接代入通项公式得答案；②求出小于0的项，然后利用等差数列的前n项和得答案．【解答】解：①∵等差数列的a1=−40，a3=−30，∴d=a3−a13−1=−30+402=5．∴a n=−40+5(n−1)=5n−45；②由a n=5n−45≤0，解得：n≤9．∴数列{a n}的前8项小于0，第9项等于0．∴数列{a n}的前8项和前9项的和相等最小，等于8×(−40)+8×7×52=−180．28.【答案】S n=n+1 nn≥2,S n−1=n n−1于是n≥2时，a n＝S n−S n−1 ;当n＝1时，a1＝2∴a n={2,n=1−1n(n−1),n≥2．【考点】数列的函数特性【解析】当已知S n求a n时，我们要明确两者之间的关系，即a n={S1,n=1S n−S n−1,n≥2．【解答】S n=n+1 nn≥2,S n−1=n n−1于是n≥2时，a n＝S n−S n−1 ;当n ＝1时，a 1＝2∴ a n ={2,n =1−1n(n−1),n ≥2 ．29.【答案】解：∵ 数列{a n }为递增数列，∴ 对于∀n ∈N ∗，a n+1>a n 都成立． ∴ (n +1)3−λ(n +1)>n 3−λn ． 化为λ<3n 2+3n +1，∵ 3n 2+3n +1=3(n +12)2−34+1≥7，∴ λ<7．∴ 实数λ的取值范围是(−∞, 7)． 【考点】数列的函数特性 【解析】由于数列{a n }为递增数列，可得对于∀n ∈N ∗，a n+1>a n 都成立．解出即可． 【解答】解：∵ 数列{a n }为递增数列，∴ 对于∀n ∈N ∗，a n+1>a n 都成立． ∴ (n +1)3−λ(n +1)>n 3−λn ． 化为λ<3n 2+3n +1，∵ 3n 2+3n +1=3(n +12)2−34+1≥7， ∴ λ<7．∴ 实数λ的取值范围是(−∞, 7)． 30.【答案】解：数列{b n }的通项为b n =na n (a >0)，∵ 当a ≥1时，数列b n =na n (a >0)，为递增数列， ∴ 不存在最大项， 当0<a <1时，b n+1b n=(1+1n)a ，随着n 的增大，比值越来越小，所以为递减数列，b 1最大． 【考点】数列的函数特性 【解析】运用作商的方法，讨论判断求解． 【解答】解：数列{b n }的通项为b n =na n (a >0)，∵ 当a ≥1时，数列b n =na n (a >0)，为递增数列， ∴ 不存在最大项， 当0<a <1时，b n+1b n=(1+1n )a ，随着n 的增大，比值越来越小，所以为递减数列，b 1最大． 31.解：∵ a n =n 2+λn ，∴ a n+1=(n +1)2+λ(n +1) ∵ a n ≤a n+1，∴ (n +1)2+λ(n +1)−n 2−λn ≥0 化简可得2n +1+λ≥0∴ λ≥−2n −1，对于任意正整数n 都成立， ∴ λ≥−3∴ λ的最小值为−3． 【考点】数列的函数特性 【解析】由题意可得a n+1=(n +1)2+λ(n +1)，要满足n ∈N ∗，a n ≤a n+1，化简可得λ≥−2n −1，只需求出−2n −1的最大值即可． 【解答】解：∵ a n =n 2+λn ，∴ a n+1=(n +1)2+λ(n +1) ∵ a n ≤a n+1，∴ (n +1)2+λ(n +1)−n 2−λn ≥0 化简可得2n +1+λ≥0∴ λ≥−2n −1，对于任意正整数n 都成立， ∴ λ≥−3∴ λ的最小值为−3． 32.【答案】解：当n ≤7时，a n ≤0；当n ≥8时，a n >0． 当n ≥8时，a n+1a n=(n−6)2(n−7)=12+12(n−7)，当n =8时，a9a 8=1；当n ≥9时，0<a n+1a n<1，a n+1<a n ．∴ 数列{a n }的最大项是a 8或a 9，且a 8=a 9=(12)8=1256． 【考点】数列的函数特性 【解析】当n ≤7时，a n ≤0；当n ≥8时，a n >0．当n ≥8时，a n+1a n=12+12(n−7)，利用数列的单调性即可得出． 【解答】解：当n ≤7时，a n ≤0；当n ≥8时，a n >0． 当n ≥8时，a n+1a n=(n−6)2(n−7)=12+12(n−7)，当n =8时，a9a 8=1；当n ≥9时，0<a n+1a n<1，a n+1<a n ．∴ 数列{a n }的最大项是a 8或a 9，且a 8=a 9=(12)8=1256． 33.解：（1）0，1，0，1，0，1…，可得a n =1+(−1)n2；（2）0.9，0.99，0.999，0.9999，…，变形为1−0.1，1−0.01，1−0.001，…，∴ a n =1−(110)n ．（3）1，3，6，10，15，21，…，3−1=2，6−3=3，10−6=4，…． 可得：a n =(a n −a n−1)+(a n−1−a n−2)+...+(a 2−a 1)+a 1 =n +(n −1)…+2+1 =n(n+1)2．【考点】数列的函数特性 【解析】（1）利用a 2k =1+(−1)2k ，a 2k−1=1+(−1)2k−1即可得出；（2）0.9，0.99，0.999，0.9999，…，变形为1−0.1，1−0.01，1−0.001，…，利用等比数列的通项公式即可得出．（3）1，3，6，10，15，21，…，3−1=2，6−3=3，10−6=4，…．利用：a n =(a n −a n−1)+(a n−1−a n−2)+...+(a 2−a 1)+a 1即可得出． 【解答】解：（1）0，1，0，1，0，1…，可得a n =1+(−1)n2；（2）0.9，0.99，0.999，0.9999，…，变形为1−0.1，1−0.01，1−0.001，…，∴ a n =1−(110)n ．（3）1，3，6，10，15，21，…，3−1=2，6−3=3，10−6=4，…． 可得：a n =(a n −a n−1)+(a n−1−a n−2)+...+(a 2−a 1)+a 1 =n +(n −1)…+2+1 =n(n+1)2．34. 【答案】a n =−n4的前5项分别为：−14，−24，−34，−44，−54； b n =2n3的前5项分别为：23，43，83，163，323； c n =2n+1n的前5项分别为：3，52，73，94，115； d n =(−1)n n的前5项分别为：−1，12，−13，14，−15．它们的图象如图：【考点】数列的函数特性【解析】根据数列的通项公式求出它的前5项，从而作出它们的图象，是一群孤立的点．【解答】a n =−n 4的前5项分别为：−14，−24，−34，−44，−54；b n =2n 3的前5项分别为：23，43，83，163，323； c n =2n+1n 的前5项分别为：3，52，73，94，115； d n =(−1)n n 的前5项分别为：−1，12，−13，14，−15．它们的图象如图：35.【答案】解：（1）∵ a n =(34)n−1[(34)n−1−1](n ∈N +)．当n =1时，a 1=(34)0[(34)0−1]=0 当n >1时，(34)n−1>0，(34)n−1−1<0，则a n =(34)n−1[(34)n−1−1](n ∈N +)<0 故数列{a n }中的最大项为a 1=0，（2）∵ a n =(34)n−1[(34)n−1−1](n ∈N +)≤0 ∴ −a n =(34)n−1[1−(34)n−1]≥0∴ −a n ≤((34)n−1+[1−(34)n−1]2)2=14 ∵ 3<log 3412+1<4当n =3时，a 3=(34)2[(34)2−1]=−63256当n =4时，a 4=(34)3[(34)3−1]=−9994096∴ 求数列{a n }中的最小项为a 3=−63256【考点】数列的函数特性【解析】（1）由已知中数列{a n }的通项公式为a n =(34)n−1[(34)n−1−1](n ∈N +)．我们可以分析出当n =1时，a n =0，当n >1时，a n <0，进而得到数列{a n }中的最大项为a 1；（2）根据数列{a n }的通项公式为a n =(34)n−1[(34)n−1−1](n ∈N +)其相乘的两项的和为定值，故我们可以利用基本不等式求出−a n 的范围，进而得到数列{a n }中的最小项及其值．【解答】解：（1）∵ a n =(34)n−1[(34)n−1−1](n ∈N +)．当n =1时，a 1=(34)0[(34)0−1]=0 当n >1时，(34)n−1>0，(34)n−1−1<0，则a n =(34)n−1[(34)n−1−1](n ∈N +)<0 故数列{a n }中的最大项为a 1=0，（2）∵ a n =(34)n−1[(34)n−1−1](n ∈N +)≤0∴ −a n =(34)n−1[1−(34)n−1]≥0∴ −a n ≤((34)n−1+[1−(34)n−1]2)2=14 ∵ 3<log 3412+1<4当n =3时，a 3=(34)2[(34)2−1]=−63256 当n =4时，a 4=(34)3[(34)3−1]=−9994096∴ 求数列{a n }中的最小项为a 3=−6325636.【答案】解：(I)排序数列为4，1，3，2．(II)证明：充分性：D当数列{a n }单调增时，∵ a 1<a 2<...<a n ，∴ 排序数列为1，2，3，…，n ．∴ 排序数列为等差数列．当数列{a n }单调减时，∵ a n <a n−1<...<a 1，∴ 排序数列为n ，n −1，n −2， (1)∴ 排序数列为等差数列．综上，数列{a n }为单调数列时，排序数列为等差数列． 必要性：∵ 排序数列为等差数列∴ 排序数列为1，2，3，…，n 或n ，n −1，n −2，…，1． ∴ a 1<a 2<...<a n 或a n <a n−1<...<a 1，∴ 数列{a n }为单调数列．【考点】数列的函数特性【解析】(1)根据排序数列的定义，即可写出2，4，3，1的排序数列；(2)根据等差数列的定义以及充要条件的定义即可证明数列{a n }的排序数列为等差数列的充要条件是数列{a n }为单调数列．【解答】解：(I)排序数列为4，1，3，2．(II)证明：充分性：D当数列{a n }单调增时，∵ a 1<a 2<...<a n ，∴ 排序数列为1，2，3，…，n ．∴ 排序数列为等差数列．当数列{a n }单调减时，∵ a n <a n−1<...<a 1，∴ 排序数列为n ，n −1，n −2， (1)∴ 排序数列为等差数列．综上，数列{a n }为单调数列时，排序数列为等差数列． 必要性：∵ 排序数列为等差数列∴ 排序数列为1，2，3，…，n 或n ，n −1，n −2，…，1． ∴ a 1<a 2<...<a n 或a n <a n−1<...<a 1，∴ 数列{a n }为单调数列．37.【答案】解：（1）a 8=28+8=136，a 10=210+10=155．（2）假设110是此数列的第n 项，则2n 2+n =110，化为n 2+n −20=0，解得n =4．故110是此数列的第4项．【考点】数列的函数特性【解析】（1）由通项公式a n =2n 2+n ．分别令n =8，10即可得出；（2）假设110是此数列的第n 项，则2n 2+n =110，解得n 若为正整数即可．【解答】解：（1）a 8=282+8=136，a 10=2102+10=155．（2）假设110是此数列的第n 项，则2n 2+n =110，化为n 2+n −20=0，解得n =4． 故110是此数列的第4项．38.【答案】解：由a n+1a n =(n+1)⋅(910)nn⋅(910)n−1=9n+910n=910+910n，可知：910+910n(n∈N∗)是关于n的单调递减数列，并且当n<9时，a n+1a n>1，即a n<a n+1；当n=9时，a n+1a n=1，即a9=a10；当n>9时，a n+1a n<1，即a n>a n+1．综上可得：a1<a2<...<a9=a10>a11>…．∴数列{a n}中的最大项是a9，a10，最小项与n有关系．【考点】数列的函数特性【解析】由a n+1a n =(n+1)⋅(910)nn⋅(910)n−1=9n+910n=910+910n，可知：910+910n(n∈N∗)是关于n的单调递减数列，对n分类讨论即可得出．【解答】解：由a n+1a n =(n+1)⋅(910)nn⋅(910)n−1=9n+910n=910+910n，可知：910+910n(n∈N∗)是关于n的单调递减数列，并且当n<9时，a n+1a n>1，即a n<a n+1；当n=9时，a n+1a n=1，即a9=a10；当n>9时，a n+1a n<1，即a n>a n+1．综上可得：a1<a2<...<a9=a10>a11>…．∴数列{a n}中的最大项是a9，a10，最小项与n有关系．39.【答案】解：∵a1=2，a n+a n+1=7，∴a2=5，a3=2，a4=5，…，∴a n={2，n为正奇数5，n为正偶数．【考点】数列的函数特性【解析】由a1=2，a n+a n+1=7，即可得出．【解答】解：∵a1=2，a n+a n+1=7，∴a2=5，a3=2，a4=5，…，∴a n={2，n为正奇数5，n为正偶数．40.【答案】解：（1）∵等差数列{a n}满足：a1=8，公差d=−2．∴a n=8−2(n−1)=10−2n．（2）由a n=10−2n≥0，解得n≤5，∴当n=5或4时，S n取得最大值．最大值为：5×(8+0)2=20．【考点】数列的函数特性【解析】（1）利用等差数列的通项公式即可得出；（2）由a n=10−2n≥0，解得n即可判断出S n取得最大值时的n的值，再利用等差数列的前n项和公式即可得出．【解答】解：（1）∵等差数列{a n}满足：a1=8，公差d=−2．∴a n=8−2(n−1)=10−2n．（2）由a n=10−2n≥0，解得n≤5，∴当n=5或4时，S n取得最大值．最大值为：5×(8+0)2=20．。