后方交会计算

空间后方交会的解算一． 空间后方交会的目的摄影测量主要利用摄影的方法获取地面的信息，主要是是点位信息，属性信息，因此要对此进行空间定位和建模，并首先确定模型的参数，这就是空间后方交会的目的，用以求出模型外方位元素。

二． 空间后方交会的原理空间后方交会的原理是共线方程。

共线方程是依据相似三角形原理给出的，其形式如下111333222333()()()()()()()()()()()()A S A S A S A S A S A S AS A S A S A S A S A S a X X b Y Y c Z Z x f a X X a Y Y a Z Z a X X b Y Y c Z Z y f a X X a Y Y a Z Z -+-+-=--+-+--+-+-=--+-+-上式成为中心投影的构线方程，我们可以根据几个已知点，来计算方程的参数，一般需要六个方程，或者要三个点，为提高精度，可存在多余观测，然后利用最小二乘求其最小二乘解。

将公式利用泰勒公式线性化，取至一次项，得到其系数矩阵A ；引入改正数（残差）V ，则可将其写成矩阵形式：V AX L =-其中111333222333[,]()()()()()()()()()()()()()()Tx y A S A S A S x A S A S A S A S A S A S y A S A S A S L l l a X X b Y Y c Z Z l x x x fa X X a Y Y a Z Z a X Xb Y Yc Z Z l y y y fa X X a Y Y a Z Z =-+-+-=-=+-+-+--+-+-=-=+-+-+- 则1()T T X A A A L -=X 为外方位元素的近似改正数，由于采用泰勒展开取至一次项，为减少误差，要将的出的值作为近似值进行迭代，知道小于规定的误差三． 空间后方交会解算过程1. 已知条件近似垂直摄影00253.24mmx y 0f ===2. 解算程序流程图MATLAB 程序format long;s1=xlsread('data.xls');%读取数据a1=s1(1:4,1:2);%影像坐标b1=s1(1:4,3:5);%地面摄影测量坐标a2=s1.*10^-3;%影像坐标单位转化j1=a2(1,:)-a2(2,:);j2=j1(1,1)^2+j1(1,2)^2;lengh_a1=sqrt(j2); %相片某一长度j1=b1(1,:)-b1(1,:);j2=j1(1,1)^2+j1(1,2)^2;lengh_b1=sqrt(j2); %地面对应的长度m=lengh_b1/lengh_a1;%求出比例尺n0=0;p0=0;q0=0;x0=mean(b1(:,1));y0=mean(b1(:,2));f=153.24*10^-3;z0=m*f;x001={x0,x0,x0,x0};X0=cell2mat(x001)';y001={y0,y0,y0,y0};Y0=cell2mat(y001)';z001={z0,z0,z0,z0};Z0=cell2mat(z001)';%初始化外方位元素的值aa1=cos(n0)*cos(q0)-sin(n0)*sin(p0)*sin(q0);aa2=-sin(q0)*cos(n0)-sin(n0)*sin(p0)*cos(q0);aa3=-sin(n0)*cos(p0);bb1=sin(q0)*cos(p0);bb2=cos(q0)*cos(p0);bb3=-sin(p0);cc1=sin(n0)*cos(q0)+sin(p0)*cos(n0)*sin(q0);cc2=-sin(n0)*sin(q0)+sin(p0)*cos(q0)*cos(n0);cc3=cos(n0)*cos(p0);%计算改正数XX1=aa1.*(b1(:,1)-X0)+bb1.*(b1(:,2)-Y0)+cc1.*(b1(:,3)-Z0); XX2=aa2.*(b1(:,1)-X0)+bb2.*(b1(:,2)-Y0)+cc2.*(b1(:,3)-Z0); XX3=aa3.*(b1(:,1)-X0)+bb3.*(b1(:,2)-Y0)+cc3.*(b1(:,3)-Z0); lx=a1(:,1)+f.*(XX1./XX3);ly=a1(:,2)+f.*(XX2./XX3);l={lx',ly'};L=cell2mat(l)';%方程系数A=[-3.969*10^-5 0 2.231*10^-5 -0.2 -0.04 -0.06899;0 -3.969*10^-5 1.787*10^-5 -0.04 -0.18 0.08615;-2.88*10^-5 0 1*10^-5 -0.17 0.03 0.08211;0 -2.88*10^-5 -1.54*10^-5 0.03 -0.2 0.0534;-4.14*10^-5 0 4*10^-6 -0.15 -7.4*10^-3 -0.07663;0 -4.14*10^-5 2.07*10^-5 -7.4*10^-3 -0.19 0.01478;-2.89*10^-5 0 -1.98*10^-6 -0.15 -4.4*10^-3 0.06443;0 -2.89*10^-5 -1.22*10^-5 -4.4*10^-3 -0.18 0.01046];%L=[-1.28 3.78 -3.02 -1.45 -4.25 4.98 -4.72 -0.385]'.*10^-2; %第一次迭代X=inv(A'*A)*A'*L;3.结果X=1492.41127406195-554.4015671761941425.68660973544-0.0383847815608609 0.00911624039769785 -0.105416434087641S=1492.41127406195-554.401567176194 1425.68660973544 38436.9616152184 27963.1641162404-0.105416434087641。

单张相片后方交会目录●作业任务 (3)●解算原理 (3)●具体过程 (4)●算法描述及程序流程 (4)●计算结果 (7)●结果分析 (8)●心得体会及建议 (8)●参考文献 (9)一，作业任务已知摄影机主距f=153.24mm，四对点的像点坐标与相应地面坐标列入下表：表1-1计算近似垂直摄影情况下后方交会解。

二，解算原理【关键词1】中心投影构像方程在摄影测量学中，最重要的方程就是中心投影构像方程（图2-1）。

这个方程将地面点在地面摄影测量坐标系中的坐标（物方坐标）和地面点对应像点的像平面坐标联系起来。

在解析摄影测量与数字摄影测量中是极其有用的。

在以后将要学习到的双像摄影测量光束法、解析测图仪原理及数字影像纠正等都要用到该式。

图2-1在上述公式中：x和y分别为以像主点为原点的像点坐标，相应地面点坐标为X,Y,Z，相片主距f以及外方位元素Xs，Ys，Zs，ψ，ω，κ。

而在此次作业中，就是已知四个地面控制点的坐标以及其对应的像点坐标，通过间接平差原理来求解此张航片的外方位元素。

【关键词2】间接平差在一个平差问题中，当所选的独立参数X的个数等于必要观测值t时，可将每个观测值表达成这t个参数的函数，组成观测方程，然后依据最小二乘原理求解，这种以观测方程为函数模型的平差方法，就是间接平差方法间接平差的函数模型为：随机模型为：平差准则为：VtPV=min【关键词3】单像空间后方交会利用至少三个已知地面控制点的坐标A（Xa，Ya，Za）、B（Xb，Yb，Zb）、Z（Xc，Yc，Zc），与其影像上对应的三个像点的影像坐标a（xa，ya）、b（xb，yb）、c（xc，yc），根据共线方程，反求该像点的外方位元素Xs，Ys，Zs，ψ，ω，κ。

这种解算方法是以单张像片为基础，亦称单像空间后方交会。

在此次作业中，就是已知四个控制点在地面摄影测量坐标系中的坐标和对应的像点坐标。

由此可以列出8个误差方程，存在两个多余观测数，则n=2。

后方交会残差值误差范围后方交会是摄影测量中常用的一种方法，用于确定地面上各个点的空间坐标。

在实际应用中，由于各种误差的存在，后方交会的结果会产生一定的残差值误差。

误差范围的确定对于保证测量结果的准确性和可靠性非常重要。

本文将从后方交会的基本原理、误差来源、误差计算方法以及误差范围的确定等方面进行详细的分析和论述。

一、后方交会的基本原理后方交会是一种基于像对几何关系的摄影测量方法，通过对各个像点的位置测量和相对方位角的观测，计算出地面控制点的空间坐标。

其基本原理可以简述如下：1. 反投影原理：根据像点在像空间上的位置，利用摄影测量的几何关系反推出这些像点所对应的地面点在物空间上的位置。

反投影原理是后方交会的理论基础，也是误差产生的根源。

2. 控制点观测：确定一定数量的控制点，并测量其像点位置及相对方位角。

控制点的选择应满足精度要求和实际情况，通常采用地面测量或其他摄影测量方法进行。

3. 几何模型：根据反投影原理和控制点观测，建立几何模型，描述像空间与物空间之间的几何关系。

模型包括相机的内外参数、像点的位置和相对方位角等。

4. 误差方程：利用几何模型，建立误差方程，将测量值与真实值之间的误差表示出来。

误差方程是分析误差来源、计算误差范围的基础。

二、后方交会误差的来源后方交会的误差主要来自于以下几个方面：1. 相机内外参数的误差：相机的内外参数是后方交会的重要参数，包括焦距、主点位置、旋转矩阵、平移向量等。

由于摄影测量设备和仪器的制造和使用限制，这些参数会存在误差，从而影响后方交会的结果。

2. 观测误差：观测误差包括控制点的像点测量误差和方位角观测误差。

像点测量误差可以由像点测量精度来描述，方位角观测误差可以由方位角观测精度来描述。

观测误差是由测量设备、操作人员和环境等因素共同引起的。

3. 地面控制点的精度：后方交会的精度还受到地面控制点的精度限制。

如果地面控制点的精度较差，那么后方交会的精度也会受到影响。

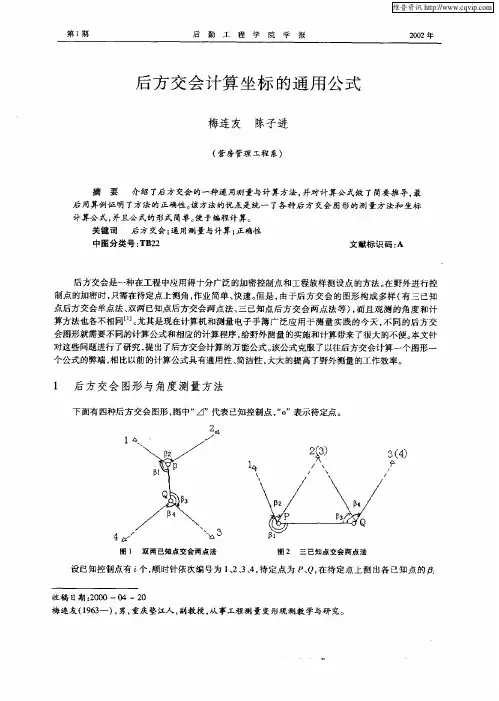
后方交会法计算推导公式
后方交会法是地理测量中一种常用的三角测量方法，用于计算未知点的坐标。

以下是后方交会法的推导公式：
假设已知的点A、B、C的坐标分别为(xA, yA)、(xB, yB)、(xC, yC)，未知点P的坐标为(xP, yP)。

1. 计算方位角α和β：
α = atan((yB - yA) / (xB - xA))
β = atan((yC - yB) / (xC - xB))
2. 计算边长AB和BC：
AB = sqrt((xB - xA)^2 + (yB - yA)^2)
BC = sqrt((xC - xB)^2 + (yC - yB)^2)
3. 计算方位角θ和γ：
θ = α + π - β
γ = atan((yC - yA) / (xC - xA))
4. 计算边长AP和PC：
AP = AB * sin(γ) / sin(θ)
PC = BC * sin(γ) / sin(θ)
5. 计算点P的坐标：
xP = xA + AP * cos(α)
yP = yA + AP * sin(α)
通过以上公式计算，可以得到未知点P的坐标(xP, yP)。

需要注意的是，这里的计算假设了已知的点A、B、C是符合三角关系的，如果存在测量误差或不满
足三角关系，可能会导致计算结果的不准确性。

在实际应用中，要考虑测量误差和进行相应的精度控制。

后方交会法计算推导公式
后方交会法是将同一个点在多个不同视角下的观测数据进行处理，最终确定该点在地图上的实际位置。

其计算推导公式如下：
1. 观测数据处理
对于同一个点，可以在多个不同位置观测到，可以通过三角化原理计算出该点在各个视角下的坐标。

假设有n个视角，则有
n个观测数据，分别为:
(X1, Y1, Z1, x1, y1)
(X2, Y2, Z2, x2, y2)
...
(Xn, Yn, Zn, xn, yn)
其中，(X, Y, Z) 表示观测视角的三维坐标，(x, y) 表示在该视
角下观测到该点的二维坐标。

2. 构建观测方程
针对每个视角，可以构建如下的观测方程：
(x - xi) / f = X / Z
(y - yi) / f = Y / Z
其中，xi 和 yi 表示该视角的二维坐标，f 表示相机的焦距，X、Y、Z 分别表示该点在三维空间中的坐标。

3. 解算观测方程
将观测方程转换为 Z 的形式，并可以得到一个关于 X、Y 和 Z 的二次方程：
aX² + bY² + cZ² + dXY + eXZ + fYZ + gX + hY + iZ + j = 0
其中，a、b、c、d、e、f、g、h、i 和 j 是该方程的系数。

4. 进行加权最小二乘法拟合
为了提高计算精度，对观测数据进行加权处理，并利用最小二乘法拟合解算方程系数。

5. 求解 X、Y 和 Z 的坐标值
利用解算出来的方程系数，可以解算出该点在三维空间中的坐标值。

单像空间后方交会测绘学院 成晓倩1 概述1.1 定义利用一定数量的地面控制点和对应像点坐标求解单张像片外方位元素的方法称为空间后方交会。

1.2 所需控制点个数与分布共线条件方程的一般形式为：⎪⎪⎩⎪⎪⎨⎧-+-+--+-+--=--+-+--+-+--=-)()()()()()()()()()()()(33322203331110S S S S S S S S S S S S Z Z c Y Y b X X a Z Z c Y Y b X X a f y y Z Z c Y Y b X X a Z Z c Y Y b X X a f x x （1）式中包含有六个外方位元素，即κωϕ、、、、、S S S Z Y X ，只有确定了这六个外方位元素的值，才能利用共线条件方程真正确定一张像片的任一像点与对应地面点的坐标关系。

个数：对任一控制点，我们已知其地面坐标)(i i i Z Y X 、、和对应像点坐标)(i i y x 、，代入共线条件方程可以列出两个方程式，因此，只少需要3个控制点才能解算出六个外方位元素。

在实际应用中，为了避免粗差，应有多余检查点，因此，一般需要4～6个控制点。

分布：为了最有效地控制整张像片，控制点应均匀分布于像片边缘，如下图所示。

由于共线条件方程是非线性的，直接答解十分困难，所以首先将共线方程改化为线性形式，然后再答解最为简单的线性方程组。

2 空间后方交会的基本思路分布合理 分布合理 分布不合理2.1 共线条件方程线性化的基本思路在共线条件方程中，令)()()()()()()()()(333222111S S S S S S S S S Z Z c Y Y b X X a Z Z Z c Y Y b X X a Y Z Z c Y Y b X X a X -+-+-=-+-+-=-+-+-= （2） 则共线方程变为⎪⎪⎩⎪⎪⎨⎧-=--=-ZY fy y Z Xf x x 00 （3） 对上式两侧同乘Z ，并移至方程同侧，则有⎩⎨⎧=-+=-+0)(0)(00Z y y Y f Z x x X f （4） 令⎩⎨⎧-+=-+=Zy y Y f Fy Zx x X f Fx )()(00 （5） 由于上式是共线方程的变形，因此，Fy Fx 、是κωϕ、、、、、S S S Z Y X 的函数。

后方交会的原理后方交会是测量学中一种常用的方法，可以用来确定点的位置，尤其是在地图制图、土地测量、建筑设计等领域中。

本文将从定义、原理、步骤、误差分析等方面详细介绍后方交会的原理。

一、定义后方交会是一种测量学方法，通过已知控制点的坐标、方位角等信息，对未知点进行定位。

它是一种基于三角测量原理的方法，通过三角形相似原理计算出未知点的坐标。

后方交会可以用来测量平面坐标、高程、方位角等，适用于各种地形和地貌。

二、原理后方交会的原理基于三角测量原理，即以三个已知点为顶点的三角形，其内部所有角度和三个顶点的距离都是已知的。

通过测量三角形内角和三边长度，可以计算出未知点的坐标。

具体来说，后方交会的原理可以分为以下几个步骤：1.测量控制点的坐标和方位角首先需要测量控制点的坐标和方位角，以确定已知点的位置和方向。

控制点可以是已知点，也可以是通过前方交会计算出的点。

2.测量未知点与控制点之间的距离和方位角接下来需要测量未知点与控制点之间的距离和方位角。

距离可以通过测距仪、激光测距仪等设备进行测量，方位角可以通过经纬仪或罗盘进行测量。

3.计算三角形内角和三边长度通过测量三角形内角和三边长度，可以计算出未知点的坐标。

其中，内角可以通过三角函数计算，三边长度可以通过勾股定理计算。

4.检验后方交会的精度最后需要对后方交会的精度进行检验，可以通过误差分析等方法进行评估。

如果误差较大，可以通过增加控制点、提高测量精度等方式进行调整。

三、步骤后方交会的步骤可以总结为以下几个：1.确定控制点的位置和方向，测量其坐标和方位角。

2.测量未知点与控制点之间的距离和方位角。

3.计算三角形内角和三边长度，确定未知点的坐标。

4.检验后方交会的精度，评估误差。

四、误差分析后方交会的精度受到多种因素的影响，如测量仪器精度、控制点布设精度、天气环境等。

误差分析可以通过以下几种方法进行： 1.重复测量法重复测量法是通过多次测量同一点来评估测量精度的方法。

后方交会法计算步骤后方交会法是一种常用的测量方法，用于确定地面上某一点的坐标。

它适用于各种测量场景，如土地测量、建筑测量等。

下面将介绍后方交会法的计算步骤。

首先，我们需要收集测量数据。

这些数据包括各个测量点的水平角、垂直角和斜距。

水平角是指测量点与基准点之间的水平夹角，垂直角是指测量点与基准点之间的垂直夹角，斜距是指测量点与基准点之间的直线距离。

接下来，我们需要建立一个坐标系。

坐标系的原点可以选择任意一个测量点，但通常选择其中一个作为基准点。

其他测量点的坐标将相对于基准点来确定。

然后，我们需要计算每个测量点相对于基准点的坐标。

这可以通过三角测量法来实现。

首先，我们可以利用水平角和斜距计算出测量点与基准点之间的水平距离。

然后，利用垂直角和斜距计算出测量点与基准点之间的垂直距离。

最后，我们可以利用三角函数计算出测量点的坐标。

在计算过程中，我们需要注意单位的转换。

通常情况下，水平角和垂直角以度为单位，而斜距以米为单位。

因此，在计算水平距离和垂直距离时，需要将角度转换为弧度。

完成上述计算后，我们可以得到每个测量点相对于基准点的坐标。

这些坐标可以表示为二维坐标系中的点，也可以表示为三维坐标系中的点，具体取决于测量场景的需求。

最后，我们可以通过绘制坐标系和标注测量点的坐标来展示测量结果。

这样可以更直观地了解测量点的位置和相对关系。

总结起来，后方交会法是一种常用的测量方法，可以用于确定地面上某一点的坐标。

它的计算步骤包括收集测量数据、建立坐标系、计算测量点的坐标和展示测量结果。

通过这些步骤，我们可以准确地确定测量点的位置，为后续的工程设计和规划提供基础数据。

前方交会法：在己知的两个（或两个以上）己知点（A,B）上架站通过测量α角和β角，计算待测点(P)坐标的方法。

如下图所示,红色字母代表的站点为架站点（A,B）：后方交会法：在待测点（P）上架站,通过使用三个己知点(A,B,C)及α角和β角计算待测点（P）坐标的方法。

如下图所示,红色字母代表的站点为架站点（P）：一、引言在工程测量中，内业资料计算占有很重要的比重，内业资料计算的准确无误与速度直接决定了测量工作是否能够快速、顺利地完成。

而内业资料的计算方法及其所需达到的精度，则又直接取决于外业所用仪器及具体的放样目标和内业计算所用到的办公软件和计算方法。

计算机辅助设计（Computer Aid Design 简写CAD，常称AutoCAD）是20世纪80年代初发展起来的一门新兴技术型应用软件。

如今在各个领域均得到了普遍的应用。

它大大提高了工程技术人员的工作效率。

AutoCAD配合AutoLisp语言，还可以编制一些常用的计算程序，得到计算结果。

AutoCAD的特性提供了测量内业资料计算的另外一种全新直观明了的图形计算方法。

结合我们现正使用的徕卡全站仪的情况，其可以很方便地进行三维坐标的测量，通过AutoCAD的内业计算，①、在放样的过程中，可以用编程计算器结合全站仪，非常方便地、快速地进行作业；②、运用AutoCAD进行计算结果的验证；③、随着全站仪的推广和普及，极坐标的放样越来越成为众多放样方法中备受测量人员青睐的一种，而坐标计算又是极坐标放样中的重点和难点，由于一般的红线放样，工程放样中的元素多为点、直线（段）、圆（弧）等，故可以充分利用AutoCAD的设定坐标系、绘图和取点的功能，以及结合我们外业所用计算器的功能，从而大大减轻我们外业的工作强度及内业的工作量。

以下以冶勒电站厂区枢纽工程的一些实例来说明三者在工程测量中的应用。

二、测区概况冶勒电站厂址位于石棉县李子坪乡南桠村，距坝址11KM，距石棉县城40KM。