郑州大学远程教育学院《线性代数》第01章在线测试

网络教育第一学期考试真题_线性代数1.下列排列中，（）是四级奇排列。

A 43212.若（-1）。

是五阶行列式【。

】的一项，则k,l之值及该项符号为（）B k=2,l=3,符号为负3.行列式【k-1 2。

】的充分必要条件是（）C k不等于-1且k不等于34.若行列式D=【a11 a12 a13。

】=M不等于0，则D1=【2a11 2a12 2a13。

】=（）C 8M5.行列式【0111】101111011110 =（）D -36.当a=（）时，行列式【-1 a 2…】=0B 17.如果行列式【a11 a12 a13 …】=d 则【3a31 3a32 3a33 …】=()B 6d8.当a=()时，行列式【a 1 1 …】=0A 19.行列式【125 64 27 8 。

】的值为（）A 1210.行列式【a 0 0 b …】中g元素的代数余子式为（）B bde-bcf11.设f(x)= 【1 1 2 。

】则f(x)=0的根为（）C 1，-1，2，-212.行列式【0 a1 0…0。

】=()D (-1)n+1 a1 a2…an-1 an114.~不能取（）时，方程组~X1+X2+X3=0…只有0解B 215.若三阶行列式D的第三行的元素依次为1，2，3它们的余子式分别为2，3，4，则D=()B 816.设行列式【a11 a12 a13…】=1,则【2a11 3a11-4a12 a13…】=()D -81.线性方程组x1+x2=1…解的情况是（）A 无解2.若线性方程组AX=B的增广矩阵A经初等行变换化为A- 【1234…】,当~不等于（）时，此线性方程组有唯一解B 0，13.已知n元线性方程组AX=B,其增广矩阵为A ，当（）时，线性方程组有解。

C r(A)=r(A)4.非齐次线性方程组AX=B中，A和增广矩阵A的秩都是4，A是4*6矩阵，则下列叙述正确的是（）B 方程组有无穷多组解5.设线性方程组AX=B有唯一解，则相应的齐次方程AX=0（）C 只有零解6.线性方程组AX=0只有零解，则AX=B(B不等于0)B 可能无解7.设有向量组a1,a2,a3和向量BA1=(1,1,1) a2=(1,1,0) a3= (1,0,0) B=(0,3,1)则向量B由向量a1,a2,a3的线性表示是（）A B=a1+2a2-3a38.向量组a1=（1.1.1）（0.2.5）（1.3.6）是（）A 线性相关9.下列向量组线性相关的是（）C （7.4.1），（-2.1.2），（3.6.5）10.向量组a1.a2…ar 线性无关的充要条件是（）B 向量线的秩等于它所含向量的个数11.向量组B1.B2…Bt可由a1.a2…as线性表示出，且B1.B2…Bt 线性无关，则s与t的关系为（）D s≥t12.n个向量a1.a2…an线性无关，去掉一个向量an，则剩下的n-1个向量（）B 线性无关13.设向量组a1.a2…as(s≥2)线性无关，且可由向量组B1.B2…Bs 线性表示，则以下结论中不能成立的是（）C 存在一个aj，向量组aj，b2…bs线性无关14.矩阵【1 0 1 0 0…】的秩为（）A 515.向量组a1.a2…as（s≥2）线性无关的充分必要条件是（）C a1.a2…as每一个向量均不可由其余向量线性表示16.若线性方程组的增广矩阵为A=【1.~.2】则~=（）时，线性方程组有无穷多解。

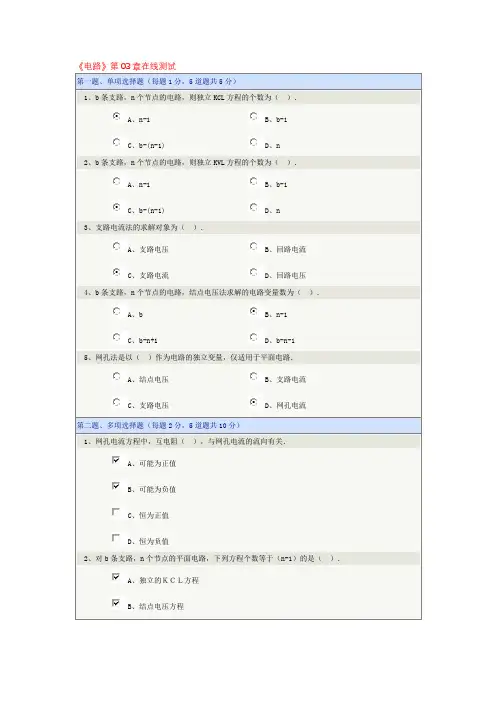
《电路》第03章在线测试第一题、单项选择题（每题1分，5道题共5分）1、b条支路，n个节点的电路，则独立KCL方程的个数为（）．A、n-1B、b-1C、b-(n-1)D、n2、b条支路，n个节点的电路，则独立KVL方程的个数为（）．A、n-1B、b-1C、b-(n-1)D、n3、支路电流法的求解对象为（）．A、支路电压B、回路电流C、支路电流D、回路电压4、b条支路，n个节点的电路，结点电压法求解的电路变量数为（）．A、bB、n-1C、b-n+1D、b-n-15、网孔法是以（）作为电路的独立变量，仅适用于平面电路．A、结点电压B、支路电流C、支路电压D、网孔电流第二题、多项选择题（每题2分，5道题共10分）1、网孔电流方程中，互电阻（），与网孔电流的流向有关．A、可能为正值B、可能为负值C、恒为正值D、恒为负值2、对b条支路，n个节点的平面电路，下列方程个数等于（n-1）的是（）．A、独立的ＫＣＬ方程B、结点电压方程C、网孔电流方程D、独立的ＫＶＬ方程3、关于网孔电流方程，下列说法正确的是（）．A、自电阻恒为正B、互电阻恒为负C、自电阻可正可负D、互电阻可正可负4、对于b个支路，n个结点的平面电路，下列说法正确的是（）．A、可以列出b个支路电流方程B、可以列出（b-n+1）个网孔电流方程C、可以列出（n-1）个网孔电流方程D、可以列出（n-1）个结点电压方程5、在网孔电流法中，网孔电流方程右端为各网孔电压源的代数和，其中的电压源包括（）．A、与电阻串联的电压源B、支路电压C、无伴电压源D、由电流源和电阻并联得到的等效电压源第三题、判断题（每题1分，5道题共5分）1、网孔电流法仅适用于平面电路．（）正确错误2、网孔电流是真实存在的，可以用电流表测出来．（）正确错误3、网孔法中的网孔电流是一种假想的，沿着网孔边缘流动的电流．（）正确错误4、支路电流法中方程的总数等于电路的支路数．（）《电路》第04章在线测试第一题、单项选择题（每题1分，5道题共5分）1、叠加定理表明在线性电路中，任一支路电流（电压），都是电路中各个独立电源单独工作时在该支路产生的电流或电压的（）．A、代数和B、差C、叠加D、商2、用电压源和电阻的串联来等效含源一端口网络时，电压源的电压等于网络的（）．A、开路电压B、短路电流C、电压源的电压D、电流源的电流3、任何一个含独立电源，线性电阻和受控源的一端口对外电路，可等效为（）和电导的并联电路．A、电压源B、受控电压源C、电流源D、受控电流源4、替代定理表明在线性电路中，替代后未被替代的支路的电压和电流将（）．A、变大B、变小C、不定D、保持不变5、叠加定理中的电压源置零是指将电压源用（）代替．A、短路线B、开路线C、受控源D、电阻第二题、多项选择题（每题2分，5道题共10分）1、叠加定理适用于下列哪些电路（）．A、线性电阻电路B、非线性电阻电路C、线性动态电路D、非线性动态电路2、在电路分析中，戴维宁定理特别适用于求解电路中某条支路的（）．A、电压B、电流C、功率D、电阻3、下面关于叠加定理的描述正确的是（）．A、可以用来直接计算线性电路的电压、电流B、叠加定理反应了线性电路的可加性C、可以用来直接计算线性电路的功率D、适用于非线性电路4、应用叠加定理计算线性电路中的电压、电流时，不作用的独立源应（）。

《线性代数》第一章习题解答1. 解：(1)31542 的逆序数=2+0+2+1=5(2)264315 的逆序数=1+4+2+1+0=8 （3）54321 的逆序数=4+3+2+1=10⑷ 246..S2）（2“）135..・HWT ）=呼2. 解：四阶彳亍列式中含有t?31的项可表示为（-1）5山％肿2//3104” '其中Ji ，J 2,J 4为2, 3, 4的全排列。

故带有负号的项有：一£?]2024°31°43，~a \3a 22a M a 44 > ~ a 23° 3\a 421 x2 4 展开式中含有%4 5的项必须每行都取含x 的项相乘,6x 1 即=x-3x-6x- x = 18x 4,含有 x 3 的项为(―1 严31)X • 3x • 6x • 7 + (一1)心24)x. 2 • X • x = -128%3关于''如何做线性代数习题”的一些说明：每个人都有自己的套学习方法，并经 过不断借鉴他人优点、总结自我经验，不断完善学习方法。

做习题是学习方法中一部分。

现介绍一种简单的习题解答方法：拿到习题后不要立即动手，应当先观察，看题目考你 的是哪个知识点；再思考，初步猜测要用哪些方法（所用定理、公式、解决技巧）来操作， 然后动手验证刚才猜测的方法是否可行，可行则解答之，不可行则换一种方法，直到找到答 案。

简单来说，这种方法步骤概括为：一停、二看、三想、四动手。

线性代数的计算题一般通过多做练习能很好的掌握,证明题对非数学专业同学而言要稍 难一些，但这仅仅是第一印象，事实证明只要认真听课、勤做练习、自我总结，每位同学都 能解决大部分证明题（非数学专业考试试题中证明题往往只占少数分值），即使自己不会做 的我们可以查阅参考资料是如何做的（对于教材每章的习题来说，教材正文中的例题也是常 用的参考资料），然后记住这种方法，记得多了做证明题的能力自然得到提高。

《线性代数》第05章在线测试
《线性代数》第05章在线测试剩余时间：59:54
答题须知：1、本卷满分20分。

2、答完题后，请一定要单击下面的“交卷”按钮交卷，否则无法记录本试卷的成绩。

3、在交卷之前，不要刷新本网页，否则你的答题结果将会被清空。

第一题、单项选择题（每题1分，5道题共5分）
1、设三阶矩阵A的特征值为1，2，-1，则|A|＝
A、-3
B、-2
C、2
D、3
2、设A是m×n矩阵，Ax＝0,只有零解，则r(A)＝＿＿.
A、n+m
B、n
C、m
D、0
3、设A为n阶方阵，r(A)＜n，下列关于齐次线性方程组Ax＝0的叙述正确的是（）
A、Ax＝0只有零解
B、Ax＝0的基础解系含r(A)个解向量
C、Ax＝0的基础解系含n-r(A)个解向量
D、Ax＝0没有解
4、设A为m×n矩阵，m≠n,则齐次线性方程组Ax＝0只有零解的充分必要条件是A的秩（）
A、小于m
B、等于m
C、小于n
D、等于n
5、下列命题中错误的是（）
A、只含有一个零向量的向量组线性相关
B、由3个2维向量组成的向量组线性相关
C、由一个非零向量组成的向量组线性相关
D、两个成比例的向量组成的向量组线性相关。

郑州大学远程继续教育学院代数考试题库一、选择题(每小题1分，共60分)下列各题A)、B)、C)、D)四个选项中，只有一个选项是正确的，请将正确选项涂写在答题卡相应位置上，答在试卷上不得分。

1，世界上不同型号的计算机，就其工作原理而论，一般认为都基于的冯·诺依曼提出的__原理。

(A)二进制数(B）布尔代数(C）开关电路(D)存储程序和控制2．下列一组数据中，最大的数是:(A)(227）(B）(1FF) (c)(1010001) (D)(789)io3．第一台电子计算机ENIAC问世的10年间，称为电子管计算机时代。

其主要的硬件电路为:(A)电子管(B）品体管(C)集成电路(D）大规模集成电路4．计算机辅助教学的英文意义为:(A)CAD (B)CAM(C)CAT(D)CAI5.MPU的含义是:(A）多媒体计算机的简称―――(B）控制器的简称(C）微处理器的简称(D)中央处理器的简称6. UPS是:(A)控制器(B)存储器(C)不间断电源(D)运算器7．在表示存储器的容量时，M的准确含义是:(A)100OK(B）1024K (c)1000 D)10248．直接用计算机能够识别的二进制编码编写的语言是:(A) BASIC(Bc(C)汇编语言(D)机器语言9．计算机只懂机器语言，而人类只熟悉高级语言，故人机通信必须借助一种中间者，此中间者就是:(A）编译程序(B）编辑程序(C〉连接程序 (D)装入程序10.下列语句中，正确的是:(A）lKB=1024X1024bytes(B)1KB=1024MB(C)1MB=1024X1024bytes (D〉1MB=1024bytes11．图标是W1ndows的重要元素之一，对图标的描述错误的是:(A)图标可以表示被组合在一起的多个程序(B)图标既可以代表程序也可以代表文档(C)图标可能是仍然在运行但窗口被最小化的程序(D)图标只能代表某个应用程序12. Windows 是一个多任务操作系统，这是指:(A)Windows可以供多个用户同时使用(B) windows可以运行很多种应用程序(C) Windows 可以同时运行多个应用程序(D) windows可以同时管理多种资源13．在Windows桌面上，不能打开资源管理器的操作是:(A)先用鼠标右键单击"我的电脑"图标，然后从弹出的菜单中选取"资源管理器(B先用鼠标右键单击"开始"按钮，然后从弹出的菜单中选取"资源管理器(C)先用鼠标左键单击"开始"按钮，然后从系统菜单中选取"资源管理器”(D)先用鼠标左键双击"我的电脑"图标，然后从窗口菜单中选取"资源管理器"图标14. Windows98 /2000桌面上，不能打开"我的电脑"的操作是:(A)在"资源管理器"中选取"我的电脑"(B)用鼠标左键双击"我的电脑"图标(C)先用鼠标右键单击"我的电脑"图标，然后在弹出的快捷菜单中选择"打开”(D)用鼠标左键单击"开始"按钮，然后在系统菜单中选取"我的电脑"15．控制面板是用来改变___的应用程序，以调整各种硬件和软件的选项。

郑州大学远程教育结构力学在线测试1-9章答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March《结构力学》第01章在线测试第一题、单项选择题（每题1分，5道题共5分）1、对结构进行强度计算的目的，是为了保证结构A、既经济又安全B、不致发生过大的变形C、美观实用D、不发生刚体运动2、结构的刚度是指A、结构保持原有平衡形式的能力B、结构抵抗失稳的能力C、结构抵抗变形的能力D、结构抵抗破坏的能力3、杆系结构中的构件的长度A、等于截面的高和宽B、与截面的高和宽是同一量级C、远远小于截面的高和宽D、远远大于截面的高和宽4、对结构进行强度计算目的是为了保证结构A、既经济又安全B、不致发生过大的变形C、美观实用D、不发生刚体运动5、固定铰支座有几个约束反力分量A、一个B、两个C、三个D、四个第二题、多项选择题（每题2分，5道题共10分）1、下列哪种情况不是平面结构A、所有杆件的轴线都位于同一平面内，荷载也作用在该平面内B、所有杆件的轴线都位于同一平面内，荷载与该平面垂直C、所有杆件的轴线都位于同一平面内，荷载与该平面平行D、所有杆件的轴线都不位于同一平面内E、荷载不作用在结构的平面内2、铰结点的约束特点是A、约束的各杆端不能相对移动B、约束的各杆端可相对转动C、约束的各杆端不能相对转动D、约束的各杆端可沿一个方向相对移动E、约束的各杆端可相对移动3、刚结点的约束特点是A、约束各杆端不能相对移动B、约束各杆端不能相对转动C、约束的各杆端可沿一个方向相对移动D、约束各杆端可相对转动E、约束各杆端可相对移动4、可动铰支座的特点是A、约束杆端不能移动B、允许杆端转动C、只有一个约束力偶D、允许杆端沿一个方向移动E、只有一个反力5、固定端支座的特点是A、不允许杆端移动B、只有一个反力C、允许杆端转动D、不允许杆端转动E、有两个反力和一个反力偶第三题、判断题（每题1分，5道题共5分）1、结构是建筑物和构筑物中承受荷载起骨架作用的部分。

《线性代数》第02章在线测试
《线性代数》第02章在线测试剩余时间：46:13
答题须知：1、本卷满分20分。

2、答完题后，请一定要单击下面的“交卷”按钮交卷，否则无法记录本试卷的成绩。

3、在交卷之前，不要刷新本网页，否则你的答题结果将会被清空。

第一题、单项选择题（每题1分，5道题共5分）
1、已知A2+A-E＝0，则矩阵A⁻¹＝（）
A、A-E
B、-A-E
C、A+E
D、-A+E
2、设矩阵A，B，C，X为同阶方阵，且A，B可逆，AXB＝C，则矩阵X＝（）
A、A⁻¹CB⁻¹
B、CA⁻¹B⁻¹
C、B⁻¹A⁻¹C
D、CB⁻¹A⁻¹
3、已知A是一个3×4矩阵，下列命题中正确的是（）
A、若矩阵A中所有3阶子式都为0，则秩（A）＝2
B、若A中存在2阶子式不为0，则秩（A）＝2
C、若秩（A）＝2，则A中所有3阶子式都为0
D、若秩（A）＝2，则A中所有2阶子式都不为0
4、设A , B , C均为n阶方阵，AB＝BA，AC＝CA，则ABC＝（）
A、ACB
B、CAB
C、CBA
D、BCA
5、设矩阵A的秩为r，则A中（）
A、所有r-1阶子式都不为0
B、所有r-1阶子式全为0
C、至少有一个r阶子式不等于0
D、所有r阶子式都不为0。

线代第一章测试题及答案一、选择题（每题5分，共20分）1. 以下哪个选项不是线性代数的研究对象？A. 向量空间B. 线性方程组C. 矩阵D. 微分方程答案：D2. 矩阵的秩是指：A. 矩阵的行数B. 矩阵的列数C. 矩阵中非零行（或列）的最大数目D. 矩阵的元素个数答案：C3. 以下哪个矩阵是可逆的？A. 零矩阵B. 单位矩阵C. 奇异矩阵D. 任意矩阵答案：B4. 向量空间的基是指：A. 空间中的任意一组向量B. 空间中的一组线性无关的向量C. 空间中的一组线性相关的向量D. 空间中的一组正交向量答案：B二、填空题（每题5分，共20分）1. 矩阵的元素个数称为矩阵的______。

答案：阶数2. 如果一个矩阵的行向量组线性无关，则该矩阵是______矩阵。

答案：满秩3. 向量空间中，一组向量如果满足线性组合的系数全为零，则称这组向量是______的。

答案：线性无关4. 一个n阶方阵的行列式等于______。

答案：0三、简答题（每题10分，共20分）1. 请简述什么是线性方程组的解。

答案：线性方程组的解是指满足方程组中所有方程的未知数的取值。

2. 请解释什么是矩阵的转置。

答案：矩阵的转置是指将矩阵的行向量变成列向量，列向量变成行向量，即交换矩阵的行和列。

四、计算题（每题15分，共40分）1. 计算矩阵A的行列式，其中A = \[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\]。

答案：\[ \text{det}(A) = (1)(4) - (2)(3) = 4 - 6 = -2 \]2. 已知矩阵B = \[\begin{bmatrix} 2 & 1 \\ 4 & 2\end{bmatrix}\]，求B的逆矩阵。

答案：\[ B^{-1} = \frac{1}{(2)(2) - (1)(4)} \begin{bmatrix} 2 & -1 \\ -4 & 2 \end{bmatrix} = \begin{bmatrix} 1 & -0.5 \\-2 & 1 \end{bmatrix} \]。

第一部分 专项同步练习第一章 行列式一、单项选择题1．下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512．如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4．=0001001001001000( ).、(A) 0 (B)1- (C) 1 (D) 25. =0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26．在函数100323211112)(x x x x x f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ，则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8．若a a a a a =22211211，则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9． 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).）(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ，则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若2235001011110403--=D ，则D 中第四行元的余子式的和为( ).(A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时，齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.|2．在六阶行列式中项261365415432a a a a a a 所带的符号是.3．四阶行列式中包含4322a a 且带正号的项是.4．若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=0100111010100111.6．行列式=-000100002000010n n .7．行列式=--001)1(2211)1(111n n n n a a a a a a .8．如果M a a a a a a a a a D ==333231232221131211，则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9．已知某5阶行列式的值为5，将其第一行与第5行交换并转置，再用2乘所有元素，则所得的新行列式的值为.10．行列式=--+---+---1111111111111111x x x x .11．n 阶行列式=+++λλλ111111111.。

习题 1.11．计算下列二阶行列式．（1）5324；（2）ααααcos sin sin cos ．解（1）146205324=−=；（2）ααααcos sin sin cos αα22sin cos −=．2．计算下列三阶行列式．（1）501721332−−；（2）00000d c b a ；（3）222111c b a c b a ；（4）cb a b a ac b a b a a c b a ++++++232．解（1）原式62072)5(1)3(12317)3(301)5(22−=××−−××−−××−××−+××+−××=（2）原式00000000000=⋅⋅−⋅⋅−⋅⋅−⋅⋅+⋅⋅+⋅⋅=d c b a c a d b ；（3）原式))()((222222b c a c a b c b ac b a c a ab bc −−−=−−−++=；（4）原式)()()2()23)((b a ac c b a ab b a ac c b a b a a +−++++++++=3)23())(2(a c b a ab c b a b a a =++−+++−．3．用行列式解下列方程组．（1）⎩⎨⎧=+=+35324y x y x ；（2）⎪⎩⎪⎨⎧=++=++=++82683321321321x x x x x x x x x ；（3）⎩⎨⎧=−=+0231322121x x x x ；（4）⎪⎩⎪⎨⎧=−+=+=−−031231232132321x x x x x x x x ．解（1）75341−==D ，253421−==D ，333212−==D 所以721==D D x ，732==D D y ．（2）2121111113−==D ，21281161181−==D ，41811611832−==D ，68216118133−==D ；所以111==D D x ，222==D Dx ，333==DD x ．（3）132332−=−=D ，220311−=−=D ，303122−==D 所以1321==D D x ，1332==D D y ．（4）8113230121−=−−−=D ，81102311211−=−−−=D ，81032101112=−−=D ；20131301213=−=D 所以111==D D x ，122−==D Dx ，333==DD x ．4．已知xx x x x x f 21112)(−−−=，求)(x f 的展开式．解xxx x x x f 21112)(−−−=22)(11)(1)(111)(2)()(2⋅⋅−⋅−⋅−⋅−⋅−−⋅⋅+−⋅⋅−+⋅−⋅=x x x x x x x x x x xx x 23223+−−=5．设b a ,为实数，问b a ,为何值时，行列式010100=−−−a b b a ．解01010022=−−=−−−b a a b b a 0,022==⇒−=⇒b a b a ．习题 1.21．求下列各排列的逆序数．（1）1527364；（2）624513；（3）435689712；（4）)2(42)12(31n n L L −．解（1）逆序数为14；62421527364it ↓↓↓↓↓↓↓ （2）逆序数为5；311624513it ↓↓↓↓↓↓ （3）逆序数为19；554310010435689712it ↓↓↓↓↓↓↓↓↓（4）逆序数为2)1(−n n ：2122210000421231↓↓−−−↓↓↓↓↓−n n n n t n i L L L L2．在由9,8,7,6,5,4,3,2,1组成的下述排列中，确定j i ,的值，使得（1）9467215j i 为奇排列；（2）4153972j i 为偶排列．解（1）j i ,为分别3和8；若8,3==j i ，则93411)946378215(=+++=τ，为奇排列；若3,8==j i ，则1234311)946873215(=++++=τ，为偶排列；（2）j i ,为分别6和8；若8,6==j i ，则205135231)397261584(=++++++=τ，为偶排列；若6,8==j i ，则215335131)397281564(=++++++=τ，为奇排列；3．在五阶行列式)det(ij a =D 展开式中，下列各项应取什么符号？为什么？（1）5145342213a a a a a ；（2）2544133251a a a a a ；（3）2344153251a a a a a ；（4）4512345321a a a a a ．解（1）因5)32451(=τ，所以前面带“-”号；（2）因7)53142(=τ，所以前面带“-”号；（3）因10)12543()53142(=+ττ，所以前面带“+”号；（4)因7)13425()25314(=+ττ，所以前面带“-”号．4．下列乘积中，那些可以构成相应阶数的行列式的项?为什么？（1）12432134a a a a ；（2）14342312a a a a ；（3）5514233241a a a a a ；（4）5512233241a a a a a ．解（1）可以，由于该项的四个元素乘积分别位于不同的行不同的列；（2）不可以，由于14342312a a a a 中的1434a a 都位于第四列，所以不是四阶行列式的项；（3）可以，由于该项的五个元素乘积分别位于不同的行不同的列；（4）不可以，由于5512233241a a a a a 中没有位于第四列的元素。

大学生校园网— 线性代数综合测试题共3页第1页×××大学线性代数期末考试题一、填空题（将正确答案填在题中横线上。

每小题2分，共10分）1. 1. 若若022150131=---x，则=c ____________________。

2．若齐次线性方程组ïîïíì=++=++=++000321321321x x x x x x x x x l l 只有零解，则l 应满足。

3 3．已知矩阵．已知矩阵n s ij c C B A ´=)(，，，满足CB AC =，则A 与B 分别是阶矩阵。

阶矩阵。

44．矩阵÷÷÷øöçççèæ=323122211211a a a a a a A 的行向量组线性。

5．n 阶方阵A 满足032=--E A A ，则=-1A。

二、判断正误（正确的在括号内填“√”，错误的在括号内填“×”。

每小题2分，共10分）1. 1. 若行列式若行列式D 中每个元素都大于零，则0ñD 。

（）2. 2. 零向量一零向量一定可以表示成任意一组向量的线性组合。

（） 3. 3. 向量组向量组m a a a ，，， 21中，如果1a 与m a 对应分量成比例，则向量组s a a a ，，， 21线性相关。

（）4. úúúúûùêêêêëé=01100000010010A ，则A A =-1。

（）5. 5. 若若l 为可逆矩阵A 的特征值，则1-A的特征值为l 。

( )三、单项选择题 (每小题仅有一个正确答案，将正确答案题号填入括号内。

每小题2分，共10分) 1. 1. 设设A 为n 阶矩阵，且2=A ，则=TA A （）。

大学生校园网—线性代数综合测试题×××大学线性代数期末考试题一、填空题〔将正确答案填在题中横线上。

每题 2 分，共 10 分〕1311. 假设05x 0 ，那么__________ 。

122x1x2x302．假设齐次线性方程组x1x2x30 只有零解，那么应满足。

x1x 2x303．矩阵A，B，C( c ij ) s n，满足AC CB ，那么 A 与 B 分别是阶矩阵。

a a11124．矩阵A a a的行向量组线性。

2122a a31325．n阶方阵A满足A 23A E0，那么A1。

二、判断正误〔正确的在括号内填“√〞，错误的在括号内填“×〞。

每题 2 分，共10 分〕1.假设行列式 D 中每个元素都大于零，那么D 0 。

〔〕2.零向量一定可以表示成任意一组向量的线性组合。

〔〕3.向量组 a1， a2，， a m中，如果a1与 a m对应的分量成比例，那么向量组a1， a2，，a s线性相关。

〔〕01001000A 。

〔〕4.A，那么 A1000100105. 假设为可逆矩阵 A 的特征值，那么 A 1的特征值为 。

( )三、单项选择题 ( 每题仅有一个正确答案，将正确答案题号填入括号内。

每题2 分，共 10 分 )1. 设 A 为 n 阶矩阵，且 A2，那么AAT〔〕。

① 2n② 2n 1③ 2n 1④ 42. n 维向量组 1 ， 2，，s 〔 3 s n 〕线性无关的充要条件是〔 〕。

①1， 2， ， s 中任意两个向量都线性无关②1， 2， ， s 中存在一个向量不能用其余向量线性表示③1， 2， ， s 中任一个向量都不能用其余向量线性表示共 3 页第 1 页大学生校园网—线性代数综合测试题④中不含零向量1， 2 ，， s3. 以下命题中正确的选项是 () 。

① 任意 n 个 n 1 维向量线性相关 ② 任意 n 个 n 1 维向量线性无关③ 任意 n 1 个 n 维向量线性相关 ④任意 n 1 个 n 维向量线性无关4. 设 A ， B 均为 n 阶方阵，下面结论正确的选项是( )。

线性代数习题参考答案(总96页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除第一章行列式§1 行列式的概念1．填空(1) 排列6427531的逆序数为，该排列为排列。

(2) i = ，j = 时，排列1274i56j9为偶排列。

(3) n阶行列式由项的代数和组成，其中每一项为行列式中位于不同行不同列的n个元素的乘积，若将每一项的各元素所在行标按自然顺序排列，那么列标构成一个n元排列。

若该排列为奇排列，则该项的符号为号；若为偶排列，该项的符号为号。

(4) 在6阶行列式中，含152332445166a a a a a a的项的符号为，含324314516625a a a a a a的项的符号为。

2．用行列式的定义计算下列行列式的值(1)112223323300 0aa aa a解：该行列式的3!项展开式中，有项不为零，它们分别为，所以行列式的值为。

(2)12,121,21,11, 12,100000nn nn n n n n n n n n nnaa aa a aa a a a------解：该行列式展开式中唯一不可能为0的项是，而它的逆序数是，故行列式值为。

3．证明：在全部n 元排列中，奇排列数与偶排列数相等。

证明：n 元排列共有!n 个，设其中奇排列数有1n 个，偶排列数为2n 个。

对于任意奇排列，交换其任意两个元的位置，就变成偶排列，故一个奇排列与许多偶排列对应，所以有1n 2n ，同理得2n 1n ，所以1n2n 。

4．若一个n 阶行列式中等于0的元素个数比n n -2多，则此行列式为0，为什么 5．n 阶行列式中，若负项的个数为偶数，则n 至少为多少（提示：利用3题的结果） 6．利用对角线法则计算下列三阶行列式（1）21141183---（2）222111ab c a b c§2 行列式的性质1．利用行列式的性质计算系列行列式。

华师网院《线性代数》练习测试题库及答案华中师范大学网络教育学院《线性代数》练习测试题库及答案一.选择题1、=-0000000000121nn a a a a （ B ）A. n n a a a 21)1(-B. n n a a a 211)1(+-C. n a a a 212、n 阶行列式00000000000a a aa=（ B ）A.na B. (1)2(1)n n n a -- C. (1)n n a -3、n21＝（ B ）A. (1)!nn - B. (1)2(1)!n n n -- C. 1(1)!n n +-4、 A 是n 阶方阵，m, l 是非负整数，以下说法不正确的是（ C ）. A. ()m lmlA A = B. m l m lA A A +?= C. m m mB A AB =)(5、A 、B 分别为m n ?、s t ?矩阵, ACB 有意义的条件是（ C ）A. C 为m t ?矩阵；B. C 为n t ?矩阵；C. C 为n s ?矩阵6、下面不一定为方阵的是（C ）A.对称矩阵.B.可逆矩阵.C. 线性方程组的系数矩阵.7、 ??-1021 的伴随矩阵是（A ） A. ??1021 B. ??-1201 C. ??-10218、分块矩阵 00A B ??（其中A 、B 为可逆矩阵）的逆矩阵是（ A ） A. 1100A B --??B. 00B AC. 1100B A --??9、线性方程组Ax b = 有唯一解的条件是（ A ）A.()()r A r A b A ==的列数B.()()r A r A b = .C.()()r A r A b A ==的行数10、线性方程组=++=++=++23213213211aax x x a x ax x x x ax 有唯一解的条件是（A ）A. 2,1-≠aB. 21-==a a 或.C. 1≠a11、的是则下面向量组线性无关），，，＝（），，，＝（)6,2,4(054312--=--γβα（B ）A. 0，，βαB. γβ，C. γα，12、设A 为正交矩阵，下面结论中错误的是（ C ）A. A T 也为正交矩阵.B. A -1也为正交矩阵.C. 总有 1A =-13、二次型()233221214321342,,,,x x x x x x x x x x f --+=的矩阵为（ C ）A 、---340402021B 、---320201011 C 、??---0000032002010011 14、设r 是实二次型),,,(21n x x x f 的秩，p 是二次型的正惯性指数，q 是二次型的负惯性指数，s 是二次型的符号差，那么（ B ）A. q p r -=；B. q p r +=；C. q p s +=； 15、下面二次型中正定的是（ B ）A. 21321),,(x x x x x f =B.2322213212),,(x x x x x x f ++=C.22213212),,(x x x x x f +=16、设A ，B 为n 阶方阵，满足等式0=AB ，则必有（）(A)0=A 或0=B ; (B)0=+B A ；（C ）0=A 或0=B ; (D)0=+B A 。