当前位置：文档之家 › 1.3 电势及其梯度

1.3 电势及其梯度

  • 格式：ppt
  • 大小：738.00 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

1-4 电势

1-4 电势

E = −∇ V v
（电势梯度）
为求电场强度
E 提供了一种新的途径
利用电场强度叠加原理 利用高斯定理 利用电势与电场强度的关系
v v V A = ∫ E ⋅ dl
A
V = 0点
电势零点选择方法： 电势零点选择方法：有限带电体以无穷远为电势 零点，实际问题中常选择地球电势为零. 零点，实际问题中常选择地球电势为零.
VA =
∫
A∞
v v E ⋅ dl
物理意义 把单位正试验电荷从点 A移到无穷远 静电场力所作的功. 时，静电场力所作的功. 电势差
x >> R
σ = ( x 2 + R 2 − x) ∫0 x 2 + r 2 2ε 0 2 R V ≈ Q 4π ε0 x 2 2 x +R ≈ x+ 电荷电势） （点电荷电势） 2x
σ 2 π r dr
1 – 4 电势及其梯度
例2
第一章 静电场
均匀带电球壳的电势. 均匀带电球壳的电势. 真空中， 的带电球壳. 真空中，有一带电为 Q ，半径为 R 的带电球壳 试求（ ）球壳外两点间的电势差；（ ；（2） 试求（1）球壳外两点间的电势差；（ ）球壳内两点 间的电势差；（ ；（3）球壳外任意点的电势；（ ；（4） 间的电势差；（ ）球壳外任意点的电势；（ ）球壳 内任意点的电势. 内任意点的电势 v + + + v 解 r < R ， E1 = 0 + + A d B r
∞ v ∞ Q v Q dr = 或 V外 ( r ) = ∫ E 2 ⋅ d r = ∫ 2 r 4π ε 0r r 4 π ε 0r
1 – 4 电势及其梯度
（4） r < R ）

电势梯度表达式

电势梯度表达式

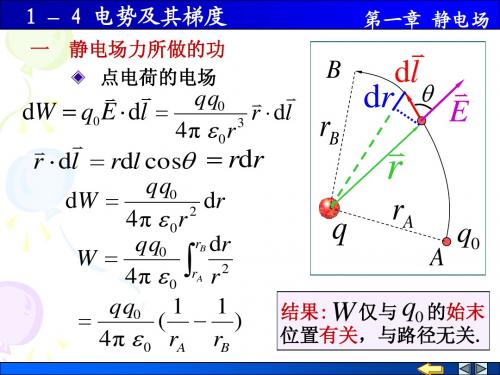
电势梯度表达式
摘要：
1.电势梯度的定义
2.电势梯度的表达式推导
3.电势梯度的物理意义
4.电势梯度在电场中的应用
正文：
电势梯度是指单位长度内电势的改变量，它是电势场的一种强度性质。

在电场中，电势梯度可以用来描述电势在空间中的变化情况。

根据电势的定义，我们知道电势是电荷在单位电荷上所具有的能量。

因此，电势梯度可以理解为单位电荷在电场中由于电势差所获得的能量。

电势梯度的表达式可以通过电势的定义和电场的基本公式推导得到。

假设在一个静电场中，我们有两个点A 和B，它们的电势分别为V_A 和V_B，那么电势梯度就可以定义为(V_A - V_B)/d，其中d 是点A 和点B 之间的距离。

这个公式表明，电势梯度等于电势的改变量除以距离。

电势梯度在电场中有很多应用，其中最主要的应用是用来描述电荷的运动。

根据电势梯度的定义，我们知道电势梯度是单位电荷在电场中所获得的能量。

因此，如果一个电荷在电场中沿着电势梯度方向移动，那么它的能量将不断增加。

这个过程可以用来推动其他电荷，从而实现电场的传输。

总之，电势梯度是描述电势在空间中变化的重要概念，它的表达式可以通过电势的定义和电场的基本公式推导得到。

1-4.电势及其梯度

1-4.电势及其梯度

1
A21 ( E p1 E p 2 ) E p 2 E p1 q0 (U 2 U1 ) 0 U 2 U1 0 U 2 U1 E 的方向为电势降低的方向。
第一章 静电场 恒定电流场
等势面的性质：
1)在静电场中，沿等势面移动电荷时，静电场力对此 电荷不作功。
证明： A q0
q0 (U a U b ) 0

b
a
E dl q0U ab
a
等势面
b
2)除电场强度为零外，电场线与等势面正交。
证明：因为将单位正电荷从等势面上M点移到N点， N 电场力做功为零，而路径不为零。 dl E dA E dl Edl cos 0
Up

p
E dl p
q 4 0 r
2
dr
q 4 0 rp
正点电荷周围的场电势为离正电荷越远，电势越低。 负点电荷周围的场电势为离负电荷越远，电势越高。
§4、电势及其梯度
第一章 静电场 恒定电流场
3、电势迭加原理 表述：一个电荷系的电场中,任一点的电势等于每一个 带电体单独存在时在该点所产生电势的代数和。 表达式： ( p) U


p
E dl ( E1 E2 ) dl
p
U ( p)
i i
U i ( p)

p
Ei dl
4 0 rip
qi
U ( p)
i
4 0 ri
qi
q1
r1 r2
p
q2
ri q3
r3
qi
（1）电势是标量，迭加的结果是求代数和； 注意： （2）要求各个点电荷的零电势点必须相同；

电势及其梯度

电势及其梯度

q E= 2 4πε 0 r
1
cosθ dl = dr
q o
r
c
θ
r E
a b rb 1 qq qq0 1 1 0 − ∴W = ∫ dW = ∫ 2 dr = a ra 4πε 4πε 0 ra rb 0 r
温州大学物理与电子信息学院
电势和电势差
结论：在点电荷的电场中， 结论：在点电荷的电场中，电场力对试验电荷所 做的功， 做的功 ， 只与试验电荷所带电量以及起点和终点 位置有关，而与所经历的路径无关． 位置有关，而与所经历的路径无关． 问题：任何带电体系产生的电场的结果如何？ 问题：任何带电体系产生的电场的结果如何？ r r r Q E = E1 + E 2 + L r r r r r r r ∴W = ∫ F ⋅ dl = q0 ∫ E ⋅ dl = q0 ∫ ( E1 + E2 + L) ⋅ dl r r r r = q0 ∫ E1 ⋅ dl + q0 ∫ E2 ⋅ dl + L
ρR 2 r Up = − ln < 0 2εo R
P r o o
温州大学物理与电子信息学院
定义法求电势
R
r ρ r r r < R E= 2ε o
r≥R
r
.
p
ρR 2 r Up = − ln 2εo R < 0
R
r ρR 2 ˆ = λ r E= r ˆ 2πεor 2εor
r<R
r= 0处， U= Umax= ρ R 2 处 2εo ε
温州大学物理与电子信息学院
电势梯度概念 等势面 定义:电势相等的曲面 定义:
U1
+q

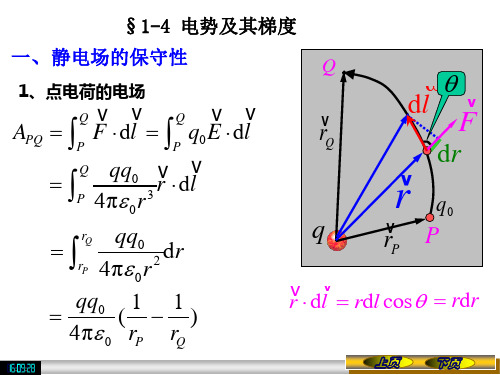
1-4电势及梯度

1-4电势及梯度
在静电场中，电场强度沿任意闭合路径的线积分恒为零.

L
E dl 0
物理意义：静电场是有源无旋场.
上页
下页
三、电势能
APQ (WQ WP ) WP WQ Q q0 E dl P Q 则 WP 令 WQ 0 q0 E dl
结论：任意静电场，静电力的功只与起、止位置有关，而与路径
无关，所以静电力是保守力，静电场是保守场，这种性质叫静电
场的保守性.
A
L
q0 E dl 0
上页 下页
A
因为
L
q0 E dl 0
所以
q0 0

L
E dl 0
二、静电场的环路定理
1、电势定义：
M0 WP uP E dl P q0
2、物理意义：某点的电势 uP 表示把单位正电荷从 该点移至M0 静电力所做的功.
上页
下页
讨论：①
M0 Wa uP E dl P q0 u只与 E 有关，可以描述电场的性质;
② u是标量，没有方向，但有正负;
u
例 点电荷的电势：
u j k) z j k )u z
Q u 4π 0 r
du Q E 2 dr 4π 0 r
上页 下页
电场强度：
qi 1 u 4π 0 ri 4π 0
qi r i
连续:
dq 1 u du 4π 0 r 4π 0
dq Q r
上页 下页
例2 均匀带电球面周围的电势分布.（已知R和Q） 解：选无穷远处电势为零. ① 球面外电势分布： 电场：
E

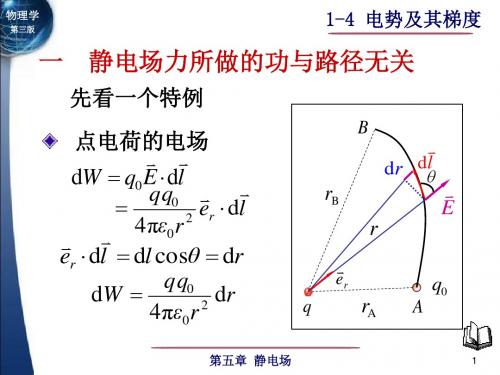
电势及其梯度

电势及其梯度
V
Q 4 π 0 R
Q 4π 0 r
R
o
rA
A
rB
B
r
o
R
r
第五章 静电场
29
物理学
第三版
1-4 电势及其梯度
例3 “无限长”带电直导线的电势. 解: 令 VB 0
有限远为电势零点 rB VP E dr r rB

o
B
P
dr r 2 π ε0 r rB ln 2 π ε0 r 讨论：能否选 V 0 ?
E dl
第五章 静电场
E
12
物理学
第三版
1-4 电势及其梯度
电 势定义：电场中任意点 a 的电 势 VA P( 0 ) Wa VA E dl a q0
单位正电荷在该点 所具有的电势能 单位正电荷从该点沿任意 路径移至电势能零点处的 过程中电场力所做的功
q0 E dl ( EpB EpA )
AB
VB EpB / q0 B点电势 令 VA EpA / q0 A点电势，
WAB E dl (VB VA ) AB q0
令 VB 0
q0
A E pA
VA
B
E pB
零点
VB
VA
A
0 r R 解: 电场分布 E Q rR 4ε r 2 0
r r Q B dr B （ 1） r R V V A B rA E dr 4πε0 rA r 2 Q 1 1 ( ) 4πε0 rA rB
（ 2） r R
rB VA VB E dr 0 rA

电势,电势差,电势梯度

电势、电势差、电势梯度1、三个相同的点电荷q ，分别放在边长为L 的等边三角形的三个顶点处，则三角形中心的电势 )4/(330L q U πε=，电场强度大小E=0=E ，将单位正电荷从中心移到无限远时，电场力作功)4/(330L q A πε= 。

2、半径为R 的均匀带电细圆环，电荷线密度为λ，则环心处的电势02/ελ=U ，场强大小0=E 。

3、静电场中某点的电势，其数值等于单位正电荷在该处的电势能，或把单位正电荷从该点移到无限远处电场力作的功。

4、下列各种说法中正确的是( B )(A)电场强度相等的地方电势一定相等。

(B)电势梯度较大的地方场强较大。

(C)带正电的导体电势一定为正。

(D)电势为零的导体一定不带电。

5、在静电场中下面叙述正确的是( B )(A)电场强度沿电力线方向逐点减弱。

(B)电势沿电力线方向逐点降低。

(C)电荷在电场力作用下一定沿电力线运动。

(D)电势能一定沿电力线方向逐点降低。

6、真空中产生电场的电荷分布确定以后，则( C )(A)电场中各点的电势具有确定值(B)电荷在电场中各点的电势能具有确定值(C)电场中任意两点的电势差具有确定值。

7、如图，在一带负电的物体A 附近有两点M 和N ，电势分别为u M 和u N ，另一带负电的点电荷处在该两点时所具有的电势能分别为W M 和W N ，则：（ C ）19(A)u M ＞u N ，W M ＞W N ；(B)u M ＞u N ，W M ＜W N ；(C) u M ＜u N ，W M ＞W N ；(D)u M ＜u N ，W M ＜W N ； 8、球壳的内半径为R 1，外半径为R 2，壳体内均匀带电，电荷体密度为ρ，A 、B 两点分别与球心0相距r 1和r 2，(r 1＞R 2，r 2＜R 1)，求A 、B 两点的电势。

解：利用均匀带电球壳产生电势的结果和电势叠加原理计算 作一半径为r ，厚度为dr 的球壳，其电量为dr r dq ρπ24=（1）r >R 2时，)4/(101r dq dU πε=()103132113/21r R R dU U R R ερ-==⎰（2）r <R 1时，)4/(02r dq dU πε=()02122222/21ερR R dU U R R -==⎰M N· ·。

《大学物理》电势能、电势、梯度 (3)


r
ε ε A
=
=q 0E .dl
= q 0E .d
q
4π
q
0
o

rb ra
cosφq
r= 4π
dr r2
q
o
0
r
2d r
q
dr φ dl
b
r b dl φφ
ra q 0 E a
2-1-5
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
1、点电荷对试验电荷作功
8 8
Wa = A a = q 0 a E .dl
(
或：Wa=A ab
=q 0
b
a E
.
dl
其中b为零势能点 )
dA =F. d l =q 0E .dl
r
=q 0E .dl cosφ
q
φ dl b
r b dl φφ
ra q 0 E
a
2-1-5
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
1、点电荷对试验电荷作功
dr
设点电荷 q、试验电荷 qo r
dA =F. d l =q 0E .dl
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
1、点电荷对试验电荷作功 设点电荷 q、试验电荷 qo
dA =F. d l =q 0E .dl
q
b r b dl φφ
ra q 0 E
a
2-1-5
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。

1.4 电势及其梯度


Ek
Q

P (E1

E2

Ek
) dl

(L) Q
q0 P E1

dl
(L) Q
q0(L)P E2

dl

q0
Q P Ek dl
(L)
(L)
(L)
总电场力对q0的功，也与路径无关。 结论：试探电荷在任何静电场中移动时，电场力所作的功只与这试探电
证明：沿着等势面把q0从P点移到Q点，电场力做功
APQ

q0 (U P

U
Q
),
(U P UQ ) 0,
APQ 0
看dA： dA q0E dl q0Edlcos 0
由于q0、E、dl均不为0，只有cos 0， 得证
16
§4 电势及其梯度
等势面的性质：
Q E dl
P
UQ
Q P
E
dl
设
UQ=0，Q点称为参考点，则
参考点


U (P) P E dl
如果带电体系局限在有限大小的空间里，一般选无穷远点为电势
的参考点，即

U (P) E dl ,
U(Q) E dl
P
Q
电势单位：伏特（V） 1V 1J 1C
作业2: 9、11、12
作业3: 15、16、20
作业4: 22、25、29
关于思考题：每个都思考！
例题14 讲看
问！
不会的画下来，
25
SUCCESS
THANK YOU
2019/10/25
例15 求均匀带电圆形细环轴线上的电势和场强分 布。环半径R，电荷线密度ηe 。

电势梯度---电磁学

4 0 ( x 2
y2 y2
z2) z2 )5/2
2
3Pxy
40(x2 y2
z2 )5/ 2
2
4
0(x2
P y2
z2 )2
4x2 y2 z2
P(0,y) y
讨论：
1. 在X轴上，y=0，z=0，则 E
P
Ex 20x3 Ey 0, Ez 0 -q
+q
2. 在Y 轴上，x=0，z=0，则
yA
r
q q r0
x
25
上节课：U
1
4 π 0
p cos
r2
4
p
π 0
(x2
x y2
z2 )3/2
Ex
U x
p
4 π0
y2 z2 2x2 (x2 y2 z2 )5/2
yA
r
r
r
q q r0
x
Ey
U y
4
p
π 0
(x2
3xy y2
z2 )5/2
Ez
26
E
Ex2
E
2 y
Ez2
P(2x2
19
例1 求一均匀带电细圆环轴线上任一点的电场强度.
解
E U
U
q
4 π 0 (x2 R2 )1 2
E
Ex
U x
y dq dl
qR
o
z
r
x
P x E
q
x
4π
0
(x2
R2
)1
2
qx
4π 0(x2 R2)3 2
20
1. 在环心O 即x=0处的电势和场强如何？ 2. 想象一下这均匀带电圆环的E 线和等势面分布。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。


Q
P
Q Q E dr E dl ( E1 E2 En )dl
P P
Q Q E1 dl E2 dl En dl A( P, Q)
Q P P P
电场力是保守力，作功和路径无关．
U ˆ gradU U n n
def
E U
电势梯度的大小为电势变化的最大值 方向沿电势降最快的方向
dl dxi dyj dzk
U E U ; U Ex ; Ez y y x z
假如U(x, y, z) 已知，则 E 可以通过求电势的梯度得到
保守力的概念
A W
做功特点
W W F .dl
b a b a
作功只与位置有关，与路径无关，可以 定义势能（位能）.
2.电势能ELECTRIC POTENTIAL ENERGY 电场力的功与路径无关只由始末两点位置决定 dr E r dr q0
/ 2
M
q
q
点电荷的等势面 同心球面 匀强电场的等势面 为垂直于电场的 平行平面 （２）沿等势面做功为零 若任意曲线的两端点在同一等势面上，则 电场力沿曲线作功为零．
12.电势梯度POTENTIAL GRADIENT U 由定义可以通过Ｅ求Ｕ．
E
U P U Q
Q
5.电势差The difference in electric potential
U PQ U P U Q
6.电势Electric potential
P
E dl

U P U P U P U
P
E dl
7.单位Unit J/C volt, V 1V=1J/C 例题 （１）点电荷的电势
偶极层的电势和电场仅与曲面 所张立体角及电偶极层强度决定
电偶极层两侧立体角有-4π的跃变
e
0
P
e
0
4
P
e e U P U P 4 4 0 0
p
U i ( p)

p
Ei dl
4 0 rip
qi
q1
U ( p)
i
4 0 ri
qi
q2
r1 r2
i
p
r 3 ri q3 qi
(2)连续分布电荷的电势The electric potential of continuous charge distributions dq U (r ) 4 0 r V 体分布
i
q
4 0 r 4 0 r l r r r r cos 2 r l q q r r cos 2 l ˆ Pe r q r r q l cos Up ( ) 2 2 4 0 r r 4 0 2 l 4 0 r 2 (r cos ) 4
2 1 2
0
1
2
Z
U ( z)
q 4 0 ( z R )
2
p
r
R
dq
11.等势面 EQUIPOTENTIAL SURFACES 和电场线一样，电势可以直观的描述，就 是等势面．电势相同的点构成的曲面是 电势面． N 性质 (1)等势面总是垂直于电场线 dl E
dAMN
E dl Edl cos 0
U ˆ U ˆ U ˆ E U { i j k) x y z
例题Sample problem 由偶极子的电势求电场分布．
ˆ Pe r U (r ) 2 4 0 r
p
r r U 2ql cos r Er q 3 q r 4 0 r l U
CHAPTER 1(3)
§4.电势及其梯度
用能量的方法研究静电场 注意静电力和万有引力的相似性 求解带电体的电势分布 电场强度和电势的联系
1. 静电场力和万有引力
注意万有引力和库仑力的相似性
万有引力
m1m2 F G r2
库仑力
q1q2 F 4 0 r 2
两者都是平方反比力，都是保守力！
rR
r
U (r ) Edr
r
R

Q 4 0 r
R
dr
Q 4 0 R
rR
（3）无限长均匀带电直线的电势 E 2 0 r p0 p' p0 U E dl E dl 0 dr p p' p ' 2 r 0
Q
P
E dl
U U
P
n
Q
现在考虑能否通过 电势求电场强度
U U E lim | | n 0 n n
E
U
n
P
l
n
Q
n l cos
U U
n
U U n l n l
U U cos E cos l n
Er 0， E
延长线上 0 2 Pe Er ， E 0 3 4 0 r
4 0 r
Pe
3
r r r q q l
４.６电偶极层
厚度为 l 的均匀曲 面薄壳，两面带符号 相反的面电荷，叫偶 极层
任意场点Ｐ的电势为
S’ S
e e
l cos dS '
E
q 4 0 r
p
2
ˆ r
p
q
q
r
2
p E
U p U p U
E dl
4 0 r
dr
q 4 0 rp
Up
q 4 0 rp
(２）均匀带电球面的电势
Q
E
R
U (r )

r
Q Q dr 2 4 0 r 4 0 r
e dV U (r ) 4 0 r V
e dS U (r ) 4 0 r S
面分布
线分布
e dl U (r ) 4 0 r L
10.例题 Examples p (1)电偶极子的电势Potential due to a dipole
U p U i ( p )

q
ˆ ˆ P e r ql r ql cos
(2)均匀带电圆环的电势Potential due to a uniformly charge ring
dU dq 4 0 r
dU 4 r
L 0
dq
2
e Rd
4 0 ( z R )
2 2
n
r' r
P
1
dS
l
U P 1
1 4 0
S'

e
e dS' dS r' 4 0 S r
1 1 e ( )dS 4 0 S r' r
1 1 1 l cos , 2 r ' r l cos r r
S’ S
e e
E r
U ql sin E 3 r 4 0 r
ˆ
U Er r
rˆ

r
U 2ql cos Er r 4 0 r 3 ˆ Pe r U ql sin U (r ) E 2 3 4 0 r r 4 0 r p 中垂面上 2
q
ˆ ˆ) q0 dA q0 E dl q0 E | dr | cos(E dr
r
q 4 0 r
2
dr
A
QHale Waihona Puke Pq0 q dA dr 2 P 4 r 0
Q
q0 q 1 1 ( ) 4 0 rP rQ
rQ
q
rP
Q
q0
P
多个点电荷A group of point charges
ln r ln r0 ln r C 2 0 2 0 2 0
r
p
p po
ro
'
8.电势叠加原理The principle of superposition （１）点电荷系的电势为各点电荷单独存在时， 电势的代数和．
U ( p)
p
E dl ( E1 E2 ) dl U i ( p)
3. 静电场的环路定理Circuit theorem of electrostatic field
E dl 0
L
Q
4.电势能差The difference in potential energy
WPQ= APQ q0

P
E dl q0 (U P U Q )
l cos dS '
n
1 1 l cos 2 r' r r
U P 1 4 0
r' r
dS
l

S
el cosdS P
r2
令
电偶极层强 度
e E U 40
e el
e e U P d 4 0 S 4 0