电场强度与电势梯度的关系

电场强度与电势
电场强度（E）和电势（V）是描述电场特性的两个重要参数。

电场强度是指单位正电荷在某点所受到的力的大小。

它的方向与力的方向相同，单位是牛顿/库仑（N/C）。

电势是指单位正电荷从无穷远处移动到某点所需的功。

它的单位是伏特（V）。

电势是标量量，它描述了电荷在电场中的势能。

电场强度和电势之间存在以下关系：
1. 电场强度为负梯度电势：E = -∇V
这个公式表示电场强度是电势的负梯度，其中∇是梯度算子。

2. 电场强度和电势的关系：E = -dV/dr
这个公式表示电场强度是电势对位置的导数，其中dV/dr表示电势对位置的变化率。

3. 电场强度和电势的关系：V = -∫E·dl
这个公式表示电势是电场强度积分后的结果，其中∫E·dl表示电场强度沿路径l的线积分。

在一维情况下，电势和电场强度之间的关系可以通过上述公式进行计算。

在三维情况下，电势和电场强度之间的关系需要考虑电场的分布情况，并使用泊松方程或拉普拉斯方程进行计算。

总之，电场强度描述了电场中的力的大小和方向，而电势描述了电荷在电场中的势能。

电场强度和电势之间存在一定的关系，可以通过公式进行计算。

电势梯度和电场强度的关系
电势梯度和电场强度是电学中两个非常重要的概念，它们之间存在着密切的关系。

电势梯度是指电势在空间中的变化率，而电场强度则是指单位电荷在电场中所受到的力的大小。

在电学中，电势梯度和电场强度的关系是非常紧密的，它们之间的关系可以用以下公式来表示：
E = -∇V
其中，E表示电场强度，V表示电势，∇表示梯度运算符。

这个公式告诉我们，电场强度的大小与电势梯度的大小成反比。

也就是说，当电势梯度越大时，电场强度就越小；反之，当电势梯度越小时，电场强度就越大。

这个公式的意义可以通过一个简单的例子来说明。

假设我们有一个电荷为Q的点电荷，它在空间中产生了一个电势场。

如果我们想知道在某一点P处的电场强度，我们可以通过以下步骤来计算：
1. 首先，我们需要计算出点P处的电势V。

2. 然后，我们需要计算出点P处的电势梯度∇V。

3. 最后，我们可以通过公式E = -∇V来计算出点P处的电场强度E。

这个例子告诉我们，电势梯度和电场强度之间的关系是非常密切的。

在电学中，我们经常使用这个公式来计算电场强度，从而更好地理解电场的性质和行为。

电势梯度和电场强度是电学中两个非常重要的概念，它们之间存在着密切的关系。

电场强度的大小与电势梯度的大小成反比，这个关系可以用公式E = -∇V来表示。

在电学中，我们可以通过这个公式来计算电场强度，从而更好地理解电场的性质和行为。

电场强度与电势梯度的关系
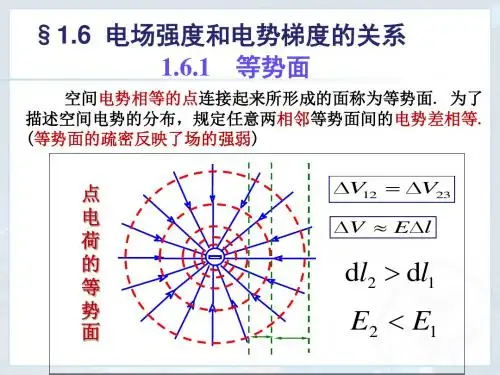
电场与电势是相互关联的，电势是电场的线积分，电场是电势的变化梯度，即电势的求导，电势变化越快的地方电场越强，有一个特殊的地方，电势零点可以任意选取，电场不为零的地方电势可以为零，电势为零的地方电场可以不为零电场线与等势面的关系：电场线越密的地方等差等势面也越密，电场线与通过该处的等势面垂直。

1、电场线与等势面的关系：电场线越密的地方等差等势面也越密，电场线与通过该处的等势面垂直。

2、场强与电势的关系：场强和电势无因果关系。

场强的方向是电势降落最快的方向，场强大小标志着沿电场线方向电势降落的快慢，场强数值和电势数值无因果关系。

3、电场线与等势面的关系：电场线越密的地方等差等势面也越密，电场线与通过该处的等势面垂直。

4．场强与电势的关系：场强和电势无因果关系。

场强的方向是电势降落最快的方向，场强大小标志着沿电场线方向电势降落的快慢，场强数值和电势数值无因果关系。

电场线假设与等势面不垂直，那么沿等势面就有分量，这样电荷在沿等势面移动时电场力就可做功，故假设不正确。

因此，电场线应与等势面垂直。

电场线越密处，电荷所受电场力大，移动相同距离电场力做功多也可能是克服电场力做功多，故在此处沿电场线方向移动相同距离比疏处电势差大。

那么相邻等势面差值一样时，电场线越密处等势面也越密。

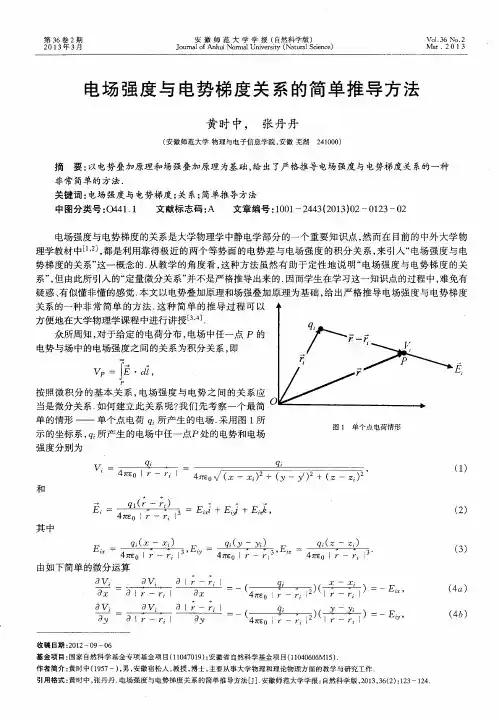
电势梯度和电场强度的关系电势梯度与电场强度是电学中两个重要的概念，它们之间存在着密切的联系和相互依赖关系。

本文将从电势梯度和电场强度的定义、计算方法以及它们之间的关系等方面展开阐述。

我们来了解一下电势梯度和电场强度的定义。

电势梯度是指电势在空间中变化的快慢程度，表示为电势的变化率。

电场强度是指单位正电荷所受的力的大小和方向，表示为电场力的大小。

电势梯度的计算方法是通过对电势函数沿着某一方向求偏导数，即电势梯度等于电势函数在某一方向上的偏导数。

电场强度的计算方法是通过库仑定律得到的，即电场强度等于单位正电荷所受力的大小。

接下来，我们来探讨电势梯度和电场强度之间的关系。

根据定义可知，电场强度是电势梯度的负梯度，即电场强度与电势梯度具有相反的方向。

这是因为电势梯度表示电势的变化率，而电场强度表示单位正电荷所受的力的大小和方向，二者之间存在着直接的关系。

进一步地，我们可以通过电势梯度和电场强度的性质来理解它们之间的关系。

首先，电势梯度的方向指向电势变化率最快的方向，而电场强度的方向指向力的作用方向。

由于力的方向是电势下降最快的方向，所以电势梯度的方向与电场强度的方向相反。

电势梯度的大小与电场强度的大小成正比。

根据电势梯度的定义可知，电势梯度的大小等于电势函数在某一方向上的偏导数。

而根据电场强度的定义可知，电场强度的大小等于单位正电荷所受力的大小。

由于电场力与电势梯度具有相反的方向，所以电场强度的大小与电势梯度的大小成正比。

我们可以通过具体的例子来进一步说明电势梯度和电场强度之间的关系。

假设有一个点电荷位于原点，我们要计算该点电荷在距离原点某一点的电场强度。

首先，我们可以通过库仑定律计算出该点电荷在距离原点某一点的电势。

然后，我们可以通过计算电势在该点的梯度得到该点电荷在该点的电场强度。

根据电势梯度和电场强度的关系可知，电场强度的大小与电势梯度的大小成正比，方向与电势梯度的方向相反。

电势梯度和电场强度之间存在着密切的关系。

电场强度与电势电场强度和电势是物理中的两个重要概念，也是研究电学领域的基础。

电场强度是指某一点上电场的大小和方向，而电势则是指某一点的电位与参考点的电位之差。

本文将详细介绍电场强度和电势的概念、计算方法以及它们的应用。

一、电场强度电场强度定义为单位正电荷在电场中受到的力的大小和方向。

在国际单位制中，电场强度的单位为牛顿/库仑(N/C)。

在某一点的电场强度的大小和方向决定了该点上其它电荷的受力情况。

电场强度可以用库仑定律计算，该定律描述了点电荷间的相互作用力与它们之间距离平方的关系，即：F=k×Q1×Q2/r2 ，其中k为库仑常数，Q1和Q2分别为两个点电荷的电量，r为它们之间的距离。

当不止一个电荷存在时，可以采用叠加原理，将每个点电荷产生的电场强度矢量相加，得到这一点所有点电荷产生的合成电场强度。

二、电势电势是在电场中一个电荷单位正电荷所具有的电势能。

电势是标量量，通常用符号V表示。

在国际单位制中，电势的单位是伏特(V)。

电势差是指两个点之间的电势差异，它等于两点之间的电场强度积分值。

电势差可以用如下公式计算：ΔV=Vb-Va=Wab/Q0，其中Vb、Va分别为电场中的两个点的电势，Wab表示从点a到点b在电场中移动的势能，Q0为一个参考电荷的电荷量。

三、电场强度与电势的关系电场强度与电势是密切相关的，电场强度是电势的负梯度。

在电位场中单位正电荷所受的电场力与沿着电势线的方向相反，大小为电势在此方向上的梯度，即：E=−ΔV/Δl。

由此可以得到电场强度和电势的关系式：E=−∇V ，其中∇是表示偏导数算符，称为“nabla算符”。

四、电场强度与电势的应用电场强度和电势在电学领域有广泛的应用，例如在电容器中电荷能够通过电场从一个极板传输到另一个极板；在电路中由于电势的差异，电子流能够产生，从而完成电能的转换和传输；在静电场中，通过对电势分布的计算，可以确定电荷在空间中的分布。

在计算实际问题中，我们通常需要根据具体情况选择使用电场强度或电势，或同时结合使用两者。

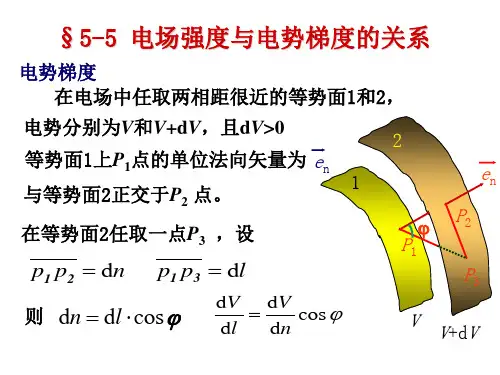
电势的提度
在匀强电场里，我们称两点间的电势差V和沿场强方向的距离l 的比为匀强电场的电势梯度，或称为匀强电场的电势陡度。

电势梯度用于描述电场中电势沿某一方向的变化率。

电势梯度概念
在匀强电场里，我们称两点间的电势差V和沿场强方向的距离l 的比为匀强电场的电势梯度，或称为匀强电场的电势陡度。

电势梯度基本原理
在匀强电场里，我们有V=El（有的版本是U=Ed，就是两点间的电势差等于电场强度和两点在场强方向的距离的乘积），把这个等式变换为：E=V/l，我们就可以得出这样一个结论：电场强度等于电势梯度，并指向电势降落的方向。

理论可以证明，这最后一个结论，不仅对匀强电场适用，而且对任何别种电场也都适用。

但由于电势梯度，除匀强电场之外，一般都不等于V/l，所以上面的等式只对匀强电场适用。

在厘米·克·秒制静电单位系中，电势梯度的单位为静伏/厘米。

匀强电场的电势梯度在数值上等于沿场强方向相隔1厘米两点间的电势差的静伏数。

电势梯度在数值上的负值等于该点场强沿相同方向发分量。

电场中的电势梯度与电场强度电场是物理学中的一个重要概念，它描述了电荷之间相互作用的力。

而电势则是描述电场中一个点的性质，它是用来度量电场对电荷所做的功。

电场强度和电势梯度是电场的两个重要性质，它们之间有着紧密的联系。

首先，让我们来了解一下电场强度。

电场强度是指单位正电荷在电场中所受到的力。

如果我们把一个正电荷放置在电场中的某一点，它将受到一个由电场引起的力。

这个力的大小和方向就是电场强度的大小和方向。

电场强度用E来表示，它的单位是牛顿每库仑（N/C）。

电场强度是一个向量，它的方向与电场力的方向相同。

在均匀电场中，电场强度的大小是恒定的，并且与电势差的变化率有关。

而在非均匀电场中，电场强度的大小和方向都可能会随着位置的改变而改变。

我们可以使用电场线来表示电场强度的方向和分布情况。

接下来，让我们来了解一下电势梯度。

电势梯度是指电势随着距离的变化率，它的大小和方向描述了电势在空间中的变化情况。

电势梯度用∇V来表示，其中∇是梯度运算符，V是电势。

电势梯度与电场强度之间存在一个重要的关系：电场强度等于电势梯度的相反数。

简单来说，电场强度是电势梯度的反向。

这是因为电势梯度描述了电势在空间中的变化情况，而电势力是电势随着距离变化的导数。

由此可以得出，电场强度指向电势值减小的方向。

这一关系可以用数学公式来表示：E = -∇V。

这意味着，如果我们已知电势的分布情况，就可以通过计算电势梯度来确定电场强度的大小和方向。

同时，如果已知电场强度的分布情况，我们也可以通过积分计算电势的分布情况。

这种关系在解决电场问题时有着广泛的应用。

例如，在求解电场力的问题时，我们可以通过计算电场强度和电荷的乘积来得到力的大小。

而在求解电势分布的问题时，我们可以通过计算电势梯度的积分来得到电势的分布情况。

总之，电场强度和电势梯度是描述电场的两个重要性质。

它们之间有着紧密的联系，电场强度等于电势梯度的相反数。

通过研究电场强度和电势梯度，我们可以更好地理解电场的性质，解决相关的物理问题。