电势,电势差,电势梯度
- 格式:doc
- 大小:53.50 KB
- 文档页数:2


大学物理静电场知识点总结1. 电荷的根本特征:〔1〕分类:正电荷〔同质子所带电荷〕,负电荷〔同电子所带电荷〕〔2〕量子化特性〔3〕是相对论性不变量〔4〕微观粒子所带电荷总是存在一种对称性2.电荷守恒定律:一个与外界没有电荷交换的孤立系统,无论发生什么变化,整个系统的电荷总量必定保持不变。
3.点电荷:点电荷是一个宏观*围的理想模型,在可忽略带电体自身的线度时才成立。
4.库仑定律:表示了两个电荷之间的静电相互作用,是电磁学的根本定律之一,是表示真空中两个静止的点电荷之间相互作用的规律121212301214q q F r r πε= 5.电场强度:是描述电场状况的最根本的物理量之一,反映了电场的基0F E q =6.电场强度的计算:〔1〕单个点电荷产生的电场强度,可直接利用库仑定律和电场强度的定义来求得〔2〕带电体产生的电场强度,可以根据电场的叠加原理来求解〔3〕具有一定对称性的带电体所产生的电场强度,可以根据高斯定理来求解〔4〕根据电荷的分布求电势,然后通过电势与电场强度的关系求得电场强度7.电场线:是一些虚构线,引入其目的是为了直观形象地表示电场强度的分布〔1〕电场线是这样的线:a .曲线上每点的切线方向与该点的电场强度方向一致b .曲线分布的疏密对应着电场强度的强弱,即越密越强,越疏越弱。
〔2〕电场线的性质:a .起于正电荷〔或无穷远〕,止于负电荷〔或无穷远〕。
b .不闭合,也不在没电荷的地方中断。
c .两条电场线在没有电荷的地方不会相交8. 电通量:φ=⋅⎰⎰e s E dS〔1〕电通量是一个抽象的概念,如果把它与电场线联系起来,可以把曲面S 的电通量理解为穿过曲面的电场线的条数。
〔2〕电通量是标量,有正负之分。
9.高斯定理:ε⋅=∑⎰⎰s S 01E dS i (里)q〔1〕定理中的E 是由空间所有的电荷〔包括高斯面内和面外的电荷〕共同产生。
〔2〕任何闭合曲面S 的电通量只决定于该闭合曲面所包围的电荷,而与S 以外的电荷无关10.静电场属于保守力:静电场属于保守力的充分必要条件是,电荷在电场中移动,电场力所做的功只与该电荷的始末位置有关,而与其经历的路径无关。




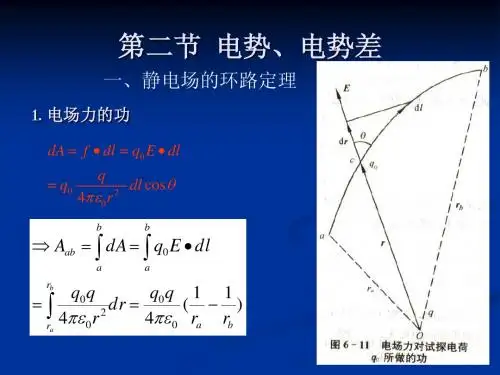

静电场的特性、电势能与梯度的关系1. 静电场的特性1.1 定义静电场是由静止电荷产生的电场。
在静电场中,任何带电粒子都会受到电场力的作用。
静电场的特点是电场强度与电荷量成正比,与距离的平方成反比。
1.2 静电场的性质(1)叠加原理:静电场中,任意一点的电场强度是由场源电荷单独产生的电场强度矢量和。
(2)高斯定律:静电场中,通过任何闭合曲面的电通量与该闭合曲面所包围的净电荷量成正比。
(3)库仑定律:静电场中,两个点电荷之间的作用力与它们的电荷量的乘积成正比,与它们之间的距离的平方成反比。
(4)电场线:用来表示静电场强度和方向的线条,电场线的疏密表示电场强度的大小,电场线从正电荷指向负电荷。
2. 电势能2.1 定义电势能是指带电粒子在电场中由于位置的改变而具有的能量。
电势能的变化等于电场力做的功。
2.2 电势能的计算电势能的计算公式为:[ U = qV ]其中,( U ) 表示电势能,( q ) 表示带电粒子的电荷量,( V ) 表示电势差。
2.3 电势差电势差是指两个点在电场中的电势差异。
电势差的计算公式为:[ V = ]其中,( V ) 表示电势差,( W ) 表示电场力做的功,( q ) 表示带电粒子的电荷量。
3. 电势梯度3.1 定义电势梯度是指电势在空间中的变化率。
它是电场强度的负值。
3.2 电势梯度的计算电势梯度的计算公式为:[ V = - ]其中,( V ) 表示电势梯度,( ) 表示电势对位置的导数。
3.3 电势梯度与电场强度的关系电势梯度与电场强度具有负相关关系。
当电势梯度较大时,电场强度较小;当电势梯度较小时,电场强度较大。
这表明电场力对带电粒子的加速作用与电势梯度成反比。
4.1 静电场的特性与电势能的关系在静电场中,电势能的变化等于电场力做的功。
根据库仑定律,静电场中两个点电荷之间的作用力与它们的电荷量的乘积成正比,与它们之间的距离的平方成反比。
因此,电势能在静电场中的变化与电荷量、距离等因素有关。



物理电势考点归纳总结图电势是物理学中的重要概念,它描述了电场中电荷所受的力和电势能之间的关系。
在学习物理电势的过程中,我们经常会遇到一些重要的考点。
本文将对这些考点进行归纳总结,并通过图表的形式展示,以便更好地理解和记忆。
1. 电势的定义- 电势是指单位正电荷在电场中所具有的电势能。
它是一个标量量,通常用符号V表示,单位为伏特(V)。
- 电势的计算公式为V = U / q,其中V为电势,U为电势能,q为电荷量。
2. 电势的基本特性- 电势与位置无关:在一个给定的电场中,不同位置的电势相同。
这意味着电势是一个标量,而不是矢量。
- 电势的线性叠加性:对于由多个电荷产生的电势,可以将它们的电势分别计算,然后求和。
- 电势的相对性:电势是相对于某一参考点来定义的,通常取无穷远处电势为零点。
3. 电势与电场强度的关系- 电势梯度:电场强度与位置的变化率称为电势梯度。
在均匀电场中,电势的梯度是恒定的。
- 电势差:沿电场方向,单位正电荷从A点移动到B点时所获得的电势能的变化量称为电势差。
电势差等于电场强度与两点之间距离的乘积。
4. 电势的计算方法- 离散点电荷:对于一个点电荷产生的电势,可以使用库仑定律计算。
公式为V = k * q / r,其中k为库仑常数,q为电荷量,r为距离。
- 连续分布电荷:对于电荷连续分布的情况,可以使用积分计算电势。
公式为V = ∫ k * dq / r,其中dq为微元电荷,r为距离。
5. 电势的应用- 电势能和势能面:电势能是指电荷在电场中具有的势能。
势能面是一个等势面的集合,表示在该面上任意点的电势相等。
- 电势与电势能的转换:电势能可以通过电势差与电荷量的乘积计算,即U = q * V。
- 电势分布:电荷形成的电势分布在空间中通常呈现出特定的形状,如球对称分布、圆柱对称分布等。
通过以上对电势的考点进行归纳总结,可以更好地理解电势的定义、特性、计算方法和应用。
图表的形式可以清晰地展示这些考点的关系,帮助我们在学习和复习中更好地理解和记忆。
和电势有关的公式
电势是描述电场中某点的电能状态的物理量,与电荷之间的相互作用有关。
以下是几个与电势有关的公式:
1.电势能与电势差的关系:电势能的变化等于电荷在电场中
移动的过程中受到的力乘以移动的距离。
ΔPE = q ΔV 其中,ΔPE表示电势能的变化量,q表示电荷的大小,ΔV表示电
势差。
2.电势差的定义:电势差(电压)是单位正电荷在电场中移
动时所需的能量。
在恒定电场中,电势差等于两点之间的
电位差。
V = ΔV / q 其中,V表示电势差(电压),ΔV表示
两点之间的电位差,q表示单位正电荷的电量。
3.电势与电场的关系:电势是电场的一种衡量。
单位正电荷
所受电势力等于单位正电荷在该点处的电势。
E = -∇V 其
中,E表示电场强度,V表示电势,∇表示梯度运算符。
4.点电荷电势的计算公式:对于一个点电荷Q,在与其距离
为r的点处的电势计算公式为: V = kQ / r 其中,V表示电
势,k表示库仑常数。
需要注意的是,上述公式是应用于简化情况中的基本公式。
在实际问题中,还需要考虑电场的分布、电荷的形状和分布等因素,以更精确地计算电势。
静电场与电势知识点总结静电场和电势是电学中重要的概念,它们在电荷分布和电场力学中起着关键作用。
本文将对静电场和电势的相关知识点进行总结,以便更好地理解和应用这些概念。
一、静电场1. 电荷和静电场:电荷是物体带有的一种基本属性,可以分为正电荷和负电荷。
当电荷分布在空间中时,会产生静电场。
静电场是由电荷周围的电场力所产生的力场,具有方向和强度。
2. 库仑定律:库仑定律描述了静电场中电荷之间的相互作用。
根据库仑定律,电荷之间的相互作用力与它们之间的距离成反比,与它们的电量成正比。
3. 静电场的叠加原理:当有多个电荷同时存在时,它们所产生的静电场可以进行叠加。
即总的静电场等于各个电荷所产生的静电场的矢量和。
4. 静电场的高斯定律:高斯定律是描述电场的重要原理之一。
它指出,通过任意闭合曲面的电场通量等于该曲面内部的电荷代数和的1/ε₀倍(ε₀为真空介电常数)。
5. 静电场的势能:静电场与静电力之间存在一种势能关系。
电荷在静电场中具有势能,当电荷在电场力的作用下发生位移时,其势能会发生改变。
二、电势1. 电势的基本概念:电势是描述一个点的位置在静电场中所具有的势能大小的物理量。
这个点可以是某个电荷周围的位置,也可以是在电场内的任意一点。
2. 电势的定义:电势定义为单位正电荷在静电场中所具有的势能大小。
单位为伏特(V)。
在静电场中,电势的数值表示了单位正电荷从无穷远处移到该点时所获得的能量。
3. 电势差:电势差是指在电场中从一个位置到另一个位置的电势之差。
用ΔV表示,ΔV = V₂ - V₁。
电势差决定了电荷在电场中的能量变化。
4. 电势与电场的关系:电场与电势之间存在着密切的关系。
电场强度是电场力对单位正电荷的作用力,而电势梯度是电势随空间位置变化的变化率。
两者之间满足关系E = -∇V,其中E为电场强度,∇为梯度算符。
5. 电势能与电势的关系:电势能是物体在电场中的位置所具有的能量,而电势是单位正电荷在电场中的势能。
关于电势的公式
定义
电势是指垂直于某一个点的电场线的方向,单位正电荷在该点具有的
电势能大小,通常用符号V表示。
公式
电势的公式为V = U/q,其中V为电势,U为某一点处的电势能,q为
单位正电荷的电荷量。
同时,如果考虑静电场具有的标量性质,电势
也可以表示为V = W/q,其中W为电场力所做的功。
单位
电势的单位为伏特(V),在国际单位制中,1伏特等同于1焦耳/库仑。
电势差的公式
电势差(电压)是指当两点之间放置一个单位正电荷时,由于电场的
作用,电荷从高电势处移动到低电势处所获得的电势能的差值。
电势
差的公式为ΔV = V2 - V1,其中ΔV为电势差,V2为高电势处的电势,V1为低电势处的电势。
电势能的公式
电势能是指由于正电荷在电场中存在而具有的能量,它与电势之间存在着关系。
电势能的公式为U = qV,其中U为电势能,q为电荷量,V 为电势。
电势的参考点
电势无法直接测量,通常需要参考某一点。
在静电场中,通常以无穷远点或导体表面的电势为参考点。
电场强度与电势的关系
电场强度与电势存在着密切的关系。
在静电场中,电势梯度的负值等于电场强度。
即E = -∆V/∆s,其中E为电场强度,∆V为电势差,∆s为两点间距离。
应用
电势是重要的物理量,它被广泛应用于电磁学、电路理论、电化学等领域。
在电路理论中,电势差是计算电路中电路元件电流和功率的重要参数;在电化学中,电势差是计算电解过程中化学反应能量的关键参数。
电势、电势差、电势梯度
1、三个相同的点电荷q ,分别放在边长为L 的等边三角形的三个顶点处,则三角形中心的电势 )4/(330L q U πε=,电场强度大小0=E ,将单位正电荷从中心移到无限远时,电场力作功)4/(330L q A πε= 。
2、半径为R 的均匀带电细圆环,电荷线密度为λ,则环心处的电势02/ελ=U ,场强大小0=E 。
3、静电场中某点的电势,其数值等于单位正电荷在该处的电势能,或把单位正电荷从该点移到无限远处电场力作的功。
4、下列各种说法中正确的是( B )
(A)电场强度相等的地方电势一定相等。
(B)电势梯度较大的地方场强较大。
(C)带正电的导体电势一定为正。
(D)电势为零的导体一定不带电。
5、在静电场中下面叙述正确的是( B )
(A)电场强度沿电场线方向逐点减弱。
(B)电势沿电场线方向逐点降低。
(C)电荷在电场力作用下一定沿电场线运动。
(D)电势能一定沿电场线方向逐点降低。
6、真空中产生电场的电荷分布确定以后,则( C )
(A)电场中各点的电势具有确定值
(B)电荷在电场中各点的电势能具有确定值
(C)电场中任意两点的电势差具有确定值。
7、如图,在一带负电的物体A 附近有两点M 和N ,电势分别为u M 和u N ,另一带负电的点电荷处在该两点时所具有的电势能分别为W M 和W N ,则:( C )
19
(A)u M >u N ,W M >W N ;
(B)u M >u N ,W M <W N ;
(C) u M <u N ,W M >W N ;
(D)u M <u N ,W M <W N ; 8、球壳的内半径为R 1,外半径为R 2,壳体内均匀带电,电荷体密度为ρ,A 、B 两点分别与球心0相距r 1和r 2,(r 1>R 2,r 2<R 1),求A 、B 两点的电势。
解:利用均匀带电球壳产生电势的结果和电势叠加原理计算 作一半径为r ,厚度为dr 的球壳,其电量为dr r dq ρπ24=
(1)r >R 2时,
)4/(101r dq dU πε=
()103132113/21r R R dU U R R ερ-==⎰
(2)r <R 1时,
)4/(02r dq dU πε=
()
02122222/21ερR R dU U R R -==⎰
M N
· ·。