诱导公式地化简与求值题

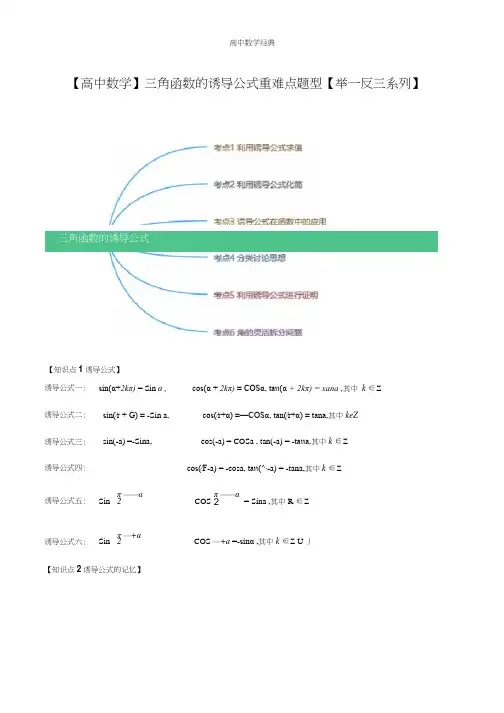
【高中数学】三角函数的诱导公式重难点题型【举一反三系列】三角函数的诱导公式【知识点1诱导公式】【知识点2诱导公式的记忆】诱导公式一: sin(α+2kπ) = Sin a ,cos(α + 2kπ) = COSα, taιι(α + 2kπ) = xana ,其中 k ∈Z 诱导公式二: sin(∕r + G) = -Sin a,cos(∕r+α) =—COSα, tan(∕r+α) = tana,其中keZ 诱导公式三: sin(-a) =-Sina, cos(-a) = COSa , tan(-a) = -taιιa ,其中k ∈Z诱导公式四:cos(∕F -a) = -cosa, taιι(^∙-a) = -tana,其中k ∈Z 诱导公式五: Sin π ——a 2 COS π ——a 2 = Sina ,其中R ∈Z诱导公式六:Sin π —+a 2 COS —+a =-sinα ,其中k ∈Z U 丿记忆11诀“奇变偶不变，符号看象限”，意思是说角k-90 ±a(k 为常整数)的三角函数值：当k 为奇数 时，正弦变余弦，余弦变正弦；当k 为偶数时，函数名不变，然后α的三角函数值前面加上当视Q 为锐角 时原函数值的符号.【考点1利用诱导公式求值】【方法点拨】对任意角求三角函数值，一般遵循“化负为正，化大为小”的化归方向，但是在具体的转化 过程中如何选用诱导公式，方法并不唯一，这就需要同学们去认真体会，适当选择，找出最好的途径，完 成求值.【例1】(2018秋•道里区校级期末)已知点P(l,l)在角Q 的终边上，求下列各式的值.T 、 COS (Λ^ + α)sin(^∙ - a)(I )------------------------------------- ；tan(∕r + α) + sin 2 (彳-a)sin(- + α)cos(- 一 a) (II) 、 2 、——召——cos^ a - sm^ a + tan(;T - a)【分析】由条件利用任意角的三角函数的定义求得smα, cosα, Sna 的值，再利用诱导公式即可求得要 求式子的值.【答案】解：∙.∙角α终边上有一点P(l,l),.x = l , y = l , r =|OP I= √7,Sill CL = — = _ , COS Ct = — = — , tan Ct — -- = It r 2 r 2 X([) cos(∕r + α)sin(%-α)、 -、，兀、 tan(^∙ + α) + sιn^ (― 一 a) ./3∕r 3π([[)SInq-+Q )COS (T _Q ) _ (γosα)(-smα) cos 2 a - sin 2 a + tan(∕r -a) cos 2a - sin 2a 一 tan a【点睛】本题主要考查任意角的三角函数的定义，诱导公式在三角函数化简求值中的应用，考查了转化思想，属于基础题.【变式1-1】 (2019春•龙潭区校级月考)己知tan(^+ «) = -!,求下列各式的值:-COSa ∙smα ton a + cos 2(x(]) 2COS (Λ∙-α)-3sin(∕r+ α)4cos(α - 2πy ) + sin(4∕r - a)(2) siιι(α-7π)cos(a + 5π).【分析】(1)由诱导公式化简后，原式分子分母除以cosα,利用同角三角函数间的基本关系化简，将tana 的值代入计算即可求出值；(2)由诱导公式化简后，原式分母“1”化为sin 2a + ∞s 2a,然后分子分母除以∞s 2a,利用同角三角函数间的基本关系化简，>'J tana 的值代入计算即可求出值.【答案】解：∙.∙tan(∕r + a) = tana =-扌,【点睛】此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键，属于基本知识的 考查.【变式1-21(2018春•陆川县校级月考)若COSa = - , a 是第四象限角，求sm(d_2”) + sin(--3∕τ)cos(-3”) 3 COS (龙-a)-COS (-Λ∙ - a) COS(a - 4π)的值.【分析】由条件利用诱导公式进行化简所给的式子，可得结果.【答案】解：∙.∙cosa =扌，a 是第四象限角，- -sina = 一JI-COS 订=_£ ,Sin(Q - 2π) + siιι(-a -3π)cos(a- 3π) _ Sillcr + Siila ・(一COS a) _ Sin a(l- COS a) _3 3 _ ∙√5 cos(∕r — a)-cos(-x-a)cos(a-4;F) — CoSa+ cosa∙cosa COSa(COSa — 1) 亠(一 1) 2【点睛】本题主要考查应用诱导公式化简三角函数式，属于基础题.【变式1-3】 (2019春•沈阳校级月考)己知SlnQ 是方程5√-7x-6 = 0的根，求sin(-a -—龙)∙sin(- π 一 a)∙tan 2 (2π - a) 4 5【分析】把SinQ 代入到方程中解出即可求出Sina 的值进而求出tan'a 的值，然后把所求的式子利用诱导公 式及同角三角函数间的基本关系进行化简，将tan j 的值代入即可求出值.【答案】解：∙.∙sinα是方程SJC-IX-6 = O 的根，二Sina = -O 或Sina = 2 (舍).5+iτ . ■> 9 “16 , 9∣ √ sm^ α = —， cos^ a = — => taιι^ a = —• 25 25 16(1) 2 COS (Λ∙ -Qf)-3 sin(π + a)4cos(α - 2π) + sin(4∕r - a) 3sinα-2cosα 4cosα-siιια 3 tail α - 2 4-tana(2) sin(α — 7π)cos(α + 5π) = Sm a COS a =SlnQCOSa SUra + COS I atanatan 2a + l 的值.「•原式=∞s α∙(-COS α)∙tan^ aSin α∙(- Sin a)∙cos2 asin2 aCOSa•(—COS α) •—____________ COS-CLSill α∙(- Sill α)∙cos2a1cos2a=sec^ a = l +tail" α = l + —=—16 16【点睛】此题要求学生灵活运用诱导公式及同角三角函数间的基本关系化简求值，解这道题的思路是利用已知求出正切函数的平方，所求的式子也要化为关于正切函数平方的关系式.【考点2利用诱导公式化简】【方法点拨】灵活应用诱导公式，应用的原则是：负化正，大化小，化到锐角就终了taιι(Λ∙ - α)cos(2∕τ —α)sin(-α + —)【例2】(2019秋•颍泉区校级期中)化简： ------------- ------ —-------- .cos(-α - π) sm(-∕r - a)【分析】由已知利用诱导公式即可化简得解.tan(∕r —α)cos(2∕r - α)sin(-α + —) 【答案］解： -------- ------ ---------- 一一cos(_a 一π)sιn(-π一a)(一tan a) COS ◎(一COS a) _ -------------------------- =—1.(一COSa)SiiIa【点睛】本题主要考查了诱导公式在三角函数化简求值中的应用，属于基础题.【变式2-1] (2019春•兰考县校级期末)化简:sιn(4—⑵ CoS(I■ + ◎) tan(5 一Q) + a) COS(2Λ,-a)sin(3τr —a) sin(- + O)【分析】利用诱导公式以及同角三角函数基本关系式化简求解即可.【答案】解sin(4Λ∙-α)cos(-÷α) _ tan(5Λ∙-a) _ sin(-αχ-Sina) _ -tana _ Sin Z a十1 I-Sin Z aSm(爭+ a)cos0-a) sm(3^-a)sin(^÷ a) " <-cosa>cos<-a> SInaCoS八CoSF 品- cos2【点睛】本题考查诱导公式以及同角三角函数基本关系式的应用，考查计算能力.sin(8 - 5Λ∙)COS( ------- θ)cos(lπ一θ)【变式2・2】(2019春•东莞市校级期末)化简----------------- F -------------------------sin(8 - #) sin(-3^∙ - θ)【分析】由条件利用诱导公式进行化简所给的式子，可得结果.【答案】解:sin(8 —5π) cos(-壬一 &)cos(7∕r —θ) Sin(^ - π >cos(y + &)・cos(/r -θ)Sin(O -夢)sin(-3;T — 6)-Sin(^- —8)∙sin(∕r - θ)-siu8»(-sin&)・(一cos8) .；---- =—Sln σ • COS8∙sin θ【点睛】本题主要考查应用诱导公式化简三角函数式，要特别注意符号的选取，这是解题的易错点，属于基础题.【变式2-3】(2019春•西安月考)化简：血Sr)SIn(-2—&)CoS(6”也cos(8 - π)siιι(5Λ∙ + θ)【分析】由条件利用诱导公式化简所给的三角函数式，可得结果.r M tan(2∕r-8)sin(-2 広一 &) COS(6兀一&) - tan 0∙(-Sill ^)∙cos θ sin 8L ⅛ 杀J W • ----------------------------------------------- = ----------------------------- =-------- = t∩ιι θ ‘COS(O - π)sin(5∕r + θ)- COS 8・(一Sm θ) COS θ【点睛】本题主要考查利用诱导公式进行化简求值，属于基础题.【考点3诱导公式在函数中的应用】cos(- + x) cos(-x) siιι(- - x)【例3】(2019春•怀化期末)已知/(X) = 一 -------------------- - -- 2——sm(-Λ- - X)CoS(2/T - x)(I )化简/(x)；(II)若X是第三象限角，且tmιx = 2,求/⑴的值.【分析】(【)由己知利用诱导公式即可化简得解；(II)由tanx=2,可得SinX=2cosx,根据角的范围利用同角三角函数基本关系式即可求解.【答案】解：([)∕α)=Eτ∙(⅜χ.SillACOSX(II) ∙.∙ta∏Λ = 2, ..sinx = 2COSΛ'» 代Asin3 x+cos2 x = l,得：5cos2 x = l,∙.∙x是第三彖限角，.■- /(X) = COSX = --Y .【点睛】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题.【变式3-1】(2019春•大武口区校级期末)己知./(«) =—)su,cos(";)_ sin(-^- - a) cos(y + a) sin(- + a)(1)化简/(«)：(2)若/(a) = *,求3sin2α-4siιιαcosof + 5cos2a的值.【分析】(1)直接利用诱导公式化简求解即可.(2)求出正切函数值，利用同角三角函数基本关系式化简表达式为正切函数的形式，代入求解即可.【答案】解：(1)弘)=一Smgm"(Yθsα)=toιm-COS a∙(- Sm QXOS a3 f(a)=-,可得：taιια = -,r . “° 3siιF α — 4sinαcosα + 5cos% 3tan 2α-4taιια + 53SIn- α-4sιnαCOS a + Scos~a = ----------------- ； -------； ----------- = ------------ ； ---------- ,siιι^ a + cos~a taιι^ α + l 将tanα =丄代入， 3Jg得 3siιι2 α-4siιιαCOS a + 5cos 1a = 一 •5 【点睛】本题考查诱导公式以及同角三角函数基本关系式的应用，考查转化思想以及计算能力•【变式3-2】 （2018秋•红塔区校级期末）己知/（α）=泅（2兀一Q ）述S + ?COS （FF ）cos （∕r - a ） tan （3;T - a ）（1） 将/（◎）化为最简形式；（2） f （a ）- f （rγ + α） = » 且 Qe （O ,兀），求 tana 的值.【分析】（1）由题意利用诱导公式，化简所给的式子，可得结果.（2）由题意可得Sina+cosa 的值,再利用同角三角函数的基本关系，求得Sina-CoSa 的值，可得Sina 的 COSa 的值，从而求得tana 的值.【答案】解：(1)由题意可得，f(a) = (~SmQf)tanQfeCOSQf) =Sinα . (-cos α)(-taιια)(2) f(a)-f(rγ + Qf) = Sina-Sm(^ + α) = Sinα + COSa = 4©»] 24平方可得 1 + 2SinaCOSQ = ----- .. 2siιιαcosα = -一<0, 25 25π 49 7因为α e (0,兀)，所以 α∈(-,Λ-) ∙ SinQ-COSa>0 , (Sina-COSa)2 =1-2SmaCOSa =—,所以SinQ-COSQ = E ②， 由①②可得：Sma = —,cosα = --,5 5 4 结果.（2）利用诱导公式化简要求的式子为sin&-cos0>0,再计算（Sin^-CoS^）2的值，可得要求式子的值.4所以taιια =——• 3【点睛】本题主要考查利用诱导公式，同角三角函数的基本关系，属于基础题.【变式0 （沁秋•汕头校级期中）己知函数蚀少二：（穿1 (1)若 f(θ)×siii — -COS^ = 0,求SineCOSe 的值.(2)若/(B)MosO= £ ,且彳v&v 普，求/(2019Λ--θ)-∞S (2018Λ∙-θ)的值; 【分析】 （1）由题意利用诱导公式求得诚=2,再根据SineCOSe = sin8cos8 sin 2 8+cos' θ总’计算求得【答案】解：(I)函数fg = (SE • +迓哄E = SIn“OS"S1∏Λ∙=若 f(0)×siιι--COS θ = sin&・--COSe = 0 •则 tan 。

三角函数诱导公式练习题含答案三角函数定义及诱导公式练习题1．将120o化为弧度为（）A．B．C．D．2．代数式的值为（）A.B.C.D.3．（）A．B．C．D．4．已知角α的终边经过点(3a，－4a)(a<0)，则inα＋coα等于()A.B.C．D．－5．已知扇形的面积为2cm2,扇形圆心角θ的弧度数是4,则扇形的周长为()(A)2cm(B)4cm(C)6cm(D)8cm6．若有一扇形的周长为60cm，那么扇形的最大面积为()A．500cm2B．60cm2C．225cm2D．30cm27．已知，则的值为（）A．B．－C．D．－8．已知，且，则（）A、B、C、D、9．若角的终边过点，则_______.10．已知点P(tanα，coα)在第二象限，则角α的终边在第________象限．11．若角θ同时满足inθ<0且tanθ<0，则角θ的终边一定落在第________象限．12．已知，则的值为．13．已知，，则_____________.14．已知，则_________.15．已知tan=3，则.16．(14分)已知tanα＝，求证：(1)=－；(2)in2α＋inαcoα＝．17．已知（1）求的值；（2）求的值；（3）若是第三象限角，求的值.18．已知in(α－3π)＝2co(α－4π)，求的值．参考答案1．B【解析】试题分析：，故.考点：弧度制与角度的相互转化.2．A.【解析】试题分析：由诱导公式以可得，in120°co210°=in60°某(-co30°)=-某=,选A.考点：诱导公式的应用．3．C【解析】试题分析：本题主要考查三角诱导公式及特殊角的三角函数值.由，选C.考点：诱导公式.4．A【解析】试题分析：,,.故选A.考点：三角函数的定义5．C【解析】设扇形的半径为R,则R2θ=2,∴R2=1R=1,∴扇形的周长为2R+θ·R=2+4=6(cm).6．C【解析】设扇形的圆心角为,弧长为cm,由题意知，∴∴当时，扇形的面积最大；这个最大值为.应选C.7．A【解析】试题分析：，=====.考点：诱导公式.8．【解析】试题分析：.又因为，所以为三象限的角，.选B.考点：三角函数的基本计算.9．【解析】试题分析：点即，该点到原点的距离为，依题意，根据任意角的三角函数的定义可知.考点：任意角的三角函数.10．四【解析】由题意，得tanα＜0且coα＞0，所以角α的终边在第四象限．11．四【解析】由inθ<0，可知θ的终边可能位于第三或第四象限，也可能与y轴的非正半轴重合．由tanθ<0，可知θ的终边可能位于第二象限或第四象限，可知θ的终边只能位于第四象限．12．-3【解析】13．【解析】试题分析：因为α是锐角所以in(π－α)＝inα＝考点：同角三角函数关系，诱导公式.14．【解析】试题分析：，又，则原式=.考点：三角函数的诱导公式.15．45【解析】试题分析：已知条件为正切值，所求分式为弦的齐次式，所以运用弦化切，即将分子分母同除以得.考点：弦化切16．证明：(1)＝－．(2)in2α＋inαcoα＝．【解析】(1)原式可以分子分母同除以co某,达到弦化切的目的.然后将tan某=2代入求值即可.（2）把”1”用替换后，然后分母也除以一个”1”，再分子分母同除以,达到弦化切的目的.证明：由已知tanα＝．(1)＝＝＝－．(2)in2α＋inαcoα＝＝＝＝．17．（1）;（2）;（3）.【解析】试题分析：（1）因为已知分子分母为齐次式，所以可以直接同除以转化为只含的式子即可求得；（2）用诱导公式将已知化简即可求得；（3）有，得，再利用同角关系，又因为是第三象限角，所以；试题解析：⑴2分．3分⑵9分．10分⑶解法1：由，得，又，故，即，12分因为是第三象限角，，所以．14分解法2：，12分因为是第三象限角，，所以．14分考点：1.诱导公式；2.同角三角函数的基本关系.18．【解析】∵in(α－3π)＝2co(α－4π)，∴－in(3π－α)＝2co(4π－α)，∴inα＝－2coα，且coα≠0.∴原式＝三角函数的诱导公式1一、选择题1．如果|co某|=co （某+π），则某的取值集合是（）A．－+2kπ≤某≤+2kπB．－+2kπ≤某≤+2kπC．+2kπ≤某≤+2kπD．（2k+1）π≤某≤2（k+1）π（以上k∈Z）2．in（－）的值是（）A．B．－C．D．－3．下列三角函数：①in（nπ+）；②co（2nπ+）；③in（2nπ+）；④co［（2n+1）π－］；⑤in［（2n+1）π－］（n∈Z）．其中函数值与in的值相同的是（）A．①②B．①③④C．②③⑤D．①③⑤4．若co（π+α）=－，且α∈（－，0），则tan（+α）的值为（）A．－B．C．－D．5．设A、B、C是三角形的三个内角，下列关系恒成立的是（）A．co（A+B）=coCB．in （A+B）=inCC．tan（A+B）=tanCD．in=in6．函数f（某）=co（某∈Z）的值域为（）A．{－1，－，0，，1}B．{－1，－，，1}C．{－1，－，0，，1}D．{－1，－，，1}二、填空题7．若α是第三象限角，则=_________．8．in21°+in22°+in23°+…+in289°=_________．三、解答题9．求值：in（－660°）co420°－tan330°cot（－690°）．10．证明：．11．已知coα=，co（α+β）=1，求证：co（2α+β）=．12．化简：．13、求证：=tanθ．14．求证：（1）in（－α）=－c oα；（2）co（+α）=inα．参考答案1一、选择题1．C2．A3．C4．B5．B6．B二、填空题7．－inα－coα8．三、解答题9．+1．10．证明：左边==－，右边=，左边=右边，∴原等式成立．11．证明：∵co（α+β）=1，∴α+β=2kπ．∴co（2α+β）=co（α+α+β）=co（α+2kπ）=coα=．12．解：=====－1．13．证明：左边==tanθ=右边，∴原等式成立．14证明：（1）in（－α）=in［π+（－α）］=－in（－α）=－coα．（2）co（+α）=co［π+（+α）］=－co（+α）=inα．三角函数的诱导公式2一、选择题：1．已知in(+α)=，则in(-α)值为（）A.B.—C.D.—2．co(+α)=—，6．co(-某)=，某∈（-，），则某的值为．7．tanα=m，则．8．|inα|=in（-+α），则α的取值范围是．三、解答题：9．．10．已知：in（某+）=，求in（+co2（-某）的值．11．求下列三角函数值：（1）in；（2）co；（3）tan（－）；12．求下列三角函数值：（1）in·co·tan；（2）in［（2n+1）π－］.13．设f（θ）=，求f（）的值.参考答案21．C2．A3．C4．C5．A6．±7．8．[(2k-1),2k]9．原式===inα10．11．解：（1）in=in（2π+）=in=.（2）co=co（4π+）=co=.（3）tan（－）=co（－4π+）=co=.（4）in（－765°）=in［360°某（－2）－45°］=in（－45°）=－in45°=－.注：利用公式（1）、公式（2）可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数，从而求值.12．解：（1）in·co·tan=in（π+）·co（4π+）·tan（π+）=（－in）·co·tan=（－）··1=－.（2）in ［（2n+1）π－］=in（π－）=in=.13．解：f（θ）======＝coθ－1，∴f（）=co－1=－1=－.三角函数公式1．同角三角函数基本关系式in2α＋co2α=1=tanαtanαcotα=12．诱导公式(奇变偶不变，符号看象限)（一）in(π－α)＝inαin(π+α)＝-inαco(π－α)＝-coαco(π+α)＝-coαtan(π－α)＝-tanαtan(π+α)＝tanαin(2π－α)＝-inαin(2π+α)＝inαco(2π－α)＝coαco(2π+α)＝coαtan(2π－α)＝-tanαtan(2π+α)＝tanα（二）in(－α)＝coαin(+α)＝coαco(－α)＝inαco(+α)＝-inαtan(－α)＝cotαtan(+α)＝-cotαin(－α)＝-coαin(+α)＝-coαco(－α)＝-inαco(+α)＝inαtan(－α)＝cotαtan(+α)＝-cotαin(－α)＝－inαco(－α)=coαtan(－α)=－tanα3．两角和与差的三角函数co(α+β)=coαcoβ－inαinβco(α－β)=coαcoβ＋inαinβin(α+β)=inαcoβ＋coαinβin(α－β)=inαcoβ－coαinβtan(α+β)=tan(α－β)=4．二倍角公式in2α=2inαcoαco2α=co2α－in2α＝2co2α－1＝1－2in2αtan2α=5．公式的变形（1）升幂公式：1＋co2α＝2co2α1—co2α＝2in2α（2）降幂公式：co2α＝in2α＝（3）正切公式变形：tanα+tanβ＝tan(α+β)（1－tanαtanβ）tanα－tanβ＝tan(α－β)（1＋tanαtanβ)（4）万能公式（用tanα表示其他三角函数值）in2α＝co2α＝tan2α＝6．插入辅助角公式ain某＋bco某=in(某+φ)(tanφ=)特殊地：in某±co某＝in(某±)7．熟悉形式的变形（如何变形）1±in某±co某1±in某1±co某tan某＋cot某若A、B是锐角，A+B＝，则（1＋tanA）(1+tanB)=28．在三角形中的结论若：A＋B＋C=π,=则有tanA＋tanB＋tanC=tanAtanBtanCtantan＋tantan＋tantan＝1很赞的文章！介绍的很全面，对我很有帮助。

运用诱导公式化简求值精选题42道一．选择题（共16小题）1．记cos（﹣80°）＝k，那么tan100°＝（）A．B．﹣C．D．﹣2．已知cos（）＝，则sinθ＝（）A．B．C．﹣D．﹣3．计算：cos210°＝（）A．B．C．D．4．cos300°＝（）A．B．﹣C．D．5．已知，则＝（）A．B．C．D．6．已知sin（α﹣）＝，则cos（）＝（）A．﹣B．C．﹣D．7．sin225°＝（）A．B．C．﹣D．8．cos330°＝（）A．B．C．D．9．角α的终边在直线y＝2x上，则＝（）A．B．1C．3D．﹣1 10．已知cos（﹣θ）＝，则sin（）的值是（）A．﹣B．﹣C．D．11．已知，则的值等于（）A．B．C．D．12．已知，则＝（）A．B．C．D．13．若，则等于（）A．B．C．D．14．sin330°等于（）A．B．C．D．15．已知tanθ＝3，则等于（）A．B．C．0D．16．已知f（α）＝，则的值为（）A．B．C．D．二．填空题（共18小题）17．已知tan（3π+α）＝2，则＝．18．已知，则＝．19．化简：＝．20．设tanα＝3，则＝．21．已知，且，则＝．22．已知，则＝．23．化简：的值为．24．化简：＝．25．若cos（﹣α）＝，则sin（+α）＝26．已知，则的值为．27．sin600°＝．28．已知，则sinα＝．29．已知角α终边上一点P（﹣4，3），则的值．30．化简：＝．31．若角θ的终边经过点（﹣3，4），则sin（+θ）+cos（π﹣θ）+tan（2π﹣θ）＝．32．已知，则tan（π﹣α）的值是．33．若α∈（0，π），且，则＝．34．已知sin（π﹣α）+2cos（π+α）＝0，则＝．三．解答题（共8小题）35．已知α是第二象限角，且sinα＝．（1）求tanα的值；（2）求的值．36．已知α是第三象限角，f（α）＝．（1）化简f（α）；（2）若cos（α﹣π）＝，求f（α）的值；（3）若α＝﹣1860°，求f（α）的值．37．若α为第二象限角，sin（+α）＝﹣，（1）求sinα的值；（2）若f（α）＝，求f（α）的值．38．已知角α为第一象限角，且sinα＝．（1）求cosα，tanα的值；（2）求的值．39．已知f（α）＝．（1）若α＝﹣，求f（α）值；（2）若α为第三象限角，且，求f（α）的值．40．已知角α的终边与单位圆交于点P（，）．（1）求sinα、cosα、tanα的值；（2）求的值．41．已知．（1）化简f（α）；（2）若，求的值．42．已知，f（α）＝．（1）化简f（α）；（2）若＝﹣，求tanα．运用诱导公式化简求值精选题42道参考答案与试题解析一．选择题（共16小题）1．记cos（﹣80°）＝k，那么tan100°＝（）A．B．﹣C．D．﹣【分析】法一：先求sin80°，然后化切为弦，求解即可．法二：先利用诱导公式化切为弦，求出求出结果．【解答】解：法一：，所以tan100°＝﹣tan80°＝．法二：cos（﹣80°）＝k⇒cos（80°）＝k，＝．故选：B．【点评】本小题主要考查诱导公式、同角三角函数关系式等三角函数知识，并突出了弦切互化这一转化思想的应用．2．已知cos（）＝，则sinθ＝（）A．B．C．﹣D．﹣【分析】利用二倍角的余弦公式、诱导公式，求得sinθ的值．【解答】解：∵cos（）＝，∴cos（﹣θ）＝2﹣1＝﹣＝sinθ，即sinθ＝﹣，故选：C．【点评】本题主要考查二倍角的余弦公式、诱导公式的应用，属于基础题．3．计算：cos210°＝（）A．B．C．D．【分析】把所求式子中的角210°变为180°+30°，利用诱导公式cos（180+α）＝﹣cosα及特殊角的三角函数值化简，即可求出原式的值．【解答】解：cos210°＝cos（180°+30°）＝﹣cos30°＝﹣．故选：B．【点评】此题考查了运用诱导公式化简求值，其中灵活变换角度，熟练掌握诱导公式是解本题的关键．4．cos300°＝（）A．B．﹣C．D．【分析】利用三角函数的诱导公式，将300°角的三角函数化成锐角三角函数求值．【解答】解：∵．故选：C．【点评】本小题主要考查诱导公式、特殊三角函数值等三角函数知识．5．已知，则＝（）A．B．C．D．【分析】由诱导公式，化简已知条件以及所求的表达式，然后求解即可．【解答】解：∵，∴sin[]＝sin（）＝，则＝sin（π﹣α+）＝﹣sin（α+）＝﹣，故选：C．【点评】本题主要考查给值求值问题，熟记诱导公式即可，属于基础题型．6．已知sin（α﹣）＝，则cos（）＝（）A．﹣B．C．﹣D．【分析】运用﹣α、﹣α的诱导公式，计算即可得到．【解答】解：sin（α﹣）＝，即为sin（﹣α）＝﹣，即有sin[﹣（+α）]＝﹣，即cos（）＝﹣．故选：A．【点评】本题考查三角函数的求值，考查三角函数的诱导公式的运用，考查运算能力，属于基础题．7．sin225°＝（）A．B．C．﹣D．【分析】把225°写为180°+45°由诱导公式二得特殊角的正弦角，由特殊角正弦值得结果．【解答】解：sin225°＝sin（180°+45°）＝﹣sin45°＝﹣．故选：A．【点评】本题考查用诱导公式化简求值，诱导公式一到四可以把任意角的三角函数化为锐角的三角函数，是基础题．8．cos330°＝（）A．B．C．D．【分析】由cos（α+2kπ）＝cosα、cos（﹣α）＝cosα解之即可．【解答】解：cos330°＝cos（360°﹣30°）＝cos（﹣30°）＝cos30°＝，故选：C．【点评】本题考查余弦函数的诱导公式．9．角α的终边在直线y＝2x上，则＝（）A．B．1C．3D．﹣1【分析】由已知求得tanα，再由同角三角函数基本关系式化弦为切求解．【解答】解：∵角α的终边在直线y＝2x上，∴tanα＝2．∴＝＝＝．故选：C．【点评】本题考查三角函数的化简求值，考查诱导公式及同角三角函数基本关系式的应用，是基础题．10．已知cos（﹣θ）＝，则sin（）的值是（）A．﹣B．﹣C．D．【分析】由已知及诱导公式即可计算求值．【解答】解：cos（﹣θ）＝sin[﹣（﹣θ）]＝sin（）＝，故选：C．【点评】本题主要考查了诱导公式在三角函数求值中的应用，属于基础题．11．已知，则的值等于（）A．B．C．D．【分析】观察发现，那么＝cos（α+）利用诱导公式求解即可．【解答】解：由，则＝cos（α+）＝sin（α﹣）＝．故选：A．【点评】本题主要考查诱导公式的灵活应用和构造思想，属于基本知识的考查．12．已知，则＝（）A．B．C．D．【分析】由已知直接利用三角函数的诱导公式化简求值．【解答】解：∵，∴＝cos[﹣（）]＝，故选：C．【点评】本题考查三角函数的化简求值，考查诱导公式的应用，是基础题．13．若，则等于（）A．B．C．D．【分析】直接利用诱导公式化简求解即可．【解答】解：，则＝sin（﹣）＝，故选：A．【点评】本题考查诱导公式的应用，三角函数化简求值．14．sin330°等于（）A．B．C．D．【分析】根据330°＝360°﹣30°，由诱导公式可得答案．【解答】解：∵故选：B．【点评】本题主要考查根据三角函数的诱导公式进行化简求值的问题．属基础题．对于三角函数的诱导公式一定要强化记忆．15．已知tanθ＝3，则等于（）A．B．C．0D．【分析】由题意利用诱导公式、同角三角函数的基本关系，化简所给的式子，可得结果．【解答】解：∵tanθ＝3，则＝＝＝＝，故选：B．【点评】本题主要考查应用诱导公式化简三角函数式，同角三角函数的基本关系，要特别注意符号的选取，这是解题的易错点，属于基础题．16．已知f（α）＝，则的值为（）A．B．C．D．【分析】已知关系式右边利用诱导公式化简确定出f（α），即可求出所求式子的值．【解答】解：f（α）＝＝cosα，则f（﹣）＝cos（﹣）＝cos（8π+）＝cos＝．故选：B．【点评】此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．二．填空题（共18小题）17．已知tan（3π+α）＝2，则＝2．【分析】利用诱导公式把tan（3π+α）＝2化简，得tanα＝2，再利用诱导公式化简所求表达式，令分式的分子分母同除cosα，得到只含有tanα的式子，把tanα＝2代入即可．【解答】解：由tan（3π+α）＝2，可得tanα＝2，则＝＝＝＝＝2，故答案为：2．【点评】本题主要考查诱导公式和同角三角函数关系式在三角函数化简求值中的应用，应用诱导公式时，注意符号的正负．18．已知，则＝．【分析】原式利用诱导公式化简，将sinα的值代入计算即可求出值．【解答】解：∵sinα＝，∴cos（+α）＝﹣sinα＝﹣．故答案为：﹣【点评】此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．19．化简：＝tanα．【分析】由已知利用诱导公式，同角三角函数基本关系式即可化简求值得解．【解答】解：＝＝＝tanα．故答案为：tanα．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，属于基础题．20．设tanα＝3，则＝2．【分析】利用诱导公式、同角三角函数的基本关系化简所给的式子，可得结果．【解答】解：∵tanα＝3，则＝＝＝＝＝2，故答案为：2．【点评】本题主要考查同角三角函数的基本关系、诱导公式的应用，属于基础题．21．已知，且，则＝．【分析】先利用同角三角函数基本关系求得sinα的值，在利用诱导公式对原式化简整理，把cosα和sinα的值代入即可求得答案．【解答】解：∵∴sinα＝﹣＝﹣∴原式＝＝＝﹣2故答案为：﹣2【点评】本题主要考查了运用诱导公式化简求值的问题．解题时注意三角函数的正负．22．已知，则＝．【分析】利用诱导公式化简求解即可．【解答】解：．故答案为：﹣．【点评】本题主要考查诱导公式．三角函数求值，是基本知识的考查．23．化简：的值为1．【分析】运用诱导公式及特殊角的三角函数值即可求值．【解答】解：＝﹣sin（3π+）+cos2640°+tan1665°＝sin+cos（360°×7+120°）+tan（360°×4+225°）＝+cos（180°﹣60°）+tan（180°+45°）＝﹣cos60°+tan45°＝﹣+1＝1．故答案为：1．【点评】本题主要考查了诱导公式及特殊角的三角函数值的应用，属于基础题．24．化简：＝﹣1．【分析】利用诱导公式化简即可求解．【解答】解：＝＝＝﹣1．故答案为：﹣1．【点评】本题主要考查了诱导公式在三角函数化简求值中的应用，属于基础题．25．若cos（﹣α）＝，则sin（+α）＝【分析】由题意利用诱导公式，求得所给式子的值．【解答】解：cos（﹣α）＝，则sin（+α）＝cos[﹣（﹣α）]＝cos（﹣α）＝，故答案为：．【点评】本题主要考查诱导公式的应用，属于基础题．26．已知，则的值为．【分析】由已知利用诱导公式可求tanα的值，进而利用诱导公式，同角三角函数基本关系式化简所求即可求解．【解答】解：因为，可得tanα＝，所以＝＝＝＝．故答案为：．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题．27．sin600°＝．【分析】利用诱导公式直接化简sin600°为﹣sin60°，然后求出它的值即可．【解答】解：sin600°＝sin（360°+240°）＝sin240°＝sin（180°+60°）＝﹣sin60°＝﹣．故答案为：．【点评】本题考查三角函数求值与化简，正确应用诱导公式是解决三角函数求值的重点，一般思路，负角化简正角，大角化小角（锐角）．28．已知，则sinα＝﹣．【分析】由已知利用诱导公式即可计算得解．【解答】解：因为，所以﹣sinα＝，则sinα＝﹣．故答案为：﹣．【点评】本题主要考查了诱导公式在三角函数化简求值中的应用，属于基础题．29．已知角α终边上一点P（﹣4，3），则的值．【分析】由条件利用任意角的三角函数的定义，求得sinα和cosα的值，再利用同角三角函数的基本关系、诱导公式求得所给式子的值．【解答】解：∵角α终边上一点P（﹣4，3），∴x＝﹣4，y＝3，r＝|OP|＝5，∴sinα＝＝，cosα＝＝﹣，∴原式＝＝﹣＝﹣＝．故答案为：．【点评】本题主要考查任意角的三角函数的定义，同角三角函数的基本关系、诱导公式的应用，属于基础题．30．化简：＝1．【分析】由条件利用诱导公式进行化简所给的式子，可得结果．【解答】解：＝••＝1，故答案为：1．【点评】本题主要考查诱导公式的应用，属于基础题．31．若角θ的终边经过点（﹣3，4），则sin（+θ）+cos（π﹣θ）+tan（2π﹣θ）＝．【分析】运用诱导公式化简所求，根据任意角的三角函数的定义即可求解．【解答】解：由诱导公式可得，又角θ的终边经过点（﹣3，4），所以，所以．故答案为：．【点评】本题主要考查了诱导公式，任意角的三角函数的定义在三角函数化简求值中的应用，考查了转化思想，属于基础题．32．已知，则tan（π﹣α）的值是﹣2．【分析】由已知利用诱导公式可得﹣2cosα＝﹣sinα，根据同角三角函数基本关系式可求tanα的值，利用诱导公式化简所求即可得解．【解答】解：∵，∴﹣2cosα＝﹣sinα，可得tanα＝2，∴tan（π﹣α）＝﹣tanα＝﹣2．故答案为：﹣2．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题．33．若α∈（0，π），且，则＝．【分析】由题意，利用诱导公式可得，从而根据诱导公式及同角三角函数的基本关系求解即可．【解答】解：∵α∈（0，π），且，∴，∴，故答案为．【点评】本题考查了诱导公式及同角三角函数的基本关系，考查了推理能力与计算能力，属于基础题．34．已知sin（π﹣α）+2cos（π+α）＝0，则＝．【分析】由已知利用诱导公式，同角三角函数基本关系式可求tanα＝2，进而利用同角三角函数基本关系式化简所求即可求值得解．【解答】解：∵sin（π﹣α）+2cos（π+α）＝0，∴sinα﹣2cosα＝0，可得tanα＝2，∴＝＝＝＝．故答案为：．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题．三．解答题（共8小题）35．已知α是第二象限角，且sinα＝．（1）求tanα的值；（2）求的值．【分析】（1）由已知利用同角三角函数基本关系式即可求值得解；（2）利用诱导公式，同角三角函数基本关系式化简所求即可求值得解．【解答】（本小题满分14分）解：（1）因为α是第二象限角，且sinα＝，所以cosα＝﹣＝﹣，所以tanα＝＝﹣2．（2）＝＝＝＝＝．【点评】本题主要考查了同角三角函数基本关系式，诱导公式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．36．已知α是第三象限角，f（α）＝．（1）化简f（α）；（2）若cos（α﹣π）＝，求f（α）的值；（3）若α＝﹣1860°，求f（α）的值．【分析】（1）f（α）利用诱导公式及同角三角函数间的基本关系化简即可得到结果；（2）由已知等式求出sinα的值，代入计算即可求出f（α）的值；（3）把α度数代入计算即可求出f（α）的值．【解答】解：（1）f（α）＝＝cosα；（2）∵cos（α﹣π）＝﹣sinα＝，即sinα＝﹣，且α为第三象限角，∴cosα＝﹣＝﹣，则f（α）＝cosα＝﹣；（3）把α＝﹣1860°代入得：f（﹣1860°）＝cos（﹣1860°）＝cosα1860°＝cos（5×360°+60°）＝cos60°＝．【点评】此题考查了同角三角函数基本关系的运用，运用诱导公式化简求值，熟练掌握基本关系是解本题的关键．37．若α为第二象限角，sin（+α）＝﹣，（1）求sinα的值；（2）若f（α）＝，求f（α）的值．【分析】（1）由已知利用诱导公式可求cosα的值，根据同角三角函数基本关系式可求sinα的值．（2）利用诱导公式即可化简求值得解．【解答】解：（1）∵α为第二象限角，sin（+α）＝cosα＝﹣，∴sinα＝＝；（2）∵f（α）＝＝＝sinα，∴f（α）＝．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．38．已知角α为第一象限角，且sinα＝．（1）求cosα，tanα的值；（2）求的值．【分析】（1）由已知利用同角三角函数基本关系式即可求解；（2）利用诱导公式，同角三角函数基本关系式即可化简求解．【解答】解：（1）∵角α为第一象限角，且sinα＝，∴cos＝，tanα＝＝．（2）＝＝3+＝3+＝7．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题．39．已知f（α）＝．（1）若α＝﹣，求f（α）值；（2）若α为第三象限角，且，求f（α）的值．【分析】（1）利用诱导公式化简函数解析式，进而根据特殊角的三角函数值即可计算得解．（2）利用诱导公式化简已知等式，结合α为第三象限角，利用同角三角函数基本关系式即可计算得解．【解答】解：（1）由于，又，所以f（α）＝＝＝﹣．（2）因为，又因为α为第三象限角，所以．【点评】本题主要考查了诱导公式，特殊角的三角函数值，同角三角函数基本关系式在三角函数化简求值中的应用，考查了转化思想，属于基础题．40．已知角α的终边与单位圆交于点P（，）．（1）求sinα、cosα、tanα的值；（2）求的值．【分析】（1）根据已知角α的终边与单位圆交于点P（，）．结合三角函数的定义即可得到sinα、cosα、tanα的值；（2）依据三角函数的诱导公式化简即可：＝，最后利用第（1）小问的结论得出答案．【解答】解：（1）已知角α的终边与单位圆交于点P（，）．∴x＝＝，r＝1，∴sinα＝；cosα＝；tanα＝；（6分）（2）＝＝．（14分）【点评】本题考查任意角的三角函数的定义，运用诱导公式化简求值．本题是基础题，解答关键是熟悉任意角的三角函数的定义，单位圆的知识．41．已知．（1）化简f（α）；（2）若，求的值．【分析】（1）利用诱导公式化简f（α）的解析式，可得结果．（2）由题意利用同角三角函数的基本关系求得sinα+cosα和sinα•cosα的值，从而求得要求式子的值．【解答】解：（1）＝+cosα＝sinα+cosα．（2）若＝sinα+cosα，∴平方可得1+2sinαcosα＝，∴sinαcosα＝﹣．∴＝＝＝﹣．【点评】本题主要考查利用诱导公式进行化简求值，同角三角函数的基本关系，属于基础题．42．已知，f（α）＝．（1）化简f（α）；（2）若＝﹣，求tanα．【分析】（1）利用诱导公式，同角三角函数基本关系式即可化简得解．（2）由（1）及已知利用诱导公式可得cosα＝﹣，分类讨论，利用同角三角函数基本关系式即可计算得解．【解答】解：（1）f（α）＝＝＝sinα．（2）∵＝﹣，∴sin（﹣α）＝﹣，可得cosα＝﹣，∴α是第二或第三象限角，当α是第二象限角时，sinα＝＝，tan＝﹣，当α是第三象限角时，sinα＝﹣＝﹣，tan＝．【点评】本题主要考查了诱导公式，同角三角函数基本关系式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．。

诱导公式的化简与求值1．已知角α终边上一点P（﹣，1）（1）求的值（2）写出角α的集合S．考点：任意角的三角函数的定义；运用诱导公式化简求值．专题：计算题．分析：先求出点P（﹣，1）到原点的距离，再由定义求出角α的三角函数值，（1）先用诱导公式化简，再代入角α的三角函数值求值；（2）写出角α的集合S，由于本题中的角是一个特殊角，故可以用终边相同的角将它表示出来．解答：解：点P（﹣，1）到原点的距离是2，由定义sinα=，cosα=﹣（1）==﹣==﹣（2）由sinα=，cosα=﹣知角α的终边与角的终边相同，故α=2kπ+，k∈z故S={α|α=2kπ+，k∈z}2．已知角α的终边经过点P（，﹣）．（1）求sinα的值．（2）求式﹣的值考点：任意角的三角函数的定义；运用诱导公式化简求值．专题：计算题．分析：（1）求出|OP|，利用三角函数的定义，直接求出sinα的值．（2）利用诱导公式化简表达式，根据角的终边所在象限，求出cosα=，可得结果．解答：解：（1）∵|OP|=，∴点P在单位圆上．（2分）由正弦函数的定义得sinα=﹣（5分）（2）原式=（9分）=..（10分）由余弦的定义可知，cosα=（11分）即所求式的值为（12分）3．已知角α终边上一点A的坐标为，（1）求角α的集合（6分）（2）化简下列式子并求其值：（6分）考点：三角函数的化简求值；终边相同的角；同角三角函数间的基本关系；诱导公式的作用．专题：计算题．分析：（1）根据角的终边过一个定点，根据三角函数的定义做出角的正弦值，根据角的终边在第四象限，写出与角终边相同的所有的角的集合．（2）首先用诱导公式进行整理，再把正割与余割变化成正弦与余弦的形式，约分整理出最简形式，得到结果．解答：解：（1）点P到原点的距离为r=根据三角函数的定义，得…．（2分）∵点P在第四象限，也就是角α在第四象限…．（4分）∴α的集合是…（6分）（2）原式=…．（8分）==﹣sinα=4．（1）已知tanα=2，求的值（2）已知cos（75°+α）=，其中﹣180°＜α＜﹣90°，求sin（105°﹣α）+cos（375°﹣α）的值．考点：同角三角函数基本关系的运用；运用诱导公式化简求值．专题：计算题．分析：（1）利用诱导公式化简表达式，应用tanα=2求出，代入化简后的表达式即可求出原式的值．（2）利用诱导公式化简sin（105°﹣α）+cos（375°﹣α），为2sin（75°+α），利用求出2sin（75°+α）即可．。

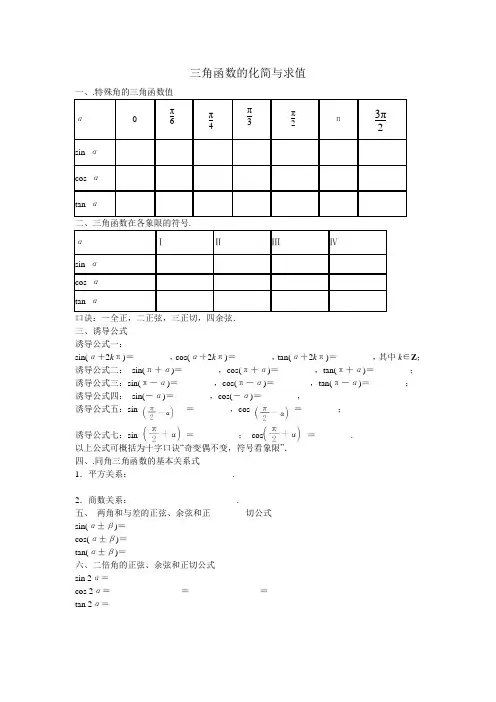
三角函数的化简与求值二、三角函数在各象限的符号. 口诀：一全正，二正弦，三正切，四余弦． 三、诱导公式 诱导公式一：sin(α＋2k π)＝________，cos(α＋2k π)＝________，tan(α＋2k π)＝________，其中k ∈Z ； 诱导公式二： sin(π＋α)＝________，cos(π＋α)＝________，tan(π＋α)＝________； 诱导公式三：sin(π－α)＝________，cos(π－α)＝________，tan(π－α)＝________； 诱导公式四： sin(－α)＝________，cos(－α)＝________，诱导公式五：sin ＝________，cos ＝________；诱导公式七：sin ＝__________； cos ＝________. 以上公式可概括为十字口诀“奇变偶不变，符号看象限”． 四、.同角三角函数的基本关系式1．平方关系：_______________________.2．商数关系：________________________.五、 两角和与差的正弦、余弦和正________切公式 sin(α±β)＝________________________ cos(α±β)＝________________________ tan(α±β)＝________________________ 六、二倍角的正弦、余弦和正切公式sin 2α＝________________cos 2α＝________________＝________________＝________________ tan 2α＝________________七、二倍角余弦公式的变式八、辅助角公式a sin x ＋b cos x ＝ sin(其中 角所在的象限由a, b 的符号确定， 角的值由tan ＝ 确定)．1． sin 330°等于( )2．求值sin 210°＝( )3．若sin α<0且tan α>0，则α是( )A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角 4．使得函数y ＝lg(tan θcos θ)有意义的角在( ) A ．第一，四象限 B ．第一，三象限 C ．第一、二象限 D ．第二、四象限5．若 － <α<0，则点Q (cos α，sin α)位于( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限6．若z ＝sin θ－ ＋i 是纯虚数，则tan θ的值为( )7.sin 15°cos 75°＋cos 15°sin 105° 等于( )8.下列各式中，值为 的是( )A ．2sin 15°cos 15°B ．︒︒-15sin 15cos 22 C ．115sin 22-︒D ．︒︒+15cos 15sin 229.记cos(－80°)＝k ，那么tan 100°＝( )π21．降幂公式：cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2；2．升幂公式：1＋cos 2α＝2cos 2α，1－cos 2α＝2sin 2α. a 2＋b 2 ()x ＋φ b a35 ⎝ ⎛⎭⎪⎫cos θ－45 A.34 B.43 C ．－34 D ．－43A.1－k 2k B ．－1－k 2kC.k 1－k 2 D ．－k 1－k2 A ．－32 B ．－12 C.12 D.32A.32 B ．－32 C.12 D ．－12A ．0 B.12C.32D ．1 3210．已知：tan(π＋α)＝－ ，则sin(α－7π)cos(α＋5π)的值是________． 11, =13.已知α为第二象限的角，sin α＝ ，则tan 2α＝ ______________.14.cos 43°cos 77°＋sin 43°cos 167°的值为________．15.已知 则f 的值为_____17.化简：(4) sin x ＋cos x; (5) x 2sin 21-＋2sin x cos x (6)x2sin＋2sin x cos x ＋3x 2cos ; (7)16．化简： (1)－sin (180°＋α)＋sin (－α)－tan (360°＋α)tan (α＋180°)＋cos (－α)＋cos (180°－α)；⎝ ⎛⎭⎪⎫－31π3 12计算：sin π4cos π3sin π2－cos πcos 3π2＋tan 2π6.cos π6tan π4sin 23π2－tan πcos 0＝________.f (α)＝sin (π－α)cos (2π－α)tan ⎝ ⎛⎭⎪⎫－α＋3π2cos (－π－α)(2)1－2sin 40°cos 40°.sin ⎝⎛⎭⎪⎫2x －π4－22sin 2x (1)1－2sin 2⎝⎛⎭⎫x ＋π8＋2sin ⎝⎛⎭⎫x ＋π8cos ⎝⎛⎭⎫x ＋π8； (2)2sin 2⎝⎛⎭⎫π4＋x －3cos 2x ；(3)cos 4x －4cos 2x ＋3.35()︒-440sin 13218.已知tan α＝2，求下列各式的值：20.已知sin α＝ ，α∈ ，tan β＝ . (1)求tan α的值； (2)求tan(α＋2β)的值．21.已知函数f (x )＝cos2x ＋sin x cos x (x ∈R )．(1)求f 的值；(2)求f (x )的单调递增区间．(1)2sin α－3cos α4sin α－9cos α；(2)2sin 2α－3cos 2α4sin 2α－9cos 2α； (3)4sin 2α－3sin αcos α－5cos 2α.tan θ＝2，求(1)cos θ＋sin θcos θ－sin θ；(2)1－sin θcos θ＋cos 2θ的值．55 ⎝⎛⎭⎪⎫0，π2 13⎝ ⎛⎭⎪⎫3π8。

诱导公式的化简求值1．已知π0,2α⎛⎫∈ ⎪⎝⎭，3sin 5α=，则9πsin sin(8π)25πsin sin(7π)2αααα⎛⎫+++ ⎪⎝⎭=⎛⎫+++ ⎪⎝⎭______．【答案】7【详解】因为3sin 5α=，且π0,2α⎛⎫∈ ⎪⎝⎭，所以4cos 5α==，所以sin 3tan cos 4ααα==．所以9πsin sin(8π)25πsin sin(7π)2αααα⎛⎫+++ ⎪⎝⎭⎛⎫+++ ⎪⎝⎭31cos sin 1tan 473cos sin 1tan 14αααααα+++====---．故答案为：7.2．若π2cos 123α⎛⎫+= ⎪⎝⎭，则2πsin 23α⎛⎫+= ⎪⎝⎭__________.【答案】19-【详解】2ππππsin 2sin 2cos 2312212ααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫+=++=+ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦22π212cos 1211239α⎛⎫⎛⎫=+-=⨯-=- ⎪ ⎪⎝⎭⎝⎭.故答案为：19-.3．计算7π5πcos sin 644πtan 3的结果为__________．【答案】4【详解】因为7πππcoscos πcos 666⎛⎫=+=-= ⎪⎝⎭5πππsin sin πsin 444⎛⎫=+=-=- ⎪⎝⎭4πππtan tan πtan 333⎛⎫=+= ⎪⎝⎭所以7π5πcos sin 22644πtan 3⎛⎫⎛⎫-⨯ ⎪ ⎪=故答案为：4.4．点()3,4A 在角θ的终边上，则sin(π)2cos πcos()cos 2θθθθ++=--__________．【答案】2【详解】因为点()3,4A 在角θ的终边上，则4tan 3θ=，所以42sin(π)2cos sin 2cos tan 232π4sin cos tan 1cos()cos 123θθθθθθθθθθ-+++-+-+===-----.故答案为：25．若1sin 3α=，则πcos 2α⎛⎫+= ⎪⎝⎭__________.【答案】13-【详解】π1cos sin 23αα⎛⎫+=-=- ⎪⎝⎭.故答案为：13-6．已知角α终边上一点()2,3P -，则()()πcos sin π23πcos πcot 2αααα⎛⎫+- ⎪⎝⎭=⎛⎫++ ⎪⎝⎭________．【答案】【详解】由诱导公式知，()()πcos sin πsin sin 2sin 3πcos (tan )cos πcot 2ααααααααα⎛⎫+- ⎪-⋅⎝⎭===--⋅-⎛⎫++ ⎪⎝⎭，因为角α终边上一点()2,3P -，所以sin α所以原式sin 13α=-=-.故答案为：7．23πtan 3⎛⎫-= ⎪⎝⎭____.【详解】23π23π2π2ππtan(tan tan(7π)tan tan 33333-=-=-+=-=8．cos660︒=________.【答案】12/0.5【详解】()()1cos660cos 236060cos 60cos602︒=⨯︒-︒=-︒=︒=故答案为：129．化简:()()()()sin 2πcos 6πcos πsin 5πθθθθ---=-+_____.【答案】1-【详解】原式=()()()()()()()sin cos sin cos 1cos πsin πcos sin θθθθθθθθ-⋅--⋅==-+⋅+-⋅-.故答案为：1-.10．若()sin π3α-=，则πcos 2α⎛⎫+= ⎪⎝⎭______．【答案】【详解】因为()sin sin παα-=所以πcos sin 2αα⎛⎫+=-=- ⎪⎝⎭.故答案为：11．()()cos πππsin cos sin π22αααα-⎛⎫⎛⎫-+ ⎪ ⎪-⎝⎭⎝⎭=____________【答案】2cos α-【详解】原式()()()2cos cos sin cos sin ααααα-=⋅⋅-=--故答案为：2cos α-.12．已知()1cos π2α+=-，3π2π2α<<，则()sin 3πα+=_________．【答案】2【详解】()1cos π2α+=- ，1cos 2α∴-=-，即1cos 2α=，3π2π2α<<，sin 2α∴==()sin 3πsin αα∴+=-=13．()()()()tan 2πsin 2πcos 6πcos π3ππsin cos 22x x x x x x -----=⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭__________【答案】sin x【详解】()()()tan 2πtan ,sin 2πsin sin x x x x x -=---=-=-，()()()cos 6πcos cos ,cos πcos x x x x x -=-=-=-，3ππsin cos ,cos sin 22x x x x ⎛⎫⎛⎫+=-= ⎪ ⎪⎝⎭⎝⎭，原式()()()()tan sin cos cos tan cos sin cos sin x x x x x x x x x-⨯-⨯⨯-==⨯=-⨯，故答案为：sin x .14．若α的终边过点()1,2-，则()()sin ππsin cos π2ααα-=⎛⎫+-+ ⎪⎝⎭______.【答案】1-【详解】因为α的终边过点(1,2)-，由三角函数的定义可得2tan 21α==--，所以()()sin πsin 11tan (2)1πcos cos 22sin cos π2ααααααα-===⨯-=-+⎛⎫+-+ ⎪⎝⎭.故答案为：1-15．已知()1sin π3α+=，则πcos()2α+=_________________.【答案】13【详解】由已知1sin(π)sin 3αα+=-=，1sin 3α=-，所以π1cos()sin 23αα+=-=．故答案为：13．16．若角α的终边过点()1,2-，则πsin 2α⎛⎫-= ⎪⎝⎭__________.【答案】【详解】角α的终边过点(1,2)-，由三角函数的定义得cos α=由诱导公式得ππsin sin cos 225ααα⎛⎫⎛⎫-=--=-=- ⎪ ⎪⎝⎭⎝⎭，故答案为：17．1717cos πsin π44⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭______．【详解】17π17π17π17πππcos sin cos sin cos 4πsin 4π444444⎛⎫⎛⎫⎛⎫⎛⎫---=+=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ππcos sin 4422=+=；.18．7πsin 3的值为__________【答案】2【详解】7πππsinsin 2πsin 3332⎛⎫=+== ⎪⎝⎭.19．已知5sin 13α=，则πcos 2α⎛⎫+= ⎪⎝⎭______.【答案】513-【详解】由π5cos sin 213αα⎛⎫+=-=- ⎪⎝⎭.故答案为：513-20．已知tan 3α=，求sin(4)3cos()92sin()sin(7)2παπαπαπα-+--=-+-+_________【答案】-6【详解】原式=sin 3cos tan 33362cos sin 2tan 23αααααα------===--+-+-+.故答案为：-6.21．已知角x 在第二象限，且π4cos ,25x ⎛⎫+=- ⎪⎝⎭则tan 2x =______．【答案】247/337【详解】π4cos 25x ⎛⎫+=- ⎪⎝⎭，即4sin 5x -=-，则4sin 5x =， 角x在第二象限，则3cos 5x ==-，则4tan 3x =-，22tan 24tan 21tan 7x x x ∴==-.故答案为：247.22．若()1sin π2A +=-，则3πcos 2A ⎛⎫-= ⎪⎝⎭____________．【答案】12-/-0.5【详解】因为()2π3π5π2A A ⎛⎫-= ⎪⎝⎭+-，所以3πcos 2A ⎛⎫-= ⎪⎝⎭()()()()5πππ1cos πcos πcos πsin π2222A A A A ⎡⎤⎡⎤⎡⎤+-=+-=-+=+=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦.故答案为：12-23．化简：()()tan cos 3ππ2co i πt 2πs n 2αααα⎛⎫- ⎪-⎝⎭⋅=+⎛⎫+ ⎪⎝⎭_________．【答案】1【详解】()()tan cos 3πcos cot 21cot 2πcos cot πi 2πs n αααααααα⎛⎫- ⎪---⎝⎭⋅=⋅=+⎛⎫+ ⎪⎝⎭.故答案为：124．已知α是第二象限角，1sin 3α=，则πsin 2α⎛⎫+= ⎪⎝⎭________．【答案】3-/【详解】因为α是第二象限角，1sin 3α=，所以πsin cos 2αα⎛⎫+==-- ⎪⎝⎭故答案为：25．已知1tan 2α=，则()cos ππcos 2αα-=⎛⎫+ ⎪⎝⎭__________．【答案】2【详解】因为1tan 2α=，所以()cos πcos 12πsin tan cos 2ααααα--===-⎛⎫+ ⎪⎝⎭.故答案为：2.26．已知1cos 2α=，3π2π2α<<，则()sin 2πα-=______.【答案】2【详解】因为13πcos ,2π22αα=<<，所以sin2α==-，所以sin(2)sinπαα-=-=.故答案为：2.27．化简：()()()π11πcosπcos cos229πcosπsinπsin2αααααα⎛⎫⎛⎫++-⎪ ⎪⎝⎭⎝⎭=⎛⎫---+⎪⎝⎭______．【答案】tanα【详解】()()()π11πcosπcos cos229πcosπsinπsin2αααααα⎛⎫⎛⎫++-⎪ ⎪⎝⎭⎝⎭⎛⎫---+⎪⎝⎭()()cos sin sin tancos sin cosααααααα-⋅--==-.故答案为：tanα.28．化简πsin(5π)cos()cos(8π)23πsin()sin(4π)2θθθθθ---=---__．【答案】sinθ【详解】πsin(5π)cos()cos(8π)(sin)sin cos2sin3πcos(sin)sin()sin(4π)2θθθθθθθθθθθ----==----．故答案为：sinθ.29．化简222sin(π)cos(π)cos(2π)3π3π1cos cos sin222παααααα+-+-⎛⎫⎛⎫⎛⎫+-++-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的结果为______.【答案】1tanα【详解】222sin(π)cos(π)cos(2π)3π3π1cos cos sin222παααααα+-+-⎛⎫⎛⎫⎛⎫+-++-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭222(sin)(cos)cosππ1cos cos cosπ22παααααα--+=⎛⎫⎛⎫+-++-⎪⎡⎤⎡⎤++⎢⎥⎢⎪⎝⎭⎝⎭⎥⎣⎦⎣⎦22222sin cos cos 2sin cos cos 1sin sin cos ππ1cos cos cos 22αααααααααααα++==++-⎡⎤⎛⎫⎛⎫+---+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦22sin cos cos (2sin 1)cos cos 12sin sin (2sin 1)sin sin tan αααααααααααα++====++.故答案为：1tan α.30．已知角θ的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点()()8,60P m m m -->．(1)求sin θ，cos θ的值；(2)求()()()()()()3πsin sin 3πcos πcos 25πsin 2πcos 3πsin sin π2θθθθθθθθ⎛⎫-⋅-⋅+⋅- ⎪⎝⎭⎛⎫-⋅-⋅-⋅- ⎪⎝⎭的值．【答案】(1)3sin 5θ=-，4cos 5θ=-；(2)34-【详解】（1）由题意知，10r m ==，∴63sin 105y m r m θ-===-，84cos 105x m r m θ-===-；（2）原式()()()()()()()322sin sin cos sin sin cos sin cos cos sin sin cos θθθθθθθθθθθθ-⋅-⋅-⋅-⋅==--⋅-⋅⋅-⋅tan θ=-，由（1）知，sin 3tan cos 4θθθ==，∴()()()()()()3πsin sin 3πcos πcos 325π4sin 2πcos 3πsin sin π2θθθθθθθθ⎛⎫-⋅-⋅+⋅- ⎪⎝⎭=-⎛⎫-⋅-⋅-⋅- ⎪⎝⎭．31．已知角θ的始边为x 轴非负半轴,终边过点(A -.(1)3ππcos sin 22θθ⎛⎫⎛⎫-++ ⎪ ⎪.(2)已知角α的始边为x 轴非负半轴,角θ和α的终边关于y 轴对称,求πsin 6α⎛⎫- ⎪⎝⎭的值.【答案】(1)2-(2)6【详解】（1）由题可知OA =则sin ,cos ,tan 33θθθ===3ππcos 222θθ⎛⎫⎛⎫-+++ ⎪ ⎪=-.（2）因为角θ和α的终边关于y 轴对称,所以sin αcos α所以π1sin sin cos 6226ααα⎛⎫-=-= ⎪⎝⎭.32．已知()()ππsin cos 223πcos πsin 2f ααααα⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭=⎛⎫-+ ⎪⎝⎭.(1)若角α的终边经过点(),2m m ，0m ≠，求()f α的值；(2)若()2f α=，求sin cos sin cos αααα+-的值.【答案】(1)2(2)3【详解】（1）()()()()ππsin cos cos sin 22tan 3πcos cos cos πsin 2f αααααααααα⎛⎫⎛⎫-+ ⎪ ⎪-⋅-⎝⎭⎝⎭===-⋅-⎛⎫-+ ⎪⎝⎭，因为角α的终边经过点(),2m m ，0m ≠，所以()2tan 2m f mαα===.（2）由（1）知()tan 2f αα==，所以sin cos tan 1213sin cos tan 121αααααα+++===---.33．已知()()()()()πsin sin tan π2tan 2πsin π+f αααααα⎛⎫--- ⎪⎝⎭=-(1)化简()f α．(2)若α为第三象限角，且3π1cos 25⎛⎫-= ⎪⎝⎭α，求()f α的值．【答案】(1)()f αcos α=(2)()f α=【详解】（1）()()()()()πsin sin tan π2tan sin πf αααααα⎛⎫--- ⎪⎝⎭=-+()()()cos sin tan tan sin ααααα⋅-⋅-=-⋅-cos α=．（2）∵α为第三象限角，且3π1cos sin 25⎛⎫-=-= ⎪⎝⎭αα，∴1sin 5α=-，()cos f αα===．34．已知()()()3πsin 2πsin 2πsin cos π2f ααααα⎛⎫-⋅- ⎪⎝⎭=⎛⎫+⋅- ⎪⎝⎭．(1)化简()f α；(2)若()2f α=，求2222sin 1sin 2cos ααα-+的值【答案】(1)()tan f αα=-(2)12【详解】（1）()()()()()3πsin 2πsin sin cos 2tan cos cos sin cos π2πf αααααααααα⎛⎫-⋅- ⎪-⋅-⎝⎭===-⋅-⎛⎫+⋅- ⎪⎝⎭；（2）由（1）得tan 2α-=，tan 2α∴=-，()2222222222222sin sin cos 2sin 1sin cos sin 2cos sin 2cos sin 2cos αααααααααααα-+--∴==+++221tan ta 1412422n αα--===++.35．（1）化简：3πtan(π)cos(2π)sin()2cos(π)sin(π)ααααα---+----；（2）已知π3cos 45x ⎛⎫+= ⎪⎝⎭，求2sin 22sin 1tan x xx --的值．【答案】（1）1-；（2）725【详解】（1）3πtan(π)cos(2π)sin()2cos(π)sin(π)ααααα---+----＝sin cos (tan )cos (cos )cos 1(cos )sin sin ααααααααα⋅-⋅⋅-=-=--⋅；（2）2sin 22sin 2sin (cos sin )2sin cos sin 1tan 1cos x x x x x x xx x x--==--，()2π331818cos cos sin cos sin 12sin cos 4552525x x x x x x x ⎛⎫+==⇒-=⇒-=⎪⎝⎭72sin cos 25x x ⇒=，因此2sin 22sin 71tan 25x x x -=-.36．已知()()()()π3πcos tan πsin 22cos πtan 3πf αααααα⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭=++.(1)若()0,2πα∈，且()12f α=-，求α的值；(2)若()3π125f f αα⎛⎫-+= ⎪⎝⎭，且π3π,22⎛⎫∈ ⎪⎝⎭α，求tan α的值.【答案】(1)7π6α=或11π6α=(2)4tan 3α=-【详解】（1）()()()()()()π3πcos tan πsin sin tan cos 22sin cos πtan 3πcos tan f αααααααααααα⎛⎫⎛⎫+-+ ⎪ ⎪---⎝⎭⎝⎭===++-，()0,2πα∈，且()1sin 2f αα==-，则7π6α=或11π6α=.（2）()3π3π1sin sin sin cos 225f f αααααα⎛⎫⎛⎫-+=-+=+=⎪ ⎪⎝⎭⎝⎭，则1sin cos 5αα=-，所以22221cos sin cos cos 15αααα⎛⎫+=+-= ⎪⎝⎭，解得4cos 5α=或3cos 5α=-，由π3π,22⎛⎫∈ ⎪⎝⎭α，则3cos 5α=-，得4sin 5α=，所以4sin 45tan 3cos 35ααα===--37．已知tan 3α=，求()()πsin 3sin π23πcos cos 5π2αααα⎛⎫+++ ⎪⎝⎭⎛⎫--+ ⎪⎝⎭的值．【答案】4【详解】因为()πsin cos ,sin πsin 2αααα⎛⎫+=+=- ⎪⎝⎭，()()3πcos sin ,cos 5πcos πcos 2ααααα⎛⎫-=-+=+=- ⎪⎝⎭，所以()()πsin 3sin πcos 3sin 13tan 23πsin cos tan 1cos cos 5π2αααααααααα⎛⎫+++ ⎪--⎝⎭==-+-+⎛⎫--+ ⎪⎝⎭，又tan 3α=，所以()()πsin 3sin π133243π31cos cos 5π2αααα⎛⎫+++ ⎪-⨯⎝⎭==-+⎛⎫--+ ⎪⎝⎭.故答案为：4.38．已知()()5πsin πsin 23π2sin sin π2αααα⎛⎫-++ ⎪⎝⎭=⎛⎫-++ ⎪⎝⎭.(1)求tan α的值；(2)求24sin cos 2cos ααα+的值.【答案】(1)7tan 4α=-(2)1613-【详解】（1）依题意得，()()5πsin πsin sin cos 2π2cos sin 2sin sin π2αααααααα⎛⎫-++ ⎪+⎝⎭=--⎛⎫-++ ⎪⎝⎭tan 132tan αα+==--，解得7tan 4α=-（2）22224sin cos 2cos 4sin cos 2cos sin cos αααααααα++=+24tan 2tan 1αα+=+1613=-.39．已知角α终边上一点(4,3),P -求()πcos()sin π211π9πcos()sin()22a a a α+----++的值．【答案】67【详解】角α终边上一点(4,3),P -3tan ,4y x α∴==-则原式32()sin sin 2tan 64.3sin cos tan 1714αααααα-⨯----====-+-++故答案为：6740．设()322π2cos sin 2cos π222cos 7πcos f θθθθθθ⎛⎫++--- ⎪⎝⎭=+++-（）（）（），求2023π3f ⎛⎫⎪⎝⎭的值.【答案】12.【详解】因为()322π2cos sin 2cos π222cos 7πcos f θθθθθθ⎛⎫++--- ⎪⎝⎭=+++-（）（）（）=322222cos cos 2cos cos 2cos cos 2cos 22cos cos 22cos cos θθθθθθθθθθθ++++==++++（），所以2023π2023πππ1cos cos 3372πcos 33332f ⎛⎫⎛⎫==⨯+== ⎪ ⎪⎝⎭⎝⎭41．已知1tan 2θ=-，求下列各式的值：(1)22cos 12sin cos θθθ-；(2)tan(π)sin(π)3πππsin cos cos 222θθθθθ--⎛⎫⎛⎫⎛⎫+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．【答案】(1)34-(2)54【详解】（1）原式()222222cos sin cos cos sin 2sin cos 2sin cos θθθθθθθθθ-+-==22111tan 3212tan 422θθ⎛⎫-- ⎪-⎝⎭===-⎛⎫⨯- ⎪⎝⎭．（2）原式tan sin (cos )sin (sin )θθθθθ=--22221sin cos cos cos θθθθ+==22151tan 124θ⎛⎫=+=+-= ⎪⎝⎭．42．已知()()()()()3sin 3πcos 2πsin π2cos πsin πf αααααα⎛⎫-⋅-⋅-+ ⎪⎝⎭=--⋅-+．(1)化简()f α；(2)若31π3α=-，()f α．【答案】(1)cos α(2)12【详解】（1）由题意可得：()()()()()()()()()3sin 3πcos 2πsin πsin πcos cos 2cos cos πsin πcos sin πf αααααααααααα⎛⎫-⋅-⋅-+ ⎪-+⋅⋅-⎝⎭===--⋅-+-⋅-+，故()cos f αα=.（2）∵31π3α=-，则()3131πππ1πcos πcos 10πcos cos 333332f f α⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=-== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，∴()12f α=.43．已知3πsin(3π)cos(2π)sin()2()cos(π)sin(π)f αααααα---+=----.(1)化简()f a ；(2)若α是第三象限角，且3π1co (s 52α-=，求π(6f α+的值；【答案】(1)()f α=cos α-；(2)110【详解】（1）3πsin(3π)cos(2π)sin()2()cos(π)sin(π)f αααααα---+=----(sin )cos (cos )cos (cos )sin αααααα-⋅⋅-==--.（2）因为3π1co (s 52α-=，又3ππcos(cos()sin 22ααα-=+=-，所以1sin 5α=-，又α是第三象限的角，所以cos α=-所以ππππ(cos()cos cos sin sin6666f αααα+=-+=-+111(()5210-=-⨯-⨯=.44．sin(2π)sin(π)cos(π)sin(3π)cos(π)ααααα-+----.【答案】sin α【详解】因为sin(2π)sin()sin ,sin(π)sin ,ααααα-=-=-+=-cos(π)cos(π)cos ααα--=+=-，sin(3π)sin(π)sin ,cos(π)cos ,ααααα-=-=-=-所以原式sin (sin )(cos )sin sin (cos )αααααα-⋅-⋅-==⋅-.45．（1）化简：()()()()()()π11πsin 2πcos πcos cos 229πcos πsin 3πsin πsin 2f ααααααααα⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫----+ ⎪⎝⎭（2）求值：cos21cos24sin159sin 204︒⋅︒+︒⋅︒．【答案】（1）tan α-；（2）2．【详解】（1）()()()()()()π11πsin 2πcos πcos cos 229πcos πsin 3πsin πsin 2f ααααααααα⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫----+ ⎪⎝⎭()()()()()()πsin cos sin cos 6π2πcos sin πsin πsin 4π2αααααααα⎡⎤⎛⎫----+ ⎪⎢⎥⎝⎭⎣⎦=⎡⎤⎛⎫---+++⎡⎤ ⎪⎣⎦⎢⎥⎝⎭⎣⎦()()()()πsin cos sin cos 2πcos sin sin sin 2αααααααα⎡⎤⎛⎫----+⎪⎢⎥⎝⎭⎣⎦=⎛⎫-+ ⎪⎝⎭()()()2222sin cos cos sin cos sin sin 2tan cos sin cos cos sin cos cos πααααααααααααααα⎛⎫-+ ⎪--⎝⎭===-=---（2）cos 21cos 24sin159sin 204cos 21cos 24sin 21sin 24︒⋅︒+︒⋅︒=︒⋅︒-︒︒()cos 2124cos 452=︒+︒=︒46．.化简下列各式：(1)π2912sin cos 6ππtan 54⎛⎫-+⋅ ⎪⎝⎭；(2)3tan(π)cos(2π)sin(π)2cos(3π)sin(π)ααααα+⋅+⋅---⋅--.【答案】(1)12-(2)1-【详解】（1）原式52sin cos 0π6π5=-+⨯2π1sin6=-=-（2）原式tan cos cos 1cos sin ααααα⋅⋅==--⋅47．已知()()()()()5πsin 2πcos πcos 29πcos πsin πsin 2x x x f x x x x ⎛⎫-+- ⎪⎝⎭=⎛⎫---+ ⎪⎝⎭．(1)化简()f x ；(2)已知()2f α=，求sin2α的值．【答案】(1)tan x -(2)45-【详解】（1）由题意得()()()()()5πsin 2πcos πcos 29πcos πsin πsin 2x x x f x x x x ⎛⎫-+- ⎪⎝⎭=⎛⎫---+ ⎪⎝⎭(sin )(cos )sin sin tan (cos )sin cos cos x x x xx x x x x--==-=--.（2）由()2f α=，可得tan 2,tan 2αα-=∴=-，则2222sin cos 2tan 4sin2sin cos tan 15ααααααα===-++.48．（1）已知()2tan π3α-=-，求cos 3sin cos 9sin α-αα+α的值；（2）化简()()()()3πsin πsin tan 2π2πsin tan πcos 2θθθθθθ⎛⎫--- ⎪⎝⎭⎛⎫-+- ⎪⎝⎭.【答案】（1）17-；（2）tan θ.【详解】（1）因为()2tan πtan 3αα-=-=-，可得2tan 3α=，所以213cos 3sin 13tan 132cos 9sin 19tan 7193αααααα-⨯--===-+++⨯；（2）()()()()()()23πsin πsin tan 2πsin cos tan 2tan πcos tan sin tan πcos 2θθθθθθθθθθθθ⎛⎫--- ⎪--⎝⎭==⎛⎫-+- ⎪⎝⎭.49．已知sin 2cos αα=，求：(1)化简()()πcos 2sin 2πcos 2π5πsin 2αααα⎛⎫- ⎪⎝⎭--⎛⎫+ ⎪⎝⎭；(2)求2sin2sin sin cos cos21ααααα+--的值.【答案】(1)45(2)1【详解】（1）因为sin 2cos αα=，22sin cos 1αα+=，所以22sin sin 12αα⎛⎫+= ⎪⎝⎭，即24sin 5α=，()()2πcos sin 42sin 2πcos 2πsin cos sin 5πcos 5sin 2ααααααααα⎛⎫- ⎪⎝⎭--===⎛⎫+ ⎪⎝⎭.（2）sin tan 2cos ααα== ，2sin2sin sin cos cos21ααααα∴+--()222sin cos sin sin cos 2cos 11αααααα=+---222sin cos sin sin cos 2cos αααααα=+-222tan tan tan 2221222ααα=+-⨯==+-.50．化简以下式子：()()()()()7πsin cos πtan 3π2sin 2πtan πcos 9παααααα⎛⎫++- ⎪⎝⎭--+-【答案】1tan α-【详解】()()()()()7πsin cos πtan 3π2sin 2πtan πcos 9παααααα⎛⎫++- ⎪⎝⎭--+-()()()()3πsin cos tan 2sin tan cos παααααα⎛⎫+-- ⎪⎝⎭=--()()()()()cos cos tan sin tan cos αααααα---=--cos 1sin tan ααα=-=-.。

诱导公式的化简与求值20题一.解答题(共20小题)1.已知角a终边上一点P (—二，1)cos (晋+a ) sin ( - JL - a )(1 )求，.. 的值cos I ―-。

】sin I —r-+ )(2)写出角a的集合S.2.已知角a的终边经过点P(-, — ?(1) 求 sin %的值.的值(3n - a)sin ( a + 兀) cos(2)求式3 .已知角a终边上一点A的坐标为(1)求角a的集合(6 分)(2)化简下列式子并求其值:sin (2兀-CL ) tan (兀+ CI ) cot ( - a -兀)sin 4. ( 1)已知 tan a =2求----- esc (一 a ) cos ( JT - CL ) tan(3兀一口〔兀-a ) cos (2兀-a ) sin ( - a + "兀、2 砧/古.二一' __n ' '：的值(6分)(2)已知 cos (75° +a =£，其中—180° v aV—90°,求 sin (105°— a +cos (375°— a)的值.sin (兀一 a ) cos (2 兀一tan ( ~ a5 .已知a是第三象限角，且-■ 1(1)化简 f ( a)；(2)若I | ':一，求 f (a)2 5的值.6 .已知角a的终边上一点 P (X, 4)，且3 cos a ——.(1 )求x的值；(2 )求 sin ( a + n)的值;2(3)将角a的终边沿顺时针旋转g n弧度得到角3,求sin B的值.sin (5兀-a) w cos ( 'cos (兀+ a ) 7 .已知:：_. |sin ( Q 一—T-) *cos ( ^+―) *tan ( 口一3兀)■u u(1)化简 f (a)(2 )若a是第三象限角，且I ' ■，求f (a)的值.2 58.求值：① si n870 +c os660 +ta n1215 - tan (— 300 ° +cot (- 330 ° ②^10.已知'.Z '.'I, . _2.i, _ .2(1 )求 sinx - cosx 的值；(2)求： 1 1: 二的值cos (180c +x) *cos(90* - x) + cos^ J11 .已知a是第四象限角，且11 -.5(1 )求tan a的值；sin (舟兀- a) +2cos ( □+弓)(2 )求的值.sin ( a - TT ) - 3cos ( 2兀~ CL )sin (2 兀- a) cos ( TT + Ct ) cos12.已知：:- " ■2sin (3TT + a ) sin ( - TT - a ) sin (+a )①化简f( a .2②右sin o是方程10x +x - 3=0的根，且a在第三象限，求f (a)的值.③若a=…I.,求f (a)的值.sin ( d - %) cos (2兀-口 )tan ( - a -兀)sin(57l+a ) tan2( - a~ 2X)(1)化简 f ( a)；JT 1(2)若a是第三象限角，且cos O :'，求f ( ⑶若」J 1,求 f(a)的值.cos (TT - 6 J an〔3兀一 6 )13.14.已知 f (a)=a + n的值;，求 sin - cos %的值.(1)已知-：i 1- 'I - 1-■sin (a -cos (~ a) tan 兀一且) 15•已知 f (a) =— ■tan (一&一 5兀)sin (a 3TT )(1) 化简 f (a);(2) 若角a 的终边经过点P (- 2, 3),求f (a)的值.(1)化简 f (a)；(2 )若 tan ( n- a =- 2,求 f (a)的值; (3 )若 a=- 420° 求 f (a)的值.sin (2兀-a ) cos (兀+Q ) cos) cos (】叮-□)19. 已知:■-：：..cos t K - CL ) sin (3兀 一。

三角函数公式1． 同角三角函数根本关系式 sin 2α＋cos 2α=1 sin αcos α=tan α tan αcot α=12． 诱导公式 (奇变偶不变，符号看象限)（一） sin(π－α)＝sin α sin(π+α)＝-sin αcos(π－α)＝-cos α cos(π+α)＝-cos α tan(π－α)＝-tan α tan(π+α)＝tan α sin(2π－α)＝-sin α sin(2π+α)＝sin α cos(2π－α)＝cos α cos(2π+α)＝cos α tan(2π－α)＝-tan α tan(2π+α)＝tan α 〔二〕 sin(π2 －α)＝cos α sin(π2+α)＝cos αcos(π2 －α)＝sin α cos(π2 +α)＝- sin αtan(π2 －α)＝cot α tan(π2 +α)＝-cot αsin(3π2 －α)＝-cos α sin(3π2 +α)＝-cos αcos(3π2 －α)＝-sin α cos(3π2 +α)＝sin αtan(3π2 －α)＝cot α tan(3π2+α)＝-cot αsin(－α)＝－sin α cos(－α)=cos α tan(－α)=－tan α3． 两角和与差的三角函数cos(α+β)=cos αcos β－sin αsin β cos(α－β)=cos αcos β＋sin αsin β sin (α+β)=sin αcos β＋cos αsin β sin (α－β)=sin αcos β－cos αsin β tan(α+β)=tan α+tan β1－tan αtan βtan(α－β)=tan α－tan β1＋tan αtan β4． 二倍角公式 sin2α=2sin αcos αcos2α=cos 2α－sin 2α＝2 cos 2α－1＝1－2 sin 2α tan2α=2tan α1－tan 2α5．公式的变形（1）升幂公式：1＋cos2α＝2cos2α1—cos2α＝2sin2α（2）降幂公式：cos2α＝1＋cos2α2sin2α＝1－cos2α2（3）正切公式变形：tanα+tanβ＝tan(α+β)〔1－tanαtanβ〕tanα－tanβ＝tan(α－β)〔1＋tanαtanβ) （4）万能公式〔用tanα表示其他三角函数值〕sin2α＝2tanα1+tan2αcos2α＝1－tan2α1+tan2αtan2α＝2tanα1－tan2α6．插入辅助角公式asinx＋bcosx=a2+b2sin(x+φ) (tanφ= b a)特殊地：sinx±cosx＝ 2 sin(x±π4)7．熟悉形式的变形〔如何变形〕1±sinx±cosx 1±sinx 1±cosx tanx＋cotx1－tanα1＋tanα1＋tanα1－tanα假设A、B是锐角，A+B＝π4，那么〔1＋tanA〕(1+tanB)=28．在三角形中的结论假设：A＋B＋C=π, A+B+C2=π2那么有tanA＋tanB＋tanC=tanAtanBtanCtan A2tanB2＋tanB2tanC2＋tanC2tanA2＝1三角函数的诱导公式1一、选择题1．如果|cos x |=cos 〔x +π〕，那么x 的取值集合是〔 〕 A ．－2π+2k π≤x ≤2π+2k π B ．－2π+2k π≤x ≤2π3+2k πC ．2π+2k π≤x ≤2π3+2k π D ．〔2k +1〕π≤x ≤2〔k +1〕π〔以上k ∈Z 〕2．sin 〔－6π19〕的值是〔 〕 A ．21 B ．－21 C ．23 D ．－23 3．以下三角函数：①sin 〔n π+3π4〕；②cos 〔2n π+6π〕；③sin 〔2n π+3π〕；④cos ［〔2n +1〕π－6π］；⑤sin ［〔2n +1〕π－3π］〔n ∈Z 〕．其中函数值与sin 3π的值相同的是〔 〕 A ．①② B ．①③④ C ．②③⑤ D ．①③⑤4．假设cos 〔π+α〕=－510，且α∈〔－2π，0〕，那么tan 〔2π3+α〕的值为〔 〕 A ．－36B ．36C ．－26 D ．26 5．设A 、B 、C 是三角形的三个内角，以下关系恒成立的是〔 〕 A ．cos 〔A +B 〕=cos C B ．sin 〔A +B 〕=sin C C ．tan 〔A +B 〕=tan CD ．sin2B A +=sin 2C6．函数f 〔x 〕=cos 3πx〔x ∈Z 〕的值域为〔 〕 A ．{－1，－21，0，21，1} B ．{－1，－21，21，1} C ．{－1，－23，0，23，1}D ．{－1，－23，23，1} 二、填空题7．假设α是第三象限角，那么)πcos()πsin(21αα---=_________． 8．sin 21°+sin 22°+sin 23°+…+sin 289°=_________． 三、解答题9．求值：sin 〔－660°〕cos420°－tan330°cot 〔－690°〕．10．证明：1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ．11．cos α=31，cos 〔α+β〕=1，求证：cos 〔2α+β〕=31．12． 化简：︒+︒︒︒+790cos 250sin 430cos 290sin 21．13、求证：)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ．14． 求证：〔1〕sin 〔2π3－α〕=－cos α； 〔2〕cos 〔2π3+α〕=sin α．参考答案1一、选择题1．C 2．A 3．C 4．B 5．B 6．B 二、填空题7．－sin α－cos α 8．289 三、解答题 9．43+1． 10．证明：左边=θθθθ22sin cos cos sin 2-1--=－θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++，右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--， 左边=右边，∴原等式成立．11．证明：∵cos 〔α+β〕=1，∴α+β=2k π．∴cos 〔2α+β〕=cos 〔α+α+β〕=cos 〔α+2k π〕=cos α=31．12．解：︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21=︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =－1．13．证明：左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tan θ=右边，∴原等式成立．14证明：〔1〕sin 〔2π3－α〕=sin ［π+〔2π－α〕］=－sin 〔2π－α〕=－cos α． 〔2〕cos 〔2π3+α〕=cos ［π+〔2π+α〕］=－cos 〔2π+α〕=sin α．三角函数的诱导公式2一、选择题： 1．sin(4π+α)=23，那么sin(43π-α)值为〔 〕 A.21 B. —21 C. 23 D. —23 2．cos(π+α)= —21，23π<α<π2,sin(π2-α) 值为〔 〕 A.23 B. 21 C. 23± D. —233．化简：)2cos()2sin(21-•-+ππ得〔 〕A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2) 4．α和β的终边关于x 轴对称，那么以下各式中正确的选项是〔 〕 A.sinα=sinβ B. sin(α-π2) =sinβ C.cosα=cosβ D. cos(π2-α) =-cosβ 5．设tanθ=-2, 2π-<θ<0，那么sin 2θ+cos(θ-π2)的值等于〔 〕， A. 51〔4+5〕 B. 51〔4-5〕 C. 51〔4±5〕 D. 51〔5-4〕二、填空题： 6．cos(π-x)=23，x ∈〔-π，π〕，那么x 的值为 ． 7．tanα=m ，那么=+-+++)cos(-sin()cos(3sin(απα）απ）απ ．8．|sinα|=sin 〔-π+α〕，那么α的取值范围是 ． 三、解答题： 9．)cos(·3sin()cos()n(s 2sin(απα）παπα）π----+-απi ．10．：sin 〔x+6π〕=41，求sin 〔)67x +π+cos 2〔65π-x 〕的值．11． 求以下三角函数值： 〔1〕sin 3π7；〔2〕cos 4π17；〔3〕tan 〔－6π23〕；12． 求以下三角函数值：〔1〕sin3π4·cos 6π25·tan 4π5； 〔2〕sin ［〔2n +1〕π－3π2］.13．设f 〔θ〕=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+，求f 〔3π〕的值.参考答案21．C 2．A 3．C 4．C 5．A 6．±65π7．11-+m m 8．[(2k-1) π,2k π]9．原式=)cos (·sin()cos()n s (sin αα）παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sinα 10．161111．解：〔1〕sin 3π7=sin 〔2π+3π〕=sin 3π=23.〔2〕cos4π17=cos 〔4π+4π〕=cos 4π=22.〔3〕tan 〔－6π23〕=cos 〔－4π+6π〕=cos 6π=23.〔4〕sin 〔－765°〕=sin ［360°×〔－2〕－45°］=sin 〔－45°〕=－sin45°=－22. 注：利用公式〔1〕、公式〔2〕可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数，从而求值.12．解：〔1〕sin 3π4·cos 6π25·tan 4π5=sin 〔π+3π〕·cos 〔4π+6π〕·tan 〔π+4π〕 =〔－sin3π〕·cos 6π·tan 4π=〔－23〕·23·1=－43.〔2〕sin ［〔2n +1〕π－3π2］=sin 〔π－3π2〕=sin 3π=23.13．解：f 〔θ〕=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++---=θθθθθcos cos 22)1(cos cos )1(cos 223++---=θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-＝cos θ－1， ∴f 〔3π〕=cos 3π－1=21－1=－21.。

[基础巩固]1．已知sin(π－α)＝13，则sin(α－2021π)的值为( ) A ．223B ．－223C ．13D ．－13解析 由sin(π－α)＝sin α得sin α＝13， 所以sin(α－2021π)＝sin[(α－π)－2020π]＝sin(α－π)＝－sin(π－α)＝－sin α＝－13. 答案 D2．若sin(－110°)＝a ，则tan 70°等于( )A ．a 1－a 2 B ．－a 1－a 2 C.a 1＋a 2D ．－a 1＋a 2 解析 ∵sin(－110°)＝－sin 110°＝－sin(180°－70°)＝－sin 70°＝a ，∴sin 70°＝－a ，∴cos 70°＝1－(－a )2＝1－a 2，∴tan 70°＝sin 70°cos 70°＝－a 1－a 2. 答案 B3．若tan(5π＋α)＝m (m ≠±1)，则sin (α－3π)＋cos (π－α)sin (－α)－cos (π＋α)的值为( ) A ．m ＋1m －1B ．m －1m ＋1C ．－1D ．1解析 ∵tan(5π＋α)＝tan α＝m ，∴原式＝sin α＋cos αsin α－cos α＝tan α＋1tan α－1＝m ＋1m －1. 答案 A4．若P (－4,3)是角α终边上一点，则cos (α－3π)·tan (α－2π)sin 2(π－α)的值为________．解析 由题意知sin α＝35，原式＝(－cos α)·tan αsin 2α＝－sin αsin 2α＝－1sin α＝－53. 答案 －535.cos (－585°)sin 495°＋sin (－570°)的值是________． 解析 原式＝cos (360°＋225°)sin (360°＋135°)－sin (360°＋210°)＝cos 225°sin 135°－sin 210° ＝cos (180°＋45°)sin (180°－45°)－sin (180°＋30°)＝－cos 45°sin 45°＋sin 30°＝－2222＋12＝2－2. 答案 2－2 6．化简下列各式：(1)sin ⎝⎛⎭⎫－193πcos 76π； (2)sin(－960°)cos 1470°－cos(－240°)sin(－210°)．解析 (1)sin ⎝⎛⎭⎫－193πcos 76π ＝－sin ⎝⎛⎭⎫6π＋π3cos ⎝⎛⎭⎫π＋π6 ＝sin π3cos π6＝34. (2)sin(－960°)cos 1470°－cos(－240°)sin(－210°)＝－sin(180°＋60°＋2×360°)cos(30°＋4×360°)＋cos(180°＋60°)sin(180°＋30°) ＝sin 60°cos 30°＋cos 60°sin 30°＝1.[能力提升]7．(多选)已知角α和β的终边关于x 轴对称，则下列各式不正确的是( )A ．sin α＝sin βB ．sin(α－2π)＝sin βC ．cos α＝cos βD ．cos(2π－α)＝－cos β解析 由角α和β的终边关于x 轴对称，可知β＝－α＋2k π(k ∈Z )，故cos α＝cos β. 答案 ABD8．若cos(π＋α)＝－12，32π<α<2π，则sin(α－2π)＝____________ . 解析 由cos(π＋α)＝－12，得cos α＝12， 故sin(α－2π)＝sin α＝－1－cos 2α ＝－ 1－⎝⎛⎭⎫122＝－32(α为第四象限角)． 答案 －32 9．已知a ＝tan ⎝⎛⎭⎫－7π6，b ＝cos 23π4，c ＝sin ⎝⎛⎭⎫－33π4，则a ，b ，c 的大小关系是________． 解析 a ＝－tan 7π6＝－tan π6＝－33， b ＝cos ⎝⎛⎭⎫6π－π4＝cos π4＝22， c ＝－sin 33π4＝－sin π4＝－22， ∴b >a >c .答案 b >a >c 10．若cos(α－π)＝－23，求： sin (α－2π)＋sin (－α－3π)cos (α－3π)cos (π－α)－cos (－π－α)cos (α－4π)的值． 解析 原式＝－sin (2π－α)－sin (3π＋α)cos (3π－α)－cos α－(－cos α)cos α＝sin α－sin αcos α－cos α＋cos 2α＝sin α(1－cos α)－cos α(1－cos α)＝－tan α. ∵cos(α－π)＝cos(π－α)＝－cos α＝－23， ∴cos α＝23. ∴α为第一象限角或第四象限角．当α为第一象限角时，cos α＝23， sin α＝ 1－cos 2α＝53，∴tan α＝sin αcos α＝52， ∴原式＝－52. 当α为第四象限角时，cos α＝23，sin α＝－ 1－cos 2α＝－53， ∴tan α＝sin αcos α＝－52，∴原式＝52. 综上，原式＝±52. [探索创新]11．在△ABC 中，若sin(2π－A )＝－2sin(π－B )，3cos A ＝－2cos(π－B )，求△ABC 的三个内角．解析 由条件得sin A ＝2sin B ，3cos A ＝2cos B ，平方相加得2cos 2A ＝1，cos A ＝±22， 又∵A ∈(0，π)，∴A ＝π4或34π. 当A ＝34π时，cos B ＝－32<0， ∴B ∈⎝⎛⎭⎫π2，π，∴A ，B 均为钝角，不合题意，舍去．∴A ＝π4，cos B ＝32， ∴B ＝π6，∴C ＝712π. 综上所述，A ＝π4，B ＝π6，C ＝712π.。

高三数学诱导公式试题答案及解析1.化简=()A．-2B．-C．-1D．1【答案】C【解析】===-1.2.已知，且，则（）A．B．C．D．【答案】【解析】.又因为，所以为三象限的角，.选B.【考点】三角函数的基本计算.3.在中,,,则的面积为．【答案】或；【解析】解三角形问题，往往需要利用对角进行消元.因为所以或或，所以的面积为或.【考点】诱导公式4.已知，，则= ．【答案】【解析】由，得从而所以解决三角函数给值求值问题，关键从角的关系上进行分析.【考点】三角函数给值求值.5.已知,,则 .【答案】【解析】，又，则【考点】三角函数运算.6.在中，角A、B、C的对边分别为a、b、c，且角A、B、C成等差教列．(I)若，求边c的值；(II)设，求的最大值．【答案】（Ⅰ）.（Ⅱ）.【解析】（Ⅰ）由角成等差数列，及，首先得到.进一步应用余弦定理即得所求.（Ⅱ）根据，可化简得到根据,即可得到时，有最大值.试题解析：（Ⅰ）因为角成等差数列，所以，因为，所以. 2分因为，，,所以.所以或(舍去)． 6分（Ⅱ）因为，所以9分因为，所以,所以当，即时，有最大值. 12分【考点】等差数列，和差倍半的三角函数，，三角函数的性质，余弦定理的应用.7.已知向量，，(Ⅰ)若，求的值；(Ⅱ)在中，角的对边分别是，且满足，求函数的取值范围．【答案】（1）；（2）.【解析】本题主要考查两角和与差的正弦公式、二倍角公式、余弦定理、三角函数的值域等基础知识，考查运用三角公式进行三角变换的能力和基本的运算能力.第一问，利用向量的数量积将坐标代入得表达式，利用倍角公式、两角和的正弦公式化简表达式，因为，所以得到，而所求中的角是的2倍，利用二倍角公式计算；第二问，利用余弦定理将已知转化，得到，得到，得到角的范围，代入到中求值域.试题解析：（Ⅰ）∵，而，∴，∴，（Ⅱ）∵，∴，即，∴，又∵，∴，又∵，∴，∴.【考点】1.向量的数量积；2.倍角公式；3.两角和与差的正弦公式；4.余弦公式；5.三角函数的值域.8.已知，，则的值是( )A．B．C．D．1【答案】C【解析】∵,∴，又∵，∴，∴.【考点】1.诱导公式；2.平方关系；3.两角和与差的正弦公式.9.已知向量，，（1）若，求向量、的夹角；（2）当时，求函数的最大值.【答案】（1）向量与的夹角为；（2）函数在区间的最大值为.【解析】（1）将代入向量的坐标，再利用向量的数量积计算）向量与的夹角；（2）先根据向量的数量积求出函数的解析式，并化简为，计算在区间的取值范围，然后结合正弦曲线确定函数的最大值.试题解析：（1）当时，，，，所以、的夹角为；（2），，，，当，即.时，.【考点】1.平面向量的数量积；2.二倍角公式；3.辅助角公式；4.三角函数的最值10.已知向量函数.（1）求函数的最小正周期及单调递减区间；（2）在锐角三角形ABC中，的对边分别是，且满足求的取值范围.【答案】（1），；（2）【解析】（1）首先利用向量的坐标运算和两角和差公式求出函数的表达式，然后再根据三角函数的周期公式求出周期，由正弦函数的单调性可得，解出x，即得所求的单调减区间，.（2）利用正弦公式把已知等式转化为角的三角函数式，再利用两角和差公式，把和角展开，整理可得sinC=2cosAsinC，即1=2cosA.得，在根据三角形的内角和定理和B是锐角，求出角B的取值范围为，即，可得，所以=.试题解析：解：（1） 3分函数的最小正周期为T 4分函数的单调递减区间为，。

三角函数的诱导公式（二）[学习目标] 1.掌握诱导公式五、六的推导 ，并能应用解决简单的求值、化简与证明问题.2.对诱导公式一至六，能作综合归纳，体会六组公式的共性与个性，培养由特殊到一般的数学推理意识和能力.3.继续体会知识的“发生”、“发现”过程，培养研究问题、发现问题、解决问题的能力．知识点一 诱导公式五～六(1)公式五：sin ⎝⎛⎭⎫π2－α＝cos α；cos ⎝⎛⎭⎫π2－α＝sin α. 以－α替代公式五中的α，可得公式六．(2)公式六：sin ⎝⎛⎭⎫π2＋α＝cos α；cos ⎝⎛⎭⎫π2＋α＝－sin α. 思考1 根据任意角α与π2－α的终边关于直线y ＝x 对称，推导诱导公式五．思考2 根据π2＋α＝π－(π2－α)这一等式，利用诱导公式四和诱导公式五推导诱导公式六．知识点二 诱导公式的理解、记忆与灵活应用公式一～四归纳：α＋2k π(k ∈Z )，－α，π±α的三角函数值，等于角α的同名三角函数值，前面加上一个把α看成锐角时原函数值的符号，简记为：“函数名不变，符号看象限”． 公式五～六归纳：π2±α的正弦(余弦)函数值，分别等于α的余弦(正弦)函数值，前面加上一个把α看成锐角时原函数值的符号，简记为：“函数名改变，符号看象限”或“正变余、余变正、符号象限定”．六组诱导公式可以统一概括为“k ·π2±α(k ∈Z )”的诱导公式．当k 为偶数时，函数名不改变；当k 为奇数时，函数名改变；前面加一个把α视为锐角时原函数值的符号，记忆口诀为“奇变偶不变，符号看象限”．思考 请你根据上述规律，完成下列等式． sin(32π－α)＝－cos α，cos(32π－α)＝－sin α sin(32π＋α)＝－cos α，cos(32π＋α)＝sin α.题型一 利用诱导公式求值例1 已知cos ⎝⎛⎭⎫α＋π6＝35，π2≤α≤3π2，求sin ⎝⎛⎭⎫α＋2π3的值． 解 ∵α＋2π3＝⎝⎛⎭⎫α＋π6＋π2， ∴sin(α＋2π3)＝sin ⎣⎡⎦⎤⎝⎛⎭⎫α＋π6＋π2＝cos ⎝⎛⎭⎫α＋π6＝35.跟踪训练1 已知sin ⎝⎛⎭⎫π6＋α＝33，求cos ⎝⎛⎭⎫α－π3的值． 解 ∵cos ⎝⎛⎭⎫α－π3＝cos ⎝⎛⎭⎫π3－α＝cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫π6＋α ＝sin ⎝⎛⎭⎫π6＋α＝33.题型二 利用诱导公式证明恒等式例2 求证：tan (2π－α)sin (－2π－α)cos (6π－α)sin ⎝⎛⎭⎫α＋3π2cos ⎝⎛⎭⎫α＋3π2＝－tan α.证明 左边＝tan (－α)·sin (－α)·cos (－α)sin ⎣⎡⎦⎤2π－⎝⎛⎭⎫π2－α·cos ⎣⎡⎦⎤2π－⎝⎛⎭⎫π2－α＝(－tan α)·(－sin α)·cos αsin ⎣⎡⎦⎤－⎝⎛⎭⎫π2－αcos ⎣⎡⎦⎤－⎝⎛⎭⎫π2－α＝sin 2α－sin ⎝⎛⎭⎫π2－αcos ⎝⎛⎭⎫π2－α ＝sin 2α－cos α·sin α＝－sin αcos α＝－tan α＝右边．∴原等式成立．跟踪训练2 求证：2sin ⎝⎛⎭⎫θ－3π2cos ⎝⎛⎭⎫θ＋π2－11－2sin 2 (π＋θ)＝tan (9π＋θ)＋1tan (π＋θ)－1. 证明 左边＝－2sin ⎝⎛⎭⎫3π2－θ·(－sin θ)－11－2sin 2θ＝2sin ⎣⎡⎦⎤π＋⎝⎛⎭⎫π2－θsin θ－11－2sin 2θ＝－2sin ⎝⎛⎭⎫π2－θsin θ－11－2sin 2θ＝－2cos θsin θ－1cos 2θ＋sin 2θ－2sin 2θ ＝(sin θ＋cos θ)2sin 2θ－cos 2θ＝sin θ＋cos θsin θ－cos θ. 右边＝tan θ＋1tan θ－1＝sin θ＋cos θsin θ－cos θ.∴左边＝右边，故原等式成立． 题型三 诱导公式的综合应用例3 已知f (α)＝sin (α－3π)cos (2π－α)sin ⎝⎛⎭⎫－α＋3π2cos (－π－α)sin (－π－α).(1)化简f (α)；(2)若α是第三象限的角，且cos ⎝⎛⎭⎫α－3π2＝15，求f (α)的值； (3)若α＝－31π3，求f (α)的值．解 (1)f (α)＝(－sin α)·cos α·(－cos α)(－cos α)sin α＝－cos α.(2)∵cos ⎝⎛⎭⎫α－3π2＝－sin α＝15，∴sin α＝－15， 又α是第三象限的角， ∴cos α＝－1－⎝⎛⎭⎫－152＝－265，∴f (α)＝265. (3)f ⎝⎛⎭⎫－31π3＝－cos ⎝⎛⎭⎫－31π3＝－cos ⎝⎛⎭⎫－6×2π＋5π3 ＝－cos5π3＝－cos π3＝－12. 跟踪训练3 已知cos(α－75°)＝－13，且α为第四象限角，求sin(105°＋α)的值．解 ∵cos(α－75°)＝－13<0，且α为第四象限角，∴α－75°是第三象限角．∴sin(α－75°)＝－1－cos 2(α－75°) ＝－1－－132＝－223.∴sin(105°＋α)＝sin[180°＋(α－75°)] ＝－sin(α－75°)＝223.诱导公式的应用例4 已知cos ⎝⎛⎭⎫π2＋α＝2sin ⎝⎛⎭⎫α－π2， 求sin 3(π－α)＋cos (α＋π)5cos ⎝⎛⎭⎫5π2－α＋3sin ⎝⎛⎭⎫7π2－α的值．解 ∵cos ⎝⎛⎭⎫π2＋α＝2sin ⎝⎛⎭⎫α－π2， －sin α＝－2sin(π2－α)，∴sin α＝2cos α，∴tan α＝2. ∴sin 3(π－α)＋cos (α＋π)5cos ⎝⎛⎭⎫5π2－α＋3sin ⎝⎛⎭⎫7π2－α＝sin 3α－cos α5cos (π2－α)－3sin ⎝⎛⎭⎫π2＋α＝sin 3α－cos α5sin α－3cos α＝sin 2α·tan α－15tan α－3＝2sin 2α－110－3＝2sin 2α－17＝2sin 2α－(sin 2α＋cos 2α)7(sin 2α＋cos 2α)＝sin 2α－cos 2α7(sin 2α＋cos 2α) ＝tan 2α－17(tan 2α＋1) ＝4－17×(4＋1)＝335.1．若sin α＝12，则cos(π2＋α)的值为( )A.12B.32 C ．－12 D ．－32 2．已知sin ⎝⎛⎭⎫α－π6＝13，则cos ⎝⎛⎭⎫α＋π3的值为( ) A ．－233 B.233 C.13 D ．－133．代数式sin 2(A ＋45°)＋sin 2(A －45°)的化简结果是 ． 4．已知sin(π＋α)＝－13.计算：(1)cos ⎝⎛⎭⎫α－3π2； (2)sin ⎝⎛⎭⎫π2＋α； (3)tan(5π－α)．5．已知sin(5π－θ)＋sin ⎝⎛⎭⎫52π－θ＝72，求sin 4⎝⎛⎭⎫π2－θ＋cos 4⎝⎛⎭⎫32π＋θ的值．一、选择题1．已知sin(5π2＋α)＝15，那么cos α等于( )A ．－25B ．－15 C.15 D.252．若sin(3π＋α)＝－12，则cos(7π2－α)等于( )A ．－12 B.12 C.32 D ．－323．已知sin ⎝⎛⎭⎫α－π4＝13，则cos ⎝⎛⎭⎫π4＋α的值等于( ) A ．－13 B.13 C ．－223 D.2234．若sin(π＋α)＋cos ⎝⎛⎭⎫π2＋α＝－m ，则cos ⎝⎛⎭⎫32π－α＋2sin(2π－α)的值为( ) A ．－2m 3 B.2m 3 C ．－3m 2 D.3m25．已知cos(π2＋φ)＝32，且|φ|<π2，则tan φ等于( )A ．－33 B.33C ．－ 3 D. 3 6．已知cos(75°＋α)＝13，则sin(α－15°)＋cos(105°－α)的值是( )A.13B.23 C ．－13 D ．－23 二、填空题7．式子cos 2(π4－α)＋cos 2(π4＋α)＝ .8．若sin(α＋π12)＝13，则cos(α＋7π12)＝ .9．已知f (α)＝tan (π－α)·cos (2π－α)·sin (π2＋α)cos (－α－π)，化简f (α)＝ .10．已知tan(3π＋α)＝2，则sin (α－3π)＋cos (π－α)＋sin (π2－α)－2cos (π2＋α)－sin (－α)＋cos (π＋α)＝ .三、解答题11．已知角α终边经过点P (－4,3)，求 cos (π2＋α)sin (－π－α)cos (11π2－α)sin (9π2＋α)的值．12．已知sin(θ－32π)＋cos(32π＋θ)＝35，求sin 3(π2＋θ)－cos 3(3π2－θ)．当堂检测答案1．答案 C解析 ∵sin α＝12，∴cos(π2＋α)＝－sin α＝－12.2．答案 D解析 cos ⎝⎛⎭⎫α＋π3＝cos ⎣⎡⎦⎤π2＋⎝⎛⎭⎫α－π6＝－sin ⎝⎛⎭⎫α－π6＝－13. 3．答案 1解析 原式＝sin 2(A ＋45°)＋sin 2(45°－A ) ＝sin 2(A ＋45°)＋cos 2(A ＋45°)＝1.4．解 ∵sin(π＋α)＝－sin α＝－13，∴sin α＝13.(1)cos ⎝⎛⎭⎫α－3π2＝cos ⎝⎛⎭⎫3π2－α＝－sin α＝－13. (2)sin ⎝⎛⎭⎫π2＋α＝cos α，cos 2α＝1－sin 2 α＝1－19＝89. ∵sin α＝13，∴α为第一或第二象限角．①当α为第一象限角时，sin ⎝⎛⎭⎫π2＋α＝cos α＝223. ②当α为第二象限角时，sin ⎝⎛⎭⎫π2＋α＝cos α＝－223. (3)tan(5π－α)＝tan(π－α)＝－tan α， ∵sin α＝13，∴α为第一或第二象限角．①当α为第一象限角时，cos α＝223，∴tan α＝24，∴tan(5π－α)＝－tan α＝－24. ②当α为第二象限角时，cos α＝－223，tan α＝－24，∴tan(5π－α)＝－tan α＝24.5．解 ∵sin(5π－θ)＋sin ⎝⎛⎭⎫52π－θ ＝sin(π－θ)＋sin ⎝⎛⎭⎫π2－θ ＝sin θ＋cos θ＝72， ∴sin θcos θ＝12[(sin θ＋cos θ)2－1]＝12⎣⎡⎦⎤⎝⎛⎭⎫722－1＝38，∴sin 4⎝⎛⎭⎫π2－θ＋cos 4⎝⎛⎭⎫32π＋θ＝cos 4θ＋sin 4θ ＝(sin 2θ＋cos 2θ)2－2sin 2θcos 2θ ＝1－2×⎝⎛⎭⎫382＝2332.课时精练答案一、选择题 1．答案 C解析 sin(5π2＋α)＝cos α，故cos α＝15，故选C.2．答案 A解析 ∵sin(3π＋α)＝－sin α，∴sin α＝12，∴cos(7π2－α)＝cos(3π2－α)＝－cos(π2－α)＝－sin α＝－12.3．答案 A解析 cos ⎝⎛⎭⎫π4＋α＝sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4＋α ＝sin ⎝⎛⎭⎫π4－α＝－sin ⎝⎛⎭⎫α－π4＝－13.4．答案 C解析 ∵sin(π＋α)＋cos ⎝⎛⎭⎫π2＋α＝－sin α－sin α＝－m ， ∴sin α＝m2.故cos ⎝⎛⎭⎫32π－α＋2sin(2π－α)＝－sin α－2sin α ＝－3sin α＝－32m .5．答案 C解析 由cos(π2＋φ)＝－sin φ＝32，得sin φ＝－32，又∵|φ|<π2，∴φ＝－π3，∴tan φ＝－ 3.6．答案 D解析 sin(α－15°)＋cos(105°－α)＝sin [(75°＋α)－90°]＋cos [180°－(75°＋α)] ＝－sin [90°－(75°＋α)]－cos(75°＋α) ＝－cos(75°＋α)－cos(75°＋α) ＝－2cos(75°＋α)＝－23.二、填空题 7．答案 1解析 原式＝sin 2[π2－(π4－α)]＋cos 2(π4＋α)＝sin 2(π4＋α)＋cos 2(π4＋α)＝1.8．答案 －13解析 cos(α＋7π12)＝cos[π2＋(α＋π12)]＝－sin(α＋π12)＝－13.9．答案 sin α解析 f (α)＝tan (π－α)·cos (2π－α)·sin (π2＋α)cos (－α－π)＝－tan α·cos α·cos α－cos α＝sin α.10．答案 2解析 ∵tan(3π＋α)＝2，∴tan α＝2， ∴原式＝sin αsin α－cos α＝tan αtan α－1＝22－1＝2. 三、解答题11．解 ∵角α终边经过点P (－4,3)， ∴tan α＝y x ＝－34，11 ∴cos (π2＋α)sin (－π－α)cos (11π2－α)sin (9π2＋α)＝－sin α·sin α－sin α·cos α＝tan α ＝－34.12．解 ∵sin(θ－32π)＋cos(32π＋θ)＝－sin(32π－θ)－cos(π2＋θ)＝sin(π2－θ)＋sin θ＝sin θ＋cos θ＝35.∴sin θcos θ＝12[(sin θ＋cos θ)2－1]＝12(925－1)＝－825.∴sin 3(π2＋θ)－cos 3(3π2－θ)＝cos 3θ＋cos 3(π2－θ)＝cos 3θ＋sin 3θ＝(sin θ＋cos θ)(sin 2θ－sin θcos θ＋cos 2θ) ＝35×[1－(－825)]＝99125.。

三角函数的诱导公式(一)【学问梳理】1．诱导公式二(1)角π＋α与角α的终边关于原点对称． 如图所示． (2)公式：sin(π＋α)＝－sin_α.cos(π＋α)＝－cos_α.tan(π＋α)＝tan_α.2．诱导公式三(1)角－α与角α的终边关于x 轴对称．如图所示．(2)公式：sin(－α)＝－sin_α.cos(－α)＝cos_α.tan(－α)＝－tan_α.3．诱导公式四(1)角π－α与角α的终边关于y 轴对称．如图所示．(2)公式：sin(π－α)＝sin_α.cos(π－α)＝－cos_α.tan(π－α)＝－tan_α.【常考题型】题型一、给角求值问题【例1】 求下列三角函数值：(1)sin(－1 200°)；(2)tan 945°；(3)cos 119π6. [解] (1)sin(－1 200°)＝－sin 1 200°＝－sin(3×360°＋120°)＝－sin 120°＝－sin(180°－60°)＝－sin 60°＝－32； (2)tan 945°＝tan(2×360°＋225°)＝tan 225°＝tan(180°＋45°)＝tan 45°＝1；(3)cos 119π6＝cos ⎝⎛⎭⎫20π－π6＝cos ⎝⎛⎭⎫－π6＝cos π6＝32.【类题通法】利用诱导公式解决给角求值问题的步骤【对点训练】求sin 585°cos 1 290°＋cos(－30°)sin 210°＋tan 135°的值．解：sin 585°cos 1 290°＋cos(－30°)sin 210°＋tan 135°＝sin(360°＋225°)cos(3×360°＋210)＋cos 30°sin 210°＋tan(180°－45°)＝sin 225°cos 210°＋cos 30°sin 210°－tan 45°＝sin(180°＋45°)cos(180°＋30°)＋cos 30°·sin(180°＋30°)－tan 45°＝sin 45°cos 30°－cos 30°sin 30°－tan 45°＝22×32－32×12－1＝6－3－44. 题型二、化简求值问题【例2】 (1)化简：cos (－α)tan (7π＋α)sin (π－α)＝________； (2)化简sin (1 440°＋α)·cos (α－1 080°)cos (－180°－α)·sin (－α－180°). (1)[解析]cos (－α)tan (7π＋α)sin (π－α)＝cos αtan (π＋α)sin α＝cos α·tan αsin α＝sin αsin α＝1. [答案] 1(2)[解] 原式＝sin (4×360°＋α)·cos (3×360°－α)cos (180°＋α)·[－sin (180°＋α)]＝sin α·cos (－α)(－cos α)·sin α＝cos α－cos α＝－1. 【类题通法】利用诱导公式一～四化简应留意的问题(1)利用诱导公式主要是进行角的转化，从而达到统一角的目的；(2)化简时函数名没有变更，但肯定要留意函数的符号有没有变更；(3)同时有切(正切)与弦(正弦、余弦)的式子化简，一般采纳切化弦，有时也将弦化切．【对点训练】化简：tan (2π－θ)sin (2π－θ)cos (6π－θ)(－cos θ)sin (5π＋θ). 解：原式＝tan (－θ)sin (－θ)cos (－θ)(－cos θ)sin (π＋θ)＝tan θsin θcos θcos θsin θ＝tan θ. 题型三、给角（或式）求值问题【例3】 (1)已知sin β＝13，cos(α＋β)＝－1，则sin(α＋2β)的值为( ) A ．1 B ．－1C.13 D ．－13 (2)已知cos(α－55°)＝－13，且α为第四象限角，求sin(α＋125°)的值． (1)[解析] ∵cos(α＋β)＝－1，∴α＋β＝π＋2k π，k ∈Z ，∴sin(α＋2β)＝sin[(α＋β)＋β]＝sin(π＋β)＝－sin β＝－13. [答案] D(2)[解] ∵cos(α－55°)＝－13<0，且α是第四象限角． ∴α－55°是第三象限角．sin(α－55°)＝－1－cos 2(α－55°)＝－223. ∵α＋125°＝180°＋(α－55°)，∴sin(α＋125°)＝sin[180°＋(α－55°)]＝－sin(α－55°)＝223. 【类题通法】解决条件求值问题的策略(1)解决条件求值问题，首先要细致视察条件与所求式之间的角、函数名称及有关运算之间的差异及联系．(2)可以将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化．【对点训练】已知sin(π＋α)＝－13，求cos(5π＋α)的值． 解：由诱导公式得，sin(π＋α)＝－sin α，所以sin α＝13，所以α是第一象限或其次象限角． 当α是第一象限角时，cos α＝ 1－sin 2α＝223， 此时，cos(5π＋α)＝cos(π＋α)＝－cos α＝－223. 当α是其次象限角时，cos α＝－1－sin 2α＝－223， 此时，cos(5π＋α)＝cos(π＋α)＝－cos α＝223. 【练习反馈】1.如图所示，角θ的终边与单位圆交于点P ⎝⎛⎭⎫－55，255，则cos(π－θ)的值为( )A ．－255B ．－55C.55D.255解析：选C ∵r ＝1，∴cos θ＝－55， ∴cos(π－θ)＝－cos θ＝55. 2．已知sin(π＋α)＝45，且α是第四象限角，则cos(α－2π)的值是( ) A ．－35B.35 C ．±35 D.45解析：选B sin α＝－45，又α是第四象限角， ∴cos(α－2π)＝cos α＝1－sin 2α＝35. 3．设tan(5π＋α)＝m ，则sin (α－3π)＋cos (π－α)sin (－α)－cos (π＋α)＝________. 解析：∵tan(5π＋α)＝tan α＝m ，∴原式＝－sin α－cos α－sin α＋cos α＝－tan α－1－tan α＋1＝－m －1－m ＋1＝m ＋1m －1. 答案：m ＋1m －14.cos (－585°)sin 495°＋sin (－570°)的值是________． 解析：原式＝cos (360°＋225°)sin (360°＋135°)－sin (210°＋360°)＝cos 225°sin 135°－sin 210°＝cos (180°＋45°)sin (180°－45°)－sin (180°＋30°)＝－cos 45°sin 45°＋sin 30°＝－2222＋12＝2－2. 答案：2－25．已知cos ⎝⎛⎭⎫π6－α＝33，求cos ⎝⎛⎭⎫α＋5π6的值． 解：cos ⎝⎛⎭⎫π＋5π6＝－cos ⎣⎡⎦⎤π－⎝⎛⎭⎫α＋5π6＝ －cos ⎝⎛⎭⎫π6－α＝－33.。

三角函数诱导公式专项练习学校:_____________________________________考号：___________ 一、单选题1．〔A． B． C． D．2．的值为〔A． B． C ． D．3．已知,则cos〔60°–α的值为A． B．C． D．–4．已知,且,则〔A． B． C． D．5．已知sin<π－α>＝－,且α∈<－,0>,则tan<2π－α>的值为< >A ． B．－ C．± D．6．已知,则=< >A． B． C． D．7．已知,,则〔A ． B． C ． D．8．已知,则〔A． B． - C ． D ． -9．如果,那么A． - B． C． 1 D． -110．已知,则〔A． B． C． D．1 / 1911．化简的值是〔A． B． C． D．12．的值是〔A． B． C． D．13．已知角的终边经过点,则的值等于A． B． C． D．14．已知,则〔A． B． C． D．15．已知的值为〔A． B． C． D．16．已知则〔A． B． C． D．17．已知,且是第四象限角,则的值是< > A． B． C． D．18．已知sin＝,则cos＝< >A． B． C．－ D．－19．已知cos α＝k,k∈R,α∈,则sin<π＋α>＝< >A．－ B．C．± D．－k20．＝< >A． sin 2－cos 2 B． sin 2＋cos 2C．±<sin 2－cos 2> D． cos 2－sin 221．的值为A． B． C． D．22．〔A ． B． C． D ．23．若,,则的值为〔A． B． C． D ．24．已知且,则〔A． B． C． D．25．已知,则< >A． B ． C． D．26．若,且,则〔A． B． C． D．27．已知,则< >A． B ． C ． D．28．已知,则的值为〔A． B． C． D．29．若,,则的值为〔A． B ． C ． D．30．已知,则的大小关系是< > A． B ． C． D．31．A． B． C． D．32．的值等于〔A． B． C． D．33．的值的〔3 / 19A． B． C． D．34．已知,,则等于〔．A． B． C． D．35．已知,则的值为〔A． B． C． D．36．点在直角坐标平面上位于〔A．第一象限 B．第二象限 C．第三象限 D．第四象限37．如果,那么等于〔A． B． C． D．38．已知角的终边过点,若,则实数A． B． C． D．39．A． B． C． D．40．已知,则的值为〔A． B． C． D．参考答案1．D[解析][分析]直接运用诱导公式,转化为特殊角的三角函数值求解。

重点突破：利用诱导公式化简求值姓名：___________班级：___________1、诱导公式主要是用来化简[,2]2ππ内的角，锐角不用化简，超过2π的角先去掉周期后再利用诱导公式。

2、诱导公式的口诀“奇变偶不变，符号看象限”。

“奇变偶不变”针对函数名称而言，先将角度整理为2n πα⨯+的模式，若n 为奇数将函数名称sin 变成cos ，或者cos 变成sin ；若n 为偶数那么函数名称不发生改变。

这里与n 的正负无关。

3、“符号看象限”是针对未化简前的角度，在原函数中的符号。

4、注意在利用诱导公式化简中，角度2n πα⨯+中的α，不管题目有无限制条件都看成锐角，化简完成后在考虑角的范围。

1．如果sin π−α=13，那么sin π+α−cos −α等于（）A.−23B.23 C.D.−2．已知sin (π3−x)=35,则cos (5π6−x)等于（）A.35B.45C.−35D.−453．若sin (π2−α)=cos 2α等于（）A.29B.−29C.13D.−134．若α∈(0,π)，sin (π−α)+cos α=sin α−cos α的值为（）A.B. C.43D.−435．若sin (π6−α)=13，则cos (2π3+2α)的值为（）A.−79B.79 C.13D.−136．已知sin (π2+θ)+3cos (θ−π)=sin (−θ)，则sin θcos θ+cos 2θ=()A.15B.35C.25D.457．已知函数f x =−x 2−2x,x ≥0x 2−2x,x <0，又α,β为锐角三角形两锐角，则（）A.f sin α>f cos βB.f sin α<f cos βC.f sin α>f sin βD.f cos α>f cos β8．已知数列{a n }满足a 1＝1，a 2＝2，a n ＋2＝(1＋cos 22n π)a n ＋sin 22n π，则该数列的前10项和为()A.2101B.1067C.1012D.2012本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

要点导学各个击破利用诱导公式进行化简与求值(1) 已知cos(π+α)=-12,32π<α<2π,求sin(2π-α)的值;(2) 已知12()2-(-)sinsinπθθ++=117,求tan(θ-π)cos(θ-π)的值.[思维引导]将已知条件转化为单角的三角函数,再利用诱导公式求解.[解答](1) 由已知得cos α=1 2.又32π<α<2π,则sin α<0,所以sin(2π-α)=-sin α.(2) 因为12()2-(-)sinsinπθθ++=117,所以1-22sinsinθθ+=117,所以sin θ=-35,所以tan(θ-π)cos(θ-π)=tan θ(-cos θ)=-sin θ=3 5.[精要点评]使用诱导公式求解数学问题时,一要注意函数名是否改变,二要注意是否改变符号.已知f(α)=-(2-)(-3)2()2sin cos tantan sinπαπααπππαα⎛⎫+⎪⎝⎭⎛⎫++⎪⎝⎭.(1) 化简f(α);(2) 若α是第三象限角,且cos3-2πα⎛⎫⎪⎝⎭=15,求f(α)的值.[思维引导]解本题的关键是熟练地应用诱导公式和记住特殊角的三角函数值,特别注意符号以及名称的变化.[解答](1) f(α)=(-)cos cos tantan cosααααα=-cosα.(2) 因为cos3-2πα⎛⎫⎪⎝⎭=-sinα,所以sinα=-15.又α是第三象限角,所以cosα,所以f(α.[精要点评]重视三角函数的“三变”:“三变”是指“变角、变名、变式”.变角为:对角的拆分要尽可能化为同名、同角、特殊角;变名:尽可能减少函数名称;变式:对式子变形一般要尽可能有理化、整式化、降低次数等.在解决求值、化简、证明问题时,一般是观察角度、函数名、所求(或所证明)问题的整体形式中的差异,再选择适当的三角公式恒等变形.(2014·湖南联考)设α是第三象限角,且tan α=2,则-()232sin cossinπαπαπα⎛⎫+⎪⎝⎭⎛⎫+⎪⎝⎭=.[答案][解析]-()232sin cossinπαπαπα⎛⎫+⎪⎝⎭⎛⎫+⎪⎝⎭=·(-)-ocos cosc sααα=cosα,又tanα=2,α是第三象限角,所以cosα含相同变量的复合角与诱导公式的综合已知cos(75°+α)=13,且α是第三象限角,求cos(15°-α)+sin(α-15°)的值.[思维引导]结合诱导公式把cos(15°-α)与sin(α-15°)用条件cos(75°+α)=13分别求出.[解答]因为cos(15°-α)=cos[90°-(75°+α)]=sin(75°+α), 由于α是第三象限角,所以sin(75°+α)<0,所以sin(75°+α.因为sin(α-15°)=sin[-90°+(75°+α)]=-sin[90°-(75°+α)]=-cos(75°+α)=-13,所以cos(15°-α)+sin(α-15°[精要点评]利用诱导公式时,要注意已知角与未知角之间的联系,善于转化.已知sin -6πθ⎛⎫⎪⎝⎭=a,那么cos 2-3πθ⎛⎫ ⎪⎝⎭= . [答案]-a[解析]cos 2-3πθ⎛⎫ ⎪⎝⎭=cos -26ππθ⎡⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦=-sin （6π-θ）=-a. 已知sin 6x π⎛⎫+ ⎪⎝⎭=13,求sin 76x π⎛⎫+ ⎪⎝⎭+cos 25-6x π⎛⎫ ⎪⎝⎭的值.[解答]因为6x π⎛⎫+ ⎪⎝⎭+5-6x π⎛⎫⎪⎝⎭=π, 76π+x=π+6x π⎛⎫+ ⎪⎝⎭, 所以原式=sin 6x ππ⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦+cos 2-6x ππ⎡⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦ =-sin 6x π⎛⎫+ ⎪⎝⎭+2-6cos x π⎡⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦=-13+11-9⎛⎫ ⎪⎝⎭=59.已知sin(3π-αcos 32πβ⎛⎫+⎪⎝⎭αcos(π+β),0<α<π,0<β<π,求α,β的值.[思维引导]求角的大小必须先求出含这个角的某个三角函数的值,再求出这个角的大小.[解答]由已知等式可得sin αsin β,①αβ.②两式平方相加,得sin 2α+3cos 2α=2sin 2β+2cos 2β=2,即sin 2α+3(1-sin 2α)=2,则sin α=.又因为0<α<π,所以sin α,α=4π或34π.当α=4π时,由①②可得sin β=12,cos β,又0<β<π,所以β=6π;当α=34π时,由①②可得sin β=12,cos β,又0<β<π,所以β=56π.故,46παπβ⎧=⎪⎪⎨⎪=⎪⎩或3,45.6παπβ⎧=⎪⎪⎨⎪=⎪⎩ [精要点评]求角的大小时一定要注意角的范围,再结合三角函数值的大小完成.已知sin(θ-3π)=2cos(θ-4π).(1) 求(-)5(2-)32-θ-(-)2sin cossin sinπθπθπθ+⎛⎫⎪⎝⎭的值;(2) 求cos524πθ⎛⎫+⎪⎝⎭的值.[规范答题](1) 因为sin(θ-3π)=2cos(θ-4π), 所以-sin(3π-θ)=2cos(4π-θ),所以sin θ=-2cos θ.(3分)所以原式=5-2sin coscos sinθθθθ++ (5分)=-25-2-2cos coscos cosθθθθ+=-34. (7分)(2) 由(1)可知tan θ=-2,(8分) 所以原式=-cos24πθ⎛⎫+⎪⎝⎭ (9分)=-2-244cos cos sin sinππθθ⎛⎫⎪⎝⎭ (11分)=-222222-2-cos sin sin cos cos sin cos sinθθθθθθθθ⎫⎪++⎝⎭=-2221-2-11tan tantan tanθθθθ⎫⎪++⎝⎭ (13分)×1-4-4-1414⎛⎫⎪++⎝⎭. (14分)1. 计算:sin585°=.[答案][解析]sin585°=sin(360°+225°)=sin(180°+45°)=-sin45°.2. 已知sin 52πα⎛⎫+⎪⎝⎭=15,那么cos α= . [答案]153. (2014·肇庆二模改编)已知α∈0,2π⎛⎫⎪⎝⎭,sin 2πα⎛⎫+ ⎪⎝⎭=35,那么sin(π+α)= . [答案]-45[解析]由sin 2πα⎛⎫+ ⎪⎝⎭=35,得cos α=35,因为α∈0,2π⎛⎫ ⎪⎝⎭,所以sin α=45,sin(π+α)=-sin α=-45.4. 若cos α=13,则(2-)?()·(3-)2cos sin sin tan παπαπαπα+⎛⎫+ ⎪⎝⎭= . [答案]13[解析](2-)?()·(3-)2cos sin sin tan παπααπα+⎛⎫+ ⎪⎝⎭=·(-)·(-)cos sin cos tan αααα=cos α=13.[温馨提醒]趁热打铁,事半功倍.请老师布置同学们完成《配套检测与评估》中的练习(第45-46页).。