2011届强化训练(14)向量

即 B1D⊥EG，B1D⊥EF，因此 B1D⊥平面 EGF. 结合(1)可知平面 EGF∥平面 ABD.
题型二
利用空间向量求线线角、线面角
【例 2】(2010· 课标全国)如图，已知四棱椎 P－ABCD 的底 面为等腰梯形，AB∥CD，AC⊥BD，垂足为 H，PH 是四棱锥的高，E 为 AD 中点． (1)证明：PE⊥BC； (2)若∠APB＝∠ADB＝60° ，求直线 PA 与平面 PEH 所成角的正弦值． 解：以 H 为原点，HA，HB，HP 分别为 x，y，z 轴， 线段 HA 的长为单位长，建立空间直角坐标系如图， 则 A(1,0,0)B(0,1,0)． (1)证明：设 C(m,0,0)， P(0,0，n)(m<0，n>0)，
3．模、夹角和距离公式 (1)设 a＝(a1，a2，a3)，b＝(b1，b2，b3)， 则|a|＝ a· a＝ a2＋a2＋a2， 1 2 3 a1b1＋a2b2＋a3b3 a· b cos 〈a，b〉＝ ＝ 2 . 2 |a||b| a1＋a2＋a2· b2＋b2＋b2 3 1 2 3 (2)距离公式 设 A(x1，y1，z1)，B(x2，y2，z2)， 则 dAB＝ x1－x22＋y1－y22＋z1－z22. (3)平面的法向量 如果表示向量 a 的有向线段所在直线垂直于平面 α，则称这个 向量垂直于平面 α，记作 a⊥α. 如果 a⊥α，那么向量 a 叫做平面 α 的法向量．
(2)在棱 C1D1 上存在点 F，使 B1F∥平面 A1BE. 事实上，如图(b)所示，分别取 C1D1 和 CD 的中点 F，G，连结 EG，BG，CD1，FG.因 A1D1∥B1C1∥BC，且 A1D1＝BC，所以 四边形 A1BCD1 是平行四边形，因此 D1C∥A1B.又 E，G 分别为 D1D，CD 的中点，所以 EG∥D1C，从而 EG∥A1B.这说明 A1，B， G，E 共面．所以 BG⊂平面 A1BE. 因四边形 C1CDD1 与 B1BCC1 皆为正方形，F，G 分别为 C1D1 和 CD 的中点，所以 FG∥C1C∥B1B，且 FG＝C1C＝B1B，因此四边 形 B1BGF 是平行四边形，所以 B1F∥BG.而 B1F⊄平面 A1BE，BG⊂ 平面 A1BE，故 B1F∥平面 A1BE.

y＝1， x＝－1或－3.
∴a＝(－1,1)或(－3,1)． 15．(2009· 朝阳 4 月)在△ABC 中，角 A、B、C 所对的边分别为 a、b、c.若∠B＝45° ，b＝ 2，a＝1， 则∠C 等于________度． 答案：105 asinB 1 解析：由正弦定理得 sinA＝ ＝ ，A＝30° 或 150° (舍去)，则∠C＝105° ，故填 105. b 2 16．已知△ABC 中，角 A、B、C 所对的边分别为 a、b、c.若 a＝1，∠B＝45° ，△ABC 的面积 S＝2， 那么△ABC 的外接圆的直径等于__________． 答案：5 2
1 1 解析：∵S＝ acsinB＝2，∴ ×1×c×sin45° ＝2， 2 2 ∴c＝4 2， ∴b2＝a2＋c2－2accosB＝1＋32－2×1×4 2×cos45° ， ∴b2＝25，b＝5. b 所以△ABC 的外接圆的直径等于 ＝5 2. sinB 三、解答题(本大题共 6 小题，共 70 分，解答应写出文字说明、演算步骤或证明过程。) 17．(本小题满分 10 分)已知|a|＝1，|b|＝ 2. (1)若 a∥b，求 a· b； (2)若 a，b 的夹角为 135° ，求|a＋b|. 解析：(1)∵a∥b， ∴若 a，b 同向，则 a· b＝|a||b|＝ 2； 若 a，b 反向，则 a· b＝－|a||b|＝－ 2. (2)∵a，b 的夹角为 135° ， ∴a· b＝|a||b|cos135° ＝－1， ∴|a＋b|2＝(a＋b)2＝a2＋b2＋2a· b＝1＋2－2＝1， ∴|a＋b|＝1. 18． (2009· 江苏， 15)(本小题满分 12 分)设向量 a＝(4cosα， sinα)， b＝(sinβ， 4cosβ)， c＝(cosβ， －4sinβ)． (1)若 a 与 b－2c 垂直，求 tan(α＋β)的值； (2)求|b＋c|的最大值； (3)若 tanαtanβ＝16.求证 a∥b. 解析：(1)由 a 与 b－2c 垂直 则 a· (b－2c)＝a· b－2a· c＝0， 即 4sin(α＋β)＝8cos(α＋β)，tan(α＋β)＝2. (2)∵b＋c＝(sinβ＋cosβ，4cosβ－4sinβ)， 则|b＋c|2＝sin2β＋2sinβcosβ＋cos2β＋16cos2β－32cosβsinβ＋16sin2β＝17－30sinβcosβ＝17－15sin2β， 最 大值为 32，所以|b＋c|的最大值为 4 2. (3)由 tanαtanβ＝16，得 sinαsinβ＝16cosαcosβ， 即 4cosα· 4cosβ－sinαsinβ＝0，故 a∥b. 19．(2009· 四川，17)(本小题满分 12 分)在△ABC 中，A、B 为锐角，角 A、B、C 所对的边分别为 a、 3 10 b、c，且 cos2A＝ ，sinB＝ . 5 10 (1)求 A＋B 的值； (2)若 a－b＝ 2－1，求 a、b、c 的值． 命题意图：本小题主要考查同角三角函数间的关系、两角和差的三角函数、二倍角公式、正弦定理等 基础知识及基本运算能力． 10 解析：(1)∵A、B 为锐角，sinB＝ ， 10 3 10 ∴cosB＝ 1－sin2B＝ . 10 3 又 cos2A＝1－2sin2A＝ ， 5 5 2 5 ∴sinA＝ ，cosA＝ 1－sin2A＝ . 5 5 ∴cos(A＋B)＝cosAcosB－sinAsinB＝

强化训练14立体几何——大题备考第二次作业1．[2022·广东深圳二模]如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面P AD是正三角形，M是侧棱PD的中点，且AM⊥平面PC D.(1)求证：平面P AD⊥平面ABCD；(2)求AM与平面PBC所成角的正弦值．2．[2022·河北唐山二模]如图，△ABC是边长为43的等边三角形，E，F分别为AB，AC的中点，G是△ABC的中心，以EF为折痕把△AEF折起，使点A到达点P的位置，且PG⊥平面AB C.(1)证明：PB⊥AC；(2)求平面PEF与平面PBF所成二面角的正弦值．3.[2022·山东淄博三模]已知如图，在多面体ABCEF 中，AC ＝BC ＝2，∠ACB ＝120°，D 为AB 的中点，EF ∥CD ，EF ＝1，BF ⊥平面AEF .(1)证明：四边形EFDC 为矩形； (2)当三棱锥A - BEF 体积最大时，求平面AEF 与平面ABE 夹角的余弦值．4．[2022·山东德州二模]《九章算术》是中国古代张苍，耿寿昌所撰写的一部数学专著，是《算经十书》中最重要的一部，成于公元一世纪左右，是当时世界上最简练有效的应用数学专著，它的出现标志着中国古代数学形成了完整的体系．在《九章算术·商功》篇中提到“阳马”这一几何体，是指底面为矩形，有一条侧棱垂直于底面的四棱锥，现有“阳马”P - ABCD ，底面为边长为2的正方形，侧棱P A ⊥平面ABCD ，P A ＝2，E 、F 为边BC 、CD 上的点，CE → ＝λCB → ，CF → ＝λCD →，点M 为AD 的中点．(1)若λ＝12，证明：平面PBM ⊥平面P AF ；(2)是否存在实数λ，使二面角P - EF - A 的大小为45°？如果不存在，请说明理由；如果存在，求此时直线BM 与平面PEF 所成角的正弦值．强化训练15 统计、统计案例与概率——小题备考一、单项选择题(本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一个是符合题目要求的)1．[2022·山东潍坊三模]某省新高考改革方案推行“3＋1＋2”模式，要求学生在语数外3门全国统考科目之外，在历史和物理2门科目中必选且只选1门，再从化学、生物、地理、政治4门科目中任选2门．某学生各门功课均比较优异，因此决定按方案要求任意选择，则该生选考物理、生物和政治这3门科目的概率为( )A ．12B ．13C ．16D ．1122．[2022·山东威海三模]甲、乙两人相约在某健身房锻炼身体，他们分别在两个网站查看这家健身房的评价．甲在网站A 查到共有840人参与评价，其中好评率为95%，乙在网站B 查到共有1 260人参与评价，其中好评率为85%.综合考虑这两个网站的信息，则这家健身房的总好评率为( )A ．88%B ．89%C ．91%D ．92% 3．[2022·辽宁葫芦岛一模]有一组样本数据x 1，x 2，…，x n ，由这组数据得到新样本数据，y 1，y 2，…，y n ，其中y i ＝x i ＋c (i ＝1，2，…，n )c 为非零常数，则( )A ．两组样本数据的样本方差相同B ．两组样本数据的样本众数相同C ．两组样本数据的样本平均数相同D ．两组样本数据的样本中位数相同 4．[2022·辽宁辽阳二模]为了解某地高三学生的期末语文考试成绩，研究人员随机抽取了100名学生对其进行调查，根据所得数据制成如图所示的频率分布直方图，已知不低于90分为及格，则这100名学生期末语文成绩的及格率为( )A ．40%B ．50%C ．60%D ．65% 5．[2022·河北保定二模]某研究机构为了了解初中生语文成绩的平均分y (单位：分)与每周课外阅读时间x (单位：分钟)是否存在线性关系，搜集了100组数据(∑i ＝1100x i ＝3 000，∑i ＝1100y i ＝7 900)，并据此求得y 关于x 的回归直线方程为y ＝0.3x ＋a.若一位初中生的每周课外阅读时间为2个小时，则可估计她的语文成绩的平均分为()A ．70.6B ．100C ．106D ．110 6．[2022·山东青岛一模]甲乙两选手进行象棋比赛，已知每局比赛甲获胜的概率为0.6，乙获胜的概率为0.4，若采用三局二胜制，则甲最终获胜的概率为( )A ．0.36B ．0.352C ．0.288D ．0.648 7．[2022·湖北武汉模拟]通过随机询问某中学110名中学生是否爱好跳绳，得到如下列联表：已知χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），则以下结论正确的是(A .根据小概率值α＝0.001的独立性检验，爱好跳绳与性别无关B .根据小概率值α＝0.001的独立性检验，爱好跳绳与性别无关，这个结论犯错误的概率不超过0.001C .根据小概率值α＝0.01的独立性检验，有99%以上的把握认为“爱好跳绳与性别无关”D .根据小概率值α＝0.01的独立性检验，在犯错误的概率不超过1%的前提下，认为“爱好跳绳与性别无关”8．[2022·湖南长沙模拟]第24届冬季奥林匹克运动会于2022年2月4日至20日在北京和张家口举行．某特许产品100件，其中一等品98件，二等品2件，从中不放回的依次抽取10件产品(每次抽取1件).甲表示事件“第一次取出的是一等品”，乙表示事件“第二次取出的是二等品”，记取出的二等品件数为X ，则下列结论正确的是( )A .甲与乙相互独立B ．甲与乙互斥C .X ～B(10，0.02)D ．E(X)＝0.2二、多项选择题(本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多个符合题目要求，全部选对得5分，部分选对得2分，选错或多选得0分)9．[2022·辽宁大连二模]为评估一种农作物的种植效果，选了10块地作试验田．这10块地的亩产量(单位：kg )互不相等，且从小到大分别为x 1，x 2，…，x 10，则下列说法正确的有( )A .x 1，x 2，…，x 10的平均数可以用来评估这种农作物亩产量稳定程度B .x 1，x 2，…，x 10的标准差可以用来评估这种农作物亩产量稳定程度C .x 10－x 1可以用来评估这种农作物亩产量稳定程度D .x 1，x 2，…，x 10的中位数为x 5 10．[2022·山东枣庄三模]下列结论正确的有( ) A .若随机变量ξ，η满足η＝2ξ＋1，则D(η)＝2D(ξ)＋1B .若随机变量ξ～N(3，σ2)，且P(ξ<6)＝0.84，则P(3<ξ<6)＝0.34C .若样本数据(x i ，y i )(i ＝1，2，3，…，n)线性相关，则用最小二乘估计得到的回归直线经过该组数据的中心点(x － ，y －)D .根据分类变量X 与Y 的成对样本数据，计算得到χ2＝4.712.依据α＝0.05的独立性检验(x 0.05＝3.841)，可判断X 与Y 有关且犯错误的概率不超过0.0511．[2022·福建福州三模]某质量指标的测量结果服从正态分布N(80，σ2)，则在一次测量中( )A .该质量指标大于80的概率为0.5B .σ越大，该质量指标落在(70，90)的概率越大C .该质量指标小于60与大于100的概率相等D .该质量指标落在(75，90)与落在(80，95)的概率相等 12．[2022·山东淄博三模]甲箱中有5个红球，2个白球和3个黑球，乙箱中有4个红球，3个白球和3个黑球．先从甲箱中随机取出一球放入乙箱，分别以A 1，A 2和A 3表示由甲箱取出的球是红球、白球和黑球的事件；再从乙箱中随机取出一球，以B 表示由乙箱取出的球是红球的事件，则下列结论正确的是( )A .事件B 与事件A i (i ＝1，2，3)相互独立B .P(A 1B)＝522C .P(B)＝25D .P(A 2|B)＝845三、填空题(本题共4小题，每小题5分，共20分) 13．[2022·河北石家庄二模]某中学高一、高二、高三年级的学生人数分别为1 200、1 000、800，为迎接春季运动会的到来，根据要求，按照年级人数进行分层抽样，抽选出30名志愿者，则高一年级应抽选的人数为________．14．[2022·全国乙卷]从甲、乙等5名同学中随机选3名参加社区服务工作，则甲、乙都入选的概率为________．15．[2022·山东济南二模]2022年4月24日是第七个“中国航天日”，今年的主题是“航天点亮梦想”．某校组织学生参与航天知识竞答活动，某班8位同学成绩如下：7，6，8，9，8，7，10，m.若去掉m ，该组数据的第25百分位数保持不变，则整数强化训练14 立体几何1．解析：（1）证明：因为AM ⊥平面PCD ， 所以AM ⊥CD ，又底面ABCD 为正方形，所以AD ⊥CD ，又AD∩AM ＝A ，所以CD ⊥平面PAD ，又CD ⊂平面ABCD ， 所以平面PAD ⊥平面ABCD ；（2）取AD 的中点O ，连接PO ，则PO ⊥平面ABCD ， 则以O 为原点，建立如图所示空间直角坐标系：设AB ＝2，则A （1，0，0），B （1，2，0），C （－1，2，0），P （0，0，3 ），D （－1，0，0），M （－12) ，0，32 ），所以AM→ ＝（－32 ，0，32 ），PB → ＝（1，2，－ 3 ），PC → ＝（－1，2，－3 ），设平面PBC 的一个法向量为n ＝（x ，y ，z ），则⎩⎪⎨⎪⎧PB →·n ＝0PC →·n ＝0 ，即⎩⎨⎧x ＋2y －3z ＝0－x ＋2y －3z ＝0 ，令z ＝ 3 ，则y ＝32 ，x ＝0，则n ＝（0，32 ，3 ）， 设AM 与平面PBC 所成角为θ，所以sin θ＝|cos 〈AM →，n 〉|＝|AM →·n||AM →|·|n| ＝323·212＝77 .2．解析：（1）证明：连接BF ，由△ABC 为等边三角形，F 为AC 的中点，所以BF ⊥AC ，由PG ⊥平面ABC ，AC ⊂平面ABC ，所以PG ⊥AC ，又PG∩BF ＝G ，PG ，BF ⊂平面PBF ，所以AC ⊥平面PBF ， 又PB ⊂平面PBF ，所以PB ⊥AC ；（2）依题意PF ＝2 3 ，GF ＝2，在Rt △PFG 中，PG ＝22 ， 以F 为坐标原点，以FB→ 为x 轴的正方向，如图建立空间直角坐标系，则A （0，－2 3 ，0），C （0，2 3 ，0），B （6，0，0），E （3，－ 3 ，0），P （2，0，2 2 ）FP→ ＝（2，0，2 2 ），FE → ＝（3，－ 3 ，0），由（1）可知，AC → ＝（0，4 3 ，0）是平面PBF 的一个法向量，设平面PEF 的法向量为n ＝（x ，y ，z ），则⎩⎪⎨⎪⎧n·FP →＝2x ＋22z ＝0n·FE →＝3x －3y ＝0 ，令x ＝2 ，则n ＝（ 2 ， 6 ，－1），所以cos 〈AC → ，n 〉＝AC →·n |AC →|·|n | ＝63 ，所以sin 〈AC→ ，n 〉＝1－cos2〈AC→，n 〉 ＝33，所以平面PEF 与平面PBF 所成二面角的正弦值为33 .3．解析：（1）证明：因为∠ACB ＝120°，AC ＝BC ＝2，D 为AB 的中点， 所以CD ⊥AB ，且CD ＝BC sin30°＝1，又因为EF ＝1，所以CD ＝EF ，因为EF ∥CD ， 所以四边形EFDC 为平行四边形，因为BF ⊥平面AEF ，EF ⊂平面AEF ，所以BF ⊥EF ，所以CD ⊥BF ，因为BF∩AB ＝B ，BF ，AB ⊂平面ABF ，所以CD ⊥平面ABF, DF ⊂平面ABF ， 所以CD ⊥DF ，所以四边形EFDC 为矩形．（2）由（1）可知，EF ⊥平面ABF ，BF ⊥平面AEF ，AF ⊂平面AEF ，所以BF ⊥AF ，AB ＝2BC2 - CD2 ＝2 3 ，所以三棱锥A - BEF 的体积V ＝13 S △ABF·EF ＝16 AF·BF≤112 （AF2＋BF2）＝112 AB2＝1， 当且仅当AF ＝BF 时等号成立，此时FD ⊥AB ，据（1），以D 为坐标原点，分别以DA ，CD ，DF 所在的直线为x ，y ，z 轴建立空间直角坐标系D - xyz 如图所示.由已知可得下列点的坐标：A （ 3 ，0，0），B （－ 3 ，0，0），F （0，0，3 ），E （0，－1， 3 ），所以AB→ ＝（－2 3 ，0，0），AE → ＝（－ 3 ，－1， 3 ）， 设平面ABE 的法向量为m ＝（x ，y ，z ），则⎩⎪⎨⎪⎧m·AE →＝0m·AB →＝0 ，即⎩⎨⎧－3x －y ＋3z ＝0－23x ＝0，取y ＝ 3 ，则x ＝0，z ＝1， 所以平面ABE 的一个法向量为m ＝（0， 3 ，1）， 因为BF→ ＝（ 3 ，0， 3 ）是平面AEF 的法向量， 设平面AEF 与平面ABE 夹角为θ，则cos θ＝|m·BF →||m|·|BF →| ＝32·6 ＝24 ，故平面AEF 与平面ABE 夹角的余弦值为24 .4．解析：（1）证明：λ＝12 时，点E 、F 为BC 及CD 的中点． 连接AF 与BM 交于点G ，在△ABM 和△DAF 中，AB ＝AD ，AM ＝DF ，∠BAM ＝∠ADF ＝90°， 所以△ABM ≌△DAF ，于是∠ABM ＝∠FAD. 而∠FAD ＋∠BAF ＝90°， 所以∠ABM ＋∠BAF ＝90°，故∠AGB ＝90°，即BM ⊥AF.又PA ⊥平面ABCD ，BM ⊂平面ABCD ， 所以PA ⊥BM.因为BM ⊥PA ，BM ⊥AF ，PA ⊂平面PAF ，AF ⊂平面PAF ，PA∩AF ＝A ， 所以BM ⊥平面PAF.又因为BM ⊂平面PBM ，所以平面PBM ⊥平面PAF.（2）连接AC ，交EF 于点Q ，连接PQ ，记BD 与AC 交于点O ，如图：因为CE→ ＝λCB → ，CF → ＝λCD → ， 所以EF ∥BD ， 因为AC ⊥BD ，所以AC ⊥EF ，从而PQ ⊥EF ， 所以∠AQP 为二面角P - EF - A 的一个平面角．由题意，∠AQP ＝45°，从而AQ ＝PA ＝2， 所以CQ ＝2 2 －2，于是λ＝CE CB ＝CQ CO ＝22－22 ＝2－ 2 ，所以CF ＝CE ＝4－2 2 ，BE ＝DF ＝2 2 －2.如图，以AB 方向为x 轴，AD 方向为y 轴，AP 方向为z 轴建立空间直角坐标系，于是P （0，0，2），E （2，2 2 －2，0），F （2 2 －2，2，0），B （2，0，0），M （0，1，0）BM → ＝（－2，1，0），PE → ＝（ 2 ，2 2 －2，－2），PF →＝（2 2 －2，2，－2），设平面PEF 的一个法向量是n ＝（x ，y ，z ），由⎩⎪⎨⎪⎧n·PE →＝2x ＋（22－2）y －2z ＝0n·PF →＝（22－2）x ＋2y －2z ＝0 ，得：⎩⎨⎧x ＝y z ＝2x ，取x ＝1，则y ＝1，z ＝ 2 ，则n ＝（1，1， 2 ）. 所以直线BM 与平面PEF 所成角为θ，则sin θ＝|cos 〈n ，BM → 〉|＝|n·BM →||n|·|BM →| ＝⎪⎪⎪⎪⎪⎪－2＋14×5 ＝510 .。

提能拔高限时训练42 空间向量及其运算（B ）一、选择题1.平行六面体ABCD —A 1B 1C 1D 1中,M 为AC 和BD 的交点,若11B A =a ,11D A =b ,AA 1=c,则下列式子中与MB 1B 1M 相等的是( )A.-21a +21b +cB.21a +21b +c C.21a -21b +c D.- 21a-21b+c 解析:M B 1=BB 1+BM=B B 1+21（BA +BC）=AA 1-2111B A +2111D A=c-21a+21b.故选A. 答案:A2.以下命题中正确的是( ) A.若OP=21OA +31OB,则P 、A 、B 三点共线B.若{a ,b ,c }为空间的一个基底，则{a +b ,b +c ,c +a }构成空间的另一个基底C.|（a ·b ）·c |=|a |·|b |·|c |D.△ABC 为直角三角形的充要条件是AB ·AC=0解析:根据“若OD =m OA +n OB 且m+n=1,则P 、A 、B 三点共线”可知A 错误;若{a 、b 、c }为空间的一个基底,则a 、b 、c 为不共线向量.假设a +b 与b +c 共面,则存在实数λ,使a +b =λ(b +c ),即a =(λ-1)b +c .∴a 与b 、c 共面.∴假设不成立,即a +b 、b +c 不共面.可知B 正确;根据向量数量积的定义,易知C 不正确;△ABC 为直角三角形的充要条件是△ABC 三个内角∠A 、∠B 、∠C 中有一个是直角. 答案:B3.P 为正六边形ABCDEF 外一点,O 为正六边形ABCDEF 的中心,则PA +PB +PC +PE +PF +PD 等于( )A.POB.3POC.6POD.0解析:如图,PA +PD =2PO ,同理PB +PE =PC +PF =2PO ,∴原式=6PO.答案:C4.若a ，b 为非零向量，则a ·b =|a |·|b |是a 与b 平行的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 解析:因为a ,b 为非零向量，又a ·b =|a ||b |cos 〈a ,b 〉=|a ||b |, 所以cos 〈a ,b 〉=1.所以〈a ,b 〉=0,即a 与b 平行；反之，若a 与b 平行，当〈a ,b 〉=π时， a ·b =-|a |·|b |≠|a |·|b |, 由此知应选A. 答案:A5.若a=(2,2,0),b=(1,3,z),〈a ，b 〉=60°,则z 等于( )A.22B.-22C.±22D.±22解析:∵a ·b =8，|a |·|b |=2)10(22z ，cos 〈a ,b 〉=21)10(228||||2=+=•z b a b a ,∴z=±22.答案:C6.已知a =(2,-1,3),b =(-4,2,x),c =(1,-x,2),若(a +b )⊥c ,则x 等于( ) A.4 B.-4 C.21D.-6 解析:a +b =(-2,1,x+3),∵(a +b )⊥c , ∴(a +b )·c =0,即-2×1+1×(-x)+(x+3)×2=0. 解得x=-4. 答案:B7.已知a =(1-t,1-t,t),b =(2,t,t),则|b -a |的最小值为( ) A.55B.555C.553 D.511解析:∵b -a =(1+t,2t-1,0),∴|b -a |2=(b -a )2=(1+t)2+(2t-1)2+0=5t 2-2t+2. 当t=51时,|b -a |min 2=59, ∴|b -a |的最小值是553. 答案:C8.在正方体ABCD —A 1B 1C 1D 1中,棱长为a,M 、N 分别为A 1B 和AC 上的点,A 1M=AN=32a,则MN 与平面BB 1C 1C 的位置关系是( )A.相交B.平行C.垂直D.不能确定 解析:如图,建立空间直角坐标系B 1—xyz,则 M(0,32a,3a )、N(3a ,32a,a),∴MN =(3a ,0,32a).∴MN ∥平面BB 1C 1C.答案:B9.如图所示,ABCD —EFGH 是棱长为1的正方体,P 在正方体的内部且AP=43AB+21AD+32AE,则P 点到直线AB 的距离为( )A.65 B.12181 C.630 D.65 解析:建系如题图,则A(0,0,0)、B(1,0,0)、D(0,1,0)、E(0,0,1). ∴AP=43AB+21AD+32AE=(43,0,0)+(0,21,0)+(0,0,32) =(43,21,32). 又AB 为单位向量, ∴AP 在AB 上的射影为AP ·AB=43. 又|AP|=12181)32()21()43(222=++, ∴P 到AB 的距离d=65||||22=•-AB AP AP .答案:A10.在棱长为1的正方体ABCD —A 1B 1C 1D 1中，M 、N 分别为A 1B 1和BB 1的中点，那么直线AM 与CN 所成的角为( )A.arccos23 B.arccos 1010 C.arccos53 D.arccos 52 解析:如图建立空间直角坐标系，把D 点视作原点O ，分别沿DA 、DC 、1DD 方向为x 轴、y 轴、z 轴的正方向，则A （1，0，0），M （1，21，1），C （0，1，0），N （1，1，21）,∴AM=（1，21，1）-（1，0，0）=（0，21，1）, CN=（1，1，21）-（0，1，0）=（1，0，21）. 故AM ·CN =0×1+21×0+1×21=21.又|AM|=251)21(0222=++, |CN|=25)21(01222=++, 设α为直线AM 与CN 所成的角,∴cosα=52252521||||=•=CN AM CNAM . ∴α=arccos 52. 答案:D 二、填空题11.已知空间四边形ABCD ，则AB ·CD +BC ·AD +CA ·BD =_______.解析:AB ·CD +BC ·AD +CA ·BD=AB ·CD +BC ·(AB +BD )+CA ·BD =AB ·CD +BC ·AB +BC ·BD +CA ·BD=AB ·(BC +CD )+BD ·(CA +BC )=AB ·BD +BD ·BA =AB ·BD -BD ·AB=0. 答案:012.在平行六面体ABCD —A 1B 1C 1D 1中，M 为B 1C 1的中点，设AB=a ，AD=b ，1AA =c ，用a ，b ，c 表示下列向量： （1）1AC =____________________________________；（2）DM=________________________________________.解析:（1）1AC =AB +1BB +11C B =a +c +b ;（2）DM =1DC +2111B C =DC +1CC +2111B C =a +c -21b . 答案:（1）a +b +c （2）a -21b +c 13.已知A （1，0，1），B （4，4，6），C （2，2，3），D （10，14，17）,则这四个点是否共面：__________________（填“共面”或“不共面”）. 解析:∵AB=(3,4,5),AC=(1,2,2),AD=(9,14,16),∴AD =2AB +3AC.∴A、B 、C 、D 四点共面. 答案:共面14.已知点A(1,2,1),B(-1,3,4)、D(1,1,1),若AP =2PB ,则|PD |的值是_____________. 解析:设点P(x,y,z),则由AP =2PB,得(x-1,y-2,z-1)=2(-1-x,3-y,4-z),即⎪⎩⎪⎨⎧-=---=---=-,281,262,221z z y y x x 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=.3,38,31z y x则|PD |=222)13()138()131(-+-+-- =377. 答案:377 三、解答题15.四棱锥S —ABCD 中,底面ABCD 为平行四边形,侧面SBC⊥底面ABCD. 已知∠ABC=45°,AB=2,BC=22,SA=SB=3.(1)证明SA⊥BC;(2)求直线SD 与平面SAB 所成角的大小. 解法一:(1)证明:作SO⊥BC,垂足为O,连结AO, 由侧面SBC⊥底面ABCD,得SO⊥底面ABCD. 因为SA=SB,所以AO=BO.又∠ABC=45°,故△AOB 为等腰直角三角形,AO⊥BO. 由三垂线定理,得SA⊥BC.(2)由(1)知SA⊥BC,依题设AD∥BC,故SA⊥AD.由AD=BC=22,SA=3,AO=2,得SO=1,SD=11.所以△SAB 的面积S 1=21AB·2)21(22=-AB SA . 连结DB,得△DAB 的面积S 2=21AB·ADsin135°=2. 设D 到平面SAB 的距离为h, 由V D —SAB =V S —ABD ,得31h·S 1=31SO·S 2, 解得h=2.设SD 与平面SAB 所成角为α,则sinα=1122112==SD h . 所以直线SD 与平面SAB 所成的角为arcsin1122. 解法二:(1)证明:作SO⊥BC,垂足为O,连结AO, 由侧面SBC⊥底面ABCD,得SO⊥平面ABCD. 因为SA=SB, 所以AO=BO.又∠ABC=45°,所以△AOB 为等腰直角三角形,AO⊥OB.如图,以O 为坐标原点,OA 为x 轴正向,建立空间直角坐标系O —xyz,则A(2,0,0),B(0,2,0),C(0,-2,0),S(0,0,1),SA=(2,0,-1),CB=(0,22,0),SA ·CB=0,所以SA⊥BC. (2)取AB 的中点E,E(22,22,0).连结SE,取SE 的中点G,连结OG,则 G(42,42,21),OG=(42,42,21), SE=(22,22,-1),AB=(-2,2,0).SE ·OG =0, AB ·OG =0,OG 与平面SAB 内两条相交直线SE 、AB 垂直,所以OG⊥平面SAB.OG 与DS 的夹角记为α,SD 与平面SAB 所成的角记为β,则α与β互余.D(2,-22,0),DS =(-2,22,1),cosα=1122||||=•DS OG DS OG ,sinβ=1122, 所以直线SD 与平面SAB 所成的角为arcsin1122. 16.如图,四边形PCBM 是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM 与直线PC 所成的角为60°.(1)求证:平面PAC⊥平面ABC; (2)求二面角M —AC —B 的大小; (3)求三棱锥P —MAC 的体积.解法一:(1)证明:∵PC⊥AB,PC⊥BC,AB∩BC=B, ∴PC⊥平面ABC. 又∵PC ⊂平面PAC, ∴平面PAC⊥平面ABC.(2)取BC 的中点N,则CN=1,连结AN 、MN,∵PM CN,∴MNPC.从而MN⊥平面ABC.作N H⊥AC,交AC 的延长线于H,连结MH,则由三垂线定理,知AC⊥NH, 从而∠MHN 为二面角MACB 的平面角, 直线AM 与直线PC 所成的角为60°, ∴∠AMN=60°.在△ACN 中,由余弦定理,得AN=3120cos 222=••-+ CN AC CN AC ,在Rt△AMN 中,MN=AN ·cot ∠AMN =3×33=1, 在Rt△CNH 中,NH=CN ·sin ∠NCH =1×23=23, 在Rt△MNH 中,tan ∠MHN=332231==NH MN . 故二面角M —AC —B 的平面角大小为arctan 332. (3)由(2),知四边形PCNM 为正方形, ∴V P —MAC =V A —PCM =V A —MNC =V M —ACN =31×21AC ·CN ·sin120°·MN=123. 解法二:(1)同解法一(1).(2)在平面ABC 内,过C 作CD⊥CB,交AB 于D,建立空间直角坐标系C —xyz(如图).由题意有A(23,-21,0),设P(0,0,z 0)(z 0＞0), 则M(0,1,z 0), AM =(-23,23,z 0), CP =(0,0,z 0), 由直线AM 与直线PC 所成的角为60°,得 AM ·CP=｜AM ｜｜CP ｜cos60°,即z 02=32120+z ·z 0, 解得z 0=1. ∴CM =(0,1,1), CA CA=(23,-21,0). 设平面MAC 的一个法向量为n =(x 1,y 1,z 1), 则⎪⎩⎪⎨⎧=-=+,02123,01111y x z y 取x 1=1,得n =(1,3,-3).平面ABC 的法向量取为m =(0,0,1),设m 与n 所成角为θ,则cosθ=73||||-=•n m n m , 显然,二面角M —AC —B 的平面角为锐角.故二面角M —AC —B 的大小为arccos 721. (3)取平面PCM 的法向量为n 1=(1,0,0),则点A 到平面PCM 的距离 h=23||||11=•n n CA . ∵｜PC ｜=1,｜PM ｜=1,∴V P —MAC =V A —PCM =31×21｜PC ｜·｜PM ｜·h=61×1×1×23=123. 教学参考例题 志鸿优化系列丛书【例1】已知A(3,2,1)、B(1,0,4),求:(1)线段AB 的中点坐标和长度;(2)到A 、B 两点距离相等的点P(x,y,z)的坐标满足的条件.解:(1)设P(x,y,z)是AB 的中点,则OP =21(OA +OB )=21[(3,2,1)+(1,0,4)]=(2,1,25), ∴点P 的坐标是(2,1,25),d AB =2221)-(42)-(03)-(1++=17. (2)设点P(x,y,z)到A 、B 的距离相等,则2221)-(z 2)-(y 3)-(x ++=2224)-(z y 1)-(x ++.化简得4x+4y-6z+3=0,即为P 坐标应满足的条件.【例2】 棱长为a 的正方体ABCD —A 1B 1C 1D 1中,在棱DD 1上是否存在点P 使B 1D⊥面PAC ？解:以D 为坐标原点建立如图所示的空间直角坐标系,设存在点P(0,0,z),AP =(-a,0,z),AC =(-a,a,0),1DB =(a,a,a). ∵B 1D⊥面PAC,∴1DB ·AP =0,1DB ·AC =0.∴-a 2+az=0.∴z=a,即点P 与D 1重合.∴点P 与D 1重合时,DB 1⊥面PAC.【例3】如图,在三棱锥A —BCD 中,侧面ABD 、ACD 是全等的直角三角形,AD 是公共的斜边,且AD=3,BD=CD=1.另一个侧面ABC 是正三角形.(1)求证:AD⊥BC;(2)求二面角B —AC —D 的大小;(3)在线段AC 上是否存在一点E,使ED 与面BCD 成30°角?若存在,确定点E 的位置;若不存在,请说明理由.(1)证明:作AH⊥面BCD 于点H,连结BH 、CH 、DH,则四边形BHCD 是正方形,且AH=1. 以D 为原点,以DB 为x 轴,DC 为y 轴建立空间直角坐标系如下图,则B(1,0,0),C(0,1,0),A(1,1,1).BC =(-1,1,0),DA =(1,1,1), ∴BC ·DA =0,则BC⊥AD.(2)解:设平面ABC 的法向量为n 1=(x,y,z),则由n 1⊥BC ,知n 1·BC =-x+y=0; 同理由n 1⊥CA ,知n 1·CA =x+z=0.可取n 1=(1,1,-1).同理,可求得平面ACD 的一个法向量为n 2=(1,0,-1).由图可以看出,二面角BACD 的大小应等于〈n 1,n 2〉,则cos 〈n 1,n 2〉=3623101||||2121=•++=•n n n n ,即所求二面角的大小是arccos 36. (3)解:设E(x,y,z)是线段AC 上一点, 则x=z ＞0,y=1,平面BCD 的一个法向量为n =(0,0,1),DE=(x,1,x),要使ED 与面BCD 成30°角,由图可知DE 与n 的夹角为60°, ∴cos〈DE ,n 〉=221||||x xn DE n DE +=• =cos60°=21.则2x=22x 1+,解得x=22,则CE=2x=1.故线段AC 上存在E 点,且CE=1时,ED 与平面BCD 成30°角.。

训练13 平面向量（一）一、选择题（方法：直接选择法、特殊化法、估算选择法、特征选择法、数形结合法、结论选择法）1.（2010安徽文）(3)设向量()1,0a =, 11,22b ⎛⎫= ⎪⎝⎭ ,则下列结论中正确的是（ ）(A) a b =(B)a b ⋅=(C) //a b (D) a b - 与b垂直2.（2010湖南理）4、在Rt ABC ∆中，C ∠=90°，AC=4，则AB AC ⋅uu u r uu u r等于（ ）A 、-16B 、-8C 、8D 、163.（2010重庆文）（3）若向量()3,a m = ，()2,1b =-，0a b ⋅= ，则实数m 的值为（ ）（A ）32-（B ）32（C ）2 （D ）64.（2010重庆理）(2) 已知向量,a b满足0,1,2a b a b ⋅=== ，则2a b -= （ ）A. 0B.D. 85.（2009重庆卷理）已知()1,6,2a b a b a ==⋅-=，则向量a 与向量b 的夹角是（ ）A ．6π B ．4π C ．3π D ．2π 6.（2010四川理）（5）设点M 是线段BC 的中点，点A 在直线BC 外，216,B C A B A C A B A C =∣+∣=∣-, 则AM ∣∣= （ ）（A ）8 （B ）4 （C ） 2 （D ）17.（2010辽宁理）(8)平面上O,A,B 三点不共线，设,OA a OB b ==，则△OAB 的面积等于（ ）(A)8.（2010湖北文）8.已知ABC ∆和点M 满足0MA MB MC ++=.若存在实m 使得AB AC m AM += 成立，则m =（ ）A.2B.3C.4D.59.（2010全国卷2理）（8）ABC V 中，点D 在AB 上，CD 平方ACB ∠．若CB a = ，CA b =，1a = ，2b =，则CD =u u u r （ ）（A ）1233a b + （B ）2133a b + （C ）3455a b + （D ）4355a b +10.（2010山东文）（12）定义平面向量之间的一种运算“ ”如下：对任意的(),a m n =，(),b p q = ，令a b mq np =-，下面说法错误的是（ ）(A)若a 与b 共线，则0a b =(B) a b b a =(C)对任意的R λ∈，有()()a b a b λλ=(D) ()()2222a b a ba b +⋅=11.（2007湖北）设()4,3a = ，a 在b b在x 轴上的投影为2，且14b ≤ ，则b为（ ）A ．(214)，B ．227⎛⎫-⎪⎝⎭， C ．227⎛⎫- ⎪⎝⎭，D ．(28)，12.（2010全国卷1文）（11）已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为两切点，那么PA PB ∙的最小值为（ ）(A) 4- (B)3-(C) 4-+(D)3-+二、填空题（策略：快--运算要快；稳--变形要稳；全--答案要全；细--审题要细。

2011年高考数学试题汇编4——平面向量（北京4）已知O 是A B C △所在平面内一点，D 为B C 边中点，且2OA OB OC ++=0，那么（ Ａ ） Ａ．AO O D = Ｂ．2AO OD =Ｃ．3AO OD =Ｄ．2AO OD =（辽宁3）若向量a 与b 不共线，0≠ a b ，且⎛⎫ ⎪⎝⎭a ac =a -b a b，则向量a 与c 的夹角为（ D ）A ．0B ．π6C ．π3D ．π2（辽宁6）若函数()y f x =的图象按向量a 平移后，得到函数(1)2y f x =+-的图象，则向量a =（ A ） A ．(12)--，B ．(12)-，C ．(12)-，D ．(12)，（宁夏，海南4）已知平面向量(11)(11)==-，，，a b ，则向量1322-=a b （ Ｄ ）Ａ．(21)--， Ｂ．(21)-，Ｃ．(10)-，Ｄ．(12)，（福建4）对于向量，，a b c 和实数λ，下列命题中真命题是（ B ） A ．若=0 a b ，则0a =或0b =B ．若λ0a =，则0λ=或=0aC ．若22=a b ，则=a b 或-a =bD ．若 a b =a c ，则b =c（湖北2）将π2cos 36x y ⎛⎫=+⎪⎝⎭的图象按向量π24⎛⎫=-- ⎪⎝⎭，a 平移，则平移后所得图象的解析式为（Ａ ）Ａ．π2cos 234x y ⎛⎫=+- ⎪⎝⎭Ｂ．π2cos 234x y ⎛⎫=-+ ⎪⎝⎭Ｃ．π2cos 2312x y ⎛⎫=--⎪⎝⎭Ｄ．π2cos 2312x y ⎛⎫=++⎪⎝⎭（湖北文9）设(43)=，a ，a 在b 上的投影为522，b 在x 轴上的投影为2，且||14≤b ，则b 为（ Ｂ ）A ．(214)，B ．227⎛⎫-⎪⎝⎭， C ．227⎛⎫- ⎪⎝⎭，D ．(28)， （湖南4）设，a b 是非零向量，若函数()()()f x x x =+- a b a b 的图象是一条直线，则必有（ A ） A ．⊥a bB ．∥a bC ．||||=a bD ．||||≠a b （湖南文2）若O E F ，，是不共线的任意三点，则以下各式中成立的是（ B ） A ．EF OF OE =+B ．EF OF OE =-C ．EF OF OE =-+D ．EF OF OE =--（四川7）设A ｛a ,1｝，B ｛2，b ｝，C ｛4,5｝，为坐标平面上三点，O 为坐标原点，若方向在与→→→OC OB OA 上的投影相同，则a 与b 满足的关系式为 （ A ） (A)354=-b a(B)345=-b a (C)1454=+b a(D)1445=+b a（天津10）设两个向量22(2cos )λλα=+-，a 和sin 2m m α⎛⎫=+ ⎪⎝⎭，b ，其中m λα，，为实数．若2=a b ，则mλ的取值范围是（ Ａ ）Ａ．[-6，1] Ｂ．[48]，Ｃ．（-6，1] Ｄ．[-1，6]（浙江7）若非零向量，a b 满足+=a b b ，则（ Ｃ ） Ａ．2>2+a a b Ｂ．22<+a a b Ｃ．2>+2b a bＤ． 22<+b a b（浙江文9）若非零向量a 、b 满足｜a 一b ｜＝｜b｜，则（Ａ） (A) ｜2b ｜＞｜a 一2b ｜ (B) ｜2b ｜＜｜a 一2b｜(C) ｜2a ｜＞｜2a 一b ｜ (D) ｜2a ｜＜｜2a 一b｜（山东11）在直角A B C ∆中，C D 是斜边A B 上的高，则下列等式不成立的是（ C ） （A ）2AC AC AB =⋅（B ） 2BCBA BC =⋅（C ）2ABAC CD =⋅（D ） 22()()AC AB BA BC C DAB⋅⨯⋅= （山东文5）已知向量(1)(1)n n ==-，，，a b ，若2-a b 与b 垂直，则=a （ Ｃ ） A ．1B ．2C ．2D ．4（重庆5）在A B C △中，3AB =，45A = ，75C = ，则B C =（ Ａ ）Ａ．33-Ｂ．2 Ｃ．2 Ｄ．33+（重庆10）如题（10）图，在四边形A B C D 中，4AB BD D C ++=，4AB BD BD D C +=，0AB BD BD DC == ，则()A B D C A C +的值为（ Ｃ ）Ａ．2 Ｂ．22 Ｃ．4 Ｄ．42（上海14）直角坐标系x O y 中，i j，分别是与x y ，轴正方向同向的单位向量．在直角三角形A B C 中，若j k i AC j i AB+=+=3,2，则k 的可能值个数是（ B ）Ａ．1 Ｂ．2 Ｃ．3 Ｄ．4 （全国Ⅰ3）已知向量(56)=-，a ，(65)=，b ，则a 与b （ A ） A ．垂直 B ．不垂直也不平行 C ．平行且同向 D ．平行且反向（全国Ⅱ5）在A B C △中，已知D 是A B 边上一点，若123A D DBCD C A C B λ==+，，则λ=（ A ） DCA B 题（10）图A ．23B ．13C ．13-D ．23-二、填空题 （安徽13）在四面体O A B C -中，OA OB OC D === ，，，a b c 为B C 的中点，E 为A D 的中点，则O E =111244++a b c（用，，a b c 表示）．（北京11．）已知向量2411()()，，，a =b =．若向量()λ⊥b a +b ，则实数λ的值是3-（北京12．）在A B C △中，若1tan 3A =，150C = ，1BC =，则A B =102（广东10. ）若向量a 、b 满足b a b a 与,1==的夹角为120°，则b a b a ··+＝ 21. （湖南12．）在A B C △中，角A B C ，，所对的边分别为a b c ，，，若1a =，b =7，3c =，则B = 5π6 ．（湖南文12．）在A B C △中，角A B C ，，所对的边分别为a b c ，，，若1a =，3c =，π3C =，则A = π6 ．（江西15．）如图，在A B C △中，点O 是B C 的中点，过点O 的直线分别交直线A B ，A C 于不同的两点M N ，，若A B mA M = ，AC n AN =，则m n +的值为2 ．（江西文13．）在平面直角坐标系中，正方形O A B C 的对角线O B 的两端点分别为(00)O ，，(11)B ，，则AB AC =1．（陕西15. ）如图，平面内有三个向量OA 、OB 、OC ,其中与OA 与OB 的夹角为120°，OA 与OC 的夹角为30°,且|OA |＝|OB |＝1，|OC |＝32，若OC ＝λOA +μOB （λ，μ∈R ）,则λ+μ的值为 6 . （天津15．）如图，在A B C △中，12021B A C A B A C ∠===，，°，D 是边B C 上一点，2D C B D =，则A D B C =·83- ．（天津文15）在A B C △中，2A B =，3A C =，D 是边B C 的中点，则AD BC =52．（重庆文（13））在△ABC 中，AB =1,B C =2,B =60°，则AC ＝ 3。

2011年高考数学试题分类汇编（必修Ⅳ——向量）（一）选择题1、【08安徽理3】在平行四边形ABCD 中，AC 为一条对角线，若(2,4)A B =，(1,3)AC =,则AB =（ B ） A ． （－2，－4）B ．（－3，－5）C ．（3，5）D ．（2，4）2、【08安徽文2】若(2,4)A B = ，(1,3)AC =, 则BC = （ B ） A ． （1，1）B ．（－1，－1）C ．（3，7）D ．（-3,-7）3、【08广东文3】已知平面向量(1,2)a = ，(2,)b m =-，且a //b ，则23a b + ＝（ B ）A 、(5,10)--B 、(4,8)--C 、(3,6)--D 、(2,4)--4、【08湖北文1】设(1,2),(3,4),(3,2),(2)a b c a b c =-=-=+= 则（C ）A.(15,12)-B.0C.-3D.-115、【08湖南理7】设D 、E 、F 分别是△ABC 的三边BC 、CA 、AB 上的点，且2,D C BD = 2,C E E A =2,AF FB =则AD BE CF ++ 与BC （A ）A.反向平行B.同向平行C.互相垂直D.既不平行也不垂直6、【08辽宁理5】已知,,O A B 是平面上的三个点,直线A B 上有一点C ,满足2AC CB +=0 ,则O C等于(A ) A.2OA OB - B.2OA OB -+ C.2133O A O B - D.1233O A O B -+7、【08宁夏理8】平面向量a ，b 共线的充要条件是（ D ）A ．a ，b 方向相同B ．a ，b 两向量中至少有一个为零向量C ．λ∈R ∃，λ=b aD ．存在不全为零的实数1λ，2λ，12λλ+=0a b8、【08宁夏文5】已知平面向量(13)=-，a ，(42)=-，b ，λ+a b 与a 垂直， 则λ=（ A ） A ．1- B ．1C ．2-D ．29、【08全国Ⅰ理3】在A B C △中，AB = c ，AC = b ．若点D 满足2BD DC = ，则AD =（ A ） A ．2133+b cB ．5233-c b C ．2133-b c D ．1233+b c10、【08全国Ⅰ文5】在A B C △中，AB c = ，AC b = ．若点D 满足2BD DC = ，则AD=（ A ）A ．2133b c +B ．5233c b -C ．2133b c -D ．1233b c +11、【08浙江理9】已知，a b 是平面内两个互相垂直的单位向量，若向量c 满足()()0--= a c b c ，则c 的最大值是（ C ） A ．1B ．2C ．2D ．22（二）填空题12、【08江苏5】b a ,的夹角为 120，1,3a b == ，则5a b -= 713、【08江西理13】直角坐标平面内三点()()()1,23,29,7A B C -、、，若E F 、为线段B C 的三等分点，则AE ·AF＝ 22 ．14、【08江西文16】如图，正六边形A B C D E F 中，有下列四个命题：A ．2AC AF BC +=B ．22AD AB AF =+C ．AC AD AD AB ⋅=⋅D ．()()AD AF EF AD AF EF ⋅=⋅其中真命题的代号是 A,B,D （写出所有真命题的代号）15、【08北京文11】已知向量a 与b 的夹角为120 ，且4==a b ，那么 a b 的值为 -8 16、【08宁夏理13】已知向量(011)=-，，a ，(410)=，，b ，29λ+=a b 且0λ>，则λ= 3 ．17、【08全国Ⅱ理13】设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ 2 ． 18、【08陕西理15】关于平面向量，，a b c ．有下列三个命题：①若 a b =a c ，则=b c ．②若(1)(26)k ==-，，，a b ，∥a b ，则3k =-．③非零向量a 和b 满足||||||==-a b a b ，则a 与+a b 的夹角为60．其中真命题的序号为 ② ．（写出所有真命题的序号）19、【08上海理5】若向量→a 、→b 满足|→a |＝1，|→b |＝2，且→a 与→b 的夹角为π3，则|→a +→b |＝ 720、【08天津文14】已知平面向量(24)=，a ，(12)=-，b ，若()=- c a a b b ，则=c 82 ．21、【08浙江理11】已知0a >，若平面内三点23(1)(2)(3)A a B a C a -，，，，，共线，则a = 12+22、【08浙江文16】已知a 是平面内的单位向量，若向量b 满足()0b a b -=，则||b 的取值范围是 [0,1] 。

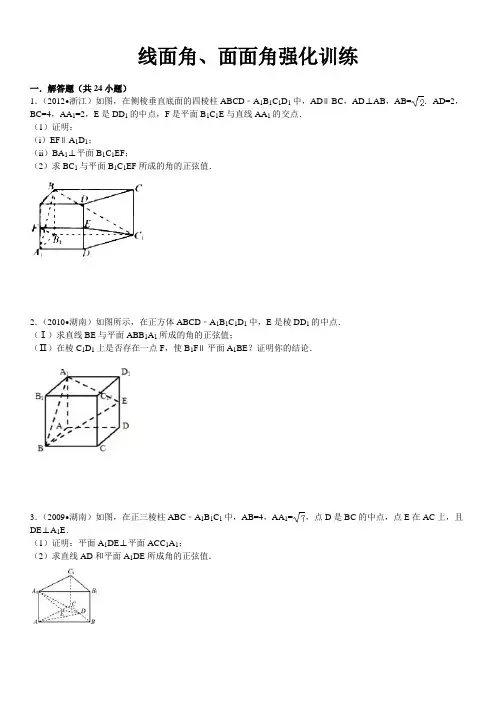
线面角、面面角强化训练一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．线面角、面面角强化训练参考答案与试题解析一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．B=B=，即∠，BH=，H=，2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．BE=中，所成的角的正弦值为3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．），，﹣，，﹣所成角的正弦值为4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．EF=（5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．EF DGa所成角的正弦值为所成角为，∴）解：由，得，∴所成的角为所成的角为．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．的法向量为锐角时，所求的角即为它的余角；当=MD=SM=（，y==，，＞==，＞arcsin7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．，则，代入公式可求的法向量的法向量，，﹣，，，=|）知，设的法向量令的法向量所以的法向量=0t=PA=8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．ADC=DP=利用勾股定理求得等于，，的坐标表示．设平面的法向量为，，表示出和在向量的距离为，∴，所成角的大小为．的距离为．，，•=0•=0•（，﹣，．在向量=）上的投影的绝对值，的距离为9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．=λ，与AC，AB=，CE=CBCED==所成角的余弦值（（Ⅰ）∵=0⊥，，=∥（Ⅲ）∵=，＞所成角的余弦值为10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．距离的的一个法向量，结合然后求出距离的，再利用向量的射影公式直接求点的中点可得即，则，，由PN=（．）可知所求距离为．的一个法向量，由可得：，所以所求角的大小为，所以，则距离的，设点．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．（Ⅰ）利用，求出．即可．．通过，得到．求出，，由已知，．解得，所以（Ⅰ）因为．即．，所以．．则，）则，则，由已知，，解得，∴（Ⅰ）因为，．即．，所以12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．，（2），﹣=，（）•==0•=0），（的法向量为，则，=，则，﹣），∴•﹣，（﹣，﹣，＞==13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．=．=，得D=，D=2=．=，﹣得=0，2，）=，=，则⊥，⊥取=（=，则⊥，，即取得，＞==．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．=，从而D=．所以=，，，从而，，﹣，故，2，，=，则有⊥，⊥•且•，即，取=，=，则⊥，⊥，即且=0，＞=，所以二面角的平面角的余弦值15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．的法向量，AQ=2AC=AB=中，（﹣，（），的平面角的余弦值为BD=AM=PB=AE=AQ=2BPC=MQ=．QE=，∴AEQ=的平面角的余弦值为16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．OP=与平面OP=，，OC====．为原点，建立空间直角坐标系．则）=2=，则由得出，取﹣，所以（﹣===．OP=，，，所以=2 =）为平面==arcsin（Ⅱ）由（Ⅰ）知，，，=，则由得出，，则，所以=，的一个法向量为==arccos17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．，﹣，，因此（，﹣==，则•，•y=z，则==，＞=，所以二面角CB=CGFGC=的余弦值为18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．求出则、、由向量积的运算易得•，•、、的坐标，的法向量法向量，==••=即因此可取，=，＞﹣的余弦值为﹣19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．的坐标，求出向量，和平面BD=，，，，=的法向量为，则因此可取（，=，==﹣的余弦值为：﹣20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．D=21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．，求，））=的法向量=，则，）∴的距离为的法向量（，的法向量，的余弦值为22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．FO=中，中，所成的角大小为，可得的大小为23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．坐标，代入向量数量积公式，易得满足，的一个法向量为，的一个法向量为24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．（Ⅰ）求出通过，相关向量，计算，求二面角，∴，的距离是，．的大小是。

第五章 平面向量【考试要求】（1）理解向量的概念，掌握向量的几何表示，了解共线向量的概念． （2）掌握向量的加法和减法．（3）掌握实数与向量的积，理解两个向量共线的充要条件．（4）了解平面向量的基本定理.理解平面向量的坐标的概念，掌握平面向量的坐标运算．（5）掌握平面向量的数量积及其几何意义，了解用平面向量的数量积可以处理有关长度、角度和垂直的问题，掌握向量垂直的条件．（6）掌握平面两点间的距离公式，以及线段的定比分点和中点坐标公式，并且能熟练运用掌握平移公式．（7）掌握正弦定理、余弦定理，并能初步运用它们解斜三角形．【考题】1、 （全国Ⅰ新卷文2）a ，b 为平面向量，已知a=（4，3），2a+b=（3，18），则a ，b 夹角的余弦值等于（ ）A ．865 B ．865- C ．1665 D ．1665- 2、 （重庆卷理2）已知向量a ，b 满足0,1,2,a b a b •===，则2a b -=（ ）A ． 0B ．C ． 4D ． 83、 （重庆卷文3）若向量a=（3,m ）,b=（2,-1）,a·b=0,则实数m 的值为（ ）A ．32-B ．32C ．2D ．6 4、 （安徽卷理3文3）设向量()1,0=a ，11,22⎛⎫=⎪⎝⎭b ，则下列结论中正确的是（ ）A ．=a bB ．2•=a b C ．-a b 与b 垂直 D ．a ∥b5、 （湖北卷理3）在ABC ∆中，a=15,b=10,A=60°，则cos B =（ ）A ．－3 B ．3C ．－3D ．36、 （北京卷文4）若a,b 是非零向量，且a b ⊥，a b ≠，则函数()()()f x xa b xb a =+⋅-是（ ）A ．一次函数且是奇函数B ．一次函数但不是奇函数C ．二次函数且是偶函数D ．二次函数但不是偶函数7、 （湖南卷理4）在Rt ABC ∆中，C ∠=90°AC=4，则AB AC ⋅等于（ ）A ．-16B ．-8C ．8D ．168、 （广东卷文5）若向量a=（1,1），b=（2,5），c =（3,x ）满足条件 （8a－b）·c=30，则x =（ ）A ．6B ．5C ．4D ．39、 （四川卷理5文6）设点M 是线段BC 的中点，点A 在直线BC 外，216,BC AB AC AB AC =∣+∣=∣-∣,则AM ∣∣=（ ）A ．8B ．4C ． 2D ．110、（湖北卷理5文8）已知ABC ∆和点M 满足0MA MB MC --→--→--→+=+.若存在实数m 使得AB AC AM m --→--→--→+=成立，则m=（ ）A ．2B ．3C ．4D ．511、（湖南卷文6）若非零向量a ，b 满足||||,(2)0a b a b b =+⋅=，则a 与b 的夹角为（ ）A ． 300B ． 600C ． 1200D ． 1500 12、（北京卷理6）a ，b 为非零向量。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年江苏省常州市高中数学人教B 版 必修三-向量数的量积-强化训练(14)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟 满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）48-8-41. 已知向量 ， 在方向上的投影向量为 ， 则（ ）A. B. C. D.2. 已知向量 ， 满足 ， ， ，则 与 的夹角为（ ）A. B. C. D.f(x)在(0， )上单调递增f(x)在(0，)上单调递减f(x)在(0， )上单调递增f(x)在(0，)上单调递减3. 设函数f(x)＝sin(wx ＋)＋sin(wx －)(w ＞0)的最小正周期为π，则（）A. B. C. D. ,,,,4. 已知a ，b ，c 为△ABC 的三个内角A ，B ，C 的对边，向量=（ ， ﹣1），=（cosA，sinA ）．若⊥ ，且αcosB+bc osA=csinC ，则角A ，B 的大小分别为（ ）A. B. C. D. 5. 若 ， 则X 可以为（ ）A. B. C. D.等腰直角三角形等腰三角形直角三角形等边三角形6. 在 中，若 ，那么一定是（ ）A. B. C. D. 7. 已知 为单位向量，且 与垂直，则 的夹角为（ ）30°60°120°150°A. B. C. D. 锐角三角形钝角三角形直角三角形等腰直角三角形8. 在中，若 ， 则是 ( )A. B. C. D. 9. 已知向量 在向量 方向上的投影为 ，且，则 （ ）A. B. C. D.2110. 已知 ， 与 的夹角为 ，则 在 上的投影为（ ）A. B. C. D.11. 已知 ，则 的值为（ ）A. B. C. D.--12. 若sin （﹣θ）= ， 则cos （+2θ）的值为（ ）A. B. C. D. 13. 已知向量 ， ，若 ，则 的最小值为 ．14. 若θ∈（ ， ），sin2θ= ， 则cosθ﹣sinθ的值是15. 在三角形ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．已知， 则角 ；若 ，， 成等比数列，则 ．16. 计算：=17. 已知 ， ， .(1) 求 和 的值；(2) 求的值.18. 已知α，β为锐角，，，求α+2β．19. 在①，②，③这三个条件中，任选一个，补充在下面问题中，问题：在中，a，b，c分别为角A，B，C所对的边，， ____．(1) 求角B﹔(2) 求的范围．20. 已知函数，在下列三个条件中，选择可以确定和m的值的两个条件作为已知．条件①：的最小正周期为；条件②：的最大值与最小值之和为0；条件③：．(1) 求的值；(2) 若函数在区间上是增函数，求实数a的最大值；(3) 令，若在上恒成立，求实数t的取值范围．21. 已知函数的部分图象如图所示.(1) 求函数的解析式；(2) 求函数的单调递增区间.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)18.19.(1)(2)20.(1)(2)(3)21.(1)(2)。

巩固1．已知向量a 与向量b 的夹角为120°，若向量c ＝a ＋b ，且a⊥c ，则|a ||b |的值为( ) A.12 B.233C ．2 D. 3解析：选A.c ·a ＝(a ＋b )·a ＝|a |2＋a ·b ＝|a |2＋|a ||b |·cos120°＝|a |2－12|a ||b |＝0，∴|a ||b |＝12.故选A. 2．(2009年高考陕西卷)在△ABC 中，M 是BC 的中点，AM ＝1，点P 在AM 上且满足＝2，则·(＋)等于( )A ．－49B ．－43C.43D.49解析：选A.M 是BC 的中点，则·(＋)＝·2＝·A＝－()2＝－(23)2＝－49.3．(2010年江苏四市调研)已知圆O 的半径为a ，A ，B 是其圆周上的两个三等分点，则·＝( )A.32a 2 B ．－32a 2C.32a 2 D ．－32a 2 解析：选 B.结合图形易知两向量夹角为5π6，且||＝a ，||＝3a ，故·＝||×||×cos 5π6＝－3a 22.4．已知平面向量a ＝(2,4)，b ＝(－1,2)，若c ＝a －(a ·b )b ，则|c |＝________.解析：由a ＝(2,4)，b ＝(－1,2)，得a ·b ＝－2＋8＝6，∴c ＝(2,4)－6(－1,2)＝(8，－8)，∴|c |＝82＋(－8)2＝8 2.答案：8 25．(原创题)三角形ABC 中AP 为BC 边上的中线，||＝3，·＝－2，则||＝________.解析：·＝12(＋)·(－)＝12(||2－||2)＝－2∴||＝ 5. 答案： 56．已知|a |＝4，|b |＝8，a 与b 的夹角是120°.(1)计算|4a －2b |；(2)当k 为何值时，(a ＋2b )⊥(k a －b )?解：由已知，a ·b ＝4×8×(－12)＝－16.(1)∵|4a －2b |2＝16a 2－16a ·b ＋4b 2＝16×16－16×(－16)＋4×64＝3×162∴|4a －2b |＝16 3.(2)若(a ＋2b )⊥(k a －b )，则(a ＋2b )·(k a －b )＝0，∴k a 2＋(2k －1)a ·b －2b 2＝0.16k －16(2k －1)－2×64＝0，∴k ＝－7.练习1．(2009年高考全国卷Ⅰ)设非零向量a 、b 、c 满足|a |＝|b |＝|c |，a ＋b ＝c ，则〈a ，b 〉＝( )A ．150°B ．120°C ．60°D ．30°解析：选B.∵a ＋b ＝c ，∴|c |2＝|a ＋b |2＝a 2＋2a ·b ＋b 2.又|a |＝|b |＝|c |，∴2a ·b ＝－b 2，即2|a ||b |cos 〈a ，b 〉＝－|b |2.∴cos 〈a ，b 〉＝－12，∴〈a ，b 〉＝120°.2．共点力F 1(lg2，lg2)，F 2(lg5，lg2)作用在物体M 上，产生位移s ＝(2lg5,1)，则共点力对物体做的功W 为( )A ．lg2B ．lg5C ．1D ．2解析：选D.F 1与F 2的合力F ＝(lg2＋lg5,2lg2)＝(1,2lg2)又s ＝(2lg5,1)所以W ＝F ·s ＝2lg5＋2lg2＝2.3．已知向量a ＝(1,2)，b ＝(－2，－4)，|c |＝5，若(a ＋b )·c ＝52，则a 与c 的夹角为( )A ．30°或150°B ．60°或120°C ．120°D ．150°解析：选C.由题意容易得出向量a 、b 共线，且向量a 与向量a ＋b 的夹角为π，可设向量a ＋b 与向量c 的夹角为α，则(a ＋b )·c ＝|a＋b |·|c |·cos α＝5cos α＝52，所以cos α＝12，α＝60°，则向量a 与向量c所夹的角应为120°.答案为C.4．若向量a 与b 不共线，a ·b ≠0，且c ＝a －(a ·a a ·b)b ，则向量a 与c 的夹角为( )A ．0 B.π6C.π3D.π2解析：选D.∵a ·c ＝a ·[a －(a ·a a ·b )b ]＝a ·a －(a ·a a ·b)(a ·b )＝0. ∴a ⊥c ，故选D.5.设A (a,1)，B (2，b )，C (4,5)为坐标平面上三点，O 为坐标原点，若与在方向上的投影相等，则a 与b 满足的关系式为( )A ．4a －5b ＝3B ．5a －4b ＝3C ．4a ＋5b ＝14D ．5a ＋4b ＝14解析：选A.由投影计算公式可得：＝，即：4a ＋5＝8＋5b ，即4a －5b ＝3，故选A.6．在△ABC 中，(＋)·＝||2，则三角形ABC 的形状一定是( )A ．等边三角形B ．等腰三角形C ．直角三角形D ．等腰直角三角形解析：选C.由(＋)·＝||2，得·(＋－)＝0，即·(＋＋)＝0，∴·2＝0，∴⊥，∴∠A ＝90°.7．已知向量＝(2,2)，＝(4,1)，在x 轴上一点P ，使·有最小值，则P 点的坐标是________．解析：设P (x,0)，则＝(x －2，－2)，＝(x －4，－1)．因此，·＝(x －4)(x －2)＋2＝x 2－6x ＋10＝(x －3)2＋1.∴当x ＝3时，·取得最小值1，此时P (3,0)．答案：(3,0)8．关于平面向量a ，b ，c ，有下列三个命题：①(a ·b )c －(c ·a )b ＝0②|a |－|b |<|a －b |；③(b ·c )a －(c ·a )b 不与c 垂直；④非零向量a 和b 满足|a |＝|b |＝|a －b |，则a 与a ＋b 的夹角为60°. 其中真命题的序号为________(写出所有真命题的序号)．解析：平面向量的数量积不满足结合律，故①假；由向量的减法运算可知|a |、|b |、|a －b |恰为一个三角形的三条边长，而三角形的两边之差小于第三边，故②是真命题．因为[(b·c)a－(c·a)b]·c＝(b·c)a·c －(c·a)b·c＝0，所以垂直，故③假．由|a|＝|b|＝|a－b|，再结合平行四边形法则可得a与a＋b的夹角为30°，命题④错误．答案：②9．在长江南岸渡口处，江水以12.5 km/h的速度向东流，渡船的速度为25 km/h.渡船要垂直地渡过长江，则航向为________．解析：如图，渡船速度为，水流速度为，船实际垂直过江的速度为，依题意知，||＝12.5，||＝25，由于四边形OADB为平行四边形，则||＝||，又OD⊥BD，∴在Rt△OBD中，∠BOD＝30°，∴航向为北偏西30°.答案：北偏西30°10．已知|a|＝3，|b|＝2.(1)若a与b的夹角为150°，求|a＋2b|；(2)若a－b与a垂直，求a与b的夹角大小．解：(1)∵|a＋2b|2＝(a＋2b)2＝a2＋4a·b＋4b2＝|a|2＋4|a||b|cos150°＋4|b|2＝(3)2＋4×3×2×cos150°＋4×22＝7，∴|a＋2b|＝7.(2)∵(a－b)⊥a，∴(a－b)·a＝|a|2－a·b＝0.∴a·b＝|a|2.∴cos〈a，b〉＝a·b|a||b|＝|a|2|a||b|＝|a||b|＝32.又∵0°≤〈a ，b 〉≤180°，∴〈a ，b 〉＝30°.11.(2009年高考湖北卷)已知向量a ＝(cos α，sin α)，b ＝(cos β，sin β)，c ＝(－1,0)．(1)求向量b ＋c 的长度的最大值；(2)设α＝π4，且a ⊥(b ＋c )，求cos β的值．解：(1)法一：b ＋c ＝(cos β－1，sin β)，则|b ＋c |2＝(cos β－1)2＋sin 2β＝2(1－cos β)．∵－1≤cos β≤1，∴0≤|b ＋c |2≤4，即0≤|b ＋c |≤2.当cos β＝－1时，有|b ＋c |＝2，所以向量b ＋c 的长度的最大值为2.法二：∵|b |＝1，|c |＝1，|b ＋c |≤|b |＋|c |＝2，当cos β＝－1时，有b ＋c ＝(－2,0)，即|b ＋c |＝2.所以向量b ＋c 的长度的最大值为2.(2)法一：由已知可得b ＋c ＝(cos β－1，sin β)，a ·(b ＋c )＝cos αcos β＋sin αsin β－cos α＝cos(α－β)－cos α.∵a ⊥(b ＋c )，∴a ·(b ＋c )＝0，即cos(α－β)＝cos α.由α＝π4，得cos(π4－β)＝cos π4，即β－π4＝2k π±π4(k ∈Z )，∴β＝2k π＋π2或β＝2k π，k ∈Z ，于是cos β＝0或cos β＝1.法二：若α＝π4，则a ＝(22，22)．又由b ＝(cos β，sin β)，c ＝(－1,0)得a ·(b ＋c )＝(22，22)·(cos β－1，sin β)∵a ⊥(b ＋c )，∴a ·(b ＋c )＝0，即cos β＋sin β＝1.∴sin β＝1－cos β，平方后化简得cos β(cos β－1)＝0，解得cos β＝0或cos β＝1.经检验，cos β＝0或cos β＝1即为所求．12．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .已知m ＝(cos 3A 2，sin 3A 2)，n ＝(cos A 2，sin A 2)，且满足|m ＋n |＝ 3.(1)求角A 的大小；(2)若||＋||＝3||，试判断△ABC 的形状．解：(1)由|m ＋n |＝3，得m 2＋n 2＋2m ·n ＝3， 即1＋1＋2(cos 3A 2cos A 2＋sin 3A 2sin A 2)＝3，∴cos A ＝12，∵0<A <π，∴A ＝π3.(2)∵||＋||＝3||，∴b ＋c ＝3a ，∴sin B ＋sin C ＝3sin A ，∴sin B ＋sin(2π3－B )＝3×32，即32sin B ＋12cos B ＝32，∴sin(B ＋π6)＝32.∵0<B <2π3，∴π6<B ＋π6<5π6，∴B ＋π6＝π3或2π3，故B ＝π6或π2.当B ＝π6时，C ＝π2；当B ＝π2时，C ＝π6.故△ABC 是直角三角形．。

南师附中2011届高三模拟考试数 学(满分160分，考试时间120分钟)2011．05一、 填空题：本大题共14小题，每小题5分，共70分．1. 已知全集U ＝R ，集合A ＝{x |log 2x ＞1}，则∁U A ＝______________.2. 已知复数z ＝2i1＋i，则该复数的虚部为______________．3. 已知双曲线过点(2,1)且一条渐近线方程为x －y ＝0，则该双曲线的标准方程为__________．4. 在如图所示的流程图中，输出的结果是__________．(第4题)5. 在△ABC 中，三边a 、b 、c 所对的角分别为A 、B 、C ，若A ＝30°，a ＝1，b ＝2，则B ＝____________.6. 已知向量a 与b 的夹角为150°，且|a|＝2，|b|＝3，则(2a ＋b )·a ＝____________.7. 已知函数f (x )＝⎩⎨⎧x (x ≥0)，－x 2－4x (x ＜0)，若f (x )≤3，则x 的取值范围是____________．8. 如图是函数y ＝A sin(ωx ＋φ)⎝⎛⎭⎫A ＞0，ω＞0，|φ|＜π2图象的一部分，则此函数的表达式为____________．(第8题)9. 某人2011年初向银行申请个人住房公积金贷款a (a ＞0)元购买住房，年利率为r (r ＞0)，按复利计算，每年等额还贷一次，并从贷款后的次年初开始还贷．如果10年还清，那么每年应还贷款__________元．(用a 、r 表示)10. 已知函数f (x )＝xx ＋a，若函数y ＝f (x ＋2)－1为奇函数，则实数a ＝____________.11. 已知等差数列{a n }的公差不为零且a 3、a 5、a 8依次成等比数列，则S 5a 9＝______________.12. 已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右准线与x 轴交于点A ，点B 的坐标为(0，a )，若椭圆上的点M 满足AB →＝2AM →，则椭圆C 的离心率为____________．13. 在平面直角坐标系xOy 中，集合M ＝{(x ，y )|x ＋y ≤1，且x ≥0，y ≥0}，N ＝{(x －y ，x ＋y )|(x ，y )∈M }，则当(x ，y )∈N 时，z ＝x －2y 的最大值为______________．14. 已知函数f (x )＝4x ＋k ·2x ＋14x ＋2x ＋1，若对于任意实数x 1、x 2、x 3，均存在以f (x 1)、f (x 2)、f (x 3)为三边边长的三角形，则实数k 的取值范围是____________．二、 解答题：本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤．15. (本小题满分14分)某学科在市模考后从全年级抽出50名学生的学科成绩作为样本进行分析，得到样本频率分布直方图如图所示．(1) 估计该次考试该学科的平均成绩；(2) 为详细了解每题的答题情况，从样本中成绩在70～90之间的试卷中任选2份进行分析，求至少有1份试卷成绩在70～80之间的概率．16.(本小题满分14分)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且cos A ＝13.(1) 求2sin 2⎝⎛⎭⎫π3＋B ＋C 2＋sin 4π3cos ⎝⎛⎭⎫π2＋A 的值； (2) 若a ＝3，求三角形面积的最大值．17. (本小题满分14分)如图，在四棱锥P —ABCD 中，四边形ABCD 为矩形，AB ⊥BP ，M 、N 分别为AC 、PD 的中点．求证：(1) MN ∥平面ABP ；(2) 平面ABP ⊥平面APC 的充要条件是BP ⊥PC .18. (本小题满分16分)已知直线l 1、l 2分别与抛物线x 2＝4y 相切于点A 、B ，且A 、B 两点的横坐标分别为a 、b (a 、b ∈R )．(1) 求直线l 1、l 2的方程；(2) 若l 1、l 2与x 轴分别交于P 、Q ，且l 1、l 2交于点R ，经过P 、Q 、R 三点作⊙C . ① 当a ＝4，b ＝－2时，求⊙C 的方程；② 当a ，b 变化时，⊙C 是否过定点？若是，求出所有定点坐标；若不是，请说明理由．19. (本小题满分16分)已知数列{a n }的前n 项的和为S n ，且S n ＝2n ＋7－2a n . (1) 求证：{a n －2}为等比数列；(2) 是否存在实数k ，使得a n ≤n 3＋kn 2＋9n 对于任意的n ∈N *都成立？若存在，求出实数k 的取值范围；若不存在，说明理由．20. (本小题满分16分)已知函数f (x )＝12ax 2－2x ＋2＋ln x ，a ∈R .(1) 当a ＝0时，求f (x )的单调增区间；(2) 若f (x )在(1，＋∞)上只有一个极值点，求实数a 的取值范围；(3) 对于任意x 1、x 2∈(0,1]，都有|x 1－x 2|≤|f (x 1)－f (x 2)|，求实数a 的取值范围.南京市名校2011届高三模拟考试数学附加题(满分40分，考试时间30分钟)21. [选做题]在A 、B 、C 、D 四小题中只能选做2题，每小题10分．解答应写出文字说明、证明过程或演算步骤．A. 选修41：几何证明选讲如图，D 为△ABC 的BC 边上的一点，⊙O 1经过点B 、D ，交AB 于另一点E ，⊙O 2经过点C 、D ，交AC 于另一点F ，⊙O 1、⊙O 2交于点G .求证：(1) ∠BAC ＋∠EGF ＝180°； (2) ∠EAG ＝∠EFG .B. 选修42：矩阵与变换已知M ＝⎣⎢⎡⎦⎥⎤3－22－2，β＝⎣⎢⎡⎦⎥⎤45，试计算M 9β.C. 选修44：坐标系与参数方程已知曲线⎩⎨⎧ x ＝2cos θ，y ＝3sin θ(θ为参数)和曲线⎩⎪⎨⎪⎧x ＝－2t ＋2，y ＝3t (t 为参数)相交于两点A 、B ，求A 、B 的坐标．D. 选修45：不等式选讲已知x 、y 均为正数，且x >y ，求证：2x ＋1x 2－2xy ＋y 2≥2y ＋3.[必做题]第22、23题，每小题10分，共20分．解答应写出文字说明、证明过程或演算步骤．22. 如图，已知正四棱柱ABCD —A 1B 1C 1D 1中，AB ＝2，AA 1＝4，E 为BC 的中点，F为直线CC 1上的动点，设C 1F →＝λFC →.(1) 当λ＝1时，求二面角F —DE —C 的余弦值； (2) 当λ为何值时，有BD 1⊥EF?23. 某养鸡场对疑似有传染病的100只鸡进行抽血化验，根据流行病学理论这些鸡的感染率为10%，为了减少抽检次数，首先把这些鸡平均分成若干组，每组n 只，并把同组的n 只鸡抽到的血混合在一起化验一次，若发现有问题，再分别对该组n 只鸡逐只化验．(1) 当n ＝4时，记某一组中病鸡的数量为X ，求X 的概率分布和数学期望； (2) 当n 为多少时，化验次数最少？并说明理由．南京市名校2011届高三模拟考试数学参考答案及评分标准1. (－∞，2]2. 13. x 23－y 23＝1 4. 10 5. 45°或135° 6. 5 7. [－1,9]∪(－∞，－3]8. y ＝2sin ⎝⎛⎭⎫2x ＋π6 9. ar (1＋r )10(1＋r )10－110. －2 11. 2 12. 22 13. 3 14. －12≤k ≤4 15. 解：(1) 用每组中的平均值作为每组中的样本数据，直接算得平均成绩为103.4.(5分)(2) 样本中成绩在70～80之间有2人，设其编号为①②，样本中成绩在80～90之间有4人，设其编号为③④⑤⑥，从上述6人中任取2人的所有选取可能为：①②，①③，①④，①⑤，①⑥；②③，②④，②⑤，②⑥； ③④，③⑤，③⑥；④⑤，④⑥；⑤⑥.(9分)故从样本中成绩在70～90之间任选2人所有可能结果数为15，(12分)至少有1人成绩在70～80之间可能结果数为9，因此，所求概率为P 2＝0.6.(14分)16. 解：(1) 2sin 2⎝⎛⎭⎫π3＋B ＋C 2＋sin 4π3cos ⎝⎛⎭⎫π2＋A ＝1＋cos ⎝⎛⎭⎫2π3＋B ＋C ＋sin π3sin A (2分) ＝1＋cos ⎝⎛⎭⎫5π3－A ＋sin π3sin A ＝1＋cos 5π3cos A ＋sin 5π3sin A ＋sin π3sin A＝1＋cos π3cos A －sin π3sin A ＋sin π3sin A＝76.(6分) (2) ∵ b 2＋c 2－a 22bc ＝cos A ＝13，∴ 23bc ＝b 2＋c 2－a 2≥2bc －a 2.(8分)又a ＝3，∴ bc ≤94，当且仅当b ＝c ＝32时，bc ＝94，故bc 的最大值是94.(10分)∵ cos A ＝13，∴ sin A ＝223，S ＝12bc sin A ≤342.(12分)故三角形面积的最大值是324.(14分)17. 证明：(1) 连结BD ，由已知，M 为AC 和BD 的中点．又N 为PD 的中点，∴ MN ∥BP .∵ MN ⊂面ABP ，∴ MN ∥面ABP .(6分) (2) ∵ AB ⊥BP ，AB ⊥BC ，∴ AB ⊥面BPC ， ∴ AB ⊥PC .(8分) 充分性：∵ BP ⊥PC ，∴ PC ⊥面ABP ， 平面ABP ⊥平面APC .(10分)必要性：过点B 作BE ⊥AP 于E ， ∵ 平面ABP ⊥平面APC ， ∴ BE ⊥面APC ，∴ BE ⊥PC .∵ PC ⊥AB ， ∴ PC ⊥面ABP ， ∴ BP ⊥PC .(14分)18. 解：(1) A ⎝⎛⎭⎫a ，a 24，B ⎝⎛⎭⎫b ，b 24，记f (x )＝x 24，f ′(x )＝x 2，则l 1的方程为y －a 24＝a 2(x －a )，即y ＝a 2x －a 24；同理得l 2的方程为y ＝b 2x －b24.(6分)(2) 由题意a ≠b 且a 、b 不为零，联立方程组可求得P ⎝⎛⎭⎫a 2，0，Q ⎝⎛⎭⎫b 2，0，R ⎝⎛⎭⎫a ＋b2，ab .(8分)抛物线的焦点F (0,1)，∵ K PF ＝－2a，∴ K PF ·K P A ＝－1，故l 1⊥PF ，同理l 2⊥RF .(10分)∴ 经过P 、Q 、R 三点的⊙C 就是以FR 为直径的圆，∴ ⊙C ：x ⎝⎛⎭⎫x －a ＋b 2＋(y －1)(y －ab )＝0，当a ＝4，b ＝－2时，⊙C ：x 2＋y 2－x ＋7y －8＝0，(14分) 显然当a ≠b 且a 、b 不为零时，⊙C 总过定点F (0,1)．(16分) 19. (1) 证明：n ＝1时，a 1＝S 1＝2＋7－2a 1，解得a 1＝3.(2分) n ≥2时，a n ＝S n －S n －1＝2－2a n ＋2a n －1，即3a n ＝2a n －1＋2，可得a n －2＝23(a n －1－2)，所以{a n －2}是首项为1，公比为23的等比数列．(6分)(2) 解：由(1)可得：a n －2＝⎝⎛⎭⎫23n －1，所以a n ＝2＋⎝⎛⎭⎫23n －1.由2＋⎝⎛⎭⎫23n －1≤n 3＋kn 2＋9n 得k ≥2n 2＋⎝⎛⎭⎫23n －1n2－⎝⎛⎭⎫n ＋9n ，(8分) 只需求出p (n )＝2n 2＋⎝⎛⎭⎫23n －1n2－⎝⎛⎭⎫n ＋9n 的最大值即可． 设f (n )＝2n 2，g (n )＝⎝⎛⎭⎫23n －1n2，h (n )＝－⎝⎛⎭⎫n ＋9n ，(10分) 易得f (n )单调递减，g (n )g (n ＋1)＝⎝⎛⎭⎫23n －1n 2÷⎝⎛⎭⎫23n (n ＋1)2＝32⎝⎛⎫n ＋1n 2＞1，所以g (n )＜g (n ＋1)，(12分) 故g (n )单调递减，h (n )－h (n ＋1)＝⎝⎛⎭⎫n ＋1＋9n ＋1－⎝⎛⎭⎫n ＋9n ＝n 2＋n －9n (n ＋1)，当n ≥3时，h (n )＞h (n ＋1)，故n ≥3时，h (n )单调递减，所以n ≥3时，p (n )＝2n 2＋⎝⎛⎭⎫23n －1n2－⎝⎛⎭⎫n ＋9n 随着n 的增大而减小，(14分) 而p (1)＝－7，p (2)＝－356，p (3)＝－46481，所以p (n )的最大值为p (3)＝－46481，故k ≥－46481.(16分)20. 解：(1) 当a ＝0时，f (x )＝－2x ＋2＋ln x ，令f ′(x )＝1x －2＝1－2x x ＞0，解出：0＜x＜12， 所以f (x )的单调增区间为⎝⎛⎭⎫0，12或⎝⎛⎦⎤0，12.(3分) (2) 令f ′(x )＝ax －x ＋1x ＝ax 2－2x ＋1x＝0，f (x )在(1，＋∞)上只有一个极值点⇔f ′(x )＝0在(1，＋∞)上只有一个根且不是重根．(5分)令g (x )＝ax 2－2x ＋1，x ∈(1，＋∞)，① 当a ＝0时，g (x )＝－2x ＋1，不在(1，＋∞)上有一个根，舍去；② 当a ＞0时，g (x )＝ax 2－2x ＋1，在(1，＋∞)上只有一个根且不是重根⇔g (1)＜0⇔0＜a ＜1；③ 当a ＜0时，g (x )＝ax 2－2x ＋1，在(1，＋∞)上只有一个根且不是重根⇔g (1)＞0⇔a ＞1；矛盾．综上所述，实数a 的取值范围是0＜a ＜1.(8分) 注：②③可以合并为：ag (1)＜0⇔0＜a ＜1.(3) 当x 1＝x 2，显然满足，以下讨论x 1≠x 2的情况．① 当a ≥1时，f ′(x )＝ax 2－2x ＋1x ＝a ⎝⎛⎭⎫x －1a 2－1a＋1x，∵ x ∈(0,1]，1a ∈(0,1]，∴ a ⎝⎛⎭⎫x －1a 2－1a ＋1≥1－1a≥0，得到f ′(x )≥0， 即f (x )在(0,1]上单调递增．(10分)对于任意x 1、x 2∈(0,1]，不妨设x 1＜x 2，则有f (x 1)＜f (x 2)，且x 2＞x 1代入不等式 |x 1－x 2|≤|f (x 1)－f (x 2)|⇔f (x 2)－f (x 1)≥x 2－x 1⇔f (x 2)－x 2≥f (x 1)－x 1，引入新函数：h (x )＝f (x )－x ＝12ax 2－3x ＋2＋ln x ，h ′(x )＝ax －3＋1x ＝ax 2－3x ＋1x，所以问题转化为h ′(x )≥0，x ∈(0,1]上恒成立⇔ax 2－3x ＋1≥0⇔a ≥3x －1x 2⇔a ≥⎝⎛⎭⎫3x －1x 2max .令l (x )＝3x －1x 2，通过求导或不等式判断都可以：l ′(x )＝2－3x x 3，当0＜x ＜23，l ′(x )＞0；23＜x ＜1，l ′(x )＜0，所以当x ＝23，l (x )max ＝l ⎝⎛⎭⎫23＝94，所以a ≥94；(13分)② 当a ＜1且a ≠0时，f ′(x )＝ax 2－2x ＋1x，令k (x )＝ax 2－2x ＋1＝0，方程判别式Δ＝4－4a ＞0，且k (1)＝a －1＜0；所以f (x )在(0,1)上只有一个极大值．不妨设极大值点为x 1，记A (x 1，f (x 1))，在A 点处的切线的斜率为0；过A 点作一条割线AB ，肯定存在点B (x 2，f (x 2))使得|k AB |＜1.因为|k AB |慢慢变成0.这样存在x 1、x 2，使得|f (x 1)－f (x 2)||x 1－x 2|＜1与|x 1－x 2|≤|f (x 1)－f (x 2)|矛盾．当a ＝0时，f (x )在(0,1)上只有一个极大值，同样得出矛盾．综上所述，求实数a 的取值范围为a ≥94.(16分)第 10 页 共 11 页 金太阳新课标资源网南京市高三数学附加题参考答案 第页(共2页)南京市名校2011届高三模拟考试数学附加题参考答案及评分标准21. A. 证明：(1)连结GD ，由B 、D 、E 、G 四点共圆，可得∠EGA ＝∠B ，同理∠FGA ＝∠C ，故∠BAC ＋∠EGF ＝∠BAC ＋∠B ＋∠C ＝180°.(5分)(2) 由题知E 、G 、F 、A 四点共圆，故∠EAG ＝∠EFG .(10分)B. 解：由⎪⎪⎪⎪⎪⎪λ－32－2λ＋2＝(λ－3)(λ＋2)＋4＝λ2－λ－2＝0，得λ1＝2，λ2＝－1.(4分)当λ1＝2时，对应的特征向量为α1＝⎣⎢⎡⎦⎥⎤21； 当λ1＝－1时，对应的特征向量为α2＝⎣⎢⎡⎦⎥⎤12，β＝⎣⎢⎡⎦⎥⎤45＝α1＋2α2，(8分)所以M 9β＝29⎣⎢⎡⎦⎥⎤21＋(－1)92⎣⎢⎡⎦⎥⎤12＝⎣⎢⎡⎦⎥⎤1 022 508.(10分)C. (2,0)和⎝⎛⎭⎫1，32(10分) D. 证明： 因为x ＞0，y ＞0，x －y ＞0，所以2x ＋1x 2－2xy ＋y 2－2y ＝2(x －y )＋1(x －y )2(4分) ＝(x －y )＋(x －y )＋1(x －y )2≥33(x －y )2·1(x －y )2＝3， 所以2x ＋1x 2－2xy ＋y 2≥2y ＋3.(10分)22. (1) 解：建立空间直角坐标系，则E (1,0,0)，F (0,0,1)，EF →＝(－1,0,1)． 设平面ABCD 的法向量为n ，则n ＝(0,0,1)．D (0，－2,0)，F (0,0,2)，∴ EF →＝(－1,0,2)，DF →＝(0,2,2)．设平面FDE 的法向量为m ，则m·DF →＝0，m ·EF →＝0，m ＝(2，－1,1)．(4分)∴ cos 〈m ，n 〉＝m·n|m||n|＝66.∴ 二面角F —DE —C 的余弦值为66.(6分)(2) 显然D 1(0，－2,4)，B (2,0,0)，设F (0,0，t )，则EF →＝(－1,0，t )，BD 1＝(－2，－2,4)．要使EF ⊥BD 1，只要EF →·BD 1→＝0,2＋4t ＝0，t ＝－12. ∴ λ＝－9.(10分)23. 解：(1) 由题意X 服从B (4,0.9)，概率分布略，E (X )＝4×0.9＝0.36.(4分) (2) 由题意n ＝1,2,4,5,10,20,25,50,100.当n ＝1或100时，就是逐只检验，检验次数为100.(5分) 当n ∈{2,4,5,10,20,25,50}，将100只鸡平均分成100n组，每组n 只，设X 为n 只鸡中的病鸡数，则X 服从B (n,0.9)，这n 只鸡中无病鸡的概率为0.9n ，这时化验1次；若n 只鸡中有病鸡，其概率为1－0.9n ，金太阳新课标资源网 第 11 页 共 11 页 金太阳新课标资源网 此时化验n ＋1次．设Y 为nE (Y )＝0.9n ＋(n ＋1)(1－0.9n )－0.1)n . 则100n组共需化验次数为 E (Y )＝100n[n ＋1－n ·(1－0.1)n ] ≈100n ⎣⎡⎦⎤n ＋1－n ·⎝⎛⎭⎫1－0.1n ＋n 2－n 2×0.12 ＝100n ⎝⎛⎭⎫1＋0.1n 2－n 2－n 200 ＝100n＋9.5n ＋0.5，(8分) 函数f (x )＝100x＋9.5x 在(0,3]内递减，在[4，＋∞)内递增． 又f (2)＝69，f (4)＝63，故n ＝4时，化验次数最少．(10分)。

平面向量 题组一一、选择题1．（宁夏银川一中2011届高三第五次月考试题全解全析理）),(,,2121R ，∈+=+=λλλλ若是不共线的向量，则A 、B 、C 三点共线的充要条件为（ ） A ．121-==λλ B ．121==λλ C ．0121=+⋅λλ D ．0121=-λλ【答案】D【分析】由于向量,AC AB 由公共起点，因此三点,,A B C 共线只要,AC AB共线即可，根据向量共线的条件即存在实数λ使得AC AB λ=，然后根据平面向量基本定理得到两个方程，消掉λ即得结论。

【解析】只要要,AC AB共线即可，根据向量共线的条件即存在实数λ使得AC AB λ= ，即21()a b a b λλλ+=+ ，由于,a b不共线，根据平面向量基本定理得11λλ=且2λλ=，消掉λ得121λλ=。

【考点】平面向量。

【点评】向量的共线定理和平面向量基本定理是平面向量中的两个带有根本意义的定理，平面向量基本定理是平面内任意一个向量都可以用两个不共线的向量唯一地线性表示，这个定理的一个极为重要的导出结果是，如果,a b不共线，那么1212a b a b λλμμ+=+ 的充要条件是11λμ=且22λμ=。

2．（浙江省金丽衢十二校2011届高三第一次联考文）平面向量b a 与的夹角为120,a (2,0),|b |1,||a b ︒=-=+ 则（ ）A ．3B C ．7D 答案 B.3. （山东省日照市2011届高三第一次调研考试文）设平面向量(1,2),(1,)a b m ==-，若//a b ，则实数m 的值为(A)1- (B)2- (C)1 (D)2 答案 B.4.（山东省莱阳市2011届高三上学期期末数学模拟6理）已知)5,6(),6,5(=-=b a ，则a 与（ ）A 、垂直B 、不垂直也不平行C 、平行且同向D 、平行且反向 答案 A. 5．（吉林省东北师大附中2011届高三上学期第三次模底考试理）已知向量()()75751515a cos sin b cos sin |a b |==-，，，，那么的值是 （ ）A ．21B ．22 C ．23 D ．1答案 D. 6．（湖南省嘉禾一中2011届高三上学期1月高考押题卷）在平行四边形ABCD 中，AC 与BD交于点O E ，是线段OD 的中点，AE 的延长线与CD 交于点F ．若AC a = ，BD b =，则AF =（ ）A ．1142a b +B ．2133a b +C ．1124a b +D ．1233a b +答案 B. 7．（湖北省涟源一中、双峰一中2011届高三第五次月考理）已知ABC ∆和点M 满足0MA MB MC ++=．若存在实m 使得 AB AC mAM +=成立，则m =（ ）A ．2B ．3C ．4D ．5答案 B.8．（湖北省八校2011届高三第一次联考理）如图，在ABC ∆中，13A N N C =，P 是BN 上的一点，若2 11AP m AB AC =+，则实数m 的值为（ ）.A 911 .B 511.C 311 .D 211答案 C.9．（黑龙江省佳木斯大学附属中学2011届高三上学期期末考试理）已知向量a=(－2,1)，b =(－3，0)，则a 在b方向上的投影为 ( )A ．－2B ．5C ．2 D答案 C. 10．（黑龙江省哈九中2011届高三期末考试试题理）已知(2,0),(2,2),cos sin )OB OC CA αα===，则OA 与OB 夹角的取值范围是（ ）A ．,123ππ⎡⎤⎢⎥⎣⎦ B ．5,412ππ⎡⎤⎢⎥⎣⎦ C ．5,1212ππ⎡⎤⎢⎥⎣⎦ D ．5,122ππ⎡⎤⎢⎥⎣⎦答案 C.11．（河南省鹿邑县五校2011届高三12月联考理）若两个非零向量a ，b满足2a b a b a +=-=，则向量a b + 与a b - 的夹角是（ ）CABN PA ．6π B ．3π C ．23π D ．56π答案 C.12. （河南省焦作市部分学校2011届高三上学期期终调研测试理）如图，向量等于A ．B ．C ．D ．答案 D.13．（广东省高州市南塘中学2011届高三上学期16周抽考理）已知向量(2,3),(5,1)a b ==-- ，若ma nb + (0)m ≠与a 垂直，则nm等于（ ）A ．1-B ．0C ．1D ．2答案 C.14.（广东六校2011届高三12月联考文） 已知平面向量(3,1),(,3)a b x ==-，且a b ⊥ ，则x =A ．3- B.1- C.1D. 3答案 C.15．（北京四中2011届高三上学期开学测试理科试题）已知为非零的平面向量，甲：，乙：，则甲是乙的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 答案 B.16.（北京五中2011届高三上学期期中考试试题理） 设非零向量,满足+==，则与+的夹角为（ ）)(A 30° )(B 60° )(C 90° )(D 120°答案 D. 17．（福建省安溪梧桐中学2011届高三第三次阶段考试理）已知向量a b a 且)1,(sin ),2,(cos αα=-=∥b，则2sin cos αα等于（ ）A ．3B ．－3C ．45 D ．－45答案 D.18.（福建省惠安荷山中学2011届高三第三次月考理科试卷）已知),(,,2121R ，∈+=+=λλλλ若是不共线的向量，则A 、B 、C 三点共线的充要条件为 ( ) A ．121-==λλ B 121==λλC ．0121=-λλD ．1210λλ⋅+=答案 B.19.（福建省四地六校2011届高三上学期第三次联考试题理） 已知向量与则),2,1,1(),1,2,0(--==的夹角为（ ）A ．0°B ．45°C ．90°D ．180°答案 C. 20．（福建省厦门双十中学2011届高三12月月考题理） 设向量"//""2"),3,1(),1,1(x x x 是则=+=-=的（ ） A ．充分但不必要条件 B ．必要但不充分条件 C ．充要条件 D ．既不充分也不必要条件 答案 A.21.（福建省厦门外国语学校2011届高三11月月考理）已知),(,,2121R b a AC b a AB ，b a ∈+=+=λλλλ若是不共线的向量，则A 、B 、C 三点共线的充要条件为 A ．121-==λλ B 121==λλC ．0121=-λλD ．1121=+⋅λλ答案 C. 二、填空题22．（宁夏银川一中2011届高三第五次月考试题全解全析理）已知和b的夹角为120︒，||1,||3a b ===- ．【分析】根据向量模的含义222()()2a b a b a b a b a b -=--=+-，讲已知代入即可。

题型一
空间几何体的三视图、 空间几何体的三视图、直观图
)
北京)一个长方体去掉一个小长方体 【例 1】 (1)(2010·北京 一个长方体去掉一个小长方体，所得几何体的 】 北京 一个长方体去掉一个小长方体， 视图与侧(左 视图分别如下图所示 则该几何体的俯视图为( 视图分别如下图所示， 正(主)视图与侧 左)视图分别如下图所示，则该几何体的俯视图为 主 视图与侧
(3)正棱台的性质 正棱台的性质 侧面是全等的等腰梯形；斜高相等；棱台的高、 侧面是全等的等腰梯形；斜高相等；棱台的高、斜高和两底面的边心 距组成一个直角梯形；棱台的高、 距组成一个直角梯形；棱台的高、侧棱和两底面外接圆的半径组成一 个直角梯形；棱台的斜高、 个直角梯形；棱台的斜高、侧棱和两底面边长的一半也组成一个直角 梯形． 梯形． 2．圆柱、圆锥、圆台 ．圆柱、圆锥、 (1)圆柱、圆锥、圆台的概念 圆柱、圆锥、 圆柱 分别以矩形的一边、直角三角形的一直角边、 分别以矩形的一边、直角三角形的一直角边、直角梯形垂直于底边 的腰所在的直线为旋转轴， 的腰所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几 何体分别叫做圆柱、圆锥、圆台． 何体分别叫做圆柱、圆锥、圆台． (2)圆柱、圆锥、圆台的性质 圆柱、圆锥、 圆柱 轴截面分别是矩形、等腰三角形、等腰梯形； 轴截面分别是矩形、等腰三角形、等腰梯形；平行于底面的截面都是 圆．
3．球 ． (1)球面与球的概念 球面与球的概念 半圆以它的直径所在直线为旋转轴旋转一周所成的曲面叫做球面． 半圆以它的直径所在直线为旋转轴旋转一周所成的曲面叫做球面．以半 圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体叫做球体， 圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体叫做球体， 简称球，半圆的圆心叫做球的球心． 简称球，半圆的圆心叫做球的球心． (2)球的截面性质 球的截面性质 球心和截面圆心的连线垂直于截面；球心到截面的距离 d 与球的半径 球心和截面圆心的连线垂直于截面； R 及截面圆的半径 r 的关系为 d＝ R2－r2. ＝ 4．柱体、锥体、台体的表面积(不要求记忆 ．柱体、锥体、台体的表面积 不要求记忆 不要求记忆) (1)直棱柱、正棱锥、正棱台的侧面积 直棱柱、正棱锥、 直棱柱 1 1 S 直棱柱侧＝Ch，S 正棱锥侧＝ Ch′，S 正棱台侧＝ (C＋C′)h′(其中 C、C′为 ， ′ 2 2 ＋ ′ ′ 其中 、 ′ 底面周长， 为高， ′为斜高)． 底面周长，h 为高，h′斜二测画法的步骤： ．水平放置的平面图形的直观图的斜二测画法的步骤： (1)在已知图形中取互相垂直的 x 轴和 y 轴，两轴相交于 O 点， 在已知图形中取互相垂直的 画直观图时， 画直观图时，把它们画成对应的 x′轴与 y′轴，两轴相交于 O′ ′ ′ ′ 且使∠ ′ ′ ′ 且使∠x′O′y′＝45°，用它们确定的平面表示水平面； ，用它们确定的平面表示水平面； (2)已知图形中平行于 x 轴或 y 轴的线段，在直观图中，分别画成 已知图形中平行于 轴的线段，在直观图中， 平行于 x′轴或 y′轴的线段； ′ ′轴的线段； (3)已知图形中平行于 x 轴的线段，在直观图中保持原长度不变，平 已知图形中平行于 轴的线段，在直观图中保持原长度不变， 行于 y 轴的线段，长度变为原来的一半. 轴的线段，长度变为原来的一半

7． （2） ， （4）
11． C 1, 3
12． 7 ≤ a 1
二、解答题：本大题共 6 小题，共 90 分． 15． （本题满分 14 分） 解： （1）由|a－b|=2，得|a－b| 2 a 2 2a· b b 2 4 1 2 a· b 4 ，∴ a· b
AB 于点 E，连接 EC，求∠OEC． 交劣弧
B．选修 4－2：矩阵与变换
1 2 曲线 C1 : x 2 2 y 2 1 在矩阵 M 的作用下变换为曲线 C2 ， 0 1
求 C2 的方程． C．选修 4－4：坐标系与参数方程
x 1 cos x 1 2t P 为曲线 C1 ： （ 为参数）上一点，求它到直线 C2 ： （ t 为参数）距离 y 2 y sin
π ，∴ AE BE ． 2
„„„„„„„„„„„6 分
又∵直线 BC⊥平面 ABE，∴ AE BC ． 又 BC BE B ，∴直线 AE 平面 BCE ． „„„„„„„„„„„„„„„„8 分
数学试卷
第 5 页 （共 11 页）
由（1）知，FG∥AE，∴直线 FG 平面 BCE ．
①最多有几项在 1～100 之间？ ②最多有几项是 1～100 之间的整数？ （2）当 q＞1 时，在数列{an}中，最多有几项是 100～1000 之间的整数？ （参考数据：lg3=0.477，lg2=0.301） ．
数学试卷
第 3 页 （共 11 页）
B．附加题部分 21． 【选做题】本题包括 A，B，C，D 共 4 小题，请从这 4 题中选做 2 小题，每小题 10 分，共 20 分．请在答题卡上准确填涂题目标记，解答时应写出文字说明、证明过程或演算步骤． A．选修 4－1：几何证明选讲 锐角三角形 ABC 内接于⊙O，∠ABC=60，∠BAC=40．作 OE⊥AB

巩固1．设平面α的法向量为(1,2，－2)，平面β的法向量为(－2，－4，k )，若α∥β，则k ＝( )A ．2B ．－4C ．4D ．－2解析：选C.∵α∥β，∴(－2，－4，k )＝λ(1,2，－2)，∴－2＝λ，k ＝－2λ，∴k ＝4.2．(原创题)如果平面的一条斜线和它在这个平面上的射影的方向向量分别是a ＝(0,2,1)，b ＝(2，5，5)，那么这条斜线与平面的夹角是( )A ．90°B ．60°C ．45°D ．30°解析：选D.cos θ＝a ·b |a ||b |＝32，因此a 与b 的夹角为30°. 3．(2008年高考福建卷)如图，在长方体ABCD －A 1B 1C 1D 1中，AB ＝BC ＝2，AA 1＝1，则BC 1与平面BB 1D 1D 所成角的正弦值为( ) A.63 B.255C.155D.105解析：选D.以D 点为坐标原点，以DA 、DC 、DD 1所在的直线为x 轴、y 轴、z 轴，建立空间直角坐标系(图略)，则A (2,0,0)，B (2,2,0)，C (0,2,0)，C 1(0,2,1)∴＝(－2,0,1)，＝(－2,2,0)，且为平面BB 1D 1D 的一个法向量．∴cos 〈，〉＝＝45·8＝105.4.长方体ABCD －A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝1，E 为CC 1的中点，则异面直线BC 1与AE 所成角的余弦值为__________．解析：建立坐标系如图，则A (1,0,0)，E (0,2,1)，B (1,2,0)，C 1(0,2,2)，＝(－1,0,2)，＝(－1,2,1)， cos 〈，〉＝＝3010.答案：30105．在空间直角坐标系中，定义：平面α的一般方程为：Ax ＋By ＋Cz ＋D ＝0(A ，B ，C ，D ∈R ，且A ，B ，C 不同时为零)，点P (x 0，y 0，z 0)到平面α的距离为：d ＝|Ax 0＋By 0＋Cz 0＋D |A 2＋B 2＋C 2.则在底面边长与高都为2的正四棱锥中，底面中心O 到侧面的距离等于__________．解析：如图，以底面中心O 为原点建立空间直角坐标系O －xyz ，则A (1,1,0)，B (－1,1,0)，P (0,0,2)，设平面P AB 的方程为Ax ＋By ＋Cz ＋D ＝0，将以上3个坐标代入计算得A ＝0，B ＝－D ，C ＝－12D ，∴－Dy －12Dz ＋D ＝0，即2y ＋z －2＝0，∴d ＝|2×0＋0－2|22＋1＝255.答案：2556．如图，在四棱锥P －ABCD 中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD ＝DC ，E 、F 分别是AB 、PB 的中点．(1)求证：EF ⊥CD ；(2)求DB 与平面DEF 所成角的正弦值．解：以DA ，DC ，DP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系(如图)．设AD ＝a ，则D (0,0,0)，A (a,0,0)，B (a ，a,0)，C (0，a,0)，E (a ，a 2，0)，P (0,0，a )，F (a 2，a 2，a 2)．(1)证明：∵·＝(－a 2，0，a 2)·(0，a,0)＝0，∴⊥，∴EF ⊥CD .(2)设平面DEF 的法向量为n ＝(x ，y ，z )，由，得⎩⎪⎨⎪⎧ (x ，y ，z )·(a 2，a 2，a 2)＝0(x ，y ，z )·(a ，a 2，0)＝0， 即⎩⎪⎨⎪⎧ a 2(x ＋y ＋z )＝0ax ＋a 2y ＝0，取x ＝1，则y ＝－2，z ＝1，∴n ＝(1，－2,1)，∴cos 〈，n 〉＝＝－a 2a ·6＝－36. 设DB 与平面DEF 所成角为θ，则sin θ＝36.练习1．(2010年北京西城调研)下列命题中，正确命题的个数为( ) ①若n 1，n 2分别是平面α，β的法向量，则n 1∥n 2⇔α∥β；②若n 1，n 2分别是平面α，β的法向量，则α⊥β⇔n 1·n 2＝0；③若n 是平面α的法向量，a 与α共面，则n ·a ＝0；④若两个平面的法向量不垂直，则这两个平面一定不垂直．A ．1B ．2C ．3D ．4解析：选C.①中平面α，β可能平行，也可能重合，结合平面法向量的概念，易知②③④正确，故选C.2．已知平面α内有一个点M (1，－1,2)，平面α的一个法向量是n ＝(6，－3,6)，则下列点P 中在平面α内的是( )A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)解析：选A.∵n ＝(6，－3,6)是平面α的法向量，∴n ⊥，在选项A 中，＝(1,4,1)，∴n ·＝0.3．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为( )A ．75°B ．60°C ．45°D ．30°解析：选C.如图，四棱锥P －ABCD 中，过P 作PO ⊥平面ABCD 于O ，连结AO ，则AO 是AP 在底面ABCD 上的射影，∴∠P AO 即为所求线面角，∵AO ＝22，P A ＝1，∴cos ∠P AO ＝AO P A ＝22.∴∠P AO ＝45°，即所求线面角为45°.4.如右图所示，正方体ABCD －A1B 1C 1D 1中，E 、F 分别是正方形ADD 1A 1和ABCD 的中心，G 是CC 1的中点，设GF 、C 1E 与AB所成的角分别为α、β，则α＋β等于( )A ．120°B ．60°C ．75°D ．90°解析：选D.建立坐标系如图，B (2,0,0)，A (2,2,0)，G (0,0,1)，F (1,1,0)，C 1(0,0,2)，E (1,2,1)．则＝(0,2,0)，＝(1,1，－1)，＝(1,2，－1)，∴cos 〈，〉＝13， cos 〈，〉＝23，∴cos α＝13， cos β＝23，sin β＝13，∴α＋β＝90°， 故选D.5．若正三棱锥的侧面都是直角三角形，则侧面与底面所成二面角的余弦值是( ) A.63 B.33 C.23 D.13解析：选B.以正三棱锥O －ABC 的顶点O 为原点，OA ，OB ，OC 为x ，y ，z 轴建系(图略)，设侧棱长为1，则A (1,0,0)，B (0,1,0)，C (0,0,1)，侧面OAB 的法向量为＝(0,0,1)，底面ABC 的法向量为n ＝(13，13，13)，∴cos 〈， n 〉＝＝131·(13)2＋(13)2＋(13)2＝33. 6．在正方体ABCD －A 1B 1C 1D 1中，若E 为A 1C 1中点，则直线CE 垂直于( )A ．ACB ．BDC ．A 1D D ．A 1A解析：选B.以A 为原点，AB 、AD 、AA 1所在直线分别为x ，y ，z 轴建系(图略)，设正方体棱长为1，则A (0,0,0)，C (1,1,0)，B (1,0,0)，D (0,1,0)，A 1(0,0,1)，E (12，12，1)，∴＝(－12，－12，1)， ＝(1,1,0)，＝(－1,1,0)，＝(0,1，－1)，＝(0,0，－1)，显然·＝12－12＋0＝0，∴⊥，即CE ⊥BD .7．正四棱锥S －ABCD 中，O 为顶点在底面上的射影，P 为侧棱SD 的中点，且SO ＝OD ，则直线BC 与平面P AC 所成的角是__________．解析：如图，以O 为原点建立空间直角坐标系O －xyz .设OD ＝SO ＝OA ＝OB ＝OC ＝a ，则A (a,0,0)，B (0，a,0)，C (－a,0,0)，P (0，－a 2，a 2)，则＝(2a,0,0)，＝(－a ，－a 2，a 2)，＝(a ，a,0)，设平面P AC 的法向量为n ，可求得n ＝(0,1,1)，则cos 〈，n 〉＝＝a 2a 2·2＝12， ∴〈， n 〉＝60°，∴直线BC 与平面P AC 所成的角为90°－60°＝30°.答案：30°8．如图，正方体ABCD －A1B 1C 1D 1的棱长为1，E 、F 分别是棱BC 、DD 1上的点，如果B 1E ⊥平面ABF ，则CE 与DF 的和的值等于__________．解析：以D 1A 1、D 1C 1、D 1D 所在直线分别为x 、y 、z 轴建立空间直角坐标系(图略)，设CE ＝x ，DF ＝y ，则易知E (x,1,1)，B 1(1,1,0)⇒＝(x －1,0,1)，又F (0,0,1－y )，B (1,1,1)⇒＝(1,1，y )，由于AB ⊥B 1E ，故若B 1E ⊥平面ABF ，只需·＝(1,1，y )·(x －1,0,1)＝0⇒x ＋y ＝1.答案：19.如图，在正三棱柱ABC －A1B 1C 1中，AB ＝1，AA 1＝2，则二面角C 1－AB －C 的余弦值为__________．解析：如图建立空间直角坐标系，则A (0,0,0)，＝(0,1,2)，＝(32，12，0)．设n ＝(x ，y ，z )为平面ABC 1的法向量则⎩⎨⎧ 32x ＋12y ＝0，y ＋2z ＝0.取n ＝(－233，2，－1)，取m ＝(0,0,1)，作为平面ABC 的法向量．则cos 〈m ，n 〉＝－1193＝－5719.∴二面角C 1－AB －C 的余弦值为5719.答案：571910．如图，在正四棱柱ABCD －A1B 1C 1D 1中，AB ＝2，AA 1＝4，E 为BC 的中点，F 为CC 1的中点．(1)求EF 与平面ABCD 所成的角的余弦值；(2)求二面角F －DE －C 的余弦值．解：建立如图所示的空间直角坐标系D －xyz ，则D (0,0,0)，A (2,0,0)，C (0,2,0)，B (2,2,0)，E (1,2,0)，F (0,2,2)．(1)＝(－1,0,2)．易得平面ABCD 的一个法向量为n ＝(0,0,1)，设与n 的夹角为θ，则cos θ＝＝255，∴EF 与平面ABCD 所成的角的余弦值为55.(2)＝(－1,0,2)，＝(0,2,2)．设平面DEF的一个法向量为m，则m·＝0，m·＝0，可得m＝(2，－1,1)，∴cos〈m，n〉＝m·n|m||n|＝66，∴二面角F－DE－C的余弦值为6 6.11．正三棱柱ABC－A1B1C1的所有棱长均为2，P是侧棱AA1上任意一点．(1)求正三棱柱ABC－A1B1C1的体积；(2)判断直线B1P与平面ACC1A1是否垂直，请证明你的结论；(3)当BC1⊥B1P时，求二面角C－B1P －C1的余弦值．解：(1)V ABC－A1B1C1＝S△ABC·AA1＝34×22×2＝2 3.(2)不垂直．建立如图所示的空间直角坐标系O－xyz，设AP＝a，则A，C，B1，P的坐标分别为(0，－1,0)，(0,1,0)，(3，0,2)，(0，－1，a)，＝(0,2,0)，＝(－3，－1，a－2)，·＝－2≠0，∴B1P不垂直AC，∴直线B1P不可能与平面ACC1A1垂直．(3)＝(－3，1,2)，由BC1⊥B1P，得·＝0，即2＋2(a－2)＝0，∴a＝1.又BC1⊥B1C，∴BC1⊥平面CB1P，∴＝(－3，1,2)是平面CB1P的法向量．设平面C1B1P的法向量为n＝(1，y，z)，设二面角C －B 1P －C 1的大小为α，则cos α＝＝64，∴二面角C －B 1P －C 1的余弦值的大小为64.12．如图，四棱锥P －ABCD 中，底面ABCD 是矩形，P A ⊥底面ABCD ，P A ＝AB ＝1，AD ＝3，点F 是PB 的中点，点E 在边BC 上移动．(1)点E 为BC 的中点时，试判断EF 与平面P AC 的位置关系，并说明理由；(2)求证：无论点E 在BC 边的何处，都有PE ⊥AF ；(3)当BE 为何值时，P A 与平面PDE 所成角的大小为45°？ 解：(1)当点E 为BC 的中点时，EF 与平面P AC 平行．∵在△PBC 中，E 、F 分别为BC 、PB 的中点，∴EF ∥PC .又EF ⊄平面P AC ，而PC ⊂平面P AC ，∴EF ∥平面P AC .(2)证明：建立如图所示空间直角坐标系，则P (0,0,1)，B (0,1,0)，F (0，12，12)，D (3，0,0)，设BE ＝x (0≤x ≤3)，则E (x,1,0)， ·＝(x,1，－1)·(0，12，12)＝0，∴PE ⊥AF .(3)设平面PDE 的法向量为m ＝(p ，q,1)，（高考、中考、考研、留学英国） 由，得m ＝(13，1－x 3，1)． 而＝(0,0,1)，依题意P A 与平面PDE 所成角为45°，所以sin45°＝22＝， ∴113＋(1－x 3)2＋1＝12， 得BE ＝x ＝3－2或BE ＝x ＝3＋2>3(舍)． 故BE ＝3－2时，P A 与平面PDE 所成角为45°.。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年北京市高中数学人教A 版选修一空间向量与立体几何强化训练(14)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）1. 将边长为 的正方形 及其内部)绕 旋转一周形成圆柱，如图，长为， 长为，其中 与在平面的同侧，则直线与平面所成的角的正弦值为（ ）A. B. C.D.+-++---++2. 如图，在平行六面体ABCD ﹣A 1B 1C 1D 1中，若= ， = ，= ， 则=（ ）A. B. C. D. 3. 在正方体 中，M ，N 分别为AD ， 的中点，O 为侧面 的中心，则异面直线MN 与 所成角的余弦值为（ ）A.B. C. D.4.如图，平面ABCD 平面ABEF ，四边形ABCD 是正方形，四边形ABEF 是矩形，且， G 是EF 的中点，则GB 与平面AGC 所成角的正弦值为（ ）A. B. C. D.-10105. 已知空间向量 ，， 且 ， 则的值为（ ）A. B. C. D.在轴上在平面内在平面内在平面内6. 点(2，0，1)在空间直角坐标系中的位置是（ ）A. B. C. D. 7. 若向量、、的起点与终点M 、A 、B 、C 互不重合且无三点共线，且满足下列关系（O 是空间任一点），则能使向量、、成为空间一组基底的关系是（ ）A. B.C. D.8. 在三棱锥中，若为的中点，则（ ）A.B.C. D.9. 已知P 是正六边形ABCDEF 外一点，O 为正六边形ABCDEF 的中心，则等于（）A. B. C. D. 1，-2，-3-2，1，-3-2，1，3-1，2，310. 设（其中是两两垂直的单位向量），若，则实数的值分别是（ ）A. B. C. D. 11. 已知大小为的二面角棱上有两点A 、B，，，，， 若，，， 则的长为（ ）2240A. B. C. D.4-4-612. 已知=（2，﹣1，3），=（﹣4，2，x ），=（1，﹣x ，2），若（+）⊥ ， 则x 等于（ ）A. B. C.D. 13. 已知 ， ，则线段 的中点坐标为 ； .14. 已知直线是曲线及抛物线的公切线，切点分别为， 则，若， 则.15. 已知点是正方体表面上一动点，且满足 ， 设 与平面所成的角为 ， 则的最大值是 .16. 已知半径为 的球面上有 、 、 、 四点，满足 ，，，则球心 到平面的距离为 ，三棱锥体积的最大值为 .17. (1) 已知，，求，， ；(2) 已知空间内三点，，.求以向量，为一组邻边的平行四边形的面积 .18. 在四棱锥P−ABCD 中，平面PAD ⊥平面ABCD ，O 为AD 的中点，DC//AB ，DC ⊥AD ，PA=PD ，PO=AB=2DC ，BC=CD，(1) 求证：平面PBC ⊥平面POC ；(2) 求平面PAB与平面PCB所成角的余弦值.19. 如图，已知三棱柱，底面，，，为的中点.（I）证明：面；（Ⅱ）求直线与平面所成角的正弦值.20. 如图，在空间几何体中，平面平面，平面，与都是以为底的等腰三角形，为的中点，，．(1) 证明：点在平面内；(2) 已知，，求二面角的余弦值．21. 如图，在直三棱柱中，平面侧面．(1) 求证：；(2) 若直线AC与平面所成的角为，二面角的大小为，试判断与的大小关系，并予以证明．答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)(1)(2)19.20.(1)(2)21.(1)(2)。