初中几何中常见的基本图形1

初中数学常见的几何图形名称1.点（Point）：在几何学中，点是最基本的几何对象，不具有大小和形状，仅有位置。

2.直线（Line）：直线是由无限多个点连成的，它没有弯曲或弯折。

3.线段（Line Segment）：线段是由两个端点和它们之间所有点构成的部分。

4.射线（Ray）：射线是由一个起点和一个方向组成的直线。

5.角（Angle）：两条射线共享一个起点所形成的图形。

6.三角形（Triangle）：由三条边和三个顶点组成的图形。

7.直角三角形（Right Triangle）：一个内角为90度的三角形。

8.直观三角形（Obtuse Triangle）：一个内角大于90度的三角形。

9.锐角三角形（Acute Triangle）：所有内角都小于90度的三角形。

10.等腰三角形（Isosceles Triangle）：两边长度相等的三角形。

11.等边三角形（Equilateral Triangle）：所有边长度相等的三角形。

12.四边形（Quadrilateral）：由四条边和四个顶点组成的图形。

13.矩形（Rectangle）：具有四个直角的四边形。

14.平行四边形（Parallelogram）：具有两对平行边的四边形。

15.正方形（___）：具有四个相等边和四个直角的四边形。

16.梯形（Trapezoid）：具有一对平行边的四边形。

17.圆（Circle）：由一条连续曲线上所有点的集合组成的图形。

18.弧（Arc）：是圆上的一部分，由两个端点和圆弧之间的弦构成。

19.扇形（Sector）：是圆心角和圆弧所围成的区域。

20.椭圆（Ellipse）：离两个固定点距离之和等于常数的点的集合。

以上是初中数学中常见的几何图形和名称说明。

了解这些概念将有助于学生在学习几何学时更好地理解和应用。

初中几何基本图形归纳(基本图形+常考图形)初中几何常见基本图形1.基本图形及结论A、B、C、D分别为四边形的顶点，AC=BD，AD=BC，∠AOC=∠BOD，∠AOD=∠BOC。

2.直角三角形在直角三角形ABC中，∠C=90°，OA为斜边的中线，OD⊥XXX。

3.等腰三角形在等腰三角形ABC中，AB=AC，AD为角A的平分线，BD=CD。

4.三角形的面积公式在三角形ABC中，AB2=BD×BC，AC2=CD×BC。

5.三角形内角和公式在三角形ABC中，∠A+∠B+∠C=180°。

6.平行四边形在平行四边形ABCD中，∠A+∠B=∠C+∠D，AC平分∠BAD。

7.直角三角形的斜边中线在直角三角形ABC中，BD为斜边AC的中线，∠B=∠D。

8.直角三角形的高线在直角三角形ABC中，PA⊥AB，PB⊥AC，PC⊥BC，且PA=PB+PC，∠P=∠A/2.9.直角三角形的内心在直角三角形ABC中，∠P=∠A/2，PD为角A的平分线，AD=BD=AC=DC。

10.直角三角形的外心在直角三角形ABC中，∠P=90°-∠A/2，以AB的中点O为圆心，AB为半径作圆，交AC于点P，则P为三角形ABC的外心。

11.等腰三角形的中线在等腰三角形ABC中，AB=CB，BD为角B的平分线，且BC∥AD。

12.等边三角形在等边三角形ABC中，AB=AC=BC。

13.等角三角形在等角三角形ABC中，∠A=∠B=∠C。

14.三角形的相似在三角形ABC和DEF中，如果∠A=∠D，∠B=∠E，∠C=∠F，则称三角形ABC与DEF相似。

15.圆的基本性质在圆O中，AB为直径，则∠C=90°，且AC=BC=OD。

16.圆的切线在圆O中，以点A为圆心，AB为半径作圆，则CD为圆O的切线。

17.圆的割线在圆O中，以点A为圆心，AC为半径作圆，则BD为圆O的割线。

18.圆的弦在圆O中，AB为圆O的弦，R为圆O的半径，则弦长公式为AB2=BD×BC，且弦AB平分∠AOB。

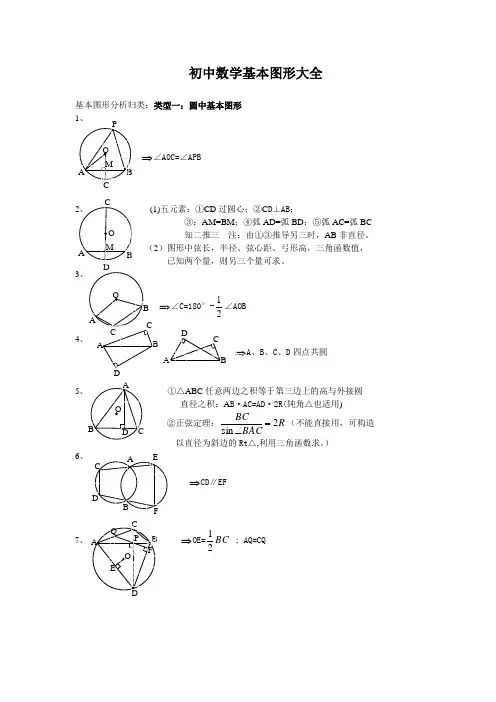
初中数学基本图形大全基本图形分析归类：类型一：圆中基本图形D⊥AB；弧BD；⑤弧AC=弧BCAB非直径。

、C、D四点共圆·2R(钝角△也适用)=（不能直接用，可构造R2）8、（弧AC=弧EC ） ⇒AM=CM=FM ;AC=EC;AE CD 21=; ABAD AE AM AC ⋅=⋅=2;BF OM 21=9∽CDE, △ABD ∽△AEC ∽BED,·AC=AD ·AE,AE ·DE=BE ·CEBAD ∠cos 2 关注∠BAC 为特殊角时图形的 10 AC 、AB 的对称点在⊙O 上，11DC 切⊙O 于C 点 知二推一12 ,BO ⊥DE , ∠DEF=90°-21∠A 13 14CE 切⊙O 于点E,知二推一15⇒C △PDE=PA+PB ∠DOE=)180(21P ∠-16 ①EA 切⊙O 于点A AE ∥CF ③AP=EP 知二推一17、 △ABD 、△ACE 为等边△⇒ BE=CD,BE 、CD 相交所成锐角为60° 18、正方形ABDE 、正方形ACFG ⇒EC=BG ,BG ⊥CE注：条件可为等腰Rt △19、①AD 平分∠CAB, ②DE ∥AC,③AE=DE 知二推一20、 △ABC 为等腰Rt △，AE 平分∠CAB ，BD ⊥AD⇒AE=2BD21、⇒C △ADE=AB+ACA B C DEA B C D E F G A B CD E A B C D E A B C D E M22、 △ACD 、△BCE 为等边△，A 、C 、B 三点共线⇒ △ACE ≌△DCB , △ACM ≌△DCN , △MCE ≌△NCB AE=BD,AM=DN,EM=BN,CM=CN,AE 、BD 相交所成锐角为60° AO=DO+CO,BO=EO+CO,OM+ON=OC,OC 平分∠AOB 注：△BCE 旋转时，结论有变化。

初中常见几何模型结论全文共四篇示例，供读者参考第一篇示例：初中阶段学习几何模型是数学学习的一个重要组成部分，通过学习几何模型可以帮助学生理解几何概念，培养其逻辑思维和空间想象能力。

在初中课本中，涉及到的常见几何模型有三角形、四边形、圆等，学生需要掌握这些模型的性质和结论。

本文将从几何模型的性质和结论入手，详细介绍初中常见几何模型的相关知识。

一、三角形三角形是几何学中的基本图形之一，包括等腰三角形、等边三角形、直角三角形等。

在初中阶段，学生主要需要掌握三角形的性质和定理，如三角形内角和为180度、三角形外角和等于其对应内角等。

还要掌握利用角平分线、垂直平分线等相关知识解决三角形问题。

常见的三角形结论包括：1.等腰三角形的底角相等，等边三角形的三个角都相等。

2.三角形内角和为180度，即三角形的三条边可以围成一个封闭的图形。

3.等腰直角三角形的斜边等于底边的平方和。

二、四边形四边形是指有四条边的多边形，包括矩形、正方形、菱形等。

在初中阶段，学生需要掌握四边形的性质和定理，如内角和、对角线交点的性质、边的性质等。

学生还需要学会利用平行线、垂直线等概念解决四边形问题。

1.矩形的对角线相等且互相垂直。

4.平行四边形的对角线相等、同一条对角线上的内角互补。

三、圆圆是一个重要的几何模型，具有许多独特的性质和特点。

在初中阶段，学生需要掌握圆的周长、面积计算方法，以及圆的心、弦、弧等概念。

学生还需要掌握切线和切于圆的定理，并能够运用这些知识解决有关圆的问题。

1.圆的周长等于其直径乘以π，面积等于半径的平方乘以π。

2.圆的直径、弧、弦之间的关系满足弧长公式、角度公式等。

3.相交圆中的两条切线互相垂直。

4.相交圆的切线与切点处的切线垂直。

总结：通过学习初中常见几何模型的相关知识，可以帮助学生建立对几何概念的深刻理解，培养其解决实际问题的能力和创造力。

在学习几何模型的过程中，学生需要不断巩固掌握相关的性质和定理，灵活运用这些知识解决各种几何问题。

解析几何中的常见图形在解析几何中，常见的图形有点、直线、射线、线段、角、三角形、四边形和圆等。

这些图形在几何学中起着重要的作用，并且是我们在求解几何问题时常常会遇到的基本元素。

1. 点点是解析几何中最基本的图形，它是空间中没有大小的位置。

用大写字母表示点，比如A、B、C等。

点没有长度、宽度和厚度，它只有一个确定的位置。

2. 直线直线是由无穷多个点组成的，无限延伸的路径。

直线是解析几何中最基本的图形之一。

我们可以用两个点之间的直线段来表示一条直线，也可以用一条箭头来表示一条无限延伸的直线。

3. 射线射线也是由无穷多个点组成的路径，但它只延伸到一个方向。

射线有一个起点，表示为一个点，然后延伸到一个方向，不会结束。

4. 线段线段是由两个点之间的有限个点组成的路径。

线段有一个起点和一个终点，表示为两个点。

线段有确定的长度，在两个点之间有一个明确的终止点。

5. 角角是由两条射线或线段的交点和其它点组成的图形。

角的大小可以根据两条射线或线段之间的夹角来确定。

6. 三角形三角形是由三条线段组成的图形。

三角形有三个顶点和三条边。

根据三角形的边和角的性质，我们可以判断三角形的类型，如等边三角形、等腰三角形和直角三角形等。

7. 四边形四边形是由四条线段组成的图形。

四边形有四个顶点和四条边。

根据四边形的边和角的性质，我们可以判断四边形的类型，如矩形、正方形、平行四边形和菱形等。

8. 圆圆是由一个中心和一条半径组成的图形。

圆的所有点到中心的距离都相等。

圆在解析几何中有许多重要的性质和定理，在几何问题的求解中经常会用到。

以上就是解析几何中常见的图形。

通过理解和掌握这些图形的性质和特点，我们可以更好地进行几何问题的分析和求解。

初中数学专题——几何介绍几何是数学中的重要分支，主要研究空间、图形的形状、大小和相互关系。

在初中数学中，几何是一个重要的专题，涉及到的知识点较多。

基本概念在几何中，有一些重要的基本概念需要掌握：- 点：几何中最基本的几何对象，没有大小和形状，只有位置。

- 直线：由无数个点构成，没有宽度和厚度。

- 射线：由一个起始点和一个方向组成，无限延伸。

- 线段：由两个点确定，有固定的长度。

- 角：由两条射线共享一个起始点构成。

- 等边三角形：三边长度相等的三角形。

- 直角三角形：一个角为直角（90°）的三角形。

- 圆：由一个固定的中心和一条半径组成。

基本性质在几何中，有一些基本性质需要了解：- 直线上的两点可以确定一条直线；- 一条直线上的任意两点构成的线段是这条直线上最短的；- 三角形的内角和等于180°；- 直角三角形中，斜边的平方等于两直角边的平方和；- 三角形中，两边之和大于第三边；- 圆的周长等于直径的π倍；- 圆的面积等于半径的平方乘以π。

常见形状在初中几何中，有一些常见的形状需要熟悉：- 正方形：四条边长相等的四边形。

- 长方形：两对边分别相等的四边形。

- 三角形：三条边和三个内角的关系决定了不同的类型。

- 梯形：有两个平行边的四边形。

- 圆：所有点到圆心的距离相等的图形。

探索几何在研究几何时，可以进行一些探索性的研究活动来加深理解：1. 通过尺子、直尺等工具，自己画出各种形状，并测量它们的长度、面积等特征。

2. 观察周围的环境，找到一些具有几何特征的事物，比如建筑物、家具等，并描述它们的形状、大小等特征。

总结几何是初中数学中的重要专题，掌握几何的基本概念、基本性质以及常见形状对于研究数学有很大的帮助。

通过探索几何，可以加深对几何的理解，提高解题能力。

以上是关于初中数学专题——几何的简单介绍。

希望对你的学习有所帮助！。

七年级数学几何知识点梳理数学几何是初中数学的重要组成部分之一。

在初中阶段，学生们需要学习并掌握基本的几何知识和技能，为高中和大学学习打下坚实基础。

本文将为大家梳理七年级数学几何知识点，帮助同学们更好地学习和掌握数学几何。

一、点、线、面的基本概念点是几何的基本要素，它是没有长、宽、高的，用大写字母表示。

线是由无数个点在同一方向上依次排列组成，用小写字母表示。

面是由无数个点和线在同一平面上组成的，用大写字母表示。

二、角的概念和性质角是由两条射线公共端点组成的图形，用小写希腊字母表示。

角是几何中的重要概念，学习角的概念和性质是初中几何学习的重点之一。

（1）角的度量单位是度，在逆时针方向旋转一度可以使一条线段的一端向前移动约0.0015个单位长度。

（2）对顶角的度数相等，即∠ABC=∠DEF。

（3）平分线所分割的角相等，即∠ABD=∠CBD。

（4）相邻角互补，即∠ABC和∠CBD互补，它们的和为90度。

（5）邻补角相等，即∠ABC和∠CBD邻补，它们的和为180度。

三、三角形的性质三角形的性质是初中几何的重点之一，它是几何中最基本的图形之一。

根据三角形内角和定理，三角形的三个内角和为180度，可以推出以下性质：（1）等腰三角形的两个底角相等。

（2）等边三角形的三个内角相等。

（3）直角三角形的两条直角边上的直角角平分三角形的直角角。

（4）全等三角形对应的边和角相等。

（5）相似三角形对应的角相等。

四、正方形、长方形和平行四边形的性质正方形、长方形和平行四边形是初中几何中的基本图形，学习它们的性质对于初中学生而言非常重要。

（1）正方形的特点是四条边相等、四个角相等、对角线相等垂直相交。

（2）长方形的特点是两对相等的边、四个角都是直角。

（3）平行四边形的特点是两组对边分别平行、对边相等、对角线互相平分。

五、圆的性质圆是初中几何中的另一个重要图形，学习圆的性质可以帮助初中学生更好地理解圆的概念。

（1）圆的直径是圆上任意两个点之间的最长线段，其长度等于圆的半径的两倍。

几何图形初步1.几何图形1.1立体图形立体图形（1）概念：有些几何图形的各部分不都在，它们是立体图形．．（2）几种常见的立体图形：柱体：，；锥体：，；台体：，；球体：。

【答案】（1）同一平面内；（2）圆柱，棱柱，圆锥，棱锥，圆台，棱台；球。

注意：主要从以下几个方面来认识几何体：①由几个面围成，是平面还是曲面；②有无顶点，有几个顶点；③侧面是平面还是曲面；④底面是什么形状，是多边形还是圆，有几个底面等1.1.1立体图形的相关概念展开图1.1.2立体图形的展开图（1）概念：有些立体图形是由一些平面图形围成的，将它们的表面适当，可以展开成．这样的平面图形称为相应立体图形的展开图．【答案】（1）剪开，平面图形；（2）几种常见的立体图形的展开图如表：【答案】（1）相同(2)唯一确定，同一个；1.1.3正方体的展开图立正方形的展开图（1）正方体的展开图的11种情况，可分为四类：“二二二型”“三三型”“二三一型”“一四一型”如；，如；，如；【答案】（1）排成一排(2)“四”字型；（3）“凹”字型；1.2平面图形1.2.1平面图形（1）概念：有些几何图形的各部分都在内，它们是平面图形几种常见的平面图形：直线、射线、线段、三角形、长方形、正方形、梯形、平行四边形、圆、扇形。

【答案】同一平面1.2.2点、线、面、体点、线、面、体的定义1.体：几何体也简称体．我们学过的长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体．2.面：包围着体的是面．面有和两种．3.线：面和面的地方形成线．线分为和两种．例如，长方体的6个面相交成的12条棱(线)是直的，圆柱的侧面与底面相交得到的圆是曲的．4.点：线和线的地方是点5.点、线、面、体之间的关系：。

【答案】1.平面,曲面2.相交，直线，曲线3.相交4.点动成线，线动成面，面动成体2.直线、射线、线段2.1直线、射线、线段1.直线的特征：无，无，向两方。

2.直线的表示方法：（1）用一条直线上的点表示（2）用一个字母表示3.射线的概念：直线上一点和它一旁的部分叫做，这一点叫做射线的4.射线的特征：有端点，无，向方向无限延伸5.射线的表示方法：（1）用表示射线的端点和直线上另外一点的两个字母表示（表示端点的字母必须写在）（2）用一个小写字母表示6.线段的概念：直线上两点及两点间的部分叫做，这两个点叫做线段的。

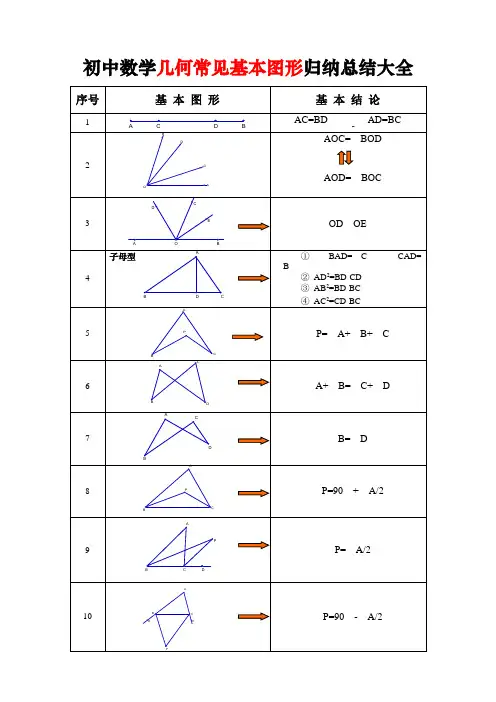
初中数学几何模型归纳1. 直线模型：直线是最基本的几何图形，可以用直线方程y = kx + b 来表示。

其中，k 是斜率，b 是截距。

2. 点模型：点是几何图形中的基本元素，可以用坐标(x, y) 来表示。

3. 线段模型：线段是由两个端点确定的有限长度的直线部分。

线段可以用起点和终点的坐标来表示。

4. 射线模型：射线是由一个端点和一个方向确定的无限延伸的直线部分。

射线可以用起点和方向向量来表示。

5. 角模型：角是由两条射线的公共端点和这两条射线之间的夹角组成的。

角可以用顶点、始边和终边来表示。

6. 三角形模型：三角形是由三条边和三个内角组成的多边形。

三角形可以用三边的长度和三个内角的大小来表示。

7. 四边形模型：四边形是由四条边和四个内角组成的多边形。

四边形可以用四边的长度和四个内角的大小来表示。

8. 圆模型：圆是由一个圆心和一个半径确定的平面上的所有点到圆心的距离都等于半径的图形。

圆可以用圆心和半径来表示。

9. 椭圆模型：椭圆是由两个焦点和一个长轴、短轴确定的平面上的所有点到两个焦点的距离之和等于常数的图形。

椭圆可以用两个焦点和长轴、短轴的长度来表示。

10. 双曲线模型：双曲线是由两个焦点和一个实轴、虚轴确定的平面上的所有点到两个焦点的距离之差等于常数的图形。

双曲线可以用两个焦点和实轴、虚轴的长度来表示。

11. 正多边形模型：正多边形是由相等的边和相等的内角组成的多边形。

正多边形可以用边数和内角度数来表示。

12. 梯形模型：梯形是由一对平行边和一对非平行边组成的四边形。

梯形可以用两对边的长度和夹角来表示。

13. 矩形模型：矩形是由四个直角和两对相等的边组成的四边形。

矩形可以用两对边的长度和夹角来表示。

14. 正方形模型：正方形是特殊的矩形，它的四个边都相等且四个角都是直角。

正方形可以用边长来表示。

15. 三角形面积模型：三角形的面积可以通过底边长度和高来计算，公式为S = (底边长度×高) / 2。

初中数学中的几何图形性质几何学是数学的一个重要分支，研究的是空间和形状之间的关系。

而对于初中学生来说，学习几何图形的性质是必不可少的一部分。

通过对几何图形性质的学习，学生能够提高空间思维能力，培养逻辑思维和观察能力。

本文将介绍一些初中数学中常见的几何图形性质，帮助学生加深对这些性质的理解。

1. 直线和角度的性质在几何学中，直线是一个基本概念。

直线没有起点和终点，它由无数个点组成，且任意两点之间都可以连成一条直线。

而角是由两条射线共享一个端点组成的，可以用度数来度量。

在学习几何图形的性质时，直线的平行性质和角的性质是重要的基础。

2. 三角形的性质三角形是最简单的多边形之一，由三条边和三个角组成。

对于三角形的性质，有很多重要的定理需要掌握。

例如，三角形的内角和等于180度，这是三角形的基本定理之一；三角形的边长之间也存在着一些特殊的关系，比如勾股定理和正弦定理。

通过学习三角形的性质，我们可以解决一些实际问题，比如测量不规则形状的土地面积。

3. 四边形的性质四边形是指由四条线段组成的图形，其中一个特殊的四边形是矩形。

矩形的性质是四边形中最为重要的之一，它具有四个直角和四条相等的边。

学习矩形的性质可以帮助我们理解平行四边形和菱形的性质，并能够应用到实际中，比如计算长方形的面积和周长。

4. 圆的性质圆是具有无限个同心圆的一组点的集合。

圆的性质主要包括圆心、半径、弧长以及圆心角等。

其中，圆心角是指圆上的两条射线所夹的角，它的度数等于所对的弧的一半。

利用圆的性质，我们可以解决一些与圆有关的问题，例如求解圆的面积、推导圆的弧长公式等。

5. 多边形的性质多边形是由一系列连续的线段组成的封闭图形，其中最常见的多边形是正多边形。

正多边形具有相等的边长和相等的内角，而任意多边形的内角和等于180度乘以多边形的边数减去2。

通过研究多边形的性质，学生可以解决一些与多边形有关的问题，比如寻找规律、计算不规则多边形的面积等。

通过对初中数学中几何图形性质的学习，学生不仅可以提高空间思维和观察能力，还能够培养逻辑思维和解决问题的能力。

初中几何图形知识点整理在初中数学的学习中，几何图形是一个重要的组成部分。

它不仅能够帮助我们更好地理解和描述现实世界中的物体和空间关系，还能锻炼我们的逻辑思维和空间想象力。

接下来，让我们一起对初中几何图形的知识点进行整理。

一、点、线、面、体点是构成几何图形的最基本元素，没有大小和形状。

线是由无数个点组成的，分为直线和曲线。

直线没有端点，可以向两端无限延伸；曲线则是弯曲的线。

面是由线围成的，有平面和曲面之分。

平面是平的，曲面则不是平的。

体是由面围成的，如正方体、长方体、圆柱体等。

二、线段、射线、直线线段有两个端点，长度是可以测量的。

射线有一个端点，另一端可以无限延伸，长度不可测量。

直线没有端点，向两端无限延伸，长度也不可测量。

在直线上，两点之间的部分叫做线段。

两点确定一条直线，这是一个非常重要的性质。

三、角角是由两条有公共端点的射线组成的图形。

这个公共端点叫做角的顶点，这两条射线叫做角的边。

角可以分为锐角、直角、钝角、平角和周角。

锐角是小于 90 度的角，直角是等于 90 度的角，钝角是大于 90 度小于 180 度的角，平角是等于 180 度的角，周角是等于 360 度的角。

角的度量单位是度、分、秒。

1 度＝ 60 分，1 分＝ 60 秒。

四、相交线两条直线相交，会形成四个角。

对顶角相等，邻补角互补。

垂线是两条直线相交的特殊情况，当两条直线相交所成的四个角中有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

点到直线的距离是指从直线外一点到这条直线的垂线段的长度。

五、平行线在同一平面内，不相交的两条直线叫做平行线。

经过直线外一点，有且只有一条直线与这条直线平行。

如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

平行线的判定方法有：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行。

平行线的性质有：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。

初中数学几何图形知识点掌握几何图形知识非常的丰富,因此我们的学习也是非常的紧张,获得的知识也就非常的多。

下面是为大家整理的关于初中数学几何图形知识点掌握，希望对您有所帮助!初一上册数学几何图形初步知识点归纳1.几何图形：点、线、面、体这些可帮助人们有效的刻画错综复杂的世界，它们都称为几何图形。

从实物中抽象出的各种图形统称为几何图形。

有些几何图形的各部分不在同一平面内，叫做立体图形。

有些几何图形的各部分都在同一平面内，叫做平面图形。

虽然立体图形与平面图形是两类不同的几何图形，但它们是互相联系的。

2.几何图形的分类：几何图形一般分为立体图形和平面图形。

3.直线：几何学基本概念，是点在空间内沿相同或相反方向运动的轨迹。

从平面解析几何的角度来看，平面上的直线就是由平面直角坐标系中的一个二元一次方程所表示的图形。

求两条直线的.交点，只需把这两个二元一次方程联立求解，当这个联立方程组无解时，二直线平行;有无穷多解时，二直线重合;只有一解时，二直线相交于一点。

常用直线与X轴正向的夹角(叫直线的倾斜角)或该角的正切(称直线的斜率)来表示平面上直线(对于X轴)的倾斜程度。

4.射线：在欧几里德几何学中，直线上的一点和它一旁的部分所组成的图形称为射线或半直线。

5.线段：指一个或一个以上不同线素组成一段连续的或不连续的图线，如实线的线段或由“长划、短间隔、点、短间隔、点、短间隔”组成的双点长划线的线段。

线段有如下性质：两点之间线段最短。

6. 两点间的距离：连接两点间线段的长度叫做这两点间的距离。

7. 端点：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

线段用表示它两个端点的字母或一个小写字母表示，有时这些字母也表示线段长度，记作线段AB或线段BA，线段a。

其中AB表示直线上的任意两点。

8.直线、射线、线段区别：直线没有距离。

射线也没有距离。

因为直线没有端点，射线只有一个端点，可以无限延长。

9.角：具有公共端点的两条不重合的射线组成的图形叫做角。

初中几何线段数量关系
1. 线段的定义
线段是几何学中最基本的图形之一，是由端点和两个端点之间的
所有点组成的一段线。

2. 线段的数量
在几何学中，线段的数量是许多重要概念和关系的基础。

线段的
数量可以通过以下几种方式来表示。

2.1 点和线段的关系
一个点可以与另一个点连接成一条线段，所以当有n个点时，就
可以连接成n(n-1)/2条线段。

例如，当有3个点时，可以连接成3条
线段；当有4个点时，可以连接成6条线段；当有5个点时，可以连
接成10条线段。

2.2 图形中线段的数量
许多几何图形中包含的线段数量与其形状有关。

例如，一个正方
形有4条边，每条边可以看作是一条线段，所以一个正方形中有4条
线段。

同样地，一个三角形中有3条线段，一个四边形中有4条线段。

2.3 直线上线段的数量
在同一条直线上，若有n个点，则有n-1个线段。

例如，直线上
有3个点时，有2条线段；直线上有4个点时，有3条线段。

2.4 平面内线段的数量
在平面内，若有n条线段，则交点的数量为n(n-1)/2。

例如，当平面内有3条线段时，它们最多有3个交点；平面内有4条线段时，最多有6个交点。

3. 总结
线段数量在几何学中是一个非常重要的概念。

掌握线段数量的各种表示方法，可以帮助我们更好地理解几何图形和解决几何问题。

初中数学（几何）知识点总结图形的初步认识考点一、直线、射线和线段1、几何图形：从实物中抽象出来的各种图形，包括立体图形和平面图形。

立体图形：有些几何图形的各个部分不都在同一平面内，它们是立体图形。

平面图形：有些几何图形的各个部分都在同一平面内，它们是平面图形。

2、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形中最基本的图形。

线：面和面相交的地方是线，分为直线和曲线。

面：包围着体的是面，分为平面和曲面。

体：几何体也简称体。

（2）点动成线，线动成面，面动成体。

3、直线的概念：一根拉得很紧的线，就给我们以直线的形象，直线是直的，并且是向两方无限延伸的。

4、射线的概念：直线上一点和它一旁的部分叫做射线。

这个点叫做射线的端点。

5、线段的概念：直线上两个点和它们之间的部分叫做线段。

这两个点叫做线段的端点。

6、点、直线、射线和线段的表示在几何里，我们常用字母表示图形。

一个点可以用一个大写字母表示。

一条直线可以用一个小写字母表示。

一条射线可以用端点和射线上另一点来表示。

一条线段可用它的端点的两个大写字母来表示。

注意：（1）表示点、直线、射线、线段时，都要在字母前面注明点、直线、射线、线段。

（2）直线和射线无长度，线段有长度。

（3）直线无端点，射线有一个端点，线段有两个端点。

（4）点和直线的位置关系有线面两种：①点在直线上，或者说直线经过这个点。

②点在直线外，或者说直线不经过这个点。

7、直线的性质（1）直线公理：经过两个点有一条直线，并且只有一条直线。

它可以简单地说成：过两点有且只有一条直线。

（2）过一点的直线有无数条。

（3）直线是是向两方面无限延伸的，无端点，不可度量，不能比较大小。

（4）直线上有无穷多个点。

（5）两条不同的直线至多有一个公共点。

8、线段的性质（1）线段公理：所有连接两点的线中，线段最短。

也可简单说成：两点之间线段最短。

（2）连接两点的线段的长度，叫做这两点的距离。

（3）线段的中点到两端点的距离相等。