buck电路 小信号模型传递函数

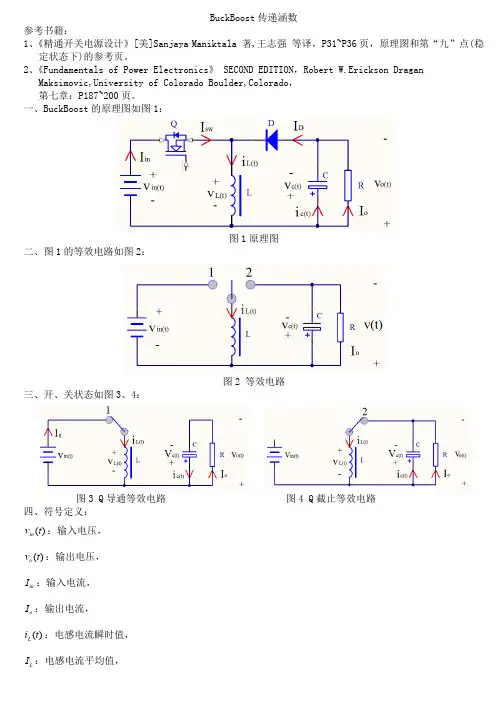
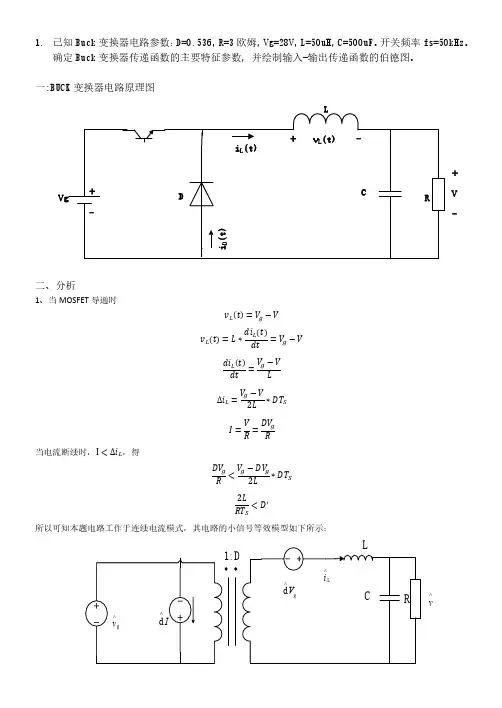
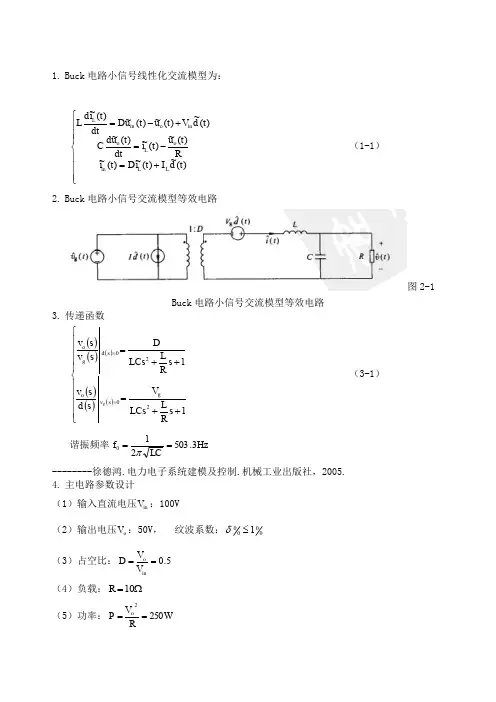
1. Buck 电路小信号线性化交流模型为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=-=+-=)(~)(~)(~)(~)(~)(~)(~)(~)(~)(~o o o t d I t i D t i R t u t i dt t u d C t d V t u t u D dt t i d L L L in L in in L （1-1）2. Buck 电路小信号交流模型等效电路图2-1Buck 电路小信号交流模型等效电路3. 传递函数 ()()()()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++=++===112020s R L LCs V s d s v s R L LCs D s v s v g s v o s d g o g （3-1） 谐振频率Hz LC f 3.503210==π--------徐德鸿.电力电子系统建模及控制.机械工业出版社，2005.4. 主电路参数设计（1）输入直流电压in V ：100V（2）输出电压o V ：50V ， 纹波系数：00001≤δ（3）占空比：5.0o ==inV V D （4）负载：Ω=10R（5）功率：W R V P 2502o ==（6）开关频率：kHz f s 10=（7）开关管由于是小功率DC-DC 变换器，所以选用功率MOSFET 作为开关器件，MOSFET 的型号选择IRF250（V U DS 200=,A I D 30=,()Ω=085.0on DS R )。

（8）电感电感的大小决定了开关电源主回路处于CCM 还是DCM 模式，由Buck 电路工作于电感电流连续状态下的条件：21D RT L S -≥ （4-1）得： S RT D L 21-≥（4-2） 所以mH L 25.0≥,取mH L 1=（9）电容电容的作用是保持恒定的输出电压，可根据允许的输出电压纹波值来选择电容的大小： 所以F C μ5.62=，取F C μ100=--------[1] 裴云庆，杨旭，王兆安.开关稳压电源的设计和应用[M].机械工业出版社，2010.[2] 英飞凌公司.IRF250 数据手册.[3] 巩鲁洪, 曹文思. 基于BUCK 变换器的建模与设计[J]. 科学之友,2008.5. 扰动信号占空比扰动：)2sin()(~t f d t d sd π=其中： 005.05.01001=⨯≤d kHz kHz f sd 110101=⨯≤ 输入电压扰动：)2sin()(~t f u t u su in π= 其中： V V u 5.0501001=⨯≤kHz kHz f sd 110101=⨯≤ 负载扰动：)2sin()(~t f i t i si o π=其中： A A I 05.051001=⨯≤kHz kHz f sd 110101=⨯≤ 6. 仿真因素电路与小信号模型对比输入电压小扰动)(~t u in占空比小扰动)(~t d → 输出电压)(~o t u 纹波等稳态性能负载小扰动7. 仿真结果分析电路与小信号模型对比，模型是否精确？加各种扰动，对输出电压的影响？。

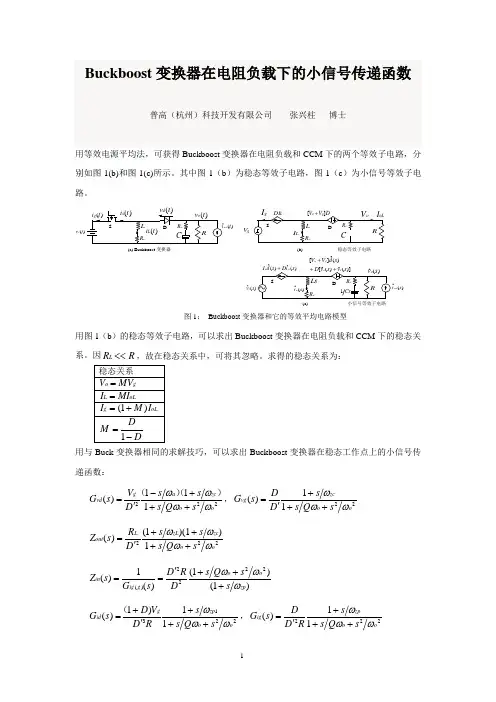
Buckboost 变换器在电阻负载下的小信号传递函数普高（杭州）科技开发有限公司 张兴柱 博士用等效电源平均法，可获得Buckboost 变换器在电阻负载和CCM 下的两个等效子电路，分别如图1(b)和图1(c)所示。

其中图1（b ）为稳态等效子电路，图1（c ）为小信号等效子电路。

)(t v g )(tgV(ˆs vg )(ˆ][s dV V g o +)(ˆs oL图1： Buckboost 变换器和它的等效平均电路模型用图1（b ）的稳态等效子电路，可以求出Buckboost 变换器在电阻负载和CCM 下的稳态关系。

因R R L <<，故在稳态关系中，可将其忽略。

求得的稳态关系为：Buckboost 变换器在稳态工作点上的小信号传递函数：222111)(o o zc a g vd s Q s s s D V s G ωωωω+++−′=）（）（，2211)(o o zc vg s Q s s D Ds Gωωω+++′= 2221)1)(1()(oo zc zL L out s Q s s s D R s Z ωωωω++++′=)1()1()(1)(2222)(zp o o g ig in s s Q s D R D s G s Z ωωω+++′== 221311)1)(o o zp g id s Q s s R D V D s G ωωω+++′+=（，22211)(oo zpig s Q s s R D D s G ωωω+++′=22111)(o o zcii s Q s s D s G ωωω+++′=其中：D D −=′1，LC D o ′=ω，])([122C D R R R D L Q L c o ′++′=ω，DL R D a 2′=ω L R L zL =ω，C R C zc 1=ω，RC zp 1=ω，RCD zp +=11ω有两个小信号传递函数，即)()(s G g id ，)()(s G g ii 没有给出，有兴趣的读者，可以作为作业自己去推导。

在已知环路其他部分的传递函数表达式后，即可设计电压误差放大器了。

由于KLC提供了一个零点和两个谐振极点，因此，一般将E/A设计成PI调节器即可，KEA=KP(1＋ωz/s)。

其中ωz用于消除稳态误差，一般取为KLC零极点的1/10以下；KP用于使剪切频率处的开环增益以－20dB/十倍频穿越0dB线，相角裕量略小于90°。

2 电压模式控制（VMC）电压模式控制方法仅采用单电压环进行校正，比较简单，容易实现，可以满足大多数情况下的性能要求，如图2所示。

图2中，当电压误差放大器（E/A）增益较低、带宽很窄时，Vc波形近似直流电平，并有D=Vc/Vs （15）d=Vc'/Vs （16）式（16）为式（15）的小信号波动方程。

整个电路的环路结构如图3所示。

图3没有考虑输入电压的变化，即假设Uin=0。

图3中，（一般为0）及分别为电压给定与电压输出的小信号波动；KFB=UREF/Uo，为反馈系数；误差e为输出采样值偏离稳态点的波动值，经电压误差放大器KEA放大后，得；KMOD为脉冲宽度调制器增益，KMOD=d/=1/Vs；KPWR为主电路增益，KPWR=/d=Uin；KLC为输出滤波器传递函数，KLC=(1+sCRe)/[S2LC+s(ReC+L/Ro)+1]。

在已知环路其他部分的传递函数表达式后，即可设计电压误差放大器了。

由于KLC提供了一个零点和两个谐振极点，因此，一般将E/A设计成PI调节器即可，KEA=KP(1＋ωz/s)。

其中ωz用于消除稳态误差，一般取为KLC零极点的1/10以下；KP用于使剪切频率处的开环增益以－20dB/十倍频穿越0dB线，相角裕量略小于90°。

VMC方法有以下缺点：1）没有可预测输入电压影响的电压前馈机制，对瞬变的输入电压响应较慢，需要很高的环路增益；2）对由L和C产生的二阶极点（产生180°的相移）没有构成补偿，动态响应较慢。

VMC的缺点可用下面将要介绍的CMC方法克服。

buck电路小信号模型传递函数Buck电路是一种常用的DC-DC转换电路，其特点在于输入电压高于输出电压，并且可以通过调节占空比来控制输出电压。

在设计和分析Buck电路时，需要推导出其小信号模型和传递函数。

下面将分步骤阐述如何进行这些推导。

1. Buck电路的基本原理Buck电路由开关管、输出电容和负载组成。

当开关管导通时，电感存储了电流，然后当开关管关断时，电感的电流通过输出电容和负载产生输出电压。

通过调节开关管的导通时间占空比，可以控制输出电压的大小。

2. 推导Buck电路的小信号模型为了推导Buck电路的小信号模型，需要采用线性化的方法，将非线性元件进行虚拟短路或虚拟开路。

以Buck电路为例，假设开关管T的导通时间为DT，开关管关断时间为（1-D）T。

因此，开关管T的小信号模型可以表示为：I = gm(Vgs-Vth)Vds = VdVgs = Vin – Vout其中，I为T管的源电流，gm为T管的跨导，Vgs为T管的栅极-源极电压，Vth为T管的阈值电压，Vds为T管的漏极-源极电压，Vin 为输入电压，Vout为输出电压。

3. 推导Buck电路的传递函数Buck电路的传递函数为输出电压与输入电压之比。

在推导传递函数时，可以采用控制电压法或控制电流法。

以控制电压法为例，假设输入电压为Vin，输出电压为Vout，输出电容为C，开关管导通时间为DT，电感为L，电阻为R。

则可以得到以下方程：Vin = Vout + L(di/dt) + Vrdi/dt = (Vout – Vc)/L其中，Vr为开关管的二极管反向电压，di/dt为电感电流的变化速率，Vc为电容器的电压。

带入传递函数公式：Vout/Vin = 1/（1-D）可以得到Buck电路的传递函数为1/（1-D），这意味着通过调节开关管的占空比，可以控制输出电压的大小。

总结：Buck电路的小信号模型和传递函数的推导可以帮助我们更好地理解Buck电路的工作原理，并在电路设计和分析中应用。

Buck 变换器小信号模型
本文为大家介绍Buck 电路电感电流连续时的小信号模型。

Buck 电路电感电流连续时的小信号模型
图1 为典型的Buck 电路，为了简化分析，假定功率开关管S 和D 为理想开关，滤波电感L 为理想电感（电阻为0），电路工作在连续电流模式（CCM）下。

Re 为滤波电容C 的等效串联电阻，R0 为负栽电阻。

各状态变量的正方向定义如下图中所示。

图1 典型buck 电路
s 导通时，对电感列状态方程
s 断开时，D1 续流导通时，状态方程变成
占空比为D 时，一个开关周期过程中，式（1）及式（2）分别持续了DTs 和（1-D）Ts 的时间（Ts 为开关周期），因此，一个周期内电感的平均状态方程为。

峰值电流型控制Buck 等效功率级的小信号传递函数普高（杭州）科技开发有限公司 张兴柱 博士Buck 变换器在峰值电流型控制下的等效功率级小信号传递函数（CCM ）： )1)(1()1()(220n n p p zc vc vc s Q s s s G s G ωωωω++++′≈′ )1)(1()1()(220n n p p zc vg vg s Q s s s G s G ωωωω++++′≈′ )1()1()(0p zc out s s R s Z ωω++′≈′ 其中：101F R R G i vc =′，120F F L RT G s vg =′，10F R R =′ 11F RC p =ω，)5.0(1−′=D m Q c p π，C R c zc 1=ω，sn T πω= )5.0(11−′+=D m LRT F c s ，)]21([2D D m D F c −−′=，n e c S S m +=1 i o g n R L V V S ×−= 从求得的峰值电流控制Buck 等效功率级的三个CCM 小信号传递函数，我们可以来分析这种控制的特点。

其峰值电流控制等效功率级的控制电压到输出电压小信号传递函数)(s G vc ′，和输入电压到输出电压小信号传递函数)(s G vg ′，形式完全相同，所不同的只是零频分量。

它由一个左半平面单极点，一个1/2开关频率处的双极点和一个因输出滤波电容ESR 引起的左半平面单零点组成。

双极点的频率在1/2开关频率，比起开关电源的带宽要高得多，故一般情况下可将其忽略。

在R.Ridely 引入采样函数之前的分析文章中，所得到的结果都是用一阶小信号传递函数近似，所以就不能解释在实验中出现的子谐波振荡现象。

所谓的子谐波振荡是峰值电流型控制的等效功率级，在工作占空比大于0.5时和无外部补偿斜波时，会在输出产生一种1/2开关频率的有规则的振荡，可在MOSFET 的ds V 波形上反映出来，它在时钟的相邻开关周期内，具有不同的导通时间和截止时间，一长一短，其波形示意图如图1所示。

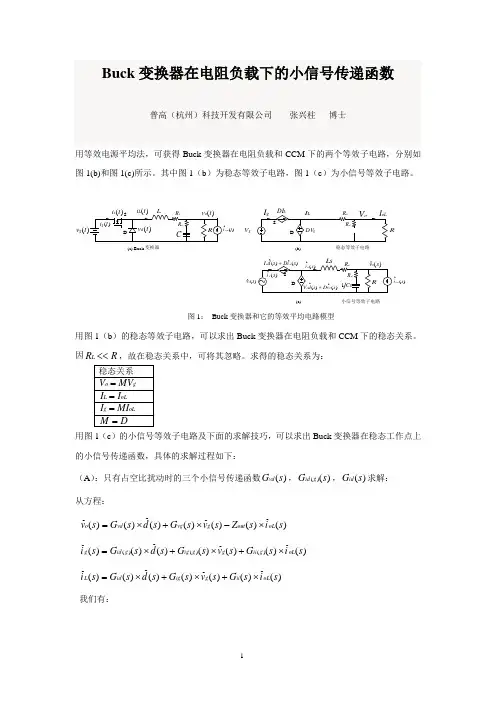
Buck 变换器在电阻负载下的小信号传递函数普高（杭州）科技开发有限公司 张兴柱 博士用等效电源平均法，可获得Buck 变换器在电阻负载和CCM 下的两个等效子电路，分别如图1(b)和图1(c)所示。

其中图1（b ）为稳态等效子电路，图1（c ）为小信号等效子电路。

)(t oL (t v ggV(ˆs vg )(s oL (c)图1： Buck 变换器和它的等效平均电路模型用图1（b ）的稳态等效子电路，可以求出Buck 变换器在电阻负载和CCM 下的稳态关系。

因R R L <<，故在稳态关系中，可将其忽略。

求得的稳态关系为：稳态关系g o MV V =oL L I I = oL g MI I = D M =用图1（c ）的小信号等效子电路及下面的求解技巧，可以求出Buck 变换器在稳态工作点上的小信号传递函数，具体的求解过程如下：（A ）：只有占空比扰动时的三个小信号传递函数)(s G vd ，)()(s G g id ，)(s G id 求解： 从方程：)(ˆ)()(ˆ)()(ˆ)()(ˆs i s Z s v s G s d s G s voL out g vg vd o ×−×+×= )(ˆ)()(ˆ)()(ˆ)()(ˆ)()()(s i s G s v s G s d s G s ioL g ii g g ig g id g ×+×+×= )(ˆ)()(ˆ)()(ˆ)()(ˆs i s G s v s G s d s G s ioL ii g ig id L ×+×+×= 我们有：0ˆ,0ˆ)(ˆ)(ˆ)(===oL g o vd i vs ds vs G 0ˆ,0ˆ)(ˆ)(ˆ)()(===oL g g g id i vs ds is G 0ˆ,0ˆ)(ˆ)(ˆ)(===oL g d id i vs ds is G图2： Buck 变换器只有占空比扰动时的小信号等效电路所以图1（c ）的小信号等效电路可简化为图2所示。

平均电流模式控制Buck 电路小信号分析平均电流模式控制在电池充电电路以及PFC 中有着广泛的应用。

因其电流环和电压环均需补偿，故分析其小信号特性相当必要。

本文将采用参考[1]的建模方法来分析平均电流模式下buck 电路的特性，给出了其简化等式，并利用K 因子方法设计了补偿电路。

一 电流环补偿设计图一所示为电路的方框图及其小信号模型。

占空比到输出以及到电感电流的传递函数为[2]图一 电路方框图及小信号模型其中图二 Gvd 和Gid 传递函数输入和输出的反馈为从Vcl 到Ri V 的传递函数为其中 因Go<<1，故上式简化形式为其高频近似为此处采用Type II 来补偿，参考[3][4]给出了避免电路不稳定的补偿中频增益的限制，其中选定中频增益后，电流环的交越频率也随之确定利用K 因子法，确定补偿的零点为则有补偿的极点为进而有补偿的传函为电流环传递函数为图3 电流环bode 图 交越频率和相位裕量计算如下二 电压环补偿设计控制Vc 到输出的传递函数为 其近似为其低频近似为为了减少电流环对电压环的影响，后者交越频率要小于前者。

设定电压环交越频率 fc利用K 因子法，确定补偿的零点为补偿的极点为补偿的传函为则电压环传函为图4 Gvc Bode 图图5电压环bode 图交越频率和相位裕量计算如下参考：[1]. Philip Cooke." Modeling Average Current Control". Unitrode Integrated Circuits Corporation(TI).2005.[2].Doaer"buck".[3].Lloyd Dixon."Average Current Mode Control of Switching Power Supplies"Unitrode(TI) Application Note .[4].Jian Sun. Richard M.Bass."Modeling and Practical Design Issues for Average Current Control".1999 IEEE。

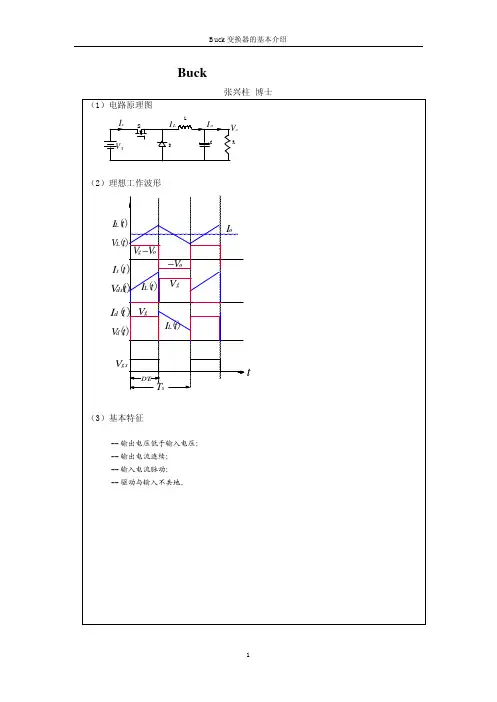
系统建模作业——BUCK电路的建模一．BUCK 电路简介BUCK 电路是一种降压式变换电路，降压变换器输出电压平均值U 0总是小于输出电压U D 通常电感中的电流是否连续，取决于开关频率、滤波电感L 和电容C 的数值。

二．BUCK 电路建模1. BUCK 电路基本结构Va)VVb) c)图1. BUCK 电路基本结构a) Buck 变换器 b)开关处于通态[t ，t+DTs] c)开关处于断态[t+DTs ，t+Ts]2．符号说明1、 输入直流电压(Vg)：2、 输出电压(Vo)：3、 输入电流(Ig)：4、 输出电流(Io)：5、 电感电压(VL)：6、 电感电流(IL)：7、 电容电流(IC)：3. Buck 变换器达到稳态时的电压电流关系当Buck 变换器达到稳态时，电感电压为()()()ss L s0L L T I t T I t V t LT +-==（1）并且()()()()sss ss L L L L ss 11d d d t T t DT t T g o T tt t DT v t V t t V t t V t t V D V T T ++++⎡⎤==+=-⎢⎥⎣⎦⎰⎰⎰ （2） 则结合（1）和（2），其稳态电压传输比为：goV D V = （3）若略去开关损耗，则Buck 变换器的输入输出功率平衡有：g g o o V I V I =，得o g DI I =。

4.大信号模型在开关管处于通态时，即时间在[t ，t+DT s ]区间时，电感两段电压为:()()()()L g d d L o I t V t LV t V t t==- （4）通过电容的电流为：()()()()C d d o og V t V t I t CI t t R==- （5）当开关管处于断态时，即时间[t+DT s ，t+T s ]区间时，电感两端电压为：()()()L d d L o I t V t LV t t==- （6）通过电容的电流为：。