小信号模型

小信号模型的原理与应用1. 小信号模型的概述小信号模型是指将非线性电路在某工作点处进行线性化处理，以线性矩阵来近似描述电路的动态行为。

小信号模型能够有效地分析电路的频率响应以及信号增益等参数，对于电路设计和分析非常重要。

2. 小信号模型的原理小信号模型基于线性近似原理，将非线性电路在某工作点线性化，并将线性化的电路表示为参数形式的等效电路。

在小信号模型中，将电路中的所有非线性元件均视作线性单端增益元件，并用电压和电流的增益参数描述。

通过将电路中的各个元件进行线性化，可以得到不同环节的增益参数，从而形成小信号模型。

具体而言，小信号模型的基本原理如下： - 对于非线性电路，选择合适的工作点进行线性化处理； - 将非线性元件视作线性单端增益元件，并用增益参数描述；- 采用等效电路的参数形式，将线性化的电路表示为常数项和一阶项的线性组合；- 利用线性化得到的小信号模型，进行频率响应和信号增益等参数的分析。

3. 小信号模型的应用小信号模型在电路设计和分析中具有广泛的应用，主要应用于以下几个方面：3.1. 频率响应分析小信号模型能够有效地分析电路的频率响应特性。

通过线性化处理，可以得到电路在不同频率下的增益和相位等信息。

这对于滤波器、放大器等电路的设计和优化非常重要。

通过对小信号模型进行分析，可以选择合适的工作频率范围，使得电路在该范围内具有良好的性能。

3.2. 信号增益分析小信号模型可以用于分析电路的信号增益。

通过线性化处理，可以得到电路的增益参数，从而了解电路对不同信号的放大程度。

这对于放大器等电路的设计和评估非常重要。

通过对小信号模型进行分析，可以选择合适的增益参数，使得电路能够实现所需的放大功能。

3.3. 稳定性分析小信号模型还可以用于分析电路的稳定性。

通过线性化处理，可以得到电路的传输函数和极点位置。

根据极点的位置，可以判断电路是否稳定。

这对于反馈电路和振荡电路等的设计和分析非常重要。

通过对小信号模型进行分析，可以调整电路的参数，以满足稳定性的要求。

小信号模型的原理及应用1. 引言小信号模型是一种用于分析线性电路中微小信号变化的数学模型。

它通过线性化并简化非线性电路，使得我们能够更容易地理解和预测电路的行为。

本文将介绍小信号模型的基本原理以及它在电子电路设计和分析中的应用。

2. 小信号模型的基本原理小信号模型基于两个假设：线性性和小信号假设。

2.1. 线性性线性性意味着电路中的元件满足线性关系，即输出响应是输入信号的线性函数。

线性性允许我们使用简单的数学工具（如线性代数）来分析电路。

当输入信号较小时，大多数电路元件可以被近似为线性的。

2.2. 小信号假设小信号假设是基于输入信号较小的假设。

它要求输入信号的振幅足够小，以至于它的变化不会引起电路中元件的非线性饱和。

根据小信号假设，我们可以在电路中线性化非线性元件，并将它们建模为简单的电阻、电容和电感。

3. 小信号模型的应用小信号模型在电子电路设计和分析中有广泛的应用。

下面列举了一些主要的应用场景：3.1. 放大器设计小信号模型允许我们将放大器建模为线性电路，从而更容易分析和设计放大器的性能。

通过分析小信号模型，我们可以确定放大器的增益、带宽和稳定性。

3.2. 滤波器设计滤波器通常用于信号处理和频率选择。

小信号模型可以帮助我们分析滤波器的频率响应以及阻带和通带的特性。

这有助于我们设计和优化各种类型的滤波器。

3.3. 振荡器设计振荡器是一种产生周期性信号的电路。

小信号模型可以帮助我们分析振荡器的稳定性和频率。

这对于设计高性能的振荡器非常重要。

3.4. 反馈控制系统分析反馈控制系统常用于稳定性控制和误差校正。

小信号模型可以用来分析系统的稳定性，并预测系统的频率响应和阶跃响应。

这对于设计和优化反馈控制系统非常有用。

4. 小结小信号模型是一种在电子电路设计和分析中广泛使用的工具。

它通过线性化和简化电路，使得我们能够更好地理解和预测电路的行为。

在放大器、滤波器、振荡器和反馈控制系统等方面，小信号模型都有重要的应用价值。

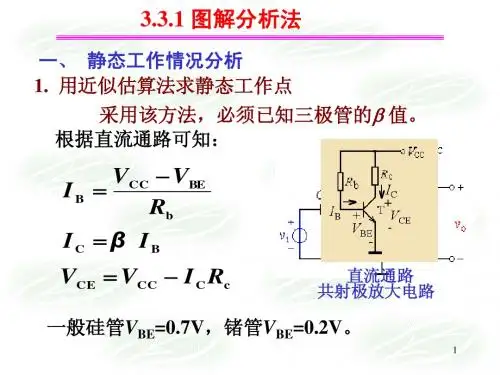
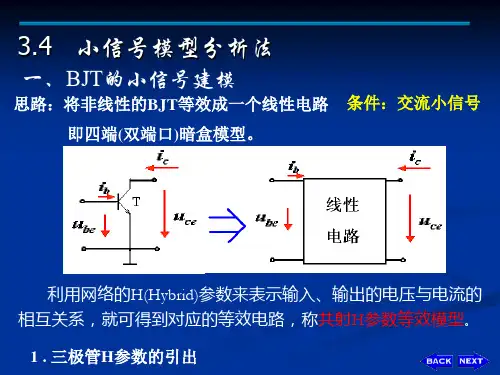
回忆BJT三极管的小信号模型BJT双口网络BJT管小信号模型4.4 小信号模型分析4.4.1 MOSFET小信号模型分析（1）模型iD Kn (vGS VT )2 Kn (VGSQ vgs VT )2 Kn[(VGSQ VT ) vgs ]2 Kn (VGSQ VT )2 2Kn (VGSQ VT )vgs Kn vg2s IDQ gm vgs Kn vg2s静态值 （直流）动态值 （交流）非线性 失真项gm 2Kn (vGS VT )当 vgs<< 2(VGSQ- VT )时， iD IDQ gmvgs IDQ id直流+交流3. 小信号模型分析 FET低频小信号模型SiO2 绝缘层(1)输入回路g、s间: iG 0, rgs= 106~109Ω， g、s开路(2)输出回路d、s间: id gmvgs 电压控制电流源rds vDS iD 1ID0时λ=0时， rds= ∞4.4.2 共源极放大电路分析例4.4.1 VDD = 5V， Rd=3.9k Rg1=60k， Rg2=40k。

VT = 1V， Kn = 0.8mA/V2，＝0.02V-1 。

计算 静态值， 小信号电压增益Av，Ri， Ro电路分析： vig极组态判断 vod极剩 s极 共用＝0.02共源极放大电路例4.4.1（1）电路的静态值（画直流通路）解：VGSQ Rg2 Rg1 Rg2 VDD 40 5V 2V 60 40+ VGS ID + VDS IDQ Kn(VGS VT )2 (0.8)(2 1)2mA 0.8mA直流通路VDSQ VDD IDRd [5 0.8 3.9]V 1.88V满足 VGS VT ,VDS (VGS VT ) ,工作在饱和区（2）放大电路动态分析 小信号等效电路：①直流电源VDD短路 — 接地； ②电容Cb1、 Cb2短路；例4.4.1 （2）放大电路动态分析gm 2Kn (VGSQ VT ) 2 0.8 (2 1)mS 1.6mSsRg2rds [Kn (vGS VT )2 ]11ID小信号等效电路IDQ Kn (VGS VT )2 1 k 62.5k 0.02 0.8Avvo vigmvgs (rds v gs// Rd ) gm (rds // Rd ) 5.87Ri Rg1 // Rg2 24k Ro rds // Rd 3.67ksRg2小信号等效电路4.4.3 带源极电阻的共源极放大电路（稳Q点）电路分析： vig极组态判断： vod极剩 s极 共用共源极放大电路sis比较分压式射极偏置电路: 稳Q点4.4.3 带源极电阻的共源极放大电路（稳Q点）1. 求 静态工作点（画直流通路）VGS VG VS[Rg2 Rg1 Rg2(VDDVSS)VSS]sis ( ID Rs VSS )ID Kn (VGS VT )2IDVDS (VDD VSS ) ID ( Rd Rs )+验证是否满足 VGS VT ,VDS (VGS VT ) 饱和区条件：VG +VGSVS VDS s直流通路（2）放大电路动态分析小信号等效电路：①直流电源VDD、VSS短路 — 接地；②电容Cb1、 Cb2短路；sis（2）放大电路动态分析rds [Kn (vGS VT )2 ]11IDgm 2Kn (VGSQ VT )Av vo vi gmvgs Rd v gs gmvgs Rssi gm Rd 1 gm RsRi Rg1 // Rg2Ro Rd＝0, rds→∞isRg2s小信号等效电路Avsvo vSvo vivi vSAvRiRi RSi。

放大电路分析方法放大电路是一种用于提高信号幅度的电路，广泛应用于各种电子设备中。

对于放大电路的分析，有许多不同的方法可供选择。

本文将介绍放大电路的几种常用分析方法，并重点讨论小信号模型法和大信号模型法。

一、小信号模型法小信号模型法是一种基于线性近似的方法，适用于分析非线性电路以及在其中一工作点附近的放大电路。

该方法的基本思想是将非线性电路视为线性电路的叠加，通过线性电路的分析求解非线性电路的行为。

以下是使用小信号模型法进行分析时需要遵循的步骤：1.选取工作点：首先，需要确定放大电路的工作点。

这通常涉及使用直流偏置电路来确定电路的直流工作条件。

2.建立小信号模型：其次，需要将放大电路线性化为小信号模型。

这涉及将非线性的器件（如晶体管）进行局部分析，并简化为线性等效电路。

3.求解等效电路：然后，需要对等效电路进行分析。

这通常涉及使用网络理论和线性系统的分析技巧来求解电路的响应。

4.评估放大性能：最后，需要根据等效电路的分析结果评估放大电路的性能。

这通常涉及计算增益、输入阻抗、输出阻抗等指标。

小信号模型法的优点是可以提供对放大电路行为的定量分析。

然而，由于其基于线性近似，只适用于工作点附近的小信号分析。

二、大信号模型法大信号模型法是一种基于非线性分析的方法，适用于分析工作点偏离很远的放大电路，或者涉及大信号激励的情况。

该方法的基本思想是直接分析非线性放大电路的行为，忽略器件的非线性特性。

以下是使用大信号模型法进行分析时需要遵循的步骤：1.建立非线性模型：首先，需要建立器件的非线性模型。

这可以通过等效电路、传输特性等方式实现。

2.求解非线性方程：其次，需要根据非线性模型和电路拓扑关系，建立非线性方程。

这通常涉及使用基本的电路分析技巧，如基尔霍夫定律。

3.进行数值模拟：然后，可以使用数值模拟工具，如SPICE软件，来求解非线性方程。

这可以提供对电路行为的详细分析。

4.评估放大性能：最后，可以根据数值模拟结果评估放大电路的性能。

小信号模型小信号模型是指在电子电路分析中使用的一种简化模型，用于分析电路中的微小变化或者交流信号的响应。

通过小信号模型，我们可以更好地了解电路的稳定性、频率响应以及信号传输特性。

在电子技术领域，小信号模型起着至关重要的作用，为工程师们设计和优化电路提供了有效的工具和方法。

小信号模型的基本概念小信号模型通过将非线性电路元件在工作点处的导纳或者电阻转换成等效的线性模型来描述电路的动态特性。

在小信号模型中，电路中的电容、电阻和电感等元件被简化为等效的小信号模型参数，这样可以更方便地进行分析和计算。

通常情况下，小信号模型可以通过微分方程或者迪拜电路等方法来建立。

通过对电路中各个元件的微分导纳、微分阻抗以及微分电容等参数进行计算，可以得到小信号模型的等效电路。

这样一来，我们就可以分析电路在频率响应、幅频特性和传输特性上的变化。

小信号模型在电路分析中的应用小信号模型在电子电路设计和分析中有着广泛的应用。

在放大器设计中，通过建立放大器的小信号模型，可以快速地分析放大器的增益、带宽、稳定性以及噪声等特性。

此外，小信号模型还可以在滤波器设计、功率放大器设计以及交流耦合等领域发挥作用。

在通信系统设计中，小信号模型常常用于分析调制解调器、射频前端、混频器等模块的频率响应和信号传输特性。

利用小信号模型，工程师们可以更好地优化电路的性能，提高系统的整体性能和稳定性。

结语小信号模型作为一种电子电路分析的重要方法，为工程师们提供了便利和实用的工具。

通过建立准确的小信号模型，我们可以更深入地了解电路的特性和性能，从而优化设计、提高效率。

希望通过本文的介绍，读者对小信号模型有了更清晰的认识，并在实际工程应用中能够灵活运用这一方法。

三极管小信号等效模型三极管是一种常用的电子元件，广泛应用于各种电子设备中。

在电子电路设计中，为了简化复杂的电路结构，提高分析和计算的效率，通常会使用等效模型来代替实际的三极管。

本文将介绍三极管的小信号等效模型及其应用。

一、小信号等效模型的概念小信号等效模型是指在三极管工作于小信号条件下，将其非线性特性近似为线性特性的模型。

它可以将三极管的输入输出关系简化为电流和电压之间的线性关系，便于电路设计与分析。

二、三极管的小信号等效模型三极管的小信号等效模型包括输入端的电流源以及输出端的电压源。

其中，输入端的电流源称为输入电流源，表示输入信号对三极管的控制作用；输出端的电压源称为输出电压源，表示三极管输出信号的变化。

1. 输入电流源输入电流源的大小与输入信号的变化有关，通常用电流放大倍数β表示。

当输入信号为直流信号时，输入电流源的值为0。

而当输入信号为交流信号时，输入电流源的值与输入信号的变化成正比。

2. 输出电压源输出电压源的大小与输出信号的变化有关，通常用输出电压增益Av 表示。

当输出信号为直流信号时，输出电压源的值为0。

而当输出信号为交流信号时，输出电压源的值与输出信号的变化成正比。

三、小信号等效模型的应用小信号等效模型在电子电路设计中有广泛的应用。

它可以简化复杂的电路结构，使得电路分析和计算更加方便快捷。

同时，小信号等效模型也可以用于分析三极管的放大性能以及频率特性。

1. 放大性能分析通过小信号等效模型，可以方便地计算三极管的电流放大倍数β，以及输入输出电阻等参数。

这些参数可以用来评估三极管的放大性能，判断其是否适合特定的应用场景。

2. 频率特性分析通过小信号等效模型，可以方便地计算三极管的截止频率、增益带宽积等参数。

这些参数可以用来评估三极管的频率特性，确定其在不同频率下的工作范围。

四、小信号等效模型的限制小信号等效模型的基本假设是电路工作在小信号条件下，即输入信号的幅度相对于静态工作点来说是很小的。

小信号模型的原理和应用1. 什么是小信号模型小信号模型是一种用于分析和设计电子电路的工具。

正常情况下，电子元件的工作状态一般采用大信号模型进行分析，但在某些情况下，当输入信号非常小，以至于可以忽略的时候，采用小信号模型进行分析可以更加简化和有效。

2. 小信号模型的基本原理小信号模型的基本原理是将电路中的非线性元件（如晶体管）抽象成线性元件（如电阻，电容）的组合，从而简化分析过程。

其可以采用各种线性化技术，如小信号分析、增量分析、微分等方法进行建模和求解。

3. 小信号模型的应用小信号模型在电子电路设计和信号处理中有着广泛的应用。

下面列举了几个常见的应用领域：3.1 放大器设计小信号模型可以用于设计和优化放大器电路。

通过对放大器进行小信号模型化，可以更好地理解和调整电路的频率响应、增益和失真等特性。

同时，小信号模型也可以用于估计放大器的输入和输出阻抗，从而实现匹配和调谐。

3.2 滤波器设计小信号模型可以用于分析和设计各种类型的滤波器电路，如低通滤波器、带通滤波器、高通滤波器等。

通过对滤波器进行小信号模型化，可以更好地了解滤波器的频率特性、可调节性和稳定性。

3.3 系统建模和控制小信号模型可以用于系统建模和控制。

对于复杂的控制系统，小信号模型可以将其简化成一个线性动态系统，从而方便对系统进行分析和控制算法的设计。

此外，小信号模型也可以用于估计系统的稳定性和鲁棒性。

3.4 集成电路设计小信号模型在集成电路设计中有着重要的应用。

通过对集成电路进行小信号分析，可以更好地了解电路的稳定性、功耗和噪声等特性，从而优化电路设计和性能。

3.5 通信系统设计小信号模型在通信系统设计中也有广泛的应用。

通过对系统中各个组件进行小信号分析，可以更好地了解系统的频率响应、噪声特性和信号传输能力，从而提高系统的性能和可靠性。

4. 总结小信号模型是一种重要的工具，可以用于分析和设计电子电路。

它通过将非线性元件线性化，简化了电路分析的过程，提供了更好的抽象和分析能力。

运放的等效小信号模型
运放（Operational Amplifier，简称Op-Amp）的等效小信号模型是用来描述运放在小信号条件下的行为的模型。

在小信号分析中，我们通常将运放看作是一个理想的电压控制电压源（Voltage-Controlled Voltage Source，简称VCVS），它的等效小信号模型可以用一个简单的电路图来表示。

常见的运放等效小信号模型包括以下几个主要部分：
1．输入阻抗（Input Impedance）：在小信号条件下，运放的输入阻抗非常高，近似为无穷大，因此可以忽略不计。

2．输入电压（Input Voltage）：运放的等效输入电压为零，即差模输入电压为零。

3．增益（Gain）：运放的等效增益非常大，近似为无穷大。

4．输出阻抗（Output Impedance）：在小信号条件下，运放的输出阻抗非常低，近似为零，因此可以忽略不计。

5．输出电压（Output Voltage）：运放的输出电压与差模输入电压之间存在一个线性关系，通常表示为V out=A∙(V+−V−)，其中A 是运放的差模增益。

6．功率供应（Power Supply）：运放的等效小信号模型通常不考虑功率供应。

综上所述，运放的等效小信号模型可以简化为一个理想的差模电压控制电压源（VCVS）电路图，其中输入电压为零，增益无穷大，输入阻抗无穷大，输出阻抗为零。

这个简化模型使得在小信号条件下对
运放进行分析和设计更加方便。

但需要注意的是，在实际应用中，运放的实际性能可能会与理想模型有所不同，因此需要根据具体情况进行分析和验证。