【小初高学习]2018年高中数学 黄金100题系列 第65题 空间角的计算 理
- 格式:doc
- 大小:2.18 MB
- 文档页数:32
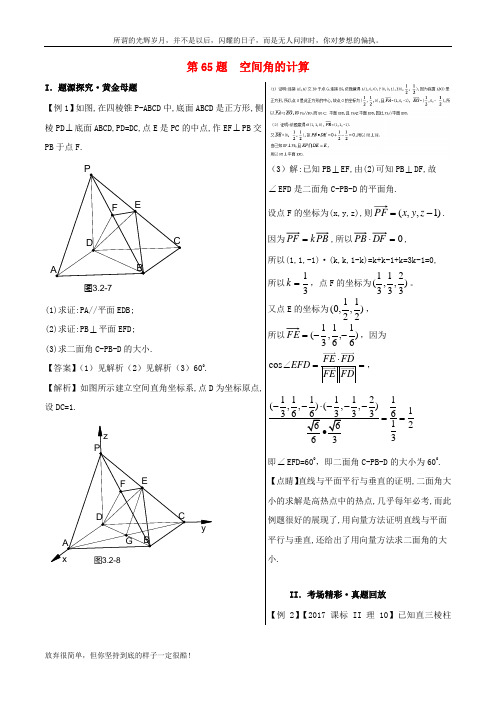
第65题 空间角的计算I .题源探究·黄金母题【例1】如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD,PD=DC,点E 是PC 的中点,作EF ⊥PB 交PB 于点F.图3.2-7EADBCPF(1)求证:PA//平面EDB; (2)求证:PB ⊥平面EFD; (3)求二面角C-PB-D 的大小.【答案】(1)见解析(2)见解析(3)600.【解析】如图所示建立空间直角坐标系,点D 为坐标原点,设DC=1.yxz 图3.2-8GE A DBCPF(3)解:已知PB ⊥EF,由(2)可知PB ⊥DF,故∠EFD 是二面角C-PB-D 的平面角.设点F 的坐标为(x,y,z),则)1,,(-=z y x .因为k =,所以0=⋅, 所以(1,1,-1)·(k,k,1-k)=k+k-1+k=3k-1=0,所以31=k ,点F 的坐标为)32,31,31(。
又点E 的坐标为)21,21,0(,所以)61,61,31(--=,因为cos FE FD EFD FE FD⋅∠==,1111121(,,)(,,)1366333612663--⋅---==•即∠EFD=600,即二面角C-PB-D 的大小为600.【点睛】直线与平面平行与垂直的证明,二面角大小的求解是高热点中的热点,几乎每年必考,而此例题很好的展现了,用向量方法证明直线与平面平行与垂直,还给出了用向量方法求二面角的大小.II .考场精彩·真题回放【例2】【2017课标II 理10】已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A .32B .155C .105D .33【答案】C【解析】分析:如图所示,补成四棱柱1111ABCD A B C D - , 11,2,BC D BC ∠=则所求角为201121221cos603,5BD C D AB =+-⨯⨯⨯=== 因此1210cos 55BC D ∠== ,故选C 。



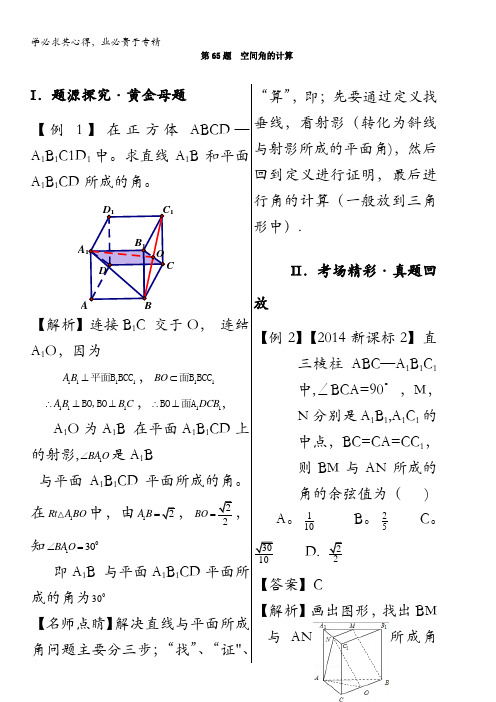
OCC 1D 1D B 1ABA 1第65题 空间角的计算I .题源探究·黄金母题【例1】在正方体ABCD —A 1B 1C1D 1中。
求直线A 1B 和平面A 1B 1CD 所成的角。
【解析】连接B 1C 交于O , 连结A 1O ,因为1111A B ⊥平面B BCC ,11BO ⊂面B BCC 111A B B C ∴⊥⊥BO,BO ,11DCB ∴⊥BO 面A ,A 1O 为A 1B 在平面A 1B 1CD 上的射影,1BAO ∠是A 1B与平面A 1B 1CD 平面所成的角。
在1RtA BO 中,由12AB =,22BO =,知0130BAO ∠=即A 1B 与平面A 1B 1CD 平面所成的角为030【名师点睛】解决直线与平面所成角问题主要分三步;“找”、“证"、“算”,即;先要通过定义找垂线,看射影(转化为斜线与射影所成的平面角),然后回到定义进行证明,最后进行角的计算(一般放到三角形中).II .考场精彩·真题回放【例2】【2014新课标2】直三棱柱ABC —A 1B 1C 1中,∠BCA=90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC=CA=CC 1,则BM 与AN 所成的角的余弦值为( )A 。
110B 。
25C 。
30D.22【答案】C【解析】画出图形,找出BM 与AN所成角的平面角,利用解三角形求出BM 与 AN 所成角的余弦值.解:直三棱柱ABC ﹣A 1B 1C 1中,∠BCA=90°,M ,N 分别是A 1B 1,A 1C 1 的中点,如图:BC 的中点为O,连结ON,1112MN B C OB ==且11MN B C ,则MN0B 是平行四边形,BM 与AN 所成角就是∠ANO ,∵BC=CA=CC 1,设BC=CA=CC 1=2,∴CO=1,AO=,AN=,MB=22211226B M BB +=+=在△ANO 中,由余弦定理可得:cos∠ANO=222630210256AN ON AO AN NO +-==⨯⨯故选:C .【例3】【2016高考新课标1文数】平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ,11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( ) (A )32(B )22(C )33(D )13【答案】A【解析】分析:如图,设平面11CB D 平面ABCD ='m ,平面11CB D 平面11ABB A ='n ,因为//α平面11CB D ,所以//',//'m m n n ,则,m n 所成的角等于','m n 所成的角。

2018年高考数学专题34空间中线线角、线面角的求法黄金解题模板专题34 空间中线线角、线面角的求法【高考地位】立体几何是高考数学命题的一个重点,空间中线线角、线面角的考查更是重中之重. 其求解的策略主要有两种方法:其一是一般方法,即按照“作——证——解”的顺序进行;其一是空间向量法,即建立直角坐标系进行求解. 在高考中常常以解答题出现,其试题难度属中高档题.【方法点评】类型一空间中线线角的求法方法一平移法使用情景:空间中线线角的求法解题模板:第一步首先将两异面直线平移到同一平面中;第二步然后运用余弦定理等知识进行求解;第三步得出结论.例1正四面体ABCD 中, E F ,分别为棱AD BC ,的中点,则异面直线EF 与CD 所成的角为A. 6π B. 4π C. 3π D. 2π 【答案】B平移;利用特殊点(线段的端点或中点)作平行线平移;补形平移.计算异面直线所成的角通常转化为解三角形的问题处理,要注意异面直线所成角的范围为0,2π?。
【变式演练1】如图,四边形ABCD 是矩形,沿直线BD 将ABD ?翻折成'A BD ?,异面直线CD 与'A D 所成的角为α, 则()A .'A CA α<∠B .'A CA α>∠C.'A CD α<∠ D .'A CD α>∠【答案】B考点:异面直线所成角的定义及运用.【变式演练2】【2018年衡水联考】在棱长为1的正方体1111ABCD A BC D -中,点E , F 分别是侧面11AA D D 与底面ABCD 的中心,则下列命题中错误的个数为()①//DF 平面11D EB ;②异面直线DF 与1B C 所成角为60?;③1ED 与平面1B DC 垂直;④1112F CDB V -=. A. 0 B. 1 C. 2 D. 3【答案】A【解析】对于①,∵DF 11//B D ,DF ?平面11D EB , 11B D ?平面11D EB ,∴//DF 平面11D EB ,正确;对于②,∵DF 11//B D ,∴异面直线DF 与1B C 所成角即异面直线11B D 与1B C 所成角,△11C B D 为等边三角形,故异面直线DF 与1B C 所成角为60?,正确;对于③,∵1ED ⊥1A D ,1E D ⊥CD,且1A D ?CD=D ,∴1E D ⊥平面11A B DC ,即1E D ⊥平面1B DC ,正确;。
规范答题示例7 空间角的计算问题典例7 (12分)如图,AB 是圆O 的直径,C 是圆O 上异于A ,B 的一个动点,DC 垂直于圆O 所在的平面,DC ∥EB ,DC =EB =1,AB =4. (1)求证:DE ⊥平面ACD ;(2)若AC =BC ,求平面AED 与平面ABE 所成的锐二面角的余弦值. 审题路线图(1)(2)CA ,CB ,CD 两两垂直―→建立空间直角坐标系―→写各点坐标―→求平面AED 与平面ABE 的法向量―→将所求二面角转化为两个向量的夹角ACB 中,AB =4,AC =BC , ,为原点建立空间直角坐标系,,D (0,0,1),B (0,22,0),评分细则(1)第(1)问中证明DC⊥BC和AC⊥BC各给1分,证明DE∥BC给1分,证明BC⊥平面ACD时缺少AC∩DC=C,AC,DC⊂平面ACD,不扣分.(2)第(2)问中建系给1分,两个法向量求出1个给2分,没有最后结论扣1分,法向量取其他形式同样给分.跟踪演练7 (2017·山东)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是DF的中点.(1)设P是CE上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E—AG—C的大小.解(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP.又BP⊂平面ABP,所以BE⊥BP,又∠EBC=120°,所以∠CBP=30°.(2)方法一取EC的中点H,连接EH,GH,CH.因为∠EBC=120°,所以四边形BEHC为菱形,所以AE=GE=AC=GC=32+22=13.取AG 的中点M ,连接EM ,CM ,EC , 则EM ⊥AG ,CM ⊥AG ,所以∠EMC 为所求二面角的平面角. 又AM =1,所以EM =CM =13-1=2 3. 在△BEC 中,由于∠EBC =120°,由余弦定理得EC 2=22+22-2×2×2×cos 120°=12, 所以EC =23,因此△EMC 为等边三角形, 故所求的角为60°.方法二 以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系. 由题意得A (0,0,3),E (2,0,0),G (1,3,3),C (-1,3,0),故AE →=(2,0,-3),AG →=(1,3,0),CG →=(2,0,3), 设m =(x 1,y 1,z 1)是平面AEG 的一个法向量. 由⎩⎪⎨⎪⎧m · AE →=0,m ·AG →=0,可得⎩⎨⎧2x 1-3z 1=0,x 1+3y 1=0.取z 1=2,可得平面AEG 的一个法向量m =(3,-3,2). 设n =(x 2,y 2,z 2)是平面ACG 的一个法向量. 由⎩⎪⎨⎪⎧n ·AG →=0,n ·CG →=0,可得⎩⎨⎧x 2+3y 2=0,2x 2+3z 2=0.取z 2=-2,可得平面ACG 的一个法向量n =(3,-3,-2).所以cos 〈m ,n 〉=m ·n |m ||n |=12.因此所求的角为60°.。
第65题空间角的计算I.题源探究·黄金母题【例1】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.图3.2-7(1)求证:PA//平面EDB;(2)求证:PB⊥平面EFD;(3)求二面角C-PB-D的大小.【答案】(1)见解析(2)见解析(3)600.【解析】如图所示建立空间直角坐标系,点D为坐标原点,设DC=1.(3)解:已知PB⊥EF,由(2)可知PB⊥DF,故∠EFD是二面角C-PB-D的平面角.设点F的坐标为(x,y,z),则)1,,(-=zyx. 因为k=,所以0=⋅,所以(1,1,-1)·(k,k,1-k)=k+k-1+k=3k-1=0,所以31=k,点F的坐标为)32,31,31(。
又点E的坐标为)21,21,0(,所以)61,61,31(--=,因为cosFE FDEFDFEFD⋅∠==,1111121(,,)(,,)16123--⋅---==即∠EFD=600,即二面角C-PB-D的大小为600. 【点睛】直线与平面平行与垂直的证明,二面角大小的求解是高热点中的热点,几乎每年必考,而此例题很好的展现了,用向量方法证明直线与平面平行与垂直,还给出了用向量方法求二面角的大小.II.考场精彩·真题回放【例2】【2017课标II理10】已知直三棱柱111C C AB -A B 中,C 120∠A B=,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A.B. C.5D.3【答案】C【解析】分析:如图所示,补成四棱柱1111ABCD A B C D -, 11,BC D BC ∠=则所求角为11BD C D AB ====因此1cos 5BC D ∠== ,故选C 。
【名师点睛】平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角;②认定:证明作出的角就是所求异面直线所成的角;③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角。
求异面直线所成的角要特别注意异面直线之间所成角的范围。
【例3】【2016高考浙江】如图,已知平面四边形ABCD ,AB =BC =3,CD =1,AD ∠ADC =90°.沿直线AC 将△ACD 翻折成△CD 'A ,直线AC 与D'B 所成角的余弦的最大值是______.【答案】9【解析】分析:设直线AC 与'BD 所成角为θ.设O是AC 中点,由已知得AC =,如图,以OB 为x 轴,OA 为y 轴,过O 与平面ABC 垂直的直线为z 轴,建立空间直角坐标系,由(0,2A ,2B ,(0,2C -,作DH AC ⊥于H ,翻折过程中,'D H 始终与AC 垂直,2CD CH CA ===,则3OH=,6DH ==,因此可设,,)636D αα-,则'()6236BD αα=--uuu r , 与CA uu r平行的单位向量为(0,1,0)n =r ,所以cos cos ',BD n θ=<>uuu r r ''BD nBD n ⋅=uuu r ruuu r r =cos 1α=时, cos θC【点睛】先建立空间直角坐标系,再计算与C A 平行的单位向量n 和D 'B ,进而可得直线C A 与D 'B 所成角的余弦值,最后利用三角函数的性质可得直线C A 与D 'B 所成角的余弦值的最大值.【例4】【2017浙江9】如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CRQC RA==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面角为α,β,γ,则A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α【答案】B【解析】设O 为三角形ABC 中心,则O 到PQ 距离最小,O 到PR 距离最大,O 到RQ 距离居中,而高相等.【例5】【2017课标3理16】a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC为旋转轴旋转,有下列结论:①当直线AB 与a 成60°角时,AB 与b 成30°角; ②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°; ④直线AB 与a 所成角的最小值为60°.其中正确的是________.(填写所有正确结论的编号) 【答案】②③【解析】由题意,AB 是以AC 为轴,BC 为底面半径的圆锥的母线,由,AC a AC b ⊥⊥ ,又AC ⊥圆锥底面,在底面内可以过点B ,作B D a ,交底面圆C 于点D ,如图所示,连结DE ,则DE ⊥BD ,DE b ∴ ,连结AD ,等腰△ABD中,AB AD ==当直线AB 与a 成60°角时,60ABD ∠= ,故BD = ,又在B D ERt △中,2,BE DE =∴=,过点B 作BF ∥DE ,交圆C 于点F ,连结AF ,由圆的对称性BF DE ==ABF ∴△ 为等边三角形,60ABF ∴∠= ,即AB 与b 成60°角,②正确,①错误.由最小角定理可知③正确;很明显,可以满足平面ABC ⊥直线a ,直线AB 与a 所成的最大角为90°,④错误. 正确的说法为②③.【例6】【2017课标1理18】如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=.(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=,求二面角A -PB -C 的余弦值.【解析】分析:(1)根据题设条件可以得出AB ⊥AP ,CD ⊥PD .而AB ∥CD ,就可证明出AB ⊥平面PAD .进而证明平面PAB ⊥平面PAD .(2)先找出AD 中点,找出相互垂直的线,建立以F 为坐标原点,FA 的方向为x 轴正方向,||AB 为单位长,的空间直角坐标系,列出所需要的点的坐标,设(,,)x y z =n 是平面PCB 的法向量,(,,)x y z =m 是平面PAB的法向量,根据垂直关系,求出(0,1,=-n 和(1,0,1)=m ,利用数量积公式可求出二面角的平面角.解析:(1)由已知90BAP CDP ∠=∠=︒,得AB ⊥AP ,CD ⊥PD .由于AB ∥CD ,故AB ⊥PD ,从而AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD . (2)在平面PAD 内作PF AD ⊥,垂足为F , 由(1)可知,AB ⊥平面PAD ,故AB PF ⊥,可得PF ⊥平面ABCD .以F 为坐标原点,FA 的方向为x 轴正方向,||AB 为单位长,建立如图所示的空间直角坐标系F xyz -.由(1)及已知可得2A,(0,0,2P,2B,(,1,0)2C -.所以(,1,)22PC =--,(2,0,0)CB =,2(22PA =-,(0,1,0)AB =. 设(,,)x y z =n 是平面PCB 的法向量,则00PC CB ⎧⋅=⎪⎨⋅=⎪⎩n n,即0220x y z ⎧-+-=⎪⎨=,可取(0,1,=-n .设(,,)x y z =m 是平面PAB 的法向量,则00PA AB ⎧⋅=⎪⎨⋅=⎪⎩m m,即0220x z y -=⎨⎪=⎩, 可取(1,0,1)=m .则cos ,||||3⋅==-<>n m n m n m , 所以二面角A PB C --的余弦值为3-【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面:①求异面直线所成的角,关键是转化为两直线的方向向量的夹角;②求直线与平面所成的角,关键是转化直线的方向向量和平面的法向量的夹角;③求二面角,关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.【例7】【2017课标II 理19】如图,四棱锥P -ABCD 中,侧面PAD 为等比三角形且垂直于底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点。
(1)证明:直线//CE 平面PAB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为o 45 ,求二面角M AB D --的余弦值。
【答案】(1)证明略;。
【解析】分析:(1) 取PA 的中点F ,连结EF ,BF ,由题意证得CE ∥BF ,利用线面平行的判断定理即可证得结论;(2)建立空间直角坐标系,求得半平面的法向量:()0,=m ,()0,0,1=n ,然后利用空间向量的结论可求得二面角M -AB -D。
解析:(1)取PA 的中点F ,连结EF ,BF 。
因为E 是PD 的中点,所以EF ∥AD ,12EF AD =, 由90BAD ABC ∠=∠=得BC ∥AD ,又12BC AD =, 所以EF BC ∥。
四边形BCEF 为平行四边形,CE ∥BF 。
又BF ⊂平面PAB ,CE ⊄平面PAB , 故CE ∥平面PAB 。
(2)由已知得BA AD ⊥,以A 为坐标原点,AB 的方向为x 轴正方向,AB 为单位长,建立如图所示的空间直角坐标系A xyz -,则()0,0,0A ,()1,0,0B ,()1,1,0C,(P,(10PC =,,,(100)AB =,,,设()(),,01M x y z x <<则()(1,,,,1,BM x y z PM x y z =-=-,因为BM 与底面ABCD 所成的角为45°, 而()0,0,1=n 是底面ABCD 的法向量, 所以cos ,sin 45BM =n ,2=, 即()22210x y z -+-=。
①又M 在棱PC 上,设PM PC λ=,则,1,x y z λ===。
②由①,②解得121x y z ⎧=+⎪⎪⎪=⎨⎪⎪=⎪⎩(舍去),121x y z ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩。
所以122M ⎛-⎝⎭,从而122AM ⎛⎫=- ⎪ ⎪⎝⎭。
设()000,,x y z =m 是平面ABM 的法向量,则0,0,AM AB ⎧⋅=⎪⎨⋅=⎪⎩m m即(0000220,0,x y x ⎧+=⎪⎨=⎪⎩所以可取()0,=m 。