【名师一号】2014-2015学年高中数学 1-3-1 函数的单调性与导数双基限时训练 新人教版选修2-2

教学设计中学数学教学设计：§1.3.《函数的单调性》教学设计一【教材分析】《函数单调性》是高中数学新教材必修一第二章第三节的内容。

在此之前，学生已学习了函数的概念、定义域、值域及表示法，这为过渡到本节的学习起着铺垫作用。

本节内容是高中数学中相当重要的一个基础知识点，是研究和讨论初等函数有关性质的基础。

掌握本节内容不仅为今后的函数学习打下理论基础，还有利于培养学生的抽象思维能力，及分析问题和解决问题的能力.二【学生分析】从学生的知识上看，学生已经学过一次函数，二次函数，反比例函数等简单函数，函数的概念及函数的表示，接下来的任务是对函数应该继续研究什么,从各种函数关系中研究它们的共同属性，应该是顺理成章的。

从学生现有的学习能力看，通过初中对函数的认识与实验，学生已具备了一定的观察事物的能力，积累了一些研究问题的经验，在一定程度上具备了抽象、概括的能力和语言转换能力。

从学生的心理学习心理上看，学生头脑中虽有一些函数性质的实物实例，但并没有上升为“概念”的水平，如何给函数性质以数学描述?如何“定性”“定量”地描述函数性质是学生关注的问题，也是学习的重点问题。

函数的单调性是学生从已经学习的函数中比较容易发现的一个性质，学生也容易产生共鸣，通过对比产生顿悟，渴望获得这种学习的积极心向是学生学好本节课的情感基础。

三【教学目标】1、知识与技能：（1）建立增（减）函数的概念通过观察一些函数图象的特征，形成增（减）函数的直观认识. 再通过具体函数值的大小比较，认识函数值随自变量的增大（减小）的规律，由此得出增（减）函数单调性的定义 . 掌握用定义证明函数单调性的步骤。

（2）函数单调性的研究经历了从直观到抽象，以图识数的过程，在这个过程中，让学生通过自主探究活动，体验数学概念的形成过程的真谛。

2、过程与方法（1）通过已学过的函数特别是二次函数，理解函数的单调性及其几何意义；（2）学会运用函数图象理解和研究函数的性质；（3）能够熟练应用定义判断与证明函数在某区间上的单调性．3、情态与价值，使学生感到学习函数单调性的必要性与重要性，增强学习函数的紧迫感.四【教学重点与难点】重点：函数的单调性及其几何意义．难点：利用函数的单调性定义判断、证明函数的单调性．五【学法与教学用具】1、从观察具体函数图象引入，直观认识增减函数，利用这定义证明函数单调性。

3.3.1 函数的单调性与导数教学目标重点：利用导数研究函数的单调性，会求函数的单调区间. 难点：⒈探究函数的单调性与导数的关系;⒉如何用导数判断函数的单调性. 知识点：1.探索函数的单调性与导数的关系;2.会利用导数判断函数的单调性并求函数的单调区间.能力点：1.通过本节的学习，掌握用导数研究单调性的方法.2.在探索过程中培养学生的观察、分析、概括的能力渗透数形结合思想、转化思想.教具准备：多媒体课件,三角板 课堂模式：学案导学 一.引入新课师：判断函数的单调性有哪些方法？比如判断2x y =的单调性，如何进行？ 生：用定义法、图像法.师：因为二次函数的图像我们非常熟悉,可以画出其图像，指出其单调区间，再想一下，有没有需要注意的地方？ 生：注意定义域.师：如果遇到函数x x y 33-=，如何判断单调性呢？你能画出该函数的图像吗？ 师：定义是解决问题的最根本方法，但定义法较繁琐,又不能画出它的图像，那该如何解决呢？揭示并板书课题：函数的单调性与导数【设计意图】通过复习回顾，巩固旧知.从已学过的知识（判断二次函数的单调性）入手，提出新的问题（判断三次函数的单调性），引起认知冲突，激发学习的兴趣.师：函数是描述客观世界变化规律的重要数学模型，研究函数时，了解函数的增与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的．通过研究函数的这些性质，我们可以对数量的变化规律有一个基本的了解．函数的单调性与函数的导数一样都是反映函数变化情况的，那么函数的单调性与函数的导数是否有着某种内在的联系呢? 二．探究新知师：如图（1），它表示跳水运动中高度h 随时间t 变化的函数2() 4.9 6.510h t t t =-++的图像，图（2）表示高台跳水运动员的速度v 随时间t 变化的函数'()()9.8 6.5v t h t t ==-+的图像．运动员从起跳到最高点，以及从最高点到入水这两段时间的运动状态有什么区别？ 生：通过观察图像，可以发现：（1）运动员从起点到最高点，离水面的高度h 随时间t 的增加而增加，即()h t 是增函数．相应地，'()()0v t h t =>．（2）从最高点到入水，运动员离水面的高度h 随时间t 的增加而减少，即()h t 是减函数．相应地，'()()0v t h t =<．【设计意图】从具体的实际情景出发，提出本节课要探索的问题，函数的单调性与导数的关系.为学生提供一个联想的“源”，巧妙设问，把学习任务转移给学生；让学生完成对函数单调性与导数关系的第一次认识，明确研究课题.师：导数的几何意义是函数在该点处的切线的斜率，函数图象上每个点处的切线的斜率都是变化的，那么函数的单调性与导数有什么关系呢？观察下面函数的图像，探讨函数的单调性与其导数正负的关系．（1）函数x y =的定义域为R ，并且在定义域上是增函数，其导数01/>=y ； （2）函数2x y =的定义域为R ，在),(+∞-∞上单调递减，在),0(+∞上单调递增；而x y 2/=，当0<x 时，其导数0/<y ；当0>x 时，其导数0/>y ；当0=x 时，其导数0/=y ．（3）函数3x y =的定义域为R ，在定义域上为增函数；而2/3x y =，若0≠x ，则其导数032>x ，当0=x 时，其导数032=x ；（4）函数x y 1=的定义域为),0()0,(+∞⋃-∞，在)0,(-∞上单调递减，在),0(+∞上单调递减,而2/1xy -=，因为0≠x ,所以0/<y .师：以上四个函数的单调性及其导数符号的关系说明，在区间),(b a 内,如果0)(/>x f ，那么函数)(x f y =在这个区间内单调递增；如果0)(/<x f ，那么函数)(x f y =在这个区间内单调递减.【设计意图】从具体的函数出发，体会数形结合思想的运用.让学生体会从特殊到一般，从具体到抽象的过程，降低思维难度，让学生在老师的引导下自主学习和探索，提高学习的成就感和自信心. 三. 理解新知师：如图，导数'0()f x 表示函数)(x f 在点00(,)x y 处的切线的斜率．观察图像回答，函数在某个点处的导数值与函数在该点处的单调性是怎样的关系？生:在0x x =处，'0()0f x >，切线是“左下右上”式的，这时，函数)(x f 在0x 附近单调递增；在1x x =处，0)(1/<x f ，切线是“左上右下”式的，这时，函数)(x f 在1x 附近单调递减．师生共同总结：函数的单调性与导数的关系: 在某个区间),(b a 内，如果0)(/>x f ，那么函数)(x f y =在这个区间内单调递增；如果0)(/<x f ，那么函数)(x f y =在这个区间内单调递减．说明：如果0)(/=x f ，那么函数)(x f y =在这个区间内是常函数．【设计意图】通过导数的几何意义来验证由具体函数所得到的结论，形成一般性结论.让学生经历观察、分析、归纳、发现规律的过程，体会函数单调性与导数的关系. 四．运用新知例1、已知导函数'()f x 的下列信息：当14x <<时，'()0f x >； 当4x >，或1x <时，'()0f x <； 当4x =，或1x =时，'()0f x = 试画出函数()y f x =图像的大致形状．解：当14x <<时，'()0f x >，可知()y f x =在此区间内单调递增；当4x >，或1x <时，'()0f x <；可知()y f x =在此区间内单调递减； 当4x =，或1x =时，'()0f x =，这两点比较特殊，我们把它称为“临界点”． 综上，函数()y f x =图像的大致形状如图所示． 学生思考，并在纸上画出函数图像教师投影若干学生的作业情况,学生共同分析.【设计意图】让学生通过此题加深理解导函数是如何影响原函数的,这是今后利用 导函数研究函数的必备技能.这里让学生切实理解，为今后学习扫清障碍. 例2、判断下列函数的单调性，并求出单调区间． （1）3()3f x x x =+；（2）2()23f x x x =--（3）()sin (0,)f x x x x π=-∈；（4）32()23241f x x x x =+-+ 解：（1）因为3()3f x x x =+，所以，'22()333(1)0f x x x =+=+>因此，3()3f x x x =+在R 上单调递增，如图1所示．（2）因为2()23f x x x =--，所以，()'()2221f x x x =-=-当'()0f x >，即1x >时，函数2()23f x x x =--单调递增； 当'()0f x <，即1x <时，函数2()23f x x x =--单调递减； 函数2()23f x x x =--的图像如图2所示．（3）因为()sin (0,)f x x x x π=-∈，所以，'()cos 10f x x =-<因此，函数()sin f x x x =-在(0,)π单调递减，如图3所示． （4）因为32()23241f x x x x =+-+，所以．当'()0f x >，即时，函数2()23f x x x =--； 当'()0f x <，即时，函数2()23f x x x =--； 函数32()23241f x x x x =+-+的图像如图4所示．【设计意图】让学生初步体会用导数的方法确定函数单调性的简便. 【师生活动】总结求()y f x =单调区间的步骤： （1）确定函数()y f x =的定义域；（2）求导数''()y f x =；（3）解不等式'()0f x >，解集在定义域内的部分为增区间； （4）解不等式'()0f x <，解集在定义域内的部分为减区间． 例3．已知函数xx y 1+=，试讨论出此函数的单调区间. 解：2222//)1)(1(111)1(x x x x x x x x y +-=-=-=+=２令0)1)(1(2>+-xx x . 解得11-<>x x 或∴xx y 1+=的单调增区间是：),1()1-,(+∞-∞和 令0)1)(1(2<+-x x x ，解得1001<<<<-x x 或 ∴xx y 1+=的单调减区间是：)1,0()0,1(和-五.课堂小结（1）函数的单调性与导数的关系 （2）求解函数()yf x =单调区间【设计意图】通过师生共同反思，优化学生的认知结构. 六. 布置作业 必做：课本A 组 1,2【设计意图】体现了分层、有梯度的教学，学生动手练习,加强学生的应用意识. 七、板书设计。

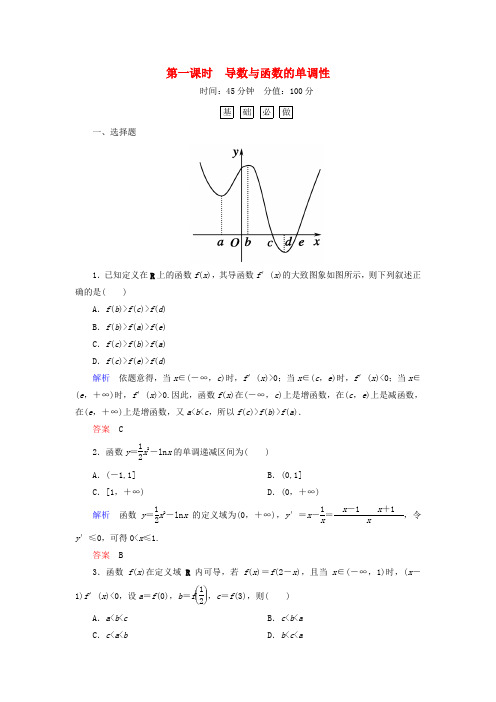
第一课时 导数与函数的单调性时间：45分钟 分值：100分基 础 必 做一、选择题1．已知定义在R 上的函数f (x )，其导函数f ′(x )的大致图象如图所示，则下列叙述正确的是( )A ．f (b )>f (c )>f (d )B ．f (b )>f (a )>f (e )C ．f (c )>f (b )>f (a )D ．f (c )>f (e )>f (d )解析 依题意得，当x ∈(－∞，c )时，f ′(x )>0；当x ∈(c ，e )时，f ′(x )<0；当x ∈(e ，＋∞)时，f ′(x )>0.因此，函数f (x )在(－∞，c )上是增函数，在(c ，e )上是减函数，在(e ，＋∞)上是增函数，又a <b <c ，所以f (c )>f (b )>f (a )．答案 C2．函数y ＝12x 2－ln x 的单调递减区间为( )A ．(－1,1]B ．(0,1]C ．[1，＋∞)D ．(0，＋∞)解析 函数y ＝12x 2－ln x 的定义域为(0，＋∞)，y ′＝x －1x＝x －x ＋x，令y ′≤0，可得0<x ≤1.答案 B3．函数f (x )在定义域R 内可导，若f (x )＝f (2－x )，且当x ∈(－∞，1)时，(x －1)f ′(x )<0，设a ＝f (0)，b ＝f ⎝ ⎛⎭⎪⎫12，c ＝f (3)，则( )A ．a <b <cB ．c <b <aC ．c <a <bD ．b <c <a解析 依题意得，当x <1时，f ′(x )>0，f (x )为增函数；又f (3)＝f (－1)，且－1<0<12<1，因此有f (－1)<f (0)<f ⎝ ⎛⎭⎪⎫12， 即有f (3)<f (0)<f ⎝ ⎛⎭⎪⎫12，即c <a <b . 答案 C4．若函数f (x )＝x 2＋ax ＋1x 在⎝ ⎛⎭⎪⎫12，＋∞上是增函数，则a 的取值范围是( )A ．[－1,0]B ．[－1，＋∞)C ．[0,3]D ．[3，＋∞)解析 f ′(x )＝2x ＋a －1x 2，因为函数在⎝ ⎛⎭⎪⎫12，＋∞上是增函数，所以f ′(x )≥0在⎝ ⎛⎭⎪⎫12，＋∞上恒成立，即a ≥1x 2－2x 在⎝ ⎛⎭⎪⎫12，＋∞上恒成立，设g (x )＝1x 2－2x ，g ′(x )＝－2x 3－2，令g ′(x )＝－2x 3－2＝0，得x ＝－1，当x ∈⎝ ⎛⎭⎪⎫12，＋∞时，g ′(x )<0，故g (x )max ＝g ⎝ ⎛⎭⎪⎫12＝4－1＝3，所以a ≥3，故选D.答案 D5．若f (x )＝ln xx，e<a <b ，则( )A ．f (a )>f (b )B ．f (a )＝f (b )C ．f (a )<f (b )D ．f (a )f (b )>1解析 f ′(x )＝1－ln xx2，当x >e 时，f ′(x )<0， 则f (x )在(e ，＋∞)上为减函数，f (a )>f (b )． 答案 A6．已知a ≤1－x x ＋ln x 对任意x ∈⎣⎢⎡⎦⎥⎤12，2恒成立，则a 的最大值为( )A ．0B ．1C ．2D ．3解析 设f (x )＝1－x x ＋ln x ＝1x＋ln x －1，则f ′(x )＝－1x 2＋1x ＝x －1x2.当x ∈⎣⎢⎡⎭⎪⎫12，1时，f ′(x )<0，故函数f (x )在⎣⎢⎡⎭⎪⎫12，1上单调递减； 当x ∈(1,2]时，f ′(x )>0， 故函数f (x )在(1,2]上单调递增． ∴f (x )min ＝f (1)＝0.∴a ≤0，故a 的最大值为0.故选A. 答案 A 二、填空题7．函数f (x )＝1＋x －sin x 在(0,2π)上的单调情况是________． 解析 在(0,2π)上有f ′(x )＝1－cos x >0， 所以f (x )在(0,2π)上单调递增． 答案 单调递增8．若函数f (x )＝13x 3－32x 2＋ax ＋4恰在[－1,4]上单调递减，则实数a 的值为________．解析 ∵f (x )＝13x 3－32x 2＋ax ＋4，∴f ′(x )＝x 2－3x ＋a ，又函数f (x )恰在[－1,4]上单调递减，∴－1,4是f ′(x )＝0的两根，∴a ＝(－1)×4＝－4.答案 －49．已知函数f (x )＝(m －2)x 2＋(m 2－4)x ＋m 是偶函数，函数g (x )＝－x 3＋2x 2＋mx ＋5在(－∞，＋∞)内单调递减，则实数m ＝________.解析 若f (x )＝(m －2)x 2＋(m 2－4)x ＋m 是偶函数， 则m 2－4＝0，m ＝±2.若g ′(x )＝－3x 2＋4x ＋m ≤0恒成立，则Δ＝16＋4×3m ≤0，解得m ≤－43，故m ＝－2.答案 －2 三、解答题10．已知函数f (x )＝ax 2＋b ln x 在x ＝1处有极值12.(1)求a ，b 的值；(2)求函数y ＝f (x )的单调区间．解 (1)f ′(x )＝2ax ＋b x .又f (x )在x ＝1处有极值12.得⎩⎪⎨⎪⎧f＝12，f＝0，即⎩⎪⎨⎪⎧a ＝12，2a ＋b ＝0.解之得a ＝12，b ＝－1.(2)由(1)可知f (x )＝12x 2－ln x ，其定义域是(0，＋∞)，且f ′(x )＝x －1x＝x ＋x －x.由f ′(x )<0，得0<x <1； 由f ′(x )>0，得x >1.所以函数y ＝f (x )的单调减区间是(0,1)，单调增区间是(1，＋∞)． 11．(2015·长春模拟)已知函数f (x )＝x 2＋a ln x . (1)当a ＝－2时，求函数f (x )的单调区间；(2)若g (x )＝f (x )＋2x在[1，＋∞)上是单调函数，求实数a 的取值范围．解 (1)由已知，函数的定义域为(0，＋∞)． 当a ＝－2时，f (x )＝x 2－2ln x ， 所以f ′(x )＝2x －2x＝x －x ＋x，则当x ∈(0,1)时，f ′(x )<0， 所以(0,1)为f (x )的单调递减区间．当x ∈(1，＋∞)时，f ′(x )>0，(1，＋∞)为f (x )的单调递增区间．(2)由题意得g ′(x )＝2x ＋a x －2x2，函数g (x )在[1，＋∞)上是单调函数．(ⅰ)若函数g (x )为[1，＋∞)上的单调增函数， 则g ′(x )≥0在[1，＋∞)上恒成立， 即a ≥2x－2x 2在[1，＋∞)上恒成立，设φ(x )＝2x－2x 2，因为φ(x )在[1，＋∞]上单调递减，所以φ(x )max ＝φ(1)＝0，所以a ≥0.(ⅱ)若函数g (x )为[1，＋∞)上的单调减函数， 则g ′(x )≤0在[1，＋∞)上恒成立，不可能． 综上，实数a 的取值范围是[0，＋∞)．培 优 演 练1．(理)(2014·辽宁卷)当x ∈[－2,1]时，不等式ax 3－x 2＋4x ＋3≥0恒成立，则实数a 的取值范围是( )A ．[－5，－3] B.⎣⎢⎡⎦⎥⎤－6，－98 C ．[－6，－2]D ．[－4，－3]解析 不等式等价于ax 3≥x 2－4x －3恒成立． 当x ＝0时式子恒成立．当x >0时，a ≥1x －4x 2－3x3恒成立．令1x＝t ，x ∈(0,1]，∴t ≥1.∴a ≥t －4t 2－3t 3恒成立．令g (t )＝t －4t 2－3t 3，g ′(t )＝1－8t －9t 2. 对称轴t ＝－818＝－49.∴函数g ′(t )在[1，＋∞)上为减函数． 而且g ′(1)＝－16<0，∴g ′(t )<0在[1，＋∞)上成立． ∴g (t )在[1，＋∞)上是减函数． ∴g (t )max ＝g (1)＝－6，∴a ≥－6. 当x <0时，a ≤1x －4x 2－3x3恒成立．∵x ∈[－2,0)，∴t ≤－12，令g ′(t )＝0，得t ＝－1.∴g (t )在(－∞，－1]上为减函数，在⎝ ⎛⎦⎥⎤－1，－12上为增函数．∴g (t )min ＝g (－1)＝－2，∴a ≤－2.综上，－6≤a ≤－2. 答案 C(文)对于在R 上可导的任意函数f (x )，若满足(x －a )f ′(x )≥0，则必有( ) A ．f (x )≥f (a ) B ．f (x )≤f (a ) C ．f (x )>f (a )D ．f (x )<f (a )解析 由(x －a )f ′(x )≥0知，当x >a 时，f ′(x )≥0；当x <a 时，f ′(x )≤0.∴当x ＝a 时，函数f (x )取得最小值，则f (x )≥f (a )．答案 A2．已知函数f (x )＝－12x 2＋4x －3ln x 在[t ，t ＋1]上不单调，则t 的取值范围是________．解析 由题意知f ′(x )＝－x ＋4－3x ＝－x 2＋4x －3x＝－x －x －x.由f ′(x )＝0得函数f (x )的两个极值点为1,3. 则只要这两个极值点有一个在区间(t ，t ＋1)内， 函数f (x )在区间[t ，t ＋1]上就不单调， 由t <1<t ＋1或t <3<t ＋1，得0<t <1或2<t <3. 答案 (0,1)∪(2,3)3．已知函数f (x )＝a x ＋x 2－x ln a －b (a ，b ∈R ，a >1)，e 是自然对数的底数． (1)试判断函数f (x )在区间(0，＋∞)上的单调性；(2)当a ＝e ，b ＝4时，求整数k 的值，使得函数f (x )在区间(k ，k ＋1)上存在零点． 解 (1)f ′(x )＝a x ln a ＋2x －ln a ＝2x ＋(a x－1)ln a . ∵a >1，∴当x ∈(0，＋∞)时，ln a >0，a x－1>0. ∴f ′(x )>0.∴函数f (x )在(0，＋∞)上单调递增．(2)∵f (x )＝e x＋x 2－x －4，∴f ′(x )＝e x＋2x －1，∴f ′(0)＝0. 当x >0时，e x >1，∴f ′(x )>0. ∴f (x )是(0，＋∞)上的增函数； 同理，f (x )是(－∞，0)上的减函数． 又f (0)＝－3<0，f (1)＝e －4<0，f (2)＝e 2－2>0，当x >2时，f (x )>0，∴当x >0时，函数f (x )的零点在(1,2)内． ∴k ＝1满足条件；f (0)＝－3<0，f (－1)＝1e－2<0， f (－2)＝1e2＋2>0，当x <－2时，f (x )>0；∴当x <0时，函数f (x )的零点在(－2，－1)内． ∴k ＝－2满足条件． 综上所述，k ＝1或－2.。

1.理解函数的单调性、最大值、最小值及其几何意义．2.会运用基本初等函数的图象分析函数的性质.★备考知考情1.函数的单调性是函数的一个重要性质，是高考的热点，常见问题有：求单调区间，判断函数的单调性，求参数的取值，利用函数单调性比较数的大小，以及解不等式等．客观题主要考查函数的单调性，最值的确定与简单应用．2.题型多以选择题、填空题的形式出现，若与导数交汇命题，则以解答题的形式出现.一、知识梳理《名师一号》P15注意：研究函数单调性必须先求函数的定义域，函数的单调区间是定义域的子集单调区间不能并！知识点一函数的单调性1.单调函数的定义专业整理专业整理2.单调性、单调区间的定义若函数f (x )在区间D 上是增函数或减函数，则称函数f (x )在这一区间上具有(严格的)单调性，区间D 叫做f (x )的单调区间.注意： 1、《名师一号》P16 问题探究 问题1 关于函数单调性的定义应注意哪些问题？(1)定义中x 1，x 2具有任意性，不能是规定的特定值． (2)函数的单调区间必须是定义域的子集； (3)定义的两种变式：设任意x 1，x 2∈[a ，b ]且x 1<x 2，那么①1212()()0->-f x f x x x ⇔f (x )在[a ，b ]上是增函数；专业整理1212()()0-<-f x f x x x ⇔f (x )在[a ，b ]上是减函数．②(x 1－x 2)[f (x 1)－f (x 2)]>0⇔f (x )在[a ，b ]上是增函数； (x 1－x 2)[f (x 1)－f (x 2)]<0⇔f (x )在[a ，b ]上是减函数．2、《名师一号》P16 问题探究 问题2单调区间的表示注意哪些问题？单调区间只能用区间表示，不能用集合或不等式表示； 如有多个单调区间应分别写，不能用并集符号“∪”联结，也不能用“或”联结．知识点二 单调性的证明方法：定义法及导数法 《名师一号》P16 高频考点 例1 规律方法 (1) 定义法:利用定义证明函数单调性的一般步骤是： ①任取x 1、x 2∈D ，且x 1<x 2；②作差f (x 1)－f (x 2)，并适当变形(“分解因式”、配方成同号项的和等)； ③依据差式的符号确定其增减性． (2) 导数法:设函数y ＝f (x )在某区间D 内可导．如果f ′(x )>0，则f (x )在区间D 内为增函数；如果f ′(x )<0，则f (x )在区间D 内为减函数． 注意：(补充)（1）若使得f ′(x )=0的x 的值只有有限个，专业整理则如果f ′(x )0≥，则f (x )在区间D 内为增函数； 如果f ′(x ) 0≤，则f (x )在区间D 内为减函数． （2）单调性的判断方法：《名师一号》P17 高频考点 例2 规律方法定义法及导数法、图象法、复合函数的单调性(同增异减)、 用已知函数的单调性等(补充)单调性的有关结论1．若f (x )，g (x )均为增(减)函数， 则f (x )＋g (x )仍为增(减)函数． 2．若f (x )为增(减)函数，则－f (x )为减(增)函数，如果同时有f (x )>0， 则()1f x 为减(增)(减)函数．3．互为反函数的两个函数有相同的单调性． 4．y ＝f [g (x )]是定义在M 上的函数， 若f (x )与g (x )的单调性相同，则其复合函数f [g (x )]为增函数； 若f (x )、g (x )的单调性相反，则其复合函数f [g (x )]为减函数． 简称”同增异减”5. 奇函数在关于原点对称的两个区间上的单调性相同； 偶函数在关于原点对称的两个区间上的单调性相反．专业整理函数单调性的应用《名师一号》P17 特色专题 (1)求某些函数的值域或最值．(2)比较函数值或自变量值的大小． (3)解、证不等式．(4)求参数的取值范围或值． (5)作函数图象．二、例题分析：（一) 函数单调性的判断与证明 例1.（1）《名师一号》P16 对点自测 1 判断下列说法是否正确(1)函数f (x )＝2x ＋1在(－∞，＋∞)上是增函数．( )(2)函数f (x )＝1x在其定义域上是减函数．( )(3)已知f (x )＝x ，g (x )＝－2x ，则y ＝f (x )－g (x )在定义域上是增函数．( )答案： √ × √例1.（2）《名师一号》P16 高频考点例1（1）(2014·北京卷)下列函数中，在区间(0，＋∞)上为增函数的是( )A．y＝x＋1 B．y＝(x－1)2C．y＝2－x D．y＝log0.5(x＋1)答案：A.例2.（1）《名师一号》P16 高频考点例1（2）判断函数f(x)＝axx＋1在(－1，＋∞)上的单调性，并证明．法一：定义法设－1<x1<x2，则f(x1)－f(x2)＝ax1x1＋1－ax2x2＋1＝ax1x2＋1－ax2x1＋1x1＋1x2＋1＝a x1－x2x1＋1x2＋1专业整理∵－1<x1<x2，∴x1－x2<0，x1＋1>0，x2＋1>0.∴当a>0时，f(x1)－f(x2)<0，即f(x1)<f(x2)，∴函数y＝f(x)在(－1，＋∞)上单调递增．同理当a<0时，f(x1)－f(x2)>0，即f(x1)>f(x2)，∴函数y＝f(x)在(－1，＋∞)上单调递减．法二：导数法注意：《名师一号》P17 高频考点例1 规律方法1.判断函数的单调性应先求定义域；2.用定义法判断(或证明)函数单调性的一般步骤为：取值—作差—变形—判号—定论，其中变形为关键，而变形的方法有因式分解、配方法等；3.用导数判断函数的单调性简单快捷，应引起足够的重视（二）求复合函数、分段函数的单调性区间例1.《名师一号》P16 高频考点例2（1）求函数y＝x－|1－x|的单调增区间；专业整理专业整理y ＝x －|1－x |＝⎩⎨⎧1，x ≥1，2x －1，x <1.作出该函数的图象如图所示．由图象可知，该函数的单调增区间是(－∞，1]．例2.（1）《名师一号》P16 高频考点 例2（2） 求函数y ＝log 13(x 2－4x ＋3)的单调区间．解析:令u ＝x 2－4x ＋3，原函数可以看作y ＝log 13u 与u ＝x 2－4x ＋3的复合函数．令u ＝x 2－4x ＋3>0.则x <1或x >3.∴函数y ＝log 13(x 2－4x ＋3)的定义域为(－∞，1)∪(3，＋∞)．又u＝x2－4x＋3的图象的对称轴为x＝2，且开口向上，∴u＝x2－4x＋3在(－∞，1)上是减函数，在(3，＋∞)上是增函数．而函数y＝log13u在(0，＋∞)上是减函数，∴y＝log13(x2－4x＋3)的单调递减区间为(3，＋∞)，单调递增区间为(－∞，1)．注意：《名师一号》P17 高频考点例2 规律方法求函数的单调区间的常用方法(1)利用已知函数的单调性，即转化为已知函数的和、差或复合函数，求单调区间．(2)定义法：先求定义域，再利用单调性定义．(3)图象法：如果f(x)是以图象形式给出的，或者f(x)的图象易作出，可由图象的直观性写出它的单调区间．(4)导数法：利用导数的正负确定函数的单调区间．例2.（2）(补充)21122log4log⎛⎫=-⎪⎝⎭y x x专业整理专业整理答案：增区间：1,4⎛⎫+∞ ⎪⎝⎭；减区间：10,4⎛⎫ ⎪⎝⎭练习:()222log log y x x =-答案：增区间：)+∞；减区间：(（三）利用单调性解（证）不等式及比较大小 例1.（1）《名师一号》P17 特色专题 典例(1)已知函数f (x )＝log 2x ＋11－x，若x 1∈(1,2)，x 2∈(2，＋∞)，则( )A ．f (x 1)<0，f (x 2)<0B ．f (x 1)<0，f (x 2)>0C ．f (x 1)>0，f (x 2)<0D ．f (x 1)>0，f (x 2)>0【规范解答】 ∵函数f (x )＝log 2x ＋11－x在(1，＋∞)上为增函数，且f (2)＝0，∴当x 1∈(1,2)时，f (x 1)<f (2)＝0， 当x 2∈(2，＋∞)时，f (x 2)>f (2)＝0， 即f (x 1)<0，f (x 2)>0.专业整理例1.（2）《名师一号》P17 特色专题 典例(2)已知函数f (x )＝⎩⎨⎧x 2－4x ＋3，x ≤0，－x 2－2x ＋3，x >0，则不等式 f (a 2－4)>f (3a )的解集为( )A ．(2,6)B ．(－1,4)C ．(1,4)D ．(－3,5)【规范解答】作出函数f (x )的图象，如图所示，则函数f (x )在R 上是单调递减的．由f (a 2－4)>f (3a )，可得a 2－4<3a ，整理得a 2－3a －4<0，即(a ＋1)(a －4)<0，解得－1<a <4，所以不等式的解集为(－1,4)．注意:本例分段函数的单调区间可以并!（四）已知单调性求参数的值或取值范围例1.(1)《名师一号》P17 特色专题 典例(3)专业整理已知函数()()2,211,22x a x x f x x ⎧-≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩满足对任意的实数x 1≠x 2，都有1212()()0-<-f x f x x x 成立，则实数a 的取值范围为( )A ．(－∞，2) B.⎝ ⎛⎦⎥⎤－∞，138 C ．(－∞，2] D.⎣⎢⎡⎭⎪⎫138，2【规范解答】函数f (x )是R 上的减函数，于是有⎩⎨⎧ a －2<0，a －2×2≤⎝ ⎛⎭⎪⎫122－1，由此解得a ≤138， 即实数a 的取值范围是⎝⎛⎦⎥⎤－∞，138.例2.(1) （补充）如果函数f (x )＝ax 2＋2x －3在区间(－∞，4)上单调递增，则实数a 的取值范围是________．[答案][－14，0][解析](1)当a＝0时，f(x)＝2x－3，在定义域R上单调递增，故在(－∞，4)上单调递增；(2)当a≠0时，二次函数f(x)的对称轴为直线x＝－1 a ，因为f(x)在(－∞，4)上单调递增，所以a<0，且－1a≥4，解得－14≤a<0.综上所述－14≤a≤0.例2.(2)（补充）若f(x)＝x3－6ax的单调递减区间是(－2,2)，则a的取值范围是( )A．(－∞，0] B．[－2,2] C．{2} D．[2，＋∞)专业整理[答案] C[解析]f′(x)＝3x2－6a，若a≤0，则f′(x)≥0，∴f(x)单调增，排除A；若a>0，则由f′(x)＝0得x＝±2a，当x<－2a和x>2a时，f′(x)>0，f(x)单调增，当－2a<x<2a时，f(x)单调减，∴f(x)的单调减区间为(－2a，2a)，从而2a＝2，∴a＝2.变式：若f(x)＝x3－6ax在区间(－2,2)单调递减，则a的取值范围是？[点评] f(x)的单调递减区间是(－2,2)和f(x)在(－2，2)上单调递减是不同的，应加以区分．本例亦可用x＝±2是方程f′(x)＝3x2－6a＝0的两根解得a＝2.专业整理专业整理例2.(3) （补充） 若函数)2,3()(log )(321---=在ax x x f 上单调递减， 则实数a 的取值范围是 （ ）A ．[9，12]B ．[4，12]C ．[4，27]D ．[9，27]答案：A温故知新P23 第9题若函数()()212log 3=-+f x x ax a 在区间 [)2,+∞上单调递减，则实数a 的取值范围是《计时双基练》P217 基础7《计时双基练》P217 基础8、10 8、设函数()12+=+ax f x x a在区间()2,-+∞上是增函数, 那么a 的取值范围是答案: [)1,+∞专业整理10、设函数()()=≠-x f x x a x a（2）若0>a 且()f x 在区间()1,+∞内单调递减, 求a 的取值范围.答案: [)1,+∞（五）抽象函数的单调性例1.（补充）已知f (x )为R 上的减函数，那么满足 f (|1x|)<f (1)的实数x 的取值范围是( ) A ．(－1,1) B ．(0,1)C ．(－1,0)∪(0,1)D ．(－∞，－1)∪(1，＋∞)答案：C解析：因为f (x )为减函数，f (|1x |)<f (1)，所以|1x |>1，则|x |<1且x ≠0，即x ∈(－1,0)∪(0,1)．专业整理练习：()y f x =是定义在[]1,1-上的增函数，解不等式2(1)(1)f x f x -<-答案：()0,1温故知新 P12 第8题注意：解抽象函数的不等式通常立足单调性定义或借助图像求解例2. 《计时双基练》P216 培优4函数()f x 的定义域为()0,+∞，且对一切0,0>>x y 都有()()()=-x f f x f y y，当1>x 时，有()0>f x 。