重庆市渝北区2012-2013上期八年级期末数学试题

（第8题）A D EB CO （第7题） 2012-2013学年度八年级上学期期末考试数 学 试 卷(第Ⅰ卷)命题人：黄建立注意：将第Ⅰ卷地答案都填在第Ⅱ卷相应地位置上.一、选择题：（本大题共12小题，每小题3分，共36分，每题只有一项是正确地.） 1．式子中x 地取值范围是（ ）(A) x ＞-2 (B) x≥0(C) x≥-2 (D) x≥2 2．下列计算中，正确地是（ ）(A)(B)(C)(D)3．下列各点中不在函数图象上地点是（ ） (A)(B)(C)(D)4．下列图形中，轴对称图形有（ ）(A) 1个 (B) 2个(C)3个(D)4个5．已知，则地值是( )(A) 2 (B) 3 (C) 4 (D) 6 6．均匀地向一个如图所示地容器中注水，最后把容器注满，在注水过程中水面高度随时间变化地函数图象大致是（）7．尺规作图作地平分线方法如下：以为圆心，任意长为半径画弧交、于、，再分别以点、为圆心，以大于长为半径画弧，两弧交于点，作射线由作法得地根据是（ ）(A) SAS (B) ASA (C) SSS (D) AAS8．如图，等腰△ABC 地周长为21，底边BC ＝ 5，AB 地垂直平分线DE 交AB 于点D ，交AC 于点E ，则△BEC 地周长为（ ）(A) 13 (B) 14 (C)15 (D)16(A) (B) (C) (D)mnnn （2（1（第11BAC （第10题）B ADE （第16题） 9．如果式子是一个完全平方式，则地值是（ ）(A)±6(B) 6(C)12(D)±1210．如图，，若，则地度数是（ ） (A)(B)(C)(D)11．如图（1），把一个长为、宽为地长方形（）沿虚线剪开，拼接成图（2），成为一个大正方形在一角去掉一个小正方形，则去掉地小正方形地边长为（ ）(A)(B)(C)(D)12．已知一次函数，且y 随x 地增大而减少，点M（，）、N（，）是它地图像上不同地两点．若，则 ( ) (A) t≤0(B) t=0(C) t ＞0(D) t ＜0二、填空题（本大题共6小题，每小题3分，共18分．） 13．地算术平方根是 ．14．若,，则地值为 ．15．一个正方体地表面积为，这个正方体地棱长为． 16．如图，点B 、F 、C 、E 在同一直线上，并且BF ＝CE ，∠B ＝∠E ．请你只添加一个条件(不再加辅助线)，使得△ABC ≌△DEF ．你添加地条件是： ．17．将一些半径相同地小圆按如图所示地规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，……，依次规律，第 19个图形有 个小圆．18．某物流公司地快递车和货车同时从甲地出发，以各自地速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车地速度为60千M ／时，两车之间地距离y(千M)与货车行驶时间x(小时)之间地函数图象如图所示，现有以下4个结论：①甲、乙两地之间地距离为120千M ； ②快递车从甲地到乙地地速度为100千M ／时；第1个图形 第2个图形 第3个图形 第4个图形 … )C③图中点B地坐标为(3.75，75)；④快递车从乙地返回时地速度为90千M／时．以上4个结论中正确地是 (填序号)2012-2013学年度八年级上学期期末考试数 学 试 卷（第Ⅱ卷）命题人：黄建立完卷时间：120分钟；满分120分一、请把选择题地答案填到下面地框里（每小题3分，共36分）二、填空题（本大题共6小题，每小题3分，共18分，将答案直接写在横线上．） 13． ； 14．____________； 15．_____________；16． ； 17． ； 18．_____________.三、解答下列各题（共7大题，共66分，解答应写文字说明、演算步骤或证明过程.） 19. (两小题各4分，共8分) （1）计算（2）化简：·，20. (本小题10分，每小题5分)（1）分解因式（2）先化简，再求值：，其中．21.（本小题9分）如图是由边长为1地小正方形组成地方格,在方格图中建立平面直角坐标系，使点地坐标为，点地坐标为； （1）在图中作出点关于x 轴地对称点,点地坐标是 ；（2）若点Q 是x 轴上使得QA 十QB 地值最小地点，在图中作出点Q 地位置，并写出点Q地坐标是 。

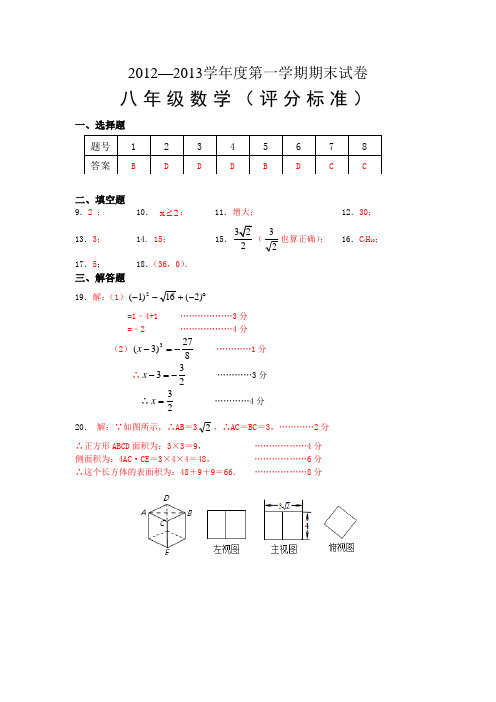
2012—2013学年度第一学期期末试卷八年级数学（评分标准）一、选择题二、填空题9．2 ； 10． x 2≥； 11．增大； 12．30； 13．3； 14. 15； 15．32（23也算正确）； 16．C 4H 10； 17．5； 18．（36，0）．三、解答题19．解：（1）︒-+--)2(16)1(2=1﹣4+1 ………………3分=﹣2 ………………4分（2）827)3(3-=-x …………1分 ∴233-=-x …………3分∴23=x …………4分20． 解：∵如图所示，∴AB ＝32，∴AC ＝BC ＝3，…………2分 ∴正方形ABCD 面积为：3×3＝9， ………………4分 侧面积为：4AC ·CE ＝3×4×4＝48， ………………6分 ∴这个长方体的表面积为：48＋9＋9＝66． ………………8分题号 12345678答案 BDDDBDCC21． 解（1）如图所示：……………… 4分（2）四边形ABCD 的面积=1222122ABD S ∆=⨯⨯⨯=．………………8分 22．解答：（1）证明：∵ABCD 是正方形∴AD=BC，∠ADC=∠BCD=90° …………1分 又∵三角形CDE 是等边三角形∴CE=CD，∠EDC=∠ECD=60°………………2分 ∴∠ADE=∠ECB ………………3分 ∴△ADE≌△BCE．………………4分（2）解：∵△CDE 是等边三角形，∴CE=CD=BC ………………5分∴△CBE 为等腰三角形，且顶角∠ECB=90°﹣60°=30° ∴∠EBC=21（180°﹣30°）=75°…………6分 ∵AD∥BC ………………7分∴∠AFB=∠EBC=75°． ……………………8分23． 解： y=223x -+与x 轴、y 轴的交点坐标为(3,0),(0,2)。

2012-2013学年度第一学期期末学情调研八年级数学试卷注意事项：1．本试卷考试时间为120分钟，试卷满分150分，考试形式闭卷． 2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．3．答题前，务必将姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上． 一、选择题（本大题共有8小题，每小题3分，共24分） 1．下列各组数中，能构成直角三角形的一组是（ ▲ ）A ．2，2，5B ．1，3，2C ．4，5，6D ．6，8，122．下列各选项的图形中，不是．．轴对称图形的是（ ▲ ）A B C D3．在平行四边形ABCD 中，若∠A：∠B=5： 4，则∠C 的度数为（ ▲ ） A ．60° B ．80° C ．90°D ．100°4．点P （m+3，m+1）在x 轴上，则点P 坐标为（ ▲ ） A ．（0，-2） B ．（2，0）C ．（4，0）D ．（0，-4） 5．下列函数中，是一次函数的有（ ▲ ）个.①y=x； ②xy 3=；③65+=x y ；④32y x =-；⑤23x y =.A ．1B ．2C ．3D ．46．某校9名初中毕业生的中考体育考试成绩如下：25 26 26 26 26 27 28 29 29，这些成绩的中位数．．．是（ ▲ ） A ．25B ．26C ．26.5D ．307．下列各式中不是．．一元一次不等式组的是（ ▲ ） A ．1,35y y ⎧<-⎪⎨⎪>-⎩B ．350,420x x ->⎧⎨+<⎩ C ．10,20a b -<⎧⎨+>⎩ D ．5020x x ->⎧⎨+≤⎩ 8．如图，平行四边形ABCD 的对角线相交于点O ，AO=4，OD=7，△DBC 的周长比△ABC 的周长（ ▲ ）A ．长6B ．短6C ．短3D ．长3二、填空题（本大题共10小题，每小题3分，共30分） 9．实数0.09的算术平方根．．．．．是 ▲ ． 10．已知直角△ABC 的周长为为 ▲ ．11．已知点A （3，4）先向左平移5个单位，再向下平移2个单位得到点B ，则点B 的坐标为 ▲ ．12．如图，已知△ABC 与△ADE 是成中心对称的两个图形，点A 是对称中心，点B 的对称点为点 ▲ ．13．如图所示，在△ABC 中，AC=6 cm ， BC=8 cm ，AB=10 cm ，D 、E 、F 分别是AB 、BC 、CA的中点，则△DEF 的面积是 ▲ cm 2．14．若一次函数y=(m-3)x+(m-1)的图像经过原点，则m= ▲ ．15．对于一次函数23y x =--，当x 满足 ▲ 条件时，图象在x 轴下方． 16．一组数据：1、2、4、3、2、4、2、5、6、1，它们的众数为 ▲ ． 17．一个钝角的度数为(535)x -°，则x 的取值范围是 ▲ ．18．如图，将一个边长分别为2、4的长方形纸片ABCD 折叠，使C 点与A 点重合，则线段DF 的长是 ▲ ．三、解答题（本大题共有10小题，共96分．解答时应写出文字说明、推理过程或演算步骤） 19．（本题8分）解下列不等式，并将解集分别用数轴表示出来：第12题第13题FEDCBA第18题（1）6876a a +<- （2）233154x x ++≥ 20．（本题8分）用图象法解下列二元一次方程组： （1）40210x y x y +-=⎧⎨-+=⎩ （2）220260x y x y +-=⎧⎨--=⎩21．（本题8分）解下列不等式组：（1）22211x x -<⎧⎨-≥⎩ （2）20331x x x-<⎧⎨-≤-⎩22．（本题8分）等腰三角形的周长为30 cm.（1）若底边长为x cm ，腰长为y cm ，写出y 与x 的函数关系式； （2）若腰长为x cm ，底边长为y cm ，写出y 与x 的函数关系式．23．（本题10分）在由边长为1的小正方形组成的网格中，建立如图所示的平面直角坐标系．（1）写出图中A、B两点的坐标；（2）已知点M（－2，1）、N（－4，－2），点P（3，2）关于原点对称的点是点Q，请在图形上标出M、N、P、Q这四点的位置，标出相应字母；（3）画出线段AB关于y24．（本题10分）如图，E、F是平行四边形ABCD的对角线AC上的点，CE=AF．请你用平行四边形有关知识来猜想：BE与DF有怎样的位置．．关系和数量．．关系？并对你的猜想加以说明．25．（本题10分）如图，每个小正方形的边长都是1．ACDEF。

2012--2013学年八年级上学期期末数学试卷D-21O yxD ．325()x x =4. 分式||22x x --的值为零，则x 的值为 A ．0 B ．2 C ．-2 D ．2或-25. 下列各式从左到右的变形是因式分解的是A.)(222y x y x -=-B.22))((y xy x y x -=-+C.2)1(3222++=++x x x D.ay ax y x a +=+)( 6. 已知点（-4，1y ），（2，2y ）都在直线221+-=x y 上，则1y 、2y 大小关系是A. 1y >2y B. 1y =2y C.1y <2y D.不能比较7. 已知一次函数y kx b =+的图象如图所示，当y 0>时，x 的取值范围是（ ）A ．x>-2B ．x>1C ．x<-2D ．x<18. 如图，直线是经过点（1,0）且与y 轴平行的直线．Rt △ABC 中直角边AC=4，BC=3．将BC 边在直线上滑动，使A ，B 在函数xk y =的图象上，那么k 的值是A ．3B ．6C ．12D ．415 二、填空题（每小题3分，共12分） 9. 函数2-=x x y 中自变量x 的取值范围是___________. 10. 如图，已知函数y ax b =+和y kx =的图象交于点P,则根据图象可得，关于y ax b y kx=+⎧⎨=⎩的二元一次方程组的解是___________. 11. 在2011,,4,3,2,1 中，共有 个无理数. 12. 已知n是正整数，111222(,),(,),,(,),n n n P x y P x y P x y 是反比例函数k y x=图象上的一列点，其中 121,2,,,n x x x n ===． 记112A x y =，223Ax y =，1n n n A x y +=，，若1A a =（a 是非零常数），则A 1·A 2·…·A n 的值是___________（用含a 和n 的代数式表示）．三、解答题（共64分）13．分解因式：33ax y axy - 14．分解因式：22882n mn m +- 15．计算：0119(π4)22----- 16．计算：29631aa --+17．解方程：423532=-+-xx x18．计算：2)2()3)(2()2)(2(y x y x y x y x y x ---+--+19．已知210x x +-=，求222(1)(1)(1)121x x x x x x x --÷+---+的值．20．某学校准备组织部分学生到少年宫参加活动，陈老师从少年宫带回来两条信息：信息一：按原来报名参加的人数，共需要交费用320元，如果参加的人数能够增加到原来人数的2倍，就可以享受优惠，此时只需交费用480元；信息二：如果能享受优惠，那么参加活动的每位同学平均分摊的费用比原来少4元．根据以上信息，原来报名参加的学生有多少人？ 21．设22113-=a，22235-=a，22357-=a……（1）写出na （n 为大于0的自然数）的表达式；（2）探究na 是否为8的倍数，并用文字语言表述你所获得的结论；（3）若一个数的算术平方根是一个自然数，则这个数是“完全平方数”，试找出1a ，2a ，3a ，……，na 这一列数中从小到大排列的前4个完全平方数；并说出当n 满足什么条件时, na 为完全平方数(不必说明理由).22．如图，已知A(n ，-2)，B(1，4)是一次函数b kx y +=的图象和反比例函数y=x m 的图象的两个交点，直线 (1)求反比例函数和一次函数的关系式； (2)求△AO B 的面积；(3)求不等式0<-+xm b kx 的解集(直接写出答案)．23．某蒜薹生产基地喜获丰收收蒜薹200吨。

2012—2013学年八年级(上)期末数学复习(三)一、填空题（每小题3分，共18分）1.等腰三角形的一边长是8，另一边长是5，则周长为 ________________2.在实数－32，0，2，π，9中，无理数有_____个.3.若20n 是整数，则正整数n 的最小值为________________．4.把多项式a 3—2a 2+a 分解因式的结果是 5.若2x －3的立方根5，则x 的平方根是____.6.如图，直线l 1，l 2交于点A 。

观察图象，点A 的坐标可以看作方程组 的解.二、选择题（每小题3分，共21分） 7.下列图案是轴对称图形的是 （ ）A ．B ．C ．D ．8.已知|a ﹣1|+=0，则a +b =（ ）A ．﹣8B ．﹣6C ．6D ．8 9.下列计算正确的是A ．a ＋a ＝2aB ．b 3·b 3＝2b 3C ．a 3÷a ＝a 3D ．(a 5)2＝a 7 10..函数1y=x 3的自变量x 的取值范围是（ ）A. x ＞3B. x ≥3C. x ≠3D. x ＜－311.在算式（）□（）的□中填上运算符号，使结果最大，这个运算符号是（ ）A ．加号B ．减号C ．乘号D ．除号 12.下列各组图形中，是全等形的是 （ ）A ．两个含60°角的直角三角形B ．腰对应相等的两个等腰直角三角形C ．边长为3和4的两个等腰三角形D ．一个钝角相等的两个等腰三角形13.如图，两个边长相等的正方形ABCD和EFGH，正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S，旋转的角度为θ，S与θ的函数关系的大致图象是（）A B C D三、解答题（每小题6分，共18分）14求代数式（a+2b）（a－2b）+（a+2b）2－4ab的值，其中a=1，b=1 10.15.如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，求CE的长度16.在三个整式2222,2,x xy y xy x++中，请你任意选出两个进行加（或减）运算，使所得整式可以因式分解，并进行因式分解．四、(每小题8分，共24分）17如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合.求∠CEF的度数18.如图，一次函数2y=23x-+的图象分别与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等腰Rt△ABC，∠BAC=90°．求过B、C两点直线的解析式．19.将4个数a b c d，，，排成2行、2列，两边各加一条竖直线记成a bc d，定义a b c da db c=-，上述记号就叫做2阶行列式．若1 1811x xx x+-=-+，求x的值.五、（每小题9分，共27分）20、某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨1.9元收费．如果超过20吨，未超过的部分按每吨1.9元收费，超过的部分按每吨2.8元收费．设某户每月用水量为x吨，应收水费为y元．（1）分别写出每月用水量未超过20吨和超过20吨，y与x间的函数关系式．（2）若该城市某户5月份水费平均为每吨2.2元，求该户5月份用水多少吨？21.感知：如图①，点E在正方形ABCD的BC边上，BF⊥AE于点F，DG⊥AE于点G．可知△ADG≌△BAF.（不要求证明）拓展：如图②，点B、C在∠MAN的边AM、AN上，点E, F在∠MAN内部的射线AD 上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC,∠1=∠2=∠BAC.求证：△ABE≌△CAF.应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边B上．CD=2BD.点E, F在线段AD上．∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为_________.22. 图l、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．点A和点B在小正方形的顶点上．(1)在图1中画出△ABC(点C在小正方形的顶点上)，使△ABC为直角三角形(画一个即可)；(2)在图2中画出△ABD(点D在小正方形的顶点上)，使△ABD为等腰三角形(画一个即可)；23．某校为开展好大课间活动，欲购买单价为20元的排球和单价为80元的篮球共100个．（1）设购买排球数为x（个），购买两种球的总费用为y（元），请你写出y与x的函数关系式（不要求写出自变量的取值范围）；（2）如果购买两种球的总费用不超过6620元，并且篮球数不少于排球数的3倍，那么有哪几种购买方案？（3）从节约开支的角度来看，你认为采用哪种方案更合算？参考答案1. 18或21.2. 2个.3. 54. a(a－1)25. ±86.{y=－X+2 ;y=2X－1)7.D8.B9.A10.A11.D12.B13.B14.解：原式=a2－4b2+a2+4ab+4b2－4ab=2a2=215.解：∵在等边三角形ABC中，AB=6，∴BC=AB=6，∵BC=3BD，∴BD=BC=2，∵△ABD绕点A旋转后得到△ACE，∴△ABD≌△ACE，∴CE=BD=2．故答案为：2．16.．解：222++=+=+(2)222();x xy x x xy x x y或222++=+(2)();y xy x x y或2222+-+=-=+-x xy y xy x y x y x y(2)(2)()();17.解：连接BO，∵∠BAC＝50°，∠BAC的平分线与AB的中垂线交于点O，∴∠OAB＝∠ABO＝25°，∵等腰△ABC中，AB＝AC，∠BAC＝50°，∴∠ABC＝∠ACB＝65°，∴∠OBC＝65°－25°＝40°，∵，∴△ABO≌△ACO，∴BO＝CO，∴∠OBC＝∠OCB＝40°，∵点C沿EF折叠后与点O重合，∴EO＝EC，∠CEF＝∠FEO，∴∠CEF ＝∠FEO ＝＝50°，故答案为：50°． 18.解：一次函数2y=23x -+中，令x =0得：y =2；令y =0，解得x =3．则A 的坐标是（0，2），C 的坐标是（3，0）． 作CD ⊥x 轴于点D ．∵∠BAC =90°， ∴∠OAB +∠CAD =90°， 又∵∠CAD +∠ACD =90°， ∴∠ACD =∠BAO又∵AB =AC ，∠BOA =∠CDA =90° ∴△ABO ≌△CAD ，∴AD =OB =2，CD =OA =3，OD =OA +AD =5． 则C 的坐标是（5，3）． 设BC 的解析式是y =kx +b ， 根据题意得：，解得：．则BC 的解析式是：125y x =+．19.解：根据题意化简1 181 1x x x x +-=-+，得：22(1)(1)8x x +--= ，整理得：2221(12)8x x x x ++--+= ，即48x =， 解得：2x = ． 故答案为：220.解：（1）当x ≤20时，y =1.9x ；当x ＞20时，y =1.9×20+（x ﹣20）×2.8=2.8x ﹣18；（2）∵5月份水费平均为每吨2.2元，用水量如果未超过20吨，按每吨1.9元收费． ∴用水量超过了20吨．2.8x ﹣18=2.2x ， 解得x =30．答：该户5月份用水30吨．21.证明：如图②∵∠1=∠2=∠BAC ∠1=∠BAE +∠EBA∠2=∠FCA +∠FAC ∠BAC =∠BAE +∠FAC ∴ ∠BAE =∠FCA ∠ABE =∠FAC ∵ AB =AC ∴△ABE ≌△CAF .解：如图③则△ABE 与△CDF 的面积之和为6. ∵由上题可知：△ABE ≌△CAF .∴△ABE 与△CDF 的面积之和=△CAF 与△CDF 的面积之和=△CAD 的面积 ∵ CD =2BD . △ABC 的面积为9。

2012年八年级数学上册期末考试卷2012年八年级数学上册期末考试卷一、选择题(共30分)1、观察下列图形，既是轴对称图形，又是中心对称图形的是 ( )A B C D2、不能判定四边形ABCD是平行四边形的是 ( )A、AB = CD，AD = BCB、AB∥CD，AB = CDC、AD∥BC，AB = CDD、AB∥CD，AD∥BC3、点P(-1，2)关于y轴对称的点的坐标为 ( )A、(1，-2)B、(-1，-2)C、(1，2)D、(2，1)4.在平面直角坐标系中，点A(1，-3)在( )A第一象限 B第二象限C第三象限 D第四象限5、众志成城，抗震救灾.某小组7名同学积极捐出自己的零花钱支援灾区，他们捐款的数额分别是(单位：元)：50，20，50，30，50，25，135.这组数据的众数和中位数分别是( )A.50，20B.50，30C.50，50D.135，506.下列各组数值是二元一次方程的解的是( )A BC D7.下列说法正确的是( )A 矩形的对角线互相垂直B 等腰梯形的对角线相等C 有两个角为直角的四边形是矩形D 对角线互相垂直的四边形是菱形8. 一辆客车从泉州出发开往宁德，设客车出发t小时后与宁德的距离为s千米，下列图象能大致反映s与t之间的函数关系的是( )A B C D9, 八年级学生开会,若每条长凳坐5人,则少10条长凳;若每条长凳坐6人,则多两条长凳,设八年级学生的人数为x，长凳数为y,由题意得方程组( )A BC D10.在平面直角坐标系中，已知一次函数的图象大致如图所示，则下列结论正确的是( )新|课|标 | 第| 一|网A gt;0, gt;0B gt;0, lt;0C lt;0, gt;0D lt;0, lt;0.二、填空题(每题3分，共30分)1.实数，中，是无理数有 ;2.如右图，数轴上点A表示的数是 ;3. 的平方根是 ;4、菱形ABCD的边长为5cm，其中一条对角线长为6cm，则菱形ABCD的面积为 cm2.5、已知正比例函数，当 ,则当x=2时y= ;6在下面的多边形中：①正三角形;②正方形;③正五边形;④正六边形，如果只用一种正多边形进行镶嵌，那么不能镶嵌成一个平面的有 (只填序号)7.如果某公司一销售人员的个人月收入与其每月的销售量成一次函数(如图所示)，那么此销售人员的销售量在4千件时的月收入是元。

2012~2013 学年度上期八年级期末教学质量监测数 学 试 卷(全卷共六个大题，满分 100 分， 90 分钟完卷）一、选择题（共 10 个小题，每小题 3 分，共 30 分）每小题下面都有代号为 A 、 B 、 C 、D 四个答案选项，其中只有一个选项是正确的，请把正确选项的代号填在题后的括号内，填写正确记 3 分，不填、填错或填出的代号超过一个均记0分。

1. 无理数 ）A . B.C. D. 2. 点 A （1,23）关于y 轴对称点 A ′的坐标是（ ） A.1(,2)3- B . 1(2,)3 C.1(,2)3- D . 1(2,)3-3. 下列图形是轴对称图形的有（ ）A . 1 个B . 2 个C . 3 个D . 4 个4. 下列计算正确的是（ ）A . 235a a a += B. 632a a a ÷= C . 22431x x -= D. ()326328x yx y -=-5. 下列条件中，不能判定三角形全等的是（ ）A. 有三边对应相等B. 有两边及夹角对应相等C. 有两角及一边对应相等D. 有两边及一角对应相等6. 按下列程序计算，最后输出的答案是（ ）A . 3aB . 21a +C . 2aD . a7. 如图： AB 是线段 CD 的垂直平分线，则图中全等三角形的对数有（ ）A.2对B.3 对C.4 对D.5 对8. 关于一次函数23y x =-，下列结论正确的是（ ）A. 图像经过点（一 3 , 3 )B. 图像经过第二、四象限C. 当32x >时，y > 0 D. y 随 x 的增大而减小 9. 如图：在△ABC 中，∠C = 90°, AC = BC , AD 平分∠BAC 交边 BC于点 D , DE ⊥AB 于 E ，若 △DEB 的周长为 10cm ，则 AB 的长为（ ）A . 8cmB . 10cmC . 12cmD . 20cm10. 已知等式()()()222252510ax bx ax bx c ax bx +-+++=++，那么c 的值为（ ）. A . 5 B . 25 C . 125 D . 225二、填空题（本大题共 8 个小题，每小题 3 分，共 24 分），请将答案直接写在题中横线上。

2012～2013学年度第一学期八年级数学试卷姓名--------------分数-------------一．选择题（每小题3分，共30分）1. 化简22x yx y--的结果…………………………………………………………… ……【 】 A.x ＋y B.x －y C.y － x D.－x －y2.从∠A 、∠B 、∠C 、∠D 的度数之比中，能判定四边形ABCD 是平行四边形的是…………【 】A.1∶2∶3∶4B.2∶2∶3∶3C.2∶3∶2∶3D.1∶2∶2∶33.下面的性质中,平行四边形不一定具有的是……………………………………… 【 】Ａ.对角互补 Ｂ.邻角互补 Ｃ.对角相等 Ｄ.对边相等4. 平行四边形一边长12cm ，那么它的两条对角线的长度可能是……………………【 】A.8cm 和16cmB.10cm 和16cmC.8cm 和14cmD.8cm 和12cm5．下列命题中正确的是……………………………………………………………………【 】 A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形 C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是菱形 6. 如图，D 是△ABC 内一点，BD ⊥CD ，BD=4，CD=3，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，且四边形EFGH 的周长是14，则AD 的长是……………………【 】 A.5 B.7 C.8 D.9 7. 给出四个特征：(1)两条对角线相等；(2)任一组对角互补；(3)任一组邻角互补； (4)是轴对称图形但不是中心对称图形.其中属于矩形和等腰梯形共同具有的特征的共有…………………………………………【 】 A.1个 B.2个 C.3个 D.4个8．下列说法中错误的是……………………………………………………………… ……【 】A ．两条对角线互相平分的四边形是平行四边形；B ．两条对角线互相垂直的矩形是正方形；C ．两条对角线相等的四边形是矩形；D ．两条对角线相等的菱形是正方形．9．如图，将一边长为12的正方形纸片ABCD 的顶点A 折叠至DC 边上的点E ，使DE ＝5，折痕为PQ ，则PQ 的长为……………………………………………………………【 】A.12B.13C.14D.1510. 在□ABCD 中，点A 1、A 2、A 3、A 4和C 1、C 2、C 3、C 4分别是AB 和CD 的五等分点，点B 1、B 2、和D 1、D 2分别是BC 和DA 的三等分点，已知四边形A 4B 2C 4D 2的面积为1，则□ABCD 的面积为……………【 】 A.2 B.53 C.35D.15二、填空题（每小题4分，共16分）11. 在□ABCD 中，若∠A －∠B ＝40°，则∠A ＝______，∠B ＝______． 12. 菱形两对角线长分别为24cm 和10cm,则菱形的高为__________13. 如图，梯形ABCD 中，AD ∥BC ，AB ＝CD ＝AD ＝1，∠B ＝60°，直线MN 为梯形ABCD 的对称轴，P 为MN 上一点，那么PC ＋PD 的最小值为______．14．已知：四边形ABCD 中,AD ∥BC.分别添加下列条件∶①AB ∥CD ；②AB=DC ；③AD=BC ；④∠A=∠C ⑤∠B=∠C.能使四边形成为平行四边形的条件的序号有____________.（把你认为正确的序号都填在横线上）三. 解答题（共54分）15. (本小题满分6分) 在等腰梯形ABCD 中，AD ∥BC ，E 是AD 的中点，求证：BE=CE.第6题图第9题图第13题图第15题图第10题图16．(本小题满分8分) 如图,平行四边形ABCD 中,AE ⊥BD,CF ⊥BD,垂足分别为E 、F,求证：四边形AECF 是平行四边形. 【证明】17. (本小题满分8分) 如图所示，折叠矩形的一边AD ，使点D 落在BC 边上的点F 处，已知AB=8cm ，BC=10cm ，求EC 的长. 【解】18. (本小题满分10分) 已知：如图，在□ABCD 中，E 、F 分别为边AB 、CD 的中点，BD 是对角线，AG ∥DB交CB 的延长线于G. (1)求证∶△ADE ≌△CBF ；(2)若四边形 BEDF 是菱形，则四边形AGBD 是什么特殊四边形？并证明你的结论. 【证明】19. (本小题满分10分) 如图，四边形ABCD 、AEFG 均为正方形连接DE 、BG ，试判断DE 与BG 的关系，并加以证明． 【证明】20. (本小题满分12分) 如图，在直角坐标系中，矩形OABC 的顶点O 与坐标原点重合，顶点A ，C 分别在坐标轴上，顶点B 的坐标为（4，2）．过点D （0，3）和E （6，0）的直线分别与AB ，BC 交于点M ，N ．（1）求直线DE 的解析式和点M 的坐标； （2）若反比例函数xmy =（x ＞0）的图象经过点M ，求该反比例函数的解析式，并通过计算判断点N 是否在该函数的图象上； （3）若反比例函数xmy =（x ＞0）的图象与△MNB 有公共点，请直接．．写出m 的取值范围____________； （4）试写出：过MB 中点且把矩形OABC 的面积平均分成两部分的直线的解析式是________________.【解】参考答案一、1A 2C 3A 4B 5D 6D 7B 8C 9B 10C 二、11.110° 70° 12.12013①③④ 三、15.∵ABCD 是等腰梯形，AD ∥BC ，∴AB=DC ，∠A=∠D …………2分 又∵E 是AD 中点，∴AE=DE ，∴△ABE ≌△DCE(SAS)…………4分 ∴BE=CE …………6分16.∵AE ⊥BD,CF ⊥BD ，∴∠AEB=∠CFD=90°，AE ∥CF ，………3分 又∵ABCD 是平行四边形，∴ AB=CD ，AB ∥CD ，∠ABE=∠CDF ， ∴△ABE ≌△DCF(AAS)…………6分 ∴AE=CF …………7分，∴AECF 是平行四边形.…………………8分17.由题意：AF=AD=10，AB=8，由勾股定理得：BF=6， ∴FC=4，……4分设CE=x ，则EF=DE=8－x ，……6分第19题图 第18题图第16题图第17题图 第20题图第16题图再由勾股定理得：()22284x x -=+，解得x=3，∴EC=3cm.……8分18. （1）∵四边形ABCD 是平行四边形， ∴∠1＝∠C ，AD ＝CB ，AB ＝CD .………2分 ∵点E 、F 分别是AB 、CD 的中点，∴AE ＝21AB ，CF ＝21CD.∴AE ＝CF .…………4分∴△ADE ≌△CBF .………………………5分（2）当四边形BEDF 是菱形时，四边形 AGBD 是矩形. ∵四边形ABCD 是平行四边形，∴AD ∥BC .∵AG ∥BD ，∴四边形 AGBD 是平行四边形.……7分 ∵四边形 BEDF 是菱形，∴DE ＝BE . ∵AE ＝BE ， ∴AE ＝BE ＝DE .∴∠1＝∠2，∠3＝∠4.∵∠1＋∠2＋∠3＋∠4＝180°， ∴2∠2＋2∠3＝180°.∴∠2＋∠3＝90°.即∠ADB ＝90°.……9分 ∴四边形AGBD 是矩形.…………………10分19.DE=BG 且DE ⊥BG.………………2分 理由是：ABCD 、AEFG 是正方形 ∴AD=AB ，AE=AG ，∠DAB=∠GAE=90°，……4分 ∴∠DAB ＋∠BAE=∠GAE ＋∠BAE ， 即∠DAE=∠BAG∴△DAE ≌△BAG(SAS)∴DE=BG ……………………………6分 延长DH 交BG 于H ， ∵△DAE ≌△BAG ，∴∠ABH=∠EDA ，∠AED=∠BEH∴∠BEH ＋∠ABH=∠AED ＋∠EDA=90°……8分 ∴∠BHE=90°即DP ⊥EF ……………………10分20.解：（1）设直线DE 的解析式为y=kx ＋b∵点D （0,3）和E （6，0）在图象上∴360b k b =⎧⎨+=⎩→⎪⎩⎪⎨⎧=-=321b k ∴直线DE 的关系式为：y=12x -+3 ………………………2分 当y=2时，12-x+3=2得x=2 ∴点M 的坐标为（2,2）……………………………………4分 （2）由（1）知：m=2×2=4∴反比例函数的解析式为y= x4 …………………………6分将x=4代入y=12x -+3得y=1 即点N 坐标为（4,1），而4×1=4∴点N 在其图象上 ……………………………………………8分 （3）4≤m ≤8………………………………………………………10分 （4）y=x －1…………………………………………………………12分。

重庆市渝北区上期八年级期末数学试题(总6页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--3号洞42号洞1号洞（第4题图） 八年级数学试卷一、选择题（每小题4分，共40分）在每个小题的下面都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请把正确答案的代号填在题后的表格中。

1．在2,1001,1010010001.0,722,0,2π⋅⋅⋅-中，无理数有( ) A ．3个 B ．4个 C ．5个 D ．6个 2．下列计算正确的是（ ）A ．1243a a a =⋅B ．532)(a a =C ．326a a a =÷D ．222)(b a ab =-3．下列图案中，属于轴对称图形的有（ ）A ．1个B ．2个C ．3个D ．4个 4．如图是一个台球桌示意图，四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出（球可以经过多次反射），则该球最后落入的球洞将是（ ）A ．1号洞B ．2号洞C ．3号洞D ．4号洞 5．若216x mx ++为完全平方式，则m 的值为（ ） A ． 8 B ． －8 C ． ±8 D ． ±46．下列条件中，能判定△ABC 与△DEF 全等的是 （ ） A ．∠A=∠E ，AB=EF ，∠B=∠D ； B ．AB=DE ，BC=EF ，∠C=∠F ；C ．AB=DE ，BC=EF ，∠A=∠E ；D ．∠A=∠D ，AB=DE ，∠B=∠E 7. 若等腰三角形的一个内角是50°，则这个等腰三角形的底角是（ ） °或80° °或40° °或50° °或80° 8．已知一次函数(1)y a x b =-+的图象如图所示，则a 、b 的取值范围是（ ）A.a ＞1 , b ＞0B.a ＜1, b ＜0C.a ＞0, b ＜0D.a ＜0, b ＞09．如图，函数b ax y +=和kx y =的图象交于点P,则关于y x ,的方程组⎩⎨⎧=-=-0y kx bax y 的解是（ ） A.无法确定 B.2,3-- C.3,2-- D.⎩⎨⎧-=-=23y x10．如图，将ABC ∆沿DE 折叠，使点A 与BC 边的中点F 重合，下列结论正确的有（ ）①EF AB ∥； ②12ADFE S AF DE =⨯四边形； ③BAF CAF ∠=∠； ④2BDF FEC BAC ∠+∠=∠． A ．1个B ．2个C ．3个D ．4个二、填空题 （每小题4分，共24分）请将每小题的答案填在该题后的横线上。

2012～2013学年度上期末统考八年级数学试题（全卷总分100分，120分钟完卷）一、 选择题（每小题2分，共30分）1、一次函数 12+-=x y 的图象经过点 （ ） A ．（2，-3） B.（1，0） C.（-2，3） D.（0，-1）2、能直观地反映出某种股票的涨跌情况，应选择 （ ）A.条形的统计图B.扇形的统计图C.折线的统计图D.直方图 3、要了解某地区八年级学生中，体重在某一范围内的学生所占的比例大小，需要求出样本的 （ ）A.平均数B.频数C.频率D.方差4、 计算a a a a ÷-÷-4322)()(的结果是 （ ） A. 2a - B. 3a - C. 4a D. 4a -5、下列从左到右的变形中是因式分解的有 ( ) ①1))((122--+=--y x y x y x ②)1(34+=+m m m m x x x x ③2222)(y xy x y x +-=- ④)3)(3(922y x y x y x -+=- A ．1个 B ．2 个 C ．3个 D ．4个6、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度n(厘米)与燃烧时间t(时)的函数关系的图象是 ( )7、 将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘以-1，所得图形与原图形的关系是 （ ） A 、关于x 轴对称 B 、关于y 轴对称 C 、关于原点对称 D 、无法确定 8、下列图案中，是轴对称图形的是 （ ）A DB C9、从镜子里面看到背后墙上电子钟显示数是: ，这时的时间是（ ）A .21:05B. 21:15 C .20:15 D.20:05 10、等腰三角形的周长是18cm ，其中一边长为4cm ，其它两边长分别为（ ） A ．4cm ，10cm B ．7cm ，7cm C ．4cm ，10cm 或7cm ，7cm D ．无法确定 11、如图，OA=OC ，OB=OD ，则图中全等三角形有（ ） A.2对 B.3对C.4对D.5对12、如图，AB 与CD 相交于点E ，EA=EC ，DE=BE ， 若使△AED ≌△CEB ，则 ( )A ． 应补充条件∠A=∠CB ． 应补充条件∠B=∠DC ． 不用补充条件D ． 以上说法都不正确13、)()(2x y y x ---因式分解的结果是 （ ） A ．(y-x)(x-y) B ．(x-y)(x-y-1)C ．(y-x)(y-x+1)D ．(y-x)(y-x-1)14、=⎪⎭⎫⎝⎛⨯⎪⎭⎫ ⎝⎛20042005522125( )A 1B 125 C 522D2003125⎪⎭⎫ ⎝⎛15、如图，已知AF 平分∠BAC ，过F 作FD ⊥BC ，若∠B 比∠C 大20度，则∠F 的度数是 （ ）A. 20度B 40度 C. 10度 D. 不能确定BE DF C A A DB C B C A E D （第12题）C（第11题）二、填空题（每题2分，共20分）1、点A （－3，4）关于原点对称的点的坐标为 。