专题训练反比例函数中k的几何意义(含答案)

专题01 用几何意义探究反比例函数中k 值问题的多种解法如图，反比例函数k y x =（k >0），A 、C 是第一象限上两点，S △OAB =S △OCD =2k ；S △OAC =S 梯形ABDC 在已知面积或比例线段解答反比例函数的问题中，善于利用k 与面积的关系，往往可以事半功倍．典例1．知面积比值，求k 值（2022•山东聊城中考真题）如图，直线与反比例函数在第一象限内的图象交于点，与y 轴交于点B ，过双曲线上的一点C 作x 轴的垂线，垂足为点D ，交直线于点E ，且．()30y px p =+¹()0k y k x=>()2,A q 3y px =+:3:4AOB COD S S =△△(1)求k ，p 的值；(2)若OE 将四边形BOCE 分成两个面积相等的三角形，求点C 的坐标．【答案】(1)，；(2)点C 的坐标为(4，2)【解析】【方法一】坐标法（1）解：∵直线与y 轴交点为B ，∴，即．∵点A 的横坐标为2，∴．∵，∴△COD 的面积为4，设，∴，解得．∵点在双曲线上，∴，把点代入，得，∴，；8k =12p =3y px =+()0,3B 3OB =13232AOB S =´´=V :3:4AOB COD S S =△△,k C m m æöç÷èø142k m m×=8k =()2,A q 8y x=4q =()2,4A 3y px =+12p =8k =12p =（2）解：由（1）得8,C m m æöç÷èø，∴．∵OE 将四边形BOCE 分成两个面积相等的三角形，∴，∵32BOE S m =△，，∴，解得或（不符合题意，舍去），∴点的坐标为（4，2）．【方法二】k 的几何意义法解：（1）由题意知，△ABO 的面积为3，又，得：△OCD 的面积为4，故k =2S △OCD =8，所以，A （2,4），把点代入，得（2）如图，过A ，E 作y 轴垂线，垂足为M ，N则四边形ODEN 为矩形，所以，S △OEN =S △OED ，又S △OBE =S △OCE ，所以S △BEN =S △OCD =4，1,32E m m æö+ç÷èøBOE COE S S =△△13422COE m S m æö=+-ç÷èø△3134222m m m æö=+-ç÷èø4m =4m =-C :3:4AOB COD S S =△△()2,4A 3y px =+12p =所以S △ABM =1，∵AM ∥NE ，∴△ABM ∽△EBN ，其面积比为1:4，∴AM ：NE =1:2，即NE =4，∴C 点坐标为（4,2）典例2．知比例线段，求k 值（2022•贵州铜仁中考真题）如图，点A 、B 在反比例函数k y x=的图象上，AC y ^轴，垂足为D ，BC AC ^．若四边形AOBC 的面积为6，12AD AC =，则k 的值为_______．【答案】3．【解析】【方法一】坐标法设点,k A a a æöç÷èø，∵AC y ^轴，∴AD a =，k OD a =，∵12AD AC =，∴AC 2a =，∴CD =3a ，∵BC AC ^．AC y ^轴，∴BC ∥y 轴，∴点B 3,3æöç÷èøk a a ，∴233k k k BC a a a=-=，∵AOD AOBC OBCD S S S =+V 四边形梯形，四边形AOBC 间面积为6，∴12136232k k a k a a æö+´=+ç÷èø，解得：3k =．【方法二】k 的几何意义法如图，连接OC ，延长CB 交x 轴于E ，则S △AOD =S △BOE =12k ，因为AD ：AC =1:2，所以S △AOC =2S △AOD =k ，S △BOC =6-k ，又四边形DOEC 为矩形，OC 为对角线，所以，S △COD =S △COE ，所以12k +k =6-k +12k ，解得：k =3．典例3．知面积值，求k 值（2022•内蒙古呼伦贝尔中考真题）如图，在平面直角坐标系中，Rt OAB △的直角顶点B 在x 轴的正半轴上，点O 与原点重合，点A 在第一象限，反比例函数k y x=（0x >）的图象经过OA 的中点C ，交AB 于点D ，连接CD ．若ACD △的面积是1，则k 的值是_________．【答案】43．【解析】【方法一】坐标法解：设C （m ，k m），因为C 为OA 中点，所以A （2m ，2k m），则D （2m ，2k m ），又△ACD 的面积为1，所以12122k k m m m æö×-=ç÷èø，解得：k =43【方法二】k 的几何意义法解：连接OD ，过C 作CE AB ∥，交x 轴于E ，∵∠ABO ＝90°，反比例函数k y x =（x ＞0）的图象经过OA 的中点C ，1ACD S =V ，∴12COE BOD S S k ==△△，1ACD OCD S S ==V V ，2OC =OA ，∵CE AB ∥，∴△OCE ∽△OAB ，∴221124OCE S OC S OA æöæö===ç÷ç÷èøèø△△O A B ，∴4OCE OAB ACD OCD OBD S S S S S ==++V V V V V ，∴1141122k k ´=++，∴k ＝43，故答案为：43．1.（2022•辽宁锦州中考真题）如图，在平面直角坐标系中，△AOB 的边OB 在y 轴上，边AB 与x 轴交于点D ，且BD =AD ，反比例函数y =k x(x >0)的图像经过点A ，若S △OAB =1，则k 的值为___________．【答案】2．【解析】【方法一】坐标法解：设A(a，b) ，如图，作A过x轴的垂线与x轴交于C，则：AC=b，OC=a，AC∥OB，∴∠ACD=∠BOD=90°，∠ADC=∠BDO，∴△ADC≌△BDO，∴S△ADC=S△BDO，∴S△OAC=S△AOD+ S△ADC=S△AOD+ S△BDO= S△OAB=1，∴12×OC×AC=12ab=1，∴ab=2，∵A(a，b) 在y=kx上，∴k=ab=2 ．【方法二】k的几何意义法由上知，S△AOC=1，所以，k=2S△AOC=2故答案为：2．2.（2022•辽宁鞍山中考真题）如图，在平面直角坐标系中，O 是坐标原点．在Rt OAB V 中，90OAB Ð=°，边OA 在y 轴上，点D 是边OB 上一点，且:1:2OD DB =，反比例函数()0ky x x=>的图象经过点D 交AB 于点C ，连接OC ．若4OBC S =△，则k 的值为_________．【答案】1．【解析】【方法一】坐标法解：∵反比例函数()0k y x x=>的图象经过点D ，∠OAB ＝90°，∴D （m ，k m ），∵OD ：DB ＝1：2，∴B （3m ，3k m），∴AB ＝3m ，OA ＝3k m ，∴反比例函数()0k y x x =>的图象经过点D 交AB 于点C ，∠OAB ＝90°，∴12AOC S k =△，∵4OBC S △＝，∴4AOB AOC S S -△△＝，即1313422k m k m ´×-=，解得k ＝1【方法二】k 的几何意义法如图，过D 作DE ⊥x 轴，则DE ∥AB ，因为OD ：BD =1:2，所以DE ：AB =1:3，所以S △ODE ：S △OAB =1：9，又S △ODE =S △OAC =12k ，所以12k +4=92k ，解得：k =13.（2022•江苏南通中考真题）平面直角坐标系中，已知点是函数图象上的三点．若，则k 的值为___________．【答案】【解析】【方法一】坐标法解：∵点是函数图象上的三点，∴，，∴m ＝n ，∴，，∴点B 、C 关于原点对称，∴设直线BC 的解析式为，代入得：，解得：，∴直线BC 的解析式为，xOy (,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x=¹2ABC S =△34(,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x =¹260k m =>6k mn =(3,2)B m m (3,2)C m m --()0y kx k =¹(3,2)B m m 23m mk =23k =23y x =不妨设m ＞0，如图，过点A 作x 轴的垂线交BC 于D ，把x ＝m 代入得：，∴D （m ，），∴AD ＝，∴，∴，∴，而当m ＜0时，可得，故答案为：．【方法二】由题意知，S △OAB =12632m n m m ×-×，O 为BC 中点，因为所以，S △OAB =12632m n m m ×-×=1，即291mn m -=①，又632m m m n k ×=×=②，23y x =23y m =23m 216633m m m -=()11633223ABC S m m m =´×+=V 218m =2136684k m ==´=34k =342ABC S =△由①②可得：4.（2022•湖北十堰中考真题）如图，正方形ABCD 的顶点分别在反比例函数()110k y k x=>和()220k y k x =>的图象上．若BD y ∥轴，点D 的横坐标为3，则12k k +=（ ）A ．36B ．18C ．12D ．9【答案】B ．【解析】【方法一】解：连接AC ，与BD 相交于点P ，设PA =PB =PC =PD =t （t ≠0）．∴点D 的坐标为（3，23k ），∴点C 的坐标为（3-t ，23k +t ）．∵点C 在反比例函数y =2k x 的图象上，34k=∴（3-t ）（23k +t ）=k 2，化简得：t =3-23k ，∴点B 的纵坐标为23k +2t =23k +2（3-23k ）=6-23k ，∴点B 的坐标为（3，6-23k ），∴3×（6-23k ）=1k ，整理，得：1k +2k =18．【方法二】先利用D 点坐标，表示出A 和C 点坐标，再根据四边形ABCD 为正方形，BD 与y 轴平行，知AC 平行于x 轴，那么，A 和C 点的纵坐标相等，进而求解23,3k D æöç÷èø，13,3k B æöç÷èø，122123,636k k k C k k æöç÷--ç÷-ç÷-èø，121123,636k k k A k k æöç÷-+ç÷-ç÷+èø所以2112123366k k k k k k =---+，整理得：()212212180k k k k ---=即()()1212108k k k k -+=-因为()120k k -¹所以()12018k k +-=，即1218k k +=5.（2022•黑龙江龙东中考真题）如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上，顶点A 在反比例函数k y x=的图象上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（ ）A ．2B ．1C ．1-D ．2-【答案】D ．【解析】解：设B点坐标为3,mmæöç÷èø，则A3,3kmmæöç÷èø，因为平行四边形OBAD的面积是5，所以353kmmmæö-×=ç÷èø，解得k=-2【方法二】解：如图，连接OA，设AB交y轴于点C，∵四边形OBAD是平行四边形，平行四边形OBAD的面积是5，∴1522AOB OBADS S==V Y，AB∥OD，∴AB⊥y轴，∵点B在反比例函数3yx=的图象上，顶点A在反比例函数kyx=的图象上，∴3,22 COB COAkS S==-V V，∴35222 AOB COB COAkS S S=+=-=V V V，解得：2k=-．故选：D．6.（2022•湖北黄石中考真题）如图，反比例函数kyx=的图象经过矩形ABCD对角线的交点E和点A，点B、C在x轴上，OCE△的面积为6，则k=______________．【答案】8．【解析】设C （m ，0），由题意知E 为AC 中点，因为△OCE 面积为6，所以E 点纵坐标为12m，所以E 12,12km m æöç÷èø，A 24,6km m m æö-ç÷èø，又A 在反比例函数图像上所以246km m k mæö-×=ç÷èø解得k =8【方法二】解：如图作EF ⊥BC ，则12EF AB =，设E 点坐标为（a ，b ），则A 点的纵坐标为2b ，则可设A 点坐标为（c ，2b ），∵点A ，E 在反比例函数k y x=上，∴ab =k =2bc ，解得：a =2c ，故BF =FC =2c -c =c ，∴OC =3c ，故113622OEC S OC EF c b =´´=´´=V ，解得：bc =4，∴k =2bc =8，故答案为：8．7.（2022•贵州六盘水中考真题）如图，正比例函数与反比例函数的图象交于，两点．y x =4y x=A B(1)求，两点的坐标；(2)将直线向下平移个单位长度，与反比例函数在第一象限的图象交于点，与轴交于点，与轴交于点，若，求的值．【答案】(1)；(2)【解析】（1）解：联立与，解得，；（2）【方法一】解：如图，过点作轴于点，A B y x =a C x D y E 13CD DE =a ()()2,2,2,2A B --3a =y x =4y x=121222,22x x y y ==-ììíí==-îî()()2,2,2,2A B \--C CF y ^F，，，直线向下平移个单位长度得到，根据图象可知,令，得，令，得，，，，，与反比例函数在第一象限的图象交于点，，将代入，得，解得或（舍去）．【方法二】CF OD \∥Q 13CD DE =13OF CD OE DE \==Q y x =a y x a =-0a >0x =y a =-0y =x a =()0,E a \-(),0D a 10,3F a æö\ç÷èø13c y a \=Q y x a =-4y x=C 41213c x aa \==121,3C a a æöç÷èøy x a =-1123a a a=-3a =3a =-如图，连接OC ，过C 作CE ⊥x 轴，因为CD ：DE =1:3，CE ∥OE则△CDE ∽△EDO ，相似比为1:3，面积比为1:9，易知△ODE 面积为212a ，△OCE 的面积为12k =2，所以△OCD 的面积为2-2118a ，又△OCD 与△ODE 的面积比为1:3，所以2-2118a =21132a ´，解得：a =3或a =-3（舍）8.（2022•安徽中考真题）如图，平行四边形OABC 的顶点O 是坐标原点，A 在x 轴的正半轴上，B ，C 在第一象限，反比例函数1y x =的图象经过点C ，()0k y k x=¹的图象经过点B ．若OC AC =，则k =________．【答案】3．【解析】【方法一】设C 1,m m æöç÷èø，因为OC =AC所以A ()2,0m ，又OABC 为平行四边形所以B 13,m m æöç÷èø因为B 点在k y x =上，所以k =133m m ×=【方法二】解：过点C 作CD ⊥OA 于D ，过点B 作BE ⊥x 轴于E ，∴CD ∥BE ，∵四边形ABCO 为平行四边形，∴CB OA ∥ ，即CB DE ∥，OC =AB ，∴四边形CDEB 为平行四边形，∵CD ⊥OA ，∴四边形CDEB 为矩形，∴CD =BE ，∴在Rt △COD 和Rt △BAE 中，OC AB CD EB =ìí=î，∴Rt △COD ≌Rt △BAE （HL ），∴S △OCD =S △ABE ，∵OC =AC ，CD ⊥OA ，∴OD =AD ，∵反比例函数1yx=的图象经过点C，∴S△OCD=S△CAD=12，∴S平行四边形OCBA=4S△OCD=2，∴S△OBA=11 2OCBAS=平行四边形，∴S△OBE=S△OBA+S△ABE=13122+=，∴3232k=´=．故答案为3．。

备考2024年中考数学二轮复习-函数_反比例函数_反比例函数系数k的几何意义-综合题专训及答案反比例函数系数k的几何意义综合题专训1、(2019盘锦.中考真卷) 如图，四边形ABCD是矩形，点A在第四象限y1＝﹣的图象上，点B在第一象限y2＝的图象上，AB交x轴于点E，点C与点D在y轴上，AD＝，S矩形OCBE＝ S矩形ODAE.（1）求点B的坐标.（2）若点P在x轴上，S△BPE＝3，求直线BP的解析式.2、(2019镇江.中考真卷) 如图，点和点是反比例函数图象上的两点，一次函数的图象经过点，与轴交于点，与轴交于点，过点作轴，垂足为，连接 .已知与的面积满足 .（1）＝，＝；（2）已知点在线段上，当时，求点的坐标.3、(2018常州.中考真卷) 如图，已知点A在反比例函数y= （x＞0）的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图象经过点A，与y轴的正半轴交于点B．（1）求点A的坐标；（2）若四边形ABOC的面积是3，求一次函数y=kx+b的表达式．4、(2017兴化.中考模拟) 已知点A（1，2）、点 B在双曲线y= （x＞0）上，过B作BC⊥x轴于点C，如图，P是y轴上一点，（1）求k的值及△PBC的面积；（2）设点M（x1，y1）、N（x2，y2）（x2＞x1＞0）是双曲线y= （x＞0）上的任意两点，s= ，t= ，试判断s与t 的大小关系，并说明理由．5、(2018深圳.中考模拟) 如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数y= 的图象在第二象限交于点C，CE⊥x轴，垂足为点E，tan∠ABO= ，OB=4，OE=2．（1）求反比例函数的解析式；（2）若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF．如果S△BAF=4S△DFO，求点D的坐标．6、(2018河南.中考模拟) 如图，点P是反比例函数y= （k＞0）图象在第一象限上的一个动点，过P作x轴的垂线，垂足为M，若△POM的面积为2．（1）求反比例函数的解析式；（2）若点B坐标为（0，﹣2），点A为直线y=x与反比例函数y= （k＞0）图象在第一象限上的交点，连接AB，过A作AC⊥y 轴于点C，若△ABC与△POM相似，求点P的坐标．7、(2017黄冈.中考模拟) 如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y= （k＞0，x＞0）的图象上点P（m，n）是函数图象上任意一点，过点P分别作x轴y轴的垂线，垂足分别为E，F．并设矩形OEPF和正方形OABC不重合的部分的面积为S．（1）求k的值；（2）当S= 时，求P点的坐标；（3）写出S关于m的关系式．8、(2017黄冈.中考模拟) 反比例函数y= 在第一象限的图象如图所示，过点A（1，0）作x轴的垂线，交反比例函数y= 的图象于点M，△AOM的面积为3．（1）求反比例函数的解析式；（2）设点B的坐标为（t，0），其中t＞1．若以AB为一边的正方形有一个顶点在反比例函数y= 的图象上，求t的值．9、(2020辽宁.中考模拟) 如图，已知∠AOB=90°，∠OAB=30°，反比例函数的图象过点，反比例函数的图象过点A.（1）求和的值.（2）过点B作BC∥x轴，与双曲线交于点C.求△OAC的面积.10、(2017湖北.中考真卷) 如图，∠AOB=90°，反比例函数y=﹣（x＜0）的图象过点A（﹣1，a），反比例函数y= （k＞0，x＞0）的图象过点B，且AB∥x轴．（1）求a和k的值；（2）过点B作MN∥OA，交x轴于点M，交y轴于点N，交双曲线y= 于另一点，求△OBC的面积．11、(2018株洲.中考真卷) 如图，已知函数的图象与一次函数的图象相交不同的点A、B，过点A作AD⊥轴于点D，连接AO，其中点A的横坐标为，△AOD的面积为2.（1）求的值及 =4时的值；（2）记表示为不超过的最大整数，例如：，，设 ,若，求值12、(2017常德.中考真卷) 如图，已知反比例函数y= 的图象经过点A（4，m），AB⊥x轴，且△AOB的面积为2．（1）求k和m的值；（2）若点C（x，y）也在反比例函数y= 的图象上，当﹣3≤x≤﹣1时，求函数值y的取值范围．13、(2018深圳.中考模拟) 如图，直线y=3x与双曲线y= （k≠0，且x＞0）交于点A，点A的横坐标是1．（1）求点A的坐标及双曲线的解析式；（2）点B是双曲线上一点，且点B的纵坐标是1，连接OB，AB，求△AOB的面积．14、(2018广州.中考真卷) 设P（x，0）是x轴上的一个动点，它与原点的距离为。

反比例函数K 的几何意义专项训练及答案（中考复习）1、如图（1）所示，已知反比例函数 y =x k 和 y =x 1分别过点 A 和点 B ，且 AB // x 轴， S ABC △ =23，点C 是 x 轴上任意一点，则 k =____________. 2、如图（2）所示,矩形ABOC 的顶点B ，C 分别在x 轴，y 轴上,顶点A 在第二象限,点B 的坐标为(-2,0)，将线段OC 绕点O 逆时针旋转60°至线段0D,若反比例函数y=xk （k ≠0）的图像经过A ，D 两点，则k 的值为_____________. 3、如图（3）所示,面积为25的Rt △OAB 的斜边OB 在x 轴上，∠ABO=30°，反比例函数y=xk 的图象恰好经过点A ，则k 的值为______________.4、如图(4)所示,A ⎪⎭⎫ ⎝⎛1y 21，，B ()2y 2，为反比例数y=x 2图象上的两点，动点P(x,0)在x 轴上运动,当|AP-BPI 的值最大时，连接OA ，则△AOP 的面积为_________.5、如图(5)所示,反比例函数y=x12在第一象限内的分支经过菱形OACB 的顶点A,B,且点A,B 的横纵坐标都为正整数,则点C 的坐标为__________________.6、如图（6）所示,在反比例函数y=xk 的图象上有A,B 两点,过点A 作AC ⊥x 轴，交x 轴于点C ，连接BC 并延长交y 轴于点D,连接AB,AD,若BD=4CD,ABD S △=8,则k 的值为__________________.（1）（2） （3）7、如图（7）所示,直线y=3x-6分别交x ，y 轴于点A ，B ，M 是反比例函数y=xa (x>0)的图象上位于直线AB 上方的一点，MC//x 轴交AB 于点C,MD ⊥MC 交AB 于点D,若AC ·BD=43则a 的值为__________.8如图(8)所示，正方形ABCD 的顶点A.B 分别在x ，y 轴上，tan ABO=3,正方形的面积为10,反比例函数y=xk 的图象经过点D,则k 的值是_______________. 9如图（9）所示,在平面直角坐标系中,△OAB 的顶点A 在反比例函数y=x 1上，顶点B 在反比例函数y=xk 上,AB ∥x 轴,△OAB 的面积是3，则k 的值为____________. 10、如图（10）所示,在平面直角坐标系中,等边三角形的顶点 A 在反比例函数y=x 1（x>0）上,顶点B,C 在反比例函数y=xk (x>0)上,且点B,C 关于直线y=x 对称.若等边三角形的边长为62，则k 的值为________________.（4） （5） （6） （7） （8） （9） （10）参考答案1、-22、3316-3、5-4、55、（13,13）或（8,8）或（7,7）6、-47、-38、-69、7 10、13。

2023年中考数学重难点专题练习-反比例函数系数k 的几何意义1．如图，点C 是反比例函数k y x=图象的一点，点C 的坐标为(4,)1-．(1)求反比例函数解析式；(2)若一次函数3y ax =+与反比例函数k y x=相交于A ，C 点，求点A 的坐标； (3)在x 轴上是否存在一个点P ，使得PAC △的面积为10，如果存在，求出点P 的坐标，如果不存在，请说明理由．2．如图，已知反比例函数k y x=（k 为常数，0k ≠）的图像经过第二象限内的点A ，过A 点作AB x ⊥轴，垂足为B ，AOB 的面积为1，A 的半径为1．(1)k =___________，当A 与x 轴相切时，A 点坐标为___________(2)点C 为y 轴上一动点，当AOB 为等腰直角三角形且AOC 面积为3时，求出点C 坐标．3．如图，已知反比例函数y ＝k x图象的一支经过点A （2，3）和点B （点B 在点A 的右侧），作BC ⊥y 轴，垂足为C ，连接AC ，AB ．(1)求反比例函数的解析式；(2)若⊥ABC 的面积为7，求B 点的坐标．4．如图，一次函数1y x =+与反比例函数k y x=的图象相交于2A m （，），B 两点，分别连接OA ，OB ．(1)求这个反比例函数的表达式(2)求AOB ∆的面积．5．如图，点A 为函数()>0k y x x=图象上的一点，过点A 作x 轴的平行线交 y 轴于点B ，连接OA ，如果AOB 的面积为2，求k 的值．6．如图，已知在平面直角坐标系xOy 中，Rt OAB ∆的直角顶点B 在x 轴的正半轴上，点A 在第一象限，反比例函数(0)k y x x =>的图象经过OA 的中点C ．交AB 于点D ，连结CD ．若ACD ∆的面积是43，则k 的值是_____．7．如图，已知反比例函数1m y x =和一次函数2y kx b =+的图像交于点()3,,621A B n ⎛⎫ ⎪⎝⎭，两点．(1)求m 、n 的值；(2)连接OA OB 、，求AOB 的面积．8．如图，一次函数()20y kx k k =-≠的图象与反比例函数1(10)m y m x-=-≠的图象交于点C ，与x 轴交于点A ，过点C 作CB y ⊥轴，垂足为B ，若3ABC S =△．（1）求点A 的坐标及m 的值；（2）若AB =9．如图，已知一次函数1y kx b =+与反比例函数2k y x=的图象交于第一象限内的点(16)A ，和(6)B m ，，与x 轴交于点C ，交y 轴于点D ．(1)分别求出这两个函数的表达式；(2)连接OA 、OB ，求AOB ∆的面积；(3)点P 为坐标平面内的点，若点O ，A ，C ，P 组成的四边形是平行四边形，请直接写出点P 的坐标．10．如图，直线2y x =-+与反比例函数k y x=（0k ≠）的图象交于(),3A a ，()3,B b 两点，过点A 作AC x ⊥轴于点C ，过点B 作BD x ⊥轴于点D ．(1)求a 、b 的值及反比例函数的解析式；(2)若点P 在直线2y x =-+上，且ACP BDP SS =，请求出此时点P 的坐标．11．如图，点A 、B 分别在反比例函数11(0)k y x x =>和22(0)k y x x =>的图象上，线段AB 与x 轴相交于点P ．(1)如图⊥，若AB x ⊥轴，且||2||AP PB =，121k k +=．求1k 、2k 的值；(2)如图⊥，若点P 是线段AB 的中点，且OAB 的面积为2．求12k k -的值．12．如图，点P 在反比例函数6y x=第一象限的图象上，PA x ⊥轴于点A ，则OPA 的面积为___________．13．如图，Rt ⊥ABO 的顶点A 是双曲线k y x =与直线y ＝－x ＋（k ＋1）在第四象限的交点，AB ⊥x 轴于B ，且32ABO S ∆=．(1)求这两个函数的解析式；(2)求直线与双曲线的两个交点A 、C 的坐标和⊥AOC 的面积．14．如图，已知一次函数22y x =+的图像与x 轴交于点A ，与y 轴交于点B ，与反比例函数(0,0)k y k x x=>>的图像交于点C ，且2BC AB =，点(,1)E a 在反比例函数的图像上．(1)求反比例函数的表达式；(2)若直线EC 交y 轴于点D ，求BCD △的面积．15．如图，一次函数(0)y kx b k =+≠与反比例函数m y x=(0m ≠，0)x >的图象交于(1,6)A ，(3,)B n 两点，AE x ⊥轴于点E ，BC x ⊥轴于点C ．(1)求反比例函数和一次函数的表达式；(2)根据图象直接写出+kx b >m x(0)x >时的x 的取值范围； (3)求AOB 的面积．16．如图，一次函数()10y k x b k =+≠与反比例函数()20k y x x =>的图像交于()1,6A ，()3,B m 两点．(1)求反比例函数和一次函数的解析式：(2)根据图象直接写出21k k x b x +<时，x 的取值范围： (3)求AOB 的面积．17．如图，反比例函数1(0)k y x x =>的图像与一次函数2y ax b =+的图像交于A （1，m ），B （3，n ）两点，过点A 作AC 垂直于x 轴于点C ， 3.OAC S ∆=(1)求反比例函数和一次函数的表达式；(2)当12y y >时，求x 的取值范围．参考答案：1．(1)4y x=-； (2)()14-，； (3)存在，P 点的坐标为()1,0-或()7,0．2．(1)2-，()2,1-；(2)(或(0,-．3．(1)6y x =； (2)209(,)310B4．(1)2y x =； (2)32 ．5．46．1697．(1)6m =，4n = (2)454AOB S =△8．（1）（2，0），m =-5；（2）2455y x -=+ 9．(1)6y x=，7y x =-+ (2)352 (3)点P 的坐标为：(86)，，(66)-，，(66)-，10．(1)a =-1，b =-1，3y x=- (2)()0,2P 或()3,5-11．(1)12k =，21k =-；(2)124k k -=．12．313．(1)3y x=-，y =-x -2 (2)A （1，-3），C （-3，1），Δ4AOC S =14．(1)12(0)y x x=> (2)515．(1)6y x =，28y x =-+ (2)13x <<(3)816．(1)28y x =-+，6y x=(2)01x <<或3x >(3)817．(1)反比例函数关系式为16y x =，一次函数的关系式为228y x +＝- (2)0＜x ＜1或x ＞3。

专题训练（十）反比例函数中k的几何意义（本专题部分习题有难度，请根据实际情况选做）一一31 .如图，在平面直角坐标系中，点A是双曲线y = -（x > 0）上的一个动点，过点A作x轴的垂线，交x轴于点B,X点A运动过程中△AOB的面积将会（)A . 逐渐增大B .逐渐减小C.先增大后减小 D .不变.2 •如图，过反比例函数y= X2（x >0）图象上任意两点A, B分别作x轴的垂线，垂足分别为C, D,连接OA OB设AC与0B的交点为AOE与梯形ECDB勺面积分别为S, S,比较它们的大小，可得（）A . S i > S2B . S i v S2C . S i = S2D . S i、S2的大小关系不能确定k3. （鄂州中考）点A为双曲线y = x（k丰0）上一点，B为x轴上一点，且△ AOE为等边三角形，△ AOB的边长为2,则k的值为（）A . 2 :3B . ± 2 3C. D . ± .34. 设P是函数y = 2■在第一象限的图象上的任意一点，点P关于原点的对称点为点P',过点P作PA平行于y轴,x过点P'作P' A平行于x轴，PA与P' A交于A点，侧厶PAP的面积（）A .随P点的变化而变化B .等于1C .等于2D .等于4k5. 如图，点A是反比例函数y = -图象上的一点，过点A作AB丄x轴，垂足为点B,点C为y轴上的一点，连接AC,xBC.若厶ABC的面积为3，贝U k的值是（）A . 3B . —3C . 6D . —6k （黔西南中考）如图，点A 是反比例函数y =-图象上的一个动点，过点A 作AB 丄x 轴，ACL y 轴，垂足点分别为 XC,矩形ABOC 的面积为4,贝y k = ______ . 4 （临沂中考）如图，反比例函数 y = -的图象 经过直角厶OAB 的顶点A, D 为斜边OA 的中点，则过点 D 的反比例函 X数的表达式为 _________ .一 一 69.如图，矩形ABCD 的边AB 与y 轴平行，顶点 A 的坐标为（1 , 2），点B 与点D 在反比例函数y = -（x > 0）的图象上, X则点C 的坐标为 _________ .的面积为2,贝U k 的值是11.（资阳中考）如图，在平面直角坐标系中，点 M 为x 轴正半轴上一点，过点 M 的直线I // y 轴，且直线I 分别与B 、 4 y =-的图象交于A, 8. 10.（铁岭中考）如图，点P 是正比例函数7.B 两点，则四边形 MAOB 勺面积为 y 轴的垂线与反比例函数 PAL OP 交x 轴于点A , △ POA求k 和m 的值.ii y =-的图象于点A, PD 丄y 轴，垂足为D,交y = -的图象于点B.已知点A(m , 1)为线段PC 的中点. X—(1)求m 和k 的值； ⑵求四边形OAPB 的面积. 参考答案11. D2. C3. D4. D5. D6. — 47. 108. y = -9. (3 , 6) 10. 2 11. — 20 12.设点 A 的坐标为(—,y) . v— 1 1△ AOB 的面积为飞：3,「. 2凶 Tyl = 2同=1： 3.解得|k| = 2苓3又v k v 0,「. k = — 2 3.二反比例函数 表达式为y = .解得 m = 2.综上可知：k =— 2 \3, n = 2. 13. (1)把1 A(m, 1)代入y = -，得m= 1,二A 点坐标为(1 , 1) .v 点A(1 , 1)为线段PC 的中点，.••点 P 坐标为(1 , 2).把(1 , —k 1 2)代入y = -，得k = 1X 2= 2.(2) v 点P 坐标为(1 , 2) ,•••四边形 OCPD 勺面积为1 X 2= 2.又：公ODB 的面积为-, — 21 1 1 △ OAQ 的面积为§，•四边形 OAPB 的面积为2 — 2 — 2= 1.反比例函数y = 8(x > 0)和 y = X (x >0)的图象交于P 、Q 两点，若 &PO F 14,则k 的值为12.如图，已知反比例函数k y = x (k v 0)的图象经过点 A( — .'3, m),过点A 作AB 丄x 轴于点B ,且厶AOB 的面积为 13 .反比例函数y = f 和y = X (k 丰0)在第一象限内的图象如图所示，点k P 在 y =x 的图象上, 年3. v 反比例函数图象经过点 A( — , m),「. m=—三备。

2
·|13
|＝12
Hale Waihona Puke ×13＝1 6，S 矩形 PCOD＝1，
∴S 四边形 PAOB＝1－2×16
＝2 3
11．如图，在平面直角坐标系 xOy 中，△OAB 的顶点 A 在 x 轴正半轴上，OC 是 △OAB 的中线，点 B，C 在反比例函数 y＝k) (x>0)的图象上，若△OAB 的面积等于 6，
解：作 AD⊥x 轴于 D，BE⊥x 轴于 E，BF⊥AD 于 F，如图，∵A，B 两点的横坐 标分别为 1，2，∴A(1，k)，B(2，k )，∴OD＝1，DE ＝1，AF ＝FD＝BE ，易证
2 △ABF≌△BCE，AD＝AF＋FD＝2BE，∴CE＝FB＝DE＝1，∴OC＝3，∵△AOC 的 面积为 6，∴1 ·3·k＝6，∴k＝4
x 则 k 的值为( B )
A．2 B．4 C．6 D．8
12．如图，反比例函数 y＝2 的图象经过长方形 OABC 的边 AB 的中点 D，则矩形 x
OABC 的面积为____4_____．
13．如图，A，B 是双曲线 y＝kx (x>0)上两点，A，B 两点的横坐标分别为 1，2， 线段 AB 的延长线交 x 轴于点 C，若△AOC 的面积为 6，求 k 的值．
专题训练八 反比例函数比例系数k的几何意义
1．如图，点 A 是反比例函数 y＝kx 的图象上的一点，过点 A 作 AB⊥x 轴，垂足为 B.点 C 为 y 轴上的一点，连结 AC，BC.若△ABC 的面积为 4，则 k 的值是( D )
A．4 B．－4 C．8 D．－8
2．如图，点 P 是反比例函数 y＝6 (x＞0)的图象上的任意一点，过点 P 分别作两坐 x
解：∵点 B 与点 A 关于 x 轴对称，△OAB 的面积为 6，∴△OAC 的面积为 3.

反比例函数k的几何意义专项练习1、如图.矩形AOCB的两边OC、OA分别位于x轴、y轴上.点B的坐标为B（20,53-）.D是AB边上的一点.将△ADO沿直线OD翻折.使A点恰好落在对角线OB上的点E处.若点E在一反比例函数的图像上.那么该函数的解析式是 .2、如图.点P在反比例函数的图象上.过P点作PA⊥x轴于A点.作PB⊥y轴于B点.矩形OAPB的面积为9.则该反比例函数的解析式为.3、如图, 如果函数y=－x与y=x4-的图像交于A、B两点, 过点A作AC垂直于y轴, 垂足为点C, 则△BOC的面积为___________.4、如图.正方形OABC.ADEF的顶点A.D.C在坐标轴上.点F在AB上.点B.E在函数()1y xx=>的图象上.则点E的坐标是( )5、反比例函数xky=的图象如图所示.点M是该函数图象上一点.MN垂直于x轴.垂足是点N.如果S△MON＝2.则k的值为（）(A)2 (B)-2(C)4 (D)-46、如图.A、B是反比例函数y＝x2的图象上的两点．AC、BD都垂直于x轴.垂足分别为C、D．AB的延长线交x轴于点E．若C、D的坐标分别为(1.0)、(4.0).则ΔBDE的面积与ΔACE的面积的比值是( )．A．21B．41Ｃ．81D．1617、如图.A、B是函数2yx=的图象上关于原点对称的任意两点.BC∥x轴.AC∥y轴.△ABC的面积记为S.则（）A．2S= B．4S= C．24S<< D．4S>8、如图.直线y=mx与双曲线y=xk交于A、B两点.过点A作AM⊥x轴.垂足为M.连结BM,若ABMS∆=2.则k的值是（）A．2 B、m-2 C、m D、4OBxyCA9、如图.双曲线)0(＞k xky =经过矩形QABC 的边BC 的中点 E.交AB 于点D 。

若梯形ODBC 的面积为3.则双曲线的解析式为A ．x y 1=B ．x y 2=C ． x y 3=D ．xy 6=10、如图.在直角坐标系中.点A 是x 轴正半轴上的一个定点.点B 是双曲线3y x=（0x >）上的一个动点.当点B 的横坐标逐渐增大时.OAB △的面积将会A ．逐渐增大B ．不变C ．逐渐减小D ．先增大后减小 11、如图.已知双曲线)0k (xk y ＞=经过直角三角形OAB 斜边OB 的中点 D.与直角边AB 相交于点C ．若△OBC 的面积为 3.则k ＝____________．13、如图.点A 、B 是双曲线3y x=上的点.分别经过A 、B 两点向x 轴、y 轴作垂线段.若1S =阴影，则12S S +=．14、如图.⊙A 和⊙B 都与x 轴和y 轴相切.圆心A 和圆心B 都在反比例函数1y x=的图象上.则图中阴影部分的面积等于 .15、如图.已知一次函数1y x =+的图象与反比例函数ky x=的图象在第一象限相交于点A .与x 轴相交于点C AB x ，⊥轴于点B .AOB △的面积为1.则AC 的长为xyABO1S 2SA BO xyxyOABxyBAo（保留根号）．16、如图.过原点的直线l 与反比例函数1y x=-的图象交于M .N 两点.根据图象猜想线段MN 的长的最小值是___________．17、如图11.若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 1y x=（0x >）的图象上.则点E 的坐标是（.）18、如图1.已知点C 为反比例函数6y x=-上的一点.过点C 向坐标轴引垂线.垂足分别为A 、B .那么四边形AOBC 的面积为 ．19、如图.已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D .且与直角边AB 相交于点C ．若点A 的坐标为（6-.4）.则△AOC 的面积为A ．12B ．9C ．6D ．420、如图,直线)0(<=k kx y 与双曲线xy 2-=交于),(),,(2211y x B y x A 两点,则122183y x y x -的值为( )A.-5B.-10C.5D.10OyxMNl yO x AC B图1DBAyxOC21、如图.已知梯形ABCO 的底边AO 在x 轴上.BC ∥AO .AB ⊥AO .过点C 的双曲线ky x=交OB 于D .且OD ：DB=1:2.若△OBC 的面积等于3.则k 的值（ ） A ． 等于2 B ．等于34C ．等于245D ．无法确定22、如图.已知在直角梯形AOBC 中.AC ∥OB .CB ⊥OB .OB ＝18.BC ＝12.AC ＝9.对角线OC 、AB交于点D .点E 、F 、G 分别是CD 、BD 、BC 的中点.以O 为原点.直线OB 为x 轴建立平面直角坐标系.则G 、E 、D 、F 四个点中与点A 在同一反比例函数图像上的是（ ） A ．点G B ．点E C ．点D D ．点F ．【答案】A ．23、如图.直线ｌ是经过点（1,0）且与y 轴平行的直线．Rt △ABC 中直角边AC=4.BC=3．将BC 边在直线ｌ上滑动.使A.B 在函数xky =的图象上． 那么k 的值是A ．3B ．６Ｃ．12 D ．415【答案】D24、如图.反比例函数y ＝kx(x ＞0)的图象经过矩形OABC 对角线的交点M .分别与AB 、BC 相交于点D 、E ．若四边形ODBE 的面积为6.则k 的值为A ．1B ．2C ．3D ．4 【答案】BO ABCDxy AB CD E yxOM（第10题）25、双曲线xy x y 21==与在第一象限的图象如图所示.作一条平行于y 轴的直线分别交双曲线于A 、B 两点.连接OA 、OB.则△AOB 的面积为（ ）A ．1B ．2C ．3D ．4【答案】A27、直线l 与双曲线C 在第一象限相交于A 、B 两点.其图象信息如图4所示.则阴影部分（包括边界）横、纵坐标都是整数的点（俗称格点）有： （ ）A ．4个B ．5 个C ．6个D ．8个【答案】B28、如图所示.已知菱形OABC .点C 在x 轴上.直线y =x 经过点A .菱形OABC 的面积是2.若反比例函数的图象经过点B .则此反比例函数表达式为（ ）A ．1y x=B ．2y =C ．21y +=D ．21y +=180°【答案】C29、反比例函数xky =的图象如图所示.则k 的值可能是（ ）A ．-1B ．21C ．1D ．2【答案】B 30、如图5.等腰直角三角形ABC 位于第一象限.AB=AC=2.直角顶点A 在直线y=x 上.其中A 点的横坐标为1.且两条直角边AB 、AC 分别平行于x 轴、y 轴。

备考2024年中考数学二轮复习-函数_反比例函数_反比例函数系数k的几何意义-单选题专训及答案反比例函数系数k的几何意义单选题专训1、(2012抚顺.中考真卷) 如图，过点P（2，3）分别作PC⊥x轴于点C，PD⊥y轴于点D，PC、PD分别交反比例函数y= （x＞0）的图象于点A、B，则四边形BOAP的面积为（）A . 3B . 3.5C . 4D . 52、(2017石家庄.中考模拟) 如图，在平面直角坐标系中，一条直线与反比例函数y= （x＞0）的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y= （x＞0）的图象交于两点D、E，连接DE，则四边形ABED的面积为（）A . 4B .C . 5D .3、(2019温州.中考模拟) 如图，矩形 OABC 的顶点 O 在坐标原点，顶点 A，C 分别在 x，y 轴的正半轴上，顶点 B 在反比例函数 y = （k 为常数，k＞0，x＞0）的图象上，将矩形 OABC 绕点 B 逆时针方向旋转 90°得到矩形 BC‘O’A‘，点 O 的对应点O¢ 恰好落在此反比例函数图象上.延长 A’O‘，交 x轴于点 D，若四边形C’ADO‘ 的面积为 2，则 k 的值为（）A . +1B . -1C . 2 +2D . 2 -24、(2016余姚.中考模拟) 如图，矩形OABC上，点A、C分别在x、y轴上，点B在反比例位于第二象限的图象上，矩形面积为6，则k的值是（）A . 3B . 6C . ﹣3D . ﹣65、(2017北仑.中考模拟) 如图，等腰三角形ABC的底边BC在x轴正半轴上，点A在第一象限，延长AB交y轴负半轴于点D，延长CA 到点E，使AE=AC，双曲线y= （x＞0）的图象过点E．若△BCD的面积为2 ，则k的值为（）A . 4B . 4C . 2D . 26、(2019包河.中考模拟) 如图，若反比例函数y= （x＜0）的图象经过点（- ，4），点A为图象上任意一点，点B在x轴负半轴上，连接AO，AB，当AB=OA时，△AOB的面积为（）A . 1B . 2C . 4D . 无法确定7、(2017宿州.中考模拟) 点P反比例函数y=﹣的图象上，过点P分别作坐标轴的垂线段PM、PN，则四边形OMPN的面积=（）A .B . 2C . 2D . 18、(2019夏津.中考模拟) 如图，平行于x轴的直线与函数y= （k1>0，x>0），y= （k2>0,x>0)的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k1-k2的值为（）A . 8B . -8C . 4D . -49、(2017蒙阴.中考模拟) 如图，双曲线y= （k＞0）与⊙O在第一象限内交于P、Q两点，分别过P、Q两点向x轴和y轴作垂线，已知点P坐标为（1，3），则图中阴影部分的面积为（）A . 1B . 2C . 3D . 410、(2018河南.中考模拟) 如图，已知反比例函数y= 与正比例函数y=kx（k＜0）的图象相交于A，B两点，AC垂直x轴于C，则△ABC的面积为（）A . 3B . 2C . kD . k211、(2017濮阳.中考模拟) 如图，直线l⊥x轴于点P，且与反比例函数y1= （x＞0）及y2= （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1﹣k2的值为（）A . 2B . 3C . 4D . ﹣412、(2016河南.中考真卷) 如图，过反比例函数y= （x＞0）的图象上一点A作AB⊥x轴于点B，连接AO，若S△AOB=2，则k的值为（ ）A . 2B . 3C . 4D . 513、(2019株洲.中考真卷) 如图所示，在直角平面坐标系中，点为反比例函数上不同的三点，连接，过点作轴于点，过点分别作垂直轴于点，与相交于点，记、、四边形的面积分别为、、，则（）A .B .C .D .14、(2018湛江.中考模拟) 如图，P是反比例函数图象上第二象限内一点，若矩形PEOF的面积为3，则反比例函数的解析式是（）A . y=B . y=﹣C . y=D . y=15、(2016宝安.中考模拟) 如图，在平面直角坐标系上，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，点B （1，3），将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE，恰好有一反比例函数y= 图像恰好过点D，则k的值为（）A . 6B . ﹣6C . 9D . ﹣916、(2022任城.中考模拟) 如图，是函数上两点，为一动点，作轴，轴，下列说法正确的是( )①；②；③若，则平分；④若，则A . ①③B . ②③C . ②④D . ③④17、(2011玉林.中考真卷) 如图，是反比例函数y= 和y= （k1＜k2）在第一象限的图象，直线AB∥x轴，并分别交两条曲线于A、B两点，若S△AOB=4，则k2﹣k1的值是（ ）A . 1B . 2C . 4D . 818、(2019昆明.中考模拟) 如图所示，反比例函数y＝（x＜0）的图象经过矩形OABC的对角线AC的中点M，分别与AB，BC交于点D，E，若矩形OABC的面积为8，则k的值为（）A . ﹣2B . ﹣2C . 2D . ﹣219、(2017.中考模拟) 如图，Rt△ABC的顶点B在反比例函数的图象上，AC边在x轴上，已知∠ACB=90°，∠A=30°，BC=4，则图中阴影部分的面积是（）A . 12B . 4C . 12-3D .20、(2019吉林.中考模拟) 如图，在平面直角坐标系中，▱OABC的对角线OB在y轴正半轴上，点A，C分别在函数y＝（x＞0），y＝（x＜0）的图象上，分别过点A，C作AD⊥x轴于点D，CE⊥x轴于点E，若|k1|：|k2|＝9：4，则AD：CE的值为（ ）A . 2：3B . 3：2C . 4：9D . 9：421、(2019鄂尔多斯.中考模拟) 如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数y＝（x＞0）与AB相交于点D，与BC相交于点E，若BD＝3AD，且△ODE的面积是9，则k＝（）A .B .C .D . 1222、(2020四川.中考模拟) 如图，在平面直角坐标系xOy中，⊙A切y轴于点B，且点A在反比例函数y= （x＞0）的图象上，连接OA交⊙A于点C，且点C为OA中点，则图中阴影部分的面积为（）A . 4 ﹣B . 4 -C . 2 -D . 2 -23、(2021四川.中考模拟) 如图，在平面直角坐标系中，函数 y = kx 与 y = - 的图象交于 A、B 两点，过 A 作 y 轴的垂线，交函数的图象于点 C，连接 BC，则△ABC 的面积为（）A . 2B . 4C . 6D . 824、(2020石家庄.中考模拟) 如图，点（）是反比例函数上的动点，过分别作轴，轴的垂线，垂足分别为， .随着的增大，四边形的面积（）A . 增大B . 减小C . 不确定D . 不变25、(2021满洲里.中考模拟) 如图，点A在反比例函数的图象上，过点A作轴，垂足为B，交反比例函数的图象于点C．P为y轴上一点，连接，．则的面积为（）A . 5B . 6C . 11D . 1226、(2020威海.中考真卷) 如图，点，点都在反比例函数的图象上，过点P分别向x轴、y轴作垂线，垂足分别为点M，N．连接，，．若四边形的面积记作，的面积记作，则（）A .B .C .D .27、(2020安阳.中考模拟) 如图，直线y=kx（k＞0）与双曲线y=交于A，B两点，BC⊥x轴于C，连接AC交y轴于D，下列结论：①A、B关于原点对称；②△ABC的面积为定值；③D是AC的中点；④S△AOD=．其中正确结论的个数为（ ）A . 1个B . 2个C . 3个D . 4个28、(2021三台.中考模拟) 如图，矩形ABCD的顶点A和对称中心在反比例函数（k≠0，x＞0），若矩形ABCD的面积为10，则k的值为（）A . 10B . 4C . 3D . 5 29。

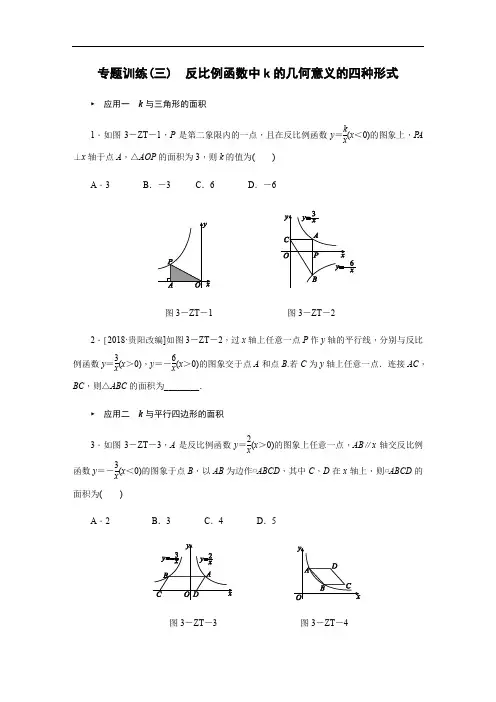
专题训练(三) 反比例函数中k 的几何意义的四种形式► 应用一 k 与三角形的面积1．如图3－ZT －1，P 是第二象限内的一点，且在反比例函数y ＝kx (x ＜0)的图象上，P A⊥x 轴于点A ，△AOP 的面积为3，则k 的值为( )A ．3B ．－3C ．6D ．－6图3－ZT －1 图3－ZT －22．[2018·贵阳改编]如图3－ZT －2，过x 轴上任意一点P 作y 轴的平行线，分别与反比例函数y ＝3x (x ＞0)，y ＝－6x (x ＞0)的图象交于点A 和点B .若C 为y 轴上任意一点．连接AC ，BC ，则△ABC 的面积为________．► 应用二 k 与平行四边形的面积3．如图3－ZT －3，A 是反比例函数y ＝2x (x ＞0)的图象上任意一点，AB ∥x 轴交反比例函数y ＝－3x (x ＜0)的图象于点B ，以AB 为边作▱ABCD ，其中C ，D 在x 轴上，则▱ABCD 的面积为( )A ．2B ．3C ．4D ．5图3－ZT －3 图3－ZT －4► 应用三 k 与特殊平行四边形的面积4．2018·抚顺如图3－ZT －4，菱形ABCD 的边AD 与x 轴平行，A ，B 两点的横坐标分别为1和3，反比例函数y ＝3x的图象经过A ，B 两点，则菱形ABCD 的面积是( )A ．42B ．4C ．22D ．25．如图3－ZT －5，在平面直角坐标系中，反比例函数y ＝kx (x ＞0)的图象与边长是6的正方形OABC 的两边AB ，BC 分别相交于M ，N 两点．△MON 的面积为10.若动点P 在x 轴上，求PM ＋PN 的最小值．图3－ZT －5► 应用四 k 与多边形的面积6．如图3－ZT －6，双曲线y ＝3x (x ＞0)经过四边形OABC 的顶点A ，C ，∠ABC ＝90°，OC 平分OA 与x 轴正半轴的夹角，AB ∥x 轴，将△ABC 沿AC 翻折后得到△AB ′C ，点B ′落在OA 上，求四边形OABC 的面积．图3－ZT－6教师详解详析1．[解析]D 根据反比例函数的几何意义可知，S △AOP ＝12|k |＝3.又∵曲线经过第二象限，∴k ＜0，则k ＝－6. 2．[答案]92[解析]设点P 的坐标为(a ，0)．则点A 的坐标为(a ，3a )，点B 的坐标为(a ，－6a )∴S △ABC ＝12AB ·OP ＝12OP ·AP ＋12OP ·BP ＝12a ·3a ＋12a ·6a ＝92.3．[解析]D 设点A 的纵坐标是b ，则点B 的纵坐标也是b .把y ＝b 代入y ＝2x ，得b ＝2x ，则x ＝2b ，即点A 的横坐标是2b .同理可得，点B 的横坐标是－3b ，则AB ＝2b －(－3b )＝5b，则S ▱ABCD ＝5b·b ＝5.4．[解析]A 作AH ⊥BC 交CB 的延长线于点H .∵反比例函数y ＝3x 的图象经过A ，B 两点，A ，B 两点的横坐标分别为1和3，∴A ，B 两点的纵坐标分别为3和1，即点A 的坐标为(1，3)，点B 的坐标为(3，1)， ∴AH ＝3－1＝2，BH ＝3－1＝2.在Rt △ABH 中，由勾股定理得，AB ＝22＋22＝2 2. ∵四边形ABCD 是菱形，∴BC ＝AB ＝22，∴菱形ABCD 的面积＝BC ·AH ＝4 2.5．解：设点M ，N 的坐标分别为(6，k 6)，(k 6，6)，则BM ＝BN ＝6－k 6.由题意可知：S △MON ＝S 正方形OABC －2S △AOM －S △BMN ， 故36－k －12(6－k6)2＝10，解得k ＝24(负值已舍去)，则AM ＝k 6＝4，BM ＝BN ＝6－k6＝2.作点M 关于x 轴的对称点M ′，连接M ′N 交x 轴于点P ，连接PM ，如图，则AM ＝AM ′＝4，PM ＝PM ′， 故PM ＋PN ＝PM ′＋PN .当M ′，P ，N 三点共线时，PM ′＋PN 的值最小，此时M ′N ＝BN 2＋M ′B 2＝22＋102＝226，即PM ＋PN 的最小值为226. 6．解：如图，延长BA 交y 轴于点E ，延长BC 交x 轴于点F .由题意易得△ABC ≌△AB ′C ，△OCF ≌△OCB ′， ∴BC ＝B ′C ＝CF .由题可知四边形OFBE 为矩形．∴设BC＝CF＝a，OF＝BE＝2b. ∵S△AOE＝S△OCF，即12·2a·AE＝12·2b·a，故AE＝b，从而AE＝AB＝b，∴S△ABC＝12S△OCF＝12×32＝34.又∵S△OCB′＝S△OCF＝3 2，∴S四边形OABC＝S△OCB′＋2S△ABC＝32＋2×34＝3.。

第六章反比例函数及反比例函数k的几何意义专题训练北师大版2024—2025学年九年级上册反比例函数比例系数k的几何意义（1）意义：从反比例函数y＝(k≠0)图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.（2）常见的面积类型：例1.如图，点P是反比例函数y＝（k≠0）的图象上任意一点，过点P作PM⊥x轴，垂足为M，若△POM的面积等于3，则k的值等于（）A．﹣6B．6C．﹣3D．3变式1.如图，在▱AOBC中，对角线AB、OC交于点E，双曲线经过A、E两点，若▱AOBC的面积为18，则k的值是（）A．5B．6C．7D．8变式2.如图，平行于x轴的直线与函数y＝（k1＞0，x＞0），y＝（k2＞0，x＞0）的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点．若△ABC的面积为4，则k1﹣k2的值为（）A．8B．﹣8C．4D．﹣4变式3.如图，点P是反比例函数图象上的一点，PF⊥x轴于F点，且Rt△POF面积为4．则k的值为（）A．8B．﹣8C．﹣4D．4变式4.如图，点M是反比例函数y＝（x＜0）图象上一点，MN⊥y 轴于点N．若P为x轴上的一个动点，则△MNP的面积为（）A．2B．4C．6D．无法确定变式5.如图，点P是双曲线C：y＝（x＞0）上的一点，过点P作x轴的垂线交直线AB：y＝x﹣2于点Q，连接OP，OQ，当点P在曲线C上运动，且点P在Q上方时，△POQ面积的最大值为（）A．2B．3C．4D．6变式6．如图，已知点A为反比例函数y＝（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B，若△OAB的面积为3，则k的值为（）A．3B．﹣3C．6D．﹣6变式7.关于x的反比例函数y＝的图象如图，A、P为该图象上的点，且关于原点成中心对称．△P AB中，PB∥y轴，AB∥x轴，PB 与AB相交于点B．若△P AB的面积大于12，则关于x的方程（a ﹣1）x2﹣x+＝0的根的情况是（）A．2个不相等的实数根B．2个相等的实数根C．1个实数根D．无实数根变式8.如图，两个反比例函数y1＝和y2＝在第一象限内的图象分别是C1和C2，设点P在C1上，P A⊥x轴于点A，交C2于点B，则△POB的面积为（）A．4B．2C．1D．6变式9.如图，若反比例函数的图象经过点A，AB⊥x轴于点B，C点是y轴上一点，且△ABC的面积4，则k的值为（）A．﹣8B．﹣4C．4D．8变式10.如图，反比例函数的图象经过矩形OABC的边AB的中点D，若矩形OABC的面积为6，则k的值为（）A．﹣3B．3C．﹣6D．6变式11.如图，点A是反比例函数的图象上的一点，过点A作AB ⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC 的面积为3，则k的值是（）A．3B．﹣6C．6D．﹣3变式12.下面四个图中反比例函数的表达式均为，则阴影部分的图形的面积为3的有（）A．1个B．2个C．3个D．4个变式13.如图，将一块含30°角的三角板AOB按如图所示摆放在平面直角坐标系中，∠B＝60°，∠BAO＝90°，△AOB的面积为4，BO与x轴的夹角为30°，若反比例函数的图象经过点A，则k的值为（）A．3B．C．6D．9变式14.如图1，在△OAB中，∠AOB＝45°，点B的坐标为，点A在反比例函数的图象上，设△OAB的面积为S1；如图2，在△ABC中，AB＝AC，BC在x轴上，且OB：BC＝1：2，点A在反比例函数的图象上，设△ABC的面积为S2，则S1+S2的值为（）A．B．5C．D．变式15.如图，已知四边形OABC是矩形，边OA在x轴上，边OC在y轴上，双曲线过OB的中点E，且与边BC交于点D，若△DOE的面积为7.5，则k的值是（）A．5B．10C．15D．变式16.如图，点A是反比例函数y＝（x＞0）图象上的一点，AB垂直于x轴，垂足为B，△OAB的面积为8．若点P（a，4）也在此函数的图象上，则a的值是（）A．2B．﹣2C．4D．﹣4变式17.如图，在平面直角坐标系xOy中，点A、B分别在y、x 轴上，BC⊥x轴，点M、N分别在线段BC、AC上，BM＝CM，NC＝2AN，反比例函数y＝（x＞0）的图象经过M、N两点，P为x轴正半轴上一点，且OP：BP＝1：4，△APN的面积为3，则k的值为（）A．B．C．D．变式18.如图，在平面直角坐标系中，平行四边形ABCD与y轴分别交于E、F两点，对角线BD在x轴上，反比例函数的图象过点A并交AD于点G，连接DF．若BE：AE＝1：2，AG：GD＝3：2，且△FCD的面积为，则k的值是（）A．B．3C．D．5变式19.如图，平面直角坐标系中，矩形OABC的边与函数y＝（x＞0）图象交于E，F两点，且F是BC的中点，则四边形ACFE的面积等于（）A．4B．6C．8D．不能确定例2.如图，矩形OABC的顶点A，C分别在x轴、y轴的正半轴上，它的对角线OB与函数的图象相交于点D，且，若矩形OABC的面积为24，则k的值是．变式1.如图，已知在平面直角坐标系xOy中，点P是▱ABCO对角线OB的中点，反比例函数的图象经过点A，点P．若▱ABCO的面积为30，且y轴将▱ABCO的面积分为1：3，则k的值为．变式2.如图，在平面直角坐标系xOy中，点A，B都在反比例函数y＝（x＞0）的图象上，延长AB交y轴于点C，过点A作AD⊥y轴于点D，连接BD并延长，交x轴于点E，连接CE．若AB＝2BC，△BCE的面积是4.5，则k的值为．变式3.如图，在平面直角坐标系xOy中，等腰Rt△OAB，∠B＝90°，点A在x轴正半轴上，点B在第一象限内，反比例函数y＝的图象与AB交于点C，连接OC，若BC＝2AC，△OBC的面积为6，则k的值为．变式4.如图，在平面直角坐标系中，C，A分别为x轴、y轴正半轴上的点，以OA，OC为边，在第一象限内作矩形OABC，且S矩形OABC＝8，将矩形OABC翻折，使点B与原点O重合，折痕为MN，点C的对应点C'落在第四象限，过M点的反比例函数y＝（k ≠0）的图象恰好过MN的中点，则点C'的坐标为．变式5.如图，在平面直角坐标系中，点A、C在y轴上，且，点B（﹣2，0）在x轴上，将△ABC绕点A逆时针旋转90°后得到△AB'C′，线段AB′与双曲线交于点D，连接B′C、C′C，当点D为AB′中点，且S△B'CC′＝6时，则k的值是．变式6.如图，在△AOB中，OC平分∠AOB，＝，反比例函数y＝（k＜0）图象经过点A、C两点，点B在x轴上，若△AOB的面积为9，则k的值为．变式7.如图，点A，B，C，D是菱形的四个顶点，其中点A，D在反比例函数y＝（m＞0，x＞0）的图象上，点B，C在反比例函数y＝（n＜0）的图象上，且点B，C关于原点成中心对称，点A，C的横坐标相等，则的值为；过点A作AE∥x轴交反比例函数y＝（n＜0）的图象于点E，连结ED并延长交x轴于点F，连结OD．若S△DOF＝7，则m的值为．变式8.如图，A（a，b）、B（﹣a，﹣b）是反比例函数y＝的图象上的两点，分别过点A、B作y轴的平行线，与反比例函数y＝的图象交于点C、D，若四边形ACBD的面积是8，则m、n之间的关系是．变式9.如图，平面直角坐标系xOy中，Rt△ABO的斜边BO在x轴正半轴上，OB＝5，反比例函数y＝（x＞0）的图象过点A，与AB边交于点C，且AC＝3BC，则a的值为，射线OA，射线OC分别交反比例函数y＝（b＞a＞0）的图象于点D，E，连接DE，DC，若△DEC的面积为45，则b的值为．变式10.如图，点A、B在反比例函数y＝（x＞0）的图象上，延长AB交x轴于C点，若△AOC的面积是12，且点B是AC的中点，则k＝．变式11.如图，菱形ABCD中，∠ABC＝120°，顶点A，C在双曲线上，顶点B，D在双曲线上，且BD经过点O．若k1+k2＝2，则菱形ABCD面积的最小值是．变式12.如图，在平面直角坐标系xOy中，正方形ABCD的顶点A、C恰好落在双曲线上，且点O在AC上，AD交x轴于点E．①当A点坐标为（1，m）时，D点的坐标为；②当CE平分∠ACD时，正方形ABCD的面积为．例3.如图，O为坐标原点，点A（﹣1，5）和点B（m，﹣1）均在反比例函数图象上（1）求m，k的值；（2）当x满足什么条件时，﹣x+4＞﹣；（3）P为y轴上一点，若△ABP的面积是△ABO面积的2倍，直接写出点P的坐标．变式1.已知点A（a，ma+2）、B（b，mb+2）是反比例函数y＝图象上的两个点，且a＞0，b＜0，m＞0．（1）求证：a+b＝﹣；（2）若OA2+OB2＝2a2+2b2，求m的值；（3）若S△OAB＝3S△OCD，求km的值．变式2.如图，双曲线y＝上的一点A（m，n），其中n＞m＞0，过点A作AB⊥x轴于点B，连接OA．（1）已知△AOB的面积是3，求k的值；（2）将△AOB绕点A逆时针旋转90°得到△ACD，且点O的对应点C恰好落在该双曲线上，求的值．。

反比例函数中K的几何意义专题训练【知识梳理】1．反比例函数图象中有关图形的面积2．涉及三角形的面积型当一次函数与反比例函数结合时，可通过面积作和或作差的形式来求解．（1）正比例函数与一次函数所围成的三角形面积.如图①，S△ABC=2S△ACO=|k|；（2）如图②，已知一次函数与反比例函数y=kx交于A、B两点，且一次函数与x轴交于点C，则S△AOB=S△AOC+S△BOC=12OC⋅|y A|+12OC⋅|y B|=12OC⋅(|y A|+|y B|)；（3）如图③，已知反比例函数y=kx的图象上的两点，其坐标分别为(x A，y A)，(x B，y B)，C为AB延长线与x轴的交点，则S△AOB=S△AOC–S△BOC=12OC⋅|y A|–12OC⋅|y B|=12OC⋅(|y A|−|y B|)．【精典训练】【01】如图，反比例函数y=kx(k≠0)的图象上有一点A，AB平行于x轴交y轴于点B，△ABO 的面积是3，则反比例函数的解析式是()A. y=32x B. y=3xC. y=6xD. y=34x【02】如图，P是反比例函数图象在第二象限上的一点，矩形PEOF的面积为5，则反比例函数的表达式是________．【03】如图，点A在反比例函数y=kx（x＞0）的图象上，过点A作AD⊥y轴于点D，延长AD至点C，使AD＝DC，过点A作AB⊥x轴于点B，连接BC交y轴于点E．若△ABC 的面积为6，则k的值为．【04】如图，在平面直角坐标系xOy中，反比例函数y=−8x在第二象限的图象上有一点A，过点A作AB⊥x轴于点B，则S△AOB＝．【05】如图，双曲线y=kx与△OAB交于点A，C，已知A，B，C三点横坐标的比为5：5：2，且S△OAB＝21，则k＝．【06】如图，矩形ABCD的顶点A和对称中心在反比例函数y=kx（k≠0，x＞0）的图象上，若矩形ABCD的面积为12，则k的值为（）A．6 B．3√3C．4√2D．12【07】如图，点A、B在反比例函数y=kx的图象上，过点A、B作x轴的垂线，垂足分别是M、N，射线AB交x轴于点C，若OM＝MN＝NC，四边形AMNB的面积是3，则k的值为（）A．-2 B．-4 C．2 D．4【08】如图，在平面直角坐标系中，矩形ABCO的两边OA，OC落在坐标轴上，反比例函数y=kx 的图象分别交BC，OB于点D，点E，且BDCD=54，若S△AOE＝24，则k的值为．【09】如图，过原点的直线与反比例函数y=kx(k>0)的图象交于A，B两点，点A在第一象限点C在x轴正半轴上，连结AC交反比例函数图象于点D.AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连结DE.若AC=3DC，ΔADE的面积为8，则k的值为________.【10】如图，在平面直角坐标系中，△OAB的顶点A在x轴正半轴上，OC是△OAB的中线，点B、C在反比例函数y=2x（x＞0）的图象上，则△OAB的面积等于．【11】如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=kx(x＞0)经过斜边OA的中点C，与另一直角边交于点D．若S△OCD＝9，则S△OBD的值为．【12】在平面直角坐标系中，对于不在坐标轴上的任意一点A(x,y)，我们把点B(1x ,1y)称为点A的“倒数点”．如图，矩形OCDE的顶点C为(3,0)，顶点E在y轴上，函数y=2x(x>0)的图象与DE交于点A．若点B是点A的“倒数点”，且点B在矩形OCDE的一边上，则△OBC的面积为_________．【13】如图，经过原点O 的直线与反比例函数y ＝ax （a ＞0）的图象交于A ，D 两点（点A 在第一象限），点B ，C ，E 在反比例函数y ＝bx （b ＜0）的图象上，AB ∥y 轴，AE ∥CD ∥x 轴，五边形ABCDE 的面积为56，四边形ABCD 的面积为32，则a ﹣b 的值为__，ba 的值为__．【14】如图，直线l ⊥x 轴于点P ，且与反比例函数y 1=k 1x（x ＞0）及y 2=k 2x（x ＞0）的图象分别交于点A ，B ，连接OA ，OB ，已知△OAB 的面积为3，则k 1﹣k 2＝ ．【15】双曲线C 1：y =k 1x和C 2：y =k 2x如图所示，点A 是C 1上一点，分别过点A 作AB ⊥x 轴，AC ⊥y 轴，垂足分别为点B 、点C ，AB ，AC 与C 2分别交于点D 、点E ，若四边形ADOE 的面积为4，则k 1﹣k 2＝ ．【16】如图，点A 是第一象限内双曲线y =mx （m ＞0）上一点，过点A 作AB ∥x 轴，交双曲线y =nx （n ＜0）于点B ，作AC ∥y 轴，交双曲线y =nx （n ＜0）于点C ，连接BC ．若△ABC 的面积为92，则m ，n 的值不可能是（ ）A．m=19，n=−109B．m=14，n=−54C．m＝1，n＝﹣2 D．m＝4，n＝﹣2。

专题1 反比例函数中比例系数k 的几何意义及运用（解析版）类型一 一个反比例函数（一）一个点及一条垂线1．如图，等边三角形OAB ，点B 在x 轴正半轴上，S △OAB ＝4，若反比例函数y ＝（k ≠0）图象的一支经过点A ，则k 的值是 4　．【思路引领】根据正三角形的性质以及反比例函数系数k 的几何意义，得出S △AOC ＝S △AOB ＝2＝|k |，即可求出k 的值．【解答】解：如图，过点A 作AC ⊥OB 于点C ，∵△OAB 是正三角形，∴OC ＝BC ，∴S △AOC ＝S △AOB ＝2＝|k |，又∵k ＞0，∴k ＝4，故答案为：4．【总结提升】本题考查等边三角形的性质，反比例函数系数k 的几何意义，掌握等边三角形的性质以及反比例函数系数k 的几何意义是正确解答的前提．2．如图，平行四边形ABCD 的顶点A 在x 轴上，点D 在上，且AD ⊥x 轴，CA 的延长线交y轴于点E ．若S △ABE ＝5，则k ＝　10　．【思路引领】连接OD ，OE ，过点D 作DH ⊥CE 于H ，BT ⊥EC 于T ，先证△ABT 和△DCH 全等得BT ＝DH ，由此得S △ADE ＝S △ABE ＝5，再由AD ⊥x 轴得AD ∥OE ，进而得S △ADO ＝S △ADE ＝5，然后根据反比例函数比例系数的几何意义得S △ADO ＝|k |，据此可求出k 的值．【解答】解：连接OD ，OE ，过点D 作DH ⊥CE 于H ，BT ⊥EC 于T ，如图所示：则∠BTA ＝∠DHC ＝90°，∵四边形ABCD 为平行四边形，∴AB ＝CD ，AB ∥CD ，AD ∥BC ，∴∠BAT ＝∠DCH ，在△ABT 和△DCH 中，，∴△ABT ≌△DCH （AAS ），∴BT ＝DH ，∴△ADE 和△ABE 同底等高，∴S △ADE ＝S △ABE ＝5，∵AD ⊥x 轴，∴AD ∥OE ，∴△ADO 和△ADE 同底等高，∴S △ADO ＝S △ADE ＝5，根据反比例函数比例系数的几何意义得：S △ADO ＝|k |，∴|k |＝2S △ADO ＝10，∵反比例函数的图象在第一象限，∴k ＝10．故答案为：10．【总结提升】此题主要考查了反比例函数的图象，反比例函数比例系数k 的几何意义，平行四边形的性质，准确识图，熟练掌握反比例函数比例系数k 的几何意义，理解等底（同底）等高（同高）的两个三角形的面积相等．3．如图，已知一次函数y ＝ax +b （a ≠0）的图象与反比例函数（k ≠0，x ＞0）的图象交于第一象限内点A ，与x 轴负半轴交于点B ，过点A 作AC ⊥x 轴于点C ，D 为AB 的中点，线段CD 交y 轴于点E ，连接BE ．若△BEC 的面积是6，则k 的值是 12　.【思路引领】设OC ＝a ，OE ＝b ，OB ＝c ，由△BEC 的面积是6，可得b （a +c ）＝12，再根据直角三角形斜边中线等于斜边一半可得CD ＝AD ＝BD ，由等腰三角形的性质可得∠ECO ＝∠ABC ，进而看得出△ACB ∽△EOC ，由对应边成比例可求出AC ＝，进而表示出点A 的坐标，代入函数关系式可求出k 的值．【解答】解：设OC ＝a ，OE ＝b ，OB ＝c ，∵△BEC的面积是BC•OE＝6，∴b（a+c）＝6，即b（a+c）＝12，∴D是AB的中点，△ABC是Rt△，∴CD＝AD＝BD，∴∠ECO＝∠ABC，∴∠ACB＝∠EOC＝90°，∴△ACB∽△EOC，∴＝，即＝，∴AC＝＝，∴点A（a，），∵点A（a，）在反比例函数y＝的图象上，∴k＝xy＝a×＝12，故答案为：12．【总结提升】本题考查反比例函数图象上点的坐标特征，反比例函数与一次函数图象的交点，用代数式表示出点A的坐标是解决问题的关键．（二）一个点及两条垂线4．如图，在平面直角坐标系中，矩形ABCD的边AB在y轴上，点C坐标为（4，﹣4），并且AO：BO＝1：2，点D在函数（x＞0）的图象上，则k的值为　8　．【思路引领】根据C点坐标表示出BO、BC的长，再利用AO：BO＝1：2表示出D点的坐标即可求出k的值．【解答】解：∵点C坐标为（4，﹣4），∴BO＝BC＝4，又∵AO：BO＝1：2，∴AO＝2，而四边形ABCD为矩形，∴点D坐标为（4，2），将D（4，2）代入函数y＝中得：k＝4×2＝8，故答案为：8．【总结提升】本题考查待定系数法求反比例函数解析式，利用矩形性质结合题干已知条件表示出D点坐标是解题关键．5．如图，在平面直角坐标系xOy中，点A（0，6），B（5，6），将△ABO向右平移到△CDE位置，点A、O 的对应点分别是C、E，函数的图象经过点C和DE的中点F，则k的值是（ ）A．6B．12C．15D．30【思路引领】设AC＝EO＝BD＝a，则E（a，0），再求出C（a，6），D（5+a，6），由F是DE的中点，得到，再由函数的图象经过点C和点F，得到，由此即可求出答案．【解答】解：由平移的性质可知AC＝EO＝BD，设AC＝EO＝BD＝a，则E（a，0），∵A（0，6），B（5，6），∴OA＝6，AB＝5，AB∥x轴，C（a，6），∴AD＝AB+BD＝5+a，∴D（5+a，6）．∵F是DE的中点，∴，∵函数的图象经过点C和点F，∴，解得k＝6a＝15．故选：C．【总结提升】本题主要考查的是求反比例函数图象上点的坐标特点及平移的性质，熟知正确用a表示出点C和点F的坐标是解题的关键．类型二反比例函数与正比例函数综合（一）两交点及一条垂线6．如图，直线y＝mx与双曲线y＝交于A，B两点，过点A作AM⊥x轴，垂足为点M，连接BM，若S△ABM＝2，则k的值为　﹣2　．【思路引领】根据反比例的图象关于原点中心对称得到点A与点B关于原点中心对称，则S△OAM ＝S△OBM，而S△ABM＝2，S△OAM＝1，然后根据反比例函数y＝（k≠0）系数k的几何意义即可得到k＝﹣2．【解答】解：∵直线y＝mx与双曲线y＝交于A，B两点，∴点A与点B关于原点中心对称，∴S△OAM ＝S△OBM，而S△ABM＝2，∴S△OAM＝1，∴|k|＝1，∵反比例函数图象在第二、四象限，∴k＜0，∴k＝﹣2．故答案为：﹣2．【总结提升】本题考查了反比例函数与一次函数的交点问题，熟知从反比例函数y＝（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|是解答此题的关键．（二）两交点及两条垂线7．如图，正比例函数y＝kx与函数的图象交于A，B两点，BC∥x轴，AC∥y轴，则S＝　△ABC 8　．【思路引领】先设A点坐标，根据反比例函数正比例函数的中心对称性再确定B点坐标，于是可得到C 点坐标，然后根据三角形面积公式进行计算．【解答】解：设A点坐标为（m，），则B点坐标为（﹣m，﹣），∴C点坐标为（m，﹣），∴AC＝，BC＝2m，∴△ABC的面积＝AC•BC＝•2m•＝8．故答案为：8．【总结提升】本题考查了反比例函数一次函数的交点问题，根据函数的性质得出A、B、C的坐标是解题的关键．8．如图，在平面直角坐标系xOy中，一次函数y＝﹣x的图象与反比例函数的图象交于A、B两点．①根据图象求k的值；②点P在y轴上，且满足以点A、B、P为顶点的三角形是直角三角形，试写出点P所有可能的坐标．【思路引领】（①求出A的坐标，代入反比例函数的解析式求出即可；②以A或B为直角顶点求出P的坐标是（0，2）和（0，﹣2），以P为直角顶点求出P的坐标是（0，），（0，﹣）．【解答】解：①把x＝﹣1代入y＝﹣x得：y＝1，即A的坐标是（﹣1，1），∵反比例函数y＝经过A点，∴k＝﹣1×1＝﹣1；②若∠PAB是直角，则OP2＝2OA2，则P（0，2），若∠PBA是直角，则OP2＝2OB2，则P（0，﹣2），若∠APB是直角，则PA2+PB2＝AB2，则P（0，），（0，﹣），∴点P的所有可能的坐标是（0，），（0，﹣），（0，2），（0，﹣2）．【总结提升】本题考查了一次函数与反比例函数的交点问题和直角三角形的判定的应用，主要考查学生的计算能力，用了分类讨论思想．类型三反比例函数与一次函数（非正比例函数）综合（一）两函数比例系数同号（两交点在不同象限）9．如图，在平面直角坐标系xOy中，一次函数y＝x+1的图象与反比例函数y＝的图象交于A，B两点，若点P是第一象限内反比例函数图象上一点，且△ABP的面积是△AOB的面积的2倍，则点P的横坐标为　2或　．【思路引领】分点P在AB下方、点P在AB上方两种情况，分别求解即可．【解答】解：①当点P在AB下方时作AB的平行线l，使点O到直线AB和到直线l的距离相等，则△ABP的面积是△AOB的面积的2倍，直线AB与x轴交点的坐标为（﹣1，0），则直线l与x轴交点的坐标C（1，0），设直线l的表达式为：y＝x+b，将点C的坐标代入上式并解得：b＝﹣1，故直线l的表达式为y＝x﹣1①，而反比例函数的表达式为：y＝②，联立①②并解得：x＝2或﹣1（舍去）；②当点P在AB上方时，同理可得，直线l的函数表达式为：y＝x+3③，联立②③并解得：x＝（舍去负值）；故答案为：2或．【总结提升】本题考查了反比例函数与一次函数的交点，当有两个函数的时候，着重使用一次函数，体现了方程思想，综合性较强．（二）两函数比例系数异号（两交点在同一象限）10．如图，矩形OABC中，A（1，0），C（0，2），双曲线y＝（0＜k＜2）的图象分别交AB，CB于点E，F ，连接OE ，OF ，EF ，S △OEF ﹣＝2S △BEF ，则k 值为（ ）A ．B ．1C ．D ．【思路引领】设E 点坐标为（1，m ），则F 点坐标为（，2），根据三角形面积公式得到S △BEF ＝（1﹣）（2﹣m ），根据反比例函数k 的几何意义得到S △OFC ＝S △OAE ＝m ，由于S △OEF ＝S 矩形ABCO ﹣S △OCF﹣S △OEA ﹣S △BEF ，列方程即可得到结论．【解答】解：∵四边形OABC 是矩形，BA ⊥OA ，A （1，0），∴设E 点坐标为（1，m ），则F 点坐标为（，2），则S △BEF ＝（1﹣）（2﹣m ），S △OFC ＝S △OAE ＝m ，∴S △OEF ＝S 矩形ABCO ﹣S △OCF ﹣S △OEA ﹣S △BEF ＝2﹣m ﹣m ﹣（1﹣）（2﹣m ），∵S △OEF ＝2S △BEF ，∴2﹣m ﹣m ﹣（1﹣）（2﹣m ）＝2•（1﹣）（2﹣m ），整理得（m ﹣2）2+m ﹣2＝0，解得m 1＝2（舍去），m 2＝，∴E 点坐标为（1，）；∴k ＝，故选：A ．【总结提升】本题考查了反比例函数k 的几何意义和矩形的性质，正确利用面积的和差计算不规则图形的面积是解题关键．11．如图，在平面直角坐标系xOy 中，菱形ABCD 的顶点D 在第二象限，其余顶点都在第一象限，AB ∥x轴，AO ⊥AD ，AO ＝AD ．过点A 作AE ⊥CD ，垂足为E ，DE ＝4CE ．反比例函数（x ＞0）的图象经过点E，与边AB交于点F，连接OE，OF，EF．若，则k的值为（ ）A．B．C．D．【思路引领】延长EA交x轴于点G，过点F作FH⊥x轴于点H，AB∥x轴，AE⊥CD，AB∥CD，可得AG⊥x轴；利用AO⊥AD，AO＝AD可得△ADE≌△OAG，得到DE＝AG，AE＝OG；利用DE＝4CE，四边形ABCD是菱形，可得AD＝CD＝DE；设DE＝4a，则AD＝OA＝5a，由勾股定理可得EA＝3a，EG＝AE+AG＝7a，可得点E的坐标为（3a，7a），所以k＝21a2，由四边形AGHF为矩形，FH＝AG＝4a，可得点F的坐标，得到OH，GH的长，利用△OEF的面积列出方程，求得a的值，即可得到k的值．【解答】解：如图，延长EA交x轴于点G，过点F作FH⊥x轴于点H，∵AB∥x轴，AE⊥CD，AB//CD，∴AG⊥x轴，∵AO⊥AD，∴∠DAE+∠OAG＝90°，∵AE⊥CD，∴∠DAE+∠D＝90°，∴∠D＝∠OAG，在△DAE和△AOG中，，∴△DAE≌△AOG（AAS），∴DE＝AG，AE＝OG，∴四边形ABCD是菱形，DE＝4CE，∴AD ＝CD ＝DE ，设DE ＝4a ，则AD ＝OA ＝5a ，∴OG ＝AE ＝＝3a ，∴EG ＝AE +AG ＝7a ，∴E （3a ，7a ），∵反比例函数y ＝（x ＞0）的图象经过点E ，∴k ＝21a 2，∵AG ⊥GH ，FH ⊥GH ，AF ⊥AG ，∴四边形AGHF 为矩形，∴HF ＝AG ＝4a ，∵点F 在反比例函数y ＝（x ＞0）的图象上，∴x ＝＝a ，∴F （a ，4a ），∴OH ＝a ，FH ＝4a ，∴GH ＝OH ﹣OG ＝a ，∵S △OEF ＝S △OEG +S 梯形EGHF ﹣S △OFH ，S △EOF ＝，∴×OG ×EG +（EG +FH ）×GH ﹣OH ×HF ＝，∴×3a ×7a +×（7a +4a ）×a ﹣×21a 2＝，解得：a 2＝，∴k ＝21a 2＝21×＝，故选：A ．【总结提升】本题主要考查了反比例函数系数k的几何意义，待定系数法求得反比例函数的解析式，反比例函数图象上点的坐标特征，三角形全等的判定与性质，等腰直角三角形，菱形的性质，利用点的坐标表示相应的线段长度和利用线段长度表示相应的坐标是解题的关键．12．如图，点A、B在反比例函数y＝（x＞0）的图象上，延长AB交x轴于C点，若△AOC的面积是16，且点B是AC的中点，则k＝（ ）A．4B．8C．D．【思路引领】先根据B是AC的中点，表示出△BOC的面积，再利用k的几何意义表示出△AOH和△BOG 的面积，即可得出△AHC和△BGC的面积，易证△AHC∽△BGC，根据面积的比等于相似比的平方，列方程即可求出k的值．【解答】解：连接OB，过点A作AH⊥x轴于点H，过点B作GB⊥x轴于点G，如图所示：∵B是AC的中点，∴＝×16＝8，根据k的几何意义，S△AOH ＝S△BOG＝，∴S△AHC ＝S△AOC﹣S△AOH＝16﹣，S△BGC ＝S△BOC﹣S△BOG＝8﹣，∵∠AHC＝∠BGC＝90°，∠ACH＝∠BCG，∴△AHC∽△BGC，∵B是AC的中点，∴相似比为1：2，∴面积的比为1：4，即S△BGC ：S△AHC＝1：4，∴（8﹣）：（16﹣）＝1：4，解得k＝．故选：C．【总结提升】本题考查了反比例函数的几何意义，运用三角形中线的性质以及相似三角形的性质是解决本题的关键．13．如图，在反比例函数y＝（x＞0）的图象上，有点P1，P2，P3，P4，…，它们的横坐标依次为2，4，6，8，…分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次记为S1，S2，S3，…，则S1+S2+S3＝　7.5　，S1+S2+S3+…+S n＝ （用含n的代数式表示，n为正整数）．【思路引领】过点P1、点P n+1作y轴的垂线段，垂足分别是点A、B，过点P1作x轴的垂线段，垂足是点C，P1C交BP n+1于点D，所有的阴影部分平移到左边，阴影部分的面积之和就等于矩形P1ABD的面积，即可得到答案．【解答】解：如图，过点P1、点P n+1作y轴的垂线段，垂足分别是点A、B，过点P1作x轴的垂线段，垂足是点C，P1C交BP n+1于点D，则点P n+1的坐标为（2n+2，），∵点P1，p2，p3的坐标f分别为（2，5）（4，）（6，）；∴S1+S2+S3＝2×5﹣2×＝7.5；OB＝，∴AB＝5﹣，∴S1+S2+S3+…+S n＝S矩形AP1DB＝2（5﹣）＝10﹣＝，故答案为：7.5，．【总结提升】本题考查了反比例函数系数k的几何意义，正确记忆反比例函数图象上点的坐标特征解题关键．类型四两个反比例函数（一）两函数k值同号14．如图，矩形OABC与反比例函数（k1是非零常数，x＞0）的图象交于点M，N，反比例函数（k2是非零常数，x＞0）的图象交于点B，连接OM，ON．若四边形OMBN的面积为3，则2k2﹣2k1＝　6　．【思路引领】根据反比例函数中k的几何意义：反比例函数图象上点向坐标轴作垂线，与原点构成的直角三角形面积等于，数形结合可以得到，根据图象均在第一象限可知k1＞0，k2＞0，再由四边形OMBN的面积为3，得到，即可得到答案．【解答】解：∵矩形OABC与反比例函数（k1是非零常数，x＞0）的图象交于点M，N，∴由反比例函数中k的几何意义知，，∵矩形OABC与反比例函数（k2是非零常数，x＞0）的图象交于点B，∴由反比例函数中k的几何意义知，S矩形OABC＝|k2|，∵四边形OMBN的面积为3，∴由图可知，S矩形OABC ＝S△AOM+S△CON+S四边形OMBN，即，解得k2﹣k1＝3，∴2k2﹣2k1＝6，故答案为：6．【总结提升】本题考查反比例函数中k的几何意义的应用，读懂题意，数形结合，将所求代数式准确用k 的几何意义对应的图形面积表示出来是解决问题的关键．15．如图，正方形ABCD的顶点分别在函数和的图象上，若BD∥y轴，点C的纵坐标为4，则k1+k2的值为（ ）A．26B．28C．30D．32【思路引领】连接AC交BD于E，延长BD交x轴于F，连接OD、OB，设AE＝BE＝CE＝DE＝m，C （a，4），根据BD∥y轴，可得B（a+m，4+m），A（a+2m，4），D（a+m，4﹣m），即知k1＝4（a+2m）＝（4+m）（a+m），从而m＝4﹣a，B（4，8﹣a），由B（4，8﹣a）在反比例函数的图象上，D（4，a）在的图象上，得k1＝4（8﹣a）＝32﹣4a，k2＝4a，即得k1+k2＝32．【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图，∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，C（a，4），∵BD∥y轴，∴B（a+m，4+m），A（a+2m，4），D（a+m，4﹣m），∵A，B都在反比例函数的图象上，∴k1＝4（a+2m）＝（4+m）（a+m），∵m≠0，∴m＝4﹣a，∴B（4，8﹣a），∵B（4，8﹣a）在反比例函数的图象上，D（4，a）在的图象上，∴k1＝4（8﹣a）＝32﹣4a，k2＝4a，∴k1+k2＝32﹣4a+4a＝32；故选：D．【总结提升】本题考查反比例函数及应用，涉及正方形性质，解题的关键是用含字母的代数式表示相关点坐标．16．如图，在平面直角坐标系中，一条直线与反比例函数y＝（x＞0）的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y＝（x＞0）的图象交于两点D、E，连接DE，则四边形ABED的面积为（ ）A．4B．C．5D．【思路引领】根据点A、B在反比例函数y＝（x＞0）的图象上，可设出点B坐标为（，m），再根据B为线段AC的中点可用m表示出来A点的坐标，由AD∥x轴、BE∥x轴，即可用m表示出来点D、E的坐标，结合梯形的面积公式即可得出结论．【解答】解：∵点A、B在反比例函数y＝（x＞0）的图象上，设点B的坐标为（，m），∵点B为线段AC的中点，且点C在x轴上，∴点A的坐标为（，2m）．∵AD∥x轴、BE∥x轴，且点D、E在反比例函数y＝（x＞0）的图象上，∴点D 的坐标为（，2m ），点E 的坐标为（，m ）．∴S 梯形ABED ＝（﹣+﹣）×（2m ﹣m ）＝．故选：B ．【总结提升】本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及梯形的面积，解题的关键是用m 表示出来A 、B 、E 、D 四点的坐标．本题属于基础题，难度不大，解决该题型题目时，只要设出一个点的坐标，再由该点坐标所含的字母表示出其他点的坐标即可．（二）两函数k 值异号17．如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l ∥y 轴，且直线l 分别与反比例函数y ＝（x ＞0）和y ＝（x ＞0）的图象交于P ，Q 两点，若S △POQ ＝12，则k 的值为　﹣16　．【思路引领】由于S △POQ ＝S △OMQ +S △OMP ，根据反比例函数比例系数k 的几何意义得到|k |+×|8|＝12，然后结合函数y ＝的图象所在的象限解方程得到满足条件的k 的值．【解答】解：∵S △POQ ＝S △OMQ +S △OMP ，∴|k |+×|8|＝12，∴|k |＝16，而k ＜0，∴k ＝﹣16．故答案为：﹣16．【总结提升】本题考查了反比例函数比例系数k 的几何意义：在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k |，且保持不变．也考查了反比例函数与一次函数的交点问题．18．如图，点A是反比例函数的图象上任意一点，AB∥x轴交反比例函数的图象于点B，以AB为边作平行四边形ABCD，其中C、D在x轴上，若平行四边形ABCD的面积为11，则k的值为　6　．【思路引领】过点B作BM⊥x轴，过点A作AN⊥x轴，可证得△BCM≌△ADN（AAS），得出S▱ABCD＝S＝11，然后根据k的几何意义求解．矩形ABMN【解答】解：过点B作BM⊥x轴，过点A作AN⊥x轴，则∠BMC＝∠AND＝90°，∵四边形ABCD为平行四边形，∴BC∥AD，BC＝AD，∴∠BCM＝∠ADN，在△BCM和△ADN中，∴△BCM≌△ADN（AAS），＝11，∴S▱ABCD＝S矩形ABMN又∵S＝k+5，矩形ABMN∴k+5＝11，∴k＝6．故答案为：6．【总结提升】本题考查了反比例函数k的几何含义，平行四边形的性质．需要我们熟练掌握把已知图形转化为模型图形（与k相关的矩形或三角形）的能力．。

专训1 用反比例函数系数k 的几何意义解与面积相关问题名师点金：反比例函数的系数k 具有一定的几何意义，|k |等于反比例函数y ＝kx (k ≠0)图象上任意一点向两坐标轴所作垂线与坐标轴所围成的矩形的面积．在反比例函数的图象中，涉及三角形或矩形的面积时，常用系数k 的几何意义求解．反比例函数的系数k 与面积的关系1．如图，过y 轴上任意一点P ，作x 轴的平行线，分别与反比例函数y ＝－4x 和y ＝2x 的图象交于A 点和B 点，若C 为x 轴上的任意一点，连接AC ，BC ，则△ABC 的面积为( )A ．3B ．4C ．5D ．6(第1题) (第2题) (第3题)2．如图，P 是反比例函数y ＝kx 的图象上一点，过P 点分别向x 轴，y 轴作垂线，所得到的图中阴影部分的面积为6，则这个反比例函数的表达式为( )A ．y ＝－6xB ．y ＝6xC ．y ＝－3xD ．y ＝3x3．【2016·菏泽】如图，△OAC 和△BAD 都是等腰直角三角形，∠ACO ＝∠ADB ＝90°，反比例函数y ＝6x 在第一象限的图象经过点B ，则△OAC 与△BAD 的面积之差S △OAC －S △BAD为( )A ．36B ．12C ．6D ．3(第4题) (第5题) (第6题)4．如图，正比例函数y ＝x 与反比例函数y ＝1x 的图象相交于A ，B 两点，BC ⊥x 轴于点C ，则△ABC 的面积为( )A ．1B ．2C ．3D ．45．如图，函数y ＝－x 与函数y ＝－4x 的图象相交于A ，B 两点，过A ，B 两点分别作y轴的垂线，垂足分别为点C ，D ，则四边形ACBD 的面积为( )A ．2B ．4C ．6D ．86．【2016·本溪】如图，点A ，C 为反比例函数y ＝kx (x ＜0)图象上的点，过点A ，C 分别作AB ⊥x 轴，CD ⊥x 轴，垂足分别为B ，D ，连接OA ，AC ，OC ，线段OC 交AB 于点E ，点E 恰好为OC 的中点，当△AEC 的面积为32时，k 的值为( )A ．4B ．6C ．－4D ．－6已知面积求反比例函数的表达式题型1 已知三角形面积求函数表达式7．如图，在平面直角坐标系xOy 中，直线AB 与x 轴交于点A (－2，0)，与反比例函数在第一象限内的图象交于点B (2，n )，连接BO ，已知S △AOB ＝4.(1)求该反比例函数的表达式和直线AB 对应的函数表达式； (2)若直线AB 与y 轴的交点为C ，求△OCB 的面积．(第7题)题型2 已知四边形面积求函数表达式8．如图，矩形ABOD 的顶点A 是函数y ＝－x －(k ＋1)的图象与函数y ＝kx 在第二象限的图象的交点，AB ⊥x 轴于B ，AD ⊥y 轴于D ，且矩形ABOD 的面积为3.(1)求两函数的表达式；(2)求两函数图象的交点A ，C 的坐标；(3)若点P 是y 轴上一动点，且S △APC ＝5，求点P 的坐标．(第8题)已知反比例函数表达式求图形的面积题型1 利用对称性求面积9．如图，是由四条曲线围成的广告标志，建立平面直角坐标系，双曲线对应的函数表达式分别为y ＝－6x ，y ＝6x ，现用四根钢条固定这四条曲线．这种钢条加工成矩形产品按面积计算，每单位面积25元，请你帮助工人师傅计算一下，所需钢条一共要花多少钱？(第9题)题型2 利用点的坐标及面积公式求面积10．如图，直线y ＝k 1x ＋b 与反比例函数y ＝k 2x (x ＜0)的图象相交于点A ，点B ，与x 轴交于点C ，其中点A 的坐标为(－2，4)，点B 的横坐标为－4.(1)试确定反比例函数的表达式； (2)求△AOC 的面积．(第10题)题型3 利用面积关系求点的坐标11．【2016·兰州】如图，在平面直角坐标系中，OA ⊥OB ，AB ⊥x 轴于点C ，点A (3，1)在反比例函数y ＝kx的图象上．(1)求反比例函数y ＝kx的表达式；(2)在x 轴的负半轴上存在一点P ，使得S △AOP ＝12S △AOB ，求点P 的坐标；(3)若将△BOA 绕点B 按逆时针方向旋转60°得到△BDE ，点A ，O 的对应点分别为点E ，D .直接写出点E 的坐标，并判断点E 是否在该反比例函数的图象上，说明理由．(第11题)参考答案1．A 点拨：设△ABC 的边AB 上的高为h ，则 S △ABC ＝12AB ·h＝12(AP ＋BP )·h ＝12(AP ·h ＋BP ·h ) ＝12(|－4|＋|2|) ＝12×6 ＝3. 故选A . 2．A3．D 点拨：设△OAC 和△BAD 的直角边长分别为a ，b ，可得出B 点坐标为(a ＋b ，a －b )．因为点B 在反比例函数y ＝6x 第一象限的图象上，所以(a ＋b )(a －b )＝a 2－b 2＝6.所以S △AOC －S △BAD ＝12a 2－12b 2＝12(a 2－b 2)＝12×6＝3.故选D .4．A5．D 点拨：由题意，易得出S △ODB ＝S △AOC ＝12×|－4|＝2.易知OC ＝OD ，AC ＝BD ，所以S △AOC ＝S △ODA ＝S △ODB ＝S △OBC ＝2.所以四边形ACBD 的面积为S △AOC ＋S △ODA ＋S △ODB ＋S △OBC ＝8.6．C 点拨：设点C 的坐标为⎝⎛⎭⎫m ，k m ，则点E ⎝⎛⎭⎫12m ，k 2m ，A ⎝⎛⎭⎫12m ，2km ，根据三角形的面积公式可得出S △AEC ＝－38k ＝32，由此即可求出k 值．7．解：(1)如图，过点B 作BD ⊥x 轴，垂足为D . 由题易知OA ＝2，BD ＝n .∴S △AOB ＝12OA ·BD ＝12×2n ＝4.∴n ＝4.∴B 点的坐标为(2，4)．∴反比例函数的表达式为y ＝8x.设直线AB 对应的函数表达式为y ＝kx ＋b ，由题意得⎩⎪⎨⎪⎧－2k ＋b ＝0，2k ＋b ＝4，解得⎩⎪⎨⎪⎧k ＝1，b ＝2. ∴直线AB 对应的函数表达式为y ＝x ＋2.(第7题)(2)对于y ＝x ＋2，当x ＝0时，y ＝0＋2＝2，∴C 点的坐标为(0，2)． ∴OC ＝2.∴S △OCB ＝S △AOB －S △AOC ＝4－12×2×2＝2.8．解：(1)由题中图象知k ＜0，由已知条件得|k |＝3，∴k ＝－3. ∴反比例函数的表达式为y ＝－3x ，一次函数的表达式为y ＝－x ＋2. (2)由⎩⎪⎨⎪⎧y ＝－3x ，y ＝－x ＋2，解得⎩⎪⎨⎪⎧x 1＝－1，y 1＝3，⎩⎪⎨⎪⎧x 2＝3，y 2＝－1.∴点A ，C 的坐标分别为(－1，3)，(3，－1)．(3)设点P 的坐标为(0，m )，直线y ＝－x ＋2与y 轴的交点为M ，则点M 的坐标为(0，2)．∵S △APC ＝S △AMP ＋S △CMP ＝12PM (|－1|＋|3|)＝5，∴PM ＝52，即|m －2|＝52.∴m ＝92或m ＝－12.∴点P 的坐标为⎝⎛⎭⎫0，92或⎝⎛⎭⎫0，－12. 9．解：由反比例函数图象的对称性可知，两条坐标轴将矩形ABCD 分成四个全等的小矩形．因为点A 为y ＝6x 的图象上的一点，所以S 矩形AEOH ＝6.所以S 矩形ABCD ＝4×6＝24.所以总费用为25×24＝600(元)．所以所需钢条一共要花600元．10．解：(1)∵点A (－2，4)在反比例函数y ＝k 2x 的图象上，∴k 2＝－8.∴反比例函数的表达式为y ＝－8x.(2)∵点B 的横坐标为－4，且点B 在反比例函数y ＝－8x 的图象上，∴其纵坐标为2.∴点B 的坐标为(－4，2)．∵点A (－2，4)，B (－4，2)在直线y ＝k 1x ＋b 上，∴⎩⎪⎨⎪⎧4＝－2k 1＋b ，2＝－4k 1＋b ，解得⎩⎪⎨⎪⎧k 1＝1，b ＝6.∴直线AB 对应的函数表达式为y ＝x ＋6.当y ＝0时，x ＝－6. ∴点C 的坐标为(－6，0)． ∴S △AOC ＝12×6×4＝12.11．解：(1)∵点A (3，1)在反比例函数y ＝kx 的图象上，∴k ＝3×1＝ 3.∴反比例函数的表达式为y ＝3x. (2)∵A (3，1)，AB ⊥x 轴于点C ， ∴OC ＝3，AC ＝1.由题意易得△AOC ∽△OBC ， ∴OC BC ＝AC OC. ∴BC ＝OC 2AC＝3.∴B 点坐标为(3，－3)． ∴S △AOB ＝12×3×(1＋3)＝2 3.∴S △AOP ＝12S △AOB ＝ 3.设点P 的坐标为(m ，0)， ∴12×|m |×1＝ 3. ∴|m |＝2 3.∵P 是x 轴的负半轴上的点， ∴m ＝－2 3.∴点P 的坐标为(－23，0)． (3)点E 的坐标为(－3，－1)．点E 在该反比例函数的图象上，理由如下： ∵－3×(－1)＝3＝k ，∴点E在该反比例函数的图象上．。

专题训练(十) 反比例函数中k 的几何意义(本专题部分习题有难度，请根据实际情况选做)1．如图，在平面直角坐标系中，点A 是双曲线y ＝3x (x ＞0)上的一个动点，过点A 作x 轴的垂线，交x 轴于点B ，点A 运动过程中△AOB 的面积将会( ) A ．逐渐增大 B ．逐渐减小 C ．先增大后减小 D ．不变2．如图，过反比例函数y ＝2x (x ＞0)图象上任意两点A ，B 分别作x 轴的垂线，垂足分别为C ，D ，连接OA ，OB ，设AC 与OB 的交点为E ，△AOE 与梯形ECDB 的面积分别为S 1，S 2，比较它们的大小，可得( ) A ．S 1＞S 2 B ．S 1＜S 2 C ．S 1＝S 2D ．S 1、S 2的大小关系不能确定3．(鄂州中考)点A 为双曲线y ＝kx (k ≠0)上一点，B 为x 轴上一点，且△AOB 为等边三角形，△AOB 的边长为2，则k 的值为( )A ．2 3B ．±2 3 C. 3 D ．± 34．设P 是函数y ＝2x 在第一象限的图象上的任意一点，点P 关于原点的对称点为点P ′，过点P 作PA 平行于y 轴，过点P ′作P ′A 平行于x 轴，PA 与P ′A 交于A 点，则△PAP ′的面积( ) A ．随P 点的变化而变化 B ．等于1 C ．等于2 D ．等于45．如图，点A 是反比例函数y ＝kx 图象上的一点，过点A 作AB ⊥x 轴，垂足为点B ，点C 为y 轴上的一点，连接AC ，BC.若△ABC 的面积为3，则k 的值是( ) A ．3 B ．－3 C ．6 D ．－66．(黔西南中考)如图，点A 是反比例函数y ＝kx 图象上的一个动点，过点A 作AB ⊥x 轴，AC ⊥y 轴，垂足点分别为B 、C ，矩形ABOC 的面积为4，则k ＝________．7．(陕西中考)如图，在平面直角坐标系中，过点M(－3，2)分别作x 轴，y 轴的垂线与反比例函数y ＝4x 的图象交于A ，B 两点，则四边形MAOB 的面积为________．8．(临沂中考)如图，反比例函数y ＝4x 的图象经过直角△OAB 的顶点A ，D 为斜边OA 的中点，则过点D 的反比例函数的表达式为________．9．如图，矩形ABCD 的边AB 与y 轴平行，顶点A 的坐标为(1，2)，点B 与点D 在反比例函数y ＝6x (x ＞0)的图象上，则点C 的坐标为________．10．(铁岭中考)如图，点P 是正比例函数y ＝x 与反比例函数y ＝kx 在第一象限内的交点，PA ⊥OP 交x 轴于点A ，△POA的面积为2，则k 的值是________．11．(资阳中考)如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l ∥y 轴，且直线l 分别与反比例函数y ＝8x (x ＞0)和y ＝kx(x ＞0)的图象交于P 、Q 两点，若S △POQ ＝14，则k 的值为________．12．如图，已知反比例函数y ＝kx (k ＜0)的图象经过点A(－3，m)，过点A 作AB ⊥x 轴于点B ，且△AOB 的面积为 3.求k 和m 的值．13．反比例函数y ＝1x 和y ＝k x (k ≠0)在第一象限内的图象如图所示，点P 在y ＝kx 的图象上，PC ⊥x 轴，垂足为C ，交y ＝1x 的图象于点A ，PD ⊥y 轴，垂足为D ，交y ＝1x 的图象于点B.已知点A(m ，1)为线段PC 的中点． (1)求m 和k 的值；(2)求四边形OAPB 的面积．参考答案1．D 2.C 3.D 4.D 5.D 6.－4 7.10 8.y ＝1x 9.(3，6) 10.2 11.－20 12.设点A 的坐标为(x ，y)．∵△AOB 的面积为3，∴12|x|·|y|＝12|k|＝ 3.解得|k|＝2 3.又∵k ＜0，∴k ＝－2 3.∴反比例函数表达式为y ＝－23x .∵反比例函数图象经过点A(－3，m)，∴m ＝－23－3.解得m ＝2.综上可知：k ＝－23，m ＝2. 13.(1)把A(m ，1)代入y ＝1x ，得m ＝1，∴A 点坐标为(1，1)．∵点A(1，1)为线段PC 的中点，∴点P 坐标为(1，2)．把(1，2)代入y ＝k x ，得k ＝1×2＝2.(2)∵点P 坐标为(1，2)，∴四边形OCPD 的面积为1×2＝2.又∵△ODB 的面积为12，△OAC 的面积为12，∴四边形O APB 的面积为2－12－12＝1.。

2023年中考数学高频考点二轮专题训练--反比例函数系数k的几何意义一、综合题1．如图，在△AOB中，△ABO=90°，OB=4，AB=8，反比例函数y= k x在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=4．（1）求反比例函数解析式；（2）求点C的坐标．2．过反比例函数y= k x(k < 0)的图象上一点A 作x 轴的垂线交x 轴于点B ，O 为坐标原点，且△ABO 的面积S△ABO = 4 ．（1）求k 的值；（2）若二次函数y = ax2与反比例函数y= k x(k < 0)的图象交于点C(-2，m) ，请结合函数的图象写出满足ax2< k x的x的取值范围．3．如图，一次函数y＝mx＋5的图象与反比例函数y＝k x（k≠0）在第一象限的图象交于A（1，n）和B（4，1）两点，过点A作y轴的垂线，垂足为M.（1）求一次函数和反比例函数的解析式；（2）求△OAM的面积S；（3）在y轴上求一点P，使PA＋PB最小.4．如图，一次函数y=−12x+52的图象与反比例函数y=kx(k>0)的图象交于A，B两点，过点A做x轴的垂线，垂足为M，△AOM面积为1.（1）求反比例函数的解析式；（2）在x轴上求一点P，使|PA−PB|的值最大，并求出其最大值和P点坐标.5．如图，在平面直角坐标系中，点O为坐标原点，直角三角形AOB的直角顶点B在x轴正半轴上，点A在第一象限，OB＝2，tan△AOB＝2．（1）求图象经过点A的反比例函数的解析式；（2）点C是（1）中反比例函数图象上一点，连接OC交AB于点D，连接AC，若D为OC中点，求△ADC的面积．6．如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，△ABO=90°，△AOB=30°，OB=2 √3，反比例函数y= kx（x＞0）的图象经过OA的中点C，交AB于点D．（1）求反比例函数的关系式；（2）连接CD，求四边形CDBO的面积．7．如图，已知反比例函数y=m−7x的图象的一支位于第一象限．（1）该函数图象的另一分支位于第象限，m的取值范围是；（2）已知点A在反比例函数图象上，AB△x轴于点B，△AOB的面积为3，求m的值．8．如图，四边形ABCD是矩形，点A在第四象限y1＝﹣2x的图象上，点B在第一象限y2＝k x的图象上，AB交x轴于点E，点C与点D在y轴上，AD＝32，S矩形OCBE＝32S矩形ODAE.（1）求点B的坐标.（2）若点P在x轴上，S△BPE＝3，求直线BP的解析式.9．如图，点P(3，2)在反比例函数y= k x(x>0)的图象上，过点P作PM△x轴交反比例函数y= 2x的图象于点M，作PNIIy轴交反比例函数y= 2x的图象于点N，连接MN。