反比例函数中K的几何意义(微课课件)

总结词
k值决定了反比例函数图像的形状和 位置。
详细描述
在反比例函数y=k/x中，k值决定了图 像的形状和位置。当k>0时，图像出 现在第一象限和第三象限；当k<0时 ，图像出现在第二象限和第四象限。
k的正负与图像的位置
总结词
k的正负决定了图像所在的象限。
详细描述
当k>0时，图像分布在第一象限和第三象限；当k<0时，图像分布在第二象限和 第四象限。
拓展反比例函数的应用领域
随着科学技术的发展，反比例函数的应用领域也在不断扩大。未来我们可以尝试将反比例 函数应用于其他领域，如经济学、生物学等，以解决实际问题。
探索与其他数学知识的联系
反比例函数作为数学中的一个重要概念，与其他数学知识有着密切的联系。未来我们可以 进一步探索反比例函数与其他数学知识之间的联系，以促进数学学科的发展。
k值对反比例函数图像的影响
随着k值的增大或减小，反比例函数的图像会向内或
反比例函数在实际生活中有着广泛的应用，如电流与电阻、电容与电压
等物理量之间的关系可以用反比例函数来描述。
对反比例函数的研究展望
深入探究反比例函数的性质
尽管我们已经对反比例函数的性质有了一定的了解，但仍有许多未知的性质等待我们去发 现和研究。例如，反比例函数的极限行为、奇偶性等性质。
反比例函数的性质
反比例函数具有以下性质：当 x 增大时，y 值会减小；当 x 减小 时，y 值会增大。这是因为 xy =
k 的关系。
在图像上，反比例函数的两个分 支在 x 轴和 y 轴上分别趋于无穷
大和无穷小。
反比例函数在坐标系中的图像是 不闭合的，且无限接近于坐标轴
。
Part
02

，求$k$的值。
利用K值解决实际问题
例题3：某工厂生产A、B两种配套产品 ，其中每天生产$x$吨A产品，需生产 $y$吨B产品。已知生产A产品的成本与 产量的平方成正比。经测算，生产1吨 A产品需要4万元，而B产品的成本为每
吨8万元。求
(1)生产A、B两种配套产品的平均成本 的最小值；
(2)若原料供应商对这种小型工厂供货 办法使得该工厂每天生产A产品的产量 $x$在$0 < x leqslant 2$的范围内， 那么在这种情况下，该工厂应生产A产
当$K < 0$时，距离公式同样适用， 只是图像位于第二、四象限。
K值与角度关系
对于反比例函数图像上任意一点，其与原点连线的倾斜角$theta$与该点 的横坐标$x$和纵坐标$y$满足关系：$tantheta = frac{y}{x} = frac{K}{x^2}$。
当$K > 0$时，$theta$为锐角或直角；当$K < 0$时，$theta$为钝角或 直角。
随着$|K|$的增大，倾斜角$theta$也逐渐增大，但始终不会超过直角。
05
典型例题解析
求反比例函数中K值
01
例题1
已知反比例函数$y = frac{k}{x}$的图像经过点 $A(2,3)$，求$k$的值。
02
例题2
已知反比例函数$y = frac{k}{x}$的图像经过点 $B(m,n)$和$C(p,q)$，且$mn = 6$，$pq = 8$
06
课堂小结与拓展延伸
课堂小结
反比例函数$y = frac{k}{x}$（$k neq 0$）中，比例系数$k$的几 何意义：过双曲线上任意一点引 $x$轴、$y$轴垂线，所得矩形面
积为$|k|$。

坐标轴围成的矩形的面积，发现，无论图像
上的点如何移动，矩形的面积却始终不变，
且刚好为 。接着，我们发现双曲线上的点
||
与坐标轴围成的三角形的面积始终为 ，可
2
见值常常与图形的面积相联系。
PPT模板：/moban/
PPT素材：/sucai/
PPT背景：/beijing/
3
相交于、两

点，过作 ⊥ 轴，过作 ⊥ 轴，则
图中阴影部分的面积为（ ）
A、2
B、3
C、4
D、6
3

点和点都在反比例函数 = 的图像上
⊥ 轴， ⊥ 轴
△ = △
3
=
2
阴影部分的面积就是两个三角形面积之和，为3
正确答案是选项B。
我们通过探究反比例函数图像上的点与
历史课件：/kejian/lishi/
PPT背景：/beijing/
PPT图表：/tubiao/
PPT下载：/xiazai/
PPT教程： /powerpoint/
资料下载：/ziliao/
数学课件：/kejian/shuxue/
英语课件：/kejian/yingyu/
美术课件：/kejian/meishu/
科学课件：/kejian/kexue/
物理课件：/kejian/wuli/
PPT图表：/tubiao/
PPT下载：/xiazai/
PPT教程： /powerpoint/
A、2
B、4
C、6
D、8
两个矩形的面积相等，且都为比例系数4。
1 = 矩形 − 阴影矩形 = 4 − 1 = 3
2 = 矩形 − 阴影矩形 = 4 − 1 = 3

别向x轴、y轴作垂线
⑴若P的坐标是（-1,3）则PM=__3__,PN=_1___
⑵若F的坐标是（0.5，-6），则FB=_6___,FA=_0_.5__
⑶若P的坐标是（x，y），则PM=__y__,PN=__x__ y
P
N
B
x
M0
平面直角坐标系内任意一点P(x,y)
.
AF
P到x轴的距离是这点纵坐标的绝对值即是 y
1
1.理解并掌握反比例函数中 ∣K∣的几何意义； 2.能灵活运用∣K∣的几何 意义求图形面积； 3.能根据图形面积求出K值
2
概念回顾
定义
形如__y_＝__kx___(k≠0，k为常数)的函数叫 做反比例函数
关系式
防错 提醒
y k 或y＝kx－1或xy＝k(k≠0) x
(1)k≠0；(2)自变量x≠0；(3)函数值y≠0
5 2
B
D
x
14
变式练习

y 6
已知：如图,反比例函数
与x一次函数
y=kx+1的图像交于A、B两点,点A的纵坐标是3.
（1）求这个一次函数的解析式 （2）求△AOB的面积.
解
:
(2)
y


6 x
,
y x 1.
解得xy

3,2或xy

2, 3.
A(2,3),B(3,2).
为什么？数缺形时少直觉， 形少数时难入微．
21
反比例函数 y kx上一点P（x0，y0），过点P 分别作PA⊥y轴，PB⊥X轴，垂足分别为A、
B，则矩形AOBP的面积为 k ；
且S△AOP= S△BOP = k

6

拓展3 : A（x1，y1）在反比例函数y= （＞）图像上
2

(3) 如图 ，点B（x2，y2 ）为反比例函数y=- （x <0）图像上一点.求△OAB的面积.
补
E
S△AOB= S梯形ABEF-S△AOF-S△BOE
=S梯形ABEF-3-1
=S梯形ABEF-4
| −
|(| |+| | )
2
(1) 如图，点B（x2，y2 ）为反比例函数y= （x＞0）图像上一点.

若A，B为两函数同一象限的点，求 △ OAB的面积.
S△AOE≠S△BOF
S△AOB= S梯形AEFB+S△AOE-S△BOF
=S梯形AEFB+3-1
=S梯aAEFB+2
E
F
| − |(| |+| | )
=
等底等高，
面积不变
N
x
利用平行转化解决面积问题
变形
等底等高，
面积不变
变形
利用平行转化解决面积问题
1、如图6, P是反比例函数y=(x>0)图象上的一点,PM⊥y,点Q,N在x轴
4
上,QN∥PM，且QN=PM,四边形PMQN的面积为4,则k=____________.
6
D
2、如图，已知点A在反比例函数y=
6

1、如图，反比例函数y= 的图像经过A（1，6），B（3，2）两点，求△AOB 的面积
.
F
方法2: S△AOB= S△AOE-S△BOE
或S△AOB= S△OBF-S△OAF
补
E
F
G
E
方法3: S△AOB= S矩形OEGF-S△BOE-S△ABG- S△OAF

随着x的增大或减小，曲线会逐渐靠近 坐标轴，但永远不会与坐标轴相交。
曲线形状
图像是由两支分别位于第一和第三象 限的曲线组成，这两支曲线关于原点 对称。
k<0时图像特征
1 2
图像位于第二、四象限
当k<0时，反比例函数的图像会出现在第二和第 四象限。
曲线形状
图像同样是由两支分别位于第二和第四象限的曲 线组成，这两支曲线也关于原点对称。
图像的性质。
总结
反比例函数的图像性质与 $k$ 的 正负有关。当 $k > 0$ 时，图像 位于第一、三象限；当 $k < 0$
时，图像位于第二、四象限。
涉及综合应用问题
01
例题5
已知反比例函数 $y = frac{k}{x}$ 的图像与一次函数 $y = ax + b$ 的
图像交于点 $M(2,1)$ 和 $N(-1,-2)$，求这两个函数的解析式。
反比例函数的极限与连续性问题
讨论反比例函数在特定点的极限行为，以 及在定义域内的连续性。
反比例函数与其他函数的复合问 题
研究反比例函数与其他基本函数（如幂函 数、三角函数等）的复合性质及图像特征 。
THANK YOU
06
总结回顾与拓展延伸
重点知识点总结回顾
反比例函数图像的基本性质
反比例函数图像为双曲线，当k>0时，图像位于第一、三象限；当k<0时，图像位于第二 、四象限。
k的几何意义
k的绝对值表示双曲线与坐标轴所围成的矩形的面积。当k>0时，矩形在第一象限；当 k<0时，矩形在第二象限。
反比例函数图像的对称性
通过中心对称性，我们可以更好 地理解反比例函数的性质和行为 ，以及它在解决实际问题中的应

（2022·日照）如图，矩形 OABC 与反比例函数 y1＝
2

1

（ k1是非零常数，
x ＞0）的图象交于点 M , N ，与反比例函数 y2＝ ( k2是非零常数, x ＞0)的图
象交于点 B ，连接 OM ,ON . 若四边形 OMBN 的面积为3，则 k1－ k2=（ B ）
A. 3
B. －3

一象限的图象经过 A ， C 两点.若△ ABO 的面积为6，则 k 的值为（ B ）
A. 3
B. 4
C. 5
D. 6
【解析】如图，过点 A 作 AE ⊥ x 轴于点 E . 设 A （ m ，


）， B
（ n ，0）.∵点 C 为线段 AB 的中点，∴由中点坐标公式，可得 C
＋

，
2
2
. ∵点 C 在反比例函数的图象上，∴
接 QO ， QA ， QP ， QB . 若△ QOA ，△ QPB 的面积之和是5，则 k ＝
10
⁠
.
【解析】设 Q （ m ， n ）， m ＜0， n ＜0.
1
2
1
2
∴ S△ QOA ＝ OA ·（－ m ）， S△ QPB ＝ OA ·（ OB ＋ m ）.
∵△ QOA ，△ QPB 的面积之和是5，
－ S△ OCN ＝3，∴ k2－ k1＝3.∴ k1－ k2＝－3.故选B.


【点拨】反比例函数系数中 k 的几何意义：在反比例函数 y ＝ 图象上任取一点，
过这点向 x 轴和 y 轴分别作垂线，与坐标轴围成的矩形的面积是定值｜ k ｜.
返回目录
数学 九年级上册 BS版

y
CA
O
x
DB
B
9
思路方法小结
有关反比例函数与几何综合的问题的 处理思路： 从关键点入手．通过关键点坐标和横 平竖直线段长的互相转化，结合 K的 几何意义，可将函数特征与几何特征 综合在一起进行研究． 对函数特征和几何特征进行转化、组 合，列方程求解．
B
10
变式训练2
1、如图，△OAB中，∠OAB=90º，双曲线 y kx（x > 0） 分别与OB、AB交于C、D两点，将△BCD沿直线CD折叠
，与BC交于点D，S△BOD=21，则K 的值
为__8______。（2015深圳中考15题）
E
B
8
【例2】（2016.5龙华二模16题）如图，已知点A是函数 y 3 (x 0) x
的图象上一点，点B是函数
y k (x 0) 上的图象上一点，且
x
4
OB⊥OA，若OA :OB=3:2 ， 则k 的值为 3 .
“数无形，少直观，形无数，难入 微”。 “数形结合”是数学中最重 要的，也是最基本的思想方法之一， 是解决许多数学问题的有效思想。利 用“数形结合”可使所要研究的问题 化难为易，化繁为简，使抽象变得直 观。
B
15
K S △2
B
3
一、基础应用
1、如图，若反比例函数 y
k x
的图象过点A，矩形ABபைடு நூலகம்C
的面积为4，则k= .
由图形面积求K值（解析式）
B
4
2、如图，过反比例函数y＝ 2 （x＞0）图象上一点A作 AM⊥x轴于点M ， x
连接OA，则 S AOM =
.
y A
OM
x
由K值（解析式）求图形面积

求反比例函数解析式的方法是什么？
待定系数法
学习目标
1.理解并掌握反比例函数中∣K∣的几何意 义； 2.能灵活运用∣K∣的几何意义求图形面 积； 3.能根据图形面积求出K值
复习反馈，导入新课
1、若点P（2,3）在反比例函数 y k 的图像上，则k= 6 _ x
2、若点P(m,n)在反比例函数
y 6 图像上，则mn= _
归纳小结
y
P(m,n) B
o
A
x
k
这就是反比例函
2、如图，连接OM，则
SOAP
1 2
OA•
AP
1 2
m
•
n
1 2
k
数中K的几何意义
S矩形OAPB=|k|
S△OAP= |k|
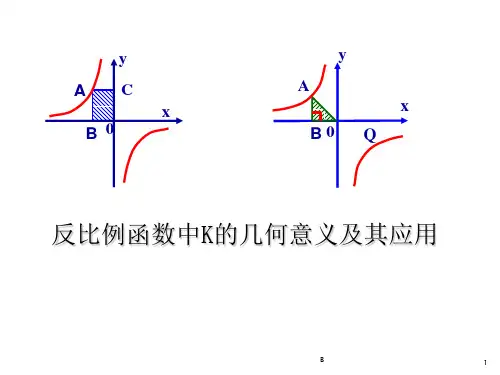
k的几何意义:过双曲线上任意一点P作x轴、y轴 的垂线,两垂线与坐标轴所围成的矩形面积为|k|.
学以致用 小试身手
1.如图,点P是反比例函数
2 x
图象上的一点
,PA⊥x轴于A, PB⊥y轴于B.求长方形PAOB的面积。
解：S矩形PAOB =OA·P.A
y
= m•n
=k
P(m,n) B
=2
o
A
x
1、过反比例函数y k 中,任意一点 x
P(m, n)分别作x轴, y轴的垂线, 垂足分别为A, B, 则S矩形OAPB OA•APLeabharlann m•n6xA
D
3、如图，S矩形ABCD=
S△A6BD=___
3
S矩形ABCD与S△ABD有何关系？
2
1 S△ABD= 2 S矩形ABCD
B
3
C
复习反馈，导入新课
4、如图,点P是反比例函数图象上的一点,过点P分别向x轴