地下水渗流基本方程及数学模型共71页文档

根据裘布依公式，径向渗流流速为
流量为
Q2rMkdz
dr
v kJk dz dr
浸润线方程： zh Q lnr
2kM r0
流量公式：
Q 2 .73 kM 2 H h 2 .73k 2Ms
lg R lg r 0
lg R lg r 0
影响半径：参照普通完全井
裘布依假定： ——在任一竖直线上，各点渗流方向水平； ——在同一竖直线上，各点渗流流速相等。
v k dzk dh
dl
dl
其合理性取决于 θ 的大小
dz tan
dl
单井
井是一种汲取地下水或排水用的集水建筑物，在水文地 质勘探工作和开发地下水资源中有着广泛的应用。
根据水文地质条件，可将井按其所在的位置可分为潜水 井和承压井两种基本类型。
井群
井群——多个井同时工作， 井间距离小于影响 半径，各井出水量 与单井时的出水量 不同。
普通完全井井群工作时的浸润面方程：
z2H 20 .7kQ 30 2 lg R 1 nlg r 1 r2 rn
渗流对建筑物安全稳定的影响 1.扬压力（浮力、渗透压力） 作用在建筑物基底上的力，对建筑物有倾覆的危险。
由于渗流流速很小，所流速水头忽略不计； 总水头=测压管水头；
Jp=J。
达西定律——渗流线性定律
达西定律——渗流能量损失与渗 流流速之间的关系（均匀流）。
vukJ
式中k为渗透系数。
适用范围：
Re vd1~10
式中d土壤颗粒有效直径， 取d10；即重量10%.
渗透系数k的确定：
1.实验室测定法： 2.现场测定法： 3.经验法。见相关资料

p减少 有效应力增大会引起固体颗粒的压缩变形。固 体颗粒的压缩变形比多孔介质中空隙的变形小得多，通
常可忽略。
（二）含水层的状态方程

含水层弹性存储的概念： 弹性储存：当地下水水头（水压）降低（或升高）时， 含水层、弱透水层释放（或储存）地下水的性质。 含水层弹性存储的物理意义：

（承压含水层）弹性储存与（潜水）重力储存不同；
第一步：化简方程左端项： 当渗流满足达西定律，且取坐标与各向异性主轴方向一致，有：
H v x K xx x
H v y K yy y
H v z K zz z
( v x ) H H H ( K xx ) [ K xx (K xx )] x x x x x x x
§5 描述地下水运动的数学模型及解算方法
一、各向异性含水层中地下水三维流的基本微 分方程的推导 二、地下水运动微分方程的各种形式 三、地下水运动数学模型的建立及求解
§5 描述地下水运动的数学模型及解算方法
一、各向异性含水层中地下水三维流基本微分方程的推导 为反映含水层地下水运动的普遍规律，研究选定在各向 异性多孔介质中建立地下三维不稳定流动连续性方程。 水均衡的基本思想，对某一研究对象：
描述地下水运动的数学模型及解算方法二地下水运动微分方程的各种形式zzyyxxzzyyxx使潜水面边界处理的简单化直接近似地在微分方程中处理dsdh此时1潜水面比较平缓等水头面呈铅直水流基本水平可忽略渗流速度的垂直分量v2隔水底板水平铅垂剖面上各点的水头都相等各点的水力坡度和渗流速度都相等sin可以近似地用tg代替此即著名的dupuit假设
m d( )

m
1 d d ( )

2
H 0
n 2
——隔水边界
第三类边界条件 H aH b n
例：弱透水边界
K H Hn H 0 n m1 / K1
溶质运移问题的边界条件
第一类边界条件
c(x,
y, z,t) 1

c1(x,
y, z,t)
——给定浓度边界
第二类边界条件 c
Di, j x j ni 2 f2 (xi , t)
u(x, y, z,t) t0 0(x, y, z)
• 2、边界条件
第一类边界条件 u(x, y, z,t) 1 1(x, y, z,t)
第二类边界条件
u n
2
1(x, y, z,t)
第三类边界条件
u



u n
3
3x,
y, z,t
水流问题的边界条件
Reynolds数小于1~10
• 有些情况下，用液体压强表示更为方便
– 例如：油水两相流动
vx

K
H x
vy

K
H y
vz

K
H z
K g k
H z p
g

k p
vx



x
v y


k
p y
vz


k


K ( d
)
dhc
C

t

x
K( )
x


y
K
(

)
y


z
K (

安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
*范围值：n×10-3~ n×10-5； 范围值：0.05~ 0.30。实际测出的值往往小于理论值。
上述两参数之间的不同，还在于潜水含水层存在滞后疏干现象。 弹性释水与重力给水: 对于含水层而言，由于受埋藏条件的限制，抽水时，水的给 出存在着不同。 潜水含水层在抽水过程中，大部分水在重力作用下排出，疏干作用于水位变动带（
为反映含水层地下水运动的普遍规律，我们选定在各向异性多孔介 质中建立地下三维不稳定流动连续性方程。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
由于渗流场中各点的渗流速度大小、方向都不同，为了反映液体运动的 质量守恒关系，需要在三维空间中建立微分方程形式表达的连续性方程。
则有：
即：
将
代入整理得：
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
所以有
上式为三维流微分方程，也可写成：
物理意义：渗流空间内任一单位体积含水层在单位时间内流入与流出该体 积含水层中的弹性水量的变化量，即单位体积含水层的水量均衡方程。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
= =
由含水层状态方程，
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
因为 则可得到： 所以有 ，Z为定值，则
于是连续性方程变为：

第四章 地下水运动的数值模型解析解虽然具有精确可靠的特点，但采用解析解反映自然状态和复杂人类活动干扰下的地下水运动是相当困难的。

因此，当含水层的条件严重偏离现有解析模型的简化假设时，人们通过数值模型来获得近似的地下水流场及演变趋势。

第一节 地下水流数值方法概述地下水流的数学模型采用偏微分方程描述地下水流的时间和空间连续状态，而数值模型则是采用离散（非连续）时空模型中水头的分布与演变对数学模型进行近似描述。

从精确数学模型到近似数值模型的转化，虽然会损失一些精度，但使复杂地下水流问题的分析得以通过机械计算实现，而且误差也是可控的。

把偏微分方程求解的数值方法引入到地下水流问题的求解始于20世纪70年代，主要方法包括有限差分法、有限元法和边界元法，此后又发展了有限分析法、多重网格法和无网格法等。

这些方法的共同特点是将模型空间及边界离散为由一系列的节点以及联系这些节点的单元（无网格法除外），含水层的水头在这些节点上定义，从而实现了水头分布空间连续函数向离散变量的转化，表示为2121211122111221202()02()02()002(0)k k k k k k k k k k k k k k k k k k k k k k k kkk f f f f a b c e x L x x t t t t f x f f f f a b c e x L x x t t f f f f a b c x L e x xd f dfe ef a b f c x L dx dx t t f x u---------∂∂-++=<<∂∂∆∆=-∂∂-++=<<∂∂∆∆∂∂=+++<<∂∂+-++=<<∆∆==，，，，{}(,,);1,2,3,,p H x y z H p M ⇒=⋅⋅⋅ （4.1.1）式中；H 为含水层的水头；x 、y 、z 为空间坐标；p 为数值模型的节点；M 为节点的数目。

安徽理工大学 地球与环境学院 水资源与规划系
Ch2 地下水渗流微分方程及数学模型
*范围值：n×10-3~ n×10-5； 范围值：0.05~ 0.30。实际测出的值往往小于理论值。
上述两参数之间的不同，还在于潜水含水层存在滞后疏干现象。 弹性释水与重力给水: 对于含水层而言，由于受埋藏条件的限制，抽水时，水的给 出存在着不同。 潜水含水层在抽水过程中，大部分水在重力作用下排出，疏干作用于水位变动带（
在水位下降为Δ H时，有
即作用于固体骨架上的力增加了H。
。
作用于骨架上力的增加会引起含水层的压缩，而水压力的减少将导 致水的膨胀。
含水层本来就充满了水，骨架的压缩和水的膨胀都会引起水从含水 层中释出，前者就象用手挤压充满了水的海绵会挤出水—样。
地下水动力学
安徽理工大学 地球与环境学院 水资源与规划系
Vv＝nVb；Vs＝(1-n)Vb
式中 ——多孔介质固体颗粒压缩系数，表示多孔介质中固 体颗粒本身的压缩性的指标，s<<p； ——多孔介质中孔隙压缩系数 （Compressibility of the pores of a porous medium），表示多孔介质中孔 隙的压缩性的指标。 n——多孔介质的孔隙度。 因 ，故 。
Ch2 地下水渗流微分方程及数学模型
§2-1 渗流连续方程
一、含水层的状态方程 含水层的状态方程主要包括地下水的状态方程和多孔介质的状态方程。 1、地下水的状态方程 Hooke定律：
式中：E——体积弹性系数（体积弹性模量），20℃时，
E=2.1×105N/cm2。其倒数为压缩系数。 等温条件下，水的压缩系数(coef. of compressibility)为
多孔介质压缩系数的表达式为：

§6 渗流基本微分方程
§6 渗流基本微分方程
2、假设 除与承压含水层基本微分方程有相同假设条件外： （1）当弱透水层的渗透系数K1比主含水层的渗透系数 K小很多时，近似认为水基本上是垂直地通过弱透水 层，折射90º 后在主含水层中基本上是水平流动的。 （如K1与K相差较小时，用等效渗透系数，非越流） （2）主含水层中水头看作是整个含水层厚度上水头的 平均值，即： 1 M H H ( x, y , t ) H ( x, y, z , t )dz M 0 （3）和主含水层释放的水及相邻含水层的越流量相比 ，弱透水层本身释放的水量小到可以忽略不计。
§6 渗流基本微分方程
（2）渗流场中任何一个局部，都必须满足质量守恒和 能量守恒。 4、数学意义 表示渗流空间内任一点任一时刻的渗流规律。 5、讨论 （1）各向同性介质
∂ ∂H ∂ ∂H ∂ ∂H ∂H ( K )+ ( K )+ ( K ) =μ s ∂x ∂x ∂y ∂y ∂z ∂z ∂t
§6 渗流基本微分方程
上次课复习
1、渗流连续性方程—地下水质量守恒定律 （1）表达式
ρ v y ) ∂( ∂( ρ v x ) ∂( ρ vz ) ∂ [ + + ] Δ xΔ yΔ z = ( ρ nΔ xΔ yΔ z ) ∂x ∂y ∂z ∂t
（2）物理含义 某一渗流场中，流入流出单元体的质量差等于单元 体内液体质量的变化。 （3）实质（机理） 水头变化引起含水层弹性释水（贮水）
§6 渗流基本微分方程
3、微分方程的物理意义
∂ ∂H ∂ ∂H ∂ ∂H ∂H ( K xx )+ ( K yy )+ ( K zz ) =μ s ∂x ∂x ∂y ∂y ∂z ∂z ∂t

H H * H T W T x x y y t
H H * H T yy W T xx x x y y t
H
2
x
2
v x v y v z H x y z x y z g n t x y z
根据Darcy定律： 1. 在各向同性介质中，有：
vx K H x ; vy K H y ; vz K H z

p t
x y z
于是连续性方程变为：
v x v y v z p n x y z x y z y z t x
将
p t
化为
H z
H t
：
，故有：p=γ（H-z）=ρg（H-z）
因为
p t
p

g
p t
H t
Hg
H t
t
zg
t
g
H t
H z g
t
或：
g
p
t
p t
将dρ=ρβdp代入，得： p g H 即，
t 1 p t
g
H t
p
p t
n x y z t
消去Δt得
v x v y v z n x y z x y z y z t x
此式为渗流的连续性方程（研究地下水运动的基本方程）。
§1—7 承压水运动的基本微分方程
由水的压缩系数： 得： V V dp 所以，dρ=ρβdp 前面给出了含水层厚度Δz和孔隙度n随压力p的变 化关系： d(Δz)= Δzαdp ；dn=(1-n) αdp 式中：α为多孔介质压缩系数。 将三式代入连续方程右端项得：

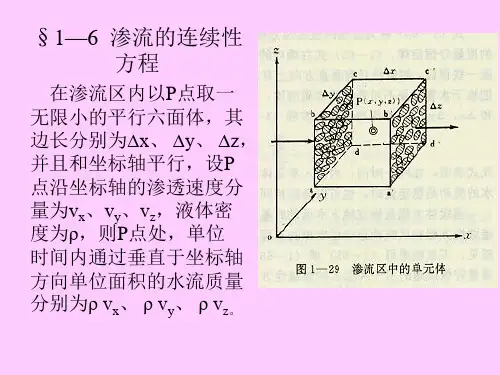
渗流的基本方程渗流是指在多孔介质中流动的现象，是水文地质学中的重要研究内容之一。

多孔介质是由许多微小的孔隙组成的，例如岩石、土壤、砂土等。

渗流的基本方程描述了多孔介质中流动的物理过程，是渗流理论的核心。

渗流的基本方程可以通过守恒原理来推导，主要包括质量守恒方程和达西-里查德森方程。

质量守恒方程是描述渗流速度分布的方程，它表达了单位时间内通过单位面积的流体质量与孔隙介质中流体储量的变化率之间的关系。

在水平地层中，质量守恒方程可以简化为二维平面问题。

其数学表示为：div（φηρv）= ∂(φηρ)/∂t + div(φηρvq)其中，div表示散度，φ表示孔隙度，η表示介质有效渗透率，ρ表示流体密度，v表示流体速度矢量，q表示流体产生或消失速率。

达西-里查德森方程则是描述渗透压梯度与渗流速度之间的关系。

达西-里查德森方程是根据流体密度不变、黏性流体和渗透性线性增大的假设下推导出来的，经过实验验证，在一定渗透条件下仍然适用。

其数学表示为：v = -K∇h其中，v表示流体速度，K表示渗透性系数，∇h表示渗透压梯度。

通过质量守恒方程和达西-里查德森方程，可以进一步推导得到渗流方程，用于描述多孔介质中任意截面内渗流速度和渗透压梯度之间的关系。

渗流方程可以用一维形式表示为：q = -K∇h其中，q表示单位面积内的流量，K表示有效渗透率，∇h表示渗透压梯度。

渗流方程是多孔介质中流动现象的数学表达式，通过解这个方程，可以求解出多孔介质中的流动速度分布、渗透压梯度分布等有关渗流过程的重要参数。

在实际应用中，渗流方程可以用来预测地下水位变化、估算地下水资源、探测地下水污染传播等。

渗流方程的求解通常依赖于一些边界条件和初值条件。

边界条件是指在孔隙介质的边界上给定的约束条件，如给定流速、压力等。

初值条件是指在求解过程中给定的初始条件。

总之，渗流的基本方程是描述多孔介质中流动现象的数学表达式，包括质量守恒方程和达西-里查德森方程。

地下水渗流偏微分方程英文回答：Groundwater flow is a complex process that can be described by partial differential equations (PDEs). These PDEs are used to model the movement of water through porous media underground. One commonly used PDE for groundwater flow is the groundwater flow equation, also known asDarcy's law.Darcy's law states that the rate of groundwater flow is proportional to the hydraulic gradient, which is the change in hydraulic head per unit distance. Mathematically, it can be written as:Q = -K A (dh/dl)。

where Q is the discharge rate of groundwater flow, K is the hydraulic conductivity of the porous medium, A is the cross-sectional area through which the groundwater flows,dh/dl is the change in hydraulic head per unit distance.This equation can be used to solve for the groundwater flow in a given system. For example, let's consider a scenario where we have a groundwater well that is pumping water out of an aquifer. The hydraulic conductivity of the aquifer is 10 m/day, and the cross-sectional area of the well is 1 m^2. If the hydraulic head at the well is 10 m higher than the hydraulic head at a distance of 100 m away, we can use Darcy's law to calculate the discharge rate of groundwater flow:Q = -10 1 (10/100) = -1 m^3/day.This means that the well is pumping out 1 cubic meter of groundwater per day.Another commonly used PDE for groundwater flow is the groundwater flow equation in transient conditions, which takes into account the change in hydraulic head over time. This equation can be written as:∂h/∂t = S ∇^2h + Q.where ∂h/∂t is the rate of change of hydraulic head with respect to time, S is the specific storage of the aquifer, ∇^2h is the Laplacian operator of the hydraulic head, and Q is the source/sink term.This equation is used to model the transient behaviorof groundwater flow, such as the response of an aquifer to pumping or recharge events. By solving this equation, wecan predict how the hydraulic head will change over time in a given system.For example, let's consider a scenario where we have a recharge event in an aquifer. The specific storage of the aquifer is 0.001 m^(-1), and the recharge rate is 0.1 m/day. If we want to determine how the hydraulic head will change over time, we can solve the groundwater flow equation in transient conditions:∂h/∂t = 0.001 ∇^2h + 0.1。

由于坡角θ很小，用 tan dH dx 代替 sin dH ds
vx
K
dH dx
(3.4.3)
Qx
KhB
dH dx
当底面水平，z以底面为原点，则近似有h=H
(3.4.4)
20
在Dupuit假设下建立的，只适用于缓变运动，在vz大 的地段不适用。
例如在有入渗的潜水分水岭地段，渗出面附近和铅 直的隔水边界附近。
t
用奥-高公式
v nd v d
x
， y
， z
v
t
d
0
v 0
t
6
渗流连续性方 程的讨论
vx
x
vy
y
vz
z
1 Vb
Vv
t
1) 稳定渗流：
vx
K
H x
vy
K
H y
vz
K
H z
渗流场不随时间变化时，右端项为0
1 Vb
Vv
t
0
通常情况：
(h H ) W dH
x x K K dt
(3.4.10)
二维情况推导类似
(h H ) (h H ) W dH
x x y y K K dt
(3.4.11)
22
潜水流的基本微分方程
当隔水底板水平时，将高程基准设在 底板面，h=H，方程变为：
(h h) (h h) W dh
27
3.5 定解条件
定解条件包括边界条件和初始条件。 1．边界条件
渗流区域几何边界上的水力性质。 （边界并不一定是外边界！） 2．初始条件 给定(t=0)时刻的渗流场内各点的水头值
28
应当注意，给定水头边

H H Q x KhB , Q y KhB x y
§6 渗流基本微分方程
3、 Boussinesq方程—潜水基本微分方程 （1）假设条件 ①符合Dupuit假设； ②忽略水的压缩和骨架的压缩—不符合弹性释（贮）水 规律。原因：潜水面是个自由面，相对压强为0； ③潜水含水层隔水底板水平； ④潜水面存在水量的垂向交换W（ W为潜水面处单位水 平面积、单位时间的入渗量, W> 0 ，入渗；W< 0 ， 蒸发） 。
（6）各向同性柱坐标系（x = rcosθ、y = rsin θ） 1 H 1 2 H 2 H s H (r ) 2 2 2 r r r r K t z 2 H 1 H 1 2 H 2 H s H 或 2 2 2 2 K t r r r r z
导压系数（a）—压力传导系数 描述含水层水头变化的传导速度的参数，其数值等 于含水层的导水系数与贮水系数之比或渗透系数与贮 水率之比。
a=
T
μ
*
=
K
μs
（2）均质各向同性介质
∂2H ∂2H ∂2H μ s ∂H 1 ∂H + 2 + 2 = = 2 K ∂t a ∂t ∂x ∂y ∂z
§6 渗流基本微分方程
§6 渗流基本微分方程
（7）有源（流入）汇（流出）项W或 一般指垂向补给或排泄。 和W分别为三维流和平面二维流的源汇。分别定义 为单位体积含水层和单位水平面积含水层柱体中，单 位时间内产生（为正值）或消耗（为负值）的水量。
∂ ∂H ∂ ∂H ∂ ∂H ∂H ( xx K )+ ( yy K )+ ( zz K )+W =μ s ∂x ∂x ∂y ∂y ∂z ∂z ∂t

渗流力学基本方程渗流力学是研究岩石、土壤等多孔介质中流体运动和物理现象的学科。

渗流力学基本方程是描述多孔介质中流体运动的数学方程组，它是研究渗流问题的基础。

渗流力学基本方程由质量守恒方程和达西定律组成。

质量守恒方程是指在多孔介质中，流体的质量在空间和时间上保持不变。

达西定律是指渗流速度与渗流力的关系，它描述了多孔介质中流体运动的规律。

质量守恒方程是渗流力学中最基本的方程之一。

它可以表示为：∂(ϕρ)/∂t + ∇·(qρ) = S，其中ϕ是多孔介质的孔隙度，ρ是流体的密度，t是时间，q是流体的渗流速度，S是源项。

这个方程描述了多孔介质中流体的密度随时间和空间的变化情况，以及流体的流动和质量的变化。

达西定律是描述多孔介质中渗流速度与渗流力的关系的方程。

它可以表示为：q = -K∇h，其中q是流体的渗流速度，K是多孔介质的渗透性，h是流体的流动势。

这个方程表明，渗流速度与渗流力负梯度成正比，且与多孔介质的渗透性有关。

渗透性越大，流体的渗流速度越大。

渗流力学基本方程还可以通过引入渗透率、渗透率张量等概念，进一步描述多孔介质中流体运动的规律。

渗透率是描述多孔介质对流体渗流的阻力的参数，它与多孔介质的孔隙度、孔隙结构、流体粘度等因素有关。

渗透率张量是描述多孔介质中渗透率随不同方向的变化的张量。

渗流力学基本方程在地下水资源开发、地下水污染治理、石油开采、岩土工程等领域具有重要的应用价值。

通过建立和求解渗流力学基本方程，可以预测多孔介质中流体的运动规律，指导工程设计和实际操作。

渗流力学基本方程是描述多孔介质中流体运动的基本数学方程组。

通过研究和解析这些方程，可以深入理解多孔介质中流体运动的规律，为工程实践提供理论依据和技术支持。

渗流力学基本方程在地下水资源开发、地下水污染治理、石油开采、岩土工程等领域具有广泛的应用前景。

地下水渗流耦合力学数值模型
在地下水渗流耦合力学数值模型中，地下水渗流方程描述了地
下水在多孔介质中的流动过程。

该方程基于达西定律和连续介质力
学原理，考虑了渗透性、孔隙度和渗透率等参数，通过计算流体的
速度和压力分布来描述地下水的运动。

与此同时，围岩力学方程描述了围岩的应力和变形行为。

这些
方程基于弹性力学理论或塑性力学理论，考虑了围岩的弹性模量、
泊松比、强度和变形特性等参数。

通过计算围岩的应力和变形分布，可以了解围岩的稳定性和变形情况。

地下水渗流耦合力学数值模型的基本原理是将地下水渗流方程
和围岩力学方程耦合在一起，形成一个联立的数学模型。

模型通过
离散化方法，如有限元法或有限差分法，将复杂的连续问题转化为
离散的代数方程组。

然后，通过迭代计算的方式，求解这个方程组，得到地下水渗流和围岩的应力和变形场。

地下水渗流耦合力学数值模型在工程领域有广泛的应用。

例如，在地下水资源开发中，可以用于模拟地下水开采对周围围岩的影响，评估地下水资源的可持续利用性。

在地下工程中，可以用于分析地
下水渗流对围岩稳定性的影响，评估工程的安全性。

在地下储气库或储水库设计中，可以用于模拟地下水渗流和围岩变形的过程，优化工程设计。

总之，地下水渗流耦合力学数值模型是一种重要的数值模拟方法，可以帮助我们理解地下水和围岩之间的相互作用，为地下工程和地下水资源管理提供科学依据。

1. 三维渗流方程1.1 连续性方程单元体水分增量=净流入速率×时间增量⎪⎭⎫ ⎝⎛∂∂-⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂-=∂∂dz z V dxdy dy y V dxdz dx x V dydz t n dxdydz z y x ρρρρ)( ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂z V y V x V t n z y x ρρρρ)( 1.2 动力方程流速与水力梯度的关系(坐标轴与渗透主轴一致);xH K V xx x ∂∂-=;y HK V yyy∂∂-=zH K V zzz ∂∂-= 1.3 贮存量的变化有效应力原理:hdH dp d p ρσσσ-=-='⇒-=' 单元体水分增量：ρρρnd dn n d +=)(有效应力减小, 骨架膨胀, 孔隙率n 增加 孔隙水压强增大，水的密度增大dH S gdH n n d s ρρβαρρ=+=])[()( 贮水率:)(βαρn g S s +=1.4 三维渗流方程忽略地下水密度空间变化的影响⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂z H K z y H K y x H K x t H S zz yy xx s2. 承压含水层方程2.1 连续性方程单元面水分增量=净流入速率×时间增量wdxdy dy y q dx dx x q dy b t n dxdy y x +⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫⎝⎛∂∂-=∂∂ρρρ)( w y q xq t n by x +⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=∂∂ρρρ)( 2.2 动力方程单宽流量与水力梯度的关系 ;x H T x H bK q xx xx x ∂∂-=∂∂-=yH T y H b K q yy yy y ∂∂-=∂∂-=导水系数:b K T b K T yy yy xx xx ==;2.3 贮存量的变化 tH S t H b S t n b s ∂∂=∂∂=∂∂ρρρ)( 贮水系数 b S S s =(弹性给水度) 2.4 承压水平面渗流方程忽略地下水密度空间变化的影响 w y H Ty x H T x tH S yyxx+⎪⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂ 均质各向同性w y H xH a t H+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂2222 2. 潜水含水层方程2.1 连续性方程单元面水分增量=净流入速率×时间增量wdxdy dy y q dx dx x q dy t M dxdy y x +⎪⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫⎝⎛∂∂-=∂∂ρρ w y q xq t My x +⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=∂∂ρρ 2.2 动力方程Dupuit 假定：忽略垂向水流速率的影响 单宽流量与水力梯度的关系;)(x H z h K q b xx x ∂∂--=yH z h K q b yy y ∂∂--=)( 2.3 贮存量的变化垂直柱：从底板到地面⎰⎰+-==00)(z hb z z dz z h n dz M bθθ给水度：μ (重力给水度); th t M ∂∂=∂∂μ2.4 潜水平面渗流方程忽略地下水密度空间变化的影响 Boussinesq 方程： w y h z h K y x h z h K x t h b yy b xx +⎥⎦⎤⎢⎣⎡∂∂-∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂=∂∂)()(μxzb ρV xdx xV V xx ∂∂+ρρ dxwyxz ρV xdx xV V xx ∂∂+ρρdxdydzxzhρV xdx xV V xx ∂∂+ρρ dxw z b。

Q=
p k (2 H - s0 ) s0 (2 H - s0 ) s0 = 1.36k R R ln lg r0 r0
• 公式表明潜水完整井的出水量Q与井内水位降深s0的二次 方成正比，这就决定了Q与s0间的抛物线关系。即随着s0 值的增大，Q的增加值将越来越小。
5.3.2地下水流向承压水完整井
根据裘布依稳定流理论，在承压完整 井中抽水时，经过一个相当长的时段， 从井内抽出来的水量和井内的水头降 落同样均能达到稳定状态，这时在井 壁周围含水层内就会形成抽水影响范 围，这种影响范围可以由承压含水层 中的水头的变化表示出来，承压水 头线的变化具有降落漏斗的形状，
i H q k H k i和Δ si可从流网图中量出。 n i 1 si
m
H
H n ，Δ
si
si
n
i i 1 si
m
m m q kH kH 取各网格的边长比例为常数、并等于1，则： n s n
自己看P52[例5.2] 。
• 5.3 地下水向完整单井的稳定渗流运动 • 提取地下水的工程设施称为取水构筑物。当取水构筑物 中地下水的水位和抽出的水量都保持不变，这时水流称为稳 定渗流运动。
。见图5.2。
n
• 渗透流速与水力坡度 H H J • 渗流区内各点的水力坡度可从下式求出： s ns ， • 式中ΔH为该处网格两边相邻等势线的水头差 s 为该网格内流线长度，渗流区内各点的渗透流速为 u kJ H 渗流量: qi k H i kH i H
• 从图5.5亦可看出：地下水向潜水完整井的流动过程中水 力坡度J是个变数，但任意断面处的水力坡度J均可表示为： J=dy/dx • 故地下水通过任意过水断面B—B/的运动方程为：