第5章地下水的稳定渗流运动
- 格式:ppt
- 大小:2.08 MB
- 文档页数:39
第五章地下水运动的基本规律5. 1 港流基本概念渗流一地卞水在岩石空隙中的运动称为渗流(渗透,地下径流)。
渗流场一发生渗流的区域。
层流运动——水的质点作有秩序的、互不混杂的流动。
紊流运动——水的质点无秩序的、互相混杂的流动。
稳定流一各个运动要素(水位、流速、流向等)不随时间改变的水流运动。
非稳定流——运动要素随时间变化的水流运动。
地卜•水总是从能量校高处流向能量较低处。
能态差异是地卜水运动的驱动力。
地下水的机械能包括动能和势能,水力学中用总水头(hydiaulic head)H表示,水总是从总水头高的地方流向总水头低的地方。
5. 2重力水运动的基本规律1.达西定律(Darcy'sLaw)1856年达西通过实验得到达西定律。
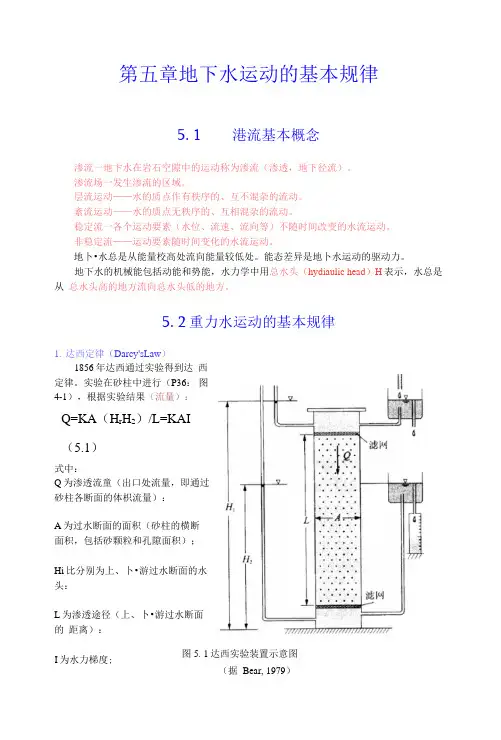
实验在砂柱中进行(P36:图4-1),根据实验结果(流量):Q=KA(H r H2)/L=KAI(5.1)式中:Q为渗透流童(出口处流量,即通过砂柱各断面的体枳流量):A为过水断面的面积(砂柱的横断面积,包括砂颗粒和孔隙面积);Hi比分别为上、卜•游过水断面的水头:L为渗透途径(上、卜•游过水断面的距离):图5. 1达西实验装置示意图I为水力梯度;(据Bear, 1979)K 为渗透系数。
由水力学:Q=vA达西定律也可以另一种形式表达(流速): 由公式(5.1)及Q=\A 得:v=KI式中:£ --- 渗透流速,m/d, cm/s ;K ----- 渗透系数,nVd, cm/s :I —水力梯度,无量纲(比值)。
具体到实际问题:计算流最:H _ HQ =川F ---------- (单位一•般为:m 3/d, L/s)L微分形式:式中:负号表示水流方向与水力梯度方向相反,水流方向(坐标方向):由水位高一 低:而水力梯度方向:由等水位线低一高。
在三维空间中(向量形式):■\v = -K x ^-i-K v ^- j-K,-51k = -KgradH dy dz或V = -KVH ,式中:K 一为渗透系数张量:gradH =更 i +更* 更 Amdy dz若用标量表示,V 的三个分最分别为:得到 v=Q/A(对地下水也适用)(5.2) (5.3)v=-KdH £Vy= ~K - dy—呻**■ dz2. 渗透流速(V ) (seepage velocity, Daicy velocity )与实际流速(u )渗透流速一水流通过整个过水断面(包括砂砾和孔隙)的流速。










岩土工程中的地下水渗流与稳定性岩土工程是土力学与岩石力学的交叉学科,研究土壤与岩石的力学性质与工程应用。
地下水渗流与稳定性是岩土工程中一个重要且复杂的问题。
地下水渗流是指地下水在岩土体中的流动现象。
在岩土工程中,地下水渗流是一个既有利也有害的因素。
利的一面是地下水能够形成有效的荷载和增强土体的稳定性。
在土体中,加入一定的水分能改善土体的力学性质,增加土体的抗剪强度,提高土体的受力性能。
然而,地下水渗流也可能带来一些不良的影响。
高含水量的土体容易软化,导致土体的变形与失稳。
地下水还可能通过长期的冲刷与侵蚀作用,导致土体的沉陷、裂缝甚至坍塌。
地下水的渗流规律对岩土工程的稳定性和设计起着至关重要的作用。
岩土体中的地下水渗流可以通过各种方法进行分析与计算。
其中,最常用的方法是通过数学模型来解决。
渗流模型可以通过碗状基因型,模拟渗流路径和渗流速度的分布。
通过观测地下水位、水质以及取样分析等,可以得到渗流模型的参数。
在地下水渗流与稳定性问题中,岩土工程师关注的重点是如何控制和管理地下水,以确保土体的稳定性。
一个常用的方法是在工程设计中加入地下水防护措施,例如设置排水系统、抽水井等。
另外,合理的排水则可以减少水分对土体力学性质的影响,并提高土体的稳定性。
为了保证地下水渗流与稳定性的研究与设计的准确性,岩土工程师还需要进行现场勘察与实测。
现场勘察可以提供地下水位、土体含水量、岩土体性质与渗透性等相关数据。
实测可以通过孔隙水压力计、土壤水分计等设备,对地下水的压力与含水量进行测量。
这些数据将为岩土工程师提供准确的参数值,以便进行地下水渗流与稳定性的计算与分析。
岩土工程中地下水渗流与稳定性问题的研究还在不断发展中。
随着科技的进步,新的理论、模型、方法和工具在岩土工程中得到了广泛的应用。
同时,对于地下水渗流与稳定性问题的研究也愈加深入,为岩土工程师们提供了更多的理论依据和实用技术。
总之,地下水渗流与稳定性是岩土工程中一个重要而复杂的问题。
地下水流的渗流力学分析地下水是地球表层下方的水体,由于地壳中的孔隙和裂隙中填充了水分,形成地下水层。
地下水流是指地下水在地下岩层中的运动过程。
为了更好地理解地下水流的运动特性,科学家们进行了渗流力学分析。
一、地下水流的渗流力学基础渗流力学研究地下水流动的原因、特征和规律,是岩石力学和流体力学的交叉学科。
渗流力学的基本原理是达西定律,即渗流速度与渗透率成正比,与流体密度和粘度成反比。
根据达西定律,我们可以计算地下水的渗流速度和渗透率,以及地下水与地下岩层之间的关系。
二、地下水流的物质平衡方程地下水流的物质平衡方程是描述地下水流动的重要工具。
该方程描述了地下水流动过程中水量的变化。
它是根据质量守恒定律推导出来的,可以表达为:∇·(qρ) + ∂(ρΦ)/∂t = S其中,q是地下水流速向量,ρ是地下水密度,Φ是地下水位势,t是时间,S是外部水源和汇水源的贡献。
这个方程可以用来分析地下水在不同区域的流动情况,并预测地下水流动的趋势。
三、地下水流的渗透率计算渗透率是描述岩层渗透性的参数,是测量岩层渗流能力的指标。
地下水流的渗透率计算可以通过实验或野外测试获得。
其中一种常用的方法是Lugeon试验,该试验通过注入标准单位水量来测量注水速度和水压变化,进而计算出地下水的渗透率。
四、地下水流的流动特征地下水流的流动特征包括流速分布、流向、流线和流量等。
地下水流速分布的分析可以通过建立二维或三维数值模型,使用流体力学方程进行数值模拟来实现。
借助计算机技术,科学家们可以获取地下水流动的详细信息,预测地下水流动的趋势。
五、地下水流的影响因素地下水流的流动过程受到众多因素的影响,主要包括岩性、裂隙特征、孔隙度和渗透率等。
岩性是决定地下水流动性质的基本因素,不同的岩性具有不同的渗透性。
裂隙特征是影响地下水流速和渗透率的重要因素,对于裂隙性岩石来说,渗透率的计算需要考虑裂隙的数量、宽度和方向等因素。
孔隙度是描述岩石中可存储和运移水的能力,是衡量地下水资源的关键指标。