第七章 虚拟变量和随机解释变量 (2)
- 格式:doc
- 大小:278.00 KB
- 文档页数:11

第七章虚拟变量第一节虚拟变量的引入一、什么是虚拟变量前面几章介绍的解释变量都是可以直接度量的,称为定量变量。
如收入、支出、价格、资金等等。
但在现实经济生活中,影响应变量变动的因素,除了这些可以直接获得实际观测数据的定量变量外,还包括一些无法定量的解释变量的影响,如性别、民族、国籍、职业、文化程度、政府经济政策变动等因素,他们只表示某种特征的存在与不存在,所以称为属性变量或定性变量。
属性变量:不能精确计量的说明某种属性或状态的定性变量。
在计量经济模型中,应当包含属性变量对应变量的影响作用。
那怎么才能把定性变量包括在模型中呢?属性变量通常是非数值变量,直接纳入回归方程中进行回归,显然是很困难的。
为此,人们采取了一种构造人工变量的方法,将这些定性变量进行量化,使其能与定量变量一样在回归模型中得以应用。
由于定性变量通常是表明某种特征或属性是否存在,如性别变量中以男性为分析基础的话,那就只有男性、非男性;政策变动变量中以政策不变为基准,则有政策不变,和政策变动;至于有两种以上的状态的话,比如学历分高中,本科,本科以上等等,我们又怎么办呢?把疑问留到后面去解决。
既然定性变量只有存在或不存在两种状态,所以量化的一般方法是取值为0或1。
称为虚拟变量。
虚拟变量:人工构造的取值为0或1的作为属性变量代表的变量。
一般常用D表示。
D=0,表示某种属性或状态不存在D=1,表示某种属性或状态存在比如前面说的性别变量,以男性为基准,则当样本为男性时,虚拟变量取0,当样本为女性时,则虚拟变量取1。
当虚拟变量作为解释变量引入计量经济模型时,对其回归系数的估计和统计检验方法都与定量解释变量相同。
二、虚拟变量的作用1、作为属性因素的代表,如,性别、种族等2、作为某些非精确计量的数量因素的代表,如:受教育程度、年龄段等;3、作为某些偶然因素或政策因素的代表,如战争、911等。
4、时间序列分析中作为季节(月份)的代表(比如对某些明显有淡季、旺季之分的产品)5、分段回归,研究斜率、截距的变动;6、比较两个回归模型;7、虚拟应变量概率模型,应变量本身是定性变量(比如你研究某产品的购买率,应变量本身就是买或不买)三、虚拟变量的设置规则1、虚拟变量D取值为0,还是取值为1,要根据研究的目的决定。

第7章含有定性信息的多元回归分析:二值(或虚拟)变量7.1复习笔记一、对定性信息的描述定性信息通常以二值信息的形式出现。
在计量经济学中,二值变量最常见的称呼是虚拟变量。
二、只有一个虚拟自变量1.只有一个虚拟自变量的简单模型考虑如下决定小时工资的简单模型:001wage female educ uβδβ=+++用0δ表示female 的参数,以强调虚拟变量参数的含义。
假定零条件均值假定() 0E u female educ =,成立,那么:()()0| 1 |0 E wage female educ E wage female educ δ==-=,,由于female=1对应于女性且female=0对应于男性,所以可以简单的把模型写为:()()0| | E wage female educ E wage male educ δ=-,,这种情况可以在图形上描绘成男性与女性之间的截距变化。
男性线的截距是0β,女性线的截距是00βδ+。
由于只有两组数据,所以只需要两个不同的截距。
这意味着,除了0β之外,只需要一个虚拟变量。
因为female+male=1,意味着male 是female 的一个完全线性函数,如果使用两个虚拟变量就会导致完全多重共线性,这就是虚拟变量陷阱。
2.当因变量为log(y)时,对虚拟解释变量系数的解释在应用研究中有一个常见的设定,当自变量中有一个或多个虚拟变量时,因变量则以对数形式出现。
在这种情况下,此系数具有一种百分比解释。
当log(y)是一个模型的因变量时,将虚拟变量的系数乘以100,可解释为y 在保持所有其他因素不变情况下的百分数差异。
当一个虚拟变量的系数意味着y 有较大比例的变化时,可以得到精确的百分数差异。
一般地,如果1ˆβ是一个虚拟变量(比方说x 1)的系数,那么,当log(y)是因变量时,在x 1=1时预测的y 相对于在x 1=0时预测的y,精确的百分数差异为:()1ˆ100exp 1β⎡⎤⋅-⎣⎦三、使用多类别虚拟变量1.在方程中包括虚拟变量的一般原则如果回归模型具有g 组或g 类不同截距,那就需要在模型中包含g-1个虚拟变量和一个截距。


习题7.1 解释概念(1)分类变量 (2)定量变量 (3)虚拟变量 ( 4)虚拟变量陷阱 (5)交互项(6)结构不稳定 (7)经季节调整后的时间序列答:(1)分类变量:在回归模型中,我们对具有某种特征或条件的情形赋值1,不具有某种特征或条件的情形赋值0,这样便定义了一个变量D :1,0,D ⎧=⎨⎩具有某种特征不具有某种特征我们称这样的变量为分类变量。
(2)具有数值特征的变量,如工资、工作年数、受教育年数等,这些变量就称为定量变量。
(3)在回归模型中,我们对具有某种特征或条件的情形赋值1,不具有某种特征或条件的情形赋值0,这样便定义了一个变量D :1,0,D ⎧=⎨⎩具有某种特征不具有某种特征 我们称这样的变量为虚拟变量(dummy variable )。
(4)虚拟变量陷阱是指回归方程包含了所有类别(特征)对应的虚拟变量以及截距项,从而导致了完全共线性问题。
(5)交互项是指虚拟变量与定量变量相乘,或者两个定量变量相乘或是两个虚拟变量相乘,甚至更复杂的形式。
比如模型:12345i i i i i i i household lwage female married female married u βββββ=++++⋅+female married ⋅就是交互项。
(6)如果利用不同的样本数据估计同一形式的计量模型,可能会得到1β、2β不同的估计结果。
如果估计的参数之间存在着显著性差异,就称为模型结构不稳定。
(7)一些重要的经济时间序列,如果是受到季节性因素影响的数据,利用季节虚拟变量或者其他方法将其中的季节成分去除,这一过程被称为经季节调整的时间序列。
7.2 如果你有连续几年的月度数据,为检验以下假设,需要引入多少个虚拟变量?如何设定这些虚拟变量?(1)一年中的每一个月份都表现出受季节因素影响;(2)只有2、7、8月表现出受季节因素影响。
答:(1)对于一年中的每个月份都受季节因素影响这一假设,需要引入三个虚拟变量。


在 Stata 中,虚拟变量(Dummy Variable)通常用于表示一个分类变量的不同水平(categories)或组。
虚拟变量是二进制的,通常被用来在回归等分析中引入分类变量的效应。
下面是关于 Stata 中虚拟变量的解释:创建虚拟变量:在 Stata 中,可以使用tabulate命令创建虚拟变量。
假设有一个名为category的分类变量,可以使用以下命令创建虚拟变量:这将为category变量的每个水平生成一个虚拟变量,变量名为dummy后加上水平的标签。
虚拟变量的解释:虚拟变量通常用于回归分析中,以表示分类变量的不同水平对因变量的影响。
例如,在一个回归模型中:其中,i.category表示将category变量转换为虚拟变量。
回归模型会为category中的每个水平引入一个虚拟变量,并拟合模型。
虚拟变量的效应:1.截距项:虚拟变量的一个水平通常被视为截距项。
其他虚拟变量的系数表示相对于这个水平的效应。
2.系数解释:虚拟变量的系数表示相对于参考水平的平均因变量的变化。
例如,如果有一个名为dummy_category的虚拟变量,其系数为 0.5,则表示相对于参考水平,该分类变量的这个水平平均因变量增加了 0.5。
注意事项:1.多重共线性:当引入虚拟变量时,需要注意多重共线性问题。
由于虚拟变量之间存在线性相关性,可能导致方差膨胀因子(VIF)较高。
2.虚拟变量陷阱:在使用虚拟变量时,要避免虚拟变量陷阱,即变量之间存在完全的线性相关性。
通常,可以通过将虚拟变量中的一个去掉来避免陷阱。
总体来说,虚拟变量是 Stata 中用于表示分类变量的一种常见方式,通过在回归分析中引入虚拟变量,可以更好地理解分类变量的效应。
第七章 虚拟变量和随机解释变量本章将讨论两种不同的模型:虚拟变量模型和随机解释变量模型,以及模型设定的其它问题。
第一节 虚拟变量模型在我们以前考虑的模型中,解释变量都是定量变量(如成本、价格、收入、产出等),但在经济研究中,因变量经常受到一些定性变量的影响(如性别、种族、季节、不同历史时期等),我们把这类定性变量称为虚拟变量。
习惯上用D表示虚拟变量,虚拟变量的取值通常为0和1。
0表示变量具备某种属性,1表示变量不具备某种属性。
一、包含一个虚拟变量的模型如果我们要研究的问题中解释变量只分为两类。
则需引入一个模拟变量。
例9.1建立模型研究中国妇女在工作中是否受到歧视。
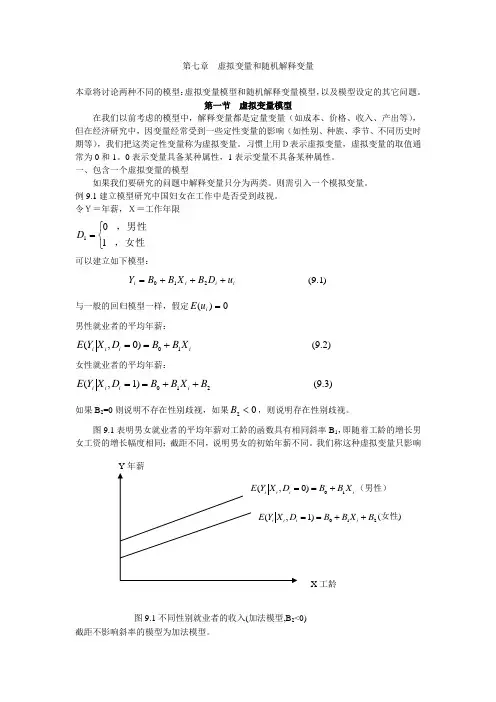
令Y=年薪,X=工作年限⎩⎨⎧=,女性,男性101D 可以建立如下模型:i i i i u D B X B B Y +++=210 )1.9( 与一般的回归模型一样,假定0)(=i u E 男性就业者的平均年薪:i i i i X B B D X Y E 10)0,(+== )2.9(女性就业者的平均年薪:210)1,(B X B B D X Y E i i i i ++== )3.9(如果B 2=0则说明不存在性别歧视,如果02<B ,则说明存在性别歧视。
图9.1表明男女就业者的平均年薪对工龄的函数具有相同斜率B 1,即随着工龄的增长男女工资的增长幅度相同;截距不同,说明男女的初始年薪不同。
我们称这种虚拟变量只影响截距不影响斜率的模型为加法模型。
图9.1不同性别就业者的收入(加法模型,B 2<0)如果随着工龄增加,男性与女性的年薪差距也发生变化,则模型(9.1)就变为i i i i i u X D B X B B Y +++=210 )4.9(图9.2描绘了男性年薪增加较快的情况。
我们称虚拟变量只影响斜率而不影响截距的模型为乘法模型如(9.4)如果男性与女性的初始年薪和年薪增加速度都有差异,我们可以将加法模型和乘法模型结合起来,得到如下模型i i i i i i u D B X D B X B B Y ++++=3210 )5.9(模型(9.5)可以用来表示截距和斜率都发生变化的模型。




计量经济学习题第7章单方程回归模型的几个专题第7章单方程回归模型的几个专题一、名词解释1、虚拟变量2、模型设定误差3、工具变量4、工具变量法5、变参数模型6、分段线性回归模型7、虚拟变量模型二、简答题1、模型中引入虚拟变量的作用是什么?2、虚拟变量引入的原则是什么?3、虚拟变量引入的方式及每种方式的作用是什么?4、判断计量经济模型优劣的基本原则是什么?5、模型设定误差的类型有那些?6、工具变量选择必须满足的条件是什么?7、滞后变量模型包括哪几种类型?写出各自的模型形式。
8、设定误差产生的主要原因是什么?9、在建立计量经济学模型时,什么时候,为什么要引入虚拟变量?三、单项选择题1、设某地区消费函数i i i x c c y μ++=10中,消费支出不仅与收入x 有关,而且与消费者的年龄构成有关,若将年龄构成分为小孩、青年人、成年人和老年人4个层次。
假设边际消费倾向不变,则考虑上述构成因素的影响时,该消费函数引入虚拟变量的个数为()A.1个B.2个C.3个D.4个2、当质的因素引进经济计量模型时,需要使用()A. 外生变量B. 前定变量C. 内生变量D. 虚拟变量3、.由于引进虚拟变量,回归模型的截距或斜率随样本观测值的改变而系统地改变,这种模型称为()A. 系统变参数模型B.系统模型C. 变参数模型D. 分段线性回归模型4、.假设回归模型为i i i x y μβα++=,其中Xi 为随机变量,Xi 与Ui 相关则β的普通最小二乘估计量( )A.无偏且一致B.无偏但不一致C.有偏但一致D.有偏且不一致5、假定正确回归模型为i i i i x x y μββα+++=2211,若遗漏了解释变量X2,且X1、X2线性相关则1β的普通最小二乘法估计量( )A.无偏且一致B.无偏但不一致C.有偏但一致D.有偏且不一致6、对于误差变量模型,模型参数的普通最小二乘法估计量是( )A.无偏且一致的B.无偏但不一致C.有偏但一致D.有偏且不一致7、系统变参数模型分为( )A.截距变动模型和斜率变动模型B.季节变动模型和斜率变动模型C.季节变动模型和截距变动模型D.截距变动模型和截距、斜率同时变动模型8、虚拟变量( )A.主要来代表质的因素,但在有些情况下可以用来代表数量因素B.只能代表质的因素C.只能代表数量因素D.只能代表季节影响因素9、. 分段线性回归模型的几何图形是( )A.平行线B.垂直线C.光滑曲线D.折线10、如果一个回归模型中不包含截距项,对一个具有m 个特征的质的因素要引入虚拟变量数目为( )A.mB.m-1C.m-2D.m+111、设某商品需求模型为Yt=β0+β1Xt+Ut ,其中Y 是商品的需求量,X 是商品的价格,为了考虑全年12个月份季节变动的影响,假设模型中引入了12个虚拟变量,则会产生的问题为()A .异方差性B .序列相关C .不完全的多重共线性D .完全的多重共线性四、多项选择题1、系统变参数模型中,参数变化是( )A.随机的B.离散的C.非随机的D.连续的E.系统的2、在包含有随机解释变量的回归模型中,可用作随机解释变量的工具变量必须具备的条件有,此工具变量( )A.与该解释变量高度相关B.与其它解释变量高度相关C.与随机误差项高度相关D.与该解释变量不相关E.与随机误差项不相关3、关于虚拟变量,下列表述正确的有()A .是质的因素的数量化B .取值为l 和0C .代表质的因素D .在有些情况下可代表数量因素E .代表数量因素4、虚拟变量的取值为0和1,分别代表某种属性的存在与否,其中()A 、0表示存在某种属性B 、0表示不存在某种属性C 、1表示存在某种属性D 、1表示不存在某种属性E 、0和1代表的内容可以随意设定5、在截距变动模型i i i x D y μβαα+++=10中,模型系数()A 、0α是基础类型截距项B 、1α是基础类型截距项C 、0α称为公共截距系数D 、1α称为公共截距系数E 、01αα-为差别截距系数6、对于线性回归模型i i i i Dx x D y μββαα++++=)(2110,其中D 为虚拟变量,有()A 、其图形是两条平行线B 、基础类型的截距项是0αC 、基础类型的截距为1βD 、差别截距系数为1αE 、差别斜率系数为12ββ-7、对于分段线性回归模型t t t t D x x x y μβββ+-++=)(*210,其中()A 、虚拟变量D 代表品质因素B 、虚拟变量D 代表数量因素C 、以*x x t =为界,前后两段回归直线的斜率不同D 、以*x x t =为界,前后两段回归直线的截距不同E 、该模型是系统变参数模型的一种特殊形式五、计算题1、家庭消费C ,除依赖于收入Y 之外,还同下列因素有关:(1)民族:汉、蒙、满、回、藏(2)家庭小孩数:没有孩子、1-2个孩子、3个及以上孩子(3)户主的文化程度:高中以下、高中、大专以上试设定该家庭消费函数的回归模型。
第7章含有定性信息的多元回归分析:二值(或虚拟)变量在前面几章中,我们的多元回归模型中的因变量和自变量都具有定量的含义。
就像小时工资率、受教育年数、大学平均成绩、空气污染量、企业销售水平和被拘捕次数等。
在每种情况下,变量的大小都传递了有用的信息。
在经验研究中,我们还必须在回归模型中考虑定性因素。
一个人的性别或种族、一个企业所属的产业(制造业、零售业等)和一个城市在美国所处的地理位置(南、北、西等)都可以被认为是定性因素。
本章的绝大部分内容都在探讨定性自变量。
我们在第7.1节介绍了描述定性信息之后,又在第7.2、7.3和7.4节中说明了,如何在多元回归模型中很容易地包含定性的解释变量。
这几节几乎涵盖了定性自变量用于横截面数据回归分析的所有流行方法。
我们在第7.5节讨论了定性因变量的一种特殊情况,即二值因变量。
这种情形下的多元回归模型具有一个有趣的含义,并被称为线性概率模型。
尽管有些计量经济学家对线性概率模型多有中伤,但其简洁性还是使之在许多经验研究中有用武之地。
虽然我们在第7.5节将指出其缺陷,但在经验研究中,这些缺陷常常都是次要的。
7.1 对定性信息的描述定性信息通常以二值信息的形式出现:一个人是男还是女;一个人有还是没有一台个人计算机;一家企业向其一类特定的雇员提供还是不提供退休金方案;一个州实行或不实行死刑。
在所有这些例子中,有关信息可通过定义一个二值变量(binary variable)或一个0-1变量来刻画。
在计量经济学中,对二值变量最常见的称呼是虚拟变量(dummy variable),尽管这个名称并不是特别形象。
在定义一个虚拟变量时,我们必须决定赋予哪个事件的值为1和哪个事件的值为0。
比如,在一项对个人工资决定的研究中,我们可能定义female为一个虚拟变Array量,并对女性取值1,而对男性取值0。
这种情形中的变量名称就是取值1的事件。
通过定义male在一个人为男性时取值1并在一个人为女性时取值0,也能刻画同样的信息。
第七章 虚拟变量和随机解释变量本章将讨论两种不同的模型:虚拟变量模型和随机解释变量模型,以及模型设定的其它问题。
第一节 虚拟变量模型在我们以前考虑的模型中,解释变量都是定量变量(如成本、价格、收入、产出等),但在经济研究中,因变量经常受到一些定性变量的影响(如性别、种族、季节、不同历史时期等),我们把这类定性变量称为虚拟变量。
习惯上用D表示虚拟变量,虚拟变量的取值通常为0和1。
0表示变量具备某种属性,1表示变量不具备某种属性。
一、包含一个虚拟变量的模型如果我们要研究的问题中解释变量只分为两类。
则需引入一个模拟变量。
例9.1建立模型研究中国妇女在工作中是否受到歧视。
令Y=年薪,X=工作年限⎩⎨⎧=,女性,男性101D 可以建立如下模型:i i i i u D B X B B Y +++=210 )1.9( 与一般的回归模型一样,假定0)(=i u E 男性就业者的平均年薪:i i i i X B B D X Y E 10)0,(+== )2.9(女性就业者的平均年薪:210)1,(B X B B D X Y E i i i i ++== )3.9(如果B 2=0则说明不存在性别歧视,如果02<B ,则说明存在性别歧视。
图9.1表明男女就业者的平均年薪对工龄的函数具有相同斜率B 1,即随着工龄的增长男女工资的增长幅度相同;截距不同,说明男女的初始年薪不同。
我们称这种虚拟变量只影响截距不影响斜率的模型为加法模型。
图9.1不同性别就业者的收入(加法模型,B 2<0)如果随着工龄增加,男性与女性的年薪差距也发生变化,则模型(9.1)就变为i i i i i u X D B X B B Y +++=210 )4.9(图9.2描绘了男性年薪增加较快的情况。
我们称虚拟变量只影响斜率而不影响截距的模型为乘法模型如(9.4)如果男性与女性的初始年薪和年薪增加速度都有差异,我们可以将加法模型和乘法模型结合起来,得到如下模型i i i i i i u D B X D B X B B Y ++++=3210 )5.9(模型(9.5)可以用来表示截距和斜率都发生变化的模型。
其图形如图9.3所示。
我们还可以用加法模型与乘法模型相结合的方式建立模型来拟合经济发展出现转折的情况。
例如,进口商品消费支出Y主要取决于国民生产总值X(作为收入的替代变量)的多少。
我们改革开放前后,由于国家政策的变化,及改革开放后外资的大量引入等因素的影响,1978年前后,Y 对X 的回归关系明显不同。
以t *=1978年为转折点,1978年的国民生产总值X *t 为临界值。
设虚拟变量⎪⎩⎪⎨⎧<≥=**01tt t t D t 进口商品支出回归方程为t t t t t t u D X X B X B B Y +-++=)(*210 )6.9(用OLS 法估计得到t t t t t D X X B X B B Y)(ˆˆˆˆ*210-++= )7.9( 当年1978*=<t t ,0=t Dt t X B B Y10ˆˆˆ+= )8.9( 当t ≥1978*=t ,1=t Dt t t X B B X B B Y)ˆˆ()ˆ(ˆ21*20++-= )9.9( 根据我国经济发展的实际情况;一般应该0ˆ2>B 。
比较(9.8)与(9.9)式中的斜率,121ˆˆˆB B B >+,说明改革开放后,随着收入的增长,我国进口商品支出增长速度较改革开放前快。
当t=t *时,X t =X *t ,所以,由(9.8)和(9.9)式计算得到的Y *t 是一样的。
两条不同时期的直线可在转折点连起成为一条折线。
如图9.4.§9.1.2 包含多个虚拟变量的模型 现在我们要研究本科生,研究生和MBA 毕业生的初职月薪有何差异。
这里有三类人员,需引入两个虚拟变量。
数据见表9.1 Y =初职月薪X t⎩⎨⎧=其他研究生011D ⎩⎨⎧=其他研究生011D表9.1研究本科生,研究生和MBA 毕业生的初职月薪 单位:人民币元根据表9.1的数据得到OLS 回归结果如下:212497719501D D Y ++= )10.9(t )45.4( )52.4( )59.15(75.128,6.1.,898.0,905.022====F W D R R根据(9.1)可以看出,截距项为本科生的平均初职月薪;D 1的系数是研究生与本科生平均初值职月薪的差额;D 2的系数是MBA 毕业生与本科生平均初职月薪的差额。
所有回归数的符号与预期的一致。
模型(9.10)表明研究生的初职月薪比本科生高143.5%。
MBA 毕业生的初值月薪比本科生高494.8%;MBA 毕业生的初职月薪比研究生高144.2%。
从这三个层次毕业生的初职月薪可以看出他们的竞争能力。
图9.5给出了模型(9.10)图9.5本科生、研究生、毕业生的初职月薪从前面讨论的例子中,我们可以发现虚拟变量实质上是“数据分类器”,它根据样本的属性(性别、种族、季节变化、经济结构的变化等)将样本分为各个不同的子群体并对每个子群体进行回归分析。
各个子群体的因变量对解释变量(定性解释变量)的不同反应表现为各子群体截距或斜率系数存在差别。
虽然虚拟变量技术非常有用,但在使用时仍需谨慎。
第一,如果回归模型包含了常数项,那么虚拟变量的个数必须比所研究问题中数据属性少1;第二虚拟变量的系数必须与基准类(所有虚拟变量都取零的一类)相关;最后,若模型中包含多个定性变量,而且每个定性变量有多种分类,则引入模型的虚拟变量将消耗大量的自由度。
因此,应当权衡进入模型的虚拟变量个数以免超过样本观察值的个数。
§9.2 随机解释变量模型回忆回归模型的古典假设这一0)(,=i i u X Cov ,即解释变量X 与随机项u 不相关。
这个假定实际上要求:或X 是确定性变量,或者X 是随机变量,但与误差项u 不相关。
显然这种假定不符合实际。
实际上解释变量的取值往往不确定,是随机的。
尤其是滞后因变量作解释变量时更不能把他当作非随机变量处理。
我们把解释变量是随机变量的模型称为随机解释变量模型。
对于随机解释变量模型,如果满足0)(,=i i u X Cov和其它古典假设。
则当X 与u 独立时,最小二乘估计量是无偏的;当X 与u 不独立时,最小二乘估计量具有一致性。
如果0)(,≠i i u X Cov ,则OLS 估计量是非一致估计量。
如何解决解释变量与随机误差项相关时模型的参数估计呢?工具变量法是一种简单的方法。
工具变量法的基本思想是当解释变量与随机项高度相关时,设法找到另外一个随机变量Z ,使得Z 与X 高度相关而与u 不相关,称Z 为工具变量,用Z 替代X 使0)(,=i i u Z Cov ,求得模型的参数估计量1。
但在实际应用中,如何选择工具变量是一个比较困难的问题。
第三节 模型的设定在前几章我们考虑了单方程回归模型,例如交通通讯支出函数,进口需求函数。
在考虑这些模型时,我们隐含地假定了所选择的模型“是对现实的真实反映”,即它正确地反映了所要研究的现象。
用专业语言说,就是我们假定所选模型中不存在设定偏差或者误差。
设定误差的产生是由于我们在不经意中估计了“不正确的”模型。
但在实践中寻找真实正确的模型就好像寻找圣杯一样,永远办不到。
我们只是希望找到一个能够合理反映现实的模型,即一个好的模型。
一、 “好的”模型具有的特性著名经济计量学家哈维2列出了可以判定模型好坏的标准。
1. 节省性。
一个模型永远无法完全把握现实,在建模过程中一定程度的抽象或简化是不可1对随机解释变量模型估计量的性质的证明和工具变量法的介绍参见《经济计量学》,张宝法编著,经济科学出版社,2000年1月,pp166-174。
避免的。
节俭原则表明模型应尽可能地简单,即简单优于复杂。
2. 可识别性。
即对给定的一组数据,每个参数只有一个估计值。
3. 拟合优度。
回归分析的基本思想是用模型中所包括的变量来尽可能地解被解释变量的变化。
比如我们可以用校正的样本决定系数2R 来度量拟合优度。
2R 越高,则认为模型就越好。
4. 理论一致性。
无论拟合度多高,一旦模型中的一个或者多个数的符号有误,该模型就不是一个好的模型。
因而,在某种商品的需求函数中,如果价格的函数为正,那么回归结果就值得怀疑。
即使模型的R 2值很高,比如0.98,我们也不能接受这个模型。
所以,在构建模型时,我们必须有一些理论基础来支撑这一模型,“没有理论的测量”经常能导致非常令人失望的结果。
5. 预测能力。
正如诺贝尔奖得主米尔顿.弗里德曼所指出的那样,“对假设(模型)的真实性唯一有效的检验就是将预测与经验值相比较”3。
因而,在货币主义模型和凯恩思模型两者之间选择时,根据这一标准,我们就应该选择理论预测能够被实际经验所验证的模型。
虽然建立一个“好的”模型没有一个统一的方法,但是我们建议读者在建立经济计量模型时应牢记这些标准。
二、设定误差的类型正如前面指出的那样。
模型应该尽可能简单,它应该包括理论上所建议的关键变量而将一些次要影响因素包括在误差项u 中。
下面我们讨论几种导致模型失效的设定误差。
1.遗漏相关变量:“过低拟合”模型由于种种原因,研究者遗漏了一个或多个本应该包括在模型中的解释变量,这样会对常用的变通最小二乘法估计结果有什么影响呢?在第七章,我们曾给出1985年到1998年期间我中国进口商品支出函数,见式(6.5),现在假定“真实”的进口商品支出函数如下:t t u X B X B B Y +++=22110 )1.8(式中的Y 为进口总额,X 1为收入,X 2 为时间趋势变量,取值从1,2,… 到14(为了使分析具有一般性,我们用Y, X 1, X 2 作为变量)。
式8.1表明:除了收以外,还有一个变量X 2也影响进口商品支出。
它可能是人口,偏好,技术,国家政策导向等因素,我们用一个包罗万象的变量--时间或趋势变量表示这些影响因素。
如果,我们在这里不估计回归方程8.1而是估计下面的方程:t t t X A A Y ν++=10 )2.8(式(8.1)与(8.2)类似,只是去掉了“相关“变量X 2 。
ν与u 都是随机误差项。
如果(8.1)是正确的模型,那么(8.2)就犯了从模型中排除重要变量的设定误差。
我们将这种设定误差称作遗漏变量偏差。
遗漏变量可能产生如下后果:(1)如果遗漏变量X 2 与模型中变量X 1 相关,则0ˆA 和 1ˆA 是有偏的,即其均值与真实值不一致 。
即0)ˆ(B A E ≠, 11)ˆ(B A E ≠3Milton, “The Methodology of Positive Economics” in Essays in Positive economics, University of Chicago(2)0ˆA 和 1ˆA 不是0B 和1B 的一致估计量。