第七章 多元回归分析-虚拟变量

关于虚拟变量（Dummy Variable ）的回归1．虚拟变量的性质● 在回归分析中，应变量不仅受量化好了的变量的影响，还受定性性质的变量的影响（如性别，种族，肤色，宗教，国籍，地震等等）● 这类定性变量指某一“性质”或属性出现或不出现。

量化这些变量的方法，是构造一个取值1或0 的人为变量，0代表某一属性不出现，而1代表该属性出现。

● 取这样的0和1 值的变量叫做虚拟变量 (dummy variable)● 在回归分析中，可以清一色的使用虚拟变量，这样的模型叫做方差分析模型（analysis of variance, ANOV A ）, 例：i i i u D Y ++=βα其中Y=学院教授的年薪 D i = 1 若是男教授= 0 若是女教授● 学院女教授的平均薪金：α==)0/(i i D Y E 学院男教授的平均薪金：βα+==)1/(i i D Y E● 截距项α给出学院女教授的平均薪金，而斜率系数β告诉我们学院男教授和女教授的平均薪金的差额，α+β反映学院男教授的平均薪金。

● 在大多数经济研究中，一个回归模型既含有一些定量的又含有一些定性的解释变量。

协方差分析（analysis of covariance ANCOV A ）2．对一个定量变量和一个两分定性变量的回归● ANCOV 的一个例子：i i i i u X D Y +++=βαα21其中Y i = 学院教授的年薪 X i = 教龄 D i = 1 若是男教授 = 0 若是女教授● 假定和平常一样E （u i ）=0，学院女教授的平均薪金：i i i X D Y E βα+==1)0/( 学院男教授的平均薪金：i i i X D Y E βαα++==)()1/(21 ● 图● 以上模型设想学院男教授和女教授的薪金作为教龄的函数，有相同的斜率，但不同的截距● 如果2α统计上显著，则表明有性别歧视● 上述虚拟变量回归模型有以下特点：（1） 为了区分两个类别，男性和女性，我们只引进了一个虚拟变量D i 。

第7章含有定性信息的多元回归分析：二值（或虚拟）变量7.1复习笔记考点一：带有虚拟自变量的回归★★★★★1．对定性信息的描述定性信息是指通常以二值信息（0-1）的形式出现的信息，如性别、是否结婚等。

在计量经济学中，二值变量又称为虚拟变量。

2．只有一个虚拟自变量（1）只有一个虚拟自变量的简单模型考虑决定小时工资的简单模型：wage＝β0＋δ0female＋β1educ＋u。

根据多元回归的解释方式，δ0表示控制educ不变时，female变化1单位给wage带来的变化。

假定零条件均值假定E（u｜female，educ）＝0成立，那么：δ0＝E（wage｜female＝1，educ）－E（wage｜female＝0，educ），其中female＝1表示女性，female＝0表示男性。

可以发现，在任意教育水平下，男性与女性的工资差异是固定的，女性工资比男性工资多δ0。

除了β0之外，模型中只需要引入一个虚拟变量。

因为female＋male＝1，所以引入两个虚拟变量会导致完全多重共线性，即虚拟变量陷阱。

（2）当因变量为log（y）时，对虚拟解释变量系数的解释当变量中有一个或多个虚拟变量，且因变量以对数的形式存在时，虚拟变量的系数可以理解为百分比的变化。

将虚拟变量的系数乘以100，表示的是在保持所有其他因素不变时y 的百分数差异，精确的百分数差异为：100·[exp（∧β1）－1]。

其中∧β1是一个虚拟变量的系数。

3．使用多类别虚拟变量（1）在方程中包括虚拟变量的一般原则如果回归模型具有g 组或g 类不同截距，一种方法是在模型中包含g－1个虚拟变量和一个截距。

基组的截距是模型的总截距，某一组的虚拟变量系数表示该组与基组在截距上的估计差异。

如果在模型中引入g 个虚拟变量和一个截距，将会导致虚拟变量陷阱。

另一种方法是只包括g 个虚拟变量，而没有总截距。

这种方法存在两个实际的缺陷：①对于相对基组差别的检验变得更繁琐；②在模型不包含总截距时，回归软件通常都会改变R 2的计算方法。

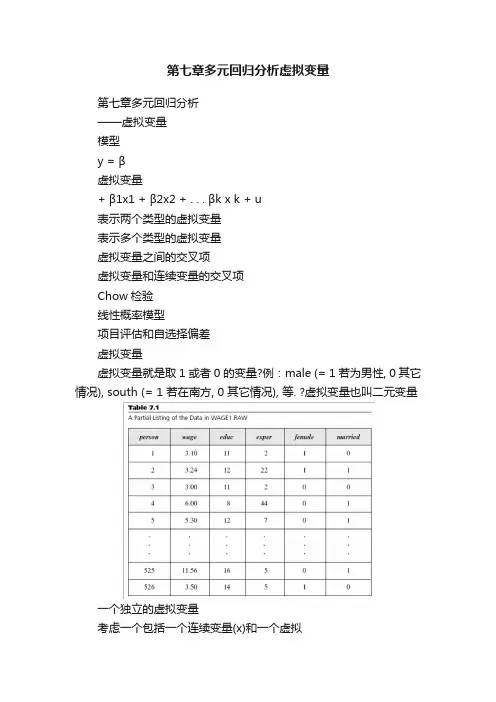
第七章多元回归分析虚拟变量第七章多元回归分析——虚拟变量模型y = β虚拟变量+ β1x1 + β2x2 + . . . βk x k + u表示两个类型的虚拟变量表示多个类型的虚拟变量虚拟变量之间的交叉项虚拟变量和连续变量的交叉项Chow检验线性概率模型项目评估和自选择偏差虚拟变量虚拟变量就是取1 或者0 的变量?例：male (= 1 若为男性, 0 其它情况), south (= 1 若在南方, 0 其它情况), 等. ?虚拟变量也叫二元变量一个独立的虚拟变量考虑一个包括一个连续变量(x)和一个虚拟变量(d)的模型y = β+ δ0d + β1x + u这可以解释成截距项的变化若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ0) + β1x + ud = 0 的样本是参照组δ0 > 0 的例子y y = (β0 + δ0) + β1xd = 1{ δslope = β1d =0 }βy = β0 + β1xx从多个数值的类型变量到虚拟变量?我们可以用虚拟变量来控制有多种类型因素?假设样本中的个人是中学辍学或者仅仅中学毕业或者大学毕业现在要拿仅仅中学毕业和大学毕业的人和中学辍学的人比较定义hsgrad = 1 如果仅仅是中学毕业, 0 其它情况; colgrad = 1 如果大学毕业, 0 其它情况多个数值的类型变量（续）?任何类型变量都可以变成一组虚拟变量?因为参照组由常数项表示了, 那么如果一共有n 个类型，就应该由n –1 虚拟变量如果有太多的类型，通常应该对其进行分组例：前10 , 11 –25, 等虚拟变量之间的交叉项求虚拟变量的交叉项就相当于对样本进行进一步分组例：有男性（male）的虚拟变量和hsgrad（仅仅中学毕业）和colgrad （大学毕业）的虚拟变量加入male*hsgrad 和male*colgrad, 共有五个虚拟变量–> 共有六种类型参照组是女性中学辍学的人此时hsgrad 代表女性仅仅中学毕业者, colgrad 表示女性大学毕业者交叉项表示男性仅仅中学毕业者和男性大学毕业者虚拟变量之间的交叉项（续）?模型可以写成y = β0 + δ1male + δ2hsgrad +δ3colgrad + δ4male*hsgrad + δ5male*colgrad+ β1x + u, 那么:若male = 0 且hsgrad = 0 且colgrad = 0则y = β0 + β1x + u若male = 0 且hsgrad = 1 且colgrad = 0则y = β0 + δ2hsgrad + β1x + u若male = 1且hsgrad = 0且colgrad = 1则y = β0 + δ1male + δ3colgrad + δ5male*colgrad+ βx + u1其它变量与虚拟变量的交叉项?也可以考虑虚拟变量d 和连续变量x 之间的交叉项y = β+ δ1d + β1x + δ2d*x + u若d = 0, 那么y = β+ β1x + u若d = 1, 那么y = (β+ δ1) + (β1+ δ2) x + u这里的两种情况可以看成是斜率的变化δ0 > 0 且δ 1 < 0的例子yy = β+ β1xd = 0d = 1y = (β0 + δ0) + (β 1 + δ1) x。

第七章多元回归分析——虚拟变量•模型•y = β•虚拟变量+ β1x1 + β2x2 + . . . βk x k + u•表示两个类型的虚拟变量•表示多个类型的虚拟变量•虚拟变量之间的交叉项•虚拟变量和连续变量的交叉项•Chow检验•线性概率模型•项目评估和自选择偏差虚拟变量•虚拟变量就是取1 或者0 的变量•例：male (= 1 若为男性, 0 其它情况), south (= 1 若在南方, 0 其它情况), 等. •虚拟变量也叫二元变量一个独立的虚拟变量•考虑一个包括一个连续变量(x)和一个虚拟变量(d)的模型•y = β+ δ0d + β1x + u•这可以解释成截距项的变化•若d = 0, 那么y = β+ β1x + u•若d = 1, 那么y = (β+ δ0) + β1x + u• d = 0 的样本是参照组δ0 > 0 的例子y y = (β0 + δ0) + β1xd = 1{ δslope = β1d =0 }βy = β0 + β1xx从多个数值的类型变量到虚拟变量•我们可以用虚拟变量来控制有多种类型因素•假设样本中的个人是中学辍学或者仅仅中学毕业或者大学毕业•现在要拿仅仅中学毕业和大学毕业的人和中学辍学的人比较•定义hsgrad = 1 如果仅仅是中学毕业, 0 其它情况; colgrad = 1 如果大学毕业, 0 其它情况多个数值的类型变量（续）•任何类型变量都可以变成一组虚拟变量•因为参照组由常数项表示了, 那么如果一共有n 个类型，就应该由n –1 虚拟变量•如果有太多的类型，通常应该对其进行分组•例：前10 , 11 –25, 等虚拟变量之间的交叉项•求虚拟变量的交叉项就相当于对样本进行进一步分组•例：有男性（male）的虚拟变量和hsgrad（仅仅中学毕业）和colgrad （大学毕业）的虚拟变量•加入male*hsgrad 和male*colgrad, 共有五个虚拟变量–> 共有六种类型•参照组是女性中学辍学的人•此时hsgrad 代表女性仅仅中学毕业者, colgrad 表示女性大学毕业者•交叉项表示男性仅仅中学毕业者和男性大学毕业者虚拟变量之间的交叉项（续）•模型可以写成y = β0 + δ1male + δ2hsgrad +δ3colgrad + δ4male*hsgrad + δ5male*colgrad+ β1x + u, 那么:•若male = 0 且hsgrad = 0 且colgrad = 0则y = β0 + β1x + u•若male = 0 且hsgrad = 1 且colgrad = 0则y = β0 + δ2hsgrad + β1x + u•若male = 1且hsgrad = 0且colgrad = 1则y = β0 + δ1male + δ3colgrad + δ5male*colgrad+ βx + u1其它变量与虚拟变量的交叉项•也可以考虑虚拟变量d 和连续变量x 之间的交叉项•y = β+ δ1d + β1x + δ2d*x + u•若d = 0, 那么y = β+ β1x + u•若d = 1, 那么y = (β+ δ1) + (β1+ δ2) x + u•这里的两种情况可以看成是斜率的变化δ0 > 0 且δ 1 < 0的例子yy = β+ β1xd = 0d = 1y = (β0 + δ0) + (β 1 + δ1) xx检验不同组之间的差异•为了检验一个回归方程对不同的组是否应该取不同的参数，我们可以检验表示组的虚拟变量及其和所有其他x变量的交叉项的显著性•因此可以估计有所有交叉项和没有交叉项两种情况下的模型，然后构造F统计量, 但这种方法不容易把握Chow 检验•也可以仅仅做没有交叉项的回归来构造适当的F统计量•如果我们对第一组样本做没有交叉项的回归，得到SSR1, 然后再对第二组样本做同样的回归，得到SSR2 •再同样对所有样本做没有交叉项的回归，得到SSR, 那么F =[()][()] SSR SSR SSR n2k1−+−+•12SSR SSR k1++12Chow 检验（续）•Chow 检验其实就是一个对排除性限制条件的F检验, 我们注意到SSR ur = SSR1 + SSR2•注，我们一共有k+ 1 限制条件（针对每一个斜率和一个截距）•注，无限制条件的模型估计了两个截距项和两组不同的系数，因此自由度（df）为n –2k–2事实上是经济过程检验•做模型回归时我们假设所有的样本观测值都来自同一个总体，如果总体发生改变，那么模型参数也将发生改变，因此检验总体也就是经济过程是否发生改变是用计量进行经济研究的主要步骤。

第七章虚拟变量回归分析姓名：耿肃竹学号：20136878 班级：经济1302【实验目的】目的在于学习基本的经济计量方法并利用Stata对经济中典型的数据，掌握虚拟变量的分析思路，掌握虚拟变量回归的基本操作方法，掌握虚拟变量回归的结果分析。

【实验软件】Stata是一套提供其使用者数据分析、数据管理以及绘制专业图表的完整及整合性统计软件。

该软件提供的功能包含线性混合模型、均衡重复反复及多项式普罗比模式。

作为流行的计量经济学软件，Stata的功能十分地全面和强大。

可以毫不夸张地说，凡是成熟的计量经济学方法，在Stata中都可以找到相应的命令，而这些命令都有许多选项以适应不同的环境或满足不同的需要。

【实验要求】利用stata软件学习多元回归分析的应用问题，并在回归结果中学会以下命令的使用对类型变量B生成虚拟变量Atabulate B, gen(A)；对包含虚拟变量的情况进行回归regress y x1 x2…A2 A3…等命令。

学会虚拟变量在回归分析中的应用进行有效分析，学以致用。

【实验内容】教材P213——C2题目【1】C2（Ⅰ）输入命令“regress lwage educ exper tenure married black south urban”:解：log(wage)=5.395497+0.0654307educ+0.014043exper+0.0117473tenure(0.113225) (0.0062504) (0.0031852) (0.002453)+0.1994171married-0.1883499black-0.0909036south+0.1839121urban (0.0390502) (0.0376666) (0.0262485) (0.0269583)n=935 R2=0.2526保持其他因素不变，黑人和非黑人之间的月薪差异近似（约等于）为0.1883499，因为P=0，所以这个差异是统计显著的。

第7章含有定性信息的多元回归分析：二值(或虚拟)变量在前面几章中，我们的多元回归模型中的因变量和自变量都具有定量的含义。

就像小时工资率、受教育年数、大学平均成绩、空气污染量、企业销售水平和被拘捕次数等。

在每种情况下，变量的大小都传递了有用的信息。

在经验研究中，我们还必须在回归模型中考虑定性因素。

一个人的性别或种族、一个企业所属的产业（制造业、零售业等）和一个城市在美国所处的地理位置（南、北、西等）都可以被认为是定性因素。

本章的绝大部分内容都在探讨定性自变量。

我们在第7.1节介绍了描述定性信息之后，又在第7.2、7.3和7.4节中说明了，如何在多元回归模型中很容易地包含定性的解释变量。

这几节几乎涵盖了定性自变量用于横截面数据回归分析的所有流行方法。

我们在第7.5节讨论了定性因变量的一种特殊情况，即二值因变量。

这种情形下的多元回归模型具有一个有趣的含义，并被称为线性概率模型。

尽管有些计量经济学家对线性概率模型多有中伤，但其简洁性还是使之在许多经验研究中有用武之地。

虽然我们在第7.5节将指出其缺陷，但在经验研究中，这些缺陷常常都是次要的。

7.1 对定性信息的描述定性信息通常以二值信息的形式出现：一个人是男还是女；一个人有还是没有一台个人计算机；一家企业向其一类特定的雇员提供还是不提供退休金方案；一个州实行或不实行死刑。

在所有这些例子中，有关信息可通过定义一个二值变量(binary variable)或一个0-1变量来刻画。

在计量经济学中，对二值变量最常见的称呼是虚拟变量(dummy variable)，尽管这个名称并不是特别形象。

在定义一个虚拟变量时，我们必须决定赋予哪个事件的值为1和哪个事件的值为0。

比如，在一项对个人工资决定的研究中，我们可能定义female为一个虚拟变Array量，并对女性取值1，而对男性取值0。

这种情形中的变量名称就是取值1的事件。

通过定义male在一个人为男性时取值1并在一个人为女性时取值0，也能刻画同样的信息。