当前位置：文档之家 › 第七章立体与立体相交

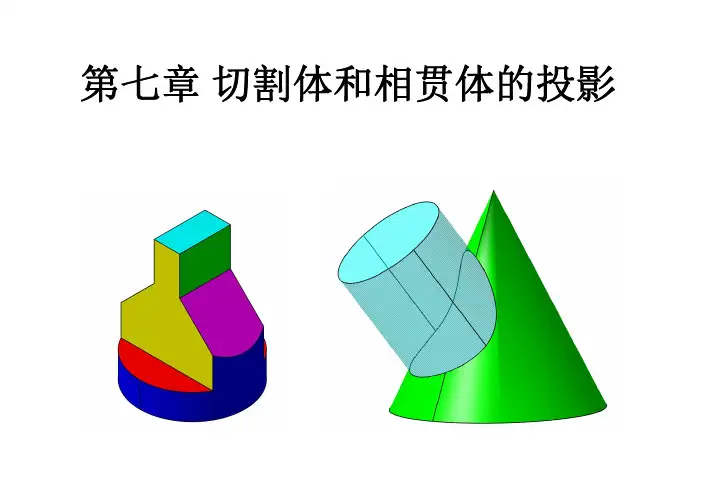
第七章立体与立体相交

  • 格式：ppt
  • 大小：2.00 MB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

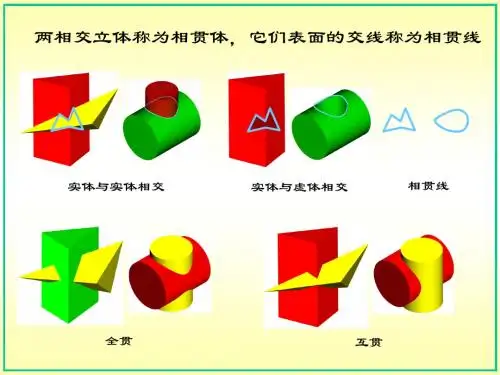
9-4立体与立体的相交

9-4立体与立体的相交

两相交立体称为相贯体，它们表面的交线称为相贯线实体与实体相交实体与虚体相交相贯线全贯互贯9.4 立体与立体相交基本要求9.4.1 平面立体与平面立体相交9.4.2 平面立体与曲面立体相交9.3.3 曲面立体与曲面立体相交基本要求9.4.1 平面立体与平面立体相交一、概述二、例题1例题2一、概述1. 相贯线是两立体表面的共有线，相贯线上的点是两立体表面的共有点;不同的立体以及不同的相贯位置,相贯线的形状也不同。

2．相贯线的形状两平面立体的相贯线通常由空间折线组成。

折线的每一段都是甲形体的一个侧面与乙形体的一个侧面的交线，折线的转折点就是一个形体的侧棱与另一形体的侧面的交点。

3．求相贯线的方法求两平面立体相贯线的方法通常有两种：一种是求各棱线对另一形体表面的交点，然后把位于甲形体同一侧面又位于乙形体同一侧面上的两点，依次连接起来。

另一种是求一形体各侧面与另一形体各侧面的交线。

4．判别相贯线可见性的原则只有位于两形体都可见的侧面上的交线才是可见的。

只要有一个侧面不可见，面上的交线就不可见。

[例题1] 完成三棱锥与三棱柱相贯体的投影图。

[例题2] 完成三棱锥与三棱柱相贯体的投影。

1"yyyy14"44'33'2'1'3"2"3．顺次地连接各点，作出相贯线，并且判别可见性；4．整理轮廓线。

2．求出相贯线上的折点Ⅰ、Ⅱ、Ⅲ、Ⅳ；解题步骤1．分析相贯线的正面投影已知，水平投影和侧面投影未知；[例题2] 两平面立体相贯，完成相贯线的投影。

9.4.2 平面立体与曲面立体相贯一、概述二、例题3例题4例题5一、概述[例题3] 完成半球与三棱柱相贯体的投影。

T S HP H35Q H 123'9'8'6'7'1'2'4'5'46789解题步骤1．分析相贯线为三段圆弧的组合；相贯线的水平投影已知，可利用表面取点法求共有点；2．求出相贯线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ；4．光滑且顺次地连接各点，作出相贯线，并且判别可见性；5．整理轮廓线。

全套机械制图教学课件-14 回转体与回转体相交

全套机械制图教学课件-14 回转体与回转体相交

11
四.回转体相对位置,大小对交线的影响 回转体相对位置,
决定相贯线空间形状和投影特点的因 除了参与相贯的立体的形状外, 素,除了参与相贯的立体的形状外,相对 位置,相对大小对交线的形状和投影均有 位置, 影响. 影响. 现以两圆柱相交为例予以讨论. 现以两圆柱相交为例予以讨论.
12
⑴. 相 对 位 置 对 交 线 的 影 响
2.步骤: 2.步骤: 步骤
分析由何种几何形体表面相交 几何形体间相互位置关系(相交方式) 几何形体间相互位置关系(相交方式) 几何形体的端面(平面) 几何形体的端面(平面)参与相交否 交线的性质(逐段分析): 交线的性质(逐段分析):
哪里有交线 交线的走向趋势 有无已知投影(利用表面积聚性投影) 有无已知投影(利用表面积聚性投影)
6
2. 圆柱与圆锥相交
注意: 注意: 辅助面法找点, 辅助面法找点, 辅助面的位置: 辅助面的位置: 平行圆柱的轴线, 平行圆柱的轴线, 垂直圆锥的轴线. 垂直圆锥的轴线.
1' b' 2',4' a' 3'
b" 4" a"
1" b" 2" 3" a"
QW PW RW
4 (a) (3) (a)
b
1 b 2
第七章 立体与立体相交
7.1 7.2 7.3 7.4 平面体与平面体相交 平面体与回转体相交 回转体与回转体相交 多形体相交
1
由曲面体, 由曲面体,平面体等组成的机件实例
2
立体与立体相交(相贯) 立体与立体相交(相贯)
1.相贯线的性质: 1.相贯线的性质: 相贯线的性质 为相交二立体表面(外或内) 为相交二立体表面(外或内)公有点的集合 2.相贯线的形状 通常为一封闭的空间折线(曲线) 相贯线的形状: 2.相贯线的形状:通常为一封闭的空间折线(曲线) 作题步骤: 3.作题步骤 3.作题步骤: 找到相贯线的已知投影

立体与立体相交PPT课件

立体与立体相交PPT课件

的交点即为相贯线
上的点。
注：辅助平面PV 、
PH应为特殊平面， 可作出回转体的素
线或纬圆
64
8
2
1
5 37
-
8’’ 1’’ 7’’
4’’
3’’
6’’
5’’
2’’
35
EXIT
<iii>、用光滑曲线连接并判别可见性：
相贯线前后对称，主 视图只画可见部分；
左视图中，相贯线 4”-6”-2”-5”-3”同时 位于圆台和球体轮廓 线左侧，为可见；相 贯线3”-7”-1”-8”-4” 位于圆台转向轮廓线 右侧，为不可见；
14
EXIT
2、<作图>：（可认为半球体被三个铅垂面截切， 依据球体截交线的求法）
<i>、作出特殊点的投影：
相贯线是由三 段椭圆圆弧组成的， 每段圆弧走向趋势 的转折点，即最高 点也应属于相贯线 上的特殊点。
在水平投影中过圆 心作棱柱侧面的垂 线，垂足即为圆弧 最高点的投影。
7’ 6’
4’
3’ ’
3、判别可见性并连线：
当点所在的所有面，在某一投影面中的投影都可见时， 则点在该投影面上的投影为可见，否则不可见。
4、检查、补全视图：
-
5
EXIT
一、两平面体相贯：
相贯线是由若干段平面直 线组成的封闭折线。相贯线 上每段线是平面体上某一棱 面与另一平面体的截交线， 既可将两平面体相贯线问题 转化为求平面截交线问题。
-
12
EXIT
例题:求三棱柱与半球体的相贯线
1、<分析>：三棱 柱只贯穿半球体的 上半部分，故相贯 线为一条封闭空间 曲线。棱柱的三个 侧面都是铅垂面， 故相贯线的水平投 影可知，其它投影 面的投影应为三段 椭圆圆弧。

习题答案-立体与立体相交演示精品PPT课件

习题答案-立体与立体相交演示精品PPT课件
平面体与平面体相交
1
85. 作左视图
2
86. 作主视图
3
平面体与回转体相交
4
87. 作左视图
5
88 作俯视图
6
89. 作左视图
7
90. 作主视图
8
91.
9
92.
10
93.
11
94.
12
两回转体相交
13
95. 作第三视图，并标出交线上特殊点的三投影。
14
96. 作第三视图，并标出交线上特殊点的三投影。
当你尽了自己的最大努力时，失败也是伟大的 ，所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
21
103. 完成两斜交圆柱的主、俯视图。
22
104. 作半圆柱与圆锥台的交线。
23
105.
24
106. 补全圆柱与圆球相交后视图中所缺的线。
25
107. 补全圆柱与圆环相交后视图中所缺的线。
26
108.
27
多形体相交
28
109.
29
110. 作俯视图
30
ห้องสมุดไป่ตู้
111. 作俯视图
31
结束语
15
97. 作第三视图，并标出交线上特殊点的三投影。
16
98. 作第三视图，并标出交线上特殊点的三投影。
17
99. 作第三视图，并标出交线上特殊点的三投影。

立体与立体相交

立体与立体相交

第7章 立体与立体相交Chapter 7 Intersection of Solids复杂零件往往是由两个或两个以上的立体组成，两立体表面的交线，称为相贯线。

因为立体分为平面立体和曲面立体，所以相贯线又有三种情况：1．平面立体与平面立体相交，如图7-1（a ）所示；2．平面立体与回转体相交，如图7-1（b ）所示；3．回转体与回转体相交，如图7-1（c ）所示。

（a ） （b ） （c ）图7-1 常见立体相贯类型本章主要通过实例介绍两平面立体相交、平面立体与曲面立体相交、两曲面立体相交及求相贯线的方法。

相贯线的性质：1．相贯线上的点是两立体表面的共有点，相贯线也就是两立体表面的共有线，具有共有性；2．由于立体有一定的范围，所以相贯线一般是闭合的空间图形，具有封闭性。

既然相贯线上的点是两立体表面的共有点，相贯线是两立体表面的共有线，即相贯线上的每一点，既在甲形体的表面上，也在乙形体的表面上。

求相贯线的一般步骤为：（1）根据两相交立体的表面形状不同（平面或曲面），分析相贯线的性质。

平面体与平面体或曲面体相交时的表面交线，组成相贯线的各截交线段都是平面曲线或直线；两曲面立体相交时的相贯线一般是闭合的空间曲线。

（2）选定合适的方法求相贯线上的特殊点和中间点。

（3）根据相贯线的性质依次连线。

（4）判断相贯线的可见性，并补全立体的投影。

本章主要学习任务：1．掌握立体表面相交时交线的作图方法。

2．灵活运用辅助平面法求相贯线。

3．熟练掌握相贯线特殊情况的画法。

117§7-1平面体与平面体表面相交［Intersections of Plane Solids］两平面立体的相贯线一般是空间闭合折线，相贯线上的每一线段是两平面体相应面的交线，而折点则是一个立体的棱线对另一立体的贯穿点。

求作两平面立体的相贯线，通常采用下面两种方法：（1）折点法 即求出甲立体上参与相交的各棱与乙立体表面的交点（即相贯线上的折点），再求出乙立体上参与相交的各棱与甲立体表面的交点，然后顺序地连接各交点，即可得到相贯线。

立体与立体相交精品PPT课件

立体与立体相交精品PPT课件
斜• 的求铅交垂线面正。 面投影 上虚实的分界点。
作图方法 辅助平面
２法。. 求用一一般个位正平置面点来。切
此模型，则切三棱柱前
SH
３线面 两线.的的 条为连两 交圆可线个 线弧见。棱 ， 。性注面 切 棱。分 球 面意别 面 上轮产 的 的廓生 交 交
UH TH
线与圆弧的交点就是三
棱柱与球面的交线上的
描点法，特殊位置点、一般位置点
相贯线作图实质是找出相贯的两立体表面的若干 共有点的投影。
§7.1 平面体与平面体相交
1.相贯线的性质
两平面体的交线在一般情况下是 折线。这条折线可以分裂成两个或更 多部分，并且都是直线组成的空间封 闭线框。
1.求解方法
两平面体的交线的各个顶点是一个平面体的棱线与另 一平面体的交点，交线的各条线段是两平面体的各棱面间 的交线。
［例题五］求两偏交圆柱的交线
SW QW TW PW RW
作图步骤
SH
QH
1. 求特殊位置点 ● ●
TH
2. 求一般位置点 ●
RH
PH 3. 连线。注意判别可见性。
擦除多余作图线后的结果
I
I 6:1
作业
P38（7） P40
P41（8）
［例题六］求两斜交圆柱的交线
投影分析
大圆柱是直立的，小
圆柱是倾斜的，直立圆柱
当两圆柱正交时，交线的投影由小圆柱内向大圆柱内弯曲。随着 小圆柱直径增大，大圆柱直径不变，交线弯曲程度越大。当两个圆柱 直径相等时，交线的投影为直线。
［例题四］补全主视图
●
●
●
●
●
●
●
●
●
● ●
● ●
●

机械工程图学习题集加详细答案 第7章

机械工程图学习题集加详细答案 第7章

7-5完成被截切圆柱的三面投影。
(2)完成水平和侧面投影
7-5完成被截切圆柱的三面投影。
(3)完成水平和正面投影
7-5完成被截切圆柱的三面投影。
(3)完成水平和正面投影
7-5完成被截切圆柱的三面投影。
(4)完成侧面投影。
7-5完成被截切圆柱的三面投影。
(4)完成水平投影。
7-5完成被截切圆柱的三面投影。
(2)完成水平及侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(2)完成水平及侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(3)完成正面和侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(3)完成正面和侧面投影(注意整理轮廓线)。
7-10完成相贯体(曲面立体与曲面立体)的投影。 (6)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (6)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (7)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (7)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (8)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (8)
7-6完成被截切圆锥的三面投影。
(4)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(5)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(5)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(6)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(6)完成水平和侧面投影。
7-10完成相贯体(曲面立体与曲面立体)的投影。 (1)

9 立体与立体相交_几何产品造型设计与分析课件

9 立体与立体相交_几何产品造型设计与分析课件
(2)分别作出辅助面与两个回转体的交线。 (3)求出交线的交点，即为两个回转体表面的共有点。
●
●
●
P
●
15
辅助平面法
（3’）（4’）（5’）
2’
6’
a’
a’
1’
7’
a’
a’
2’
6’
（3’）（4’）（5’）
3“,5"
4"
2“,6"
a"
1“,7"
a" 2“,6" 4" 3“,5"
4
3
5
PW
4 5
B 6
4
相贯线为曲线 相贯线为折线
5
3.求相贯线的方法
作图实质步骤：
1、 分析形体的相交特性。 2、 求出相贯线上特殊点的投影。 3 、求出相贯线上一定数量的一般点的投影。 4 、将各点按照位置顺序依次的平滑的连接起来，
完成相贯线。 5 、判断可见性。可见的图线画实线，不可见的
1'
2'
●
●
●
●
●
3'
1 "≡ 2"
●
3"
例：圆柱与圆柱 相贯，求相贯线 的正面投影。
1
2
●
●
3
B II
I
●
III
A
11
圆柱面相贯有外表面与外表面相贯、外表面与内表面相贯和两内表 面相贯三种形式。这三种情况的相贯线的形状和作图方法相同。
两外表面相贯
外、内表面相贯
两内表面相贯
12
相贯线与圆柱体直径的关系
9.2 回转体与回转体 相交

工程制图立体与立体相交

工程制图立体与立体相交

3.1 相贯线 的性质 3.2 相贯线投 影的求法 3.3
影响相贯 线形状的 因素
交线分析 投影分析 封闭的空间曲线 已知 H、投影作图 W投影 判别可见性 •求正面投影 光滑连线
方法1：利用积聚性投影 用面上取点的方法求解
CAD 链接
作业
上 节
回转体与 回转体 相交
内表面与外表面相贯
3.1 相贯线 的性质 3.2 相贯线投 影的求法 3.3
影响相贯 线形状的 因素
作业
上 节
回转体与 回转体 相交
3.3 影响相贯线形状的因素
相交立体表面的形状 影响相贯线形状
3.1 相贯线 的性质 3.2 相贯线投 影的求法 3.3
影响相贯 线形状的 因素
相交立体的相对位置 影响相贯线形状
作业
上 节
CAD 链接
回转体与 回转体 相交
相交立体的大小影响相贯线形状 水平圆柱小于 垂直圆柱
影响相贯 线形状的 因素
作业
上 节
CAD 链接
回转体与 回转体 相交 3.1 相贯线 的性质 3.2 相贯线投 影的求法 3.3
开方孔与开圆孔的圆锥
圆锥开矩形孔
=圆锥与四棱柱正交
圆锥开圆柱孔
=圆锥与圆柱正交
影响相贯 线形状的 因素
作业
上 节
CAD 链接
回转体与 回转体 相交
开方孔与开圆孔的球
开方孔的球
JXP13
机 械 类 作 业
答案（JXP13）
非 机 械 类 作 业
p11
非 机 械 类 作 业
P11答案
非 机 械 类 作 业
P12
非 机 械 类 作 业
P12答案
非 机 械 类 作 业

第七章 求相贯线

第七章 求相贯线

三 相贯线的形状及投影 相贯线为封闭的空间折线。 相贯线为封闭的空间折线。相贯线在非积聚 封闭的空间折线 性投影上总是向被穿的回转体里面弯折 向被穿的回转体里面弯折， 性投影上总是向被穿的回转体里面弯折，而且在 两体相交区域内不应有回转体轮廓线的投影 相交区域内不应有回转体轮廓线的投影。 两体相交区域内不应有回转体轮廓线的投影。
返回
求圆柱与圆锥的相贯线（辅助平面法） 例3 求圆柱与圆锥的相贯线（辅助平面法）
y PV QV RV
返回
例 4
辅助平面的选择原则： 辅助平面的选择原则： 选择原则 使辅助平面与 辅助平面与 两回转体表面 表面截交 两回转体表面截交 线的投影简单易画 简单易画， 线的投影简单易画， 例如直线 直线或 例如直线或圆。
圆柱才可用
返回
例2 两圆柱筒相贯 •内外分别求 内外分别求 •先求特殊点 先求特殊点 •本例以圆弧近似 本例以圆弧近似 代替相贯线
返回
2、利用辅助平面法 、利用辅助平面法
选辅助平面的原则： 选辅助平面的原则： 要使辅助平面与两立体表面交线的投影为直线 直线或 要使辅助平面与两立体表面交线的投影为直线或圆, 常用的辅助平面为投影面的平行面或垂直面。 平行面或垂直面 常用的辅助平面为投影面的平行面或垂直面。
立体与立体相交——求相贯线 第七章 立体与立体相交 求相贯线 第一节 立体相贯线的概念和性质 平面立体与回转体相交 第二节 平面立体与回转体相交 第三节 曲面立体与曲面立体相交 多体相贯 第四节 多体相贯
作业：7-2、3 、4 、5 、 6、8 看书：P72-P83
返回
第一节 立体相贯线的概念和性质
返回
4、依次连接各点 5、判断可见性 、 、
平面立体与回转体相交 第二节 平面立体与回转体相交

(6)2017秋季工程制图基础-立体与立体相交_533808557

(6)2017秋季工程制图基础-立体与立体相交_533808557

● ●
●
●
3.检查、加深
例2：求俯视图
PW
一．辅助平面法 1.两圆柱相交
交线的 已知投影
k
l
PH
P
作题步骤: 辅助平面 • 找到交线的已知投影 • 辅助面法找点(先特殊点，后中间点) • 顺序、光滑连接各点 • 完成轮廓线 • 判断可见性
L K
18
例2:偏交
3’ 4’ 5’ 6’ a’ a’ 1’ P
2’
4" 3“,5" 2“,6" a" 1“

● ● ● ●

● ●
● ● ●
●
● ●

●
●

●
★ 外表面交线 ◆ 两外表面相贯 ◆ 一内表面和一外表面相贯 ★ 内表面交线
● ● ● ●
◆ 两内表面相贯
9.4 多形体相交
29
例1： 多形体相交
3 2
三面之 共点
1与 2
1
1与3 2与3
30
例2： 补全视图中所缺的交线
2 3
有虚线
7’
a’ 6’
PW 4 3 2 a 1 a 5
6 7
PH
作题步骤 3’: • 2’ 找到相贯线的已知投影 • 辅助面法找点（先特殊点， a’ 后中间点） • 顺序、光滑连接各点 • 完成轮廓线 • 判断可见性 20
2. 圆柱与圆锥相交
注意： 辅助面法找点， 辅助面的位置： 平行圆柱的轴线， 垂直圆锥的轴线。
1’
2’,4’ a’ 3’
例4：
b’
b" 4" a"
1" b" 2" a"

第7章立体表面相交

第7章立体表面相交

第7章立体表面相交
返回
㈠ 平面立体与曲面立体相贯线的性质
1、相贯线是平面立体和曲面立体表面上的公有线， 相贯线上的点是平面立体与曲面立体表面上的 公有点；
2、相贯线是由若干段平面曲线（截交线）所组成 的空间曲线。
第7章立体表面相交
返回
㈡ 平面立体与曲面立体相贯线的求法
依次求出平面立体上参与相交的各棱面与曲面 立体表面的截交线，这些截交线即围成所求平面 立体与曲面立体相贯线。
2、棱面交线法 将两平面立体上参与相交的棱面与另一平面立体各 棱面求交线，交线即围成所求两平面立体相贯线。
第7章立体表面相交
返回
㈢ 相贯线的可见性
相贯线的可见性取决于相贯线所处立体表面的 可见性。若相贯线处于同时可见的两立体表面上， 则相贯线可见，画成实线；其它情况下均为不可 见，画成虚线。
第7章立体表面相交
相贯线上的转折点是平面立体上参与相交的棱 线与曲面立体的贯穿点。

第7章立体表面相交
返回
㈢ 相贯线的可见性
相贯线位于平面立体可见棱面上，且同时又位于 曲面立体可见曲面上，则相贯线可见，用实线绘制； 而其它情况下，相贯线均为不可见，用虚线绘制。
第7章立体表面相交
返回
例题
第7章立体表面相交
返回
【例题1】求两立体表面交线。
2
yy
4 " 3 1" 2 " y y"
返回
㈠ 两平面立体相贯线的性质
1、相贯线是两立体表面的公有线；相贯线上的点 是两立体表面的公有点。
2、相贯线的形状为封闭的空间多边形。
第7章立体表面相交
返回
㈡ 两平面立体相贯线的求法
1、棱线交点法 将两平面立体上参与相交的棱线和另一平面立体上 各棱面求交点，然后将位于甲形体同一棱面上，同时又 位于乙形体同一棱面上的两点依次连接起来，即为所求 两平面立体的相贯线。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 棱线法—求各棱线与棱面的交点 • 棱面法—求各棱面的交线
[例题一]出，四棱柱的四条棱线都穿过棱锥，所以两立体是全贯的。其交线是两条 封闭折线。前面一条是空间折线，是四棱柱与三棱锥的前面两个棱面的交线；后面一条是平面折线，是四 棱柱与三棱锥后面棱面的交线。
描点法，特殊位置点、一般位置点
相贯线作图实质是找出相贯的两立体表面的若干共有点的投影。
§7.1 平面体与平面体相交
1.相贯线的性质 两平面体的交线在一般情况下是折线。这条折线可以分裂成 两个或更多部分，并且都是直线组成的空间封闭线框。
1.求解方法 两平面体的交线的各个顶点是一个平面体的棱线与另一平面体的交点，交线的各条线段是两平 面体的各棱面间的交线。
y
圆台 圆柱 y
圆柱
擦除多余的作图线后的结果
作业
P45（15） P46（17） P48（4）
谢谢观赏！
2020/11/26
38
擦除多余作图线后的结果
§7.2 平面体与曲面体相交
1.相贯线的性质 相贯线是由若干段平面曲线（或直线）所组成的封闭曲线， 每一段平面曲线是平面体的棱面与曲面体表面的截交线。平面曲 线的交点就是平面体的棱线与曲面体的交点。
2.作图方法 求交线的实质是求各棱面与曲面的截交线及棱线与曲面的交点。
• 分析各棱面与曲面的相对位置，从而确定交线的形状。 • 求各棱面与曲面的截交线及棱线与曲面的交点。 • 连接各段交线，并判断可见性。
（ 的（ 投（ 是3投2影）1抛）影）是当物当是当椭两线两双两圆轴。轴曲轴。线线线线相相。相交交交的的的二二二次次次曲曲曲面面面中中中不有有含一一球个个面是是或扁球扁椭面椭球时球面，面时则时，它，则们则它的它们交们的线的交在交线公线在共在公对公共称共对平对称面称平上平面的面上投上的影
二次曲 抛线双物曲线线椭圆
斜的，直立圆柱的水平投影具有积
作图方法
聚性，则交线的水平投影为两圆柱 投影的公共部分。小圆柱的轴线是
辅助平面法。用正平面切此 正平线，则小圆柱的端面圆的正面
投影积聚为直线。 模型，其交线分别为四条直线，
它们的交点是相贯线上的点。
QW
PW
作图步骤 QH
1. 求特殊位置点。 ● ●
2. 用辅助平面法求一般位置点。 ● PH
3. 用光滑曲线连线，并判别可见性。
擦除多余作图线后的结果
［例题七］求圆柱与圆锥的交线
投影分析 相贯线为一光滑的封闭的空间曲线。其中圆柱面的侧面投影有积聚性，因此，相贯
线的侧面投影在柱面的侧面投影上。相贯线的正面投影、水平投影应分别求出。
辅助平面法 根据三面共点的原理，利用辅助平面求出两回转体表面上的若干共有点，从而画出相贯线的 投影。
［例题三］求两圆柱垂直相交的交线
●
●
●● ●
●
●
●
●
求相贯线的投影：
投影分析：小圆柱轴线垂直于H面，水平投影积聚为圆， 根据相贯采线用的表共面有取性点，法相，贯利线用的投水影平积投聚影性即。为该圆。大 圆柱轴线垂直于W面，侧面投影积聚为圆，相贯线的侧 面投影在☆该找圆特上殊。点
☆ 找一般位置点
☆ 光滑连接
●
●
●
●
●
●
●
●
●
解题步骤：
★ 求特殊点 ★ 用辅助平面法求中间点 ★ 光滑连接各点
擦除多余的作图线后的结果
作业
P42 P43 P44（14）
［例题八］求作两曲面体的交线
作图方法 辅助球面法—同心球面法。其基本 原理：若一回转面与一球心在其回转轴 上的球面相交，则其交线一定是圆。
同心球面法适用于当两个曲面都是 回转面时，且它们的轴线相交并平行于 投影面。
作图方法
假想用辅助平面截切两回转体，分别得出两回 转体表面的截交线。由于截交线的交点既在辅助 平面内，又在两回转体表面上，因而是相贯线上 的点。
辅助平面的选择原则 使辅助平面与两回转体表面的截交线的投影简单易画，例如直线或圆。
一般选择投影面平行面作为辅助平面
［例题七］求圆柱与圆锥的交线
● ●
● ●
投影分析 轴线为铅垂线的直立回转体的水平投 影有积聚性。倾斜圆柱的轴线为正平线， 其正面投影有积聚性。
［例题八］求作两曲面体的交线
作图步骤
1. 求特殊位置点。 ● ● 2. 求一般位置点。以两回转体 轴线的交点为球心作一个辅助 球面。 ● ●
3. 连线，并判别可见性。
擦除多余的作图线后的结果
§7.4 二次曲面的交线性质 定定 次定 定理曲理理 理3线124（若在若若4两一=两两2个般+个个二2情）二二次况，次次曲下一曲曲面，条面面有两直具切两个线有 于个二和公 第切次一共 三点曲条的 个，面三对 二则的次称 次它交曲平 曲们线线面 面的是（， ，交四4则 则线=次1它 它分+空3们 们解）间的 的为，曲交 交通或线线 线过四。在 两切条但该 条点(在4平 平=的特1面 面两+殊1上曲条+情1的线二+况1正。次)下。投曲可影线分是。解二成次两曲条线二。
在求两曲面体的交线时，若遇到这种情况，可以将交线的投影直接画出，
不必找直点径连相线等。的两圆柱
圆柱与椭圆柱
［例题九］ 补全视图
§7.5 多形体相交
作图步骤 形体分析
1. 画出分基析本组体成的模投型影的;基本几 何形体及其相互位置关系， 2. 求判大断圆哪柱些与表形面体之3的间交有线交；线， 并分析交线趋势。 3. 求形体3与小圆柱的交线；
1.相贯两立体的表面性质（外表面或内表面）。
2.相贯两立体相互位置。 3.相贯两立体的相对大小。
4.相贯两立体对投影面位置。
●
●
●● ●
●
●
★ 投影作图
●●
投影分析：小圆柱轴线垂直于H面，水 平投影积聚为圆，根据相贯线的共有性， 相贯线的水平投影即为该圆。大圆柱轴 线垂直于W面，侧面投影积聚为圆，相 贯线的侧面投影在该圆上。
第七章立体与立体相交
1
2.相贯线的主要性质
★ 表面性 相贯线位于两立体的表面上（外表面或内表面）。 ★ 封闭性
相贯线一般是封闭的空间折线（通常由直线和曲线组成）或空间曲线。 ★ 共有性 相贯线是两立体表面的共有线。 ★ 空间性 相贯线一般是空间曲线，有时也为平面曲线或直线。
3.相贯线作图的一般方法 ★ 空间分析
◆ 一内表面和一外表面相贯 ★ 内形交线
◆ 两内表面相贯
擦除多余作图线后的结果
小结 圆柱面正交，不管是内形还是外形，其作 图方法是表面取点，利用投影的积聚性。作图 步骤是先求特殊位置点，再求一般位置点，最 后连线，同时判别可见性。
［例题五］求两偏交圆柱的交线。
投影分析 两圆柱面分别垂直于水平 面和侧面，所以交线水平投影 积作聚图在方小法圆柱的水平投影上， 交线的侧面积聚在大圆柱的侧 面辅投助影平圆面弧法上。（取即一在正小平圆面柱轮 为廓辅线助之平间面的，一此段辅圆助弧平）面。切此 模型的交线都是圆柱的素线。 这些素线的交点即为相贯线上 的点。
SH UH TH
RH
擦除多余作图线后的结果
§7.3 曲面体与曲面体相交
1. 相贯线的性质 相贯线一般为光滑封闭的空间曲线，它是两回转体表面的 共有线。
2.作图方法
• 利用投影的积聚性直接找点 • 辅助平面法 • 辅助球面法 ⒊ 作图过程 • 先找特殊点 • 补充一般位置点 • 连线并判别可见性点
［例题五］求两偏交圆柱的交线
SH QH TH
RH
SW QW TW PW RW 作图步骤
1. 求特殊位置点 ● ●
2. 求一般位置点 ●
PH
3. 连线。注意判别可见性。
擦除多余作图线后的结果 I
I 6:1
作业
P38（7） P40
P41（8）
［例题六］求两斜交圆柱的交线
投影分析
大圆柱是直立的，小圆柱是倾
作图步骤
1. 先求四棱柱的两个水平棱面对三棱锥各
棱面的交线。通过四棱柱上下两个棱面作
PV
水平面P和Q，P和Q与三棱锥各个棱面的交 线分别与三棱锥的底面三角形的三条边平
行。
QV
2. 求四棱柱左右两个侧面与三棱锥的交线 。可以由四棱柱左右侧面投影的积聚性和 步骤1中求出的交线共同确定。
3. 连线。注意判别交线的可见性，在P面 内的交线可见，在Q面内的交线不可见。
[例题二] 求三棱柱与半圆球的交线
投影分析 三棱柱与半球 的作交图线步由骤三条截交线组成 。１它. 求们特的殊空位间置形点状。都是圆 弧。由投影可知，三棱柱 的• 最求后三面棱的柱棱各面条是棱正线平上面 ，的前点面。两个棱面是与正立 面• 倾求斜交的线铅正垂面面投。影上虚 实的分界点。
作图方法 辅助平面法。 ２用.一求个一正般平位面置来点切。此模型 ，则切三棱柱前面的两个 棱面分别产生两条交线， ３切. 球连面线的。交注线意为轮圆廓弧线。的棱可 见面性上。的交线与圆弧的交点 就是三棱柱与球面的交线 上的点。
4. 求大小两圆柱的交线。
3 圆柱和与之 相切的平面立
体
交线
1 小圆柱 正 交
2 大圆柱
擦除多余的作图线后的结果
［例题十］ 补全图中所缺的交线 PV
形作体图分步析骤
1. 求该小模圆型柱由与两圆个台圆的柱交和线；
PW
一个圆台组成。其中大圆 2. 柱求与两圆圆台柱同的轴交，线小。圆柱与
圆台的轴线垂直。
擦除多余作图线后的结果
讨论：当两圆柱正交时，随着直径变化，相贯线的变化趋势？
当两圆柱正交时，交线的投影由小圆柱内向大圆柱内弯曲。随着 小圆柱直径增大，大圆柱直径不变，交线弯曲程度越大。当两个圆柱 直径相等时，交线的投影为直线。
［例题四］补全主视图