平方反比定律的验证实验

引力平方反比定律
1. 表述
- 任意两个质点通过连心线方向上的力相互吸引。

该引力的大小与它们的质量乘积成正比，与它们距离的平方成反比，与两物体的化学组成和其间介质种类无关。

其数学表达式为F = G(m_1m_2)/(r^2)，其中F是两个质点间的引力，G是引力常量（G = 6.67×10^-11N· m^2/kg^2），m_1和m_2分别是两个质点的质量，r是两个质点间的距离。

1. 早期探索
- 古代哲学家对天体运动和物体之间的相互吸引就有过一些思考，但没有形成科学的理论。

例如，古希腊的亚里士多德认为物体的运动需要力来维持，这种观点在当时影响很大，但后来被证明是不准确的。

2. 科学革命时期的铺垫
3. 牛顿的贡献
1. 卡文迪许扭秤实验（间接验证）
- 实验装置：卡文迪许使用了一个扭秤，由一根轻而细长的石英丝悬挂着一根横杆，横杆两端各有一个质量为m的小铅球。

在横杆附近放置两个大铅球，质量为M。

1. 对天体力学的意义
2. 对物理学发展的意义
3. 在工程技术中的应用。

简介电的平方反比定律指出，电场强度与离源的距离的平方成反比。

这一定律是由亨利-卡文迪什于1776年首次提出的，此后一直在实验中得到验证。

这篇文章将讨论平方反比定律的历史，它的数学表述，以及它的实验验证。

平方反比定律的历史反平方律是由亨利-卡文迪许在1776年首次提出的。

他提出，当两个电荷相隔一定距离时，它们的相互作用遵循反平方律。

这意味着，如果一个电荷增加一倍，那么它们之间的力将减少到原来的四分之一。

卡文迪许的工作为理解电场如何相互作用以及它们如何与物质相互作用奠定了基础。

1820年，迈克尔-法拉第进一步发展了卡文迪许的工作，并提出电场在空气或水等介质中传播时服从反平方律。

法拉第的工作使人们对电场如何与物质相互作用有了更全面的了解，并有助于建立对电的现代理解。

平方反比定律的数学表述平方反比定律的数学表述是：如果两个电荷q_1和q_2相隔一段距离，那么它们的相互作用就遵循平方反比定律。

F = frac{q_1q_2}{4\pi\epsilon_0r^2}。

其中F是它们之间的力，q_1和q_2是它们各自的电荷，epsilon_0是自由空间的引力（8.854 x 10^{-12} C^2/Nm^2），r是它们的分离距离。

这个方程可以用来计算任何给定距离的两个电荷之间的力。

平方反比定律的实验验证自从卡文迪许在1776年首次提出平方反比定律以来，它已经在实验中得到验证。

验证这一定律的最常用方法是测量两个带电物体之间的力与它们的分离距离的函数关系。

这可以通过一个被称为静电天平的仪器来完成，该仪器使用弹簧秤或其他力传感器测量两个带电物体在不同距离上的力。

通过测量不同距离的这些力，有可能确定它们是否如理论所预测的那样服从反平方关系。

除了使用静电平衡来验证这一定律外，还可以使用库仑定律来验证，库仑定律指出。

F=frac{kq_1q_2}{r^2}。

其中k是库仑常数（8.99 x 10^9 Nm^2/C^2）。

通过使用库仑定律测量不同距离的两个带电物体之间的力，可以验证它们是否如理论所预测的那样服从反平方关系。

“光照度平方反比定律”的实验设计
作者：张静
来源：《物理教学探讨》2009年第07期
摘要:本文利用光度学的有关知识,设计了一个检验光照度的距离平方反比定律的实验。

通过这个实验可以帮助学生进一步理解光通量、发光强度、光照度的概念,以及学会用Matlab软件描点画图和分析曲线关系。

关键词:光照度;平方反比定律;实验设计
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2009)7(S)-0075-3
我们所熟悉的万有引力作用和电磁相互作用都遵循距离的平方反比定律,平方反比定律假定的基础是空间的均匀性和各向同性。

因此诸如光的照度、水的喷洒、均匀固体中热的传导等自然现象都服从平方反比关系。

本文就是通过一个简单实验来验证光照度的平方反比定律,该定律不仅可以帮助我们解释为何在众多恒星的包围下依然会有黑夜,而且可以理解天文学家如何用该定律来测量远距离的物体,甚至遥远星系。

1 实验目的
理解光通量、发光强度、光照度的概念,设计实验验证点光源的光照度满足距离平方反比定律,并能够用该定律测量距离。

2 实验原理
光的传播就是能量传播的过程。

单位时间内通过光源表面或接收面上某一面元的各种波长的总电磁辐射能称为通过该面元的辐射通量。

而光通量是指人眼所能感受到的辐射通量,光通量的多少就应以单位时间内通过某一界面的光能量的多少来衡量。

为了表征点光源发出的光通量的空间分布,我们定义点光源在某方向上单位立体角内发出的光通量为该方向的发光强度。

如图1所示,以r为轴取一立体角元dΩ,设dΩ内的光通量为dF,则沿r方向的发光强度为:。

万有引力的平方反比定律万有引力的平方反比定律是现代物理学的重要定律之一。

它由英国物理学家艾萨克·牛顿于17世纪末提出，并被广泛应用于解释天体运动、地球引力和行星轨迹等现象。

本文将全面介绍万有引力的平方反比定律的原理、实验验证和应用。

首先，让我们来了解万有引力的平方反比定律的原理。

根据牛顿的定律和引力的概念，我们知道物体之间的引力与它们的质量成正比，与它们之间的距离的平方成反比。

具体地说，如果两个物体的质量分别为m1和m2，它们之间的距离为r，则它们之间的引力F由以下公式给出：F =G * m1 * m2 / r²其中，G是一个常量，被称为万有引力常数，其值为6.67430×10^-11 N·(m/kg)²。

为了验证万有引力的平方反比定律，科学家进行了一系列的实验。

其中最著名的实验是亨利·卡文迪什于1798年进行的“开普勒斯实验”。

卡文迪什利用一个小铅球和一个地下深井构建了一个非常精确的实验装置，观察铅球在深井中的运动。

通过测量铅球的运动轨迹和时间，卡文迪什验证了万有引力的平方反比定律。

这个实验对后来爱因斯坦的相对论物理理论有着重要的影响。

实验证明，万有引力的平方反比定律在宏观尺度上成立。

例如，地球的引力能够保持人类和其他物体在地表上向下运动。

它也能够保持地球与其他行星绕着太阳运动，并维持星系之间的稳定。

通过运用万有引力的平方反比定律，科学家们能够解释和预测一系列与引力相关的现象，为太阳系和宇宙的起源和演化提供了重要线索。

此外，万有引力的平方反比定律也被广泛应用于地球上的工程和科学领域。

在航空航天工程中，科学家们利用它计算卫星和航天器的轨道，确保它们能够准确地环绕地球。

我们也可以通过万有引力的平方反比定律来计算地球上的物体的重力，为建筑物的设计和桥梁的承重能力提供了重要的依据。

尽管万有引力的平方反比定律在许多方面是有效的，但它也存在一些局限性。

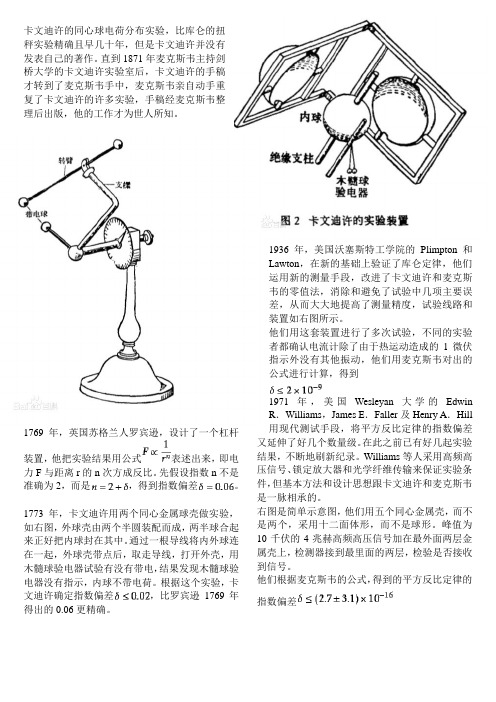
卡文迪许的同心球电荷分布实验，比库仑的扭秤实验精确且早几十年，但是卡文迪许并没有发表自己的著作。

直到1871年麦克斯韦主持剑桥大学的卡文迪许实验室后，卡文迪许的手稿才转到了麦克斯韦手中，麦克斯韦亲自动手重复了卡文迪许的许多实验，手稿经麦克斯韦整理后出版，他的工作才为世人所知。

1769年，英国苏格兰人罗宾逊，设计了一个杠杆装置，他把实验结果用公式表述出来，即电力F与距离r的n次方成反比。

先假设指数n不是准确为2，而是，得到指数偏差。

1773年，卡文迪许用两个同心金属球壳做实验，如右图，外球壳由两个半圆装配而成，两半球合起来正好把内球封在其中。

通过一根导线将内外球连在一起，外球壳带点后，取走导线，打开外壳，用木髓球验电器试验有没有带电，结果发现木髓球验电器没有指示，内球不带电荷。

根据这个实验，卡文迪许确定指数偏差，比罗宾逊1769年得出的0.06更精确。

1936年，美国沃塞斯特工学院的Plimpton和Lawton，在新的基础上验证了库仑定律，他们运用新的测量手段，改进了卡文迪许和麦克斯韦的零值法，消除和避免了试验中几项主要误差，从而大大地提高了测量精度，试验线路和装置如右图所示。

他们用这套装置进行了多次试验，不同的实验者都确认电流计除了由于热运动造成的1微伏指示外没有其他振动，他们用麦克斯韦对出的公式进行计算，得到1971年，美国Wesleyan大学的Edwin R．Williams，James E．Faller及Henry A．Hill 用现代测试手段，将平方反比定律的指数偏差又延伸了好几个数量级。

在此之前已有好几起实验结果，不断地刷新纪录。

Williams等人采用高频高压信号、锁定放大器和光学纤维传输来保证实验条件，但基本方法和设计思想跟卡文迪许和麦克斯韦是一脉相承的。

右图是简单示意图，他们用五个同心金属壳，而不是两个，采用十二面体形，而不是球形。

峰值为10千伏的4兆赫高频高压信号加在最外面两层金属壳上，检测器接到最里面的两层，检验是否接收到信号。

关于库仑定律（成立条件、精确度、使用范围）1785年（我国清代乾隆五十年），法国科学家库仑（Charles Augustin Coulomb ，1736～1806年，军事工程师，退休后从事电学研究）用扭秤实验得出：两个静止的点电荷之间的相互作用力与它们之间的距离平方成反比．这一规律的发现比牛顿发现万有引力迟100年．另外，值得指出的是，第一，在库仑做他的著名“扭秤”实验时，对电荷的量还没有明确的定义和度量方法，故在他的研究报告（《法兰西皇家科学院研究报告集》第569页）中，只强调了反平方定律，并没有明确提到电力与电荷的电量成正比．关于电量的严格定义是高斯等人在以后作出的，所以，现在我们所看到的库仑定律是后人在库仑扭秤实验结论基础上发展起来的．第二，如果真要用实验来确定两个点电荷之间的相互作用力，则应在真空中进行．如果在介质中进行，会影响测量的精确性．事实上，当初（1785年）库仑的所有测定都是在真空中做的．库仑定律不仅是静电学的基础，也是整个电磁理论的基础之一．由库仑定律可以推出静电场方程乃至整个麦克斯韦方程组，而且库仑定律还标志着：人们对电磁现象的研究由定性的观察过渡到用仪器作定量的测量，并总结出定量的规律，从而开创了用近代的科学方法研究电磁现象的道路．库仑定律在近代物理理论中也具有重要的意义，它隐含着光子的静电质量为零的结论．正因为库仑定律有如此的重要性，所以，我们有必要对库仑定律的成立条件、适用范围及平方反比的精度等问题作深入的研究和探讨．1、库仑定律的成立条件关于库仑定律的成立条件，尽管各书籍的说法不一，但归纳起来不外有三条，即，（1）电荷是点电荷；（2）在真空中；（3）电荷处于静止状态．下面，我们将逐条分析．条件（1）应该说是容易理解的，亦是正确的．因为用库仑定律计算两点电荷之间的作用力要用到距离，而只有点电荷，两带电导体之间的距离才有完全确定的意义（点电荷是个相对概念，详见扩展资料中“点电荷与检验电荷”）．然而，从微积分的观点看，任何连续分布的电荷都可看成无限多个电荷元（即点电荷）的集合，再利用叠加原理，就可求出非点电荷情况下的电场分布．所以，从上述分析可知，条件（1）确是库仑定律的成立条件，但不是限制库仑定律的使用条件．条件（2）是完全多余的（但不能说错），因为只要是两个点电荷，不管它们在什么地方（是在真空、导体还是介质中），相互作用力都遵从库仑定律．但要注意的是，在有其他物质存在时，这些物质会受到原来两电荷的电场作用，从而产生极化电荷或感应电荷．因此，原来两个电荷中的每一个，都要受到这些极化电荷或感应电荷的影响，这时它们所受的作用力一般就比较复杂了，好在有一个例子能加以说明．在均匀无限大介质（0εεεr =）中，两个点电荷之间的作用力是真空中的r ε/1倍，即2021022144r rq q r rq q F r επεπε==（1）从形式上看，（1）式似乎就是库仑定律在介质中不成立的佐证．殊不知在均匀无限大介质中，两个点电荷还要使介质产生相应的宏观极化电荷，如图所示．很明显，点电荷1q 要受到三种电荷的作用力，极化电荷1q '-均匀地包围着，由对称性可知，其对1q 的作用力为零，极化电荷2q '-由于距1q 较远，可看作点电荷，位置与2q 相同，故根据库仑定律，1q 所受到的力为：20210202144r rq q r rq q F πεπε'==（2）由电磁学理论可以证明，2q '和2q 的关系满足下式： 2021q q ⎪⎭⎫ ⎝⎛-='εε （3） 将（3）式代入（2）式可得： 2201202201414q rq q q r q F εεπεεεπε=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--'=22141rq q πε= （4）（4）式写成矢量形式为：20214r rq q F r επε=（5）可见，（5）式与（1）式完全相同．由此可见，只要我们把介质中的宏观极化电荷与自由电荷同等看待，那么，它们彼此间的作用力都遵从库仑定律，因而没有必要强调一定要在真空中库仑定律才成立．至于条件（3），即电荷处于静止状态，也可以适当放宽，不必要两个点电荷都相对于观察者静止，只要源电荷（施力电荷）保持静止就可以，受力电荷可以是静止的，也可以做任意运动．道理很简单，静止电荷在空间激发的电场是不随时间变化的，仅是空间的函数，运动电荷所受到的由静止电荷所激发的电场力只与两电荷的相对位置和它们本身的电量有关，即遵从库仑定律．反之，静止电荷所受到的由运动电荷激发的电场力，由狭义相对论电动力学可知，这个力不但与两个电荷的相对位置和电量有关，而且还与运动电荷的速度有关，即它们之间的作用不再遵从库仑定律．在这种情况下，连牛顿第三定律也不再遵守．如图所示，设点电荷1q 以速度v 匀速向右运动，点电荷2q 静止不动，则由上述观点，2q作用在1q 上的力为：2021124r rq q F πε=（6）即遵从库仑定律．但反过来，1q 作用在2q 上的力却不遵从库仑定律．根据电动力学理论，1q 在2q 处激发的电场强度为：2/3222022201114⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⋅=cr r v c v r c v rq E πε （7）式中c 是真空中的光速．因此，按qE F =计算，1q 作用在2q 上的力便为：2/3222022202121114⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⋅=cr r v c v r c v rq q F πε （8）从（8）式可知，1q 作用在2q 上的力已不再遵从库仑定律；只有当0=v 时，（8）式才退化为真空中的库仑定律．比较（6）式和（8）式还可以看出，当两个点电荷有相对运动时，它们之间的相互作用力也不再遵从牛顿第三定律．但可以证明两点电荷与它们所产生的电磁场所构成的系统满足包括电磁动量和机械动量在内的动量守恒定律．2、平方反比律的精确度 库仑定律是一个实验定律，由于实验装备的精确度是有限的，所以实验结果与库仑定律并不完全一致．验证平方反比律的一种方法是假定力按δ±2/1r变化，然后用实验测出δ的值．显然，δ值越小，实验精确度越高，从而表明库仑定律越准确．事实上，对电荷之间作用力所遵循的规律，早在库仑以前就有人进行过研究．1769年，罗比逊第一个从实验确定δ值约为0.06；1773年，卡文迪许实验测出的δ不大于0．02；1785年，库仑自己测出的δ为百分之几．关于库仑定律平方反比律精确度的研究，一直为历代物理学家高度重视，迄今未停止过．由于实验装置精确度的不断提高，至今精度最高的是1971年威廉姆斯等人所作的实验，他们测出的16102-⨯≤δ．为便于查阅，现将自罗比逊以后各次主要实验所得到的偏差值列表如下验证平方反比律的实验结果近代许多科学家之所以重新对库仑定律中的平方反比关系发生那么大的兴趣，主要是与对光子的静质量的关心有关，而光子的静质量是否为零，又与相对论的基本假设之一的光速不变原理有关．可以证明，若0≠δ，则光子的静质量将不为零．目前这方面的探讨还与磁单极的探索相联系．如果真的发现了磁单极，则光子的静质量必为零，库仑定律的平方反比关系也就严格成立了．3、库仑定律的适用范围库仑定律除了有一个平方反比律的精度问题外，还有一个适用范围的问题，因为所有验证库仑定律的实验都是囿于0210~10-米的范围内进行的．试问，超出0210~10-米这个空间范围，库仑定律是否还成立呢？库仑定律的适用范围到底有多大呢？兰姆和卢瑟福对氢原子的能级作了精确测量，与用库仑定律计算出的结果相吻合；另外，卢瑟福的X 粒子散射实验的精确测量与库仑定律也相吻合，这表明库仑定律在原子范围内（1010-米）是成立的．近代核物理实验证明在原子核的大小范围（1510-米）内，库仑定律不再成立，但在1310-米范围内，库仑定律精确成立．地球物理实验证明库仑定律在710~10米范围内是精确成立的．在更大的距离（如天文距离——26710~10米）范围内，物理学家虽然没有对库仑定律进行过实验验证，但是，在那样巨大的空间中，电磁波仍然以光速在传播，电磁场的规律仍然起作用．因此，可以推断，在那样大的范围内，库仑定律仍然有效．库仑定律的实验验证虽然都是在0210~10-米范围内进行，但其适用范围可扩展到261310~10-米．。

牛顿巧证平方反比-概述说明以及解释1.引言1.1 概述：牛顿巧证平方反比是牛顿在物理学领域所作出的重要贡献之一。

通过对重力现象的深入研究和实验，牛顿发现了物体间的引力与它们之间的距离的平方成反比的关系，即平方反比定律。

这一发现不仅在当时引起了轰动，也为后世的物理学发展奠定了基础。

本文将对牛顿的生平背景、平方反比定律的提出及其实验与证明进行探讨，在深入分析牛顿巧证平方反比的意义和他在科学上的重要贡献的基础上，对这一重要发现进行全面的论述和解析。

1.2 文章结构在本文中，我们将通过三个主要部分来探讨牛顿巧证平方反比的相关内容。

首先，在第二部分中，我们会介绍牛顿的生平背景，了解他在科学领域的成就和影响。

接着，我们将详细讨论平方反比定律的提出，探讨牛顿是如何得出这一定律的。

最后，我们会深入研究实验与证明的过程，揭示牛顿是如何通过实践验证这一定律的正确性。

通过这些内容的呈现，我们希望能全面了解牛顿巧证平方反比的意义以及他对科学领域所做出的不可磨灭的贡献。

文章1.3 目的:本文旨在探讨牛顿巧证平方反比定律的过程和意义，通过介绍牛顿的生平背景、平方反比定律的提出以及实验与证明的过程，分析牛顿在科学领域的贡献和他对物理学的重大影响。

通过对这一重要科学定律的深入研究，可以更好地理解牛顿的思想和方法，同时也可以体会到科学研究中的创新与突破。

探讨牛顿巧证平方反比的意义，可以帮助我们更全面地认识和理解自然界的规律，感受到科学探索的魅力和价值。

最终，希望通过本文的撰写，让读者更加深入地了解牛顿的科学思想，激发大家对科学研究的兴趣和热情。

2.正文2.1 牛顿的生平背景艾萨克·牛顿（Isaac Newton，1643年12月25日-1727年3月20日）是英国著名的物理学家、数学家和天文学家，也是科学史上最重要的人物之一。

他出生在英格兰的林肯郡，父母早逝，由祖母抚养长大。

牛顿在青少年时代表现出非凡的数学天赋，但由于家庭贫困，他无法接受正规的教育，只能在家自学。

高中物理18个实验及实验结论
高中物理有许多实验，以下是其中 18 个实验及实验结论的列表:
1. 平方反比定律实验：证明电流与电压成正比，与电阻成反比。

2. 单摆实验：证明物体在弹性限度内，外力愈大，振动愈短促。

3. 振动实验：证明物体振动时，振动频率与振幅无关，与外力
有关。

4. 碰撞实验：证明动量守恒定律，能量守恒定律。

5. 牛顿第一定律实验：证明任何物体都保持静止或匀速直线运
动状态，直到有外力作用于它为止。

6. 牛顿第二定律实验：证明物体所受的合外力等于物体质量与
加速度的乘积，即 F=ma。

7. 牛顿第三定律实验：证明任何作用力都有一个相等反作用力，且作用与反作用力的大小相等、方向相反。

8. 静电场实验：证明电荷守恒定律，库仑定律。

9. 直流电路实验：证明欧姆定律。

10. 波动实验：证明波的发生和传播依赖于介质。

11. 光的本性实验：证明光具有波动性和粒子性，提出“波粒二象性”理论。

12. 棱镜色散实验：证明光的颜色是由光波的振幅和频率决定的。

13. 光合作用实验：证明光合作用是光能转化为化学能的过程。

14. 浮力实验：证明物体沉浮与重力和浮力的关系。

15. 杠杆原理实验：证明杠杆的平衡条件。

16. 功和能的实验：证明功等于能量转化的量。

17. 温度实验：证明热胀冷缩规律，解释物体热胀冷缩的现象。

18. 万有引力实验：证明万有引力定律。

这些实验是物理学中非常重要的实验，它们证明了物理学中的基本定律，为物理学的发展做出了巨大贡献。