第16讲 正方形

第15讲 立体几何中的翻折问题一、学习目标1. 掌握翻折问题的基本结论；2. 掌握翻折问题的基本处理策略.翻折问题的基本结论：ABC ∆中，BC AO ⊥，将ABC ∆沿着边BC 翻折到BC A '∆，在翻折的过程中有 ①BC OA ⊥，BC OA ⊥'，'AOA ∠是二面角'A BC A --的平面角； ②'A 在底面上的投影一定在直线''AA 上； ③'BA BA =，'CA CA =；④点A 的轨迹是以O 为圆心的圆，AC AB 、的轨迹是以BC 为旋转轴的两个圆锥侧面.二、典例分析例1.（1）如图，在正方形ABCD 中，点F E 、分别是BC AB 、的中点，点G 是EF 的中点，现在沿DF DE 、及EF 把这个正方形折成一个四面体，使C B A 、、三点重合，重合后的点记为P ，则在四面体DEF A -'中必有（ ）A.⊥PD 平面EF A 'B.⊥DG 平面PEFC.⊥PE 平面DEFD.PG ⊥平面DEF9．如图，以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕，翻折ABD △和ACD △，使得平面ABD ⊥平面ACD .下列结论错误的是（ ）A ．BD AC ⊥B ．ABC 是等边三角形 C ．三棱锥D ABC -是正三棱锥D ．平面ACD ⊥平面ABC【答案】（1）C ； （2）D. 变式：（1）已知正三角形ABC 的中线AF 与中位线DE 相交于点G ，ED A '∆是AED ∆绕DE 旋转过程中的一个图形，则下列结论错误的是（ ）A.动点'A 在平面ABC 上的射影在线段AF 上B.三棱锥FED A -'的体积有最大值C.恒有平面⊥GF A '平面BCEDD.异面直线E A '与BD 不可能互相垂直【答案】D（2）如图，在矩形ABCD 中，AD AB 2=，E 为AB 的中点，将ADE ∆沿直线DE 翻折成DE A '∆，若M 是线段C A 1的中点，则在ADE ∆翻折的过程中，下列命题正确的是（ ）A.BM 是定值B.M 的轨迹是一段圆弧C.//BF 平面DE A 'D.存在某个位置，使得C A DE 1⊥【答案】D例2.（1）已知矩形ABCD ，1,2AB BC ==ABD ∆沿矩形的对角线BD 所在的直线经翻折，在翻折过程中（ ）A.存在某个位置，使得直线AC 与BD 垂直B.存在某个位置，使得直线AB 与CD 垂直C.存在某个位置，使得直线AD 与BC 垂直D.对任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直（2）如图，在菱形ABCD 中，︒=∠60BAD ，线段BD AD ,的中点分别为F E ,，现将ABD ∆沿对角线BD 翻折，则异面直线BE 与CF 所成角的取值范围是（ ）A.)3,6(ππ B.]2,6(ππ C.]2,3(ππ D.)32,3(ππ【答案】（1）B ； （2）C.. 变式：1.在正方形ABCD 中，点F E 、分别是AD BC 、的中点，将ABF ∆沿BF 所在的直线进行翻折，将CDE ∆沿DE 所在的直线进行翻折，在翻折的过程中，（ ） A.点A 与点C 在某一位置可能重合 B.点A 与点C 的最大距离为AB 3 C.直线AB 与直线CD 可能垂直 D.直线AF 与直线CE 可能垂直【答案】D2.如图，在ABC Rt ∆中，1=AC ，x BC =，D 是斜边AB 的中点，将BCD ∆沿直线CD 翻折，若在翻折过程中存在某个位置，使得AD CB ⊥，则x 的取值范围是（ ） A.]3,0( B.]2,22（ C.]32,3( D.]4,2( 【答案】A例3.（1）如图，在长方形ABCD 中，3,1AB BC ==，E 为线段DC 上一动点，现将AED ∆沿AE 折起，使得点D 在面ABC 上的射影K 在直线AE 上，当E 从D 运动到C ，则K 所形成的轨迹的长度是__________.（2）如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点．现将AFD ∆沿AF 折起，使平面ABD ⊥平面ABC ．在平面ABD 内过点D 作DK AB ⊥，K 为垂足．设AK t =，则t 的取值范围是 ．【答案】（1）3π； （2）)1,21(. 变式：1.在矩形ABCD 中，3=AB ，1=BC ，E 为DC 的三等分点（靠近C 处），F 为线段EC 上一动点（包括端点），现将AFD ∆沿AF 折起，使D 点在平面内的射影恰好落在边AB 上，则当F 运动时，二面角B AF D --的余弦值的取值范围是________.【答案】]41,91[例4.如图，在平行四边形ABCD 中，2AB BC =，120ABC ∠=︒，E 为线段AB 的中点，将ADE ∆沿直线DE 翻折成'A DE ∆，使平面'A DE ⊥平面BCD ，F 为线段'A C 的中点。

第16讲数数图形（二）专题简析：在解决数图形问题时，首先要认真分析图形的组成规律，根据图形特点选择适当的方法，既可以逐个计数，也可以把图形分成若干个部分，先对每部分按照各自构成的规律数出图形的个数，再把他们的个数合起来。

数长方形可以用公式：长边上的线段×短边上的线段=长方形的个数练习1：数一数，下面各图中分别有几个长方形？例：数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）分析与解答：图中边长为1个长度单位的正方形有3×3=9个，边长为2个长度单位的正方形有2×2=4个，边长为3个长度单位的正方形有1×1=1个。

所以图中的正方形总数为：1+4+9=14个。

经进一步分析可以发现，由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为：1×1＋2×2＋…＋n×n。

练习2：数一数下列各图中分别有多少个正方形？（每个小方格为边长是1的小正方形）例：数一数下图中有多少个正方形？（其中每个小方格都是边长为1个长度单位的正方形）分析与解答：边长是1个长度单位的正方形有3×2=6个，边长是2个长度单位的正方形有2×1=2个。

所以，图中正方形的总数为：6+2=8个。

经进一步分析可以发现，一般情况下，如果一个长方形的长被分成m等份，宽被分成n等份（长和宽的每一份都是相等的）那么正方形的总数为：mn+(m－1)(n－1)＋(m－2)(n－2)＋…＋(m－n＋1)练习31．数一数下列各图中分别有多少个正方形。

2．下图中有多少个长方形，其中有多少个是正方形？练习41，求下图中所有线段的总和。

（单位：米）2，求下图中所有线段的总和。

（单位：厘米）。

第十六讲 特殊图形一、长方体和正方体如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．①在六个面中，两个对面是全等的，即三组对面两两全等．(叠放在一起能够完全重合的两个图形称为全等图形．)②长方体的表面积和体积的计算公式是：长方体的表面积：2()S ab bc ca =++长方体；长方体的体积：V abc =长方体．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为a ，那么：26S a =正方体，3V a =正方体．二、圆柱与圆锥c b a HG F EDC B A1.掌握立体图形的特征，能通过分析图形的特征解题。

2.灵活应用公式解题。

例1：如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？【解析】我们从三个方向(前后、左右、上下)考虑，新几何体的表面积仍为原立方体的表面积：10⨯10⨯6=600．例2：右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米)．每一个面被挖去一个边长是1厘米的正方形，同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分．总的来看，每一个面都增加了4个边长是1厘米的正方形．从而，它的表面积是：96+4⨯6=120平方厘米．例3：下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同为14厘米，那么最后得到的立体图形的表面积是多少平方厘米？【解析】我们仍然从3个方向考虑．平行于上下表面的各面面积之和：2⨯2⨯2=8(平方厘米)；左右方向、前后方向：2⨯2⨯4=16(平方厘米)，1⨯1⨯4=4(平方厘米)，1 2⨯1 2⨯4=1(平方厘米)，14⨯14⨯4=14(平方厘米)，这个立体图形的表面积为：816++4+1+14=1294(平方厘米).例4：一个正方体木块，棱长是1米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少？【解析】 锯一次增加两个面，锯的总次数转化为增加的面数的公式为：锯的总次数⨯2=增加的面数．原正方体表面积：1⨯1⨯6=6(平方米)，一共锯了(2-1)+(3-1)+(4-1)=6次，6+1⨯1⨯2⨯6=18(平方米)．例5：如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？【解析】 当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木，当拼成一个333⨯⨯的正方体时，表面积最小，现在要去掉2块小积木，只有在两个角上各去掉一块小积木，或在同一个角去掉两块相邻的积木时，表面积不会增加，该几何体表面积为54.例6：要把12件同样的长a 、宽b 、高h 的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？⑴当 b =2h 时，如何打包？⑵当 b <2h 时，如何打包？⑶当 b >2h 时，如何打包？【解析】 图2和图3正面的面积相同，侧面面积=正面周长⨯长方体长，所以正面的周长愈大表面积越大，图2的正面周长是8h +6b ，图3的周长是12h +4b .两者的周长之差为2（b -2h ）.当b =2h 时，图2和图3周长相等，可随意打包；当b <2h 时，按图2打包；当b >2h 时，按图3打包.25块积木图3图2图1hba（分A/B/C易、中、难三档，每档题目数量根据课程难度自行搭配，总共不少于15道题。

第十六讲特殊图形一、长方体和正方体如右图，长方体共有六个面(每个面都是长方形)，八个顶点，十二条棱．①在六个面中，两个对面是全等的，即三组对面两两全等．(叠放在一起能够完全重合的两个图形称为全等图形．)②长方体的表面积和体积的计算公式是：长方体的表面积：；长方体的体积：．③正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形．如果它的棱长为，那么：，．二、圆柱与圆锥1.掌握立体图形的特征，能通过分析图形的特征解题。

2.灵活应用公式解题。

例1：如右图，在一个棱长为10的立方体上截取一个长为8，宽为3，高为2的小长方体，那么新的几何体的表面积是多少？【解析】我们从三个方向(前后、左右、上下)考虑，新几何体的表面积仍为原立方体的表面积：10106600．例2：右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）【解析】原正方体的表面积是44696(平方厘米)．每一个面被挖去一个边长是1厘米的正方形，同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分．总的来看，每一个面都增加了4个边长是1厘米的正方形．从而，它的表面积是：9646120平方厘米．例3：下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为厘米的正方形小洞，第三个正方形小洞的挖法和前两个相同为厘米，那么最后得到的立体图形的表面积是多少平方厘米？【解析】我们仍然从3个方向考虑．平行于上下表面的各面面积之和：2228(平方厘米)；左右方向、前后方向：22416(平方厘米)，1144(平方厘米)，41(平方厘米)，4(平方厘米)，这个立体图形的表面积为：41(平方厘米).例4：一个正方体木块，棱长是1米，沿着水平方向将它锯成2片，每片又锯成3长条，每条又锯成4小块，共得到大大小小的长方体24块，那么这24块长方体的表面积之和是多少？【解析】锯一次增加两个面，锯的总次数转化为增加的面数的公式为：锯的总次数2增加的面数．原正方体表面积：1166(平方米)，一共锯了(21)(31)(41)6次，6112618(平方米)．例5：如图，25块边长为1的正方体积木拼成一个几何体，表面积最小是多少？【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木，当拼成一个的正方体时，表面积最小，现在要去掉2块小积木，只有在两个角上各去掉一块小积木，或在同一个角去掉两块相邻的积木时，表面积不会增加，该几何体表面积为54.例6：要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体，使打包后表面积最小，该如何打包？⑴当b2h时，如何打包？⑵当b2h时，如何打包？⑶当b2h时，如何打包？【解析】图2和图3正面的面积相同，侧面面积正面周长长方体长，所以正面的周长愈大表面积越大，图2的正面周长是8h6b，图3的周长是12h4b.两者的周长之差为2（b2h）.当b2h时，图2和图3周长相等，可随意打包；当b2h时，按图2打包；当b2h时，按图3打包.（分A/B/C易、中、难三档，每档题目数量根据课程难度自行搭配，总共不少于15道题。

第十六讲完美的正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形，换句话说：正方形是各边都相等的矩形，正方形是各角都相等的菱形，正方形既是矩形又是菱形，它具有矩形和菱形的一切性质．矩形、菱形，正方形都是特殊的四边形，它们的概念交错，关系复杂，性质有许多相似之处，一些判定和性质定理又是可逆的，所以在学习中注重概念的理解，着眼于概念间的区别与联系．连正方形的对角线，能得到特殊三角形、全等三角形，由于正方形常常与直角三角形联系在一起，所以在解有关正方形问题时要用到直角三角形性质，具有代数风格，体现数形结合思想．熟悉以下基本图形，基本结论：例题求解【例1】如图，若四边形ABCD是正方形，△CDE是等边三角形，则∠EAB的度数为．(北京市竞赛题)思路点拨图中还有等腰三角形，利用等腰三角形性质计算．注可以证明，在所有用长相等的四边形中，正方形的面积最大．我们熟悉的“七巧板”，那是把一块正方形板切分成三角形、正方形、平行四边形的7块，用它可以拼出许多巧妙的图形，“七巧板”是我国古代人民智慧的结晶．【例2】如图，在正方形ABCD中，O是对角线AC、BD的交点，过O作OC⊥OF，分别交AB、BC 于E、F，若AE=4，CF=3，则EF的长为( )A．7 B．5 C．4 D．3(江苏省泰州市中考题)思路点拨AE、CF、EF不在同一个三角形中，运用全等三角形寻找相等的线段，使分散的条件集中到同一个三角形中．【例3】如图，正方形ABCD中，E、F是AB、BC边上两点，且EF=AC+FC，DG⊥EF于G，求证：DC=DA．(重庆市竞赛题)思路点拨构造AE+FC的线段是解本例的关键．【例4】已知正方形ABCD中，M是AB的中点，E是AB延长线上一点，MN⊥DM且交∠CBZ的平分线于N(如图甲)．(1)求证：MD=MN(2)若将上述条件中的“M是AB中点”改为“M是AB上的任意一点”，其余条件不变(如图乙)，则结论“MD=MN”还成立吗?如果成立，请证明：如果不成立，请说明理由．(上海市闽行区中考题)思路点拨对于图甲，取AD中点F，通过构造全等三角形证明MD=MN；这种证法能否迁移到图乙情景中去?从而作出正确的判断．注探索是学习的生命线，深入探究、学会探索是时代提出的新要求．数学解题中的探索活动可从以下几个方面进行：(1)在题设条件不变情况下，发现挖掘更多的结论；(2)通过强化或弱化来改变条件，考查结论是否改变或寻求新的结论；(3)构造逆命题．对于例3，请读者思考，在不改变题设条件的前提下，(1)∠EDF等于多少度?(2)怎样证明明逆命题?例4改变点的位置，赋以运动，从特殊到一般，(1)的结果为(2)的猜想提供了借鉴的依据，又为猜想设置了障碍，前面的证明思路是后面的证明模式．【例5】操作：将一把三角尺放在边长为l的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．探究：设A，P两点间的距离为x(1)当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论；(2)当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的关系式，并写出x的取值范围；(3)当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形?如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由(图1、图2、图3的形状大小相同，图1供操作、实验用，图2、图3备用)．思路点拨本例是探究式的操作型试题，第(1)问需抓住滑动中∠BPQ是直角这一不变量，画出滑动中一般情形的图形，通过观察提出猜想，再给予论证，第(3)问需要在操作中观察出使△PCQ是等腰三角形的两种情形．注数学学习是一个生动活泼的过程，动手实践，自主探索是学习数学的重要形式，它说明了存在的事实是怎样被发现和被发现的现象又是怎样获得证实的，解这类问题，需边操作，边观察、边思考，综合运用相关知识方法探究结论．学力训练1．如图，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PB=3，则PP′= ．河南省中考题)2．如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 延长线上一点，CE=CF ，若∠BEC=60°，则∠EFD 的度数为 ． (苏州市中考题)3．如图，∠POQ=90°，边长为2㎝的正方形ABCD 的顶点B 在OP 上，C 在OQ 上，且∠OBC=30°，则A 、D 到OP 的距离分别为 ． (南京市中考题)4．如图，正方形ABCD 中，CE ⊥MN ，若∠MCE ＝35°，则∠ANM 的度数是 ．5．如图，E 是边长为l 的正方形ABCD 的对角线BD 上一点，且BE=BC ，P 为CE 上任意一点，PQ ⊥BC 于点Q ，PR ⊥BE 于点R ，则PQ+PR 的值为( ) (河北省中考题)A ．22 B ．21 C ．23 D ．326．如图，在四边形ABCD 中，AB=BC ，∠ABC=∠CDA=90°，BE ⊥AD 于E ，8 ABCD S 四边形，则BC 的长为( )A ．2B ．3C ．3D ．22 (武汉市选拔赛试题)7．如图，在正方形ABCD 中，C 为CD 上的一点，延长月C 至F ，使CF=CE ，连结DF ，BE 与DF 相交于G ，则下面结论错误的是( )A ．BE=DFB ．BG ⊥DFC ．∠F+∠CEB=90°D ．∠FDC+∠ABG ＝90°(山东省临沂市中考题)8．如图，已知正方形ABCD 的面积为256，点F 在AD 上，点E 在AB 的延长线上，Rt △CEF 的面积为200，则BE 的值是( )A ．15B ．12C ．11D ．109．(1)如图甲，若点P 为正方形ABCD 边AB 上一点，以PA 为一边作正方形AEFP ，连BE 、DP ，并延长DP 交BE 于点H ，求证：DH ⊥BF ；(2)如图乙，若点P 为正方形ABCD 内任一点，其余条件不变，(1)的结论是否成立?若成立，请给出证明；若不成立，请说明理由．(泰州市中考题)10．如图，P为正方形ABCD的对角线BD上任一点，PF⊥CD，PE⊥BC，C、F分别为垂足，探索AP与EF的关系．11．如图，正方形ABCD中，AB=3，点E，F分别在BC、CD上，且∠BAE=30°，∠DAF=15°，求△AEF的面积．( “希望杯”邀请赛试题)12．如图，已知E、F分别是正方形ABCD的边BC、CD上的点，AE、AF分别与对角线BD相交于M、N，若∠EAF=50°，则∠CME+∠CNF= ．13．如图，在Rt△ABC中，∠C＝90°，AC=3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，OC=24，则BC边的长为．( “希望杯”邀请赛试题)14．如图，A 在线段BG 上，ABCD 和DEFG 都是正方形，面积分别为7㎝2和11㎝2，则△CDE 的面积等于 cm 2．(武汉市选拔赛试题)15．如图，将边长为12cm 的正方形ABCD 折叠，使得A 点落在边CD 上的E 点，然后压平得折痕FG ，若GF 的长为13cm ，则线段CE 的长为 ． (北京市竞赛题)16．将一个正方形分割成n 个小正方形(n>1)，则n 不可能取( )A ．4B ．5C ．8D ．9(江苏省竞赛题)17．如图，正方形ABCD 中，P 、Q 分别是BC 、CD 上的点，若∠PAQ=45°，∠BAP=20°，则∠AQP=( )A ．65°B ． 60°C ．35°D ．70°18．如图，ABCD 是边长为1的正方形，EFGH 是内接于ABCD 的正方形，AE=a ，AF=b ，若S EFGH =32，则a b 等于( )A ．22B ．32C ．23D ．33 ( “希望杯”邀请赛试题) 19．如图，BF 平行于正方形ADCD 的对角线AC ，点E 在BF 上，且AE=AC ，CF ∥AC ，则∠BCF 等于( )A ．150°B ．135°C ． 105°D ．120°20．图甲中，正方形ABDE 、CDFI 、EFGH 的面积分别为17，10，13，图乙中，DPQR 为矩形，对照图乙，计算图甲中六边形ABCIGH 的面积．(江苏省竞赛题)21．如图，在正方形ABCD中，P是CD上一点，且AP=BC+CP，Q为CD中点，求证：∠BAP=2∠QAD．22．如图，有4个动点P、Q、E、F分别从正方形ABCD的4个顶点出发，沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动．(1)判定四边形PQEF的形状；(2)PE是否总是经过某一定点，井说明理由；(3)四边形PQEF的顶点位于何处时，其面积最小、最大?各是多少?23．如图a，D为线段AE上任一点，分别以AD、DE为边作正方形ABCD和正方形DEFG，连结BF、AG、CE、BG、BE、BG、BE分别交AD，DC于P、Q两点．(1)①找出图中三对相等的线段(正方形边长相等除外)；②找出图中三对相等的钝角；③找出图中一对面积相等的钝角三角形，这两个三角形全等吗?(2)如图b，当正方形ABCD和正方形DEFG都变为菱形，且∠GDE=∠ADC时，(1)中的结论哪些成立，哪些不成立?请对不成立的情况说明理由．(3)如图“当正方形ABCD和正方形DEFG都变为矩形，且DA＞DC，DE>DG，△ABD∽△EFD时，(1)中的结论哪些不成立，哪些成立？．如果成立，请证明．(郴州市中考题)24．如图，正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形，P是EF与GH的交点，若矩形PFCH的面积恰是矩形AGPE面积的2倍，试确定∠HAF的大小，并证明你的结论．(北京市竞赛题)。

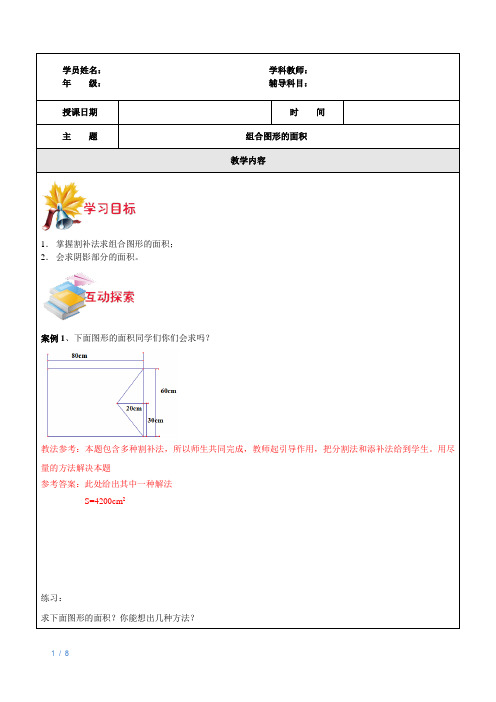
1．掌握割补法求组合图形的面积；2．会求阴影部分的面积。

案例1、下面图形的面积同学们你们会求吗？教法参考：本题包含多种割补法，所以师生共同完成，教师起引导作用，把分割法和添补法给到学生。

用尽量的方法解决本题参考答案：此处给出其中一种解法S=4200cm2练习：求下面图形的面积？你能想出几种方法？教法参考：学生在做的过程中会有不同的方法，教师可以让学生到黑板上演示自己的方法；或者让学生在一起探讨各自方法。

参考答案：总面积是525。

案例2、下图中甲和乙都是正方形，求阴影部分的面积教法参考：本题可以让学生在一起探究，教师从旁引导，在学生探究过程中遇到问题的时候给予一点的指导，并针对学生讨论时出现障碍以提问的形式引导学生思考，找到解决方法。

参考答案：阴影部分面积为18.练习：求图中阴影部分的面积。

教法参考：求阴影部分的面积同样引导学生用割补法的方法求出图形的面积。

参考答案：阴影部分面积为45.5知识点归纳：求组合图形的一般的方法：1.分割法：把一个组合图形分割成几个基础图形（平行四边形、正方形，矩形、三角形和梯形），分别求出面积，再求和；2.添补法：把一个组合图形补成一个基础图形，在从这个基础图形的面积减去几个基础图形的面积，求出它们的面积差。

（本环节可以采用学生轮流答题说解题方法，其他学生给予补充不同的解题方法）例题1、求下面图形的面积参考答案：总面积为209试一试：求下面图形的面积参考答案：1208 135.75例题2、求图形中阴影部分的面积参考答案：104 9试一试：求图形中阴影部分的面积参考答案：24例题3、如图，已知三角形ABC的面积是36平方厘米，D是AC的中点，BE=2ED，求阴影部的面积。

教法参考：本题有一定的难度，由教师主讲，引出同底等高的面积求法。

参考答案：因为D是AC的中点，所以S△ABD=S△BDC=S△ABC/2=18平方厘米因为BE=2ED，△ABE与△ADB同高，所以S△ABE=2/3*18=12.试一试：如图，已知平行四边形BCEF与长方形ABCD同底等高，AB=6厘米，BC=3厘米，CG=2DG，求梯形GFEC的面积。

（二年级）暑期备课教员：×××第16讲生活中的数学一、教学目标： 1. 学会把数学知识应用于生活实际。

2. 提高应用数学知识解决实际问题的能力。

3. 学会分析题中的条件和问题。

二、教学重点：学会分析题中的条件和问题。

三、教学难点：提高应用数学知识解决实际问题的能力。

四、教学准备：PPT、正方形和长方形五、教学过程：第一课时（50分钟）一、导入（7分)师：小朋友，在上课之前老师要问你们一个问题，你们去过超市么？生：去过。

师：去过超市的小朋友应该知道，我们在付钱的时候是要排队的，那你们知道应该怎么规范排队么？生：老师，我知道。

师：好，那这位小朋友，你上来给我们示范一下应该怎么排队。

排队一个人肯定是不够的，哪位小朋友也愿意上来给我们示范一下要怎么排队的。

恩，那就你们几个上来。

小朋友，你们觉得他们的队伍排得怎么样？生：很好，很整齐。

师：小朋友的眼睛还是雪亮的。

既然我们的小朋友的队伍排得那么整齐，为了奖励你们，老师决定考考你们。

×××（学生名字），你知道自己是排在第几个位置么？（队伍可排一排或者一列）生：我排在第2个位置。

师：你确定么？生：确定。

师：有小朋友有不同的看法么？生1：从后往前数，他是第4个位置。

生2：从前往后数，他是第2个位置。

师：是的，如果我们不知道一共有多少位小朋友人数，我们是不是可以根据×××所处的位置来计算总人数？生：可以。

师：是的，其实在排队中我们也是可以发现一些数学中的问题，所以小朋友们可不要小瞧数学。

感谢这些小朋友向我们展现应该怎么有秩序地排队，一人奖励一个大拇指。

我们的生活中处处都是有数学的。

今天就让我们一起来看看在我们的生活中会遇到的一些数学问题。

二、探索发现授课（40分）（一）例题一：（13分）几个人站成一排照相，阿派的左边和右边各有2个人。

一共有多少个人在照相？师：在拍照的时候，小朋友都是排排站好的，可是阿派这个人很粗心，他不知道自己和多少人一起拍照。

第十三站周长月日姓名【知识要点】一个图形的周长是指围成它的所有线段的长度和。

长方形周长=（长＋宽）×2 正方形周长=边长×4如果将几个长方形拼在一起，或将几个正方形拼在一起，那么图形的周长会发生变化，如果把长方形或正方形分成几个长方形或正方形，图形的周长也会发生变化。

【典型例题】例1 把3个边长3厘米的正方形拼成一个大长方形，大长方形的周长是多少厘米？例2 用一块长8分米，宽4分米的长方形与两个边长为4分米的正方形拼成一个正方形，拼成的正方形周长是多少分米？例3 一张长10厘米、宽8厘米的长方形纸片，把它剪开成两张同样的长方形纸片，每个小长方形纸片的周长是多少厘米？例4 一根铁丝长80厘米，围成一个边长为8厘米的正方形，余下的铁丝围成一个长为14厘米的长方形，这个长方形的宽是多少厘米？随堂小测姓名成绩1．把3个完全一样的小正方形拼成一个大长方形，这个长方形的周长是16分米，求每个正方形的周长。

2．用8个边长为5厘米的正方形拼成一个大长方形，拼成的大长方形的周长最大是多少？3．把一个长10厘米、宽6厘米的长方形，分成两个大小一样的长方形，每个长方形的周长是多少？4．一根铁丝围成一个边长为7厘米的正方形，余下的正好围成一个长为12厘米，宽为10厘米的长方形，这根铁丝长多少厘米？【加星题】★1．用4个同样大小的长方形和一个小正方形，拼成一个边长是24分米的大正方形，每个长方形的周长是多少？课后作业姓名成绩1．把3个边长为4厘米的正方形拼成一个大长方形，这个大长方形的周长是多少厘米？2．把一张周长是40厘米的正方形纸片，剪成5张同样大小的长方形纸片，每张长方形纸片的周长是多少厘米？3．一根铁丝可以围成一个边长为8厘米的正方形，用这根铁丝可以围成一个长为12厘米，宽为多少厘米的长方形？4．有两个相同的长方形，长12厘米，宽4厘米，如下图所示的这样子重叠在一起，这个图形的周长是多少厘米？周长练习月日姓名练1 把3个边长2厘米的正方形拼成一个大长方形，大长方形的周长比原来3个正方形周长的和少多少厘米？练习2：用一个长8厘米、宽4厘米的长方形与7个边长为4厘米的正方形，拼成一个大正方形，拼成的大正方形的周长是多少？练习3：把两个长30厘米、宽20厘米的长方形拼成一个大长方形，大长方形的周长是多少厘米？练习4：一根铁丝长100厘米，围成一个边长为10厘米的正方形，余下的铁丝围成一个宽为10厘米的长方形。

第十六讲简单的数图形．！．卡莉娅卡莉娅萱萱萱萱把相应的人物换成红字标明的人物．第一副图不要给出天安门的样子，直接给出天安门的烟花即可，剩下的不用变．生活中有许多立体图形和平面图形，你认识它们吗？今天我们一起来学习一些简单的图形，并有顺序的数一数．例题1找朋友，连一连．【提示】观察图形，找到图形特点．练习1要画出左边的图形，可以选择右边的哪个立体图形？把它圈出来．例题2你能说出下图中都有什么图形吗？【提示】你都学过什么图形呢？练习2数一数，下面2个机器人中每种图形的总个数，并回答问题．（）个（）个（）个（）个（）最多，（）最少，比多（）个，比少（）个．图形有大有小，我们在数图形的时候可以按照从小到大或从大到小的顺序数一数，这样可以保证不重不漏．例题3数图形．（）个正方形（）个正方形【提示】有没有隐藏的正方形？练习3数图形．（）个三角形（）个三角形例题4数图形．（）个长方形（）个长方形【提示】不要丢掉隐藏的长方形．练习4数图形．（）个长方形例题5下图中一共有几个长方形？【提示】2个小长方形可以构成1个长方形吗？3个呢？例题6下图中一共有几个三角形？【提示】2个小三角形可以构成1个三角形吗？3个呢？课堂内外各国国旗每个国家都有代表本国的国旗，而且每个国家的国旗都有各种各样的图形．我们来认识一下带有不同图形的国旗吧！荷兰：蓝色表示国家面临海洋，白色象征自由、平等、民主，红色代表革命胜利．捷克：红色和白色是捷克的国色，蓝色来自原来的摩拉维亚和斯洛伐克省徽章的颜色．巴哈马：黑色三角形象征人民团结一致，蓝色象征海洋环绕该岛国，黄色象征美丽的沙滩．日本：太阳旗，白色象征正直和纯洁，红色象征真诚和热忱，圆形代表太阳．老挝：红色象征革命，蓝色象征富饶，白色图轮表示圆月．德国：黑色象征对人民权利受到压抑的愤怒，红色象征人民向往自由的热情，黄色象征真理．作业1. 下图中，上排的房子图，是由下排哪些图形拼成的？用线连起来．2．按要求涂上你喜欢的颜色．（1）给涂色.（2）给涂色.3. 数一数，下图中共有几个正方形？4. 数一数，下图中共有几个三角形？5. 数一数，下图中共有几个三角形？。