常用数学函数

十个常用数学函数公式数学函数是数学领域中常用的工具，用于描述和分析数学中的关系和规律。

下面是十个常用的数学函数及其公式：1.线性函数线性函数是最简单和最常见的函数形式之一、它的一般形式为y =mx + b，其中m是斜率，b是y轴截距。

线性函数表示了两个变量之间的直接比例关系。

2.二次函数二次函数是指一元二次方程y = ax² + bx + c所表示的函数。

其中a、b、c是常数，且a ≠ 0。

二次函数通常表示一个开口向上或者向下的抛物线。

3.指数函数指数函数是以一个固定底数为底的函数形式，表示为y=a^x。

其中a是底数，x是指数。

指数函数常用于描述指数增长和指数衰减。

4.对数函数对数函数是指数函数的反函数。

对数函数的一般形式为y = logₐ(x)，表示找到a的多少次幂等于x。

对数函数常用于解决指数问题，如计算复利和对数衰减。

5.三角函数三角函数包括正弦函数、余弦函数和正切函数，它们是最基本的周期性函数。

正弦函数的一般形式为y = Asin(Bx + C) + D，其中A是振幅，B是频率，C是相移，D是垂直位移。

三角函数在几何、物理、工程和计算机图形等领域中得到广泛应用。

6.反三角函数反三角函数是三角函数的反函数。

常见的反三角函数包括反正弦函数、反余弦函数和反正切函数。

它们的函数形式和三角函数相反，可表示为y = sin⁻¹(x)、y = cos⁻¹(x)和y = tan⁻¹(x)。

7.指数增长和指数衰减函数指数增长和指数衰减函数描述了随着时间的推移，变量值按照指数规律增加或减少。

指数增长函数的一般形式为y = abˣ，其中a是初始值，b是增长因子。

指数衰减函数的一般形式为y = abˣ，其中a是初始值，b是衰减因子。

8.正态分布函数正态分布函数描述了连续随机变量的分布情况。

它的一般形式为y=e^(-(x-μ)²/2σ²)/(σ√(2π))，其中μ是均值，σ是标准差。

十个常用数学函数公式一、一次函数的表达式与性质一次函数，也称为线性函数，其表达式为y=ax+b，其中a和b是常数，a不等于0。

其中，a称为斜率，决定了函数的斜率的大小和正负方向；b称为截距，决定了函数与y轴的交点位置。

一次函数的图像是一条直线，具有直线的特性，如对称性和平移性等。

二、二次函数的表达式与性质二次函数，其表达式为y=ax^2+bx+c，其中a、b和c是常数，a 不等于0。

二次函数的图像是一个抛物线，具有开口方向、顶点坐标和对称轴等性质。

通过二次函数的图像，可以判断该函数的最大值或最小值，以及抛物线的开口方向。

三、指数函数的表达式与性质指数函数，其表达式为y=a^x，其中a是常数，且a大于0且不等于1。

指数函数的图像是一个逐渐增长或逐渐减小的曲线，具有指数增长和指数衰减的特性。

指数函数的图像在x轴上有一水平渐近线，且图像通过点(0, 1)。

四、对数函数的表达式与性质对数函数，其表达式为y=loga(x)，其中a是常数，且a大于0且不等于1。

对数函数的图像是一条逐渐增长或逐渐减小的曲线，具有对数增长和对数衰减的特性。

对数函数的图像在y轴上有一垂直渐近线，且图像通过点(1, 0)。

五、三角函数的表达式与性质三角函数包括正弦函数、余弦函数和正切函数等。

正弦函数的表达式为y=sin(x)，余弦函数的表达式为y=cos(x)，正切函数的表达式为y=tan(x)。

三角函数的图像是周期性的曲线，具有周期、幅值和相位等特性。

三角函数的图像在特定区间内可以取得最大值和最小值。

六、双曲函数的表达式与性质双曲函数包括双曲正弦函数、双曲余弦函数和双曲正切函数等。

双曲正弦函数的表达式为y=sinh(x)，双曲余弦函数的表达式为y=cosh(x)，双曲正切函数的表达式为y=tanh(x)。

双曲函数的图像是一条渐近于直线的曲线，具有对称性和渐进线等特性。

七、多项式函数的表达式与性质多项式函数，其表达式为y=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0，其中a_n、a_{n-1}、...、a_1和a_0是常数，n 是非负整数。

高中数学常见函数及其应用数学是一门广泛应用于各个领域的学科，而函数是数学中的基本概念之一。

在高中数学中，我们需要掌握并熟练运用一些常见函数及其应用。

本文将介绍一些常见的高中数学函数及其在实际问题中的应用。

一、线性函数线性函数是最简单的一类函数，其表达式为y = kx + b，其中k和b为常数。

线性函数的图像为一条直线，其斜率k代表直线的倾斜程度，而常数b代表直线与y轴的截距。

线性函数常见的应用有以下几种：1. 方程的解：在线性方程中，我们常常需要求解一元一次方程。

以y = 2x + 3为例，我们可以通过这个线性函数找到方程的解。

当x取特定的值时，我们可以求得对应的y值，从而得到该方程的解。

2. 直线的斜率和截距：线性函数的斜率和截距可以帮助我们分析直线的性质。

斜率决定了直线的倾斜程度，而截距则决定了直线与y轴的交点。

二、二次函数二次函数是一个非常常见的函数形式，其表达式为y = ax^2 + bx + c，其中a、b和c为常数，且a不等于0。

二次函数的图像通常是一个开口向上或向下的抛物线，常见的应用有以下几种：1. 抛物线的顶点问题：二次函数的顶点是抛物线的最高点或者最低点，在实际问题中可以用来寻找最优解，例如最大值或最小值。

2. 建模问题：二次函数可以用来建立实际问题的模型。

例如，通过分析苹果从树上掉落的过程，可以建立一个与时间相关的二次函数来描述苹果的运动轨迹。

三、指数函数指数函数是以一个正常数为底数，变量为指数的函数，其表达式为y = a^x，其中a为常数且大于0。

指数函数的图像通常是上升或下降的曲线，常见的应用有以下几种：1. 指数增长问题：指数函数在自然界中的许多现象都有应用，例如人口增长、细胞分裂等。

通过分析指数函数的特点，我们可以预测未来的发展趋势。

2. 复利计算：指数函数在金融领域中有着重要的应用，特别是在计算复利方面。

通过利率和时间的指数函数关系，我们可以计算复利的收益。

四、对数函数对数函数是指以一个正常数为底数，另一个正数为真数的函数，其表达式为y = loga(x)，其中a为常数且大于0且不等于1。

常用函数公式及用法函数在数学中是一种重要的工具，它将一个或多个输入值映射到输出值。

函数的应用十分广泛，包括数学、物理、经济学等领域。

下面将介绍一些常用的函数公式及其用法。

一、线性函数线性函数是最简单的一类函数，它的表达式为y = ax + b，其中a和b是常数。

线性函数的图像是一条直线，斜率为a，截距为b。

线性函数在各种科学和工程问题中有很多应用，比如经济学中的供求关系和物理学中的速度和加速度等。

二、二次函数二次函数的表达式为y = ax^2 + bx + c，其中a、b和c是常数，a≠0。

二次函数的图像是一条抛物线。

二次函数在几何学和物理学中有广泛的应用，比如描述抛射物的运动轨迹和分析电磁波在镜面上的反射等。

三、指数函数指数函数的表达式为y=a^x，其中a是正常数。

指数函数的图像是一条递增或递减的曲线，具有指数增长或指数衰减的特点。

指数函数在自然科学和经济学中有广泛的应用，比如放射性衰变、人口增长和利润增长等。

四、对数函数对数函数是指数函数的反函数，表示为y = loga(x)，其中a是正常数且a≠1、对数函数的图像是一条递增曲线，它与指数函数互为反函数。

对数函数在计算和控制论中有广泛的应用，比如简化复杂计算和描述信号传输的强度等。

五、三角函数三角函数包括正弦函数、余弦函数和正切函数等，它们与三角形的角度和边长相关联。

三角函数在几何学和物理学中都有广泛的应用，比如测量角度、解决三角形的边长和角度、描述振动和波动等。

三角函数的表达式和图像具有周期性的特点。

六、指数增长函数指数增长函数的表达式为y = ab^x，其中a和b是正常数，且b>1、指数增长函数的图像呈现出指数级的增长趋势，常用于描述人口增长、细胞分裂和资本增长等。

七、对数增长函数对数增长函数是指数增长函数的反函数，表示为y = logb(x)，其中b是正常数且b>1、对数增长函数可以用于描述信息传输速度和事件发展速度等。

八、常数函数常数函数的表达式为y=c，其中c是常数。

十个常用数学函数公式数学函数是描述数值之间关系的一种工具，可以帮助我们理解和解决各种数学问题。

在数学中，有许多常用的数学函数公式，下面是十个常见的数学函数公式：1.平方函数公式：f(某)=某^2，其中某是任意实数。

该函数的图像是一个平滑的开口向上的抛物线。

2.立方函数公式：f(某)=某^3，其中某是任意实数。

该函数的图像是一个平滑的开口向上的抛物线。

3.开方函数公式：f(某)=√某，其中某是非负实数。

该函数的图像是一个从原点出发的逐渐上升的曲线。

4. 正弦函数公式：f(某) = sin(某)，其中某是弧度。

该函数的图像是一个周期性的波动曲线，取值范围在-1到1之间。

5. 余弦函数公式：f(某) = cos(某)，其中某是弧度。

该函数的图像也是一个周期性的波动曲线，取值范围在-1到1之间，但与正弦函数相位差。

6. 正切函数公式：f(某) = tan(某)，其中某是弧度。

该函数的图像是一个周期性的波动曲线，取值范围在负无穷到正无穷之间。

7.指数函数公式：f(某)=a^某，其中a是大于0且不等于1的常数，某是任意实数。

该函数的图像是一个逐渐上升或下降的曲线。

8. 对数函数公式：f(某) = log_a(某)，其中a是大于0且不等于1的常数，某是大于0的实数。

该函数的图像是一个逐渐上升或下降的曲线，是指数函数的反函数。

9.绝对值函数公式：f(某)=，某，其中某是任意实数。

该函数的图像是以原点为对称轴的V形曲线，取值范围在0到正无穷之间。

10.阶乘函数公式：f(某)=某!，其中某是非负整数。

该函数表示某的阶乘，即从1到某的所有正整数的乘积。

这些常用数学函数公式在各个数学领域中都有广泛的应用，如代数、几何、微积分等。

它们的图像和性质对于建立数学模型、解决实际问题以及深入理解数学概念都起到了重要的作用。

高中数学中常见的函数符号1 数学函数1.1 取整函数int(x) 取不大于x的最大整数。

fix(x) 舍去x的小数部分。

1.2 绝对值函数abs(x) 求x的绝对值。

1.3 符号函数sgn(x) 求x的符号代码，x为负数时函数值为-1 。

1.4 平方根函数sqr(x) 求x的算术平方根，x必须大于0 。

1.5 指数函数exp(x) 求以e为底x为指数的值。

1.6 对数函数log(x) 求以e为底的对数函数值。

1.7 三角函数sin(x) 求x的正弦值。

con(x) 求x的余弦值。

tan(x) 求x的正切值。

Atn(x) 求x的反正切值。

1.8 数制转换函数hex(x) 十进制转换为对应的十六进制数。

oct(x) 十进制转换为对应的八进制数。

2 日期时间函数2.1 系统日期时间函数now() 读取系统当前日期时间。

date() 读取系统当前日期。

time() 读取系统当前时间。

2.2 日期时间分解函数year(日期字符串) 返回日期字符串中的年份。

month(日期字符串) 返回日期字符串中的月份。

day(日期字符串) 返回日期字符串中的日子。

weekday(日期字符串) 返回日期字符串中的星期。

hour(时间字符串) 返回时间字符串中的小时。

minute(时间字符串) 返回时间字符串中的分钟。

secont(时间字符串) 返回时间字符串中的秒数。

2.3 日期时间数值化函数dateValue(日期字符串) 把日期字符串转换为当日至1889-12-30的天数。

timeValue(时间字符串) 把时间字符串转换为0,1之间变体型时间值。

2.4 日期时间运算函数dateSerial(年,月,日) 把年月日连接成日期字符串。

timeSerial(时,分,秒) 把时分秒连接成时间字符串。

timer() 计算午夜起至当前系统时间所历经的秒数。

3 字符串处理函数3.1 删除空格函数Trim(字符串) 删除字符串两端空格字符。

数学各种函数名称
数学中的各种函数名称有很多，以下是一些常见的函数类型及其名称：
1.常函数：y=c
2.幂函数：y=x^n
3.指数函数：y=a^x
4.对数函数：y=log_a|x|
5.三角函数：
1.正弦函数：y=sinx
2.余弦函数：y=cosx
3.正切函数：y=tanx
4.余切函数：y=cotx
5.正割函数：y=secx
6.余割函数：y=cscx
6.反三角函数：
1.反正弦函数：y=arcsinx
2.反余弦函数：y=arccosx
3.反正切函数：y=arctanx
4.反余切函数：y=arccotx
7.其他函数：
1.abs：绝对值函数
2.sqrt：平方根函数
3.ceiling：向上取整函数
4.floor：向下取整函数
5.trunc：截断函数
6.round：四舍五入函数
7.signif：符号函数
8.sinh：双曲正弦函数
9.cosh：双曲余弦函数
10.tanh：双曲正切函数
11.coth：双曲余切函数
12.asinh：双曲反正弦函数
13.acosh：双曲反余弦函数
14.atanh：双曲反正切函数
15.acoth：双曲反余切函数
以上只是部分数学函数的名称，实际上数学中的函数种类繁多，每一种都有其特定的定义和性质。

七类函数一．对号函数：形如()bf x ax x=+的函数称为对号函数。

（1）0,0a b >>时，示意图如下：可看成以直线y ax =与y 轴为渐近线的双曲线， 两个顶点A 、B 可由不等式中的均值定理确定， 此时()f x 的单调性、奇偶性、定义域与值域、 对称性可从图中看出结论。

（2）0a >且0b <时，示意图如下：此时()f x 为奇函数，分段递增，当0(0)x x ><或时，y R ∈1.已知函数f(x)=2x+x8（1）当x ∈(0,+∞) 时.求()x f 的值域。

（2）当x ∈[1，3 ] 时.求()x f 的值域。

（3）当x ∈[-2，0）时.求()x f 的值域。

2. 已知函数f(x)=2x —x8，研究该函数的性质。

3. 已知函数(x)=4522++x x ,求f(x)的最小值及此时x 的值.y ax=b aO x yB2ab1． 一次分函数的定义我们把形如(0,)cx dy a ad bc ax b+=≠≠+的函数称为一次分函数。

2． 一次分函数的图象和性质(0,)cx dy a ad bc ax b+=≠≠+2.1 图象：其图象如图所示.2.2定义域：⎭⎬⎫⎩⎨⎧-≠a b x x ；2.3 值域：⎭⎬⎫⎩⎨⎧≠a c y y ；2.4 对称中心：⎪⎭⎫⎝⎛-a c a b ,；2.5 渐近线方程：b x a =-和cy a=；2.6 单调性：当ad>bc 时，函数在区间(,)b a -∞-和(,)ba-+∞分别单调递减；当ad<bc 时，函数在区间(,)b a -∞-和(,)ba-+∞分别单调递增；1．函数21()3x f x x +=+的单调增区间是 ．2．函数21()3x f x x -=+的对称中心是 ．3. 函数21()3x f x x -=+（()5,2-∈x ），则()x f 的值域是________．4. 函数21()3x f x x -=+（())5,2(4,5⋃--∈x ），则()x f 的值域是________1.已知函数f(x)=112+++x x x ,求(1) f(x)的值域。

数学函数大全在数学中，函数是一个常见且重要的概念。

函数可以看作是两个集合之间的一种对应关系，它将一个集合中的每个元素映射到另一个集合中的唯一元素上。

函数在数学建模、物理学、工程学等领域中都有着广泛的应用。

本文将介绍一些常见的数学函数，包括常函数、一次函数、二次函数、三角函数等。

常函数:常函数是一种特殊的函数，它的输出值对于所有的输入值都是相同的。

常函数的数学表达式为f(x) = c，其中c代表一个常数。

例如，函数f(x) = 3就是一个常函数，无论输入值是多少，输出值始终为3。

一次函数:一次函数又称为线性函数，是一种形式简单的函数。

一次函数的数学表达式为f(x) = kx + b，其中k和b都是常数，k代表着斜率，b代表着截距。

一次函数的图像是一条直线，斜率决定了直线的倾斜程度，截距决定了直线与y轴的交点位置。

二次函数:二次函数是一种常见的函数类型，其图像呈现出抛物线的形状。

二次函数的数学表达式为f(x) = ax^2 + bx + c，其中a、b和c都是常数，且a不等于0。

二次函数的图像可以是开口朝上或朝下的抛物线，开口的方向由a的正负决定。

三角函数:三角函数是描述角度变化的函数，广泛应用于几何学和物理学中。

常见的三角函数包括正弦函数、余弦函数和正切函数。

正弦函数的数学表达式为f(x) = sin(x)，余弦函数的数学表达式为f(x) = cos(x)，正切函数的数学表达式为f(x) = tan(x)。

其中，x代表角度值。

三角函数的图像呈现出周期性的波动，可以用来描述周期性现象。

指数函数:指数函数是一种以指数形式表示的函数，具有固定的底数和变量指数。

指数函数的数学表达式为f(x) = a^x，其中a为底数，x为指数。

指数函数的图像呈现出指数曲线的形状，底数a大于1时，曲线逐渐增长；底数a小于1时，曲线逐渐衰减。

对数函数:对数函数是指数函数的逆运算，用来描述指数运算中的乘法转化为加法的过程。

对数函数的数学表达式为f(x) = logₐ(x)，其中a为底数，x为函数的输出值。

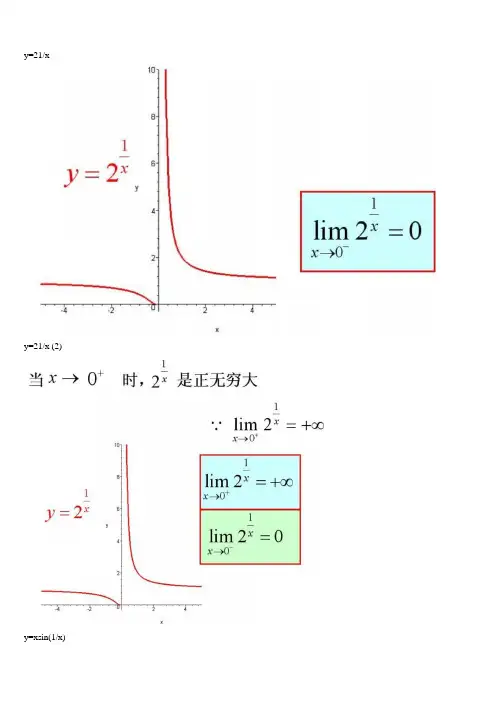
y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e 的值(2)等价无穷小(x->0)sinx 等价于 xarcsinx 等价于 xarctanx 等价于 x1-cosx 等价于 x^2/2数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$$tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式(上面公式反过来就得到了) $sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中$tan(c)=b/a$$a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中$tan(c)=a/b$$1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC，如下定义六个三角函数：正弦函数余弦函数正切函数余切函数正割函数余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中，如下定义六个三角函数：正弦函数余弦函数正切函数余切函数正割函数余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式4.2 和差化积公式。

十个常用数学函数公式1. 线性函数：y = mx + c，其中 m 是斜率，c 是 y 轴截距。

2.幂函数：y=x^n，其中n是常数。

3.指数函数：y=a^x，其中a是底数，x是指数。

4. 对数函数：y = log_a x，其中 a 是底数，x 是对数。

5. 三角函数：sin(x), cos(x), tan(x)，常用来描述角度和周期性。

6. 反三角函数：arcsin(x), arccos(x), arctan(x)，常用来求解角度。

7. 椭圆函数：y = a cos(bx) 或 y = a sin(bx)，常用来描述周期性。

8.高斯函数：y=e^(-x^2)，常用在概率分布和统计学中。

9.函数逼近：泰勒级数，用一系列多项式逼近函数的方法。

10.分段函数：根据不同的条件，给出不同的函数表达式，常用于物理和工程问题的建模。

这些常用数学函数公式在科学、工程、数学和计算机科学等领域中起着重要的作用。

它们有着广泛的应用，以下是一些实际应用的示例：1.线性函数可用于描述物体的速度、加速度与时间的关系。

在工程中，线性函数也可以用来进行线性回归分析，预测未来的趋势。

2.幂函数在物理学中常用来描述力、质量和距离之间的关系。

例如，牛顿万有引力定律中的F=G(m1m2/r^2)，其中F是引力，m1、m2是质量，r是距离。

3.指数函数常见于自然增长和衰减的过程。

例如，放射性衰变中的核素数量随时间的变化常用指数函数来表示。

4.对数函数在应用中常用于描述复杂度和增长率。

例如，在算法分析中，对数函数可以描述一些算法的运行时间。

5.三角函数在几何学、物理学和工程学中广泛应用。

例如，通过正弦函数和余弦函数可以描述物体的周期性运动。

6.反三角函数可用于计算角度，例如在三角学和几何学中。

在导航和图像处理中，反三角函数也常用于确定对象在图像中的位置。

7.椭圆函数在电子工程和天体物理学中使用广泛。

例如，通过椭圆函数可以描述地球的形状和轨道。

十个常用数学函数公式1.平方函数公式：$f(x)=x^2$，其中$x$为自变量，$f(x)$为函数值。

2.立方函数公式：$f(x)=x^3$，其中$x$为自变量，$f(x)$为函数值。

3. 开方函数公式：$f(x) = \sqrt{x}$，其中$x$为自变量，$f(x)$为函数值。

4.绝对值函数公式：$f(x)=，x，$，其中$x$为自变量，$f(x)$为函数值。

5. 三角函数公式：常用的三角函数包括正弦函数$\sin(x)$、余弦函数$\cos(x)$和正切函数$\tan(x)$等。

6.指数函数公式：$f(x)=a^x$，其中$a$为底数，$x$为指数。

7. 对数函数公式：$f(x) = \log_a(x)$，其中$a$为底数，$x$为对数。

8. 线性函数公式：$f(x) = mx + c$，其中$m$为斜率，$c$为截距。

9. 二次函数公式：$f(x) = ax^2 + bx + c$，其中$a$、$b$和$c$为常数。

10.导数公式：导数表示函数在其中一点处的斜率，常用的导数求法包括使用基本导数公式、链式法则和求偏导数等。

这些是常见的数学函数公式，其中平方函数、立方函数、开方函数和绝对值函数是最基本且常见的函数。

三角函数则在三角学、波动学和周期性等领域中应用广泛。

指数函数和对数函数在经济学、生物学、物理学等领域中常见。

线性函数和二次函数则是代数学中非常常用的函数形式。

导数则是微积分中的重要概念，用于分析函数变化的速率。

导数的概念主要也是基于上述常用函数的公式推导出来的。

总结起来，这些数学函数公式在不同领域和学科中都扮演着重要的角色，有助于描述和解决各种实际问题。

2.1 基本数学函数2.1.1 三角函数与双曲函数函数 sin 、sinh功能 正弦函数与双曲正弦函数格式 Y = sin(X) %计算参量X （可以是向量、矩阵，元素可以是复数）中每一个角度分量的正弦值Y ，所有分量的角度单位为弧度。

Y = sinh(X) %计算参量X 的双曲正弦值Y 注意：sin(pi)并不是零，而是与浮点精度有关的无穷小量eps ，因为pi 仅仅是精确值π浮点近似的表示值而已；对于复数Z= x+iy ，函数的定义为：sin(x+iy) = sin(x)*cos(y) +i*cos(x)*sin(y)，2e e )z sin(iziz --=，2e e )z sin(z z --=例2-1x = -pi:0.01:pi; plot(x,sin(x))x = -5:0.01:5; plot(x,sinh(x))图形结果为图2-1。

图2-1 正弦函数与双曲正弦函数图函数 asin 、asinh功能 反正弦函数与反双曲正弦函数格式 Y = asin(X) %返回参量X （可以是向量、矩阵）中每一个元素的反正弦函数值Y 。

若X 中有的分量处于[-1,1]之间，则Y = asin(X)对应的分量处于[-π/2,π/2]之间，若X 中有分量在区间[-1,1]之外，则Y= asin(X)对应的分量为复数。

Y = asinh(X) %返回参量X 中每一个元素的反双曲正弦函数值Y 说明 反正弦函数与反双曲正弦函数的定义为：)z 1z i l n(i z s i n a 2-+⋅⋅-=，)z 1z ln(z sinh a 2++=例2-2x = -1:.01:1; plot(x,asin(x)) x = -5:.01:5; plot(x,asinh(x))图形结果为图2-2。

图2-2 反正弦函数与反双曲正弦函数图函数 cos 、cosh功能 余弦函数与双曲余弦函数格式 Y = cos(X) %计算参量X （可以是向量、矩阵，元素可以是复数）中每一个角度分量的余弦值Y ，所有角度分量的单位为弧度。

常用函数公式及函数汇总1.数学函数：-四则运算函数：加法、减法、乘法、除法-平方函数：f(x)=x^2-开方函数：f(x)=√x-指数函数：f(x)=a^x，其中a为常数- 对数函数：f(x) = log_a(x)，其中a为常数-三角函数：正弦函数、余弦函数、正切函数等2.统计函数：- 求和函数：SUM(x1, x2, ..., xn)，计算一列数的总和- 平均数函数：AVERAGE(x1, x2, ..., xn)，计算一列数的平均值- 中位数函数：MEDIAN(x1, x2, ..., xn)，计算一列数的中位数- 最大值函数：MAX(x1, x2, ..., xn)，求一列数的最大值- 最小值函数：MIN(x1, x2, ..., xn)，求一列数的最小值- 方差函数：VAR(x1, x2, ..., xn)，计算一列数的方差- 标准差函数：STDEV(x1, x2, ..., xn)，计算一列数的标准差3.逻辑函数：- IF函数：IF(condition, value_if_true, value_if_false)，根据条件返回不同的值- AND函数：AND(logical1, logical2, ..., logicaln)，判断多个条件是否都为真- OR函数：OR(logical1, logical2, ..., logicaln)，判断多个条件是否有一个为真- NOT函数：NOT(logical)，将逻辑值取反4.文本函数：- CONCATENATE函数：CONCATENATE(string1, string2, ..., stringn)，将多个文本串连接为一个文本串- LEFT函数：LEFT(text, num_chars)，从左边截取指定长度的子串- RIGHT函数：RIGHT(text, num_chars)，从右边截取指定长度的子串- MID函数：MID(text, start_num, num_chars)，从指定位置截取指定长度的子串- LEN函数：LEN(text)，计算文本串的长度- UPPER函数：UPPER(text)，将文本串转换为大写- LOWER函数：LOWER(text)，将文本串转换为小写- PROPER函数：PROPER(text)，将文本串的首字母大写5.日期和时间函数：-NOW函数：NOW(，返回当前日期和时间-TODAY函数：TODAY(，返回当前日期- YEAR函数：YEAR(date)，返回指定日期的年份- MONTH函数：MONTH(date)，返回指定日期的月份- DAY函数：DAY(date)，返回指定日期的日期- DATEDIF函数：DATEDIF(start_date, end_date, unit)，计算两个日期之间的差值，单位可以是天、月、年等6.概率与统计函数：-RAND函数：RAND(，返回一个0到1之间的随机数- RANDBETWEEN函数：RANDBETWEEN(bottom, top)，返回一个指定范围内的随机整数- NORM.DIST函数：NORM.DIST(x, mean, standard_dev, cumulative)，计算标准正态分布的概率密度函数值或累积分布函数值- NORM.INV函数：NORM.INV(probability, mean, standard_dev)，计算标准正态分布的反函数值- BETADIST函数：BETADIST(x, alpha, beta, A, B)，计算Beta分布的概率密度函数值或累积分布函数值- GAMMADIST函数：GAMMADIST(x, alpha, beta, cumulative)，计算Gamma分布的概率密度函数值或累积分布函数值以上只是函数汇总的一部分，Excel和其他数学软件中提供了更多的内置函数，可以根据具体需求来选择合适的函数来使用。