高中数学一般常用特殊函数图像集锦(非常实用)

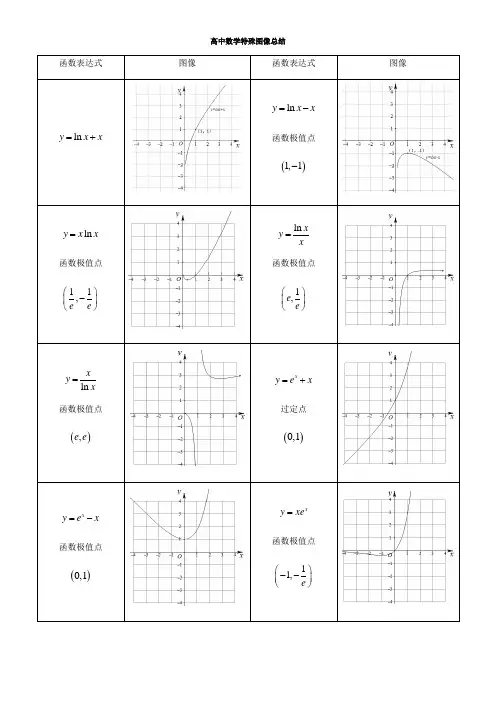
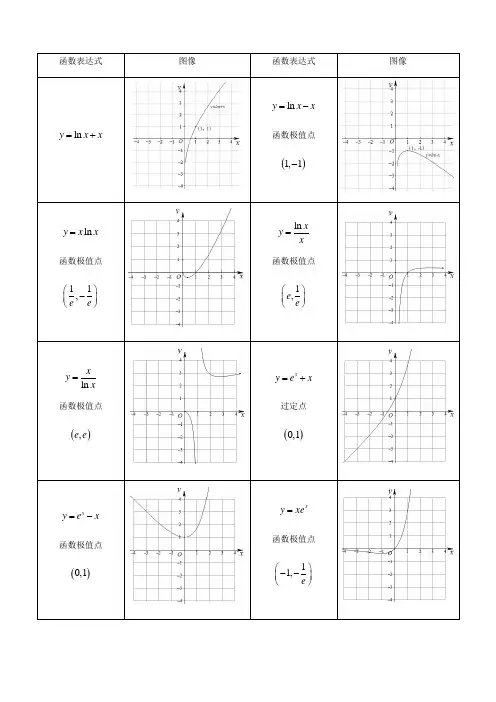
高中数学常考特殊函数图像汇总（共66个）高中数学中有许多特殊的函数，它们在图像上呈现出各种有趣的形状和特点。

本文将对这些常考的特殊函数图像进行汇总，共涉及66个函数。

让我们一起来了解它们吧！第一个函数是一次函数，也就是线性函数。

它的函数表达式为y = kx + b，其中k表示斜率，b表示截距。

这个函数的图像是一条直线，斜率决定了直线的倾斜程度，截距决定了直线与y轴的交点。

第二个函数是二次函数，它的函数表达式为y = ax² + bx + c，其中a、b、c是常数。

二次函数的图像是一个开口向上或向下的抛物线，a决定了抛物线的开口方向和大小，b决定了抛物线在x轴上的平移，c决定了抛物线在y轴上的平移。

第三个函数是立方函数，它的函数表达式为y = ax³ + bx² + cx + d，其中a、b、c、d是常数。

立方函数的图像是一个S形曲线，它在原点左右对称，并且随着x的增大，曲线呈现出逐渐增长或逐渐减小的趋势。

第四个函数是指数函数，它的函数表达式为y = a^x，其中a是常数且大于0。

指数函数的图像是一条递增或递减的曲线，具有不断增长或不断衰减的特点。

当a大于1时，曲线递增；当0＜a＜1时，曲线递减。

第五个函数是对数函数，它的函数表达式为y = loga(x)，其中a是常数且大于0且不等于1。

对数函数的图像是一条递增或递减的曲线，与指数函数相反。

当x大于1时，曲线递增；当0＜x＜1时，曲线递减。

第六个函数是正弦函数，它的函数表达式为y = a*sin(bx+c)+d，其中a、b、c、d是常数。

正弦函数的图像是一条波动的曲线，具有周期性的特点。

a决定了振幅的大小，b决定了周期的长度，c决定了曲线的左右平移，d决定了曲线的上下平移。

第七个函数是余弦函数，它的函数表达式为y = a*cos(bx+c)+d，其中a、b、c、d是常数。

余弦函数的图像也是一条波动的曲线，与正弦函数相似，但形状上有一定的差异。

函数图形基本初等函数幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2) y=xsin(1/x) y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性) 极限的性质(2) (局部保号性)极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。