第6章 连续时间系统的系统函数(2013)
- 格式:pdf
- 大小:424.01 KB
- 文档页数:25



连续系统的系统函数二、系统函数与时域响应由§5.4和§6.4可知,系统自由(固有)响应的函数(或序列)形式由()0=⋅A 的根确定,亦即由()⋅H 的极点确定,而冲激响应或单位序列响应的函数形式也由()⋅H 的极点确定。
下面讨论()⋅H 极点的位置与其所对应的响应(自由响应、冲激响应、单位序列响应等)的函数(序列)形式。
1. 连续系统连续系统的系统函数()s H 的极点,按其在s 平面上的位置可分为:左半开平面(不含虚轴的左半平面)、虚轴和有半开平面三类。
在左半开平面的极点有负实极点和共轭复极点(其实部为负)。
若系统函数有负实单极点()0>-=ααp ,则()s A 有因子()α+s ,其所对应的响应(自由响应、冲激响应等)函数为()t Ae t εα-;如有一对共轭复极点βαj p ±-=2,1,则()s A 中有因子()[]22βα++s ,其所对应的响应函数为()()t t Aetεθβα+-cos ,式中A 、θ为常数,响应均按指数衰减,当∞→t 时趋近于零。
它们的波形见图8.5-1。
如()s H 在左半开面有r 重极点,则()s A 中有因子()rs α+或()[]rs 22βα++,它们所对应的响应函数分别为()t et A tj j εα-或()()()1,,2,1,0cos -=+-r j t t et A tjj εθβα,式中j A 、jθ为常数。
用罗必塔法则不难证明,当∞→t 时,它们均趋于零。
()s H 在虚轴上的单极点0=p 或βj p ±=2,1,相应于()s A 的因子为s 或22β+s ,它们所对应的响应函数分别为()t A ε或()()t t A εθβ+cos ,其幅度不随时间变化(见图8.5-1)。
()s H 在虚轴上的r 重极点,相应于()s A 的因子为rs或()rs 22β+,其所对应的响应函数分别为()t t A j j ε或()()t t t A j j j εθβ+cos ,它们都随t 的增长而增大。



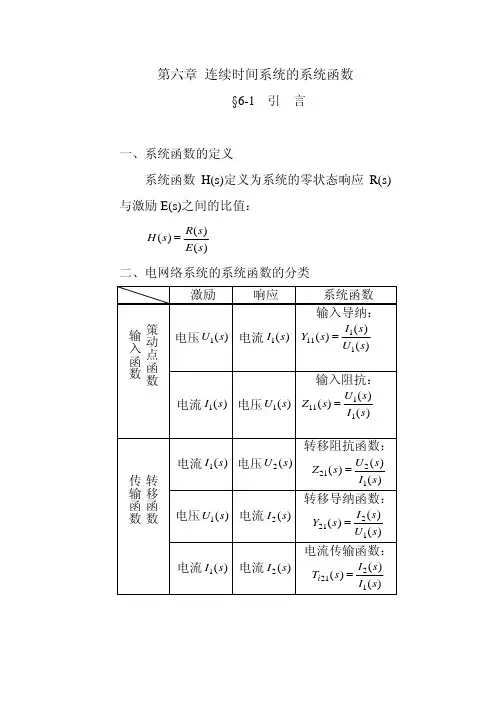
第六章 连续时间系统的系统函数§6-1 引 言一、系统函数的定义系统函数H(s)定义为系统的零状态响应R(s)与激励E(s)之间的比值:)()()(s E s R s H =二、电网络系统的系统函数的分类三、)(s H 、)(p H 、)(ωj H 、)(t h 之间关系 1、)(p H 与)(s H 形式相同,含义不同; 2、)(s H 中当ωj s =时,就得到了系统特性在频域中的表达形式)(ωj H ;3、H(s)是)(t h 的像函数,)(t h 是H(s)的原函数。
所以,得到了H(s)以后,就可以得到)(p H 、)(ωj H 和)(t h 。
通过H(s) 可以对系统进行综合和分析。
§6-2 系统函数的表示法系统函数可以用数学表达式表达,也可以用图示的方法表达。
前者比较简单,但是无法直接看出系统的特性。
后者可以直接表示出系统的特性,便于对系统的性能进行深入研究。
常用的图示法有三种:频率特性,复轨迹,极零图。
一、频率特性z 正如第四章中所见,系统特性可以用反映幅度特性随频率变化规律的幅频特性曲线和反映相位特性随频率变化规律的相频特性曲线描述。
z 频率特性主要用于研究系统的频率特性分析。
z 对于)(s H ,没有必要研究其随任意复频率变化的规律,只需要令ωj s =,得到)(ωj H ,研究沿s 平面虚轴变化的规律。
z 对于一般的(电)系统,)(s H 为s 的有理函数,其幅频特性为ω的偶函数,相频特性为ω的奇函数。
所以,只要画出0≥ω部分即可。
z 频率特性曲线有时也在对数尺度的坐标系中作出,称为波特图。
见§6-4。
z 对于因果系统而言,)(ωj H 的实部和虚部相互联系,知道其中一个,就可以推导出另一个。
证明:对于因果系统,有:)()()(t t h t h ε⋅=ωωπωωωπωπδωπωωπδωπω1*)(21)(211*)(21)(*)(211)(*)(21)(j H j j H j j H j H j j H j H +=+=⎥⎦⎤⎢⎣⎡+=∴ ωωπω1*)(21)(21j H jj H =∴[]ωωπωωπωωωπωω1*)(11*)(11*)()(1)()(j R j j X j jX j R j j jX j R −=+=+∴ ∫∫∞+∞−+∞∞−−−=−=−==∴λλωλπωωπωλλωλπωωπωd j R j R j X d j X j X j R )(11*)(1)()(11*)(1)( 根据上面两个的公式,可以从)(ωj R 计算出)(ωj X 或反之。

连续系统的系统函数二、系统函数与时域响应由§5.4和§6.4可知,系统自由(固有)响应的函数(或序列)形式由()0=⋅A 的根确定,亦即由()⋅H 的极点确定,而冲激响应或单位序列响应的函数形式也由()⋅H 的极点确定。
下面讨论()⋅H 极点的位置与其所对应的响应(自由响应、冲激响应、单位序列响应等)的函数(序列)形式。
1. 连续系统连续系统的系统函数()s H 的极点,按其在s 平面上的位置可分为:左半开平面(不含虚轴的左半平面)、虚轴和有半开平面三类。
在左半开平面的极点有负实极点和共轭复极点(其实部为负)。
若系统函数有负实单极点()0>-=ααp ,则()s A 有因子()α+s ,其所对应的响应(自由响应、冲激响应等)函数为()t Ae t εα-;如有一对共轭复极点βαj p ±-=2,1,则()s A 中有因子()[]22βα++s ,其所对应的响应函数为()()t t Aetεθβα+-cos ,式中A 、θ为常数,响应均按指数衰减,当∞→t 时趋近于零。
它们的波形见图8.5-1。
如()s H 在左半开面有r 重极点,则()s A 中有因子()rs α+或()[]rs 22βα++,它们所对应的响应函数分别为()t et A tj j εα-或()()()1,,2,1,0cos -=+-r j t t et A tjj εθβα,式中j A 、jθ为常数。
用罗必塔法则不难证明,当∞→t 时,它们均趋于零。
()s H 在虚轴上的单极点0=p 或βj p ±=2,1,相应于()s A 的因子为s 或22β+s ,它们所对应的响应函数分别为()t A ε或()()t t A εθβ+cos ,其幅度不随时间变化(见图8.5-1)。
()s H 在虚轴上的r 重极点,相应于()s A 的因子为rs或()rs 22β+,其所对应的响应函数分别为()t t A j j ε或()()t t t A j j j εθβ+cos ,它们都随t 的增长而增大。

![[计算机资料]第6章连续时间系统的系统函数](https://uimg.taocdn.com/5a9b88627e21af45b307a8e2.webp)
* 所以,不仅系统的相频特性是各个零点或极点的相频特性的叠加,而且。
所以,。
* 其中第一项是固定的常数,可以暂时不考虑;对第二项,有:如果频率也取对数,则高频渐近线是一个斜率为20的直线,其与低频渐近线(横坐标)的交点为: * 相频特性:同样可以得到相频特性在对数坐标下也可以近似表示为两段折线; * 单个极点的波特图与单个零点的波特图相似,只不过折线方向相反。
* 思考:重根如何处理? ? ? 利用计算机技术,可以很容易地得到任何系统的频率特性曲线和波特图,不用通过上面的方法画了。
但是,其中的一些结论在实际工作中依然有很重要参考价值。
* 如果系统对于有限(有界)的激励(即存在常数Me,使得|e(t)| Me在任意t的条件下都成立),有有限的响应(即存在常数Mr,使|r(t)| Mr 在任意t的条件下都成立,则称该系统为稳定系统。
* 稳定系统的H(s)的极点只能分布在s?平面的左半平面(即各个极点的实部应该小于零)。
对于三阶或以上系统,求根是很烦琐的。
于是就有了以下描述的代数稳定性判据。
设H(s)的分母为D(s)的有理代数方程 * 稳定系统的H(s)的极点只能分布在s?平面的左半平面(即各个极点的实部应该小于零)。
对于三阶或以上系统,求根是很烦琐的。
于是就有了以下描述的代数稳定性判据。
设H(s)的分母为D(s)的有理代数方程 * 思考另外一种方法 * 大小相等,符号相反的一对实根,或一对共轭虚根,或对称于虚轴的重共轭复根。
大小相等,位置径向相反的根可以通过求解辅助方程得到。
辅助方程应为偶次数的。
l????? 如果在计算中出现了一个全零行,则说明系统在虚轴上有极点,系统最多是临界稳定的。
可以直接认为系统是不稳定的(如果将临界稳定划归于不稳定之列),或者对系统是否临界稳定作出进一步判定,步骤如下: * 这说明该系统的系统函数在虚轴上有四个单极点分别为土j及土j ,系统为 * 利用罗斯―霍维茨稳定性判据还可以讨论个别参数对稳定性的影响,从而求得这些参数的取值范围。

第六章 连续时间系统的系统函数系统的响应一方面与激励有关,同时也与系统本身有关。
系统函数就是描述系统本身特性的,它在电路与系统理论中占有重要地位。
本章将介绍系统函数的定义、物理意义、分类、求法、零点与极点概念及其应用;最后介绍系统稳定性的概念及其判定方法。
6.1 系统函数的定义与分类6.1.1 定义图6.1所示零状态系统,)(t x 为激励,)(t y 为零状态响应,设系统的单位冲激励响应为()h t ,则有)()()(t x t h t y *=对上式等号两端同时求拉氏变换,并设)]([)(t y L s Y =,)]([)(t h L s H =,)]([)(t x L s X =,则有 )()()(s X s H s Y = (6.1) 故有)()()(s X s Y s H =(6.2) ()H s 称为复频域系统函数,简称系统函数。
可见系统函数()H s 就是系统零状态响应)(t y 的象函数)(s Y 与激励)(t x 的象函数)(s X 之比,也是系统单位冲激响应()h t 的拉氏变换。
由于()H s 是响应与激励的两个象函数之比,所以()H s 与系统的激励和响应的具体数值无关,它只与系统本身的结构与元件参数有关。
它充分、完整地描述了系统本身的特性。
因此,研究系统的特性,也就归结为对()H s 进行研究。
6.1.2 )(s H 的又一物理意义设系统的激励ste t x =)(,ste 称为s 域本征信号或单元信号。
此时系统的零状态响应为τττd e h e t h t y t s st )()()()(-∞∞-⎰=*=τττd e h es st-∞∞-⎰=)()(s H e st= (6.3) 式中)]([)()(t h L d e h s H s ==-∞∞-⎰τττ,为()h t 的拉氏变换。
可见,()H s 就是当激励为st e 时系统零状态图6.1(t x )(t y响应的加权函数。