曲线上涵洞坐标计算

第五篇坐标正反算通用程序(终极篇)1. 坐标正算主程序(命名为ZBZS)第1行：Lbl 0:”K=”?K:”BIAN=”? Z:”α=”?B第2行：Prog “A”第3行：”X=”:N+Zcos(F+B)◢第4行：”Y=”:E+Zsin(F+B)◢第5行：”F=”:F►DMS◢第6行：Goto 0K——计算点的里程BIAN——计算点到中桩的距离（左负右正）α——取前右夹角为正2. 坐标反算桩号和偏距主程序(命名为ZBFS)第1行：”X1=”? C:”Y1=”?D:”K1=”?K第2行：Lbl 0:Prog “A”第3行：Pol(C-N,D-E):Icos(F-J)→S:K+S→K第4行：Abs(S)>0.0001=>Goto 0第5行：”K1=”:K◢第6行：”BIAN=”:Isin(J-F)→Z◢X1——取样点的X坐标Y1——取样点的Y坐标K1——输入时为计算起始点(在线路内即可)，输出时为反算点的桩号Z——偏距（左负右正）注：在9860或9960中需将第3行替换为Pol(C-N,D-E): List Ans[1]→I ：List Ans[2]→J：Icos(J-F)→S:K+S →K，正反算主程序所有输入赋值多加一赋值符号（→），其他所有除数据库外的程序均保持不变3. 计算坐标子程序(命名为XYF)为了简洁，本程序由数据库直接调用，上述中的正反算主程序不直接调用此程序第1行：K-A→S：(Q-P)÷L→I第2行：N+∫(cos(F+X(2P+XI)×90÷π),0,S)→N第3行：E+∫(sin(F+X(2P+XI)×90÷π),0,S)→E第4行：F+S(2P+S I)×90÷π→F第5行：F<0=>F+360→F: F>360=>F-360→F4. 数据库（命名为A）第1行：K≤175.191=>Stop（超出后显示Done）第2行：175.191→A:428513.730→N:557954.037→E:92°26′40″→F:0→P:1/240→Q:70.417→L:K≤A+L =>GoTo 1（第一缓和曲线）第3行：245.607→A: 428507.298→N:558024.092→E: 100°50′59.4″→F: 1/240→P:1/240→Q:72.915→L: K≤A+L =>Goto 1（圆曲线）第4行：318.522→A: 428482.988→N:558092.538→E: 118°15′25.2″→F: 1/240→P: 0→Q: 55.104→L: K≤A+L =>Goto 1（第二缓和曲线）第5行：373.627→A:428453.283→N:558138.912→E:124°50′4.5″→F:0→P:-1/180→Q:67.222→L:K≤A+L=>Goto 1:Stop（下一曲线的第一缓和曲线，示例为S型曲线，超出后显示Done）第6行：Lbl 1:Prog “XYF”A——曲线段起点的里程N——曲线段起点的x坐标E——曲线段起点的y坐标F——曲线段起点的坐标方位角P——曲线段起点的曲率(半径倒数，直线为0，左负右正)Q——曲线段终点的曲率(半径倒数，直线为0，左负右正)L——曲线段长度（尽量使用长度，为计算断链方便）说明：（1）正算主程序可以计算一般边桩的坐标，如要计算类似涵洞端墙的坐标需增加两个变量，具体方法参考本程序集中的第1篇辛普生公式的坐标计算通用程序（2）适用于任意线形：直线（0→P、0→Q）、圆曲线（圆半径倒数→P、圆半径倒数→Q）、缓和曲线（0或圆半径倒数→P、圆半径倒数或0→Q）、卵形曲线（接起点圆的半径倒数→P、接终点圆的半径倒数→Q），曲线左转多加一负号。

第六章 涵洞设计与放样第一节 涵长计算一、正交涵洞长度计算（一）无超高加宽时： B 上=B 下=0.5BH —路基填土高度，涵底中心至路基边缘高度。

h 上、h 下——涵洞上下游洞口建筑高度。

m —路基边坡率 i0——涵底坡度L 上、L 下——涵洞上下游水平长度（m ）。

L 上=i0m 1h -H m ⋅++上）（上BL 下=i0m 1h -H m ⋅-+下）（下B涵洞总长L= L 上+L 下若缘石外低端不在路基边坡延长线时，h 上、h 下用h 上+t 、h 下+t 代替，t ——厚，a ——宽（二）有超高加宽时（设在平曲线内） 1、i0与i1方向一致 L 上=i0m 1i1B h -H m ⋅+⋅++）上（上BL 下=i0m 1W i1W h -H m ⋅-+⋅-+）下（下BB 上、B 下——半个标准路基宽 W ——路基加宽 涵洞总长L= L 上+L 下注意：路基的设计高为未超高加宽前路基内侧边缘点的高程。

图6-2有超高加宽时涵长计算12、i0与i1方向相反L 上=i0m 1i1h -H m ⋅+⋅-++）上（上W W BL 下=i0m 1i1B h -H m ⋅-⋅++）下（下B涵洞总长L= L 上+L 下（三）斜交斜做涵洞因：L 上•cos α=B 上+ m （H- h 上- L 上•i0）+a 所以： L 上=i0m c ah -H m ⋅+++αos B 上）（上同理：L 下=i0m c ah -H m ⋅-++αos B 下）（下实训项目：根据已知条件计算涵洞长度。

实训时间：2课时。

图6-3有超高加宽时涵长计算2图6-4斜交斜做涵长计算第二节 涵址测量一、 涵位中桩钉设直线上的涵位用花杆穿线的办法（经违仪）确定中桩，或用全站仪坐标法定设中桩。

曲线上的涵位用切线支距法定设中桩。

切线支距法步骤：1、预估ZY 到涵中心桩的曲线长。

2、查切线支距X 、Y ，或根据曲线长和偏角计算X 、Y 。

涵洞设计与放样涵洞放样根据涵洞设计图，在实地上把涵洞的中心线先确定下来。

根据涵洞设计尺寸，把涵洞的基础、涵身、洞口基础、洞口墙身在实地上放样出来，用桩做标记，并用白灰划线。

一、涵洞中心线的确定仪器立在涵洞中桩,根据设计的斜交角度，旋转水平度盘至涵洞中心线方向，在该方向上定出涵洞的L 上和L 下长度,定桩。

在远离涵长的该方向上确定四个方向桩（A 、B 、C 、D ），上下游各两个，注意在订桩时应该使桩相对固定。

二、涵身基础的放样 涵身基础的放样是依据涵洞中线与涵洞设计图里的基础尺寸，利用经纬仪和钢尺在实地上确定基础的轮廓线。

如图6-8，基础放样的步骤如下：1、立仪于O 点,瞄准线路方向，拨转涵洞角度，量取距离2L，订出涵洞上游长度A 点,同理定出B 点。

2、立仪于A 点，瞄准O 点，旋转900方向，量取2l，订出台基内侧边缘点1。

3、从1点在该方向上量取a,订出2点.同理订出3、4点。

C DA B路线方向涵洞方向图6-7 涵洞中心线确定ABo12434、在1、2、3、4点订桩并用白灰把四点连线,涵身的基础线则放样完毕.5、同理可以放出另一侧的涵身基础线。

三、台身的放样据图6—8，在基础样放完后，在基础线内量取台身的尺寸并划线.四、洞口放样举例洞口为八字翼墙的放样方法,如图6—9。

步骤:1、立经纬仪于A 点，对中、整平。

2、瞄准涵台台身内侧方向,倒镜1800，拨转300为翼墙方向,在该方向上量取设计图尺寸030cos W ,得墙身顶端内侧边缘点. 3、继续旋转水平度盘600，从A 点量取距离2，再量距离3，再量距离4，倒镜1800，从A 量取距离1.4、同理，可以得出洞口端部的5个点。

5、最外的两条线为基础轮廓线，靠近的两条为墙身底部线，中间等宽的部位为墙顶线.用桩订设，划白灰线。

涵洞的各构造物的端点的坐标也可通过涵洞中桩的坐标进行计算，用全站仪进行坐标放样，测定各端点。

图6-9 涵洞洞口放样。

第一部分桥梁在曲线上的布臵一、梁的布臵与基本概念1梁的布臵设在曲线上的钢筋混凝土简支梁式桥，每孔梁仍是直的，于是各孔梁中线的连接线成为折线，以适应梁上曲线线路之需要。

但若按图1所示布臵，使线路中线与梁的中线在梁端相交，则由图可以看出，线路中线总是偏在梁跨中线的外侧，当列车过桥时，外侧那片梁必然受力较大；况且列车运行时要产生离心力，使外侧的一片梁受力较大的现象更加严重。

为了使两片梁受力较为均衡，合理的布臵方案应把梁的中线向曲线外侧适当移动。

一般情况下梁的布臵有两种方案：⑴平分中矢布臵：在跨中处梁的中线平分矢距f，即梁的中线与线路中线的偏距f1=f/2；在桥墩中线处梁的中线与线路中线的偏距E=f/2。

这种布臵的特点是内外侧两片梁的偏距相同（f1=E=f/2），故两片梁的人行道加宽值相等。

⑵切线布臵：在跨中处梁的中线与线路中线相切，即偏距f1=0；在桥墩中心处梁的中线与线路中线的偏距为E=f。

（f=R-R*COS(α/2)）12图1 梁的中线连成折线示意1----线路中线 2-----梁的中线2基本概念桥梁工作线：在曲线上的桥，各孔梁中心线的连线是一折线，称桥梁工作线，与线路中线不一致，如图2， AB -BC 是桥梁工作线，abc是线路中线，E=F/2*1/COS （α/2） 桥墩中心：两相邻梁中心线之交点是桥墩中心，如图2中的A ，B 及C 各点。

基本概念中所述均指桥墩无预偏心的情况（见桥墩布臵图3）；有预偏心时见桥墩布臵图4，桥墩中心在偏距的基础上再向曲线外侧偏移一距离，偏移距离详见设计图。

桥墩轴线：过桥墩中心作一直线平分相邻二孔梁中心线的夹角，这个角平分线即桥墩横轴（又称横向中线），如图2中的Bb ；过桥墩中心作桥墩横轴的垂线为桥墩纵轴（又称纵向中线）。

桥墩中心里程：桥墩横轴与线路中线之交点称桥墩中心在线路中线上的对应点，如图2中的a 、b 及c 点。

桥墩中心里程即以其对应点的里程表示之。

偏距E ：桥墩中心与其对应点之间的距离称为偏距，如图2的Aa 、Bb 及Cc ；偏距的大小由梁长及曲线半径决定之（E=L2/16R ，L 梁长，R 曲线半径）。

第一部分桥梁在曲线上的布置一、梁的布置与基本概念1梁的布置设在曲线上的钢筋混凝土简支梁式桥，每孔梁仍是直的，于是各孔梁中线的连接线成为折线，以适应梁上曲线线路之需要。

但若按图1所示布置，使线路中线与梁的中线在梁端相交，则由图可以看出，线路中线总是偏在梁跨中线的外侧，当列车过桥时，外侧那片梁必然受力较大；况且列车运行时要产生离心力，使外侧的一片梁受力较大的现象更加严重。

为了使两片梁受力较为均衡，合理的布置方案应把梁的中线向曲线外侧适当移动。

一般情况下梁的布置有两种方案：⑴平分中矢布置：在跨中处梁的中线平分矢距f，即梁的中线与线路中线的偏距f1=f/2；在桥墩中线处梁的中线与线路中线的偏距E=f/2。

这种布置的特点是内外侧两片梁的偏距相同（f1=E=f/2），故两片梁的人行道加宽值相等。

⑵切线布置：在跨中处梁的中线与线路中线相切，即偏距f1=0；在桥墩中心处梁的中线与线路中线的偏距为E=f。

12图1 梁的中线连成折线示意1----线路中线 2-----梁的中线2基本概念桥梁工作线：在曲线上的桥，各孔梁中心线的连线是一折线，称桥梁工作线，与线路中线不一致，如图2，AB-BC是桥梁工作线，abc是线路中线。

桥墩中心：两相邻梁中心线之交点是桥墩中心，如图2中的A，B及C各点。

基本概念中所述均指桥墩无预偏心的情况（见桥墩布置图3）；有预偏心时见桥墩布置图4，桥墩中心在偏距的基础上再向曲线外侧偏移一距离，偏移距离详见设计图。

桥墩轴线：过桥墩中心作一直线平分相邻二孔梁中心线的夹角，这个角平分线即桥墩横轴（又称横向中线），如图2中的Bb；过桥墩中心作桥墩横轴的垂线为桥墩纵轴（又称纵向中线）。

桥墩中心里程：桥墩横轴与线路中线之交点称桥墩中心在线路中线上的对应点，如图2中的a、b及c点。

桥墩中心里程即以其对应点的里程表示之。

偏距E：桥墩中心与其对应点之间的距离称为偏距，如图2的Aa、Bb及Cc；偏距的大小由梁长及曲线半径决定之。

涵洞计算公式第六章涵洞设计与放样第⼀节涵长计算⼀、正交涵洞长度计算（⼀）⽆超⾼加宽时： B 上=B 下=0.5BH —路基填⼟⾼度，涵底中⼼⾄路基边缘⾼度。

h 上、h 下——涵洞上下游洞⼝建筑⾼度。

m —路基边坡率 i0——涵底坡度L 上、L 下——涵洞上下游⽔平长度（m ）。

L 上=i0m 1h -H m ?++上）（上BL 下=i0m 1h -H m ?-+下）（下B涵洞总长L= L 上+L 下若缘⽯外低端不在路基边坡延长线时，h 上、h 下⽤h 上+t 、h 下+t 代替，t ——厚，a ——宽（⼆）有超⾼加宽时（设在平曲线内） 1、i0与i1⽅向⼀致 L 上=i0m 1i1B h -H m ?+?++）上（上BL 下=i0m 1W i1W h -H m ?-+?-+）下（下BB 上、B 下——半个标准路基宽 W ——路基加宽涵洞总长L= L 上+L 下注意：路基的设计⾼为未超⾼加宽前路基内侧边缘点的⾼程。

图6-2有超⾼加宽时涵长计算12、i0与i1⽅向相反L 上=i0m 1i1h -H m ?+?-++）上（上W W BL 下=i0m 1i1B h -H m ?-?++）下（下B涵洞总长L= L 上+L 下（三）斜交斜做涵洞因：L 上?cos α=B 上+ m （H- h 上- L 上?i0）+a 所以： L 上=i0m c ah -H m ?+++αos B 上）（上同理：L 下=i0m c ah -H m ?-++αos B 下）（下实训项⽬：根据已知条件计算涵洞长度。

实训时间：2课时。

图6-3有超⾼加宽时涵长计算2图6-4斜交斜做涵长计算第⼆节涵址测量⼀、涵位中桩钉设直线上的涵位⽤花杆穿线的办法（经违仪）确定中桩，或⽤全站仪坐标法定设中桩。

曲线上的涵位⽤切线⽀距法定设中桩。

切线⽀距法步骤：1、预估ZY 到涵中⼼桩的曲线长。

2、查切线⽀距X 、Y ，或根据曲线长和偏⾓计算X 、Y 。

第一部分桥梁在曲线上的布置一、梁的布置与基本概念1梁的布置设在曲线上的钢筋混凝土简支梁式桥，每孔梁仍是直的，于是各孔梁中线的连接线成为折线，以适应梁上曲线线路之需要。

但若按图1所示布置，使线路中线与梁的中线在梁端相交，则由图可以看出，线路中线总是偏在梁跨中线的外侧，当列车过桥时，外侧那片梁必然受力较大；况且列车运行时要产生离心力，使外侧的一片梁受力较大的现象更加严重。

为了使两片梁受力较为均衡，合理的布置方案应把梁的中线向曲线外侧适当移动。

一般情况下梁的布置有两种方案：⑴平分中矢布置：在跨中处梁的中线平分矢距f，即梁的中线与线路中线的偏距f1=f/2；在桥墩中线处梁的中线与线路中线的偏距E=f/2。

这种布置的特点是内外侧两片梁的偏距相同（f1=E=f/2），故两片梁的人行道加宽值相等。

⑵切线布置：在跨中处梁的中线与线路中线相切，即偏距f1=0；在桥墩中心处梁的中线与线路中线的偏距为E=f。

（f=R-R*COS(α/2)）12图1 梁的中线连成折线示意1----线路中线 2-----梁的中线2基本概念桥梁工作线：在曲线上的桥，各孔梁中心线的连线是一折线，称桥梁工作线，与线路中线不一致，如图2，AB -BC是桥梁工作线，abc是线路中线，E=F/2*1/COS（α/2）桥墩中心：两相邻梁中心线之交点是桥墩中心，如图2中的A，B及C各点。

基本概念中所述均指桥墩无预偏心的情况（见桥墩布置图3）；有预偏心时见桥墩布置图4，桥墩中心在偏距的基础上再向曲线外侧偏移一距离，偏移距离详见设计图。

桥墩轴线：过桥墩中心作一直线平分相邻二孔梁中心线的夹角，这个角平分线即桥墩横轴（又称横向中线），如图2中的Bb；过桥墩中心作桥墩横轴的垂线为桥墩纵轴（又称纵向中线）。

桥墩中心里程：桥墩横轴与线路中线之交点称桥墩中心在线路中线上的对应点，如图2中的a、b及c点。

桥墩中心里程即以其对应点的里程表示之。

偏距E：桥墩中心与其对应点之间的距离称为偏距，如图2的Aa、Bb及Cc；偏距的大小由梁长及曲线半径决定之（E=L2/16R，L梁长，R曲线半径）。

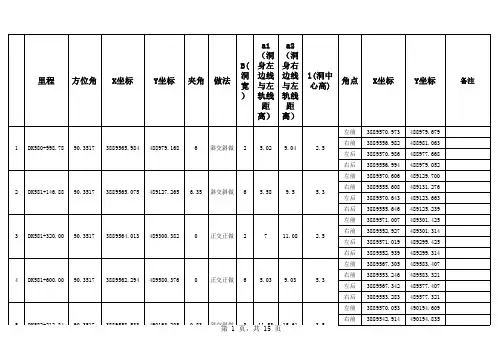
请按照线路的逐桩坐标计算出涵洞中心里程的坐标和该点的坐标方位角；利用涵洞的结构尺寸计算出其他几个（一般计算四个）角点的坐标，用全站仪进行角点放样，其后用钢尺对每一条边长进行复核，能确保施工放样无误。

圆管涵、盖板涵以及箱涵均可以采用该种计算方法，如有必要可以对各个角点以外的其他任意点（包括八字墙）进行坐标计算和施工放样。

例：已知：AK0+238盖板涵，线路中心坐标为（3132.920，88666.379）方位角为142.272504度斜交右角为110度，涵洞净宽4米，左测涵长11.91米，右侧涵长10.64米。

求解：按照大小里程左右4个角点的坐标涵 洞 坐 标 计 算
涵洞位置：K0+225
计算：1、（3134.863，88679.026）；2、（3127.997，88657.547）；3、（3138.230，88676.421）；4、（3131.363，88654.942）。

说明：斜交涵洞的里程差应为线路方向的实际里程差，即4.257米，左右涵长为图纸标注的实际长度，即11.91米和10.64米。

说得很对！！
本人理解和计算方法为：用涵洞中心坐标和切线方位角按照直线段坐标计算方法先计算出涵洞中心线路前进方向的前后两个点坐标后，分别用这两二点依然用涵洞中心的切线方位角考虑线路斜交右角的关系依照计算边桩坐标的思路分别依次求出四个角点的坐标。

axjl2202
的例子我已经计算验证是非常正确的！！！
算。

第一部分桥梁在曲线上的布置一、梁的布置与基本概念1梁的布置设在曲线上的钢筋混凝土简支梁式桥，每孔梁仍是直的，于是各孔梁中线的连接线成为折线，以适应梁上曲线线路之需要。

但若按图1所示布置，使线路中线与梁的中线在梁端相交，则由图可以看出，线路中线总是偏在梁跨中线的外侧，当列车过桥时，外侧那片梁必然受力较大；况且列车运行时要产生离心力，使外侧的一片梁受力较大的现象更加严重。

为了使两片梁受力较为均衡，合理的布置方案应把梁的中线向曲线外侧适当移动。

一般情况下梁的布置有两种方案：⑴平分中矢布置：在跨中处梁的中线平分矢距f，即梁的中线与线路中线的偏距f1=f/2；在桥墩中线处梁的中线与线路中线的偏距E=f/2。

这种布置的特点是内外侧两片梁的偏距相同（f1=E=f/2），故两片梁的人行道加宽值相等。

⑵切线布置：在跨中处梁的中线与线路中线相切，即偏距f1=0；在桥墩中心处梁的中线与线路中线的偏距为E=f。

（f=R-R*COS(α/2)）12图1 梁的中线连成折线示意1----线路中线 2-----梁的中线2基本概念桥梁工作线：在曲线上的桥，各孔梁中心线的连线是一折线，称桥梁工作线，与线路中线不一致，如图2，AB -BC是桥梁工作线，abc是线路中线，E=F/2*1/COS（α/2）桥墩中心：两相邻梁中心线之交点是桥墩中心，如图2中的A，B及C各点。

基本概念中所述均指桥墩无预偏心的情况（见桥墩布置图3）；有预偏心时见桥墩布置图4，桥墩中心在偏距的基础上再向曲线外侧偏移一距离，偏移距离详见设计图。

桥墩轴线：过桥墩中心作一直线平分相邻二孔梁中心线的夹角，这个角平分线即桥墩横轴（又称横向中线），如图2中的Bb；过桥墩中心作桥墩横轴的垂线为桥墩纵轴（又称纵向中线）。

桥墩中心里程：桥墩横轴与线路中线之交点称桥墩中心在线路中线上的对应点，如图2中的a、b及c点。

桥墩中心里程即以其对应点的里程表示之。

偏距E：桥墩中心与其对应点之间的距离称为偏距，如图2的Aa、Bb及Cc；偏距的大小由梁长及曲线半径决定之（E=L2/16R，L梁长，R曲线半径）。