北大光华管理学院金融经济学课件-课程大纲
- 格式:ppt
- 大小:213.00 KB
- 文档页数:9



课程说明1.本课程为金融学专业硕士生的必修课程,系统地讲授课程说明1.授课方式:讲授课程说明1.评估方法课程说明1.授课教师:唐国正教学内容1.什么是金融工程?什么是金融工程?定义1.包括设计、开发和实施具有创新意义的金融工具和金什么是金融工程?创新1.创新的三个层次什么是金融工程?金融工程产品作为金融创新活动的结果,金融工程产品可能是教学内容1.什么是金融工程?金融创新的动机税法与监管的变化1.Merton Miller认为:金融创新的动机减少金融约束1.Silber认为金融创新的过程实质上是公司试图放松面金融创新的社会价值R. C. Merton认为金融创新可以从三个方面提升经济公司(RJR金融创新的社会价值零和对策?1.许多经济学家认为,从全社会的角度来看,以绕开监教学内容1.什么是金融工程?金融工程的创新标准1.一种金融工具或者金融策略成为一项金融创新的条件金融工程的创新标准1.如果用Van Horne的标准来衡量,那么一些过去被认金融工程的创新标准债权-股权互换的税收套利1.A公司:金融工程的创新标准债权-股权互换的税收套利1.这笔交易对A公司来说是有意义的教学内容1.什么是金融工程?推动金融工程发展的因素在综合了Miller、Silber与Van Horne的研究成果教学内容1.什么是金融工程?应用领域综述1.开展金融工程活动的主体应用领域融资1.在融资方面,一种类型的金融工程活动是:在各种约应用领域融资4.另一种类型的金融工程活动与公司并购有关,在并购应用领域投资与现金管理1.在投资方面,金融工程师开发出了各种各样的中长期应用领域管理发行人的风险1.在风险管理领域,金融工程发挥着重要作用应用领域管理投资者的风险1.挑战性q90年代市场上出现的与股票指数挂钩的债券应用领域风险管理管理投资者的风险与管理发行人的风险迥然不同应用领域套利1.开发交易策略来利用不同地点、不同时间、不同工具教学内容1.什么是金融工程?应用领域非金融类公司1.金融工程在公司层面有着非常重要的应用应用领域非金融类公司1.对公司来说,金融工程可以用来应用领域非金融类公司安然公司(Enron) 应用领域非金融类公司1.1993年,为了便于供应商与最终消费者管理价格风教学内容1.什么是金融工程?理论基础1.作为一门应用学科,金融工程的理论基础主要来自于基本工具1.金融工程的工具可以分成两部分,一部分是基本的金来,用以实现某一特定的目标其它理论、工具1.除了应用上述理论与工具以外,金融工程活动常常还。

Principles of FinanceLecture 06Forward and Futures ContractsThe Nature of Derivatives∙ A derivative is an instrument whose value depends on the values of other more basic underlying variables∙Examples of derivatives-F orward-F utures-O ptions-S waps……Derivative Markets ∙Exchange Traded-Standard products-Trading floor or computer trading-Virtually no credit risk∙Over-the-Counter (OTC)-Non-standard products-Telephone market-Credit riskForward Contracts∙ A forward contract is an agreement made today to buy or sell an asset at a certain time in the future for a certain price (referred to as the forward price or the delivery price)∙The delivery price is usually chosen so that the initial value of the contract is zero; No money changes hands when contract is first negotiated and it is settled at maturity∙An OTC agreement between two parties and both parties are subject to credit risk∙Both parties have the obligation to honor the contractSettlement of Forward Contracts∙Physical: requires delivery of actual assets∙ Cash settled: requires only the exchange of the difference between the delivery price and the prevailing spot price at maturity∙Suppose that:Long 3-month Gold forwardDelivery price $300Spot price at t = 3 months: $320P/L from a Long Forward PositionS, TP/L from a Short Forward PositionSTFutures Contract∙Futures are standardized forward contracts.∙Whereas a forward contract is traded OTC a futures contract is traded on an exchange∙Specifications need to be defined:-The underlying asset-Delivery location-Maturity date and delivery time-Method of settlement∙Most contracts are closed out before maturityFeatures Promoting Liquidity ∙Standardized Contract-Maturity dates-Contract size-Price tick size, i.e. minimum price movement-The underlying asset (especially commodities) ∙Organized exchangesFeatures Reducing Credit Risk∙Daily settlement: Futures contracts are marked to market and settled at the end of every business day∙Margin account: To buy or sell a futures contract, the investor is required to post a specified margin to guarantee contract performance∙Clearinghouse: The clearinghouse does not take a position in any trade but interpose itself between two parties in every transactionMargin Accounts∙ A margin is cash or marketable securities deposited by an investor with his or her broker∙The balance in the margin account is adjusted to reflect daily settlement (profit or loss)∙Initial margin: The amount a trader must deposit into his/her trading account (i.e. margin account) when establishing a futures position∙When the balance in the margin account falls to, or below, a maintenance margin level, the trader receives a margin call and is requested to top up the account to the initial level. The extra funds deposited are known as a variation margin∙If the balance in the margin account exceeds the initial margin level, the trader is entitled to withdraw the excess funds in the accountExample of the Margin Account ∙An investor takes long position in $/£ futures∙Contract size: £62,500∙Initial margin: 1,485$∙Maintenance margin: 1,100$Date SettlementPrice OpeningBalance($)DailyP/L ($)ClosingBalance($)Margincall ($)Cumulative P/L ($)1.6500 1,48501/11 1.6508 1,485 50 1,535 50 02/11 1.6412 1,535 -600 935 550 -550 03/11 1.6384 1,485 -175 1,310 -725 04/11 1.6456 1,310 450 1,760 -275 05/11 1.6492 1,760 225 1,985 -50The Economic Function of Futures MarketsThe futures markets facilitate the re-allocation of exposure to commodity price risk among market participants.By providing a means to hedge the price risk associated with storing a commodity, futures contracts make it possible to separate the decision of whether to physically store a commodity from the decision to have financial exposure to price changes.The Economic Function of Futures MarketsThe existence of the futures market for wheat conveys information to all producers, distributors, and consumers; and this eliminates the necessity for market participants to gather and process information in order to forecast the future spot priceSuppose the commodity is wheat, and next year’s crop is expected to be much higher than average, then futures prices may be lower than the spot, (the spread may be negative,) nobody will store wheat.The Law of One Price and Arbitrage∙In a competitive market, if two assets are equivalent they will tend to have the same price∙The law of one price is enforced by a process called arbitrage∙Arbitrage is the purchasing of a set of assets, and immediate sale of another set of assets, in such a way as to earn a sure profit from price differences∙Arbitrage process brings two equivalent assets to the same price, this is known as market clearing.An Arbitrage Opportunity?∙Shares of General Motors (GM) are listed on both NYSE and LSE ∙The quoted price is £100 in London and $148 in New York∙The current exchange rate is $1.4500/£∙An arbitrage opportunity?Another Arbitrage Opportunity?∙There are two investment portfolios: portfolio A and portfolio B∙The payoffs at maturity are as follows:State 1 State 2Portfolio A $70 $100Portfolio B $70 $100∙The current quoted price of portfolio A is $80 and the current quoted price for portfolio B is $82∙An arbitrage opportunity?Framework for Forward/Future Pricing ∙Future price: price of the future∙Spot price: price of the underlying asset at present∙Future spot price: price of the underlying asset in the futureFramework for Forward/Future Pricing Suppose you have some spare cash, and you want to invest it in gold in a year’s time. There are 2 ways to do it:A.Buy gold at the spot price with your money, store it for a year(which means you incur some storage costs), sell it at the future spot price.B.Enter into a forward/future contract of gold, put your money in abank for a year, buy A at the forward/future price in the end of the year, sell it at the future spot price.Since the two strategies are equivalent, they must provide the same return so that there are no arbitrage opportunities.Framework for Forward/Future PricingDenote S as the spot price of gold, F as the forward/future price of gold, FS as the future spot price of gold, s as the storage cost of gold as a fraction of spot price, r as the risk-free interest rate:Return of A: FS S s S -- Return of B: FS FrS -+FS S FS Fs rS S---=+Therefore: (1)F r s S =++Framework for Forward/Future Pricing∙Forward price must be arbitrage-free∙Suppose that-The spot price of gold is US$300-The 1-year US$ interest rate is 8% per annum with annual compounding-Storage costs 2% of gold.-The forward-spot-price-parity relation implies that the one-year forward price is:+=++F⨯rs=S+08)30033002.0)1(.01(=∙Forward prices above $330 permit arbitrage-Suppose the forward price is $340-At time t = 0- Sell gold forward at $340- Borrow $300 at 8% pa- Purchase gold in the spot market at $300, store for a year (storage costs $6)-At time t = 1 year- Deliver gold and receive $340-Pay back loan with interest ($324)-Pay storage cost: ($6)- Make a profit of $10: 340-324-6=10∙Forward prices below $330 permit arbitrage-Suppose the forward price is $320-At time t = 0-Buy gold forward at $320-Sell short gold in the spot market at $300 (borrow gold and sell it immediately)-Deposit $300 at 8% pa-At time t = 1 year-Accept delivery of gold for $320: ($320)-Return the gold and receive storage cost: $6-Receive deposit with interest of $324-Make a profit of $10: 324+6-320=10Financial FuturesThe underlying asset of a financial future is a financial instrument, e.g. stock, bond, foreign currency, etc.Example: Share A has a spot price of $100 (S=100), the risk-free interest rate is 8% (r=0.08) with annual compounding, what’s the forward price?Forward-spot-price-parity for a share with no dividend with maturity of T years:T1(+=SrF)Financial FuturesThe investor has two equivalent investment strategies:1.buy one share A, hold it for a year, and sell it at the future spotprice of 1S. Cash flow in a year’s time: 1S2.buy a forward/future contract of share A at the price of F, make adeposit in a risk-free asset with future value of F, take the money out after a year, and buy the share at F, sell it in the market at the future spot price of 1S. Cash flow in a year’s time: 1SThe law of one price says that they should have the same price today since they produce the same amount of cash flow in a year’s time!Financial FuturesPrice of strategy 1: the spot price of share A: SPrice of strategy 2: the amount of cash invested into the risk-free asset so as to generate F in a year’s time: F/(1+r)Therefore: S=F/(1+r)Rearranging, we have:F+=S)1(rIf the futures contract matures in T years, it becomes:T=1(+rSF)Financial FuturesWhat if share A pays dividend of D in a year’s time?Again the investor has two equivalent strategies:Strategy 1: buy share A at the spot price S, hold it for one year, receive dividend of D, and sell the share at the future spot price of S. Cash flow in a year’s time: 1S+ D1Strategy 2: buy a forward/future contract at the price of F, make an investment in a risk-free asset with future value of F+D, take the money out after a year, buy the share at F, sell it in the market at the future spot price of 1S. Cash flow in a year’s time: 1S+DFinancial FuturesPrice of strategy 1: the spot price of share A: SPrice of strategy 2: the amount of cash invested into the risk-free assetso as to generate F+D in a year’s time (F+D)/(1+r)Applying the law of one price, we have: S=(F+D)/(1+r) Rearranging, we have the forward-spot-price-parity of a share with dividend payment:F=S(1+r)-DThe Forward Price is not a Forecast of Future Spot Price The forward price is obtained without risk from the current spot and risk free investmentThe spot value at a future date is obtained by investing in the security and accepting (market) risk, and this risk must be rewardedFX Forward RateDefine HC r and FC r as the effective interest rates at home andabroadFCHCr r S F ++=11where F and S are defined as the number of units of HC per unit of FC. For example, suppose £1=$1.6, then F =1.6 and $r r HC =, £r r FC = if you are buying a pound future; F =0.625 and £r r HC =, $r r FC = if you are buying a dollar future.The FX Forward RateSuppose an investor wants to buy a futures contract of pound sterling at F , i.e. he can buy pound at the price of £1=$F in a year’s time. The spot price of pound is S , i.e. £1=$S . So here pound is the foreign currency, dollar is the home currency. The risk-free interest rates are: $r r HC =, £r r FC =. What is the proper price of the future contract?The investor has two equivalent strategies: Stragegy 1:At t=0: Enter into a futures contract of pound with futures price of F . Cash flow: 0At t=1: Buy pound at F . Cash flow: FThe FX Forward RateStrategy 2:At t=0: Borrow )1/(£r S + of US dollars, change into £1/(1)r + of pounds, put it in a bank at the pound interest rate. Cash flow: 0At t=1, take the money out (in pound), pay back the dollar loan. Cashflow: $£11r Sr ++The FX Forward RateSince the two strategies both will give you one pound in a year’s time, the law of one price says that they have the same price, i.e. the amount of investment of these two strategies must be the same:$£11r F Sr +=+More generally:FCHCr r SF ++=11Pricing FX Forward Contract∙ Suppose that:Spot $/£: 1.4222One-year $ interest rate: %00.5 per annum with annual compounding One-year £ interest rate: %00.6 per annum with annual compounding∙ The six-month £ forward rate:415.10296.010247.014222.11111£$=++⨯=++=++=r r S r r S F FC HCAs a rule of thumb, if the foreign currency offers a higher interest rate, the future price of the foreign currency will be lower than the spot price.Corporate Applications: Hedging∙Receive FC payment at a future date ⇒ sells FC forward short∙Boeing has just sold 10 Boeing-747s to British Airways with total price of £200m payable in one year’s time∙Boeing can hedge this cash flow in £ by selling £ forward short∙If the one-year forward rate is $1.60/£, so Boeing will receive $320m no matter how exchange rate $/£ movesCorporate Applications: Hedging∙Make FC payment at a future date ⇒ buys FC forward (long)∙An US company imported some goods from Switzerland and is due to pay SFr100m in six months’ time∙The company can hedge its exposure to SFr by buying SFr forward. The six-month forward rate is SFr1.54/$, so the company is required to pay $64.94mThe Role of Expectations in Determining Exchange Rates Consider a world in which there are two countries, Domestic & Foreign, and conditions are such in each country that the yield curves are flat, with yields of 5% and 10% respectively.Further assume that the exchange rate is 1 todayThe 1-year forward is 1*1.05/1.10=0.9545The Role of Expectations in Determining Exchange Rates If the interest rate in Foreign is higher than in Domestic, one explanation may be that the rate of inflation is higher.Assume no taxes, and the interest rate difference is the result inflation being 5% and 10% respectively.Then the price dynamics of both countries will result in an exchange rate of 0.9545 next year, which is also the forward rate.The Role of Expectations in Determining Exchange Rates In real life, things are not so simple, but several mechanisms may be postulated that support the expectations hypothesis.International investor confidence, and their forecasts of inflation, place price pressure on both spot and forward exchange rates through the international bond market。


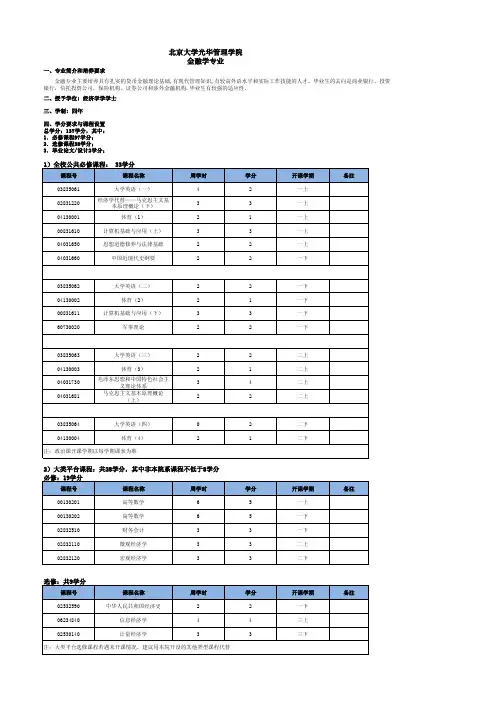


金融经济学一、课程说明课程编号:160518Z10课程名称:金融经济学/Financal Economics课程类别:专业课程学时/学分:48/3先修课程:西方经济学适用专业:金融学教材、教学参考书:1.王江主编.金融经济学.北京:中国人民大学出版社.2006.6;2.宋逢明主编.金融经济学. 北京:高等教育出版社.2006年。
二、课程设置的目的意义金融经济学旨在用经济学的一般原理和方法来分析金融问题。
本课程是金融专业的主干课程,是金融学的微观经济学理论基础。
它着重从金融市场均衡来讨论金融资产的估值与定价,以及金融资产的风险管理。
因此是金融学其他重要领域如金融工程、投资学、公司财务、金融机构管理学等必不可缺的理论基础。
三、课程的基本要求知识:本课程要求学生掌握有关金融经济学的基本理论和知识,在了解金融经济学的基本概念和意义的基础上,以建立理性金融的行为基础和基本的均衡模型为基础,了解均衡模型框架下的金融资产的套利与定价;投资组合选择理论和基金分离定理以及资产定价模型——资本资产定价模型(CAPM)。
从而使学生完整地了解金融经济学基本定理,建立对整体金融理论的认识。
能力:从对金融经济学基本理论和知识的学习,提高对社会经济和金融发展规律的认识能力、分析能力和把握能力;从对均衡模型框架下金融资产的套利与定价以及投资组合选择理论和基金分离定理等相关知识的学习和掌握,建立和提高对金融领域投资选择、金融产品开发与定价等问题深层次成因探析和把握的能力。
素质:建立在金融经济学基本理论框架下运用金融经济学基本概念、一般原理分析金融问题的思维模式,具备理解和分析金融决策的基本素质,提高对实际金融问题进行自主判断和运用的专业素质。
四、教学内容、重点难点及教学设计五、实践教学内容和基本要求无六、考核方式及成绩评定。
