当前位置：文档之家 › 氢原子和类氢离子薛定谔方程的直角坐标表示式

氢原子和类氢离子薛定谔方程的直角坐标表示式

  • 格式：ppt
  • 大小：4.69 MB
  • 文档页数：159

下载文档原格式

  / 159

合集下载

氢分子的薛定谔方程

氢分子的薛定谔方程

氢分子的薛定谔方程
氢分子的薛定谔方程是描述氢分子体系的基本定律。

它是由薛定谔方程推导而来，其中包括两个氢原子核和两个电子的相互作用。

这个方程表示了氢分子的波函数在空间中的变化规律和时间的演化。

氢分子的薛定谔方程可以写成：
HΨ= EΨ
其中，H是哈密顿算符，Ψ是氢分子的波函数，E是氢分子的能量。

哈密顿算符包括两部分，分别是动能和势能：
H = T + V
其中，T是氢分子中两个电子的动能，V是氢分子中两个电子和两个原子核之间的相互作用势能。

这个势能包括库伦势能和交换-相关势能。

解决氢分子的薛定谔方程需要用到量子力学的一些基本概念和数学方法，如波函数、本征值和本征函数等。

解得氢分子的波函数后，可以通过它来计算氢分子的性质，如能量、电荷密度、偶极矩等。

总之，氢分子的薛定谔方程是描述氢分子体系的一种数学表达方式，它是量子力学的基础之一。

物理-氢原子和类氢原子

物理-氢原子和类氢原子


r
驻波
计算表明径向波函数
的节点数
通常把节点数为零（
）的“态”，称为
圆轨道，例如：1s, 2p, 3d, …，它们极大值的位
置：
，其中 是第一玻尔轨道半径。
§2. 量子力学对（类）氢原子的描述
➢电子的几率密度随角度的变化
电子在 附近的立体角 内的几率：
Y0,0 ( ,)
1
4
Y2,0 ( ,)
1 (3 cos2 1) 4
Y1,0 ( ,)
1 cos 4
Y2,1 ( ,)
1 sin cos ei 4
Y1,1 ( ,)
1
4
sin ei
Y2,2 ( ,)
1 sin2 ei2 4
§2. 量子力学对（类）氢原子的描述
粒子概率分布随角度的变化|Ylm|2，与φ角无关
Y00 2
Y10 2
实验数据和理论结果之差异可以通过考虑原子核的质量得
到消除。即把电子质量m用约化质量 = mM/(m+M)替代。
对类氢离子（He+, Li++, Be+++等），结果都适用。 只需把核电荷+e换为+Ze（Z为核所带正电荷数）。
§2. 量子力学对（类）氢原子的描述
2）氢原子的几个光谱线系
赖曼（Lyman,1914）系：
Y11 2
Y20 2
Y21 2
Y22 2
Y30 2
Y31 2
Y32 2
Y33 2
§2. 量子力学对（类）氢原子的描述
概率密度: 2 Rnl (r)Ylm ( ,) 2 Rnl2 (r) Ylm ( ,) 2 “电子（几率）云”图象
第一节 氢原子的薛定谔方程

第一节 氢原子的薛定谔方程

A=
②常数 m（磁量子数）
由于φ是循环坐标。为了保证 Φm 是 φ的单值函数，就必须在φ变
化 1 周后保持 Φm 函数值不变。即： Φm(φ)= Φm(φ+ 2π) 即：
r Z
P
eimφ = eim(φ
则有：
+ 2π)
= eimφ • eim2π
x φ
X
o
y
Y
eim2π = eimφ-imφ = 1
∂ ∂ 1 1 + [ (sinθ ) R(r)Y(θ,φ）] + ∂θ sinθ R(r)Y(θ,φ） ∂θ ∂2 1 1 + [ R(r)Y(θ,φ）] + R(r)Y(θ,φ） sin2θ ∂φ2 1 Ze2 + （ + E）R(r)Y(θ,φ）= 0 R(r)Y(θ,φ） r
即：
ħ2 2m
Z
z
Descartes.Rene
（1596-1650）
P（数学 家，物理学家，解析几 何学奠基人之一。
0
x
Y
X
直角坐标系
2.球极坐标系
尽管用直角坐标对空间某点进行定位表述简便，但对在球状空间运动 某点的定位，却显得不便。 于是人们通过坐标换算，建立了球极坐标、椭球坐标等系。例如，对 于空间某点 P 的位置，用球极坐标可表示如下：
ħ2 T = ▽2 2m
（Kinetic energy operator ）
V = V
（Potential energy operator ）
2.H原子
如右图所示，氢原子可看成是由1个原子核及1个
核外电子构成的“双质点”体系；原子核与核外电子 只存在静电吸引势能。
+
氢原子和类氢离子一氢原子的定态schrdinger方程及其解

氢原子和类氢离子一氢原子的定态schrdinger方程及其解


(sin
)
1 sin 2
2
2
]Y
(
,)
k2Y
(
,)
Mˆ 2Y(,) l(l 1)2Y(,) k l(l 1)
其中 Y ( , ) l,m ( ) m ( )
的解 归一化条件 的解
2 0
m ( )* m' ( )d
mm'
0
l,m ( )* l'm ( ) sin d
ll '
2。角向分布图
（四）平均动能和平均位能
总能量 En
有确定值
1 2
e2 (
4 0 a 0
)(
Z n
)2
En T V
T 和V 都没有确定值，可求平均值
V Ze 2
4 0 r
V
n,l ,m
(r,
,
)(
Ze2
4 0r
)
n,l ,m
(r,
,
)r
2
sin
drdd
)(Zn22
)
1 ( e2
2 40a0
)(Z )2 n
Å a0
0h2 me2
0.529
级数终止某一项（引入量子数n ）条件是
l n 1 (n 1,2,3, l 1)
Rn,l
(r)
[c1
(
Zr a0
)l
c2
(
Zr a0
) l 1
cnl
(
Zr a0
) n1 ]e Zr
na0
nl i 1
Zr ci ( a0
)
是里德堡常数
RH
简并度为n 2
n 1
g (2l 1) n 2 l0
5 氢原子与类氢离子的定态薛定谔方程及其解

5 氢原子与类氢离子的定态薛定谔方程及其解


0
5. ()方程的解：
()方程是：
求解该方程的条件: 边界条件? 无
d 2 2 m 0 2 d
合格波函数的条件: 单值?有;连续,有限 ? 求得方程的解为： Φ
m
( ) Ae
im
式中A是归一化系数，如何求得？
归一化求A：

2
0
d
* m m
2
0
A2 e im e im d 1 1 e im 2
1 ( m m ) 2 1 ( m m ) i 2 1

1
cos m si nm

可以证明组合得到的实函数是归一化的,如:
1 1 [ 2 ( m m )]* [ 2 ( m m )]d 1 { m m d m m d 2 1 m m d m m d } 2 {1 0 0 1} 1

Zr a0
e E Z 2 2 8 0 h
2
Z2 e2 ( ) 13.6 Z 2 (e V) 2 4 0 a0
4. 将偏微分方程化为常微分方程 ——分离变量法
一般来说，偏微分方程化为常微分方程后才 能求解。
令： (r , , ) R(r )Y ( , ) R(r ) ( ) ( ) 代入薛定谔方程, 先将径向部分(只与r有关) 和角度部分分开, 分别移到方程的两边. 这样该方 程两边应等于同一个常数 . 然后在将角度部分分 离成只含一个变量的两个常微分方程 , 就将偏微 分方程分离成了三个常微分方程。
6. ()方程的解:
1 d d m2 (sin ) k 0 2 sin d d sin
氢原子的薛定谔方程

氢原子的薛定谔方程

氢原子的薛定谔方程
氢原子是最简单的原子之一，由一个质子和一个电子组成。

在量子力学中，描述氢原子的运动状态的数学模型就是薛定谔方程。

薛定谔方程是量子力学的基础方程之一，它描述了微观粒子在势场中的运动规律。

薛定谔方程是一个偏微分方程，描述了波函数随时间和空间的演化。

波函数包含了粒子的所有信息，包括位置、动量等。

在氢原子的情况下，薛定谔方程可以被简化为一个径向部分和一个角向部分的乘积。

径向部分描述了电子在原子核周围运动的距离，角向部分描述了电子在不同方向上的概率分布。

通过求解薛定谔方程，我们可以得到氢原子的能级和波函数，从而进一步研究原子的性质和行为。

薛定谔方程的求解需要考虑原子核和电子之间的相互作用，以及外加的势场对电子的影响。

通过引入适当的近似和数值方法，可以求解薛定谔方程并得到氢原子的能级和波函数。

氢原子的能级是量子化的，即只能取离散的数值。

能级越高，电子离原子核越远，能量也越大。

每个能级对应一个波函数，描述了电子在原子周围的分布情况。

薛定谔方程的求解不仅可以用于氢原子，还可以推广到其他原子和
分子系统。

通过求解薛定谔方程，我们可以理解原子和分子的结构、性质和反应规律，为化学和物理学的发展提供重要的理论基础。

薛定谔方程是描述氢原子和其他微观粒子运动的重要方程，它揭示了量子力学世界的奥秘。

通过求解薛定谔方程，我们可以深入理解原子和分子的微观世界，为科学研究和技术应用提供重要支持。

希望未来能够进一步探索量子力学的奥秘，推动科学的发展和进步。

氢原子和类氢离子薛定谔方程的直角坐标表示式

氢原子和类氢离子薛定谔方程的直角坐标表示式


pxx h

pyy h

pzz h

h
t

为满足归一化
A

h3 2
分别对x、y、z进行两次偏导，得：
p h2 2
2
42 2
x
p h2 2
2
42 y2
y
p h2 2
2
42 z2
z
三式相加，并乘以m/2
p p p h2
2d*sin
入射束
衍射束的方向性
p h/

衍射束

p 2mE
晶体
二. 实物微粒的波动性
汤姆逊电子衍射图 (示意)
n 2d sin 2
汤姆逊使用了能量较大的电子，结果也得到了类似X射线 衍射的花纹，从而也证明了德布罗意波的存在。
三、玻恩的“统计解释”:
(1) 电子的干涉作用并非两个电子的相互作用,而是 其波动本性决定.
ψ3(x) +
n=3
-+
E3
n=2
ψ2(x)
+
n=1 -
E2
ψ1(x)
+
E1
n=4 n=3 n=2 n=1
ψ42(x)
ψ32(x) ψ22(x) ψ12(x)
图 1-3.3 一维势箱中粒子的波函数、能级和几率密度
波函数的正交归一性：
l 0m
n
dx

0 1
mn mn
例 题
几率大小。
而不能确定粒子何时出现于何地。
几率大小正比于波强度。
因此：可用描述波的方法可以得到微观粒子运动的描述。 我们用波函数（Ψ）概念来代替“轨迹”，以表示微粒
第一章第六节氢原子与类氢离子的定态薛定谔方程

第一章第六节氢原子与类氢离子的定态薛定谔方程


3）、 m e 近似： 电子和核实际上是绕原子的质量中心运动，这种内部 运动的动能全部是转动能。若核不动，且为坐标原点，则 有： 2 2 Ze 2 Mm H Hamilton算符： 4 0 r M m 2
由于 m ，则折合质量 m M 直角坐标表示的薛定谔方程
第六节
氢原子与类氢离子的定 态薛定谔方程
公元前五世纪，希腊科学 家德谟克利特等人认为：万物 都是由大量的不可分割的微粒 构成， 形成了欧洲最早的朴 素唯物主义的原子论。
Δημόκριτος
19世纪初，英国科学家道尔顿提 出原子学说，认为化学元素由不可分 的微粒原子构成，它在一切化学变化 中是不可再分的最小单位；同种元素 的原子性质和质量都相同，不同元素 原子的性质和质量各不相同，原子质 量是元素基本特征之一；不同元素化 合时，原子以简单整数比结合。
类氢离子：
r
e
ze
2、采取的近似.
1）、非相对论近似 光总是必须用相对论处理，但速度不太高的电子可 用非相对论处理 电子总是具有 c 和非零的静质量 me 2）、近似 (Born Oppenheimer)定核近似 思想依据：由于 M 核 me 所以 e N ,借用经 典方法，在电子运动数周时间内原子核的空所间坐标几 乎改变，即可忽略掉核动能。
3、球极坐标
Z
z

r
y
0
x
X

Y
二、单电子原子体系的Schrö dinger方程的变数分离
三、Φ方程的解及磁量子数
四、Θ方程的解及角量子数l
五、R方程的解及主量子数n
ቤተ መጻሕፍቲ ባይዱ
六、解的综合：
JohnDalton
2019-1氢原子的薛定谔方程-文档资料

2019-1氢原子的薛定谔方程-文档资料

§18-9 量子力学中的氢原子问题
1.氢原子的薛定谔方程
氢原子中电子的势能函数 定态薛定谔方程
U e2
4 r 0
2 Ψ2 m 2 (E4e2 r)Ψ0
0
r x2y2z2
z 电子
为使求解的问题变得简便,
通常采用球坐标 (r,。,)
原核子 θ r
xφ
y
氢原子
拉普拉斯算符变为：
Y2,0 156(3co2s1)
电子的概率分布
电子的径向分布概率为 P(r)
P (r)d rR R 4r2dr
表示电子出现在 r至 rd的r球壳中的概率。
电子的概率分布
氢原子中电子径向概率分布

电子的概率分布
电子的角分布概率由 Ylm(,)决定。
Ylm(,)2与无关，表示角向概率密度对于 z轴
具有旋转对称性
由坐标原点引向曲线的长度表示 方向的概率大小
Y2 0,0
Y2 1 ,1
氢原子中电子的角分布
Y2 2,0
电子的概率分布
电子的角分布概率由 Ylm(,)决定。
Ylm(,)2与无关，表示角向概率密度对于 z轴
具有旋转对称性
由坐标原点引向曲线的长度表示 方向的概率大小
Y2 0,0
2 r12r(r2r)r2s1in(sin)
r2s1in222
设波函数为
( r ,,) R ( r ) () ()
代入薛定谔方程，采用分离变量法得到三个常 微分方程。
在解波函数时，考虑到波函数应满足的标准 条件，很自然地得到氢原子的量子化特征。
氢原子
B(z)
2
角动量的空间量 子化
o
2
L 6
氢原子的薛定谔方程

氢原子的薛定谔方程

氢原子的薛定谔方程
薛定谔方程是一个著名的电子结构理论，可以用来描述一个原子的电子状态。

它是一个带有四个变量的复合实现方程，被称为薛定谔方程。

它由20世纪伟大的物理学家Ernst Schrdinger发明，他是量子力学的创始人。

当谈到氢原子时，薛定谔方程还可以用来解释它的电子状态。

氢原子只有一个电子，因此为了解释它的电子状态，只需要一个薛定谔方程。

薛定谔方程可以如下表达：
iψ/t = ^2/2m·^2ψ + Vψ
其中，ψ表示波函数；i是虚数单位；表示普朗克常数，ψ/t表示时间导数；m是电子的质量；^2表示laplace算符；V表示电子的势能。

薛定谔方程简写为：
Hψ = εψ
其中，H表示哈密顿量，ε表示电子的能量。

对氢原子的薛定谔方程可以写为：
[^2/2m·^2+ V(r)E]ψ(r) = 0
其中，V(r)表示电子势能，E表示电子能量，r表示电子的位置半径。

解决氢原子的薛定谔方程需要一些技巧——定义一个适应性正交基函数组，利用拉普拉斯算符变换到正交空间，然后使用矩阵方法解决。

有时，哈密顿量可以被简化为一个对角矩阵，这一点取决于电
子势能的类型。

任何时候，电子能量的计算都是从在某个特定的位置的电子的能量开始的。

氢原子可以通过薛定谔方程来解释，并且可以计算出它的电子能量，解释的结果可以用来解释它的原子结构。

薛定谔方程对氢原子的电子状态起着至关重要的作用。

第二章原子构与性质§21氢原子和类氢原子的薛定谔方程及其

第二章原子构与性质§21氢原子和类氢原子的薛定谔方程及其

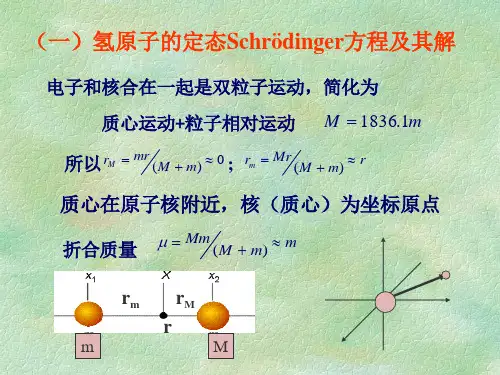
第二章 原子结构与性质§2.1.氢原子和类氢原子的薛定谔方程及其解 2.1.1.单电子原子的薛定谔方程H 原子和He +、Li 2+ 等类氢离子是单原子，它们的核电荷数为Z ，若把原子的质量中心放在坐标原点上，绕核运动的电子离核的距离为r ，电子的电荷为-e ，其静电作用势能为：r Ze V 024πε-=将势能代入薛定谔方程：得 0)(22282=ψ++ψ∇rZe h mE π或ψ=ψ-∇-E rZe mh ][22228π为了解题方便，将x 、y 、z 变量换成极坐标变量r 、θ、φ。

其关系：φθcos sin r x = φθsin sin r y =φcos r z =2222z y x r++=21)/(cos 222z y x Z ++=θx y tg /=φ})(sin )({2222sin 1sin 1212φθθθθθ∂∂∂∂∂∂∂∂∂∂++=∇r rr r 代入薛定谔方程：)()(sin )(2222222228sin 11sin 1121=ψ++++∂∂∂ψ∂∂∂∂∂∂∂rZe h mr r r rr E r πφθθθθθ2.1.2.分离变量§法：上述的方程是含三个度量的偏微分方程，要解这个方程可用度数分离法将其化为三个分别只含一个度量的常微分方程求解。

含：)()()(),,(φθθΦΘ=Φψr R r 代入方程：并乘以ΘΦR r θ22sin 移项可得：)(sin )(sin )(228sin 2sin 122222V E r r hu d d d ddr dR drdR d d ----=ΘΘΦΦθθπθθθθφ左边不含r 、θ，右边不含φ，欲左右两边相等必等于同一个常数（-m 2 ）Φ-=Φ222m d d φ, 而右边可为：（除以sin θ）)(sin )()(sin1sin 8212222θθθθπθd d d d m hur dr dR drdR V E r ΘΘ-=-+ 则有：K d d d d m =-ΘΘ)(sin sin1sin 22θθθθθK E r rZe hur dr dR drdR =++)()(2222821π2.1.3.方程解的结果 2.1.3.1.Φ（φ）方程的解0222=Φ+Φm d d φ这是一个常系数二阶齐次线性方程，有两个复函数的独立解。

氢原子与类氢离子的定态薛定谔方程及其解


r1
m1 R
m2 m2r
m1 m2
, r2
R
m1r m1 m2
x
r1
m1 C
R r2
m2 y
Ekin
1 2 1 2
m1r12
1 2
m2r22
m1( R
m2r m1 m2
)2
1 2
m2 ( R
两粒子体系示 意m1图r )2
m1 m2
1 2
(m1
m2 )R2
1 2
m1m2 m1 m2
1 r2
d dr
(r 2
dR dr
)
[
2
2
(E
Ze2 )
4 0r
l
(l r2
1)
]R
0
这是一个连属拉盖尔方程, 需要用级数法解.
求解条件: 边界条件? 无;
合格波函数条件: 有限(级数要有收敛的解)
要得到收敛结果, 无穷级数需变成多项式, 即在某
项后截断, 这要求(能量为负值时)me
2. 氢原子与类氢离子的定态
薛定谔方程的球极坐标表达式
球极坐标及其与直角坐标的关系：
x r sin cos y r sin sin z r cos
r x2 y2 z2
d r 2 sindrdd
X
0 r , 0 , 0 2
Z
r
O
P(x,y,z) (r,,) Y
函数为:
n,l,m (r, , ) Rn,l (r) Θl,m ( ) Φm ( )
nl
c{ ci i1
(
Zr a0
) l i 1
Zr
e na0
}Pl
m

强电、磁场效应中的氢及类氢原子

强电、磁场效应中的氢及类氢原子强电、磁场效应是指外加的静电场、静磁场和交变电磁场的场强大到已不能作为微扰时对原子分子体系的物理和化学性质的影响。

实验表明髙激发态里德伯原子的能级特性与外场异常敏感而且复杂。

而理论研究也很困难，在弱外场下，可用微扰法求解薛定谔方程计算能级的劈裂、移动和展宽，得到与实验一致的结果。

强外场下就不能用微扰法，需要严格求解含外场的薛定谔方程，这变得很困难。

这种困难主要在于外场的静电力、洛伦兹力和核的库仑力具有各自不同的对称性。

大多数理论计算仍集中在氢原子，或以氢原子为模型的适当修正，如碱金属原子。

由于在均匀外电场中的哈密顿量在抛物坐标中变量是可分离的，相对计算容易一些。

本文简单的记述国内关于强电、磁场中氢以及类氢原子的部分研究。

一、强电场中的氢及类氢原子高激发态里德伯原子在电场下行为主要有电离和斯塔克效应这两方面的情况。

由于氢原子和类氢离子基态s电子波函数是球对称的它的点和分布中心和原子核是重合的。

可以证明：任意一个具有确定角动量量子数l态的固有电偶极矩也为零。

但是每一个n≠1的激发态，由于对l是简并的，不同l态线型叠加的结果使固有电偶极矩不为零。

对其他多电子原子，如碱金属原子，由于轨道贯穿和极化效应，使能级对l的简并破坏，它们的固有电偶极矩也为零。

在均匀电场作用下，原子被计划，电子云中心不再与核重合，原子还能产生电偶极矩。

除了原子具有的固有电偶极矩d0之外，外场诱导的电偶极矩d1正比于场强E。

原子具有的总电偶极矩d= d0+ d1，在外电场强度E作用下产生的能级分裂为?Ee=-d*E，这就是斯塔克效应。

关于类氢原子在强电场中的电离[1]，前人有过研究。

方法是分离变量，即恒电场下类氢原子的薛定谔方程在旋转抛物座标下形式上分离变量，得到如下联立常微分方程：联立条件为。

其中，E为能量，Z为原子序，为电场强度，使用原子条件。

零边界条件为，。

在方向，；在方向远端渐进解包含出射波和入射波振幅为零。

第四节 氢原子和类氢离子


可得
π mZe α = ε 0h E = − me 8ε
2 2 4 2 0
Z h
2 2
ε 0h2 a0 = = 52.9 Pm 2 πme
Z α = a0 2 则 E = − Z R Z − ψ = N .e a 0
R =
me
2
4 2
8ε 0 h
1 ∂ ∂R (r ) 2 π mze (r 2 )+ R (r ) ∂r ∂r ε 0h 2
2
8π 2 m 2 r+ r E = k K K (1 ) 2 h
1 1 ∂ ∂ 1 ∂2 − [ (sin θ ) + ]Υ ( θ , ϕ ) = k 2 2 Υ ( θ, ϕ ) sin θ ∂θ ∂θ sin θ ∂ϕ
…………(3)
上述①②③三个方程分别叫做R(r)方程，Θ(θ)方程和 Φ(φ)方程。此时波函数被分为三部分，分别求解。注意 三个方程的变量的变化范围。
五 、 Φ方程的解
d 2Φ 2 +m Φ =0 2 dφ
此为二阶常系数齐次线性方程，有两个复数形式的独立特解：
Φ m = Ae
imφ
m =±m
2π
常数A可由归一化条件得出： A
= 13 . 6 ev
a 0为玻尔半径
r
2. 求N值
2Zr ∫ψ dτ = N ∫ exp − a0 dτ = 1
2 2
dτ = r sinθ drdθ dϕ
2
0 ≤ r p ∞,0 ≤ θ ≤ π ,0 ≤ ϕ ≤ 2π
∫ Ψ dτ = N ∫
2 1s 2
2π
0
2Zr 2 dϕ∫ sinθdθ ∫ exp − r dr =1 0 0 a0

氢原子薛定谔方程

氢原子薛定谔方程介绍薛定谔方程是量子力学中的基础方程之一，描述了微观粒子的行为。

在氢原子中，薛定谔方程被广泛应用于描述电子在氢原子中的运动。

本文将深入探讨氢原子薛定谔方程的内容。

氢原子的结构氢原子由一个质子和一个电子组成。

质子带正电荷，电子带负电荷，两者之间形成了一个静电力场。

电子在这个静电力场中运动，其行为可以用薛定谔方程来描述。

薛定谔方程的形式薛定谔方程可以写为：Ĥψ=Eψ其中，Ĥ是哈密顿算符，ψ是波函数，E是能量。

波函数的解释波函数ψ描述了电子在空间中的分布情况。

根据波函数的模的平方|ψ|2，可以得到电子在不同位置上的概率密度分布。

波函数本身是复数，其实部和虚部分别表示了不同的物理量。

分离变量法对于氢原子，可以使用分离变量法来求解薛定谔方程。

假设波函数可以写成一个径向部分和一个角向部分的乘积形式：ψ(r,θ,ϕ)=R(r)⋅Y(θ,ϕ)将波函数代入薛定谔方程，并对两个变量r和θ,ϕ分别进行分离变量，可以得到一系列关于r的径向方程和关于θ,ϕ的角向方程。

径向方程的求解径向方程可以写为：1 r2ddr(r2dRdr)+[2mℏ2(E−e24πε0r)−l(l+1)r2]R=0其中，m是电子的质量，ε0是真空介电常数，l是角量子数。

径向方程的解是球贝塞尔函数和球贝塞尔函数的导数的线性组合。

角向方程的求解角向方程可以写为：1 sinθddθ(sinθdYdθ)+[l(l+1)−m2sin2θ]Y=0其中，m是磁量子数。

角向方程的解是球谐函数。

能级和轨道通过求解径向方程和角向方程，可以得到一系列解。

每个解对应一个能级和一个轨道。

能级是电子的能量，轨道描述了电子在空间中的运动。

数值求解和定态波函数对于复杂的情况，无法通过解析方法得到薛定谔方程的解。

此时可以使用数值方法进行求解，例如使用数值计算软件。

通过数值求解可以得到氢原子的定态波函数。

结论氢原子薛定谔方程是描述氢原子中电子行为的基础方程。

通过求解薛定谔方程，可以得到氢原子的能级和轨道。

15.6.1氢原子的薛定谔方程 - 氢原子的薛定谔方程


s

1
，即
2
S
3 2
自旋角动量在外磁场方向上只有两个分量:
Sz ms
ms


1 2
ms称为自旋磁量子数
8
1 ms 2
Sz / 2
电子的自旋角动量和自旋磁量子数
z
Sz
S
Sz
1ห้องสมุดไป่ตู้
ms

1 2
2
o
S 3
2
1 2
1 ms 2
9
5 小结 原子中的电子的运动状态可由四个量子 数(n, l ,ml , ms) 来表示.
主量子数 n 决定电子的能量 副量子数 l 决定电子的轨道角动量 磁量子数 ml 决定轨道角动量的方向 自旋量子数ms决定自旋角动量的方向
10
磁量子数
h / 2π 约化普朗克常数
6
例如，l 1时，
L l(l 1) h 2 h 2 2π 2π
磁量子数 ml =0, 1， 相应的
Lz

0,
h 2π
,
h 2π
z
z
LZ
L
ħ
o
L 2
ħ
7
4 电子的自旋和自旋磁量子数
自旋角动量 S s(s 1)
式中自旋量子数
4πε0r
0
分离变量法求解,设
(r, ,) R(r)Θ( )Φ()
2
得
d 2Φ
d 2

ml 2Φ

0
ml 2
sin 2

1
Θ sin
d
d
(sin
dΘ ) l(l
d

薛定谔方程求解氢原子

§3.6 (类)氢原子的量子力学处理 (r,,)
一、氢原子的薛定谔方程
电子在原子核的库仑场中运动：
U Ze2
4 0r
定态薛定谔方程：
[ 2 2
e2
]
(r )

E
(r )
2 4 0r
氢原子问题是球对称问题，通常采用球坐标系：
x r sin cos y r sin sin z r cos
l 动量，但是大小是非连续取值的！角量子数 来自于薛定谔方程求解
过程条件限制的必然结果！ ~ l 0,1,2,3, , , , , , n 1
L l l 1
名字s.p.d. f .g.h.i. j.k
对于同一个总能级量子数第n个轨道,会有对应的n
个亚轨道，这些亚轨道对应的总能量大致相等，
亚轨道l=0,取名s轨道，对应的角动量L=0，亚轨道l=1,取名p轨道角
动量大小L= 2 ！l=2,取名d轨道，L= 6 ；l=3,取名f 轨道，
L= 12 ！
其实，不同的角动量大小对能级的能量值有细微影响
1926年，海森堡解得氢原子的
能量 En,l为



En,l


13.6 n2
L 转动惯量I 角速度 mr2 mvr
但是电子绕原子核运动形成角动量的方向并不是跟宏观一样，
方向只能取特定值！（方向量子化）而且这些特定值跟l有关,可能 存在的方向为2l+1个！
比如，n=1，亚能级只有一个，对应的
轨道量子数l=0,取名s亚能级，对应的角 动量L=0！所以不存在方向问题！对应 的能量值为[-13.6-ΔE(1,0) ]eV
L l l 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
几率大小。
而不能确定粒子何时出现于何地。
几率大小正比于波强度。
因此：可用描述波的方法可以得到微观粒子运动的描述。 我们用波函数（Ψ）概念来代替“轨迹”，以表示微粒
的运动状态。
2、波函数的性质
Ψ必须是连续的 Ψ必须是单值的 Ψ必须是有限的 Ψ可归一化
归一化：粒子在空间各点出现的几率密度之比等于波函数在这些
(2) 电子到达底片前,无法确定打在底片上的某处, 只知某处的可能性大,某处的可能性小,这是从 其粒子性上考虑.
(3) 从波动性考虑,底片黑圈处物质波的强度最大, 波峰与波峰相遇处.
结论:
空间任意一点处波的强度与该粒子出现在此处
的几率成正比,此即物质波的统计解释.
四. 波粒二象性的必然结果——“不确定关系”
不辐射能量。 （2）原子从一定态过渡到另一定态，才发射或吸收能量。
E E2 E1 h
（3）各态能量一定，角动量也一定( M=nh/2π ) 并且是量子化的，大小为 h/2π 的整数倍。
e2
4 0r 2

mv2 r
库仑引力 离心力
M nh mvr
2
-e
r
角动量
r

0h2 me 2
E n0 0 h
（2）光为一束以光速C行进的光子流。
（3）光子不但有能量，还有质量M。
（4）既然光子有质量，就必有动量。
p h/
(光源打开后,电流表指针偏转)
（5）光子与电子碰撞时服从能量守恒与动量守恒定律。
“光子说”表明了——光不仅有波动性，且有微粒性， 这就是光的波粒二象性思想。
一、三个著名实验导致“量子”概念的引入和应用
第三个实验——氢原子光谱：
氢原子激发后会发出光来，测其波长，得到原子光谱。
656.3
486.1 434.1 410.2
nm
H
H
H H
H
巴耳麦公式可写为：
1
11



RH
(
n
2 1

n
2 2
)
n2 > n1,
n1、n2为正整数
玻尔理论
为了解释以上结果，玻尔综合了普朗克的量子论， 爱因斯坦的光子说以及卢瑟福的原子有核模型，提出著 名的玻尔理论： （1）原子中有一些确定能量的稳定态，原子处于定态
具有波动性的粒子不能同时有精确坐标和动量. 当粒子的某个坐标被确定得愈精确,则其相应的 动量则愈不精确;反之亦然.但是，其位置偏差 (△x )和动量偏差(△ p )的积恒定. 即有以下关 系:
x p h
通过电子的单缝衍射可以说明这种“不确定”的确存 在。
1、波函数(Ψ)
微观粒子受不确定关系的限制，不能同时具有确定的 位置和速度，只能知道粒子在空间某处出现的可能性，即：
pxx h

pyy h

pzz h

h
t

为满足归一化
2d*sin
入射束
衍射Байду номын сангаас的方向性
p h/

衍射束

p 2mE
晶体
二. 实物微粒的波动性
汤姆逊电子衍射图 (示意)
n 2d sin 2
汤姆逊使用了能量较大的电子，结果也得到了类似X射线 衍射的花纹，从而也证明了德布罗意波的存在。
三、玻恩的“统计解释”:
(1) 电子的干涉作用并非两个电子的相互作用,而是 其波动本性决定.
按某个“能量子0”的整数倍变化。
n0
公式：
0 h0
注：n称为量子数，是整数。
一、 三个著名实验导致“量子”概念的引入和应用
第二个实验——光电效应：
为了解释光电子的动能只与入射光的 频率有关，而与光的强度无关的实验事实
爱因斯坦提出光子说：
（1）光的能量是不连续的，也是量子化的。
§1-6 氢原子及类氢离子的解的讨论
§1-7 波函数和电子云的图形表示
§1-8 多电子原子结构理论的轨道近似模型 ——原子轨道
§1-9 电子自旋
§1-10 原子整体的状态与原子光谱项
§1-11 原子内电子的排布和元素周期律
本节重点：
1、三个著名实验导致“量子”概念的引入和应用 2、实物微粒的波动性 3. 物质波的实验证明和波恩的“统计解释” 4. 波粒二象性的必然结果—— “不确定关系”
一般被看成物质的电子.原子等微粒,其实也具有波动性, 并且光的两个关系式同样适合:
h
p h / 德布罗意关系式
物质波的实验证明:
(1)戴维逊—革末实验：电子束在镍单晶上反射 (2)汤姆逊电子衍射实验
二. 实物微粒的波动性
戴维逊—革末实验
他发现当一束 50eV的电子垂直地射在镍单晶的表面 上时，在和入射束成50度角的方向上表现有反射出来最多 的电子数。且实验结果与德布罗意关系式结论很好符合。
点的模的平方比，故乘上一个常数C后，粒子在空间各点出现的几率 密度之比不变。
粒子所处的物理状态也不会改变。
即：若能满足 (x, y, z) 2 d 1
则称为归一化了的波函数。
例题
薛定谔方程的由来：
自由粒子波函数：
x、y、z、t

A
exp2i
重点公式： h p h /
E n x p h
一、三个著名实验导致“量子”概念的引入和应用
第一个实验——黑体辐射：为了让理论计算得到的“能量 密度按频率（波长）分布”的曲线与黑体辐射实验得
到
普郎的克曲提线相出符“合量子论”：主张振子能量有不连续性。
黑体由不同频率的谐振子组成，每个谐振子的能量总是
按照经典物理学, 原子是 不稳定的,如下示意图
但事实上,原子是稳 定的,如下示意图
表明：在原子内，电子与核之间的各种吸引与排斥作用，与宏观质点的
运动有质的差异，单用经典物理学的规律无法说明，必须以一种新的力学 理论(量子力学)来加以研究。
§1-1 经典物理学的困难和量子论的诞生 §1-2 实物微粒运动状态的表示法及态叠加原理 §1-3 实物微粒的运动规律—— 薛定谔方程 §1-4 定态薛定谔方程的算符表达式： §1-5 氢原子与类氢离子的薛定谔方程及其解
n2

52.9n2 (
pm)
n 1,2,3
+e
E

1 mv2 2
e2
me4
( 4 0r ) 80h2
1 n2

1 n2
R
h

En2
En1

R( 1 n12

1) n22
~

c

R hc
(
1 n12

1 n22
)
二. 实物微粒的波动性 德布罗意假设: