讲梁的挠曲线方程与积分解法
- 格式:pptx
- 大小:497.50 KB
- 文档页数:23









6、塔式简支梁的弯曲。
如图所示两端简支的梁,梁的抗弯刚度不均匀,梁的中间有一段刚度为2EI ,其为梁长2l 的一半,梁两端各有一段刚度为EI ,其长为2/l ,如果梁的中间受均布荷载q ,用里兹法求梁中点最大挠度和近似挠度曲线。
里兹法:解:设OB 段的挠曲线为321123()()2l w a x l a x l a x ⎛⎫=-+-+- ⎪⎝⎭BC 段的挠曲线为2212()()w a x l a x l =-+-从中可以看出,这两个函数满足2()0w l =;1222l l w w ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭;''1222l l w w ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭又由'1(0)0w =得2123324a a l a l =-所以3221232332()()42l w a l a l x l a x l a x ⎛⎫⎛⎫=--+-+- ⎪ ⎪⎝⎭⎝⎭22223232()()4w a l a l x l a x l ⎛⎫=--+- ⎪⎝⎭由对称性可得''2''22222122233022()()3(22)lll U EI w dx EI w dx EIl a a a l a l =+=-+⎰⎰321230111721232lq E qw dx ql a a l ⎛⎫=-=- ⎪⎝⎭⎰故总势能222322332311173(22)1232=+q U E EIl a a a l a l ql a a l ∏⎛⎫+=-+-⎪⎝⎭由势能驻值条件20a ∏∂=∂;30a ∏∂=∂得 3232432116(2)012176()032EIl a a l ql EIl a l a ql -+=--=联立得2237576ql a EI=-;37288ql a EI =则33221169377()()11525762882ql ql ql l w x l x l x EI EI EI ⎛⎫=----+- ⎪⎝⎭322216937()()1152576ql ql w x l x l EI EI=----DO 段近似挠曲线可相应由对称性得到,且跨中挠度4161(0)768ql w EI=.积分法求解挠曲线及跨中挠度: OB 段的挠曲线微分方程为2''221111132()()22228l EIw M x q x ql l x qx ql ⎛⎫=-=---=- ⎪⎝⎭则'321113268EIw qx ql x A =-+ 4221121322416EIw qx ql x A x A =-++OB 段的挠曲线微分方程为''222111()()222EIw M x ql l x qlx ql =-=--=-则'22211142EIw qlx ql x B =-+ 32221211124EIw qlx ql x B x B =-++由边界条件及连续性条件'1(0)0w =;12(2)(2)//w l w l =;''12(2)(2)//w l w l =;2()0=w l得10A =;4265384=A ql ;31548B ql =;42116B ql = 所以4224113654832768w qx ql x ql EI EI EI =-+ 32234211511244816w qlx ql x ql x ql EI EI =-++跨中挠度4165(0)768ql w EI=.里兹法相对于积分法跨中挠度相对误差为444616565 6.15%768768768=ql ql ql EI EI EI-。
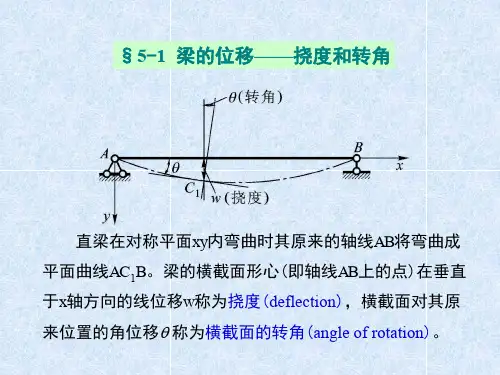

§8-3 用积分法求梁的挠度和转角梁是一种常见的结构,在结构设计和分析中经常需要求解梁的挠度和转角。
挠度和转角是评价梁在受载过程中变形情况的重要指标,对于保证梁的安全性和使用寿命有着重要作用。
本文将介绍用积分法求解梁的挠度和转角的方法。
首先,需要明确梁的基本假设及其约束条件。
梁的基本假设包括:梁轴线是直线、截面内部应力分布均匀、横截面形状及尺寸在受力过程中不变、截面在平面内转动的角度很小、且不影响梁内部的应力分布等。
约束条件一般有:端部固定或支承等。
接着,需要根据约束条件和配重条件列出梁的弯曲方程和边界条件。
假设梁长度为L,x轴方向为梁轴线方向,则弯曲方程为:d^2y/dx^2+M/(EI)=0其中,y是梁的挠度,M是弯矩,E是杨氏模量,I是梁的截面惯性矩,上述方程即为梁的弯曲方程。
根据约束条件和配重条件,可以列出边界条件。
对于悬臂梁,端点处有一个支承,因此边界条件为y(0)=0,d^2y/dx^2(0)=0;对于双端支承梁,两端都有支承,因此边界条件为y(0)=y(L)=0,d^2y/dx^2(0)=d^2y/dx^2(L)=0。
根据弯曲方程和边界条件可以解出梁的挠度和转角。
但是,弯曲方程中的弯矩是未知的,需要通过力学分析求解。
通常的做法是,将梁截面分成若干小段,每段长度为dx,考虑该段上下两点的受力平衡条件,可以得到该段的弯矩M。
然后将弯矩代入弯曲方程求解,就可以得到该段的挠度和转角。
最后将所有小段的挠度和转角相加即可得到整个梁的挠度和转角。
具体的计算过程可以用数值方法进行,也可以用解析方法求解。
下面介绍解析方法的两种常用技巧:超定积分法和欧拉-伯努利积分法。
超定积分法是一种较为简单和常用的求解梁挠度和转角的方法。
它的基本思想是将弯曲方程两端同时积分两次,得到整个梁的挠度函数和转角函数,然后根据边界条件解出各个常数。
以悬臂梁为例,弯曲方程为:将上式积分两次,得到:其中,b1和b2是积分常数,需要根据边界条件求解。
10.2 梁的挠曲线近似微分方程及其积分纯弯曲 EIM =ρ1挠曲线曲率()322"1w w κ=⎡⎤'+⎣⎦EIM ±=d θFFxd xyxρ O正负号的确定xyOxyOM > 0w ″< 0M < 0w ″>0M 与 w ″异号()322"1w w κ=⎡⎤'+⎣⎦EIM ±=()3221w M EIw ''=-⎡⎤'+⎣⎦小变形:转角 w ′ ≈ 0 适用条件: 1. 坐标系,正负号;2. 忽略剪力 F S 对变形的影响;3. 线弹性,小变形,w′ ≈ 0。
M w EI''=-EI ——梁的抗弯刚度, 若为等直梁,EI =C ,则 EIw M''=-挠曲线近似微分方程1'd Mw x C EIθ==-+⎰12d d M w x x C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰一次积分:二次积分:积分法计算梁的变形BAlw A = 0 w B = 0BAlw A = 0 θA =0EIw M''=-挠曲线近似微分方程 由边界条件,确定积分常数光滑连续条件——相邻挠曲线必须光滑连续。
挠曲线近似微分方程及其积分w C2= w C3θC2=θC2w B1= w B2θB1=θB2挠曲线近似微分方程及其积分——例题[例题1] 已知悬臂梁的抗弯刚度为EI,求在荷载P 作用下梁的挠曲线方程,并确定梁上的最大挠度和转角。
BAxL P有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)[解] (1)建立弯矩方程 ()()M x P L x =-()()E Iw M x P L x ''=-=--21()2xEIw P Lx C '=--+2312()26Lx x EIw P C x C =--++(3)确定积分常数 0,0x w ==0,0x w '==20C=10C=挠曲线近似微分方程及其积分——例题BALxPx(2)代入挠曲线方程并积分挠曲线近似微分方程222PLx Pxw EIθ-'==-23(3)6P Lx x w EI-=-最大挠度和转角3max()3PL f EI=↑2max2PL EIθ=挠曲线近似微分方程及其积分——例题B ALxPxmaxθmaxw挠曲线近似微分方程及其积分——例题[例题2] 已知:EI = 常数,求:1. 挠度、转角方程; 2. |θmax |, |w max |。