第一章气体的pVT关系
- 格式:doc
- 大小:74.50 KB
- 文档页数:3

第一章 气体的pVT 性质无论物质是哪一种聚集状态,都有许多宏观性质,如压力p 、体积V 、温度T 、密度ρ、内能U 、熵S 等.在重多的宏观性质中,p 、V 、T 三者是物理意义非常明确、又易于直接测定的基本性质.当物质的量n 一定后,其pVT 性质不可能同时独立取值,而存在如下关系:0),,(=T V p f该函数称为状态方程.若考虑到物质的量n,则可表示为: 0),,,(=T V p n f鉴于液、固体的可压缩性一般甚小,即等温压缩率(系数) T T pVV )(1∂∂-=κ和体膨胀系数p V TVV a )(1∂∂=均较小,故在通常的物理化学计算中,常将其体积随压力和温度的变化忽略.与凝聚态相比,气体具有较大的等温压缩系数T κ和体膨胀系数V a ,其体积随温度和压力的变化较大,故一般只研究气体的pVT 性质.1.1 理想气体状态方程1.理想气体状态方程波义尔定律: 常数=pV (n,T 恒定)盖.吕萨克定律 常数=T V / (n,p 恒定)阿伏加德罗定律 常数=n V / (p,T 恒定)这三个定律都客观地反映了低压下气体服从的pVT 简单关系.将其结合可整理得到状态方程: nRT pV =此即理想气体状态方程.式中,R 是摩尔气体常数.其值经精确测定,为:11314510.8--⋅⋅=K mol J R .因摩尔体积n V V m /=,故理想气体状态方程又可写成:RT pV m = 因M m n =,Vm =ρ,故理想气体状态方程又可写成:RT Mm pV =或RT pM ρ=例: 试由上列三定律导出理想气体状态方程.解: 因任意体系均满足:0),,,(=n T V p f ,可改写成:),,(n T p f V =该式取全微分得:dn nVdT T V dp p V dV T p n p n T ,,,)()()(∂∂+∂∂+∂∂= 由波义尔定律得: 0=+Vdp pdV (T,n 恒定)此即: pV p V n T -=∂∂,)( 同理,由盖.吕萨克定律和阿伏加得罗定律可得: T V T V n p =∂∂,)(和 nV n V T p =∂∂,)( 代入全微分式得:dn nVdT T V dp p V dV ++-=)(此式即: ndn T dT p dp V dV +=+ 或 )ln()ln(nT d pV d =亦即: 0)ln(=nT pV d ,积分可得: 常数=nTpV又据阿伏加德罗定律知,当气体的p,V 一定时,体系的(V/n )为与气体各类无关的常数,故上式中的常数对任何气体都应具有相同的值,如用R 表示,则上式变为: nRT pV =这就是理想气体状态方程.2.理想气体凡在任何温度、压力下均服从方程nRT pV =的气体称理想气体. 按照上述定义,理想气体必须具备下列两个微观特征: (1).气体分子本身不占有体积,是没有大小的质点.因在T 恒定时,常数=m pV ,当0→p 时,必有0→m V (2).分子间无相互作用力.分子可近似被看作是没有体积的质点。

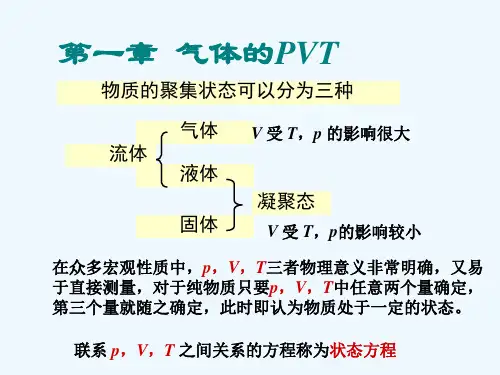
第一章 气体的pVT 关系物质的聚集状态一般可分为三种,即气体、液体和固体。
气体与液体均可流动,统称为流体;液体和固体又统称为凝聚态。
三种状态中,固体虽然结构较复杂,但粒子排步的规律性较强,对它的研究已有了较大的进展;液体的结构最复杂,人们对其认识还很不充分;气体则最为简单,最容易用分子模型进行研究,故对它的研究最多,也最为透彻。
无论物质处于哪一种聚集状态,都有许多宏观性质,如压力p ,体积V ,温度T ,密度ρ,热力学能U 等等。
众多宏观性质中,p , V , T 三者是物理意义非常明确、又易于直接测量的基本性质。
对于一定量的纯物质,只要p , V , T 中任意两个量确定后,第三个量即随之确定,此时就说物质处于一定的状态。
处于一定状态的物质,各种宏观性质都有确定的值和确定的关系①。
联系p , V , T 之间关系的方程称为状态方程。
状态方程的建立常成为研究物质其它性质的基础。
液体和固体两种凝态,其体积随压力和温度的变化均较小,即等温压缩率T T p V V ⎪⎪⎭⎫ ⎝⎛∂∂-=1κ和体膨胀系数pV T V V ⎪⎭⎫ ⎝⎛∂∂=1α都较小,故在通常的物理化学计算中常忽略其体积随压力和温度的变化。
与凝聚态相比,气体具有较大的等温压缩率κT 和体膨胀系数αV ,在改变压力和温度时,体积变化较大。
因此一般的物理化学中只讨论气体的状态方程。
根据讨论的p , T 范围及使用精度的要求,通常把气体分为理想气体和真实气体分别讨论。
§1.1 理想气体状态方程1.理想气体状态方程从17世纪中期,人们开始研究低压下(p <1 MPa )气体的p VT 关系发现了三个对各种气体均适用的经验定律:(1)波义尔(Boyle R)定律 在物质的量和温度恒定的条件下,气体的体积与压力成反比,即p V =常数 (n ,T 一定)(2)盖-吕萨克(Gay J -Lussac J )定律 在物质的量与压力恒定的条件下,气体的体积与热力学温度成正比,即V/T =常数 (n , p 一定)(3)阿伏加德罗(Avogadro A )定律 在相同的温度、压力下,1mol 任何气体占有相同体积,即V / n =常数 (T ,p 一定)将上述三个经验定律相结合,整理可得到如下的状态方程:p V = n RT (1 .1 .1a )上式称为理想气体状态方程。








第一章 气体的pVT 关系§1.1 理想气体状态方程(1)状态方程状态方程:处于一定聚集态(气体、液体或固体)的物质都有一些可以直接测量的物理量,如p 、V 、T 等,这些物理量之间存在一定的函数关系,用来描述物质状态各物理量之间的函数关系的数学表达式称物质的状态方程(也称物态方程)。
气体的状态方程可写为:0f p V T n =(,,,)p - 压力V - 体积T - 热力学温度(绝对温度)n - 气体的物质的量(2)理想气体状态方程1、波义尔定律(Boyle )波义尔定律:在恒温条件下,一定量任何气体的体积与其压力成反比,即:1V p∝,或 .pV cont = 2、盖-吕萨克定律(Gay-Lussac )盖-吕萨克定律:在恒压条件下,一定量任何气体的体积均与其绝对温度成正比,即:T V ∝,或.V cont T = 3、阿伏加德罗定律(A. Avogadro ,1811)V / n =cont (T, p 一定)4、理想气体状态方程理想气体状态方程:pV nRT =或:m pV RT =,m V V n =(摩尔体积)R - 摩尔气体常数(或气体常数)。
R =8.314J.K -1.mol -1。
理想气体的特点:①分子自身无体积;②分子间无相互作用力。
精确实验证明,只有在压力趋近于零的极限情况下,各种气体才严格服从理想气体的状态方程。
理想气体状态方程的推导:已知气体的状态方程可写为:0n T V P f =),,,( 化为:),,(n T P f V =有: dn n V dT T V dP P V dV TP n P n T ,,,⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= 根据波义尔定律:.cont PV = 得:P V P C P V 2nT -=-=⎪⎭⎫ ⎝⎛∂∂, 根据盖-吕萨克定律:.cont T V =,即 'C TV = 有:T V 'C T V n,P ==⎪⎭⎫ ⎝⎛∂∂ 对于一定量气体(dn = 0),有:dT TV dP P V dV +-= 化为:TdT P dP V dV +-= 积分得:lnV +lnP =lnT +cont.,即 .cont T PV ⋅=若气体为 1 mol ,则常数写为R ,有 RT PV m =对于 n mol 气体,有 nRT PV =§1.2 理想气体混合物(1)道尔顿(Dalton )分压定律气体能以任意比例相互混合,而液体、固体一般不能。
物理化学第一章气体的pVT 关系1.理想气体状态方程式nRTRT M m pV ==)/(或RTn V p pV ==)/(m 式中p ,V ,T 及n 单位分别为Pa ,m 3,K 及mol 。
m /V V n =称为气体的摩尔体积,其单位为m 3·mol -1。
R =8.314510J ·mol -1·K -1,称为摩尔气体常数。
此式适用于理想气体,近似地适用于低压的真实气体。
2.混合物(1)组成摩尔分数y B (或x B )=∑AAB /nn 体积分数/y B m,B B ∗=V ϕ∑∗AVy Am,A式中∑AAn为混合气体总的物质的量。
Am,∗V表示在一定T ,p 下纯气体A 的摩尔体积。
∑∗AA m,A V y 为在一定T ,p 下混合之前各纯组分体积的总和。
(2)摩尔质量∑∑∑===BBBB B BB mix //n M n m M y M 式中∑=BBmm 为混合气体的总质量,∑=BB n n 为混合气体总的物质的量。
上述各式适用于任意的气体混合物。
(3)V V p p n n y ///BB B B ∗===式中p B 为气体B ,在混合的T ,V 条件下,单独存在时所产生的压力,称为B 的分压力。
∗B V 为B 气体在混合气体的T ,p 下,单独存在时所占的体积。
2.道尔顿定律p B =y B p ,∑=BBpp 上式适用于任意气体。
对于理想气体VRT n p /B B =3.阿马加分体积定律V RT n V /B B =∗此式只适用于理想气体。
4.范德华方程RT b V V a p =−+))(/(m 2m nRTnb V V an p =−+))(/(22式中a 的单位为Pa ·m 6·mol -2,b 的单位为m 3·mol -1,a 和b 皆为只与气体的种类有关的常数,称为范德华常数。
此式适用于最高压力为几个MPa 的中压范围内实际气体p ,V ,T ,n 的相互计算。
第一章 气体的pVT 关系
主要内容
1.理想气体和理想气体状态方程
(1)理想气体
凡在任何温度、压力下均服从B V 的气体称为理想气体。
理想气体具有两个特征:
(Ⅰ)分子本身不占有体积。
(Ⅱ)分子间无相互作用力。
(2)理想气体状态方程
nRT pV = RT pV =m
理想气体状态方程适用于理想气体和低压条件下的实际气体。
2.道尔顿分压定律和阿马格分体积定律
(1)分压力
分压力定义为:在总压力为p 的混合气体中,任一组分B 的分压力B p 等于它的物质的量分数B y 与混合气体中压力p 之积。
即 p y p B B = p p =∑B B
此二式适用于理想气体混合物和非理想气体混合物。
对于理想气体有
V RT n p B B =
(2)道尔顿定律 道尔顿定律:混合气体的总压力等于各组分单独存在于混合气体的,T V 条件下所产生压力的总和。
即 V
RT n p /)(B B ∑=
此定律适用于混合理想气体和低压混合气体。
(3)分体积
分体积B V 是所含n B 的B 单独存在于混合气体的,T P 条件下占有的体积。
)/(B B p RT n V = V y V B B =
两式适用于理想气体和低压条件下的混合气体。
(4)阿马格定律
阿马格定律:混合气体各组分的分体积之和与总体积相等,即
p RT n V V V
/)(,B B B B ∑∑==
3.实际气体的PVT 性质
(1)实际气体的PVT 性质
RT pV nRT pV Z /)/( def m =
理想气体状态方程与实际气体状态方程有偏差,偏差值为修正因子,称压缩因子Z 。
Z 的数值直接表示出实际气体对理想气体的偏差程度。
(2)范德华方程与维里方程
①范德华方程
气体物质的量为1mol 的范德华方程:()m 2m a p b V RT V ⎛
⎫+-= ⎪⎝⎭
a 、范氏方程只适用中压范围。
b 、当p →0时,范氏方程可还原为理想气体方程。
②维里方程
+++=+⎪⎭⎫ ⎝⎛'+⎪⎭⎫ ⎝⎛'+'=2211Cp Bp A V C V B A pV
4.实际气体的液化与临界性质
(1)饱和蒸气压与沸点
在一定温度下,当液(或固)体与其蒸气达成液(或固)、气两相平衡时,此时气相的压力则称为该液(或固)体在该温度下的饱和蒸气压,简称蒸气压。
沸点:当液体饱和蒸气压与外压相等时,液体沸腾,此时相应的温度称为液体的沸点。
正常沸点:101.325KPa 外压下的沸点。
水是373.15K 。
(2)实际气体的液化
气体加压所允许的最高温度称为临界温度,以T c 表示;
气体在临界温度时发生液化所需的最小压力称为临界压力,以p c 表示;
物质在临界温度、临界压力的摩尔体积成为临界摩尔体积,以V m,c 表示。
T c 、p c 、V m,c 称为物质的临界参数。
它是物质固有的一种特性参数。
物质处在临界温度、临界压力下的状态称为临界状态。
5.对比参数、对应状态原理
(1)对比参数
r c r m,c m r c T T T V V V p p p ===
p r 、T r 、V r :分别称对比压力、对比温度、对比体积,又统称为气体的对比参数。
对比参数反映了气体所处状态偏离临界点的倍数。
(2)对应状态原理:各种不同的气体,只要有两个对比参数相同,则第三个对比参数必定(大致)相同。
()0,,r r r =T V p f
具有相同对比参数的气体称为处于相同的对应状态。
由于各种气体的Z C 近似相同,如果它们处于对应状态,必有相同的压缩因子。
()r r ,T p f Z =
重要公式
1.n PV RT = RT pV =m
2.y B B P P = B B P
P =∑
3.B B V V =∑ n /B B V RT P ⎛⎫= ⎪⎝⎭
∑
()m 2m a 4.b P V RT V ⎛⎫+-= ⎪⎝
⎭ 5.n PV Z RT =。