第二章 简单力系典型例题讲解
- 格式:pdf
- 大小:467.89 KB
- 文档页数:7
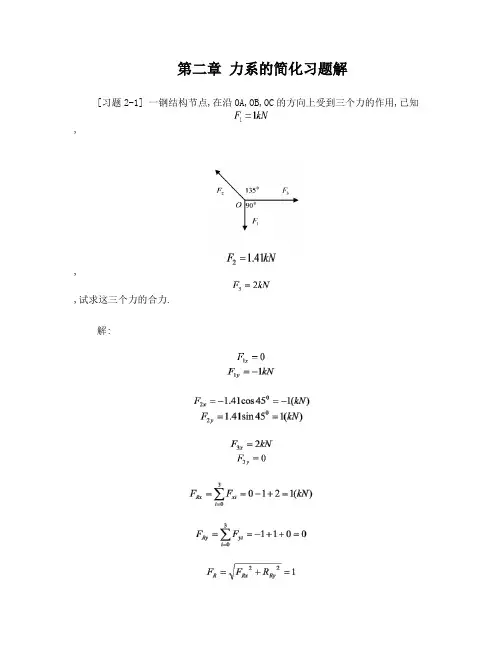
第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。
已知F1=60N,F2=400N,F3=500N,F4=200N,试将该力系向A点简化(图中长度单位为mm)。
解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成,各力大小、作用线位置和方向见图。










第二章 力系的简化 习题解答2-1在立方体的顶点A 、H 、B 、D 上分别作用四个力,大小均为F ,其中1F 沿AC ,2F 沿IG ,3F 沿BE ,4F 沿DH 。
试将此力系简化成最简形式。
解:各力均在与坐标平面平行的面内,且与所在平面的棱边成45°角。
将力系向A 点简化,主矢'R F 在坐标轴上的投影为045cos 45cos '21=-=F F F Rx ,FF F F F F Ry 245cos 45cos 45cos 45cos '4321=+-+=,F F F F Rz 245cos 45cos '43=+= 。
用解析式表示为: ()k j F +=F R 2'设立方体的边长为a ,主矩A M 在坐标轴上的投影为 045cos 45cos 32=⋅+⋅-=a F a F M Ax , Fa a F a F M Ay 245cos 45cos 42-=⋅-⋅-= ,Fa a F a F M Az 245cos 45cos 42=⋅+⋅= 。
用解析式表示为:()k j M +-=Fa A 2。
因为,0'=⋅A R M F ,所以,主矢和主矩可以进一步简化为一个力,即力系的合力。
合力的大小和方向与主矢相同,'R R F F =;合力作用点的矢径为()i MF r a F R R =⨯=2'',所以,合力大小为2F ,方向沿对角线DH 。
2-2三力321,F F ,F 分别在三个坐标平面内,并分别与三坐标轴平行,但指向可正可负。
距离c b a ,,为已知。
问:这三个力的大小满足什么关系时力系能简化为合力?又满足什么关系时能简化为力螺旋?解:这力系的主矢为k j i 321'F F F F R ++=; 对O 点的主矩为k j i a F c F b F M O 213++=。
当主矢与主矩垂直时,力系能简化为合力。
第二章 力系的简化与平衡§2.1 力向一点平移力的可传性原理 力的平移定理的过程。
重要结论:作用于刚体上的力可以平移到任一点,而不改变它对刚体的作用效应,但平移后必须附加一个力偶,附加力偶的力偶矩等于原力对平移点之矩。
力向一点平移结果表明:一个力向任一点平移,得到与之等效的一个力和一个力偶;反之,作用于同一平面内的一个力和一个力偶,也可以合成作用于另一个点的一个力。
工程实例(略)§2.2 平面力系的简化平面力系的概念 2.2.1 简化方法平面汇交力系:作用线通过同一点且在同一平面内的力系。
平面力偶系:由若干个平面力偶组成的力偶系。
2.2.2 简化结果1)∑∑==i i R F F F ``即 作用于O 点平面汇交力系的合力等于原力系诸力的矢量和,称合矢量F `R 为原力系的主矢2))(F M M M O O ∑∑==即:各附加力偶的合力偶的力偶矩等于原力系中所有对简化中心之矩的代数和。
上述结果表明:平面力系向作用平面内任意一点简化,一般情形下,得到一个力和一个力偶。
所得到的力的作用线通过简化中心,其矢量称为力系的主矢,它等于力系中所有力的矢量和;所得的力偶仍作用于原平面内,其力偶矩称为力系对简化中心的主矩,其值等于力系中所有力对简化中心之矩的代数和。
注意点:主矢与简化中心的位置无关;主矩一般与简化中心的选择有关。
因此提到主矩,必须注明是对哪一点的主矩。
故用M o 来表示力系对O 点的主矩。
主矢与合力是两个不同的概念。
主矢只有大小和方向两个要素,并不涉及作用点,可在任意点画出;而合力有三要素,除了大小和方向之外,还必须指明其作用点。
2.2.3 汇交力系简化的解析法 关于力在坐标轴上的投影力F 在X ,Y 轴上的投影分别为:X = F*cos α Y = F*sin α (2.2) 力的投影是代数量,有正负号的规定。
注意与分力F x ,F y 的区别。
只有在直角坐标系中分力的大小才与投影相等。
第2章 力系的等效简化2-1 一钢结构节点,在沿OC 、OB 、OA 的方向受到三个力的作用,已知F 1=1kN ,F 2=2kN ,F 3=2kN 。
试求此力系的合力。
解答 此平面汇交力学简化为一合力,合力大小可由几何法,即力的多边形进行计算。
作力的多边形如图(a ),由图可得合力大小kN F R 1=,水平向右。
2-2 计算图中1F 、2F 、3F 三个力的合力。
已知1F =2kN ,2F =1kN ,3F =3kN 。
解答 用解析法计算此空间汇交力系的合力。
kN F F F F ix Rx 424.26.0126.0222221=´´+=´´+=S =kN F F F iy Ry 566.08.018.022222=´´=´´=S =kN F F F F iz Rz 707.313222223=´+=´+=S =kN F F F F Rz Ry Rx R 465.4222=++=合力方向的三个方向余弦值为830.0cos ,1267.0cos ,5428.0cos ======RRz R Ry R Rx F FF F F F g b a2-3已知 N F N F N F N F 24,1,32,624321====,F 5=7N 。
求五个力合成的结果(提示:不必开根号,可使计算简化)。
解答 用解析法计算此空间汇交力系的合力。
N F F F F F ix Rx 0.460cos 45cos 537550043=´´++-=S =N F F F F F iy Ry 0.460sin 45cos 547550042=´´+-=S =N F F F F F iz Rz 0.445sin 7625041=´++-=S =N F F F F Rz Ry Rx R 93.634222==++=合力方向角:4454),(),(),(¢°=Ð=Ð=Ðz F y F x F R R R 。