第2章平面简单力系习题

习 题2-1 试计算图2-55中力F 对点O 之矩。

图2-55(a) 0)(=F O M (b) Fl M O =)(F (c) Fb M O -=)(F (d) θsin )(Fl M O =F(e) βsin )(22b l F M O +=F(f) )()(r l F M O +=F2-2 一大小为50N 的力作用在圆盘边缘的C 点上，如图2-56所示。

试分别计算此力对O 、A 、B 三点之矩。

图2-56mN 25.6m m N 625030sin 2505060cos 30sin 5060sin 30cos 50⋅=⋅=︒⨯⨯=︒⨯︒-︒⨯︒=R R M Om N 075.17825.1025.630cos 50⋅=+=⨯︒+=R M M O A m N 485.9235.325.615sin 50⋅=+=⨯︒+=R M M O B2-3 一大小为80N 的力作用于板手柄端，如图2-57所示。

(1)当︒=75θ时，求此力对螺钉中心之矩；(2)当θ为何值时，该力矩为最小值；(3) 当θ为何值时，该力矩为最大值。

图2-57(1)当︒=75θ时，（用两次简化方法）m N 21.20mm N 485.59.202128945.193183087.21sin 8025075sin 80⋅=⋅=+=⨯︒⨯+⨯︒⨯=O M (2) 力过螺钉中心 由正弦定理)13.53sin(250sin 30θθ-︒= 08955.03/2513.53cos 13.53sin tan =+︒︒=θ ︒=117.5θ(3) ︒=︒+︒=117.95117.590θ2-4 如图2-58所示，已知N 200N,300N,200N,150321='====F F F F F 。

试求力系向O 点的简化结果，并求力系合力的大小及其与原点O 的距离d 。

图2-58kN 64.1615110345cos kN 64.4375210145cos 321R321R-=+-︒-=∑='-=--︒-=∑='F F F F F F F F F F y y x x主矢RF '的大小 kN 54.466)()(22R =∑+∑='y x F F F 而 3693.064.43764.161tan RR ==''=x y F F α ︒=27.20α m N 44.21162.0511.045cos )(31⋅=-⨯+⨯︒=∑=F F M M O O Fmm 96.45m 04596.054.466/44.21/R==='=F M d O2-5 平面力系中各力大小分别为kN 60kN,260321===F F F ，作用位置如图2-59所示，图中尺寸的单位为mm 。

第2章 力系的等效与简化2－1试求图示中力F 对O 点的矩。

解：（a ）l F F M F M F M M y O y O x O O ⋅==+=αsin )()()()(F （b ）l F M O ⋅=αsin )(F（c ）)(sin cos )()()(312l l Fl F F M F M M y O x O O +--=+=ααF （d ）2221sin )()()()(l l F F M F M F M M y O y O x O O +==+=αF2－2 图示正方体的边长a =0.5m ，其上作用的力F =100N ，求力F 对O 点的矩及对x 轴的力矩。

解：)(2)()(j i k i Fr F M +-⨯+=⨯=Fa A O m kN )(36.35)(2⋅+--=+--=k j i k j i Fam kN 36.35)(⋅-=F x M2－3 曲拐手柄如图所示，已知作用于手柄上的力F =100N ，AB=100mm ，BC =400mm ，CD =200mm ，α = 30°。

试求力F 对x 、y 、z 轴之矩。

解：)cos cos sin (sin )4.03.0()(2k j i k j F r F M αααα--⨯-=⨯=F D Ak j i αααα22sin 30sin 40)sin 4.03.0(cos 100--+-=力F 对x 、y 、z 轴之矩为：m N 3.43)2.03.0(350)sin 4.03.0(cos 100)(⋅-=+-=+-=ααF x M m N 10sin 40)(2⋅-=-=αF y M m N 5.7sin 30)(2⋅-=-=αF z M2—4 正三棱柱的底面为等腰三角形，已知OA=OB =a ，在平面ABED 内沿对角线AE 有一个力F ， 图中θ =30°，试求此力对各坐标轴之矩。

习题2-1图A r A习题2-2图（a ）习题2-3图ABr(a)解：)sin 45sin cos 45cos cos ()(k j i i F r F M θθθ+︒+︒-⨯=⨯=F a A O )45sin cos sin (k j ︒+-=θθaF 力F 对x 、y 、z 轴之矩为：0)(=F x M230sin )(aF aF M y -=︒-==FFa aF M z 4645sin 30cos )(=︒︒=F2－5 如图所示，试求力F 对A 点之矩及对x 、y 、z 轴之矩。

第一、二章力和受力图、平面力系的合成与平衡测试卷一、单项选择题(每题2分，共14分)1. 对于力偶，下列说法正确的是()A. 由于力偶没有合力，因此，该力偶作用于物体上，可使物体平衡B. 力偶能用一个力来平衡C. 力偶只能用力偶来平衡D. 力偶对物体的作用效果与力矩是一样的2. “力系中所有各力在两个坐标轴上的投影的代数和分别为零”是平面汇交力系平衡的()A. 充分条件B. 必要条件C. 充分必要条件D. 无关系3. 只限制物体任何方向移动，不限制物体转动的支座称________支座。

()A. 固定铰B. 可动铰C. 固定端D. 光滑面4. 只限制物体垂直于支承面方向的移动，不限制物体向其他方向运动的支座称________支座。

()A. 固定铰B. 可动铰C. 固定端D. 光滑面5. 既限制物体任何方向运动，又限制物体转动的支座称________支座。

()A. 固定铰B. 可动铰C. 固定端D. 光滑面6. 平面汇交力系平衡的必要和充分条件是该力系的________为零。

()A. 合力B. 合力偶C. 主矢D. 主矢和主矩7. 平面平行力系合成的结果是()A. 合力B. 合力偶C. 主矩D. 主矢和主矩二、判断题(每题1分，共10分)1. 物体的平衡状态是指物体相对于地球保持静止的状态。

()2. 作用力与反作用力总是一对等值、反向、共线的力。

()3. 因作用力与反作用力大小相等，方向相反，且沿着同一直线，所以作用力与反作用力是一对平衡力。

()4. 在同一平面内的两个力偶，只要力偶矩大小相等，则这两个力偶等效。

()5. 在研究物体的运动效应时，作用在物体上的分布荷载可由集中力来代替。

()6. 光滑接触面的约束反力一定通过接触点，垂直于光滑面的压力。

()7. 两个力在坐标轴上投影相等，则这两个力一定相等。

()8. 力偶可以用一个合力来平衡。

()9. 平面一般力系简化中，主矢为零，主矩不为零，则该主矩的计算与简化中心有关。

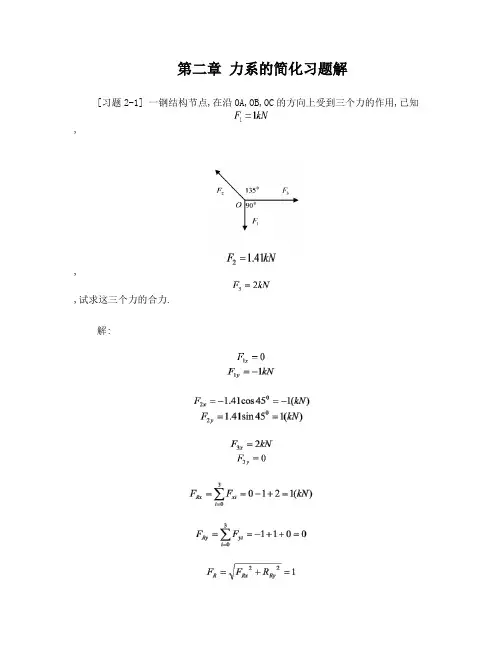
第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。

已知F1＝60Ｎ，F2＝400Ｎ，F3＝500Ｎ，F4＝200Ｎ，试将该力系向Ａ点简化(图中长度单位为mm)。

解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成，各力大小、作用线位置和方向见图。

第二章平面力系习题解2-8 平面压榨机构如题图2-8所示，A为固定铰链支座。

当在铰链B处作用一个铅直力F时，可通过压块D挤压物体E。

如果F=300N，不计摩擦和构件重量，求杆AB和BC所受的力以及物体E所受的侧向压力。

图中长度单位为cm。

2cm题2-8图解：（1）研究销钉B，受力图、坐标如图。

列平衡方程求杆AB和BC施予销钉的力：BA BCBC BABCBA BC0cos cos03001135Nsin sin02sin02xyF FF F F FFF F FFθθθθθ=⎧⎪⎧=-+=⎧⎪⎪→→===⎨⎨⎨-++==⎩⎪⎪⎩⎪⎩∑∑由作用力和反作用定理知：销钉所受BA BC、F F与杆所受的力BA BC''、F F等值、反向，BA BC'='=1135NF F，两杆均为压杆。

（2）研究压块D，受力图、坐标如图，CB'=1135NF。

列平衡方程求物体E施与的侧向压力'NEF：CB BC CB0'cos'0'cos11351125N x NEF F F F Fθθ=→-+=→===∑故，物体E所受的侧向压力NEF与压块D所受的NEF'等值、反向。

2-12 一力偶矩为M的偶作用在曲杆ADB上。

如果这曲杆用两种不同的方式支承，不计杆重，已知题2-12图中尺寸a，求每种支承情况下支座A、B对杆的约束力。

NA解：（1）以ABD杆为研究对象,画受力图如图，因力偶只能由力偶来平衡，故A、D处的反力AN B=-F F。

（2）列平衡方程，求支座A、B对杆的约束力：（a）图：NA NA20()2F F→-⋅=→=↑∑=0Mm M aa，则()2BF=↓Ma。

（b）图：NA NA0()F F→-⋅=→=←∑=0Mm M aa，则()BF=→Ma。

补充1：汽锤在锻压工件时，由于工件的位置偏离中心点，使锤头受到工件的反作用力而偏离中心线e=20mm，若已知锻压力F=1000kN，锤头高度h=200mm，不考虑锤头和导轨之间的摩擦，试计算锤头对两导轨的压力。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。

则其合力可以表示为。

①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。

所有摩擦均不计，各物自重除图中已画出的外均不计。

（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。

题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

题2-3图以AC 段电线为研究对象，三力汇交2-4 图示为一拔桩装置。

在木桩的点A 上系一绳，将绳的另一端固定在点C ，在绳的点B 系另一绳BE ，将它的另一端固定在点E 。

然后在绳的点D 用力向下拉，并使绳BD 段水平，AB 段铅直；DE 段与水平线、CB 段与铅直线成等角α=0.1rad （弧度）（当α很小时，tan α≈α）。

如向下的拉力F=800N ，求绳AB 作用于桩上的拉力。

题2-4图作BD 两节点的受力图 联合解得：kN F F F A 80100tan 2=≈=α2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，，机构在图示位置平衡。

第二章平面基本力系答案一、填空题(将正确答案填写在横线上)1.平面力系分为平面汇交力系、平面平行力系和平面一般力系。

2.共线力系是平面汇交力系的特例。

3.作用于物体上的各力作用线都在同一平面内 ,而且都汇交于一点的力系,称为平面汇交力系。

4.若力FR对某刚体的作用效果与一个力系的对该刚体的作用效果相同,则称FR为该力系的合力,力系中的每个力都是FR的分力。

5.在力的投影中,若力平行于x轴,则F X＝ F或-F ;若力平行于Y轴,则Fy＝F或-F :若力垂直于x轴,则Fx=0;若力垂直于Y轴,则Fy＝ 0 。

6.合力在任意坐标轴上的投影，等于各分力在同一轴上投影的代数和。

7.平面汇交力系平衡的解析条件为：力系中所有力在任意两坐标轴上投影的代数和均为零。

其表达式为∑Fx＝0 和∑Fy＝0 ，此表达式有称为平面汇交力系的平均方程。

8.利用平面汇交力系平衡方程式解题的步骤是：（1）选定研究对象，并画出受力图。

（2）选定适当的坐标轴，画在受力图上；并作出各个力的投影。

（3）列平衡方程，求解未知量。

9.平面汇交力系的两个平衡方程式可解两个未知量。

若求得未知力为负值，表示该力的实际指向与受力图所示方向相反。

10.在符合三力平衡条件的平衡刚体上，三力一定构成平面汇交力系。

11.用力拧紧螺丝母，其拎紧的程度不仅与力的大小有关，而且与螺丝母中心到力的作用线的距离有关。

12.力矩的大小等于力和力臂的乘积，通常规定力使物体绕矩心逆时针转动时力矩为正，反之为负。

力矩以符号Mo(F) 表示，O点称为距心，力矩的单位是N.M 。

13.由合力矩定力可知，平面汇交力系的合力对平面内任一点的力矩，等于力系中的各分力对于同一点力矩的代数和。

14.绕定点转动物体的平衡条件是：各力对转动中心O点的矩的代数和等于零。

用公式表示为∑Mo(Fi) ＝0 。

15.大小相等、方向相反、作用线平行的二力组成的力系，称为力偶。

力偶中二力之间的距离称为力偶臂。