下载文档原格式
完整三角函数公式表三角函数公式表是数学中常用的一个工具，用于计算三角函数的数值。
它包含了各种三角函数的定义和性质，能够帮助我们在解决三角函数相关问题时，快速找到所需的公式和计算方法。
以下是一个完整的三角函数公式表，包含了常见的正弦、余弦、正切、余切、正割和余割函数的公式：1. 正弦函数（sin）：- 定义：在单位圆上，从原点到圆上一点与x轴的正角对应的y坐标。
- 基本关系：sin θ = y/r，其中θ是角度，y是对应的y坐标，r是单位圆的半径（常为1）。
- 周期性：sin (θ + 2π) = sin θ。
- 奇偶性：sin (-θ) = -sin θ。
2. 余弦函数（cos）：- 定义：在单位圆上，从原点到圆上一点与x轴的正角对应的x坐标。
- 基本关系：cos θ = x/r，其中θ是角度，x是对应的x坐标，r是单位圆的半径（常为1）。
- 周期性：cos (θ + 2π) = cos θ。
- 奇偶性：cos (-θ) = cos θ。
3. 正切函数（tan）：- 定义：tan θ = sin θ / cos θ。
- 周期性：tan (θ + π) = tanθ。
- 奇偶性：tan (-θ) = -tan θ。
4. 余切函数（cot）：- 定义：cot θ = 1 / tan θ = cos θ / sin θ。
- 周期性：cot (θ + π) = cot θ。
- 奇偶性：cot (-θ) = -cot θ。
5. 正割函数（sec）：- 定义：sec θ = 1 / cos θ。
- 周期性：sec (θ + 2π) = sec θ。
- 奇偶性：sec (-θ) = sec θ。
6. 余割函数（csc）：- 定义：csc θ = 1 / sin θ。
- 周期性：csc (θ + 2π) = csc θ。
- 奇偶性：csc (-θ) = -csc θ。
此外，三角函数还有一些重要的性质：1. 三角函数的范围：sin、cos、csc、sec的值在[-1, 1]之间，tan、cot的值在整个实数范围内。
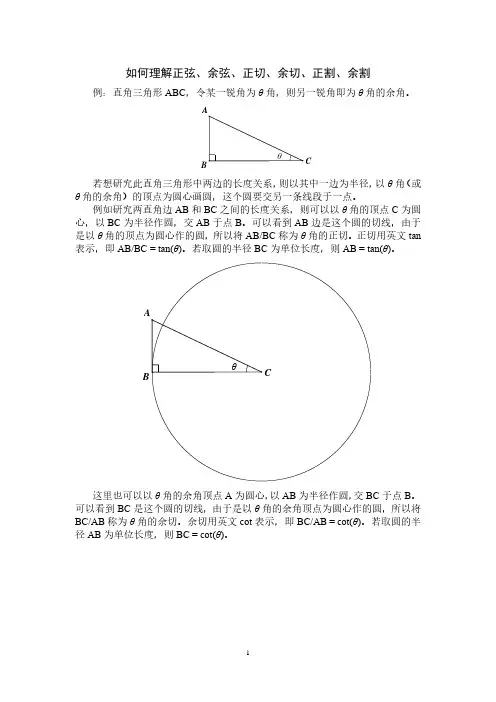
如何理解正弦、余弦、正切、余切、正割、余割例：直角三角形ABC ，令某一锐角为θ角，则另一锐角即为θ角的余角。
若想研究此直角三角形中两边的长度关系，则以其中一边为半径，以θ角（或θ角的余角）的顶点为圆心画圆，这个圆要交另一条线段于一点。
例如研究两直角边AB 和BC 之间的长度关系，则可以以θ角的顶点C 为圆心，以BC 为半径作圆，交AB 于点B 。
可以看到AB 边是这个圆的切线，由于是以θ角的顶点为圆心作的圆，所以将AB/BC 称为θ角的正切。
正切用英文tan 表示，即AB/BC = tan(θ)。
若取圆的半径BC 为单位长度，则AB = tan(θ)。
这里也可以以θ角的余角顶点A 为圆心，以AB 为半径作圆，交BC 于点B 。
可以看到BC 是这个圆的切线，由于是以θ角的余角顶点为圆心作的圆，所以将BC/AB 称为θ角的余切。
余切用英文cot 表示，即BC/AB = cot(θ)。
若取圆的半径AB 为单位长度，则BC = cot(θ)。
C研究θ角的两边AC 和BC 之间的长度关系。
则可以以θ角的顶点C 为圆心，以BC 为半径作圆，交AC 于点D 。
可以看到AC 边是这个圆的割线，由于是以θ角的顶点为圆心作的圆，所以将AC/BC 称为θ角的正割。
正割用英文sec 表示，即AC/BC = sec(θ)。
若取圆的半径BC 为单位长度，则AC = sec(θ)。
这里也可以以θ角的余角顶点A 为圆心，以AC 为半径作圆，交BC 于点C 。
若将BC 延长，则可以看到BC 边是这个圆的半弦。
由于是以θ角的余角顶点为圆心作的圆，所以将BC/AC 称为θ角的余弦。
余弦用英文cos 表示，即BC/AC = cos(θ)。
若取圆的半径AC 为单位长度，则BC = cos(θ)。
C研究θ角的余角的两边AB和AC之间的长度关系，则可以以θ角的顶点C 为圆心，以AC为半径作圆，交AB于点A。
若将AB延长，则可以看到AB边是这个圆的半弦。
分别是正弦余弦正切余切正割余割文稿归稿存档编号：[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-分别是角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数θ=y/r余弦函数θ=x/r正切函数θ=y/x余切函数θ=x/y正割函数θ=r/x余割函数θ=r/y（斜边为r，对边为y，邻边为x。
）以及两个不常用，已趋于被淘汰的函数：函数θ=1-cosθ函数θ=1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[]同角三角函数间的基本关系式：·平方关系：sin^2α＋cos^2α＝11＋tan^2α＝sec^2α1＋cot^2α＝csc^2α·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα·cotα＝1sinα·cscα＝1cosα·secα＝1商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cos α·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sin α·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1 -tanα·tanβ-ta nβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/ A))，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin²(α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tana·tan(π/3+a)·tan(π/3-a)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-c osα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/ 2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx=[sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+sinnx-sin(n-2)x+sin (n+1)x-sin(n-1)x]/2sinx（积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx=-[cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-co s(n-1)x]/(-2sinx)=-[cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos [(60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2] sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)补充：6×9＝54种诱导公式的表格以及推导方法（定名法则和定号法则）定名法则90°的奇数倍+α的三角函数，其绝对值与α三角函数的绝对值互为余函数。
初中数学什么是角的余割、正割和余切在初中数学中，我们学习了三角函数，其中包括正弦、余弦和正切函数。
除了这些常见的三角函数，还有三个与它们相关的三角函数，分别是余割、正割和余切函数。
1. 余割函数（Cosec）：余割函数是正弦函数的倒数，可以用来表示一个角的余割值。
对于一个角A，其余割值可以表示为：cosec(A) = 1 / sin(A)余割函数的定义可以解读为：余割值是对边与斜边之比的倒数。
也就是说，余割值是一个角的正弦值的倒数。
2. 正割函数（Sec）：正割函数是余弦函数的倒数，可以用来表示一个角的正割值。
对于一个角A，其正割值可以表示为：sec(A) = 1 / cos(A)正割函数的定义可以解读为：正割值是邻边与斜边之比的倒数。
也就是说，正割值是一个角的余弦值的倒数。
3. 余切函数（Cot）：余切函数是正切函数的倒数，可以用来表示一个角的余切值。
对于一个角A，其余切值可以表示为：cot(A) = 1 / tan(A)余切函数的定义可以解读为：余切值是对边与邻边之比的倒数。
也就是说，余切值是一个角的正切值的倒数。
这些角的余割、正割和余切函数在三角函数的计算和分析中起到重要的作用。
通过利用这些函数，我们可以计算和比较角的倒数值，从而得到更多的三角函数值。
此外，这些函数也可以帮助我们解决与三角函数相关的问题，例如在三角形中计算边长和角度。
总结起来，角的余割、正割和余切函数分别是正弦函数、余弦函数和正切函数的倒数。
余割函数是对边与斜边之比的倒数，正割函数是邻边与斜边之比的倒数，余切函数是对边与邻边之比的倒数。
这些函数在三角函数的计算和分析中非常有用，可以帮助我们得到更多的三角函数值，并解决与三角函数相关的问题。
分别就是正弦余弦正切余切正割余割角θ得所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中,从点Ｏ引出一条射线OＰ,设旋转角为θ,设OP=ｒ,Ｐ点得坐标为(ｘ,y)有正弦函数sｉnθ=y/r余弦函数cｏsθ＝x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ＝r/x余割函数cscθ=r／ｙ(斜边为r,对边为y,邻边为x。
)以及两个不常用,已趋于被淘汰得函数:正矢函数versinθ =1-ｃosθ余矢函数ｃoｖersθ =１—siｎθ正弦(siｎ):角α得对边比上斜边余弦(cos):角α得邻边比上斜边正切(tａn):角α得对边比上邻边余切(cot):角α得邻边比上对边正割(sec):角α得斜边比上邻边余割(ｃｓc):角α得斜边比上对边［编辑本段］同角三角函数间得基本关系式:·平方关系:sin^2α+coｓ^２α=1１+tan^2α=sｅc＾2α１＋cot^2α＝csc^2α·积得关系:sinα=tanα×cosαcoｓα＝cotα×ｓinαtanα=sinα×ｓeｃαcｏtα＝cｏsα×ｃscαsecα＝taｎα×cscαcｓcα＝ｓecα×cotα·倒数关系:taｎα ·cotα=1ｓinα ·ｃscα＝1cｏsα·sｅｃα=1商得关系:sinα/cosα＝ｔanα=ｓecα/cscαcｏsα／ｓinα＝cotα=cscα/sｅcα直角三角形ＡＢC中,角A得正弦值就等于角A得对边比斜边,余弦等于角Ａ得邻边比斜边正切等于对边比邻边,·[１]三角函数恒等变形公式·两角与与差得三角函数:coｓ(α+β)=cosα·ｃosβ-sｉnα·sinβcｏs(α—β)=cosα·cｏsβ＋siｎα·siｎβｓｉn(α±β)=siｎα·cｏｓβ±ｃｏｓα·ｓinβｔaｎ(α＋β)=(tanα+ｔanβ)/(1—tanα·ｔaｎβ)ｔaｎ(α—β)=(tａnα-tanβ)/(1＋ｔaｎα·tanβ)·三角与得三角函数:sin(α＋β+γ)=sｉnα·coｓβ·cosγ+cosα·sinβ·cｏsγ+cosα·ｃosβ·sinγ－sinα·sin β·siｎγcos(α+β+γ)＝cosα·cosβ·cｏsγ—ｃosα·sｉnβ·ｓinγ－sｉnα·cosβ·sinγ－sinα·si nβ·cosγtａｎ(α＋β+γ)=(ｔａｎα＋tａnβ+ｔａｎγ-taｎα·tanβ·tanγ)/(１—tanα·tａnβ-tan β·tａnγ-tanγ·taｎα)·辅助角公式:Ａsi nα＋Bcｏsα=(Ａ²＋B＆sｕp2;)^(１/2)sin(α+ａrｃtan(B/A)),其中ｓiｎt＝B/(A＆sｕｐ2;＋B＆sup２;)^(１/2)cost=A/(A＆sup２;+B²)^(1/2)taｎt=B/AAsinα—Bｃosα＝(A＆ｓｕp2;+Ｂ＆ｓup2;)^(1/2)cos(α-ｔ),ｔaｎt=A/Ｂ·倍角公式:ｓin(2α)＝２ｓinα·ｃoｓα＝2/(ｔａnα+ｃotα)coｓ(2α)=ｃｏｓ²(α)－siｎ＆sｕp2;(α)＝2ｃoｓ＆ｓuｐ２;(α)-１=1-2sin ＆ｓｕp2;(α)ｔan(２α)=２tａnα／[1－taｎ＆ｓup2;(α)］·三倍角公式:ｓin(3α)=3sinα-４sin&sup３;(α)=4siｎα·sin(60＋α)ｓin(60—α)cｏs(3α)＝４coｓ&sup３;(α)－3cｏsα=4ｃoｓα·coｓ(６0+α)cos(60-α)ｔan(３α)=tan a·tan(π/３+ａ)·ｔan(π／3－a)·半角公式:sin(α/２)=±√((1-ｃosα)/2)coｓ(α/2)=±√((1+coｓα)/2)tan(α/２)=±√((1-cosα)/(1＋cosα))=sｉnα/(1+coｓα)＝(１—cｏｓα)/ｓｉnα·降幂公式sin＆suｐ2;(α)=(１-ｃos(2α))/2＝versｉn(2α)/2ｃos＆sup2;(α)=(1+cos(2α))／２=cｏverｓ(2α)/２ｔan²(α)=(1-cｏｓ(２α))／(1+cｏs(２α))·万能公式:sinα=2tan(α/2)／［1＋taｎ＆sup2;(α/2)］cｏsα=［1-tan²(α/２)］/［1+taｎ＆sup2;(α／２)]tanα=２tａn(α/２)／[1－tan&ｓup２;(α/2)]·积化与差公式:siｎα·cosβ=(1/2)[sin(α+β)＋sin(α—β)］ｃoｓα·sinβ=(1/2)［sin(α＋β)—sin(α-β)］cosα·coｓβ=(1/2)［ｃos(α＋β)+ｃｏs(α－β)］siｎα·siｎβ=-(1／2)［ｃos(α+β)-ｃo s(α—β)]·与差化积公式:sinα+sinβ=2sin[(α+β)/2］coｓ［(α－β)/２]sinα－sinβ=2ｃoｓ[(α+β)/２］sin[(α－β)/２]cｏsα＋ｃosβ=2coｓ[(α+β)／2]coｓ［(α-β)/2]cosα－cosβ=－2sｉn［(α+β)/2]sin［(α—β)／2］·推导公式tanα＋cotα=2/sin2αtaｎα－cotα=-2coｔ2α１+cos2α=２cos＆ｓｕp2;α1-ｃoｓ2α=2ｓin＆sup2;α1+sｉｎα=(sｉnα／２＋cosα／2)＆sup2;·其她:ｓiｎα+siｎ(α+2π/n)＋ｓin(α+2π*2/n)+sｉn(α+2π*3/n)＋……+sin［α+2π＊(ｎ—1)/n］=０ｃosα+ｃｏs(α+２π/n)+ｃos(α+2π＊2/ｎ)+ｃoｓ(α＋2π＊3/ｎ)＋……+cｏs［α+2π*(n—１)/ｎ］=0 以及sin＆sup2;(α)+ｓiｎ&sup２;(α－2π/3)＋sin＆sup2;(α+2π/３)＝3/2tａnAｔanBtan(A＋B)+tanＡ＋tanB－tａn(A＋B)=0coｓｘ+cos2ｘ+、。
分别是-正弦-余弦-正切-余切-正割-余割维基百科正弦性质奇偶性奇定义域(-∞,∞)到达域[-1,1]周期2π特定值当x=00当x=+∞N/A当x=-∞N/A((2k+½)π,1最大值)((2k-½)π,-1最小值)其他性质渐近线N/A根kπ临界点kπ-π/2 拐点kπ不动点0k是一个整数.余弦性质奇偶性偶定义域(-∞,∞)到达域[-1,1]周期2π特定值当x=00当x=+∞N/A当x=-∞N/A最大值(2kπ,1)最小值((2k+1)π,-1)其他性质渐近线N/A根kπ-π/2临界点kπ拐点kπ-π/2不动点0k是一个整数.正切性质奇偶性奇{x|x≠kπ+π/2，定义域k∈Z}到达域(-∞,∞)周期π特定值性质奇偶性奇{x∈R〡x≠kπ，定义域k∈Z}到达域(-∞,∞)周期π特定值当x=00当x=+∞N/A当x=-∞N/A最大值∞最小值-∞其他性质渐近线N/A根kπ+不动点0k是一个整数.正割性质奇偶性偶{x|x≠kπ+π/2，定义域k∈Z}到达域|secx|≥1周期2π特定值k是一个整数.余割性质奇偶性奇定义域{x|x≠kπ，k∈Z} 到达域|csc x|≥1周期2π特定值当x=00当x=+∞N/A当x=-∞N/A(最大值,∞)(最小值,-∞)其他性质渐近线N/A根无实根临界点kπ-π/2拐点kπ不动点0k是一个整数.反正弦性质奇偶性奇定义域[-1, 1]到达域周期N/A 特定值当x=00当x=+∞N/A 当x=-∞N/A 最大值最小值其他性质渐近线N/A 根0反余弦性质奇偶性非奇非偶函数定义域[-1, 1]到达域周期N/A 特定值当x=0当x=+∞N/A 当x=-∞N/A最大值最小值其他性质渐近线N/A 根 1反正切性质奇偶性奇函数定义域实数集到达域周期N/A 特定值当x=00当x=+∞当x=-∞其他性质渐近线根0拐点原点名称常用符号定义定义域值域反正弦反余弦反正切反余切反正割反余割百度文库下载分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。
维基百科π特定值当x=+∞N/A 当x=-∞N/A 最大值∞最小值-∞其他性质N/Akπ+k是一个.反正弦性质奇[-1, 1]N/A特定值当x=+∞N/A当x=-∞N/A最大值(,∞)最小值(,-∞)其他性质N/A无实根kπ-π/2kπk 是一个.百度文库下载分别是角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设O P=r，P点的坐标为（x，y）有正弦函数θ=y/r余弦函数θ=x/r正切函数θ=y/x余切函数θ=x/y正割函数θ=r/x余割函数θ=r/y（斜边为r，对边为y，邻边为x。
）以及两个不常用，已趋于被淘汰的函数：函数θ =1-cosθ函数θ =1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[]同角三角函数间的基本关系式：·平方关系：sin^2α＋cos^2α＝11＋tan^2α＝sec^2α1＋cot^2α＝csc^2α·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边, 余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cos β·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cos β·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·t anβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/A))，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin&sup 2;(α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tan a · tan(π/3+a)· tan(π/3-a)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/si nα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]si nα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+ 2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+ 2π*(n-1)/n]=0 以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx= [sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+ sinnx-sin(n-2)x+sin(n+1)x-sin(n-1)x]/2sinx （积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx= - [cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x] /(-2sinx)=- [cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina =3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa =4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a) /2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与 -α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)补充：6×9＝54种诱导公式的表格以及推导方法（定名法则和定号法则）定名法则90°的奇数倍+α的三角函数，其绝对值与α三角函数的绝对值互为余函数。
分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。
）以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ=1-cosθ余矢函数coversθ=1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[编辑本段]同角三角函数间的基本关系式：·平方关系：sin^2α＋cos^2α＝11＋tan^2α＝sec^2α1＋cot^2α＝csc^2α·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα·cotα＝1sinα·cscα＝1cosα·secα＝1商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·si nβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-si nα·sin β·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/A))，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin² (α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tana·tan(π/3+a)·tan(π/3-a)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1) /n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π* (n-1)/n]=0以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx=[sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+sinnx-sin(n-2)x+sin(n+1)x-sin (n-1)x]/2sinx（积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx=-[cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x] /(-2sinx)=-[cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[编辑本段]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝tanαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)补充：6×9＝54种诱导公式的表格以及推导方法（定名法则和定号法定名法则90°的奇数倍+α的三角函数，其绝对值与α三角函数的绝对值互为余函数。
函数名正弦余弦正切余切正割余割这些函数都是三角函数的一部分，它们在数学和物理中都有广泛的应用。
以下是对这些函数的基本介绍：1.正弦函数（Sine Function）和余弦函数（Cosine Function）：正弦函数和余弦函数都与三角形的边长有关。
在直角三角形中，正弦函数是三角形的对边（opposite）与斜边（hypotenuse）的比值，记为sin(x)；余弦函数是三角形的邻边（adjacent）与斜边的比值，记为cos(x)。
正弦和余弦函数的图像都是周期性的，这意味着它们在一定间隔内重复。
2.正切函数（Tangent Function）和余切函数（Cotangent Function）：正切函数和余切函数是正弦函数和余弦函数的比值。
正切函数是正弦函数除以余弦函数，记为tan(x)；余切函数是余弦函数除以正弦函数，记为cot(x)。
正切函数的图像也是周期性的，但余切函数的图像并非周期性。
3.正割函数（Secant Function）和余割函数（Cosecant Function）：正割函数和余割函数分别是正弦函数和余弦函数的倒数。
正割函数是sec(x) = 1/cos(x)，余割函数是csc(x) = 1/sin(x)。
它们的图形也是周期性的。
这些函数在三角学中有着重要的应用。
例如，它们可以用来描述振动、波动、声音传播等物理现象。
在计算机图形学中，这些函数也常被用来生成旋转、缩放、平移等变换。
此外，这些函数在解决一些数学问题时也非常有用，比如求解极值、最优解、零点等。
除了基本的三角函数，还有许多派生出来的三角函数，如反正弦函数（Inverse Sine Function）、反余弦函数（Inverse Cosine Function）、反正切函数（Inverse Tangent Function）等。
这些函数的定义域是有限的，值域是整个实数集。
它们通常被用于求解一些方程的根，比如求解三角形的角度等。
高中数学六大同构函数
高中数学中存在着六大同构函数，它们分别是正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
这六个函数之间的关系是相互对称的，它们的图像形态和性质都有相似之处。
正弦函数和余弦函数是最为常见的同构函数，它们的图像都是周期为2π的曲线，只是在x轴上的位置不同。
正切函数和余切函数也是同构函数，它们的图像都是无限趋近于x轴但不会与x轴相交的曲线。
正割函数和余割函数则是对数函数和指数函数的倒数，它们的图像与对数函数和指数函数的图像相似，但形态上是关于y轴对称的。
在解决某些数学问题时，我们可以通过利用同构函数之间的关系来简化问题的求解过程。
比如，在解决三角方程时，我们可以将正切函数转化为正弦函数或余弦函数，从而更容易进行求解。
同构函数之间的关系不仅在数学中有着重要的应用，还在物理等学科中有着广泛的应用。
- 1 -。
所有三角函数的公式大全三角函数是解决三角形相关问题的数学工具。
它们包括正弦、余弦、正切、余切、正割和余割。
下面是这些三角函数的定义和重要公式：1. 正弦函数（Sine）：定义：在直角三角形中，正弦是对边与斜边的比值。
表达式：sin(θ) = 对边 / 斜边重要公式：- 正弦的平方等于1减去余弦的平方：sin²(θ) + cos²(θ) = 1- 正弦的倒数是正割：csc(θ) = 1 / sin(θ)- 正弦的倒数的平方等于余割的平方减1：csc²(θ) = cot²(θ) - 12. 余弦函数（Cosine）：定义：在直角三角形中，余弦是邻边与斜边的比值。
表达式：cos(θ) = 邻边 / 斜边重要公式：- 余弦的平方等于1减去正弦的平方：cos²(θ) + sin²(θ) = 1- 余弦的倒数是余割：sec(θ) = 1 / cos(θ)- 余弦的倒数的平方等于正割的平方减1：sec²(θ) = tan²(θ) + 13. 正切函数（Tangent）：定义：在直角三角形中，正切是正弦与余弦的比值。
表达式：tan(θ) = 正弦 / 余弦 = 对边 / 邻边重要公式：- 正切等于正弦除以余弦：tan(θ) = sin(θ) / cos(θ)- 正切的倒数是余切：cot(θ) = 1 / tan(θ)- 正切的平方等于正割的平方减1：tan²(θ) = sec²(θ) - 14. 余切函数（Cotangent）：定义：在直角三角形中，余切是余弦与正弦的比值。
表达式：cot(θ) = 余弦 / 正弦 = 邻边 / 对边重要公式：- 余切等于余弦除以正弦：cot(θ) = cos(θ) / sin(θ)- 余切的倒数是正切：tan(θ) = 1 / cot(θ)- 余切的平方等于余割的平方减1：cot²(θ) = csc²(θ) - 15. 正割函数（Secant）：定义：在直角三角形中，正割是斜边与邻边的比值。
数学三角函数公式大全数学三角函数是数学中的重要分支之一，涉及到许多重要的公式和定理。
下面是一个全面的三角函数公式大全，包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
正文:1. 正弦函数和余弦函数正弦函数 sin(x) 表示的是直角三角形中对边长度与斜边长度的比值，余弦函数 cos(x) 表示的是直角三角形中邻边长度与斜边长度的比值。
下面是它们的公式:sin(x) = 2 / (2 + x^2)cos(x) = 1 - sin^2(x)2. 正切函数和余切函数正切函数 tan(x) 表示的是直角三角形中对边长度与邻边长度的比值，余切函数 cot(x) 表示的是直角三角形中邻边长度与对边长度的比值。
下面是它们的公式:tan(x) = 2 / (1 + x^2)cot(x) = 1 / (1 + x^2)3. 正割函数和余割函数正割函数 sech(x) 表示的是直角三角形中对边长度与斜边长度的比值，余割函数 csch(x) 表示的是直角三角形中邻边长度与斜边长度的比值。
下面是它们的公式:sech(x) = 1 / (1 + x^2)csch(x) = x / (1 + x^2)4. 其他三角函数其他常见的三角函数包括正弦余弦函数、余弦正弦函数、正切余切函数、余切正切函数、正割余割函数和余割正割函数。
这些函数在三角学和物理学中都扮演着重要的角色。
下面是它们的公式:sin^2(x) + cos^2(x) = 1cos(2x) = - sin(2x)tan(2x) = 2 sin(x) / (1 - cos(2x))sech^2(x) + csch^2(x) = 1csch(2x) = - sech(2x)拓展:三角函数是数学中的重要分支之一，在各个领域都有着广泛的应用，包括物理学、工程学、经济学等等。
三角函数的公式和定理对于数学和物理学的学习都是至关重要的。
除了上面提到的公式和定理，还有许多其他的三角函数公式和定理，例如正弦定理、余弦定理、余切定理、正割定理和余割定理等等。
角9的所有三角函数（见:函数图形曲线）在平面直角坐标系xOy 中，从点O 引出一条射线OP ，设旋转角为9，设OP=r ，P 点的坐标为（x，y）有正弦函数9=y/r余弦函数9=x/r正切函数9=y/x余切函数9=x/y正割函数9=r/x余割函数9=r/y（斜边为r，对边为y，邻边为x。
）以及两个不常用，已趋于被淘汰的函数：函数9 =1-cos 9函数9 =1-sin 9正弦( sin ):角a的对边比上斜边（余弦( cos ):角a的邻边比上斜边（正切( tan ):角a的对边比上邻边（余切( cot ):角a的邻边比上对边（正割( sec ):角a的斜边比上邻边（余割( csc ):角a的斜边比上对边（[]同角三角函数间的基本关系式：平方关系：sin A2 a+ cos A2 a= 11 + tanA2 a= secA2 a1 + C0tA2 a= CSCA2 a积的关系：sin a=tan a^cos acos a=cot aX sin atan a=sin aXsec acot a=cos aX csc a sec a =tan a X csc a csc a =sec a X cot a倒数关系：tan a cot a = 1Sin a • CSC a= 1COS a • Sec a= 1商的关系：Sin a/COS a=tan a= SeC a/CSC aCOS a/Sin a=COt a= CSC a/SeC a直角三角形ABC 中,角A 的正弦值就等于角A 的对边比斜边,余弦等于角A 的邻边比斜边正切等于对边比邻边,【1]三角函数恒等变形公式两角和与差的三角函数：cos( a+ B)=cos a cos p-sin a s in Bcos( a- p)=cos a cos p+sin a sin psin( a±p)=sin a cos p±cos a sin ptan( a+p)=(tan a+tan p)/(1-tan a tan p)tan( a-p)=(ta n a-ta n p)/(1+tan a ta n p)三角和的三角函数：sin( a+ p+ Y=sin a cos p cos y+cos a sin p cos 丫+cos a cos p sin Y S in a sin p sin 丫cos( a+ p+ Y=cos a cos p cos 丫-cos a sin p sin 丫-sin a cos p sin 丫-sin a sin p cos 丫tan( a+p+y)=(tan a+tan p+tan y-tan a tan p tan y)/(1-tan a tan p-tan p tan y-tan y tan a)辅助角公式：As in a+Bcos a=(A²+B²『(1/2)s in( a+arcta n(B/A))，其中si nt=B/(A²+B²『(1/2)cost=A/(A²+B²F(1/2)tant=B/AAsin a -Bcos a =(A²+B²『(1 /2)cos( a -t) , tant=A/B倍角公式：sin(2 a)=2sin a cos a=2/(tan a+cot a)cos(2a)=cos²( a)-sin²( a )=2cos²( a) -1=1- 2sin²( a) tan(2 a)=2tan a/[1-tan²( a)]三倍角公式：sin(3 a)=3sin a-4sin³( a)=4sin a sin(60+ a)sin(60 -a)cos(3 a )=4cos³( a) -3cos a =4cos a cos(60+ a )cos(60 -a)tan(3 a )=tan a • tan( n /3+a) • tan( n /3-a)半角公式：sin( a /2)= ±V(-cos a )/2)cos( a /2)= ±V ((1+cos a )/2)tan( a /2)= ±V(-1cos a )/(1+cos a ))=sin a /(1+cos a )=(1-cos a )/sin a降幕公式sin²( a )=(1 -cos(2 a ))/2=versin(2 a )/2cos²( a )=(1+cos(2 a ))/2=covers(2 a )/2 tan²( a )=(1 -cos(2a ))/(1+cos(2 a )) 万能公式：sin a =2tan( a /2)/[1+tan²( a /2)] cos a =[1 -tan²( a /2)]/[1+tan²( a /2)] tan a =2tan( a /2)/[1 -tan²( a /2)]积化和差公式：和差化积公式：sin a +sin p =2sin[( a +p )/2]cos[( -pa )/2] sin a -sin p =2cos[( a +p )/2]sin[( -ap )/2] cos a +cos p =2cos[( a +p )/2]cos[( a -p )/2] cos a -cos p=-2sin[( a +p )/2]sin[( -pa )/2]推导公式tan a +cot a =2/sin2 a tan a -cot a=-2cot2a 1+cos2a =2cos²a 1-cos2a =2sin² a1+sin a =(sin a /2+cos a /2)²其他：sin a +sin(a +2n /n)+sin( a +2n *2/n)+sin( a +2n *3/n)+ +sin[ a +2n*(n1)/n]=0cos a +cos( a +2 n /n)+cos( a +2n *2/n)+cos( a +2n *3/n)+ +cos[ a+2n *(n -1)/n]=0 以及sin²( a )+sin²( a -2n /3)+sin²( a +2n /3)=3/2 tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0 cosx+cos2x+...+cosnx=[sin(n+1)x+sinnx-sinx]/2sinx证明：左边 =2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+ sinnx-sin(n-2)x+sin(n+1)x-sin(n-1)x]/2sinx和差)=[sin(n+1)x+sinnx-sinx]/2sinx= 右边等式得证sinx+sin2x+...+sinnx=证明 :左边 =-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x]/(-2sinx)sin a-cos p =(1/2)[sin( cos a sin p =(1/2)[sin( a +-p sin )( a -p )] cos a cos p =(1/2)[cos( a +p )+cos( -ap )] sin a sin p -(=1/2)[cos( a +p -)cos( a -p )]积化- [cos(n+1)x+cosnx-cosx-1]/2sinx=- [cos(n+1)x+cosnx-cosx-1]/2sinx= 右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[( V3/2)² -sin²a]=4sina(sin²60 ° -sin²a)=4sina(sin60 ° +sina)(sin60 °-sina)=4sina*2sin[(60+a)/2]cos[(60 ° -a)/2]*2sin[(60 °-a)/2]cos[(60 °+a)/2] =4sinasin(60 ° +a)sin(60 °-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a- (V3/2)²]=4cosa(cos²a-cos²30 °)=4cosa(cosa+cos30 °)(cosa-cos30 ° )=4cosa*2cos[(a+30 ° )/2]cos[(a-30 °)/2]*{-2sin[(a+30 °)/2]sin[(a-°)/2]}30=-4cosasin(a+30 ° )sin(a-30 °)=-4cosasin[90 ° -(60 °-a)]sin[-90 °+(60°+a)]=-4cosacos(60 ° -a)[-cos(60 °+a)]=4cosacos(60 ° -a)cos(60 °+a)上述两式相比可得tan3a=tanatan(60 ° -a)tan(60 °+a)[]三角函数的诱导公式公式一：设a为任意角，终边相同的角的同一三角函数的值相等:sin (2k n+ a)= sin aCOS ( 2k n+ a) = cos a tan ( 2k n + a)= tan a cot ( 2k n + a) = cot a 公式二:设a 为任意角，n + a 的三角函数值与 a 的三角函数值之间的关系:sin ( n+ a) =— sin a COS ( n + a) =— COs a tan ( n+ a ) = tan a COt ( n+ a) = COt a公式三:任意角 a 与-a 的三角函数值之间的关系：sin (—a = — sin a COs (—a = COs a tan (—a— tan a COt (—a— COt a公式四:利用公式二和公式三可以得到n - a 与a 的三角函数值之间的关系:sin ( n — a = sin aCOs ( n -a =— COs atan ( n 一a = — tan aCOt ( n —a = — COt a公式五:利用公式一和公式三可以得到2 n -a 与a 的三角函数值之间的关系:sin (2 n — a )= — sina COs (2 n — a):= COs a tan (2 n — a)= — tanaCOt (2 n — a )二 — COta 公式六:n /2 ±a 及 3 -兀/2 士a 与a 的三角函数值之间的关系 sin (n /2 + a = COs aCOs (n /2 + a =— sinatan (n /2 + a = — COtaCOt (n /2 + a = — tanasin (n /2 — a = COs aCOs (n /2 — a = sinatan (n /2 — a = COt acot ( n /2 — a) = tan aSin ( 3 n /2 + a)=— COS aCOS ( 3 n /2 + a) = Sin atan ( 3 n /2 + a ) =— COt a cot ( 3 n /2 + a ) =— tan aSin ( 3 n/2 —a) =— COS aCOS ( 3 n/2 — a) =—Sin atan ( 3n/2 —a ) = COt aCOt ( 3n/2 — a ) = tan a(以上k € Z)补充：6X9 = 54种诱导公式的表格以及推导方法(定名法则和定号法则)90°的奇数倍+ a的三角函数，其绝对值与a三角函数的绝对值互为余函数。
三角函数公式万能公式三角函数有六个主要的函数，分别是正弦函数（sin）、余弦函数（cos）、正切函数（tan）、余切函数（cot）、正割函数（sec）和余割函数（csc）。
这些函数之间存在着一系列的关系和公式。
1.万能公式之正弦定理：正弦定理用于计算非直角三角形的边与角之间的关系。
假设ABC是一个非直角三角形，a、b、c分别为边BC、AC、AB的长度，α、β、γ分别为对应边的对角。
则正弦定理可以表示为：sinα/a = sinβ/b = sinγ/c根据这个公式，我们可以通过已知的边长和角度来计算三角形中的其他边长和角度。
2.万能公式之余弦定理：余弦定理用于计算非直角三角形的边和角之间的关系。
假设ABC是一个非直角三角形，a、b、c分别为边BC、AC和AB的长度，α、β、γ分别为对应边的对角。
则余弦定理可以表示为：c^2 = a^2 + b^2 - 2ab*cosγ根据这个公式，我们可以通过已知的边长和角度来计算三角形中的其他边长和角度。
3.万能公式之正切定理：正切函数用于计算直角三角形的边与角之间的关系。
在一个直角三角形ABC中，A为直角，a、b、c分别为边BC、AC和AB的长度，α、β、γ分别为其他两个角。
则正切定理可以表示为：tanα = a/b这个公式可以帮助我们通过已知的边长和角度来计算三角形中的其他边长和角度。
4.万能公式之勾股定理：勾股定理用于计算直角三角形中的边之间的关系。
假设ABC是一个直角三角形，A为直角，a、b、c分别为边BC、AC和AB的长度。
勾股定理可以表示为：c^2=a^2+b^2根据这个公式，我们可以通过已知的边长来计算直角三角形中的其他边长。
5.万能公式之三角恒等式：三角函数还有许多重要的恒等式，这些恒等式为计算和简化三角函数的值提供了便利。
其中一些常见的三角恒等式包括：sin^2θ + cos^2θ = 11 + tan^2θ = sec^2θ1 + cot^2θ = csc^2θsin2θ = 2sinθcosθcos2θ = cos^2θ - sin^2θtan2θ = (2tanθ) / (1 - tan^2θ)这些恒等式可以用来简化复杂的三角函数表达式，以及推导其他三角函数的值和关系。
三角函数公式及其应用三角函数是研究三角形内角关系与边长比值的一门数学概念，是数学中基础而重要的内容之一、三角函数公式是描述三角函数之间关系的一组数学公式，它们在解决各种三角函数问题中起到了重要的作用。
三角函数包括正弦、余弦、正切、余切、正割和余割六种函数，它们分别表示一个角的三边比值。
常见三角函数公式及其应用如下：1.正弦公式：正弦公式用于计算三角形的边长：a/sinA = b/sinB = c/sinC其中a、b、c为三角形的边长，A、B、C为三角形的内角。
2.余弦公式：余弦公式用于计算三角形的边长：c^2 = a^2 + b^2 - 2ab*cosC其中a、b、c为三角形的边长，C为三角形的内角。
3.正切公式：正切公式用于计算三角形的内角大小：tanA = sinA/cosA其中A为三角形的内角。
4.余切公式：余切公式用于计算三角形的内角大小：cotA = 1/tanA = cosA/sinA其中A为三角形的内角。
5.和差化积公式：sin(A±B) = sinA*cosB ± cosA*sinBcos(A±B) = cosA*cosB ∓ sinA*sinB其中A、B为角度。
6.和差化积公式的应用：通过使用和差化积公式，可以展开复杂的三角函数表达式，简化计算过程。
7.万能公式：a/sinA = b/sinB = c/sinC = 2Ra^2 = b^2 + c^2 - 2bc*cosA其中a、b、c为三角形的边长，A、B、C为三角形的内角，R为三角形的外接圆半径。
8.万能公式的应用：万能公式可以用于计算三角形的边长和内角大小，同时也可以用于证明三角形的性质。
除了以上公式，三角函数也有一些重要的性质和恒等式，如周期性、奇偶性、反函数等，这些性质和恒等式也对解决三角函数问题具有重要的指导意义。
三角函数广泛应用于各个领域，如物理学、工程学、计算机图形学等。
在物理学中，三角函数被用于描述波动、振动等运动规律。
三角函数正弦,余弦,正切,余切是什么意思牛顿45。
正切函数为什么叫正切？正弦、余弦、正切、余切三角函数：…常见的三角函数有正弦函数、余弦函数和正切函数。
…函、数、函数，正、弦、正弦，余、弦、余弦，切：见《牛顿44》…正切：在Rt△ABC（直角三角形）中，∠C=90°，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是tanB=b/a，即tanB=AC/BC。
在物理学中，三角函数也是常用的工具。
在Rt△ABC中，如果锐角A确定，那么角A的对边与邻边的比值随之确定，这个比叫做角A的正切，记作tanA。
即：tanA=∠A的对边/∠A的邻边。
tan 为什么称为正切？正切的解释是什么？——网友提问…tan：tangent的简写……tangent（英文）：n.切线; 正切……解、释、解释：见《欧几里得56》…（…《欧几里得》：小说名…）匿名用户：首先，我们有一个角θ…θ：希腊字母西塔Theta（大写Θ，小写θ），在希腊语中，是第八个希腊字母。
国际音标：/'θi:tə/小写的θ是：数学上常代表平面的角…以角的端点为圆心，作一个单位圆（也就是半径为1的圆）然后这个圆肯定与我们的角有两个交点随便选一个交点，作一条圆的切线然后这条切线被θ角的两条射线所截，形成一条线段这条线段的长度就是tanθ，即θ的正切值…值：见《欧几里得74》…同理，我们也可以接着从这个点，作一条圆的弦这个弦被θ角的两条射线所截，形成一条线段这条线段的长度就是sinθ，即θ的正弦值至于余弦、余切。
顾名思义，正如@南中国海的一条鱼所说。
θ余角的正弦，就是θ的余弦θ余角的正切，就是θ的余切编辑于2014-12-18（39人赞同了该回答）“还在很早的时候，由于垦（kěn）殖和畜（xù）牧的需要，人们就开始作长途迁移；后来，贸易的发展和求知的欲望，又推动他们去长途旅行。
在当时，这种迁移和旅行是一种冒险的行动。
八个三角函数名称及符号中的特定函数三角函数是数学中重要的一类函数，由于其在几何学、物理学、工程学等领域的广泛应用，具有重要的意义。
常见的三角函数有八个，它们分别是正弦函数（sine function）、余弦函数（cosine function）、正切函数（tangent function）、余切函数（cotangent function）、正割函数（secant function）、余割函数（cosecant function）、反正弦函数（arcsine function）和反余弦函数（arccosine function）。
下面将分别对这八个函数进行详细解释。
1. 正弦函数（sine function）定义正弦函数是一个周期函数，记作sin(x)，其中x是角度。
正弦函数的定义域是实数集，值域是[-1, 1]。
正弦函数的图像是一条连续的波浪线，周期为360度或2π弧度，振幅为1。
用途正弦函数在几何学中被广泛应用，可以描述周期性的运动、波动等现象。
在物理学中，正弦函数可以用来描述振动、波动、周期性变化等现象。
在工程学中，正弦函数可以用来分析交流电流、声音波动等。
工作方式正弦函数的工作方式是根据给定的角度值，计算出对应的正弦值。
正弦值可以通过查表或计算器等工具来获得。
2. 余弦函数（cosine function）定义余弦函数是一个周期函数，记作cos(x)，其中x是角度。
余弦函数的定义域是实数集，值域是[-1, 1]。
余弦函数的图像是一条连续的波浪线，周期为360度或2π弧度，振幅为1。
用途余弦函数在几何学中被广泛应用，可以描述周期性的运动、波动等现象。
在物理学中，余弦函数可以用来描述振动、波动、周期性变化等现象。
在工程学中，余弦函数可以用来分析交流电流、声音波动等。
工作方式余弦函数的工作方式是根据给定的角度值，计算出对应的余弦值。
余弦值可以通过查表或计算器等工具来获得。
3. 正切函数（tangent function）定义正切函数是一个周期函数，记作tan(x)，其中x是角度。
数学三⾓函数正弦、余弦、正割、余割、正切、余切的概念深⼊解读进⼊⾼中后，同学们都要开始学习三⾓函数的知识了。
三⾓函数总共分为六个：
正弦（sin）、余弦（cos）；
正切（tan）、余切（cot）；
正割（sec）、余割（cosec）。
很多学⽣学完后的感觉就是⼀个字——绕。
这六个三⾓函数的彼此关系确实太绕了。
今天【⼗次⽼师】就为⼤家深扒⼀下它们。
名字来源
正⾓和余⾓
1. 正和余的命名原则：
在单位圆中，⾓AOB为正⾓；⾓BOE为余⾓。
这两个⾓互余。
劣弧AB为正⾓AOB所对的
弧，我们称为正弧，同理余⾓BOE所对的弧为余弧。
2. 弦、切、割的命名原则：
弦的理解
连接两个定点线段
弦的理解
切的理解
沿着边缘切
割线的理解
割开分割的含义
在单位圆中表⽰正余+弦切割
正弦+正切+正割
余弦+余割+余切
由这⼏个长度可以分别构造出两个三⾓形，我称呼他们为正⾓三⾓形和余⾓三⾓形。
如图：
正⾓三⾓形和余⾓三⾓形
这个两个三⾓形彼此相似。
有相似性可推出：
半径（1）：余切 =正切：半径（1）【正切余切互为倒数】由勾股定理可推出：
正切的平⽅+半径（1）的平⽅ = 正割的平⽅
余切的平⽅+半径（1）的平⽅ = 余割的平⽅
三⾓函数⼤⼀统图
本⽂图形采⽤GeoGebra绘制
编写不宜，希望各位看官们，随⼿点个赞。
分别是正弦余弦正切余切正割余割角θ的所有三角函数(见:函数图形曲线)在平面直角坐标系xOy中，从点O引出一条射线OP，设旋转角为θ，设OP=r，P点的坐标为（x，y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r，对边为y，邻边为x。
）以及两个不常用，已趋于被淘汰的函数：正矢函数versinθ =1-cosθ余矢函数coversθ =1-sinθ正弦（sin）:角α的对边比上斜边余弦（cos）:角α的邻边比上斜边正切（tan）:角α的对边比上邻边余切（cot）:角α的邻边比上对边正割（sec）:角α的斜边比上邻边余割（csc）:角α的斜边比上对边[编辑本段]同角三角函数间的基本关系式：·平方关系：sin^2α＋cos^2α＝11＋tan^2α＝sec^2α1＋cot^2α＝csc^2α·积的关系：sinα=tanα×cosαcosα=cotα×sinαtanα=sinα×secαcotα=cosα×cscαsecα=tanα×cscαcscα=secα×cotα·倒数关系：tanα ·cotα＝1sinα ·cscα＝1cosα ·secα＝1商的关系：sinα/cosα＝tanα＝secα/cscαcosα/sinα＝cotα＝cscα/secα直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,·[1]三角函数恒等变形公式·两角和与差的三角函数：cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tan α)·辅助角公式：Asinα+Bcosα=(A²+B²)^(1/2)sin(α+arctan(B/A))，其中sint=B/(A²+B²)^(1/2)cost=A/(A²+B²)^(1/2)tant=B/AAsinα-Bcosα=(A²+B²)^(1/2)cos(α-t)，tant=A/B·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos²(α)-sin²(α)=2cos²(α)-1=1-2sin²(α)tan(2α)=2tanα/[1-tan²(α)]·三倍角公式：sin(3α)=3sinα-4sin³(α)=4sinα·sin(60+α)sin(60-α)cos(3α)=4cos³(α)-3cosα=4cosα·cos(60+α)cos(60-α)tan(3α)=tan a · tan(π/3+a)· tan(π/3-a)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin²(α)=(1-cos(2α))/2=versin(2α)/2cos²(α)=(1+cos(2α))/2=covers(2α)/2tan²(α)=(1-cos(2α))/(1+cos(2α))·万能公式：sinα=2tan(α/2)/[1+tan²(α/2)]cosα=[1-tan²(α/2)]/[1+tan²(α/2)]tanα=2tan(α/2)/[1-tan²(α/2)]·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos²α1-cos2α=2sin²α1+sinα=(sinα/2+cosα/2)²·其他：sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0 cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0以及sin²(α)+sin²(α-2π/3)+sin²(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0cosx+cos2x+...+cosnx= [sin(n+1)x+sinnx-sinx]/2sinx证明：左边=2sinx(cosx+cos2x+...+cosnx)/2sinx=[sin2x-0+sin3x-sinx+sin4x-sin2x+...+ sinnx-sin(n-2)x+sin(n+1)x-sin(n-1)x]/2s inx （积化和差）=[sin(n+1)x+sinnx-sinx]/2sinx=右边等式得证sinx+sin2x+...+sinnx= - [cos(n+1)x+cosnx-cosx-1]/2sinx证明:左边=-2sinx[sinx+sin2x+...+sinnx]/(-2sinx)=[cos2x-cos0+cos3x-cosx+...+cosnx-cos(n-2)x+cos(n+1)x-cos(n-1)x]/(-2sinx) =- [cos(n+1)x+cosnx-cosx-1]/2sinx=右边等式得证三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)[编辑本段]三角函数的诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinαcos（2kπ＋α）＝cosαtan（2kπ＋α）＝t anαcot（2kπ＋α）＝cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）＝－sinαcos（π＋α）＝－cosαtan（π＋α）＝tanαcot（π＋α）＝cotα公式三：任意角α与-α的三角函数值之间的关系：sin（－α）＝－sinαcos（－α）＝cosαtan（－α）＝－tanαcot（－α）＝－cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π－α）＝sinαcos（π－α）＝－cosαtan（π－α）＝－tanαcot（π－α）＝－cotα公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π－α）＝－sinαcos（2π－α）＝cosαtan（2π－α）＝－tanαcot（2π－α）＝－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）＝cosαcos（π/2＋α）＝－sinαtan（π/2＋α）＝－cotαcot（π/2＋α）＝－tanαsin（π/2－α）＝cosαcos（π/2－α）＝sinαtan（π/2－α）＝cotαcot（π/2－α）＝tanαsin（3π/2＋α）＝－cosαcos（3π/2＋α）＝sinαtan（3π/2＋α）＝－cotαcot（3π/2＋α）＝－tanαsin（3π/2－α）＝－cosαcos（3π/2－α）＝－sinαtan（3π/2－α）＝cotαcot（3π/2－α）＝tanα(以上k∈Z)补充：6×9＝54种诱导公式的表格以及推导方法（定名法则和定号法则）定名法则90°的奇数倍+α的三角函数，其绝对值与α三角函数的绝对值互为余函数。
