共边共角相似的组合图形全梳理（优选）

相似三角形几种基本模型经典模型平行旋转型图形梳理：特殊情况：B 、E'、F'共线平移一般平移特殊翻折180°旋转180°平行型平行型翻折180°翻折180°斜交型斜交型■■一边平移双垂直特殊一般特殊一般C△AEF 旋转到色AE 'F 'F'一 AEF 旋转到」AE ' F '丄AEF 旋转到兰AE 'F '色AEF 旋转到二AE ' F 'C , E', F'共线相似三角形有以下几种基本类型 ：①平行线型常见的有如下两种 ，DE//BC ,则厶ADE S MBC②相交线型常见的有如下四种情形 ，如图，已知/仁/B ,则由公共角ZA 得，△ ADE s^ABCA B C△ AEF 旋转到厶AE‘ F 'A△ AEF 旋转至U 厶AE‘ F '八BC 一AEF 旋转至U 仝AE ‘ F 'AAEF 旋转到 A AE ‘ F 'E'A如下左图，已知Z1= ZB,则由公共角Z A 得，△ADC s^ACBZ1= Z得，△ ADE s^ABC 已知ZBAD= /CAE,Z B= ZD ,则厶ADE^A ABC,下图为常见的基本图形④母子型已知Z ACB=90 ° ,AB 丄CD ,则厶CBD ^A ABC^A ACD .如下右图，已知ZB= ZD,则由对顶角③旋转型相似三角形常见的图形1、下面我们来看一看相似三角形的几种基本图形（1）如图：称为平行线型”的相似三角形（有A 型”与X 型”图）反A 共角共边型”、蝶型”）⑷如图：/仁Z2，/B= ZD ,则厶ADE ^A ABC ,称为 旋转型”的相似三角形2、几种基本图形的具体应用(1)若 DE//BC (A 型和 X 型)则厶 ADE S ^ABC（2）射影定理 若CD 为Rt △ ABC 斜边上的高（双直角图形）(3) 如图：称为 垂直型”有 双垂直共角型 型”）EC双垂直共角共边型 （也称 射影定理型 ”）”三垂直如图：其中/仁Z2 ,则厶ADE S ^ABC 称为 斜交型”的相似三角形（有反A 共角型ED则Rt△ ABC^Rt△ ACD^Rt △ CBD 且AC2=AD AB , CD2=AD BD , BC2=BD AB ;(3) 满足1、AC2=AD AB, 2、/ACD= ZB, 3、/ACB= Z ADC ,都可判定△ ADC ^A ACB ./ ⑴AD AE亠亠(4) 当或AD AB=AC AE 时，△ ADE ^△ACB .AC AB。

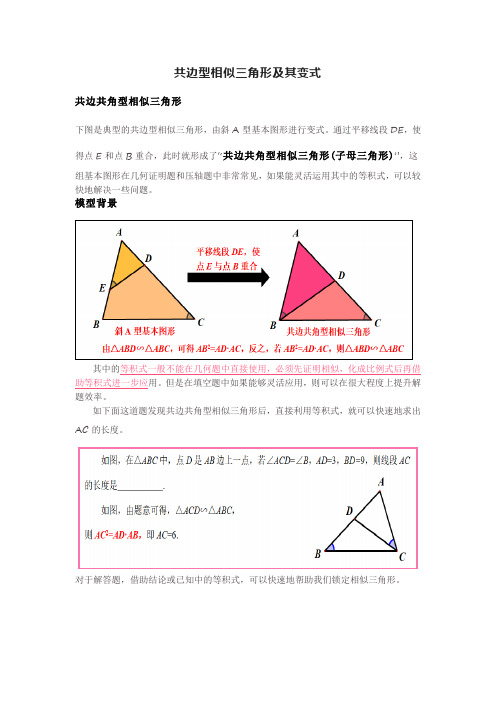
共边型相似三角形及其变式共边共角型相似三角形下图是典型的共边型相似三角形，由斜A型基本图形进行变式。

通过平移线段DE，使得点E和点B重合，此时就形成了“共边共角型相似三角形(子母三角形)”，这组基本图形在几何证明题和压轴题中非常常见，如果能灵活运用其中的等积式，可以较快地解决一些问题。

模型背景其中的等积式一般不能在几何题中直接使用，必须先证明相似，化成比例式后再借助等积式进一步应用。

但是在填空题中如果能够灵活应用，则可以在很大程度上提升解题效率。

如下面这道题发现共边共角型相似三角形后，直接利用等积式，就可以快速地求出AC的长度。

对于解答题，借助结论或已知中的等积式，可以快速地帮助我们锁定相似三角形。

射影定理射影定理是共边共角型相似三角形的变形，其图形特点就是直角三角形及其斜边上的高所组成的三个两两相似的直角三角形，其中也隐含着丰富的线段关系，也可以用等积式来表示。

模型背景我们通常也可以借助射影定理中的等积式，快速求出线段的长度。

善于发现与射影定理相关的基本图形，有助于我们快速建立线段间的比例关系。

四边形背景下的共边三角形四边形背景下，也有比较常见的“共边型”相似三角形，主要分为以下两类：模型背景此类模型的考察题型主要就是利用共边型相似三角形构造线段间的比例关系，此类题目比较灵活，以以下两道题为主。

一线三等角中的共边型三角形模型背景此类模型的特点是“一线三等角模型”的变式，为“异侧”的情况，容易忽略，此类模型常常结合45°角进行综合考察，在平面直角坐标系中考察较多。

解法分析：由题意，已知中∠CPA=45°，同时根据OC=OB=3，可以得到∠CBO=∠OBA=45°，这是另一种一线三等角模型，发现了这三个等角后，则利用▲CPB∽▲ABP，求出BP长度。

同时我们也可以借助这种模型建立线段间的比例关系：解法分析：本题考察了借助“一线三等角模型”以及“X型基本图形”搭建线段间的数量关系。

......九年级（上）第四章图形的相似(1)形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形.(1)相似多边形：如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形．相似多边形对应边长度的比叫做相似比．一．成比例线段（1）线段的比如果选用同一单位量得两条线段a,b的长度分别为m,n，那么就说这两条线段的比是a mb n，或写成a:b m:n．注：在求线段比时，线段单位要统一。

（2）成比例线段在四条线段a,b,c,d中，如果a和b的比等于c和d的比，那么这四条线段a,b,c,d叫做成比例线段，简称比例线段．注：①比例线段是有顺序的，如果说a,b,c,da c 成比例，那么应得比例式为：=．b d②在比例式a c(a：b c：d)中，a、d叫比例外项，b、c叫比例内项,如果b=c，即b da：b b：d那么b叫做a、d的比例中项，此时有b2ad。

③判断给定的四条线段是否成比例的方法：第一排：现将四条线段的长度统一单位，再按大小顺序排列好；第二算:分别算出前两条线的长度之比与后两条线段的长度之比；第三判：若两个比相等，则这四条线段是成比例线段，否则不是（3）比例的性质（注意性质立的条件：分母不能为0）基本性质：①a:b=c:d则有ad=bc（两外项之积等于两内向之积）；②②a:b b:c b2ac．注：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如a d bc，除了可化为a:b c:d，还可化为a:c b:d，c:d a:b，b:d a:c，b:a d:c，c:a d:b，d:c b:a，d:b c:a．a b，(交换内项)c da c d c（2）更比性质(交换比例的内项或外项)：，(交换外项)b d b ad b．(同时交换内外项)c a（3）合、分比性质：（4）等比性质：如果a c a b c d．b d b da c e m(b d f n 0)b d f n，那么a c e m ab d f n b．注：......①此性质的证明运用了“设k法”（即引入新的参数k）这样可以减少未知数的个数，这种方法是有关比例计算变形中一种常用方法．②应用等比性质时，要考虑到分母是否为零．③可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数，再利用等比性质也成立．如：a c e a 2c3e a 2c 3e a；其中b 2d 3f 0b d f b 2d3f b 2d 3f b．（4）比例题常用的方法有：比例合分比法，比例等比法，设参法，连等设k法，消元法二，平行线分线段成比例（1）平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例. 已知AD∥BE∥CF,A DB E可得AAAAAAAAAAAAAAAAAAAA或或或或BBBBBBBBBBBBBBBBBBBB等.C F注意：是所截的线段成比例，而跟平行线无关，所以比例线段中不可能有AD,BE,CF的比例关系（2）黄金分割：把线段AB分成两条线段AC,BC(AC BC)，且使AC是AB和B C的比例中项，即AC2AB BC，叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC 512AB≈0.618AB．即AC BC5 1AB AC2简记为：长短51＝＝全长2注：黄金三角形：顶角是360的等腰三角形。

相似图形的知识点总结（16篇）篇1：相似图形的知识点总结相似图形的知识点总结知识点1.概念把形状相同的图形叫做相似图形。

(即对应角相等、对应边的比也相等的图形)解读：(1)两个图形相似，其中一个图形可以看做由另一个图形放大或缩小得到.(2)全等形可以看成是一种特殊的相似，即不仅形状相同，大小也相同.(3)判断两个图形是否相似，就是看这两个图形是不是形状相同，与其他因素无关.知识点2.比例线段对于四条线段a,b,c,d ，如果其中两条线段的长度的比与另两条线段的长度的比相等，即(或a:b=c:d)那么这四条线段叫做成比例线段，简称比例线段.知识点3.相似多边形的性质相似多边形的性质：相似多边形的对应角相等，对应边的比相等.解读：(1)正确理解相似多边形的定义，明确“对应”关系.(2)明确相似多边形的“对应”来自于书写，且要明确相似比具有顺序性.知识点4.相似三角形的概念对应角相等，对应边之比相等的三角形叫做相似三角形.解读：(1)相似三角形是相似多边形中的一种;(2)应结合相似多边形的性质来理解相似三角形;(3)相似三角形应满足形状一样，但大小可以不同;(4)相似用“∽”表示，读作“相似于”;(5)相似三角形的对应边之比叫做相似比.知识点5.相似三角的判定方法(1)定义：对应角相等，对应边成比例的两个三角形相似;(2)平行于三角形一边的直线截其他两边(或其他两边的延长线)所构成的三角形与原三角形相似.(3)如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似.(4)如果一个三角的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似.(5)如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形相似.(6)直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似.知识点6.相似三角形的性质(1)对应角相等，对应边的比相等;(2)对应高的比，对应中线的比，对应角平分线的比都等于相似比;(3)相似三角形周长之比等于相似比;面积之比等于相似比的平方.(4)射影定理篇2：相似图形相似图形教学交流课教案:第四章相似图形教学目标：1、知道线段比的概念。

共边共角相似三角形及其应用一、基本概念：1.定义：如图，△ABC与△ACD有一条公共边AC和一个公共角∠ A，这样的两个三角形叫做共边共角三角形.这样的两个三角形若又有一个角对应相等，则两个三角形相似，那么这样的两个三角形称为共边共角相似三角形.2.性质定理：共边共角的两个相似三角形的公共边是夹公共角的另一条对应边的比例中项.如图1，在△ABC中，∠ACD=∠B，则△ACD∽△A BC，那么可得：AC2= AD·AB .特别地，当△ABC是直角三角形，且CD⊥AB时(如图2)，AC2 =AD·AB，即为射影定理.二、应用举例：例1.如图3，P为⊙O外一点，PA、PB分别切⊙O于A、B 两点，OP与AB相交于M，C是上一点. 求证：∠OPC=∠OCM .分析：若∠OPC=∠OCM，又∠O=∠O，所以必有△OCM∽△OPC，显然，这一结论只有通过“两边对应成比例，夹角相等”来实现.为此，应当设法证明= ，即OC2= OM·OP.这由OA2= OM·OP, OA= OP 即得.评析：图中△OCM与△OPC 为共边共角相似三角形.例2. 已知⊙C的半径为R，⊙O 过点C，且与⊙C相交于A、B 两点. D为⊙O上一点，弦AB、CD 相交于点E. 求证：CE·CD为定值（云南中考）分析：如图4，由于CE是线段CD的一部分，可构造以C为公共顶点的共边共角三角形.由于⊙C的半径已知为R，所以，只要能与R建立联系，即可得证. 为此，连结AC、AD 由∠ACE是公共角，及∠CAE =∠D，即得△ACE ∽△DCA，从而，CE·CD = R2为定值.评析：图中，△ACE与△D CA 是共边共角相似三角形.例3. 在圆内接四边形ABCD中，BC= CD= 4cm, AC交BD于E，AE=6 cm, 设BE=xcm ,DE = ycm , x、y 均为整数，求x、y 的值（河南省初三数学竞赛试题）解：如图5, 由相交弦定理: x·y = AE·CE = 6CE ,故要求x、y的值，必须先求CE的长. 注意到∠3 =∠1，联想到△CBE与△CAB是共边共角的相似三角形，可得：BC2 = CE·CA∴ 42= CE·（CE + 6），可得CE=2 或CE=－8（舍去），从而，x·y = 6×2 =12 ，∴x=3, y =4 或x=4, y=3 .评析：△CBE与△CAB是共边共角相似三角形例4.已知AC、AB是⊙O 的弦, AB＞AC.⑴如图6, 能否在AB 上确定一点E,使AC2 = AE·AB, 为什么?⑵如图7, 在条件⑴的结论下延长EC到P, 连结PB.如果PB=PE, 试判断PB和⊙O 的位置关系, 并说明理由.⑶在条件⑵的情况下, 如果E 是PD的中点, 那么C是PE的中点吗?为什么?(重庆中考题)分析：⑴观察图6，联想共边共角相似三角形的特征，那么只要AB上的点满足：∠ACE=∠B即可.为此连结并延长CE交⊙O于点C ' （如图6），所以只要=.故，满足题目要求的点E是存在的.作法：在优弧上取=.连CC’ ,交AB于点E,即可. 且AC2 = AE·AB.这里，△ACE与△ACB是共边共角相似三角形⑵由⑴及PB =PE 可得∠3 =∠A，过B⊙O的直径，那么可证PB是⊙O的切线( 如图7);⑶连结BD，即可证明△PBC与△PBD是共边共角的相似三角形，那么PB2 = PC·PD，又PD=2PE, PE=PB, 可得C是PE的中点 .评析：⑴中，△ACE与△ACB是共边共角相似三角形；⑶中，△PBC与△PBD是共边共角相似三角形.参考习题1. 如图8，已知⊙O的内接四边形ABCD，D 是的中点，BC、AD的延长图5线相交于点 E ，DH 切⊙O 于D ，交EB 于点H.⑴ 求证：DH 平分∠CDE ；⑵ 在图中的已知线段中找出两条线段，使它们的积等于DE 2，并加以证明.（平顶山市模拟试题）2.已知如图，在△ABC 中, AB=AC, 过点A的直线与△ABC 的外接圆O 交于D, 与BC 的延长 线交 于 点F , DE 是BD 的延长线,连接CD.求证: ⑴ DF 平分∠EDC; ⑵ AB 2=AD·AF;⑶ AF 2－AB 2=AF·DF .(四川中招)——————备 用 习 题——————1.如图，PA 切⊙O 于A ， 割线PBC 交⊙O 于B 、C 两点，D 为PC 的中点, AD 的延长线交 ⊙O 于E ，又BE 2 =DE·AE ， 求证： ⑴ PA =PD⑵ 2PB 2 = AD ·DE[ 提示: 由切割线定理证PA =2PB , ∴ B 是PD 的中点)2.如图，ΔABC 内接于⊙O ，AB = AC ，直线XY 切⊙O 于点C ，弦BD ∥XY ，AC 、BD 相交于点E ，（1）求证：ΔABE ≌ΔACD ；（2）若AB = 6cm,BC = 4 cm,求AE 的长.（吉林）3. 如图,在⊙O 中, PAB 是经过圆心的割线, PC 切⊙O于C, 若∠PAC = 120°, PA = 2cm,则PC =________cm;解：由PC 是切线，∠PAC = 120°,及AB 是直径 可得： ∠PCA=30°， 从而， AC=PA = 2cm, AB = 4cm , 再由PC 2=PA·PB ， 可得：PC=2 ；评析： 图中△PAC 与△PCB 是共边共角相似三角形 ；4 .如图，PA 为⊙O 的切线，从PA 的中点B 做割线BCD ，交圆于点C 、D ，连结PC 、PD 分别交圆于点E 、F . 求证：∠APD = ∠EFD.(河南省 中考题）（图8）（图9）5.已知如图，A 是⊙O上一点，割线PC交⊙O于B、C两点，PD是PB和PC 的比例中项，PA=PD，连结AD并延长交⊙O于E,求证：BE= CE. (四川）6.如图，已知⊙O1和⊙O2外切于点P，AB是两圆的外公切线，A、B为切点，AP的延长线交⊙O2于D，BP的延长线交⊙O1于C. 求证：⑴ AP·AD= BP·BC；⑵ AB2= AC·BD；⑶ PA·PB = PC·PD.7.如图，已知⊙O1 和⊙O2 外切于点A，直线BC切⊙O1于B，切⊙O2 于C，交O1O2于P.求证：⑴ PA2= PC·PB; ⑵. 若⊙O1与⊙O2的半径分别是方程x2－4x+ 3 = 0的两根，求△ABC的周长及PD的长.。

专题15共边共角相似模型【模型】如图，已知A A ∠=∠,要证ADC ∆∽ABC ∆,只需再知道一组对应角相等（两组对角分别相等的两三角形相似）或AC AB AB AD =（两组对应边成比例且其夹角对应相等的两三角形相似）即可证明ADC ∆∽ABC ∆【例1】如图，在Rt ABC ∆中，CD 是斜边AB 上的高，则图中的相似三角形共有（）A ．1对B ．2对C ．3对D ．4对【答案】C 【分析】根据相似三角形的判定定理及已知即可得到存在的相似三角形．【解析】∵∠ACB ＝90°，CD ⊥AB∴△ABC ∽△ACD ，△ACD ∽△CBD ，△ABC ∽△CBD所以有三对相似三角形，故选：C ．【例2】如图，在ABC 中，点D 在AB 上，请再添一个适当的条件，使ADC ACB △∽△，那么可添加的条件是__________．【答案】ACD ABC ∠=∠（答案不唯一，也可以增加条件：ADC ACB ∠=∠或2AC AD AB = ）．【分析】题目中相似的两个三角形已经有一个公共角，可以再增加一对相等的角，用两组角相等判定两三角形相似，也可以增加两组对应边成比例，利用两组边对应成比例及夹角相等判定两三角形相似．【解析】若增加条件：∠ACD =∠ABC ，∵∠ACD =∠ABC ，且∠A =∠A ，∴ADC ACB V :V ．【例3】定义：如图，若点P 在三角形的一条边上，且满足12∠=∠，则称点P 为这个三角形的“理想点”．(1)如图①，若点D 是ABC 的边AB 的中点，22AC =，4AB =，试判断点D 是不是ABC 的“理想点”，并说明理由；(2)如图②，在Rt ABC 中，90C ∠=︒，5AB =，4AC =，若点D 是ABC 的“理想点”，求CD 的长．【答案】(1)D 为ABC 的理想点,理由见解析(2)125或94【分析】（1）由已知可得AC AB AD AC =，从而ACD ABC ∆∆∽，ACD B ∠=∠，可证点D 是ABC ∆的“理想点”；（2）由D 是ABC ∆的“理想点”，分三种情况：当D 在AB 上时，CD 是AB 边上的高，根据面积法可求CD 长度；当D 在AC 上时，BDC ABC ∆∆∽，对应边成比例即可求CD 长度；D 不可能在BC 上．【解析】（1）解：点D 是ABC ∆的“理想点”，理由如下：D Q 是AB 中点，4AB =，2AD BD ∴==，8AD AB ⋅=，AC =，28AC ∴=，2AC AD AB ∴=⋅，∴AC AB AD AC=，A A ∠=∠ ，ACD ABC ∴∆∆∽，ACD B ∴∠=∠，∴点D 是ABC ∆的“理想点”；（2）①D 在AB 上时，如图：D Q 是ABC ∆的“理想点”，ACD B ∴∠=∠或BCD A ∠=∠，当ACD B ∠=∠时，90ACD BCD ∠+∠=︒ ，90BCD B ∴∠+∠=︒，90CDB ∴∠=︒，即CD 是AB 边上的高，当BCD A ∠=∠时，同理可证90CDB ∠=︒，即CD 是AB 边上的高，在Rt ABC ∆中，90ACB ∠=︒，5AB =，4AC =，3BC ∴，1122ABC S AB CD AC BC ∆=⋅=⋅ ，125CD ∴=，②4AC = ，3BC =，AC BC ∴>有B A ∠>∠，∴“理想点”D 不可能在BC 边上，③D 在AC 边上时，如图：D Q 是ABC ∆的“理想点”，DBC A ∴∠=∠，又C C ∠=∠，BDC ABC ∴∆∆∽，∴CD BC BC AC =，即334CD =，94CD ∴=，综上所述，点D 是ABC ∆的“理想点”，CD 的长为125或94．一、单选题1．如图，点P 是ABC ∆的边AB 上的一点，若添加一个条件，使ABC ∆与CBP ∆相似，则下列所添加的条件错误的是（）A ．BPC ACB∠=∠B ．A BCP ∠=∠C ．::AB BC BC PB =D ．::AC CP AB BC=【答案】D 【分析】在ABC ∆与CBP ∆中，已知有一对公共角∠B ，只需再添加一组对应角相等，或夹已知等角的两组对应边成比例，即可判断正误．【解析】A ．已知∠B=∠B,若BPC ACB ∠=∠，则可以证明两三角形相似，正确，不符合题意；B ．已知∠B=∠B,若A BCP ∠=∠，则可以证明两三角形相似，正确，不符合题意；C ．已知∠B=∠B,若::AB BC BC PB =，则可以证明两三角形相似，正确，不符合题意；D ．若::AC CP AB BC =，但夹的角不是公共等角∠B ，则不能证明两三角形相似，错误，符合题意，故选：D ．2．如图，在△ABC 中，AD ⊥BC ，点D 为垂足，为了证明∠BAC ＝90°，以下添加的等积式中，正确的有（）222•••••AD BD CD AB CD AC AD AC BC CD AB AC BD①＝②＝③＝④＝A ．1个B ．2个C ．3个D ．4个【答案】B 【分析】①由题意得出AD CD BD AD=，证明△ADC ∽△BDA ，可得出∠DAC =∠ABD ，则可证出结论；②不能证明△ABC 与△ADC 相似，得出②不符合题意；证出△ACD ∽△BCA ，由相似三角形的性质得出∠ADC =∠BAC =90°，可得出③符合题意；根据2•AB AC BD =不能证明△ABC 与△ABD 相似，则可得出结论．【解析】解：①∵AD ⊥BC ，∴∠ADC =∠ADB =90°，∵2AD BD CD =∙，∴AD CD BD AD=，∴△ADC ∽△BDA ，∴∠DAC =∠ABD ，∴∠ABD +∠BAD =∠DAC +∠BAD =90°，即∠BAC =90°，故①符合题意；②∵AB •CD =AC •AD ，∴AB AD AC CD=，∴不能证明△ABC 与△ADC 相似；故②不符合题意；③∵2•AC BC CD =，∴AC CD BC AC=，∵∠ACD =∠BCA ，∴△ACD ∽△BCA ，∴∠ADC =∠BAC =90°，故③符合题意；④由2•AB AC BD =不能证明△ABC 与△ABD 相似，故④不符合题意；故选：B ．3．如图，D 是△ABC 的边AB 上一点，要使△ACD ∽△ABC ，则具备的条件可以是（）A ．AC AD CD BC =B ．CD BC AD AB =C ．2CD AD DB =⋅D ．2AC AD AB=⋅【答案】D【分析】根据相似三角形的判定条件逐一判断即可．【解析】解：由题意得∠DAC =∠BAC ，当AC AD CD BC =时，不能证明△ACD ∽△ABC ，故A 选项不符合题意；当CD BC AD AB=时，不能证明△ACD ∽△ABC ，故B 选项不符合题意；当2=CD AD DB ⋅时，不能证明△ACD ∽△ABC ，故C 选项不符合题意；当2=AC AD AB ⋅，即=AC AD AB AC 时，能证明△ACD ∽△ABC ，故D 选项符合题意；故选D ．4．如图，D 是△ABC 的边AB 上一点，下列条件：①∠ACD ＝∠B ；②2AC AD AB =⋅；③BC CD ＝AB AC ；④∠B ＝∠ACB ，其中一定使△ABC ∽△ACD 的有（）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】△ABC 和△ACD 有公共角∠A ，然后根据相似三角形的判定方法对各个条件进行判断，从而得到答案．【解析】∵∠DAC =∠CAB ，∴当∠ACD =∠B 或∠ADC =∠ACB ，可根据有两组角对应相等的两个三角形相似可判断△ACD ∽△ABC ，故①④正确；当2AC AD AB =⋅时，可根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ACD ∽△ABC ，故②正确；当BC CD ＝AB AC时，虽∠DAC =∠CAB 但不是夹角，所以△ACD 与△ABC 不相似，故③不正确．因此有3个正确．故选：C ．5．如图，已知在等腰Rt △ABC 中，∠ACB ＝90°，AD 为BC 边的中线，过点C 作CE ⊥AD 于点E ，交AB 于点F ．若AC ＝2，则线段EF 的长为（）A ．35B ．15C ．15D ．23【答案】B【分析】过点B 作BH ⊥BC ，交CF 的延长线于H ，由勾股定理可求AD 的长，由面积法可求CE ，由“AAS”可证△ACD ≌△CBH ，可得CD ＝BH ＝1，AD ＝CH △ACF ∽△BHF ，可得BH FH AC FC=＝12，可求CF 的长，即可求解．【解析】解：如图，过点B 作BH ⊥BC ，交CF 的延长线于H ，∵AD 为BC 边的中线，AC ＝BC ＝2，∴CD ＝BD ＝1，∴AD ∵11S 22ACD AC CD AD CE =⨯⨯=⨯⨯ ，∴CE，∵∠ADC +∠BCH ＝90°，∠BCH +∠H ＝90°，∴∠ADC ＝∠H ，在△ACD 和△CBH 中，90ADC H ACD CBH AC BC ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩，∴△ACD ≌△CBH （AAS ），∴CD ＝BH ＝1，AD ＝CH ∵AC ⊥BC ，BH ⊥BC ，∴AC ∥BH ，∴△ACF ∽△BHF ，∴BH FH AC FC=＝12，∴CF∴EF ＝CF ﹣CE ＝315，故选：B ．6．如图，在△ABC 中，DE ∥BC ，过点A 作AM ⊥BC 于M ，交DE 于N ，若S △ADE ：S △ABC ＝4：9，则AN ：NM 的值是（）A ．4：9B ．3：2C ．9：4D ．2：1【答案】D 【分析】根据DE BC ∥，可得ADE ABC △△∽，再根据:4:9ADE ABC S S =△△，即可得到相似比23k =，根据相似比即可得到结果．【解析】解：∵DE BC ∥,∴ADE ABC △△∽，∵:4:9ADE ABC S S =△△，∴相似比23k =，∵AM BC ⊥，∴AN DE ⊥，∴相似比23AN k AM ==，∴:2:1AN MN =，故选：D ．7．如图，在ABC 中，点D 在AB 边上，若3AD =，4AB =，6BC =，ADC ACB ∠=∠，则线段CD 的长为（）A ．4B ．5C ．D【答案】C 【分析】根据已知条件可得ADC ACB △∽△，然后根据相似三角形的性质即可解答．【解析】解： ∠ADC ＝∠ACB ，A A ∠=∠，∴ADC ACB △∽△，AD DC AC AC BC AB∴==，∵3AD =，4AB =，6BC =，∴34AC AC =,212AC ∴=，即AC=6DC =，解得DC=故选C ．8．如图，在ABCD 中，60BAD ∠=︒，将ABCD 绕顶点A 逆时针旋转至AEFG Y ，此时点D 在AE 上，连接AC AF CF EB 、、、，线段EB 分别交CD AC 、于点H 、K ，则下列四个结论中：①60CAF ∠=︒；②DEH △是等边三角形；③23AD HK =；④当2AB AD =时，47ACF ABCD S S = △；正确的是（）A ．①②④B ．①③④C ．②③④D ．①②③【答案】A【分析】①由ABCD 绕顶点A 逆时针旋转至AEFG Y ，得到△AEF ≌△ABC ，又由∠BAD ＝60°，即可证明；②由AB CD ，得到∠EDH ＝∠DAB ＝60°，又由AD BC ，得到∠AEF ＝120°，进一步得∠DEH ＝60°，∠DHE ＝60°，结论得证；③过点H 作HM AD 交AB 于点M ，连接DM ，证明△BHC 、△DMH 和△BHM 是等边三角形，得到DH ＝HM ＝BH ＝CH ＝BC ＝AD ，点H 为CD 的中点，再证明△CKH ∽△AKB ，进一步得到AD ＝3HK ；④过点C 作CN ⊥AB 的延长线于点N ，分别用AD 表示出△ACF 和ABCD 的面积，即可得到结论．【解析】解：①∵将ABCD 绕顶点A 逆时针旋转至AEFG Y ，∴△AEF ≌△ABC ，∴∠EAF ＝∠BAC ，∵∠BAD ＝60°，∴∠CAF ＝∠EAF ＋∠CAD ＝∠BAC ＋∠CAD ＝∠BAD ＝60°，故①正确；②∵AB CD ，∴∠EDH ＝∠DAB ＝60°，∵AD BC ，∴∠AEF ＝∠ABC ＝180°－∠BAD ＝120°，∴∠DEH ＝180°－∠AEF ＝60°，∴∠DHE ＝180°－∠EDH －∠DEH ＝60°，∴∠DHE ＝∠EDH ＝∠DEH ＝60°，∴△DEH 是等边三角形，故②正确；③过点H 作HM AD 交AB 于点M ，连接DM ，如图1，∵△EDH 是等边三角形，∴∠BHC ＝∠EHD ＝60°，∵AD BC HM ，∴∠BCH ＝∠EDH ＝60°，∠DHM ＝∠BCH ＝60°，∴∠CBH ＝180°－∠BCH －∠BHC ＝60°，∠BHM ＝180°－∠DHM －∠BCH ＝60°，∴△BHC 是等边三角形，∵HM AD BC ，∴∠DHM ＝∠BCH ＝60°，∠DMH ＝∠BHM ＝60°，∴∠BHC ＝∠BHM ＝∠DHM ＝∠DMH ＝60°，∴△DMH 和△BHM 都是等边三角形，∴DH ＝HM ＝BH ＝CH ＝BC ＝AD ，∴点H 为CD 的中点，∵∠CKH ＝∠AKB ，∠CHK ＝∠ABK ，∴△CKH ∽△AKB ，∴12HK CH CH BK AB CD ===，∴111=233HK BK BH AD ==，∴AD ＝3HK ，∴2AD ＝3HK 错误，故③错误；④过点C 作CN ⊥AB 的延长线于点N ，如图2，则∠BNC ＝90°，∵AB CD ，∴∠DCN ＝180°－∠BNC ＝90°，∵∠BCD ＝60°，∴∠BCN ＝30°，∴BN ＝12BC ＝12AD ，CN ，∴AN ＝AB ＋BN ＝2AD ＋12AD ＝52AD ，∴AC AD ，由①可知，∠CAF ＝＝60°，AC ＝AF ，∴△ACF 是等边三角形，∴等边三角形△ACF AD ，∴217224ACF S AD =⨯⨯=△,∵ABCD 的边AB 上的高＝CN ＝2AD ，∴2=2ABCD S AB CN AD ⨯=⨯= ，∴47ACF ABCD S S = △，故④正确，综上，①②④正确，故选：A ．二、填空题9．如图，在△ABC 中，D 是AB 边上的一点，若∠ACD =∠B ，AD =2，BD =3，则AC 的长为．10【分析】证明△ACD ∽△ABC ，根据相似三角形的性质列出比例式，计算即可．【解析】解：∵AD =2，BD =3，∴AB =AD +BD =2+3=5，∵∠ACD =∠B ，∠A =∠A ，∴△ACD ∽△ABC ，∴AD AC AC AB =，即25AC AC =，解得，AC 10，10．10．如图，ABC A B C '''∽△△，AD 和A D ''分别是ABC 和A B C '''V 的高，若23AD A D ''==，，则ABD △与A B D '''△的周长之比为_____．ABC 与A B C '''V 的面积之比为______．【答案】2∶34∶9【分析】根据相似三角形的性质即可得到答案．【解析】∵AD 和A D ''分别是ABC 和A B C '''V 的高，，ABC A B C '''∽△△，且23AD A D ''==，，∴相似比为2：3，∴ABD △与A B D '''△的周长之比为2：3，∴ABC 与A B C '''V 的面积之比为4：9．故答案为：2∶3；4∶9．11．如图，正方形ABCD 的对角线AC 、BD 交于点O ．点E 在CD 上，且DE ：EC ＝1：3，连接BE 交AC 于点F ，若OF ＝2，则正方形的边长为_______．【答案】7【分析】过点E 作EG ⊥BD 于点G ，根据正方形的性质证明△BOF ∽△BGE ，可得OF BO GE BG =，根据DE ：EC =1：3，设DE =x ，则EC =3x ，可得DC =BC =4x ，列出方程即可求出结果．【解析】解：如图，过点E 作EG ⊥BD 于点G ，∵正方形ABCD 的对角线AC 、BD 交于点O ，∴AC ⊥BD ，∠BDC =45°，∴∠BOF =∠BGE ，∵∠OBF =∠GBE ，∴△BOF ∽△BGE ，∴OF BO GE BG=∵DE：EC=1：3，设DE=x，则EC=3x，∴DC=BC=4x，,,DGD GEB===∴,BD DGBG x=∴-=,ODOB∴===解得4x=7，∴BC=4x=7，∴正方形的边长为7．故答案为：712．如图，已知ABC DEF∽△△，:1:2AB DE=，点M、N分别是BC、EF的中点，则:=AM DN________．【答案】1：2【分析】由于ABC DEF∽△△，得出AB BCDE EF=，∠B=∠E，结合中线的定义得出AB BMDE EN=，则可证明△ABN∽△DEN，然后根据相似三角形的性质，即可得出结果．【解析】解：∵ABC DEF∽△△，∴AB BCDE EF=，∠B=∠E，∵点M、N分别是BC、EF的中点，即12BM BC=，12EN EF=，AB BMDE EN∴=，∴△ABN ∽△DEN ，12AM AB DN DE ∴==，故答案为：1：2．13．如图，在△ABC 中，D ，E 分别是AB ，AC 上的点，AF 平分∠BAC ，交DE 于点G ，交BC 于点F ．若∠AED ＝∠B ，且AG ：GF ＝3：2，则DE ：BC ＝_____．【答案】3:5【分析】先证△ADE ∽△ACB ，再根据GA 、FA 分别是△ADE 、△ABC 的角平分线可得DE BC ＝AG AF，然后再由AG ：FG ＝3：2可得AG ：AF ＝3：5即可解答．【解析】解：∵∠DAE ＝∠CAB ，∠AED ＝∠B ，∴△ADE ∽△ACB ，∵GA 、FA 分别是△ADE 、△ABC 的角平分线，∴DE BC ＝AG AF（相似三角形的对应角平分线的比等于相似比），∵AG ：FG ＝3：2，∴AG ：AF ＝3：5，∴DE ：BC ＝3：5．故答案为3：5．14．将一副三角尺（在Rt △ABC 中，∠ACB ＝90°，∠B ＝60°；在Rt △DEF 中，∠EDF ＝90°，∠E ＝45°）如图①摆放，点D 为AB 的中点，DE 交AC 于点P ，DF 经过点C ．将△DEF 绕点D 顺时针方向旋转角α（0°＜α＜60°），DE ′交AC 于点M ，DF ′交BC 于点N ，则PM CN＝________．3 3【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD＝AD＝BD＝12AB，根据等边对等角求出∠ACD＝∠A，再求出∠ADC＝120°，再根据∠ADE＝∠ADC﹣∠EDF计算得30°，根据同角的余角相等求出∠PDM＝∠CDN，再根据然后求出△BCD是等边三角形，根据等边三角形的性质求出∠BCD＝60°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD＝60°，从而得到∠CPD＝∠BCD，再根据两组角对应相等，两三角形相似判断出△DPM和△DCN相似，再根据相似三角形对应边成比例可得结论．【解析】解：∵∠ACB＝90°，点D为AB的中点，∴CD＝AD＝BD＝12 AB，∴∠ACD＝∠A＝30°，∴∠ADC＝180°﹣30°×2＝120°，∴∠ADE＝∠ADC﹣∠EDF＝120°﹣90°＝30°；∵∠EDF＝90°，∴∠PDM+∠E′DF＝∠CDN+∠E′DF＝90°，∴∠PDM＝∠CDN，∵∠B＝60°，BD＝CD，∴△BCD是等边三角形，∴∠BCD＝60°，∵∠CPD＝∠A+∠ADE＝30°+30°＝60°，∴∠CPD＝∠BCD，∴△DPM∽△DCN，∴PMCN＝PDCD，∵∠ACD＝30°，∠CDP＝90°，∴PDCD＝tan∠ACD＝tan30°33∴PM CN故答案为：3．15．如图，△ABC 中，CE ⊥AB ，BF ⊥AC ，若∠A ＝60°，EF ＝BC ＝_______．【答案】【分析】先判定△AFB ∽△AEC ，进而证明△AEF ∽△ACB ，得到EF AF CB AB=，再证明AB =2AF ，问题即可解决．【解析】解：∵CE ⊥AB ，BF ⊥AC ，∴∠AFB =∠AEC =90°，又∵∠A =∠A ，∴△AFB ∽△AEC ，∴AE AC AF AB =，即AE AF AC AB =，又∵∠A =∠A ，∴△AEF ∽△ACB ，∴EF AF CB AB=，∵BF ⊥AC ，且∠A =60°，∴∠ABF =30°，∴AF =12AB ，∴BC =2EF故答案为：16．如图，在△ABC 中，AB =AC =6．D 是AC 中点，E 是BC 上一点，BE =52，∠AED =∠B ，则CE 的长为_____________．【答案】365【分析】求出∠BAE ＝∠DEC ，证明△ABE ∽△ECD ，推出AB BE EC CD =即可解决问题．【解析】解：∵AB ＝AC ＝6，∴∠B ＝∠C ，∵∠AEC ＝∠B ＋∠BAE ＝∠AED ＋∠DEC ，∠AED ＝∠B ，∴∠BAE ＝∠DEC ，∴△ABE ∽△ECD ，∴AB BE EC CD=，∵CD ＝12AC ＝3，∴5623EC =，解得：365CE =，故答案为：365．三、解答题17．如图，在三角形ABC 中，AB ＝8cm ，BC ＝16cm ，点P 从点A 开始沿边AB 运动，速度为2cm/s ，点Q 从点B 开始沿BC 边运动，速度为4cm/s ，如果点P 、Q 两动点同时运动，何时 QBP 与 ABC 相似？【答案】经过4秒或1.6秒时，△QBC 与△ABC 相似【分析】由题意可得，2824AP t BP t BQ t ==-=，，，根据△QBC 与△ABC 相似，分情况列式计算即可．【解析】解：由题意可得，2824AP t BP t BQ t==-=，，∵∠PBQ =∠ABC ，当BP BQ AB BC =时，BPQ BAC ∽ ，即82816t t -=，解得：4t s =；当BP BQ BC BA =时，BPQ BCA ∽ ，即82168t t -=，解得： 1.6t s =；即经过4秒或1.6秒时，△QBC 与△ABC 相似．18．已知，如图，△ABC 中，AB ＝2，BC ＝4，D 为BC 边上一点，BD ＝1，AD +AC =8．（1）找出图中的一对相似三角形并证明；（2）求AC 长．【答案】（1）△BAD ∽△BCA ，理由见详解；（2）163【分析】（1）由题意易得1=2BD AB AB BC =，然后由∠B 是公共角，问题可证；（2）由（1）可得1=2AD AC ，再由AD +AC =8可求解．【解析】解：（1）△BAD ∽△BCA ，理由如下：AB ＝2，BC ＝4，BD ＝1，∴121,=242BD AB AB BC ==，∴1=2BD AB AB BC =，又 ∠B=∠B ，∴△BAD ∽△BCA ；（2）由（1）得：1=2AD AC ，即2AC AD =，AD +AC =8，∴28AD AD +=，解得：83AD =，∴163AC =．19．如图，在△ABC 中，D 为BC 边上的一点，且AC =，CD ＝4，BD ＝2，求证：△ACD ∽△BCA ．【答案】证明见解析．【分析】根据AC =CD ＝4，BD ＝2，可得AC CD BC AC =，根据∠C =∠C ，即可证明结论．【解析】解：∵AC =CD ＝4，BD ＝2∴AC BC =3CD AC ==∴AC CD BC AC=∵∠C =∠C∴△ACD ∽△BCA ．20．已知：如图，在ABC 中，D 是AC 上一点，联结BD ，且∠ABD =∠ACB ．（1）求证：△ABD ∽△ACB ；（2）若AD=5，AB=7，求AC 的长.【答案】(1)见详解；（2）495【解析】（1）证明：∵∠A=∠A,∠ABD =∠ACB,∴△ABD ∽△ACB.（2）解:∵△ABD ∽△ACB ，∴AB AD AC AB =，∴757AC =，∴495 AC=21．【基础巩固】（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．【尝试应用】（2）如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE ＝∠A．若BF＝4，BE＝3，求AD的长．【答案】（1）见解析；（2）AD=16 3．【分析】（1）证明△ADC∽△ACB，即可得出结论；（2）证明△BFE∽△BCF，得出BF2=BE•BC，求出BC，则可求出AD．【解析】（1）证明：∵∠ACD=∠B，∠A=∠A，∴△ADC∽△ACB，∴AD AC AC AB=，∴AC2=AD•AB．（2）∵四边形ABCD是平行四边形，∴AD=BC，∠A=∠C，又∵∠BFE=∠A，∴∠BFE=∠C，又∵∠FBE=∠CBF，∴△BFE∽△BCF，∴BF BE BC BF=，∴BF2=BE•BC，∴BC=2BFBE=243=163，∴AD=16 3．22．如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，且ADAC＝ACAB．（1）求证△ACD ∽△ABC ；（2）若AD ＝3，BD ＝2，求CD 的长．【答案】（1）见解析；（2【分析】（1）根据相似三角形的判定两边成比例且夹角相等的两个三角形相似，即可得出ACD ABC~ （2）由ACD ABC ~ 得90ADC ACB ∠=∠=︒，ACD B ∠=∠，推出ACD CBD ，由相似三角形的性质得=CD BD AD CD，即可求出CD 的长．【解析】（1）∵AD AC AC AB =，A A ∠=∠，∴ACD ABC ~ ；（2）∵ACD ABC ~ ，∴90ADC ACB ∠=∠=︒，ACD B ∠=∠，∴1809090CDB ACD ∠=︒-︒=︒=∠，∴ACD CBD ，∴=CD BD AD CD，即2326CD AD BD =⋅=⨯=，∴CD =23．如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 的延长线交于点P ，∠COB ＝2∠PCB ．（1）求证：CP 是⊙O 的切线；（2）若M 是弧AB 的中点，CM 交AB 于点N ，若AB ＝6，求MC •MN 的值．【答案】（1）见解析；（2）18【分析】（1）已知C 在圆上，故只需证明OC 与PC 垂直即可，根据圆周角定理，易得∠PCB +∠OCB =90°，即OC ⊥CP 即可；（2）连接MA，MB，由圆周角定理可得∠ABM＝∠BCM，进而可得△MBN∽△MCB，故BM2=MN•MC，根据锐角三角函数求出BM，代入数据可得MN•MC=BM2=18．【解析】（1）证明：∵OA＝OC，∴∠CAO＝∠ACO．又∵∠COB＝2∠CAO，∠COB＝2∠PCB，∴∠CAO＝∠ACO＝∠PCB．又∵AB是⊙O的直径，∴∠ACO+∠OCB＝90°．∴∠PCB+∠OCB＝90°．即OC⊥CP，∵OC是⊙O的半径．∴PC是⊙O的切线；（2）解：连接MA，MB，∵点M是弧AB的中点，∴¼¼AM BM=，∴∠ACM＝∠BCM．∵∠ACM＝∠ABM，∴∠BCM＝∠ABM．∵∠BMN＝∠BMC，∴△MBN∽△MCB．∴BM MN MC BM=，∴BM2＝MN•MC．∵AB是⊙O的直径，¼¼AM BM=，∴∠AMB＝90°，AM＝BM．∴∠ABM=∠BAM=45°，∵AB＝6，∴BM＝AB sin45°=62=∴MN•MC＝BM2＝18．24．如图，在△ABC 中，D 是BC 上的点，E 是AD 上一点，且AB AD AC CE=，∠BAD ＝∠ECA ．（1）求证：AC 2＝BC •CD ；（2）若AD 是△ABC 的中线，求CE AC 的值．【答案】（1）证明见解析；（2）22【分析】（1）首先利用相似三角形的判定得出BAD ACE ∽，得B EAC ∠=∠，进而求出ABC DAC △∽△，再利用相似三角形的性质得出答案即可；（2）由BAD ACE ∽可证CDE CED ∠=∠，进而得出CD CE =，再由（1）可证2AC CD =，由此即可得出线段之间关系．【解析】（1）证明：AB AD AC CE=，BAD ECA ∠=∠，BAD ACE ∴∆∆∽，B EAC ∴∠=∠，ACB DCA ∠=∠ ，ABC DAC ∴△∽△，∴AC BC CD AC=，2AC BC CD ∴= ．（2）解：BAD ACE ∽，BDA AEC ∴∠=∠，CDE CED ∴∠=∠，CD CE ∴=，AD 是△ABC 的中线，22BC BD CD ∴==，222AC BC CD CD ∴== ，即：AC =，∴2CE AC ==．25．（1）如图1，在ABC 中，D 为AB 上一点，2AC AD AB =⋅．求证：ACD B ∠=∠．（2）如图2，在ABCD 中，E 是AB 上一点，连接AC ，EC ．已知4AE =，6AC =，9CD =．求证：23AD EC =．（3）如图3，四边形ABCD 内接于O ，AC 、BD 相交于点E ．已知O 的半径为2，AE CE =，AB =，BD =ABCD 的面积．【答案】（1）见解析；（2）见解析；（3）【分析】（1）由2AC AD AB =⋅化比例，与A A ∠=∠，可证ACD △∽ABC 即可；（2）由ABCD ，可得AB CD =，AD =BC ，根据线段比值计算23AE AC =，23AC AB =，可得AE AC AC AB=，由∠EAC =∠CAB ，可证ACE ∽ABC 即可；（3）连接OA 交BD 于点F ，连接OB ，根据AE CE =，AB =，可得AC =2AE ，根据线段比值计算可得AB AE AC AB=，由∠BAC =∠EAB ，可证ABE △∽ACB △，可证∠ABD =∠ADB ，可得BF =DF ，根据勾股定理OF=1，可求ABD S ABE CBE S S = ，ADE CDE S S = ，可得S △BCD =ABD S ∆即可．【解析】（1）证明：如图1，∵2AC AD AB =⋅，∴AC AD AB AC=，又∵A A ∠=∠，∴ACD △∽ABC ，∴ACD B ∠=∠．（2）证明：如图2，∵ABCD ，∴AB CD =，AD =BC ，∵4AE =，6AC =，9CD =，∴=9AB CD =，∴4263AE AC ==，6293AC AB ==，∴AE AC AC AB=，∵∠EAC =∠CAB ，∴ACE ∽ABC ，∴AE EC AC BC =，即4263EC BC ==，∴23BC EC =．∴23AD EC =；（3）解：如图3，连接OA 交BD 于点F ，连接OB ，∵AE CE =，2AB =，∴AC =2AE ，∴2222AB AC AE ==，222AE AB AE =，∴AB AE AC AB=，∵∠BAC =∠EAB ，∴ABE △∽ACB △，∴ABD ACB ∠=∠，∵∠ADB =∠ACB ，∴∠ABD =∠ADB ，∴点A 是弧BD 的中点，BD 为弦，OA 为半径，∴OA BD ⊥，BF =DF ，∵2OA OB ==，BD =，∴BF =DF =在Rt △OBF 中，根据勾股定理OF 1==，∴1AF OF ==，∴12ABD S BD AF =⨯⨯=△∵AE CE =，∴ABE CBE S S = ，ADE CDE S S = ，∴S △BCD =S △BCE +S △DCE =+ABE CDE ABD S S S ∆= ，∴ABCD =2ABD BCD ABD S S S S ∆∆+==四边形△．26．如图1，四边形ABCD 内接于,O AC 是O 的直径， AD BD=．延长AD 交BC 的延长线于点E ．（1）证明：ACD ECD ∠=∠．（2）当8,5AB CD ==时，①求AD 的长度．②如图2，作BF 平分ABC ∠交O 于点F ，连结,DF AF ，求ADF 的面积．【答案】（1）见详解；（2）①203AD =；②259【分析】（1）由题意易得∠BAD=∠ACD ，由圆内接四边形的外角等于它的内对角得∠ECD=∠BAD ，然后问题可求解；（2）①由（1）及题意易得△CDE ∽△ABE ，则有58CD CE AB AE ==，进而可得54CE DE =，然后设5,4CE x DE x ==，最后根据勾股定理可求解；②连接CF ，过点F 作FH ⊥AE 于点H ，由题意易得∠ABF=∠ACF=∠ADF=45°，由①可得253CE =，203AD =，则有253=AC ，进而可得6AF =，△FHD 是等腰直角三角形，然后设DH=FH=x ，则203AH x =-，由勾股定理可求解x 的值，最后根据三角形面积计算公式可求解．【解析】（1）证明：∵ AD BD=，∴∠BAD=∠ACD ，∵四边形ABCD 内接于O ，∴∠ECD=∠BAD ，∴ACD ECD ∠=∠；（2）解：①由（1）得：ACD ECD ∠=∠，∵AC 是⊙O 的直径，∴∠ADC=∠CDE=90°，∵CD=CD ，∴△ADC ≌△EDC （ASA ），∴AD=DE ，AC=CE ，∵∠E=∠E ，∴△CDE ∽△ABE ，∵8,5AB CD ==，∴58CD CE AB AE ==，∴528CD CE AB DE ==，∴54CE DE =，设5,4CE x DE x ==，在Rt △CDE 中，222CE DE CD =+，∴22251625x x =+，解得：53x =，∴203AD DE ==；②连接CF ，过点F 作FH ⊥AE 于点H ，如图所示：由①得：203AD DE ==，253AC CE ==，∵BF 平分ABC ∠，∠ABC=90°，∴∠ABF=45°，∴∠ACF=∠ADF=45°，∵AC 是是⊙O 的直径，∴∠AFC=90°，∴△AFC 和△FHD 是等腰直角三角形，∴AF=FC ，FH=DH ，∴26AF AC ==，设DH=FH=x ，则203AH x =-，∴在Rt △AHF 中，222203x x ⎛⎫-+= ⎪⎝⎭⎝⎭，解得：12535,66x x ==（不符合题意，舍去）∴56FH =，∴112052522369AFD S AD FH =⋅=⨯⨯= ．27．如图1，在菱形ABCD 中，AC 是对角线，AB ＝AC ＝6，点E 、F 分别是边AB 、BC 上的动点，且满足AE ＝BF ，连接AF 与CE 相交于点G ．（1）求CGF ∠的度数．（2）如图2，作DH CE ⊥交CE 于点H ，若CF ＝4，AF =，求GH 的值．（3）如图3，点O 为线段CE 中点，将线段EO 绕点E 顺时针旋转60°得到线段EM ，当MAC∆构成等腰三角形时，请直接写出AE的长．【答案】（1）60°；（2）7；（3）2或3【分析】（1）根据菱形的性质得到△ABC ，△ACD 是等边三角形，然后根据等边三角形的性质证明△ABF ≌△CAE ，得到∠BAF ＝∠ACE ，从而结合三角形的外角性质求解即可；（2）延长GA 至点K 使得AK ＝CG ，首先结合（1）的结论推出△AFC ∽△CFG ，得到2CF FG AF =⋅，从而求出GF ，AG ，CG ，再证明△ADK ≌△CDG ，推出△DKG 是等边三角形，从而求出DG ，最后根据30°角的直角三角形的性质求解即可；（3）分别根据等腰三角形的定义进行分类讨论，并结合相似三角形的判定与性质以及全等三角形的判定与性质求解即可．【解析】解：（1）∵四边形ABCD 是菱形，AB ＝AC ，∴AB ＝AC ＝BC ＝AD ＝CD ，∴△ABC ，△ACD 是等边三角形．∴∠ABC ＝∠CAE ，在△ABF 与△CAE 中，AB CA ABF CAE BF AE =⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△CAE (SAS )，∴∠BAF ＝∠ACE ，∴∠CGF ＝∠GAC ＋∠ACG ＝∠GAC ＋∠BAF ＝∠BAC ＝60°；（2）如图所示，延长GA 至点K 使得AK ＝CG ．∵∠BAF ＝∠ACE ，∴∠FAC ＝∠GCF ，∵∠GFC ＝∠AFC ，∴△AFC ∽△CFG ，∴FG FC CG FC FA AC==,∵CF ＝4，AF =，AC ＝6，∴GF AG =CG ∵∠FGC ＝60°，∠ADC ＝60°，∴∠AGC ＋∠ADC ＝180°，∴∠GAD ＋∠GCD ＝180°，∵∠KAD ＋∠GAD ＝180°，∴∠KAD ＝∠GCD ，又∵DC =DA ，∴△ADK ≌△CDG （SAS ），∴DK ＝DG ，∠KDA ＝∠GDC ，∴∠KDG ＝∠ADC ＝60°，∴△DKG 是等边三角形，∴∠AGD ＝∠DGH ＝60°，DG ＝KG ＝AK ＋AG ＝AG ＋CG ，∵DH CE ⊥，∠DGH ＝60°，∴12GH DG =；（3）①若AM =MC ，则△MAC 为等腰三角形，此时，取AC 中点为点P ，连接OP ，OM ，BM ，∵∠MEO =60°，EO =EM ，∴△OEM 为等边三角形，∵∠FGC =60°，∴∠MEO =∠FGC ，∴ME ∥AF ，∵O 为CE 的中点，P 为AC 的中点，∴OP 为△AEC 的中位线，OP ∥AB ，∵△ABC为等边三角形，△MAC为等腰三角形，P为AC的中点，∴由“三线合一”知，B、M、P三点共线，且BP⊥AC，AP=PC=12AC=3，∠ABP=12∠ABC=30°，∵△OEM为等边三角形，∴OE=OM，∠OEM=∠OME，∵OE=OC，∴OM=OC，∠OMC=∠OCM，∴∠OEM+∠OCM=∠OME+∠OMC，即：∠OEM+∠OCM=∠EMC，∴∠EMC=90°，CM⊥EM，∴在Rt△CEM中，∠ECM=90°-60°=30°，此时，如图所示，将△AEC绕着C点逆时针旋转60°至△BNC，连接MN，则∠ACE=∠BCN，∠NBC=60°，∵∠ECM=30°，∴∠ACE+∠MCB=30°，∴∠BCN+∠MCB=∠MCN=30°，∴∠MCN=∠MCE=30°，∵CE=CN，∠MCN=∠MCE，CM=CM，∴△MCE≌△MCN，∴∠CMN=∠CME=90°，∴E、M、N三点共线，∴△ECN为等边三角形，∵∠NBC=∠ACB=60°，∴BN∥AC，∵∠BPC=90°，∴∠NBM=90°，∵∠CMN=90°，∴∠BMN+∠CMP=90°，∵∠BMN+∠BNM=90°，∴∠BNM=∠CMP，∴△BMN∽△PCM，∴BM NM PC MC，∵tan tan 30NM MCN MC =∠=︒，∴tan 30BM PC =︒=，∵PC =3，∴BM 在Rt △ABP 中，AP =3，∠ABP =30°，∴BP =∴PM =BP -BM =∵∠MBC =30°，∠OMC =90°-∠OME =30°，∴∠MBC +∠MCB =∠OMC +∠OMP ，∴∠MCB =∠OMP ，∵OP ∥AB ，∴∠OPC =∠BAC =60°，∴∠OPM =90°-60°=30°，∴△OPM ∽△MBC ，∴OP PM MB BC=，6=，∴OP =1，∵OP 为△AEC 的中位线，∴AE =2OP =2；②若AM =AC ，则△AMC 为等腰三角形，如图所示，取AC 中点P ，连接OP ，延长AO 交MC 于Q 点，由①可知，△EMC 始终为直角三角形，∠EMC =90°，∠ECM =30°，且EM 与AF 始终平行，∴∠EMC =∠AQC =90°，AQ ⊥MC 于Q 点，∵OM =OC ，∴O 点在AQ 上，∵∠COQ =60°，∠CGF =60°，∴此时O 点和G 点重合，∵∠CPO =∠CAB =60°，∠COQ =60°，∴∠APO =∠AOC =120°，∴△APO ∽△AOC ，∴AP AO OP AO AC CO==，∵AC =6，AP =3，∴23618AO AP AC ==⨯= ，∴AO=∵Rt △OCQ 中，∠OCQ =30°，∴设OQ =x ，则CQ，在Rt △CAQ 中，222CQ AQ AC +=，即：)()2226x +=，解得：4x -+=或4x --=（不合题意，舍去），∴4OQ -+=，22CO OQ -==，∴由AO OP AC CO =得：6=解得：32OP =，∵OP 是△AEC 的中位线，∴AE =2OP=3；③若AC =MC ，则E 点在AB 的延长线上，此时与E 点在边AB 上运动矛盾，故该种情况舍去；综上，AE ＝2或353．28．在Rt △ABC 中，∠ACB =90°，点D 为AB 上一点．（1）如图1，若CD ⊥AB ，求证：AC 2=AD ·AB ；（2）如图2，若AC =BC ，EF ⊥CD 交CD 于H ，交AC 于F ，且49FH HE =，求AD BD的值；（3）如图3，若AC =BC ，点H 在CD 上，∠AHD =45°，CH =3DH ，则tan ∠ACH 的值为________．【答案】（1）见解析；（2）23；（377【分析】（1）证出B ACD ∠=∠，证明CBD ∽ACD △，得出=CD BD AD CD ，即可得出结论；（2）设4FH a =，则9HE a =（0a >），同（1）得2236CH HE FH a =⋅=，则6CH a =，在Rt CHF V 中，2tan 3FH ACD CH ∠==，过D 作DP AC ⊥于P ，易证AP DP =，求出23AP DP PC PC ==，再由平行线分线段成比例定理即可得出答案；（3）过点D 作DM AH ⊥于M ，设2DH x =，则6CH x =（0x >），8CD DH CH x =+=，证明ADH ∽CDA ，得出DAH ACH ∠=∠，AD DH CD AD =，求出4AD x =，证明HDM △是等腰直角三角形，得出222DM HM DH x ===，由勾股定理得出14AM =，由三角函数定义即可得出答案．【解析】（1）证明：∵CD AB ⊥，∴90ADC CDB ∠=∠=︒，∵90ACB ∠=︒，∴90B BCD ACD BCD ∠+∠=∠+∠=︒，∴B ACD ∠=∠，∴CBD ∽ACD △，∴=CD BD AD CD，∴2CD AD DB =⋅；（2）解：∵49FH HE =，∴设4FH a =，则9HE a =（0a >），∵90ACB ∠=︒，EF CD ⊥，同（1）得：229436CH HE FH a a a =⋅=⨯=，∴6CH a =，在Rt CHF V 中，42tan 63FH a ACD CH a ∠===，过D 作DP AC ⊥于P ，如图2所示：则//DP BC ，在Rt DPC 中，2tan 3DP ACD PC ∠==，∵AC BC =，90ACB ∠=︒，∴45A ∠=︒，∴ADP △是等腰直角三角形，∴AP DP =，∴23AP DP PC PC ==，∵//DP BC ，∴23AD AP BD PC ==；（3）解：过点D 作DM AH ⊥于M ，如图3所示：∵3CH DH =，∴设2DH x =，则6CH x =（0x >），∴8CD DH CH x =+=，∵AC BC =，90ACB ∠=︒，∴45BAC ∠=︒，∴=45BAC AHD ∠=∠︒又∵ADH CDA ∠=∠，∴ADH ∽CDA ，∴DAH ACH ∠=∠，AD DH CD AD=，∴2216AD DH CD x =⋅=，∴4AD x =，∵DM AH ⊥，∴90DMH ∠=︒，∵45AHD ∠=︒，∴45HDM AHD ∠=︒=∠，∴HDM △是等腰直角三角形，∴222DM HM DH ===，∴()()22254214AM AD DM x x x =--，∴27tan tan 714DM ACH DAH AM x ∠=∠==；77．29．如图，在Rt △ABC 中，∠C=90°，AC=4cm ，BC=3cm ．动点M ，N 从点C 同时出发，均以每秒1cm 的速度分别沿CA 、CB 向终点A ，B 移动，同时动点P 从点B 出发，以每秒2cm 的速度沿BA 向终点A 移动，连接PM ，PN ，设移动时间为t （单位：秒，0＜t ＜2.5）．（1）当t 为何值时，以A ，P ，M 为顶点的三角形与△ABC 相似？（2）是否存在某一时刻t ，使四边形APNC 的面积S 有最小值？若存在，求S 的最小值；若不存在，请说明理由．【答案】（1）32；（2）当32t =时，四边形APNC 的面积S 有最小值，其最小值是215．【分析】根据勾股定理求得AB=5cm ．（1）分△AMP ∽△ABC 和△APM ∽△ABC 两种情况讨论：利用相似三角形的对应边成比例来求t 的值．（2）如图，过点P 作PH ⊥BC 于点H ，构造平行线PH ∥AC ，由平行线分线段成比例求得以t 表示的PH 的值；然后根据“S=S △ABC ﹣S △BPH ”列出S 与t 的关系式()24321S=0 2.5525t t ⎛⎫-+<< ⎪⎝⎭，则由二次函数最值的求法即可得到S 的最小值．【解析】解：∵如图，在Rt △ABC 中，∠C=90°，AC=4cm ，BC=3cm ．∴根据勾股定理，得22AB AC BC 5cm =+=．（1）以A ，P ，M 为顶点的三角形与△ABC 相似，分两种情况：①当△AMP ∽△ABC 时，AP AM AC AB =，即52445t t --=，解得32t =；②当△APM ∽△ABC 时，AM AP AC AB =，即45245t t --=，解得t=0（不合题意，舍去）．综上所述，当32t =时，以A 、P 、M 为顶点的三角形与△ABC 相似．（2）存在某一时刻t ，使四边形APNC 的面积S 有最小值．理由如下：假设存在某一时刻t ，使四边形APNC 的面积S 有最小值．如图，过点P 作PH ⊥BC 于点H ．则PH ∥AC ，∴PH BP AC BA =，即245PH t =．∴85t PH =．∴ABC BPNS S S =-△△()118343225t t =⨯⨯-⨯-⋅()24321=0 2.5525t t ⎛⎫-+<< ⎪⎝⎭．∵405>，∴S 有最小值．当32t =时，S 最小值=215．答：当32t =时，四边形APNC 的面积S 有最小值，其最小值是215．30．我们定义：对角线垂直的凸四边形叫做“准筝形”．如图1，四边形ABCD 中，AC ⊥BD ，则四边形ABCD 是“准筝形”．（1）“三条边相等的准筝形是菱形”是命题；（填“真”或“假”）（2）如图1，在准筝形ABCD 中，AD ＝3，AB ＝2，BC ＝4，求CD 的长．（3）如图2，在准筝形ABCD 中，AC 与BD 交于点O ，点P 在线段AD 上，AP ＝2，且AD ＝3，AO =32，在BD 上存在移动的线段EF ，E 在F 的左侧，且EF ＝1，使四边形AEFP 周长最小，求此时OE 的长度．【答案】（1）真；（2（3）34【分析】（1）先根据在准筝形ABCD 中，AC ⊥BD ，BC=CD=AD ，设AC 与BD 交于点O ，得出OA=OC ，OB=OD ，推出四边形ABCD 是平行四边形，再根据AD=CD ，即可证明四边形ABCD 是菱形，即可得出结论；（2）设AC 与BD 交于点O ，根据AC ⊥BD ，得到AB 2=AO 2+BO 2，AD 2=AO 2+DO 2，CD 2=CO 2+DO 2，BC 2=OB 2+OC 2，可得AB 2+CD 2=AD 2+BC 2=OA 2+OB 2+OC 2+OD 2，根据AD=3，АВ=2，BC=4，即可求出CD ；（3）过P 作PG ⊥AO 于G ，过A 作AM//EF 且AM=EF ，作M 点关于OD 的对称点N ，连接MN 交OD 于H ，交PG 于R ，连接PN 交OD 于F ，先证明四边形AEFM 是平行四边形，得到AE=MF ，根据M 、N 关于OD 对称，得出MF=NF ，推出当且仅当N 、F 、P 三点共线时，AE+PF 取得最小值，根据AP=2，EF=1，得出当AE+PE 取得最小值时，四边形AEFP 周长取得最小值，然后证明四边形AOHM 是矩形，得出АМ=ОН=EF=1，OA=MН=HN=32，根据在Rt △AOD 中，OA=32，AD=3，PG ⊥OA ，求出AG=12AP=1，，RN=HN+HR=2，证明△NHF ∽△NRP ，得出HFRP =NH NR =34，求出HF=34PR=)314=34，根据OF=ОН+HF=OE+EF ，ОН=EF=1，即可得出OЕ．【解析】解：（1）三条边相等的准筝形是菱形是真命题，，在准筝形ABCD 中，AC ⊥BD ，BC=CD=AD ，设AC 与BD 交于点O ，∴OA=OC，OB=OD，∴四边形ABCD是平行四边形，∵AD=CD，∴四边形ABCD是菱形，∴三边相等的准筝形是菱形，故答案为：真；（2）设AC与BD交于点O，∵AC⊥BD，∴AB2=AO2+BO2，AD2=AO2+DO2，CD2=CO2+DO2，BC2=OB2+OC2，∴AB2+CD2=AD2+BC2=OA2+OB2+OC2+OD2，∵AD=3，АВ=2，BC=4，∴22+CD2=32+42，∴∴CD；（3）过P作PG⊥AO于G，过A作AM//EF且AM=EF，作M点关于OD的对称点N，连接MN交OD于H，交PG于R，连接PN交OD于F，∵AM//EF，AM=EF，∴四边形AEFM是平行四边形，∴AE=MF，∵M、N关于OD对称，∴MF=NF，∴AE+PF=MF+PF=NF+PF≥PN，∴当且仅当N、F、P三点共线时，AE+PF取得最小值，∵AP=2，EF=1，∴当AE+PE取得最小值时，四边形AEFP周长取得最小值，∵AM//OD，ОA//MН，∠AOD=90°，∴四边形AOHM是矩形，∴АМ=ОН=EF=1，OA=MН=HN=3 2，在Rt△AOD中，OA=32，AD=3，∴∠ADO=30°，∵PG⊥OA，∴PG∥OD，∴∠APG=∠ADO=30°，∴AG=12AP=1，33∴3，∵HR=32-1=12，∴RN=HN+HR=2，∵PG//OD，∴△NHF∽△NRP，∴HFRP=NHNR=34，∴HF=34PR=)314∵OF=ОН+HF=OE+EF，ОН=EF=1，∴故四边形AEFP周长最小时，OE的长度为3 4．。

第4课时 共边相似三角形【知识概述】1.对于有公共边的两个相似三角形，如果相似比不为1，则公共边必定是相似三角形某两条对应边的比例中项，所谓“共边相似型，比例中项明”.在共边相似型中最常见的是共边斜A 相似型（如图），这是一种特殊的斜A 相似型，其实不仅共边而且共角，所以这种模型又称作为共边共角相似型”或“母子型相似”，由△ACD ∽△ABC ，易得2AC AD AB =，2ADk AB= （k 为△ACD 与△ABC 的相似比）.2. 共边斜A 相似型特例(1) 射影定理，又叫欧几里德定理：直角三角形中，斜边上的高线是两条直角边在斜边上的射影的比例中项，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.如图，CD 是Rt △ABC 斜边上的高，则有AC 2=AD ·AB ， BC 2=BD ·BA ， DC 2=DA ·DB .由于直角三角形斜边上的高线把这个直角三角形分割成的两个直角三角形与原直角三角形相似，所以由直角三角形和斜边上的高线组成的图形又叫做母子三角形，显然母子三角形有三对共边相似型。

注：射影定理不是现有教材的内容，在证题时请谨慎使用！ (2) 等腰三角形中的共边斜A 相似型图1与图2中各有三对相似三角形，两对共边斜A 相似型，进一步可以研究边与边、角与角之间的关系. 共边斜A 相似型母子三角形∠D=∠CAE ，∠ABC=∠△ACB ，BAD ∽△AED ∽△CEA∠DAE=∠B=∠△C ，BEA ∽△AED ∽△CAD 图2图1等腰三角形中的共边相似模型B【例题精选】例1 如图，△ABC 中，AB ＝AC ，AD 是中线，P 是AD 上一点，过C 作CF ∥AB ，延长BP 交AC 于E ，交CF 于F ．求证：2BP PE PF =⋅．思路点拨：连结PC ，由等腰三角形的轴对称性易发现PB ＝PC ，从而只要证明PC 2＝PE ·PF ，再证△EPC ∽△CPF ．例2 如图，∠ACB =∠ADC =90°，AC ，AD =2．问当AB 的长为多少时，图中两个直角三角形相似．例3 如图，点C ，D 在线段AB 上，△PCD 为等边三角形，∠APB =120°.（1）找出图中所有的相似三角形；（2）求证：CD 2=AC ·BD ．(例1)(例2)(例3)A【配套练习】1．如图，在△ABC 中，∠BAC ＝90°，D 是BC 中点，AE ⊥AD 交CB 延长线于点E ，则△BAE ∽△______．2. 如图，在△ABC 中，AB ＝AC ＝2，∠BAC ＝20°，点P 、Q 分别在线段CB 、BC 的延长线上，且满足 ∠P AQ ＝100°.设BP ＝x ，CQ ＝y ，则y 与x 之间的函数关系式为____________________.3．如图，△ABC 中，点E 在中线AD 上，∠DEB =∠ABC ． 求证：（1）2•DB DE DA = ；（2）DCE DAC ∠=∠ ．4．如图，ABC △为等边三角形，点,M N 分别在,BC AC 上，且BM CN =，AM 与BN 交于Q 点．求证：（1）2MB MQ MA =⋅；（2）2NA NQ NB =⋅．(第2题)(第1题)(第3题)Q ABCN M(第4题)5. 如图，AD 是△ABC 的角平分线，AD 的垂直平分线EF 分别交AD 于点E ，交BC 的延长线于点F ． 求证：2FD FB FC ＝.6．如图，CD 是Rt △ABC 斜边上的高线. （1）求证：222111DCBC AC =+； （2）若AC =3，BC =4，求CD 和AD 的长； （3）若AD =2，BD =3，求CD 的长.7．如图，CD 是Rt △ABC 斜边上的高线，F 为BC 上一点，CG ⊥AF 于点G ，连结DG . 求证：△ADG ∽△AFB .(第5题)(第6题)(第7题)8. 如图，在△ABC 中，∠ABC =60°，∠APB =∠BPC =120°，P A =3，PB =4. 求PC 的长.9. 如图，在△ABC 中，AB =AC =12，BC =6，点D 在边AB 上，点E 在线段CD 上，且∠BEC =∠ACB ，BE 的延长线与边AC 相交于点F ． （1）求证：BE •CD=BD •BC .（2）设AD =x ，CF =y ，求y 关于x 的函数解析式,并写出自变量x 的取值范围.10.如图，在ABC △中，90BAC ∠=︒，1AB AC ==，E F ，分别是BC 上两点，点E 在BF 上，45EAF ∠=︒，令BF =x ，CE =y ，求y 关于x 的函数关系式,及自变量x 的取值范围．(第8题)(第9题)ABCEF(第10题)例1第4课时 共边相似三角形参考答案例1 连结PC ．∵AB ＝AC ，AD 是中线，∴直线AD 是△ABC 的对称轴．∴PC ＝PB ，∠PCE ＝∠ABP ．∵CF ∥AB ，∴∠PFC ＝∠ABP ． ∴∠PCE ＝∠PFC ．又∵∠CPE ＝∠EPC ，∴△EPC ∽△CPF ． ∴PC PF ＝PEPC．即PC 2＝PE ·PF ．∴BP 2＝PE ·PF ．例2 ∵∠ADC =90°，AC=6，AD =2，∴CD =AC 2－AD 2=2．要使这两个直角三角形相似，有两种情况：(1) 当AC AD ＝AB AC 时，有Rt △ABC ∽Rt △ACD ，即AB ＝AC 2AD ＝3；(2) 当AC CD ＝AB AC 时，有Rt △ACB ∽Rt △CDA ，即AB ＝AC 2CD ＝32．故当AB 的长为3或32时，图中两个直角三角形相似．例3 (1) ∵△PCD 为等边三角形，∴∠PCD =60°，∴∠PCA =120°，∵∠APB =120°，∴∠PCA =∠APB ，又∵∠A =∠A ，∴△ACP ∽△APB ，同理△PDB ∽△APB ，∴△ACP ∽△APB ∽△PDB ．(2) ∵△ACP ∽△PDB ，∴AC CP ＝PDBD ，∴PD CP AC BD ⋅=⋅，∵CD C PD P ==，∴CD 2=AC ·BD ．【练习】1． ACE 2．y =4x3．(1)在△BDE 和△DAB 中，∵∠DEB =∠ABC ，∠BDE =∠ADB ，∴△BDE ∽△ADB ， ∴DE DB ＝DBDA，∴DB 2=DE •DA ．(2)∵AD 是中线，∴DC =DB ，∴DC 2=DE •DA ，∴DE DC ＝DCDA，又∠ADC =∠CDE ，∴△DEC ∽△DCA ，∴∠DCE =∠DAC ．4．(1)∵ABC △为等边三角形，∴AB BC =，60ABC C ∠=∠=︒．∵BM CN =，∴ABM BCN △≌△ (SAS )．∴BAM CBN ∠=∠，又∵BMA BMQ ∠=∠，∴ABM BQM △∽△，∴MB MA ＝MQMB，2MB MQ MA =⋅．(2) ∵ABC △为等边三角形，∴BAC ABC ∠=∠，由(1) 知BAM CBN ∠=∠，∴BAC BAM ABC CBN ∠-∠=∠-∠，即QAN NBA ∠=∠，类同(1) 可以证明2NA=5．连结AF ，∵AD 是角平分线，∴∠BAD =∠CAD ，又EF 为AD 的垂直平分线，∴AF =FD ，∠DAF =∠ADF ，∴∠DAC +∠CAF =∠B +∠BAD ，∴∠CAF =∠B ，∵∠AFC =∠AFC ，∴△ACF ∽△BAF ，∴FC AF ＝AF FB，∴2·AF FB FC ＝，即2·FD FB FC ＝． 6．(1) ∵CD 是RT △ABC 斜边上的高，∴AC BC CD AB ⋅=⋅ ，∴222222222211+1=AC BC AB AC BC AC BC AB DC DC +==⋅⋅； (2) ∵CD 是RT △ABC 斜边上的高，∴AB =AC 2＋BC 2=32＋42=5，2=AC AD AB ⋅ ，∴CD ＝AC ×BC AB ＝3×45＝125， AD =AC 2AB ＝325＝95；(3) ∵CD 是RT △ABC 斜边上的高，∴2=DC DA DB ⋅∴CD ．7．∵CD 是RT △ABC 斜边上的高，CG ⊥AF ，∴2==AC AD AB AG AF ⋅⋅，∴AD AF ＝AGAB ，又∵GAD BAF ∠=∠，∴△ADG ～△AFB ．8．∵∠APB =∠BPC =120°，设∠PBC =α，∠ABC =60°，则∠ABP =60°-α，∴∠BAP =∠PBC =α，∴△ABP ∽△BCP ，∴P A PB ＝PB PC ，PC=PB 2P A ＝423＝163． 9．(1) ∵AB =AC ，∴∠ABC =∠ACB ，∵∠BEC =∠ACB ，∴∠BEC =∠ABC ．又∵∠BCE =∠DCB ，∴△CBE ∽△CDB ．∴CB CD ＝BEDB，即BE •CD =BD •BC ． (2) ∵△CBE ∽△CDB ，∴∠CBE =∠CDB ．又∵∠FCB =∠CBD ．∴△FCB ∽△CBD ．∴FC CB ＝CBBD，而BD =AB -AD =12-x ，6612y x =-，3612y x =-，∵361212y x=≤-，∴9x ≤，∴自变量的取值范围为09x <≤． 10．∵∠BAC =90°，AB =AC ，∴∠B =∠C =45°，∵∠EAF =45°，∴∠EAF =∠C ，∠EF A =∠F AC +∠C =∠F AC +∠EAF =∠EAC ，∴△BAF ∽△CEA ，∴AB CE =，∴1y=，∴1y x =≤．练5。

《相似三角形》知识点归纳知识点1有关相似形的概念(1) 形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形 •(2) 如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比 (相似系数).知识点2比例线段的相关概念、比例的性质 (1)定义: 在四条线段a,b, c,d 中，如果a 和b 的比等于e 和d 的比，那么这四条线段 a,b,c,d 叫做成比例线段，简称比例线段.注：①比例线段是有顺序的，如果说 a 是b,c,d 的第四比例项，那么应得比例式为:注：①黄金三角形：顶角是 360的等腰三角形②黄金矩形：宽与长的比等于黄金数的矩形a -，(交换内项)c d②a c b d d c，(交换外项) 核心内容：ad bcb a'd -.(同时交换内外项) (2)黄金分割：把线段AB 分成两条线段 AC,BC(AC BC),且使AC 是AB 和BC 的比例中项, 即AC 2 AB BC ，叫做把线段 AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中 AC 也」AB 〜0.618 AB •即 2 AC AB BC E 1 AC 2 简记为: 长-短-V5 1全—长—2a c abed(3)合、分比性质：注：实际上，比例的合比性质可扩展为: 比例式中等号左右两个比的前项，后项之间b a d c发生同样和差变化比例仍成立•如：a c a c等等•b d a bc da b c d(4)等比性质：如果 a c e m(b d f n 0),b d f n那么a c e m ab d f n b知识点3比例线段的有关定理平行线分线段成比例定理：三条平行线截两条直线,所截得的对应线段成比例已知AD//BE// CF,可得JAB些或AB BC EFAC特别在三角形中：DF AB由DE// BC可得：如圧或BDDB EC AD EF DEEC EA知识点4相似三角形的概念匹巨或便BC等.(1)定义：对应角相等，对应边成比例的三角形，叫做相似三角形•相似用符号“S”表示，读作“相似于” 似系数)•相似三角形对应角相等，对应边成比例.•相似三角形对应边的比叫做相似比(或相注：①对应性：即把表示对应顶点的字母写在对应位置上②顺序性：相似三角形的相似比是有顺序的.③两个三角形形状一样，但大小不一定一样.④全等三角形是相似比为1的相似三角形.用轴语言表港是r 石6三角形全等 三角形相似两角夹一边对应相等(ASA)两角对应相等 两角一对边对应相等(AAS)两边对应成比例，且夹角相等 两边及夹角对应相等(SAS)三边对应成比例 三边对应相等(SSS)、(HL ) “ HL ”知识点5 相似三角形的性质相似三角形对应角相等，对应边成比例. 相似三角形周长的比等于相似比. 相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比. 相似三角形面积的比等于相似比的平方. 相似三角形的几种基本图形：称为“平行线型”的相似三角形(有“ A 型”与“ X 型”图)(2)三角形相似的判定方法 1、 平行法： 2、 判定定理 3、 判定定理 4、 判定定理 5、 判定定理 全等与相似的比较： (或两边的延长线)相交，所构成的三角形与原三角形相似 两角对应相等，两三角形相似. AA 两边对应成比例且夹角相等，两三角形相似 .SAS 三边对应成比例，两三角形相似 .SSS “HL ” (图上)平行于三角形一边的直线和其它两边 1 2 3 4 简述为： 简述为： 简述为： 直角三角形中, 则S ==> AD 2 =BD- DCS ==> AB 2 =BD- BC S ==> AC 2 =CD- BC⑴⑵⑶⑷知识点6(1)如图: / BAC=90°, AD 是斜边 BC 上的高, (3)射影定理： 如图，Rt △ ABC 中,则厶ADE^A ABC称为“斜交型”的相似三角形。

相似三角形几何模型（手拉手与十字架模型）第一部分【知识点归纳】【模型一】“手拉手（旋转）”模型图1 图222ADE ABC ABC ACF ADE ∆ ∆∆  →A 绕点旋转如图：∽如图：∽ 以上就是相似三角形中的“手拉手模型”在复杂的图形中可以由这一线索寻找新的相似形，即一转成双，由一得二（由一对相似三角形得第二对相似三角形）。

【模型二】“十字架”模型图3 图41EG AB HF BC⊥==如图3：正方形ABCD 中，EG HF,则有；EG AB HF BC ⊥=如图4：矩形ABCD 中，EG HF,则有. 以上就是矩形中的十字架模型，即矩形中两条互相垂直的线段之比等于矩形的两邻边之比。

第二部分【题型展示与方法点拨】【题型1】三角形中的的“手拉手（旋转）模型”【例1】（23-24九年级上·山西大同·期末）综合与实践-问题情境：如图1，已知在ABC 中，D E ，分别是AB AC ，上的点，且DE BC ∥．（1）操作发现：求证：AB DB =．（2）深入探究：在图1的基础上，将ADE 绕着点A 逆时针旋转一个角度得到图2，连接BD CE ，，那么（1）中的结论是否仍然成立？请判断并说明理由．拓展探究：（3）如图3，当ADE 旋转到点B D E ，，在一条直线上时，BE 与AC 交于点F ，若7BF =，9BE =，求AF CF ⋅的值．【答案】(1)见解析 (2)成立，理由见解析 (3)14【分析】本题主要考查相似三角形的判定和性质，平行线分线段成比例的综合运用，掌握相似三角形的判定是解题的关键．（1）根据平行线的性质可证ADE ABC △△∽，由此即可求解；（2）根据旋转的性质可证ABD ACE ∽，由此即可求解；（3）根据题意可得ABD ACE ∽，ABF ECF ∽△△，根据相似三角形的性质即可求解．（1）证明：∵DE BC ∥，∴ADE ABC △△∽， ∴AD AE AB AC=， ∴AB DB AC EC AB AC −−=，即DB EC AB AC =， ∴AB DB AC EC=． （2）解：成立，理由如下：由旋转的性质得BAC DAE ∠=∠， ∴BAC DAC DAE DAC ∠−∠=∠−∠，即BAD CAE ∠=∠， 由（1）得AD AE AB AC=， ∴ABD ACE ∽， ∴AB DB AC EC=， ∴（1）中的结论仍成立．（3）解：由（2）得ABD ACE ∽，∴ABD ACE ∠=∠， ∵AFB EFC ∠=∠， ∴ABF ECF ∽△△， ∴BF AF CF EF=， ∴BF EF CF AF ⋅=⋅，∵7BF =，9BE =，∴2EF BE BF =−=，∴7214AF CF ⋅=×=．【变式1】（23-24九年级上·山西晋中·期中）如图，一副三角板（90C E ∠=∠=°，30B ∠=°，45D ∠=°），AD BC =，顶点A 重合，将ADE 绕其顶点A 旋转，在旋转过程中（不添加辅助线），以下4种位置不存在相似三角形的是（ ）A ．B ．C ．D ．【答案】D【分析】本题考查了相似三角形的判定和性质，直角三角形的性质，利用相似三角形的判定方法依次判断是解决问题的关键．解：选项A ，∵90C C ∠=∠=°，30CAF B ∠=∠=°，∴ACF BCA ∽△△，故选项A 不符合题意．选项B ，如图，设CD 与AE 交于点O ，90ACO DEO ∠=∠=°∴ACO DEO △∽△，故选项B 不合题意；选项C ，∵90BCA AED ∠=∠=°，CAF DAE ∠=∠， ∴ACF AED △∽△，故选项C 不合题意；选项D 中没有相似三角形，符合题意．故选：D ．【变式2】（22-23九年级·上海·假期作业）在ABC 中，CA CB =，在AED △中，DA DE =，点D 、E 分别在CA 、AB 上．（1）如图1，若90ACB ADE ∠=∠=°，则CD 与BE 的数量关系是 ； （2）若120ACB ADE ∠=∠=°，将AED △绕点A 旋转至如图2所示的位置，则CD 与BE 的数量关系是 ．【答案】CD = CD 【分析】（1）利用平行线分线段成比例定理计算即可．（２）过点C 作CH AB ⊥交AB 于点H ，求得AC AB ，再证明ACD ABE ∆∆∽列式计算即可． 解：（1）90ACB ADE ∠=∠=° ∴DE BC ∥，∴AD DC AE EB ==，∴CD =．故答案为：CD =． （2）过点C 作CH AB ⊥交AB 于点H ，120ACB ∠=° ，30CAB ∴∠=° ，∴CA AH =，∴AC AB = 由ADE ACB ∽， 得：AD AC AE AB=， DAE CAB ∠=∠ ，∴ACD ABE △∽△，∴CDAC BE AB ==，∴CD =．故答案为：CD ． 【点拨】本题考查旋转的相关知识，等腰三角形的相关知识，三角形相似的判定和性质，直角三角形的性质，熟练掌握三角形相似的判定和性质，直角三角形的性质是解题的关键．【题型2】四边形中的的“手拉手（旋转）模型”【例2】（23-24九年级上·浙江杭州·期末）如图，四边形ABCD 与四边形BEFG 都是正方形，将正方形BEFG 绕点B 按顺时针方向旋转，连接AG ，DF ，CE ．则AG 和CE 的数量关系为 ；在正方形BEFG 绕点B 按顺时针方向旋转的过程中，DF CE的值为 ．【答案】 AE CE =【分析】此题考查了正方形的性质，相似三角形的判定和性质，全等三角形的判定和性质等知识，根据SAS证明ABG CBE ≌△△，即可证明AE CE =；连接BD BF ，．由1245∠+∠=°，2345∠+∠°得到13∠=∠．在Rt DBC △中，BD BC =在Rt FBE中，BF BE，则BD BF BC BE =，则BDF BCE ∽△△，即可得到结论．熟练掌握相似三角形的判定和性质、全等三角形的判定和性质是解题的关键．解：∵四边形ABCD 与四边形BEFG 都是正方形，∴90ABC GBE ∠=∠=°，AB BC =，BG BE =， ∴ABC GBC GBE GBC ∠−∠=∠−∠，即ABG CBE ∠=∠． 在ABG 和CBE △中，AB BC ABG CBE BG BE = ∠=∠ =， ∴()SAS ABG CBE ≌，∴AG CE =．如图，连接BD BF ，．∵1245∠+∠=°，2345∠+∠°， ∴13∠=∠．在Rt DBC △中，∵22222BD BC CD BC =+=，∴BD =，∴BD BC= 在Rt FBE中，同理可求BF BE= ∴BD BF BC BE =， ∴BDF BCE ∽△△，∴DF BD ==故答案为：AG CE =【变式1】（2023·广东广州·一模）如图，正方形ABCD 中，等腰直角EBF △绕着B 点旋转，BF EF =，90BFE ∠=°，则:DE AF = ．【分析】连接BD ，证AFB DEB ∽，得DE BD AF AB=，根据等腰直角三角形斜边与直角边的比例关系即可得出比值．解：如右图，连接BD ，由题知，四边形ABCD EBF △为等腰直角三角形45FBA ABE FBE ∠+∠=∠=° ，45ABE EBD ABD ∠+∠=∠=°，FBA EBD ∴∠=∠，由题知，EBF △为等腰直角三角形，ABD △为等腰直角三角形，FB AB BE BD ∴== AFB DEB ∴ ∽，DE BD AF AB ∴==【点拨】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、旋转变换的性质、等腰直角三角形的性质、勾股定理、直角三角形的性质等知识；本题综合性强，根据FBA EBD ∠=∠，FB AB BE BD ==AFB DEB ∽是解题的关键． 【变式2】如图，直角梯形ABCD 中，∠BCD ＝90°，AD ∥BC ，BC ＝CD ，E 为梯形内一点，且∠BEC ＝90°，将△BEC绕C 点旋转90°使BC与DC重合，得到△DCF，连EF交CD于M．已知BC＝5，CF＝3，则DM:MC 的值为（）A．5:3 B．3:5 C．4:3 D．3:4【答案】C解：由题意知△BCE绕点C顺时转动了90度，∴△BCE≌△DCF，∠ECF=∠DFC=90°，∴CD=BC=5，DF∥CE，∴∠ECD=∠CDF，∵∠EMC=∠DMF，∴△ECM∽△FDM，∴DM：MC=DF：CE，∵=4∴DM：MC=DF：CE=4：3．故选C．【题型3】正方形中的“十字架模型”【例3】（23-24九年级上·河南郑州·阶段练习）（1）如图1，正方形ABCD中，点P为线段BC上一个动=；点，若线段MN垂直AP于点E，交线段AB于点M，交线段CD于点N，证明：AP MN（2）如图2，正方形ABCD中，点P为线段BC上一动点，若线段MN垂直平分线段AP，分别交AB，AP，=+；BD，DC于点M，E，F，N．求证：EF ME FN【答案】（1）见解析；（2）见解析；【分析】（1）过B点作BH∥MN交CD于H，则AP BH⊥，根据平行四边形和正方形的性质求证()≌，然后根据三角形全等的性质即可证明；ABP BCH ASA=，然后根据等边对等角和等量代换求得（2）根据垂直平分线的性质和正方形的性质求得FP FC∠=°，根据直角三角形斜边中线的性质得到FE=190AFPAP，结合（1）问结论即可求证．2解：（1）如图1，过B点作BH∥MN交CD于H，则AP BH⊥，∥NH，BM∴四边形MBHN为平行四边形，∴=，MN BH四边形ABCD是正方形．∴=，90AB BC∠=°=∠，ABP C∠+∠=°，∴∠+∠=CBH ABH BAP ABH90∴∠=∠，BAP CBH()∴≌，ASAABP BCH∴=，BH AP∴=；MN AP（2）如图2，连接FA，FP，FC正方形ABCD 是轴对称图形，F 为对角线BD 上一点，FA FC ∴=，又FE 垂直平分AP ，FA FP ∴=，FP FC ∴=，FPC FCP ∴∠=∠，FAB FCP ∠=∠ ， FAB FPC ∴∠=∠，180FAB FPB ∴∠+∠=°，180ABC AFP ∴∠+∠=°，90AFP ∴∠=°，FE ∴=12AP ， 由（1）知，AP MN =，2MN ME EF FN AP EF ∴=++==，EF ME FN ∴=+．【点拨】本题考查了平行四边形的判定和性质，正方形的性质，三角形全等的判定和性质，等腰三角形的性质，熟练掌握各部分定理和性质是本题的关键．【变式1】（23-24九年级上·重庆南岸·期中）如图，在矩形ABCD 中，10AD =，8AB =，点E 为AD 边上一点，将ABE 沿BE 翻折到FBE 处，延长EF 交BC 于点G ，延长BF 交CD 于点H ，且FH CH =，则FG 的长是（ ）A ．95B ．94C ．45D ．185【答案】A【分析】本题考查矩形的判定与性质、翻折性质、相似三角形的判定与性质、勾股定理，综合运用相关知识求解是解答的关键．过E 作EM BC ⊥于M ，根据矩形性质和折叠的性质，结合勾股定理求得94FH CH == 941844BH =+=，根据相似三角形的性质即可得到结论．解：过E 作EM BC ⊥于M ，则90EMB EMG ∠=∠=°，四边形ABCD 是矩形，90A ABC C °∴∠=∠=∠=，10BC AD ==，ABE 沿BE 翻转到FBE 处，EF AE ∴=，8BFAB ==， 90EFB BFG A ∠=∠=∠=， 设FHCH x ==，则8BH x =+， 在Rt BCH △中，根据勾股定理得222BC CH BH +=()222108x x ∴+=+ 则94x =， 94FH CH ==， 941844BH =+=， FBG CBH =∠∠ ，BFG BCH ∠=∠BFG BCH ∴ ∽BG FG BF BH CH BC∴==8441910544BG FG === 解得：95FG =故选：A ． 【变式2】（23-24九年级上·山西太原·期末）如图，在正方形ABCD 中，点E 是DC 边的中点，AE 的垂直平分线分别交AD ，BC 边于点F ，G ，垂足为点H ．若4AB =，则GH 的长为 ．【分析】过点B 作BN GF ∥交AD 于点N ，先证明()AAS AED BNA ≌，推出AEBN FG ==，利用勾股定理求出AE ，再证明AFH AED ∽，利用相似三角形的性质求出FH =解：过点B 作BN GF ∥交AD 于点N ，如图所示：∵四边形ABCD 是正方形，4AB =，∴,4,90AD BC AD AB CD BAN D ===∠=∠=°∥， ∴四边形BGFN 是平行四边形，∴BN GF =，∵,AE FG BN GF ⊥∥，∴BN AE ⊥，∴90BNA EAD∠+∠=°， 90AED EAD∠+∠=°∴BNA AED ∠=∠， 在AED △和BNA 中，AED BNA D BAN AD AB ∠=∠ ∠=∠ =， ∴()AAS AED BNA ≌，∴AEBN FG ==， ∵点E 是DC 边的中点，∴2DECD ==，∴AE∴FG =∵H 是AE 的中点，∴12AH AE == ∵90,AHF D FAH EAD ∠=∠=°∠=∠，∴AFH AED ∽ ， ∴FH AH DE AD =，即2FH =∴FH =∴GH FG FH =−==，【点拨】本题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，构造辅助线，证明三角形全等是解题的关键．【题型4】矩形中的“十字架模型”【例4】（23-24九年级上·河南洛阳·期末）小明在学习中发现，当垂直线段出现在四边形中间时，通常有比较简明的结论．下面是他的发现过程，请补充并完成其中的问题．（1）如图1，在正方形ABCD 中，E 为AB 上一点，连接DE ，过点A 作AG DE ⊥于点F ，交BC 于G ，则AG 与DE 的数量关系是：AG ______DE （填“>”“=”“<”号）．(2)①如图2，在矩形ABCD 中，AB nBC M N =，、为AB CD 、上的点，连接MN ，过点D 作DE MN ⊥于点F ，交BC 于E ．小明发现，过M 作MG CD ⊥于点G ，可以得到MN 与DE 的数量关系．这个数量关系是什么？请说明理由；②填空：由①可得，顶点分别在矩形的每一组对边（或延长线）上且互相垂直的两条线段的比等于______； ③应用上述结论解决问题：在Rt ABC △中，9086ACB AC BC ∠°=，=，=，点D 是AB 的中点，连接CD ，过B 作CD 的垂线BE ，交直线AC 于E ，垂足是点F ，直接写出BE 的长度．【答案】(1)=(2)①数量关系为DE nMN =，理由见解析；②矩形两邻边的比；③152； 【分析】（1）证明ABG DAE ≌即可；（2）①证明MNG DEC ∽，由相似的性质即可得到MN 与DE 的数量关系；②由①的解答即可完成；③延长CD 到N ，使DN CD =，分别连接AN BN ，，则可得四边形ACBN 是矩形，且BE CN ⊥，由①的结论即可求得BE 长度．（1）解：∵四边形ABCD 是正方形， ∴90AB AD DAE ABG =∠=∠=°，， ∴90DAF BAG ∠+∠=°，∴90ADE DAF ∠+∠=°，∴ADE BAG ∠=∠， ∴(ASA)ABG DAE ≌，∴AG DE =，故答案为：=；（2）解：①数量关系为DE nMN =理由如下：∵四边形ABCD 是矩形，∴90A ADC C ∠=∠=∠=°，AD BC AB CD ==，； ∵MG CD ⊥，∴四边形ADGM 是矩形，AD MG BC ==；∵DE MN MG CD ⊥⊥，，∴90EDC MNG MNG NMG ∠+∠=∠+∠=°，∴EDC NMG ∠=∠， ∵90MGN C ∠=∠=°， ∴MNG DEC ∽， ∴MN MG DE CD=； ∵AB nBC =，∴CD nMG =， ∴1MN DE n=， 即DE nMN =；②由①知，顶点分别在矩形的每一组对边（或延长线）上且互相垂直的两条线段的比等于矩形两邻边的比；故答案为：矩形两邻边的比；③如图，延长CD 到N ，使DN CD =，分别连接AN BN ，，∵D 为AB 的中点，∴BD AD =，∴四边形ACBN 是平行四边形，∵90ACB ∠=°， ∴四边形ACBN 是矩形，∴8BNAC ==，由勾股定理得：10CN =；∵BE CN ⊥，∴由①的结论知：86CN AC BE BC ==， ∴661015882CN BE ×===．【点拨】本题考查了矩形的判定与性质，正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识，有一定的综合性．【变式1】（2024·湖南永州·一模）如图，在矩形ABCD 中，BE AC ⊥于点F ，若1,BF BC ==则DE 的长度为（ ）A ．1B C ．32 D 【答案】B 【分析】本题考查了相似三角形的判定和性质，矩形的性质，通过证明ABF BCF ∽ ，可得AF BF BF CF =，可求AF 的长，通过证明AEF CBF ∽△△，可得AF AE CF BC=，可求DE 的长． 解：∵四边形ABCD 是矩形，∴,90,AD BC AD BC ABC =∠=°∥∵BE AC ⊥，1,BF BC ==∴CF =，∵90AFB CFB ABC ∠=∠=∠=°， ∴90ABF CBF ABF BAC ∠+∠=°=∠+∠，∴BAC CBF ∠=∠， ∴ABF BCF ∽ ，∴AF BF BF CF=，∴1AF =，∴AF = ∵AD BC ∥，∴AEF CBF ∽△△，∴AF AE CF BC=，=∴AE =∴DE AD AE BC AE =−=−， 故选：B ．【变式2】（23-24九年级上·河北张家口·阶段练习）如图，在矩形ABCD 中，连接BD ，点E 在AD 上，连接CE ，交BD 于点F ，且DEF DBA ∽ ．（1）BD 与CE 是否垂直？ （填“是”或“否”）；（2）若1AB =，30CBD ∠=°，则EF CF的值为 ．【答案】 是 13【分析】（1）根据矩形ABCD 的性质可得90DAB ∠=°，已知DEF DBA ∽ 即可证得．（2）根据矩形ABCD 的性质可得AD ，根据DEF DBA ∽ 可得DF =，在证明DFC DCB ∽ ，根据相似比即可解得．（1）∵四边形ABCD 为矩形，∴90DAB ∠=°，∵DEF DBA ∽ ，∴90DFE DAB ∠=∠=°，∴BD CE ⊥；故答案为：是；（2）1AB =，30CBD ∠=°，四边形ABCD 为矩形，∴1AB CD ==，2BD =，∴AD BC ===，∵DEF DBA ∽ ，∴ EFDFAB AD =，即 1EF= ∴DF =，∵DFC BCD ∠=∠，BDC BDC ∠=∠，∴DFC DCB ∽ ，∴ DFCFCD BC =，即 1DF=∴ =，∴ 12EFCF =．故答案为： 13．第三部分【中考链接与拓展延伸】1、直通中考【例1】（2021·四川内江·中考真题）如图，矩形ABCD 中，6AB =，8BC =，对角线BD 的垂直平分线EF 交AD 于点E 、交BC 于点F ，则线段EF 的长为 ．【答案】152/7.5 【分析】根据矩形的性质和勾股定理求出BD ，证明△BOF ∽△BCD ，根据相似三角形的性质得到比例式，求出EF 即可．解：如图：四边形ABCD 是矩形，90A ∴∠=°，又6AB =，8AD BC ==，10BD ∴=，EF 是BD 的垂直平分线，5OB OD ∴==，90BOF ∠=°，又90C ∠=°，BOF BCD ∴∆∆∽， ∴OF BO CD BC =， ∴568=OF ， 解得，15OF =，四边形ABCD 是矩形，//AD BC ∴，90A ∠=°，EDO FBO ∴∠=∠，EF 是BD 的垂直平分线，BO DO ∴=，EF BD ⊥，在DEO ∆和BFO ∆中，EDO FBO BO DOEOD FOB ∠=∠ = ∠=∠， ()DEO BFO ASA ∴∆≅∆，OE OF ∴=，1522EF OF ∴==． 故答案为：152． 【点拨】本题考查的是矩形的性质、线段垂直平分线的性质以及勾股定理的应用，掌握矩形的四个角是直角、对边相等以及线段垂直平分线的定义是解题的关键．【例2】（2022·湖南娄底·中考真题）如图，已知等腰ABC 的顶角BAC ∠的大小为θ，点D 为边BC 上的动点（与B 、C 不重合），将AD 绕点A 沿顺时针方向旋转θ角度时点D 落在D 处，连接BD ′．给出下列结论：①ACD ABD ′≅△△；ACB ADD ′ △；③当BD CD =时，ADD ′ 的面积取得最小值．其中正确的结论有 （填结论对应的序号）．【答案】①②③【分析】依题意知，ABC 和ADD ′ 是顶角相等的等腰三角形，可判断②；利用SAS 证明ADC AD B ′≌△△，可判断①；利用面积比等于相似比的平方，相似比为AD AC ，故最小时ADD ′ 面积最小，即AD BC ⊥，等腰三角形三线合一，D 为中点时 .解：∵AD 绕点A 沿顺时针方向旋转θ角度得到AD ′∴DAD θ′∠=，AD AD =′ ∴CAB DAD ′∠=∠ 即CAD DAB DAB BAD ′∠+∠=∠+∠∴CAD BAD ′∠=∠ ∵AC AB CAD BAD AD AD ′= ∠=∠ =′得：ADC AD B ′≌△△（SAS ）故①对∵ABC 和ADD ′ 是顶角相等的等腰三角形∴ACB ADD ′ △△故②对 ∴2()AD D ABC S AD S AC′=△△ 即AD 最小时AD D S ′△最小当AD BC ⊥时，AD 最小点是BC 中点故③对故答案为：①②③【点拨】本题考查全等三角形的判定和性质，相似三角形的判定和性质，手拉手模型，选项③中将面积与相似比结合是解题的关键 .2、拓展延伸【例1】（2024·辽宁沈阳·二模）如图1，在Rt ABC △中，90B ∠=︒，4AB =，2BC =，点D ，E 分别是边BC ，AC 的中点，连接.DE 将CDE 绕点C 逆时针方向旋转，记旋转角为α．(1)问题发现：①当0α=°时AE BD =______； ②当180α=°时，AE BD=______． (2)拓展探究：试判断当0360α°<<°时，AE BD的大小有无变化？以下是就图2的情形给出的证明过程，请你补全：∵ECD ACB ∽，EC AC∴=③ ． 又∵旋转ECA DCB ∠=∠， ∴ECA DCB ∽△△，AE EC BD DC∴== ． (3)用以上结论解决问题：当CDE 绕点C 逆时针旋转至A ，B ，E 三点在同一条直线上时，请在备用图中画出图形，并写出求线段BD 的长 ．【答案】DC BC【分析】（1）①先利用勾股定理可得AC =AE =，1BD =，由此即可得；②先画出图形，根据旋转的性质可得90CDE°∠=，2DE CE==，1CD =，然后根据线段和差分别求出AE ，BD 的长，由此即可得；（2）根据相似三角形的判定证出ECA DCB ∽△△，再根据相似三角形的性质即可得；（3）分①点E 在AB 的延长线上和②点E 在线段AB 上，利用勾股定理求出1BE =，从而可得AE 的长，再根据AE BD= （1）解：①当0α=°时，在Rt ABC △中，90B ∠=︒，4AB =，2BC =，AC ∴=点D ，E 分别是边BC ，AC 的中点，12CE AE AC ∴===112BD CD BC ===，②如图1，点D ，E 分别是边BC ，AC 的中点，4AB =，122DE AB ==，DE AB ∥， 90ABC ∴∠=°，90CDE ABC ∠=∠=°； 如图，当180α=°时，由旋转的性质得：CDE ∠的大小不变，仍等于90°，DE 长度不变，仍等于2，CE 的长度不变，AE AC CE ∴=+=1CD ，3BD BC CD ∴=+=，AE BD ∴==（2）解：当0360α°<<°，大小没有变化； 证明：ECD ACB ∽，EC CD AC BC ∴=， 又∵旋转ECA DCB ∠=∠， ECA DCB ∴ ∽，AE EC BD DC ∴==故答案为：CD CB （3）①如图2，当点E 在AB 的延长线上时，在Rt BCE 中，CE =2BC =，1BE ∴=，415AE AB BE ∴=+=+=，AE BD∴BD ∴== ②如图3，当点E 在线段AB 上时，在Rt BCE 中，CE =2BC ，1BE ∴=，413AE AB BE ∴=−=−=，AE BD∴BD ∴==，综上，线段BD 【点拨】本题考查了旋转的性质、相似三角形的判定与性质、勾股定理、三角形中位线定理等知识点，正确分两种情况讨论是解题关键．【例2】（23-24八年级下·江苏苏州·阶段练习）（1）【问题发现】如图①，正方形ABCD ，DEFG ，将正方形DEFG 绕点D 旋转，直线AE 、CG 交于点P ，请直接写出线段AE 与CG 之间的数量关系是______，位置关系是______；（2）【拓展探究】如图2，矩形ABCD ，DEFG，22AD DE AB DG AD DG ===，，，将矩形DEFG 绕D 旋转；直线AE ,CG 交于点P ，（1）中线段之间的关系还成立吗？若成立，请写出理由；若不成立，请写出线段之间的关系；（3）【解决问题】若2428AD DE AB DG ====，，矩形DEFG 绕D 旋转过程中当点P 与点G 重合时，求线段AE 的长．【答案】（1）AE CG =，AE CG ⊥；（2）AE 、CG 的数量关系不成立，位置关系仍成立，AE 、CG 的数量关系为：2CG AE =，理由见解析；（3）AE 的长为【分析】（1）证明ADE CDG ≌得到AE 与CG 的数量关系，通过角的等量代换，求得90∠=°GPE ，得到AE 和CG 的位置关系；（2）可通过已知对应角，和对应边的比例关系，证明 ∽EDA GDC ，求得AE 和CG 的数量关系；然后利用角的等量代换，求得90∠=°GPE ，得到AE 和CG 的位置关系； （3）分情况讨论，①当点P 和点G 在边CD 上方重合时，②当点P 和点G 在边CD 下方重合时，分别求解．解：（1）AE CG =，AE CG ⊥；∵四边形ABCD ，DEFG 都是正方形，∴AD CD =，DE DG =，90ADC EDG °∠=∠=．∴ADC ADG EDG ADG ∠+∠=∠+∠，∴ADE CDG ∠=∠． ∴ADE CDG ≌．∴AE CG =，DEA DGC ∠=∠， DEA EDG DGC GPE ∠+∠=∠+∠∴90∠=°GPE ． ∴AE CG ⊥；（2）（1）中数量关系不成立，位置关系成立．2CG AE =，AE CG ⊥．理由如下：由题意知在矩形ABCD 、DEFG 中，90EDG ADC °∠=∠=，∴EDG GDA ADC GDA ∠+∠=∠+∠．∴EDA GDC ∠=∠．∵2AD DE =，2AB DG =， ∴12ED DG AD DC ==．∴ ∽EDA GDC ．∴2CG AE =，DEA DGC ∠=∠．∵DEA EDG DGC GPE ∠+∠=∠+∠，∴90GPE °∠=．∴AE CG ⊥．综上所述：2CG AE =，AE CG ⊥；（3）如解图①，AE如解图2，连接AC ，设AE x =，则2CG x =，EG AC =在Rt AGC 中，222+=AG GC AC ，222((2)++x x ，∴x ==−x综上所述，当点P 与点G 重合时，线段AE 的长为 【点拨】本题综合考查了全等三角形及相似三角形的判定及性质，以及勾股定理的应用，根据题意画出符合题意的图形是解决本题的关键．。

相似三角形（考点清单，知识导图+2个考点清单+4种题型解读）【清单01】 相似三角形的判定相似三角形的123Rt .ìïïïïíïïïD ïî预备定理：平行于三角形的直线截其它两边所在的直线，与；判定定理：，两个三角形；判定定理：且截得的三角形原三角形相似两角对应相等相似角，两个三形；判定定理：，两个三角形；相似的判定：似和对应成比例，两相两边对应成比例夹角相等三边对应成比例相斜三个边直角边直角角形相似【清单02】相似三角形的性质123ìïïíïïî基本性质：相似三角形的，；性质定理：相似三角形、和都等于；性质定理：相似三角形的等对对于；分性质比定应理应角相等对应边成比例对似：相似三角形高的比应中线的比对应角平线的相比周长的比相似比面积比的等于.的比相似的平方注：以上定理均要从文字、图形、符号三个方面去理解掌握.【考点题型一】相似三角形的性质（共8小题）【例1】（2023秋•浦东新区校级月考）如果两个相似三角形的周长比为1:4，那么它们的对应中线的比为( )A ．1:16B ．1:2C ．1:4D ．【分析】据相似三角形的周长的比等于它们的相似比1:4，然后再利用对应中线的比等于相似比求解即可．【解答】解：Q 两个相似三角形的周长比为1:4，\它们的相似比为1:4．\它们的对应中线的比为1:4，故选：C ．【点评】本题主要考查了相似三角形的性质，利用相似三角形的周长的比等于相似比是解答此题的关键．【变式1-1】（2024•崇明区）如果两个相似三角形的周长之比为1:4，那么它们对应边之比为( )A ．1:2B ．1:4C ．1:8D ．1:16【分析】直接根据相似三角形的性质进行解答即可．【解答】解：Q 两个相似三角形的周长比为1:4，\它们的对应边的比1:4=．故选：B ．【点评】本题考查的是相似三角形的性质，即相似三角形对应边的比等于相似比，面积的比等于相似比的平方．【变式1-2】（2023秋•黄浦区期末）已知：△111A B C ∽△222A B C ∽△333A B C ，如果△111A B C 与△222A B C 的相似比为2，△222A B C 与△333A B C 相似比为4，那么△111A B C 与△333A B C 的相似比为( )A ．2B ．4C ．6D ．8【分析】根据相似三角形的相似比写出对应边的比，计算出11A B 与33A B 的比值，也就是两三角形的相似比．【解答】解：Q △111A B C ∽△222A B C ∽△333A B C ，如果△111A B C 与△222A B C 的相似比为2，△222A B C 与△333A B C 相似比为41122:2:1A B A B \=，2233:4:1A B A B =，设33A B x =，则221148A B xA B x ==，1133:8:1A B A B \=，\△111A B C 与△333A B C 的相似比为8．故选：D ．【点评】根据相似三角形的相似比写出对应边的比，计算出11A B 与33A B 的比值，也就是两三角形的相似比．【变式1-3】（2023秋•浦东新区校级月考）两个相似三角形的相似比是5:7，小三角形的周长为20cm ，大三角形的周长是 cm ．【分析】根据相似三角形的性质可知，周长比等于相似比，由此即可求解．【解答】解：根据题意得，相似比为5:7，\大三角形的周长是52028()7cm ¸=，故答案为：28．【点评】本题主要考查相似三角形的性质，理解和掌握相似三角形的面积比等于相似比的平方，相似三角形的周长比等于相似比是解题的关键．【变式1-4】（2023秋•闵行区校级月考）已知两个相似三角形的周长比为4:9，那么这两个相似三角形的面积比为 　．【解答】解：Q 两个相似三角形的周长比为4:9，\相似比为4:9，\这两个相似三角形的面积比为16:81，故答案为：16:81．【点评】本题主要考查相似三角形的性质，熟练掌握相似三角形的性质是解题的关键．【变式1-5】（2023秋•虹口区期末）一个三角形框架模型的边长分别为3分米、4分米和5分米，木工要以一根长6分米的木条为一边，做与模型相似的三角形，那么做出的三角形中，面积最大的是 平方分米．【分析】由相似三角形的判定：三组对应边的比相等的两个三角形相似求出三角形最大的三边，根据勾股定理的逆定理判断新三角形是直角三角形，根据三角形的面积公式计算即可．【解答】解：当长是6分米的木条与三角形框架模型的边长最短的3分米一条边是对应边时，做出的三角形的三边最大，面积最大，设长是4分米，5分米的边的对应边的长分别是a 分米，b 分米，3:64:5:a b \==，8a \=，10b =，\其他两条边的长分别是8分米，10分米，2226810+=Q ，\做出的三角形是直角三角形，直角边分别是6分米，8分米，\做出的三角形的面积为168242´´=（平方分米）．故答案为：24．【点评】本题考查相似三角形的性质，勾股定理的逆定理，掌握当长是6分米的木条与三角形框架模型的边长最短的一条边是对应边时，做出的三角形的三边最大，是解决问题的关键．【变式1-6】（2023秋•金山区期末）在ABC D 中，6AC =，P 是AB 边上的一点，Q 为AC 边上一点，直线PQ 把ABC D 分成面积相等的两部分，且APQ D 和ABC D 相似，如果这样的直线PQ 有两条，那么边AB 长度的取值范围是 ．【分析】分两种情况进行讨论，画出图形，根据面积之比等于相似比的平方即可解答．【解答】解：如图，当APQ ABC D D ∽时，\21(2APQ ABCS AP S AB D D ==，\只要满足AP AQ AB AC ==如图，当APQ ABC D D ∽时，Q 直线PQ 把ABC D 分成面积相等的两部分，12APQ ABC S S D D \=，\21()2APQ ABCS AP S AC D D ==，\APAC=，AP \==，AQ =，APAB Q …，AQ AC …，AB \…6AB …，AB \…，当6AB AC ==时，金字塔型和子母型完全重合，此时只有一种情况，6AB \¹，综上所述，直线PQ 把ABC D 分成面积相等的两部分，且APQ D 和ABC D 相似，如果这样的直线PQ 有两条，那么边AB 长度的取值范围是AB…且6AB ¹．故答案为：AB …且6AB ¹．【点评】本题考查相似三角形的性质，熟练掌握相似三角形的性质是解题关键．【变式1-7】（2023秋•普陀区期末）如图，在ABC D 中，90ACB Ð=°，CD 是AB 边上的高，如果5AC =，4CD=，那么ACD D 与CBD D 的相似比k = ．【分析】相似三角形对应边的比叫相似比，由此即即可求解．【解答】解：CDQ是AB边上的高，90ADC\Ð=°，5AC=Q，4CD=，3AD\==，90ACBÐ=°Q，CD是AB边上的高，90ADC BDC\Ð=Ð=°，90A ACD BCD ACDÐ+Ð=Ð+Ð=°Q，A BCD\Ð=Ð，ACD CBD\D D∽，ACD\D与CBDD的相似比34ADkCD==．故答案为：34．【点评】本题考查相似三角形的性质，关键是掌握相似三角形相似比的定义．【考点题型二】7小题）【例2】（2023秋•金山区期末）如图在41´的方格中，每一个小正方形的顶点叫做格点，以其中三个格点为顶点的三角形称为格点三角形，ABCD就是一个格点三角形，现从ABCD的三个顶点中选取两个格点，再从余下的格点中选取一个格点联结成格点三角形，其中与ABCD相似的有( )A．1个B．2个C．3个D．4个【分析】根据“三边对应成比例的两个三角形相似”求解即可．【解答】解：如图，根据勾股定理得，AD ==，AC ==，BC ==BE ==，CF =，又2AB =Q ，2CD =，1BF =，\1AD CB =，1CDAB =，1ACAC =，AB BC =，AC BE ==，BC CE ==，BCBF=，AB BC ==AC CF =，\AD CD AC CB AB AC ==，AB AC BC BC BE CE ==，BC AB AC BF BC CF==，ABC CDA \D D ∽，ABC BCE D D ∽，ABC CBF D D ∽，故选：C ．【点评】此题考查了相似三角形的判定，熟记相似三角形的判定定理是解题的关键．【变式2-1】（2023秋•奉贤区期末）如图，将ABC D 绕点B 顺时针旋转，使得点A 落在边AC 上，点A 、C 的对应点分别为D 、E ，边DE 交BC 于点F ，联结CE ．下列两个三角形不一定相似的是( )A ．BAD D 与BCE DB ．BDF D 与ECF DC ．DCFD 与BEF D D ．DBF D 与DEBD 【分析】根据旋转的性质得到AB DB =，ABC DBE Ð=Ð，BC BE =，A BDD Ð=Ð，ACB DEB Ð=Ð，再根据相似三角形的判定定理判断求解即可．【解答】解：如图，根据旋转的性质得，ABC DBE D @D ，AB DB \=，ABC DBE Ð=Ð，BC BE =，A BDD Ð=Ð，ACB DEB Ð=Ð，ABD CBE \Ð=Ð，AB DBBC BE=，BAD BCE \D D ∽，故A 不符合题意；ABD CBE Ð=ÐQ ，AB AD =，BC BE =，A BDA BCE BEC \Ð=Ð=Ð=Ð，BDF ECF \Ð=Ð，又BFD EFC Ð=ÐQ ，BDF ECF \D D ∽，故B 不符合题意；DCF BEF Ð=ÐQ ，DFC BFE Ð=Ð，DCF BEF \D D ∽，故C 不符合题意；根据题意，无法求解DBF D 与DEB D 相似，故D 符合题意；故选：D ．【点评】此题考查了相似三角形的判定、旋转的性质等知识，熟练掌握相似三角形的判定、旋转的性质是解题的关键．【变式2-2】（2023秋•徐汇区期末）下列两个三角形一定相似的是( )A ．两个直角三角形B ．两个等腰三角形C ．两个等边三角形D ．两个面积相等的三角形【分析】由相似三角形的判定，即可判断．【解答】解：A 、B 、D 中的两个三角形不一定相似，故A 、B 、D 不符合题意；C 、两个等边三角形相似，故C 符合题意．故选：C ．【点评】本题考查相似三角形的判定，等边三角形、等腰三角形的性质，关键是掌握相似三角形的判定方法．【变式2-3】（2024•静安区校级模拟）如图，已知ABC D 与BDE D 都是等边三角形，点D 在边AC 上（不与点A 、C 重合），DE 与AB 相交于点F ，那么与BDF D 相似的三角形是( )A ．BEF DB ．BDA DC ．BDCD D ．AFDD 【分析】由相似三角形的判定，即可判断．【解答】解：ABC D Q 与BDE D 都是等边三角形，60E BDE EBD \Ð=Ð=Ð=°，C A ABC Ð=Ð=Ð．A 、只有60E BDF Ð=Ð=°，BEF D 和BDF D 不一定相似，故A 不符合题意；B 、由60BDF A Ð=Ð=°，DBF ABD Ð=Ð，推出BDF BAD D D ∽，故B 符合题意；C 、只有60BDF C Ð=Ð=°，BDFD 和BCD D 不一定相似，故C 不符合题意；D 、只有60BDF A Ð=Ð=°，BDF D 和AFD D 不一定相似，故D 不符合题意．故选：B ．【点评】本题考查相似三角形的判定，等边三角形，关键是掌握相似三角形的判定方法．【变式2-4】（2023秋•宝山区期末）如图，在正方形网格中，A 、B 、C 、D 、M 、N 都是格点，从A 、B 、C 、D 四个格点中选取三个构成一个与AMN D 相似的三角形，某同学得到两个三角形：①ABC D ；②ABD D ．关于这两个三角形，下列判断正确的是( )A ．只有①是B ．只有②是C ．①和②都是D ．①和②都不是【分析】根据勾股定理求出ABD D 、ABC D 、AMN D 的三边长，再根据相似三角形的对应边成比例判断即可．【解答】解：由图形可知，2AM =，4AN =，MN ==，AB ==AC ==，BC ==，AD ==，BD ==，QAB BD ADAM AN MN===，ABD MAN \D D ∽；QAB ACAM AN¹，ABC \D 与AMN D 不相似，故选：B ．【点评】本题考查了相似三角形的判定，熟记相似三角形的判定定理是解题的关键．【变式2-5】（2024•ABCD 中，//AD BC ，AC 与BD 相交于点O ，点E 在线段OB 上，AE 的延长线与BC 相交于点F ，2OD OB OE =×．（1）求证：四边形AFCD 是平行四边形；（2）如果BC BD =，AE AF AD BF ×=×，求证：ABE ACD D D ∽．【分析】（1）由已知得出OE OD OD OB =，由平行线得出AOD COB D D ∽，得出OA OD OC OB =，证出OA OEOC OD=，得出//AF CD ，即可得出结论；（2）由平行线得出AED BDC Ð=Ð，BEF BDC D D ∽，得出BE BFBD BC=，证出AEB ADC Ð=Ð．由已知得出AE AD BF AF =，由平行四边形的性质得出AF CD =，得出AE AD BE DC=，由相似三角形的判定定理即可得出结论．【解答】（1）证明：2OD OE OB =×Q ，\OE OD OD OB=，//AD BC Q ，AOD COB \D D ∽，\OA OD OC OB =\OA OE OC OD=//AF CD \，\四边形AFCD 是平行四边形；（2）证明：//AF CD Q ，AED BDC \Ð=Ð，BEF BDC D D ∽，\BE BF BD BC=，BC BD =Q ，BE BF \=，BDC BCD Ð=Ð，AED BCD \Ð=Ð．180AEB AED Ð=°-ÐQ ，ADC BCD а-Ð，AEB ADC \Ð=Ð．AE AF AD BF ×=×Q ，\AE AD BF AF=，Q 四边形AFCD 是平行四边形，AF CD \=，\AE AD BE DC=，ABE ADC \D D ∽．【点评】本题考查了相似三角形的判定与性质、平行四边形的判定与性质、梯形的性质、等腰三角形的性质等知识；熟练掌握相似三角形的判定与性质和平行四边形的判定是解题的关键．【变式2-6】（2023秋•杨浦区期中）已知：如图，在ABC D 中，点D 、E 分别在边AB 、AC 上，//DE BC ，EB 平分DEC Ð．（1）求证：AE AB ED BD=；（2）如果22BE AE BC AC=，求证：ABE ACB D D ∽．【分析】（1）根据平行线的性质得出AE AD CE BD =，BED CBE Ð=Ð，则AC AB CE BD=，根据角平分线定义及平行线的性质得到CBE BEC Ð=Ð，则BC CE =，根据相似三角形的判定与性质得出AE DE DE AC BC CE ==，根据比例的性质及等量代换即可得解；（2）结合（1）及题意推出BE DE CE BE=，结合BED BEC Ð=Ð，推出BED CEB D D ∽，根据相似三角形的性质得出DBE BCE Ð=Ð，结合BAE CAB Ð=Ð，即可判定ABE ACB D D ∽．【解答】证明：（1）//DE BC Q ，\AE AD CE BD =，BED CBE Ð=Ð，\11AE AD CE BD +=+，\AC AB CE BD=，EB Q 平分DEC Ð，BED BEC \Ð=Ð，CBE BEC \Ð=Ð，BC CE \=，//DE BC Q ，ADE ABC \D ∽，\AE DE DE AC BC CE ==，\AE AC DE CE=，Q AC AB CE BD=，\AE AB DE BD =；（2）Q 22BE AE BC AC =，BC CE =，AE DE AC CE=，\22BE DE CE CE=，\BE DE CE BE=，又BED BEC Ð=Ð，BED CEB \D D ∽，DBE BCE \Ð=Ð，即ABE ACB Ð=Ð，又BAE CAB Ð=Ð，ABE ACB \D D ∽．【点评】此题考查了相似三角形的判定与性质，熟记相似三角形的判定与性质是解题的关键．【考点题型三】相似三角形的判定与性质（共13小题）【例3】（2023秋•长宁区期末）如果点D 、E 分别在ABC D 的两边AB 、AC 上，由下列哪一组条件可以推出//(DE BC )A ．23AD BD =，23CE AE =B ．22,33AD DE AB BC ==C ．32AB AD =，12EC AE =D ．44,33AB AE AD EC ==【分析】对于选项C ，证明DAE BAC D D ∽，根据相似三角形的性质得到ADE ABC Ð=Ð，根据平行线的判定定理证明．【解答】解：A 、不能推出//DE BC ，不符合题意；B 、不能推出//DE BC ，不符合题意；C 、Q 12EC AE =，\32AC AE =，Q 32AB AD =，\AC AB AE AD =，A A Ð=ÐQ ，DAE BAC \D D ∽，ADE ABC \Ð=Ð，//DE BC \，本选项符合题意；D 、不能推出//DE BC ，不符合题意；故选：C ．【点评】本题考查的是相似三角形的判定和性质、平行线的判定，熟记相似三角形的判定定理是解题的关键．【变式3-1】（2023秋•长宁区期末）已知在ABC D 与△A B C ¢¢¢中，点D 、D ¢分别在边BC 、B C ¢¢上，（点D 不与点B 、C 重合，点D ¢不与点B ¢、C ¢重合）．如果ADC D 与△A D C ¢¢¢相似，点A 、D 分别对应点A ¢、D ¢，那么添加下列条件可以证明ABC D 与△A B C ¢¢¢相似的是( )①AD 、A D ¢¢分别是ABC D 与△A B C ¢¢¢的角平分线；②AD 、A D ¢¢分别是ABC D 与△A B C ¢¢¢的中线；③AD 、A D ¢¢分别是ABC D 与△A B C ¢¢¢的高．A ．①②B ．②③C ．①③D ．①②③【分析】根据相似三角形的判定与性质逐一判断即可得出结论．【解答】解：如图，①AD 、A D ¢¢分别是ABC D 与△A B C ¢¢¢的角平分线，BAD CAD \Ð=Ð，B A D C A D ¢¢¢¢¢¢Ð=Ð，又ADC D Q ∽△A D C ¢¢¢，CAD C A D ¢¢¢\Ð=Ð，C C ¢Ð=Ð，BAC B A C ¢¢¢\Ð=Ð，BAC \D ∽△B A C ¢¢¢，故添加条件①可以证明ABC D 与△A B C ¢¢¢相似；②AD 、A D ¢¢分别是ABC D 与△A B C ¢¢¢的中线，BD CD \=，B D C D ¢¢¢¢=，又ADC D Q ∽△A D C ¢¢¢，ADC A D C ¢¢¢\Ð=Ð，AD CD A D C D =¢¢¢¢，\AD A D BD B D ¢¢=¢¢，ADB A D B ¢¢¢Ð=Ð，ABD \D ∽△A B D ¢¢¢，B B ¢\Ð=Ð，又C C ¢Ð=ÐQ ，BAC \D ∽△B A C ¢¢¢，故添加条件②可以证明ABC D 与△A B C ¢¢¢相似；③AD 、A D ¢¢分别是ABC D 与△A B C ¢¢¢的高，ADC D ∽△A D C ¢¢¢，由图形可知，ABC D 与△A B C ¢¢¢不相似，故选：A ．【点评】本题考查了相似三角形的判定与性质，熟记相似三角形的判定与性质是解题的关键．【变式3-2】（2023秋•静安区期末）在ABC D 中，点D 、E 、F 分别在边BC 、AB 、AC 上，联结DE 、DF ，如果//DE AC ，//DF AB ，且:1:2AE EB =，那么:AF FC 的值是( )A ．3B ．13C ．2D ．12【分析】根据题目的已知条件画出图形，然后利用平行线分线段成比例解答即可．【解答】解：如图：//DE AC Q ，:1:2AE EB =，\12AE CD BE BD ==，\2BD CD=，//DF AB Q ，\2AF BD FC CD==，故选：C ．【点评】本题考查了平行线分线段成比例，熟练掌握平行线分线段成比例这个基本事实是解题的关键．【变式3-3】（2023秋•金山区期末）已知点E 是平行四边形ABCD 的边AD 上一点，联结CE 和BD 相交于点F ，如果:1:2AE ED =，那么:DF FB 为( )A ．1:2B ．1:3C ．2:3D ．2:5【分析】由平行四边形的性质得//AD CB ，AD CB =，由:1:2AE ED =，得23ED ED CB AD ==，再证明DFE BFC D D ∽，得23DF ED FB CB ==，于是得到问题的答案．【解答】解：Q 四边形ABCD 是平行四边形，//AD CB \，AD CB =，:1:2AE ED =Q ，\23ED ED CB AD ==，//ED CB Q ，DFE BFC \D D ∽，\23DF ED FB CB ==，故选：C ．【点评】此题重点考查平行四边形的判定与性质、相似三角形的判定与性质等知识，证明DFE BFC D D ∽是解题的关键．【变式3-4】（2023秋•黄浦区期末）如图，△ABC 三边上点D 、E 、F ，满足//DE BC ，//EF AB ，那么下列等式中，成立的是( )A ．DE AE EF EC =B ．AD BF DB FC =C ．DE AB EF BC =D ．AD BF DB BC=【分析】由题意可证四边形BDEF 是平行四边形，可得BD EF =，DE BF =，由相似三角形的性质和平行线分线段成比例依次判断可求解．【解答】解：//DE BC Q 、//EF AB ，ADE B EFC \Ð=Ð=Ð，AED C Ð=Ð，\△ADE ∽△EFC ，\DE AE CF EC =，故A 错误；AD DE EF CF=，//DE BC Q 、//EF AB ，\四边形BDEF 是平行四边形，BD EF \=，DE BF =，\AD BF BD FC =，故B 正确；\AB AD BC DE=，故C 错误；AD AE BF DB CE CF==，故D 错误，故选：B ．【点评】本题考查了相似三角形的判定和性质，灵活运用相似三角形的性质是本题的关键．【变式3-5】（2023秋•徐汇区期末）如图，点D 是ABC D 内一点，点E 在线段BD 的延长线上，BE 与AC 交于点O ，分别联结AD 、AE 、CE ，如果AD AE DE AB AC BC==，那么下列结论正确的是( )A ．//CE ADB ．BD AD =C ．ABE CBE Ð=ÐD ．BO AE AO BC ×=×．【分析】利用相似三角形的判定与性质解答即可．【解答】解：Q AD AE DE AB AC BC==，ADE ABC \D D ∽，ACB AED \Ð=Ð，BAC DAE Ð=Ð，BAD CAE \Ð=Ð，AOE BOC Ð=ÐQ ，AOE BOC \D D ∽，\AO BO AE BC=，BO AE AO BC \×=×．D \选项的结论正确．Q AD AE AB AC=，BAD CAE \D D ∽，ABE ACE \Ð=Ð，显然OE 与OC 不一定相等，ACE \Ð与BEC Ð不一定相等，CE \与BD 不一定平行，A \，C 不一定正确，BD Q 与AD 不一定相等，B \不一定正确．故选：D ．【点评】本题主要考查了相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．【变式3-6】（2022秋•虹口区期末）如图，点D 、E 分别在ABC D 边AB 、AC 上，3AB AE AD CE==，且AED B Ð=Ð，那么AD AC的值为( )A ．12B ．13C ．14D ．23【分析】根据题意，可以先设3AB a =，AD a =，3AE b =，CE b =，再根据题意可以得到DAE CAB D D ∽，然后即可得到AD AC的值．【解答】解：Q3AB AE AD CE ==，\设3AB a =，AD a =，3AE b =，CE b =，则4AC b =，AED B Ð=ÐQ ，DAE CAB Ð=Ð，DAE CAB \D D ∽，\AD AE AC AB =，即343a b b a=，解得2a b =，\112442AD a AC b ==´=，故选：A ．【点评】本题考查相似三角形的判定与性质，解答本题的关键是明确题意，利用数形结合的思想解答．【变式3-7】（2023秋•浦东新区校级月考）如图所示，过△ABC 的顶点C 作任一直线与边AB 及中线AD 分别交于点F 和E ，过点D 作//DM FC 交AB 于点M ．（1）若:2:3AEF MDEF S S =V 四边形，求:AE ED ．（2）试说明2AE FB AF ED ×=×．【分析】（1）利用相似三角形的性质解决问题即可．（2）利用平行线分线段成比例定理以及比例的基本性质证明即可．【解答】（1）解：//EF DM Q ，\△AEF ∽△ADM ，:2:3AEF MDEF S S =V Q 四边形，\AE AD ==\AE DE ==．（2）证明：DC DB =Q ，12FM MB FB \==，//DM CF Q ，::AE ED AF FM \=，即1::2AE ED AF FB =，:2:AE ED AF FB \=，2AE FB AF ED \×=×．【点评】此题主要考查平行线分线段成比例定理：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．同时考查了比例的性质．【变式3-8】（2022秋•长宁区期末）已知：如图，在△ABC 中，点D 在边BC 上，且AD AB =，边BC 的垂直平分线EF 交边AC 于点E ，BE 交AD 于点G ．（1）求证：△BDG ∽△CBA ；（2）如果△ADC 的面积为180，且18AB =，6DG =，求△ABG 的面积．【分析】（1）由AB AD =得到ABD ADB Ð=Ð，根据线段垂直平分线的性质得到EB EC =，则EBC C Ð=Ð，然后根据相似三角形的判定方法得到结论；（2）由（1）知△BDG ∽△CBA ，可得DG BD AB BC =，而18AB =，6DG =，即可得12BD CD =，12ABD ACD S S =V V ，又180ADC S =V ，故90ABD S =V ，因12AG =，12DG AG =，即得22906033ABG ABD S S ==´=V V ．【解答】（1）证明：AB AD =Q ，ABD ADB \Ð=Ð，EF Q 垂直平分BC ，EB EC \=，EBC C \Ð=Ð，GBD C Ð=ÐQ ，BDG CBA Ð=Ð，\△BDG ∽△CBA ；（2）解：由（1）知△BDG ∽△CBA ，\DG BD AB BC=，18AB =Q ，6DG =，\61183BD BC ==，\12BD CD =，\12ABD ACD S S =V V ，180ADC S =V Q ，90ABD S \=V ，18AD AB ==Q ，6DG =，12AG \=，\12DG AG =，\12BDG ABG S S =V V ，22906033ABG ABD S S \==´=V V ．【点评】本题考查相似三角形的判定与性质，涉及三角形面积，解题的关键是掌握相似三角形的判定定理．【变式3-9】（2022秋•杨浦区期末）如图，Rt ABC D 中，90ACB Ð=°，D 是斜边AB 上的中点，E 是边BC 上的点，AE 与CD 交于点F ，且2AC CE CB =×．（1）求证：AE CD ^；（2）连接BF ，如果点E 是BC 中点，求证：EBF EAB Ð=Ð．【分析】（1）先根据题意得出ACB ECA D D ∽，再由直角三角形的性质得出CD AD =，由90CAD ABC Ð+Ð=°可得出90ACD EAC Ð+Ð=°，进而可得出90AFC Ð=°；（2）根据AE CD ^可得出90EFC Ð=°，ACE EFC Ð=Ð，故可得出ECF EAC D D ∽，再由点E 是BC的中点可知CE BE =，故BE EF EA BE=，根据BEF AEB Ð=Ð得出BEF AEB D D ∽，进而可得出结论．【解答】证明：（1）2AC CE CB =×Q ，\AC CB CE AC=．又90ACB ECA Ð=Ð=°Q ACB ECA \D D ∽，ABC EAC \Ð=Ð．Q 点D 是AB 的中点，CD AD \=，ACD CAD\Ð=Ð90CAD ABC Ð+Ð=°Q ，90ACD EAC \Ð+Ð=°90AFC \Ð=°，AE CD\^（2）AE CD ^Q ，90EFC \Ð=°，ACE EFC\Ð=Ð又AEC CEF Ð=ÐQ ，ECF EAC\D D ∽\EC EF EA EC=Q 点E 是BC 的中点，CE BE \=，\BE EF EA BE=BEF AEB Ð=ÐQ ，BEF AEB\D D ∽EBF EAB \Ð=Ð．【点评】本题考查的是相似三角形的判定与性质，熟知相似三角形的判定定理是解答此题的关键．【变式3-10】（2022秋•嘉定区期末）如图，已知在ABC D 中，AB AC =，点D 、E 分别在边CB 、AC 的延长线上，且DAB EBC Ð=Ð，EB 的延长线交AD 于点F ．（1）求证：DBF EBC D D ∽；（2）如果AB BC =，求证：2EC DF DA =×．【分析】（1）先根据三角形外角的定义得到D E Ð=Ð，即可证明DBF EBC D D ∽；（2）先证明DBF DAB D D ∽得到2DB DA DF =×，再根据AAS 证明ADB BEC D @D ，即可证明．【解答】证明：（1）AB AC =Q ABC ACB \Ð=Ð．ABC ÐQ 、ACB Ð分别是ADB D 和BCE D 的外角，ABC DAB D \Ð=Ð+Ð，ACB EBC E Ð=Ð+Ð，DAB EBC Ð=ÐQ ，D E \Ð=Ð．又DBF EBC Ð=Ð，DBF EBC \D D ∽．（2）DBF EBC Ð=ÐQ ，DAB EBC Ð=Ð，DBF DAB \Ð=Ð．D D Ð=ÐQ ，DBF DAB \D D ∽，\DB DF DA DB=，即2DB DA DF =×．在ADB D 和BEC D 中，D E DAB EBC AB BC Ð=ÐìïÐ=Ðíï=î，()ADB BEC AAS \D @D ，BD EC \=，2EC DF DA \=×．【点评】本题考查了相似三角形的判定和性质、全等三角形的判定和性质、等腰三角形的性质，熟练掌握各知识点是解题的关键．【变式3-11】（2022秋•闵行区期末）已知：如图，在ABC D 中，AB AC =，点D 、E 分别是边AC 、AB 的中点，DF AC ^，DF 与CE 相交于点F ，AF 的延长线与BD 相交于点G ．（1）求证：ABD ACE Ð=Ð；（2）求证：2CD DG BD =×．【分析】（1）利用等腰三角形的性质和全等三角形的判定与性质解答即可；（2）利用线段垂直平分线的性质和（1）的结论，依据相似三角形的判定与性质解答即可．【解答】证明：（1）Q 点D 、E 分别是边AC 、AB 的中点，12AE AB \=，12AD AC =，AB AC =Q ，AD AE \=．在ADB D 和AEC D 中，AD AE BAD CAE AB AC =ìïÐ=Ðíï=î，()ADB AEC SAS \D @D ，ABD ACE \Ð=Ð；（2）DF AC ^Q ，点D 是边AC 的中点，DF \是AC 的垂直平分线，FA FC \=，FAC ACE \Ð=Ð．由（1）知：ABD ACE Ð=Ð，FAC ABD \Ð=Ð．ADG BDA Ð=ÐQ ，ADG BDA \D D ∽，\AD BD DG AD=，2AD DG BD \=×．Q 点D 是边的中点，12AD AC CD \==，2CD DG BD \=×．【点评】本题主要考查了等腰三角形的性质，全等三角形的判定与性质，线段垂直平分线的性质，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．【变式3-12】（2023秋•静安区期中）已知：如图，四边形ABCD 是平行四边形，在边AB 的延长线上截取BE AB =，点F 在AE 的延长线上，CE 和DF 交于点M ，BC 和DF 交于点N ．联结BD ．（1）求证：BND CNM D D ∽；（2）如果2AD AB AF =×，求证：CM AB DM CN ×=×．【分析】（1）利用平行四边形的性质得AB CD =，//AB CD ，再证明四边形BECD 为平行四边形得到//BD CE ，根据相似三角形的判定方法，由//CM DB 可判断BND CNM D D ∽；（2）先利用2AD AB AF =×可证明ADB AFD D D ∽，则1F Ð=Ð，再根据平行线的性质得4F Ð=Ð，23Ð=Ð，所以34Ð=Ð，加上NMC CMD Ð=Ð，于是可判断MNC MCD D D ∽，所以::MC MD CN CD =，然后利用CD AB =和比例的性质即可得到结论．【解答】证明：（1）Q 四边形ABCD 是平行四边形，AB CD \=，//AB CD ，而BE AB =，BE CD \=，而//BE CD ，\四边形BECD 为平行四边形，//BD CE \，//CM DB Q ，BND CNM \D D ∽；（2）2AD AB AF =×Q ，::AD AB AF AD \=，而DAB FAD Ð=Ð，ADB AFD \D D ∽，1F \Ð=Ð，//CD AF Q ，//BD CE ，4F \Ð=Ð，23Ð=Ð，34\Ð=Ð，而NMC CMD Ð=Ð，MNC MCD \D D ∽，::MC MD CN CD \=，MC CD MD CN \×=×，而CD AB =，CM AB DM CN \×=×．【点评】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．【考点题型四】相似三角形的应用（共8小题）【例4】（2024秋•静安区校级月考）某班某同学要测量学校升旗的旗杆高度，在同一时刻，量得某一同学的身高是1.5m ，影长是1m ，旗杆的影长是8m ，则旗杆的高度是 m ．【分析】因为在同一时刻同一地点任何物体的高与其影子长比值是相同的，所以同学的身高与其影子长的比值等于旗杆的高与其影子长的比值．【解答】解：设旗杆的高度为x ，根据在同一时刻同一地点任何物体的高与其影子长比值是相同的，得：1.518x =，1.58121x m ´\==，\旗杆的高度是12m ．故答案为：12．【点评】本题考查了相似三角形的应用，解题关键是知道在同一时刻同一地点任何物体的高与其影子长比值是相同的．【变式4-1】（2023秋•浦东新区校级期中）如图，在一块斜边长30cm 的直角三角形木板(Rt ACB)D 上截取一个正方形CDEF ，点D 在边BC 上，点E 在斜边AB 上，点F 在边AC 上，若:1:3AF AC =，则这块木板截取正方形CDEF 后，剩余部分的面积为 ．【分析】设AF x =，根据正方形的性质用x 表示出EF 、CF ，证明AEF ABC D D ∽，根据相似三角形的性质求出BC ，根据勾股定理列式求出x ，根据三角形的面积公式、正方形的面积公式计算即可．【解答】解：设AF x =，则3AC x =，Q 四边形CDEF 为正方形，2EF CF x \==，//EF BC ，AEF ABC \D D ∽，\13EF AF BC AC ==，6BC x \=，在Rt ABC D 中，222AB AC BC =+，即22230(3)(6)x x =+，解得，x =，AC \=，BC =，\剩余部分的面积21100()2cm =´-=，故答案为：2100cm ．【点评】本题考查的是相似三角形的应用、正方形的性质，掌握相似三角形的判定定理和性质定理是解题的关键．【变式4-2】（2024•静安区校级模拟）如图，用一个卡钳1(,)3OC OD AD BC OB OA ===测量某个零件的内孔直径AB ，量得CD 长度为6cm ，则AB 等于 cm ．AB 的长．【解答】解：Q 13OC OD OB OA ==，COD AOB Ð=Ð，COD AOB \D D ∽，:3AB CD \=，6CD cm =Q ，6318()AB cm \=´=，故答案为：18．【点评】本题考查相似三角形的应用，求出AB 的值是解答本题的关键．【变式4-2】（2023秋•浦东新区校级期中）图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB = ．【分析】高脚杯前后的两个三角形相似．根据相似三角形的判定和性质即可得出结果．【解答】解：如图：过O作OM CD^，垂足为M，过O作ON AB^，垂足为N，//CD ABQ，CDO ABO\D∽，即相似比为CD AB，\CD OMAB ON=，1578() OM cm=-=Q，1174()ON cm=-=，\684 AB=，3 AB cm\=，故答案为：3cm．【点评】本题考查相似三角形的应用，解本题的关键熟练掌握相似三角形的判定与性质．【变式4-3】（2023秋•松江区校级月考）如图，有一块面积等于21200cm的三角形纸片ABC，已知底边BC 与底边上的高的和为100cm（底边BC大于底边上的高），要把它加工成一个正方形纸片，使正方形的一边EF在边BC上，顶点D、G分别在边AB、AC上．（1）求BC和底边上的高；（2）求加工成的正方形纸片DEFG的边长．【分析】（1）设BC a=cm，BC边上的高AH为b cm，根据题意得出方程组求出BC和AH；（2）设DG DE x==cm，再由平行线得出ADG ABCD D∽，由相似三角形对应高的比等于相似比得出比例式，即可得出结果．【解答】解：（1）设BC a=cm，BC边上的高AH为b cm，DG DE x==cm，根据题意得：1001200a bab+=ìí=î，解得：6040ab=ìí=î，或4060ab=ìí=î（不合题意，舍去），60BC cm\=，40AH b cm==；（2）//DG BCQ，ADG ABC\D D∽，\AN DGAM BC=，即404060x x-=，解得：24x=，即加工成的正方形铁片DEFG的边长为24cm．【点评】本题考查了方程组的解法、相似三角形的运用；熟练掌握方程组的解法，证明三角形相似得出比例式是解决问题的关键．【变式4-4】（2023秋•宝山区期中）某社区两条平行的小道之间有一块三角形空地．如图，这两条小道m、n之间的距离为9米，ABCD表示这块空地，36BC=米．现要在空地内划出一个矩形DGHE区域建造花坛，使它的一边在BC上，其余两个顶点分别在边AB、AC上．（1）如果矩形花坛的边:1:2DG DE=，求出这时矩形花坛的两条邻边的长；（2）矩形花坛的面积能否占空地面积的59？请作出判断并说明理由．【分析】（1）过点A 作AM DE ^，垂足为M ，延长AM 交BC 于点N ，根据题意可得：9AN =米，DG MN =，AN BC ^，再根据矩形的性质可得//DE BC ，从而可得ADE ABC Ð=Ð，AED ACB Ð=Ð，然后证明A 字模型相似ADE ABC D D ∽，从而利用相似三角形的性质进行计算，即可解答；（2）设DG x =米，利用（1）的结论可得：ADE ABC D D ∽，从而利用相似三角形的性质可得(364)DE x =-米，然后根据题目的已知可得25136492x x BC AN -=´×，进行计算即可解答．【解答】解：（1）过点A 作AM DE ^，垂足为M ，延长AM 交BC 于点N ，由题意得：9AN =米，DG MN =，AN BC ^，Q 四边形DGHE 是矩形，//DE BC \，:1:2DG DE =Q ，2DE DG \=，//DE BC Q ，ADE ABC \Ð=Ð，AED ACB Ð=Ð，ADE ABC \D D ∽，\AM DE AN BC =，\92936DG DG -=，解得：6DG =，212DE DG \==，\这时矩形花坛的两条邻边的长分别为6和12；（2）矩形花坛的面积不能占空地面积的59，理由：设DG x =米，。

专题02 相似三角形重要模型-母子型（共边共角模型）相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

在相似三角形中存在众多的相似模型，其中“母子型”相似模型应用较为广泛，深入理解模型内涵，灵活运用相关结论可以显著提高解题效率，本专题重点讲解相似三角形的“母子”模型。

母子相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等；②分子和分子组成一个三角形、分母和分母组成一个三角形；③第②步成立，直接从证这两个三角形相似，逆向证明到线段乘积相等；④第②步不成立，则选择替换掉线段比例式中的个别线段，之后再重复第③步。

模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形（通常有一个公共顶点和另外一个不是公共的顶点，由于小三角形寓于大三角形中，恰似子依母怀），也是有一个“公共角”，再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似．图1 图2 图31）“母子”模型（斜射影模型）条件：如图1，∠C=∠ABD；结论：△ABD∽△ACB，AB2＝AD·AC.2）双垂直模型（射影模型）条件:如图2，∠ACB=90o，CD⊥AB；结论：△ACD∽△ABC∽△CBD；CA2＝AD·AB，BC2＝BD·BA，CD2＝DA·DB.3）“母子”模型（变形）条件:如图3，∠D=∠CAE，AB=AC；结论：△ABD∽△ECA；例1．（2022·贵州贵阳·中考真题）如图，在ABC V 中，D 是AB 边上的点，B ACD Ð=Ð，:1:2AC AB =，则ADC V 与ACB △的周长比是（ ）A．B ．1:2C ．1:3D ．1:4【答案】B 【分析】先证明△ACD ∽△ABC ，即有12AC AD CD AB AC BC ===，则可得12AC AD CD AB AC BC ++=++，问题得解．【详解】∵∠B =∠ACD ，∠A =∠A ，∴△ACD ∽△ABC ，∴AC AD CD AB AC BC ==，∵12AC AB =，∴12AC AD CD AB AC BC ===，∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++，∴△ADC 与△ACB 的周长比1:2，故选：B ．【点睛】本题主要考查了相似三角形的判定与性质，证明△ACD ∽△ABC 是解答本题的关键．例2．（2023·广东·九年级课时练习）如图，在 Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，已知AD ＝94,55BD =，那么BC ＝_______．【点睛】本题考查三角形相似的判定和性质，牢记相关知识点并能结合图形灵活应用是解题关键．例3.（2022.山西九年级期中）如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．证明：（1）∵△PCD是等边三角形，∴∠PCD＝∠PDC＝∠CPD＝60°，∴∠ACP＝∠PDB＝120°，∵∠APB＝120°，∴∠APC+∠BPD＝60°，∵∠CAP+∠APC＝60°∴∠BPD＝∠CAP，∴△ACP∽△PDB；（2）由（1）得△ACP∽△PDB，∴，∵△PCD是等边三角形，∴PC＝PD＝CD，∴，∴CD2＝AC•BD．例4．（2022·浙江·九年级期中）如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，且ADAC＝ACAB．（1）求证△ACD∽△ABC；（2）若AD＝3，BD＝2，求CD的长．【点睛】本题考查相似三角形的判定与性质，掌握相似三角形的判定定理与性质是解题的关键．例5．（2022.浙江中考模拟）如图，在V ABC中，∠ACB＝90°，CD⊥AB．（1）图1中共有 对相似三角形，写出来分别为　（不需证明）：（2）已知AB＝5，AC＝4，请你求出CD的长：（3）在（2）的情况下，如果以AB为x轴，CD为y轴，点D为坐标原点O，建立直角坐标系（如图2），若点P从C点出发，以每秒1个单位的速度沿线段CB运动，点Q出B点出发，以每秒1个单位的速度沿线段BA运动，其中一点最先到达线段的端点时，两点即刻同时停止运动；设运动时间为t秒是否存在点P，使以点B、P、Q为顶点的三角形与△ABC相似？若存在，请求出点P的坐标；若不存在，请说明理由．【答案】（1）3，V ABC∽V ACD，V ABC∽V CBD，V ACD∽V CBD；（2）125；（3）存在，(2740，32)，(98，910)【分析】（1）根据两角对应相等的两三角形相似即可得到3对相似三角形，分别为：△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD．（2）先在△ABC中由勾股定理求出BC的长，再根据△ABC的面积不变得到1 2AB•CD＝12AC•BC，即可求出CD的长．（3）由于∠B公共，所以以点B、P、Q为顶点的三角形与△ABC相似时，分两种情况进行讨论：①△PQB∽△ACB；②△QPB∽△ACB．【详解】解：（1）图1中共有3对相似三角形，分别为：△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD．证明：∵CD⊥AB，∴∠ADC=∠ACB=90°，又∵∠A=∠A，∴△ADC∽△ACB同理可证：△ABC∽△CBD，△ACD∽△CBD．故答案为：3；△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD．（2）如图2中，在△ABC中，∵∠ACB＝90°，AB＝5，AC＝4，∴BC3．∵△ABC的面积＝12AB•CD＝12AC•BC，∴CD＝AC BCAB×＝125．（3）存在点P，使以点B、P、Q为顶点的三角形与△ABC相似，理由如下：在△BOC中，∵∠COB＝90°，BC＝3，OC＝125，∴OB＝95．分两种情况：①当∠BQP ＝90°时，如图2①，此时△PQB ∽△ACB ，∴BP AB ＝BQ BC ，∴353t t -=，解得t ＝98，即98BQ CP ==，∴915388BP BC CP =-=-=．在△BPQ 中，由勾股定理，得32PQ ===，∴点P 的坐标为273(,)402；②当∠BPQ ＝90°时，如图2②，此时△QPB ∽△ACB ，∴BP BQ BC AB =，∴335t t -=，解得t ＝158，即15159,3888BQ cP BP BC CP ===-=-=，过点P 作PE ⊥x 轴于点E ．∵△QPB ∽△ACB，∴PE BQ COAB ×=，即1581255PE =，∴PE ＝910．在△BPE 中，2740BE ===，∴92795408OE OB BE =-=-=，∴点P 的坐标为99(,)810，综上可得，点P 的坐标为(2740，32)；(98，910)．【点睛】本题属于相似形综合题，考查了相似三角形的判定与性质，勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题，属于中考常考题型．例6．（2022·浙江绍兴·九年级期末）如果两个相似三角形的对应边存在2倍关系，则称这两个相似三角形互为母子三角形．（1）如果DEF V 与ABC V 互为母子三角形，则DE AB的值可能为（ ）A ．2 B ．12 C ．2或12（2）已知：如图1，ABC V 中，AD 是BAC Ð的角平分线，2,AB AD ADE B =Ð=Ð．求证：ABD △与ADE V 互为母子三角形．（3）如图2，ABC V 中，AD 是中线，过射线CA 上点E 作//EG BC ，交射线DA 于点G ，连结BE ，射线BE 与射线DA 交于点F ，若AGE V 与ADC V 互为母子三角形．求AG GF 的值．AG DG \=，DBF △．A ．ABP CÐ=ÐB ．APB Ð【答案】C 【分析】根据相似三角形的判定方法逐项判断即可．2.（2023成都市九年级期中）如图，矩形ABCD 中，F 是DC 上一点，BF ⊥AC ，垂足为E ，AD AB =12，△CEF 的面积为S 1，△AEB 的面积为S 2，则S 1S 2的值等于（ ）A ．116B ．15C ．14D ．125【解答】解：∵AD AB =12，∴设AD ＝BC ＝a ，则AB ＝CD ＝2a ，∴AC =，∵BF ⊥AC ，∴△CBE ∽△CAB ，△AEB ∽△ABC ，∴BC 2＝CE •CA ，AB 2＝AE •AC∴a 2＝CE ，4a 2＝AE ，∴CE AE =，∴CE AE =14，∵△CEF ∽△AEB ，∴S 1S 2=（CE AE）2=116，故选：A ．3.（2023浙江九年级期中）如图，在△ABC 中，∠ACB ＝90°，CD 是AB 边上的高．如果BD ＝4，CD ＝6，那么BC ：AC 是（ ）A ．3：2B ．2：3C ．3D ．2【答案】B 【解答】解：∵∠ACB ＝90°，CD 是AB 边上的高，∴∠ADC ＝∠CDB ＝∠ACB ＝90°，∵∠A +∠B ＝90°，∠A +∠ACD ＝90°，∴∠ACD ＝∠B ，∴△ACD ∽△CBD ，∴AC=CD =6=3∴BC =2，故选：B ．【答案】12【分析】过点B 作BM AC ∥交CG 的延长线于点96ACG BCG S AG AC S GB BC ===V V 32=，即可求解．【详解】解：如图所示，过点B 作BM AC ∥5．（2023•宜宾）如图，已知直角△ABC 中，CD 是斜边AB 上的高，AC ＝4，BC ＝3，则AD ＝ ．【分析】根据勾股定理求出AB ，根据射影定理列式计算即可．【解答】解：在Rt △ABC 中，AB ＝＝5，由射影定理得，AC 2＝AD •AB ，∴AD ＝＝，故答案为：．【点评】本题考查的是射影定理、勾股定理，在直角三角形中，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．6．（2022·江苏盐城·中考真题）如图，在ABC V 与A B C ¢¢¢V 中，点D 、D ¢分别在边BC 、B C¢¢上，且ACD A C D ¢¢¢∽△△，若___________，则ABDA BD¢¢¢△∽△．请从①BD B D CD C D ¢¢=¢¢；②AB A B CD C D ¢¢=¢¢；③BAD B A D ¢¢¢Ð=Ð这三个选项中选择一个作为条件（写序号），并加以证明．【答案】4【分析】根据条件证明ACD ~V 【详解】解：ADC ACB Ð=ÐQ AC AD AB AC\=，即2AC AB AD =×，8.（2022•惠山区九年级专项）如图，在Rt △ABC 中，∠BAC =90o ，AD ⊥BC 于D ．（1）图中有多少对相似三角形？（2）求证：AB 2=BD g BC ，AC 2=CD g CB ，AD 2=BD g CD ；（3）求证：AB g AC =BC g AD【解析】（1）三对．分别是：△ABD ∽△CBA ；△ACD ∽△BCA ；△ABD ∽△CADD CB A（2）∵△ABD ∽△CBA ，∴AB BD BC AB=．∴AB 2=BD g BC ，∵△ACD ∽△BCA ∴AC CD CB AC =．∴AC 2=CD g CB ，∵△ABD ∽△CAD ，∴AD BD CD AD =，∴AD 2=BC g CD （3）1122ABC S AB AC BC AD ==V g g ，∴AB g AC =BC g AD【答案】(1)是，证明见解析(2)125【分析】（1）由已知可得AC AB AD AC=，从而ACD ABC △∽△，（2）由D 是ABC V 的“理想点”，当D 在AB 上时，证明CD 【详解】（1）解：点D 是ABC V 的“理想点”，理由如下：D Q 是ABC V 的“理想点”，当ACD B Ð=Ð时，ACD ÐQ 90CDB \Ð=°，即CD 是【答案】(1)证明见解析(2)15【分析】（1）根据相似三角形的判断方法，两角分别相等的两个三角形相似，证明即可；（2）根据相似三角形的性质，得BC AB2BAC B BAD ÐÐÐ=\=Q ，ACD BCA ACD ÐÐ=\~Q V ，AC DC AD BC AC AB\==设DC x =，则AD BD a ==-任务：(1)上述材料中的证法似”）．(2)请补全证法2剩余的部分．ABD D \Ð=Ð，CAB Ð\2CAB ABC ÐÐ=Q ，ACB BCD Ð=ÐQ ，AC BC BC CD \=，b a \=【点睛】本题考查了等边对等角，三角形外角的性质，相似三角形的判定与性质．解题的关键在于对知识的熟练掌握与灵活运用．12．（2022·湖北武汉·一模）在Rt △ABC 中，∠ACB =90°，点D 为AB 上一点．（1）如图1，若CD ⊥AB ，求证：AC 2=AD ·AB ；（2）如图2，若AC =BC ，EF ⊥CD 交CD 于H ，交AC 于F ，且49FH HE =，求AD BD的值；（3）如图3，若AC =BC ，点H 在CD 上，∠AHD =45°，CH =3DH ，则tan ∠ACH 的值为________．13．（2023·安徽合肥·九年级期中）ABC V 中，90ABC Ð=°，BD AC ^，点E 为BD 的中点，连接AE 并延长交BC 于点F ，且有AF CF =，过F 点作FH AC ^于点H ．（1）求证：ADE CDB V V ∽；（2）求证：=2AE EF ；（3）若FH BC 的长．14．如图1，在ABC V 中，在BC 边上取一点P ，在AC 边上取一点D ，连AP 、PD ，如果APD △是等腰三角形且ABP △与CDP V 相似，我们称APD △是AC 边上的“等腰邻相似三角形”．（1）如图2，在ABC V 中AB AC =，50B Ð=°，APD △是AB 边上的“等腰邻相似三角形”，且AD DP =，PAC BPD Ð=Ð，请直接写出PAC Ð的度数；（2）如图3，在ABC V 中，2A C Ð=Ð，在AC 边上至少存在一个“等腰邻相似APD △”，请画出一个AC 边上的“等腰邻相似APD △”，并说明理由；（3）如图4，在Rt ABC △中4AB AC ==，APD △是AB 边上的“等腰邻相似三角形”，求出AD 长度的所有可能值．【答案】（1）30°；（2）见解析；（3）28-【分析】（1）只要证明∠A =∠PAB 即可解决问题．（2）如图3中，作∠BAC 的平分线AP 交BC 于P ，作PD ∥AB 交AC 于D ，只要证明DP =DA ，即可解决问题．（3）分三种情形讨论①如图3′中，当DA =DP 时．②如图4中，当PA =PD 时．③如图5中，当AP =AD 时．分别求解即可解决问题．【详解】解：（1）如图2中，∵AB =AC ，DA =DP ，∴∠B =∠C ，∠DAP =∠DPA ，∵∠PAC =∠BPD ，∴∠APC =∠BDP =∠DAP +∠DPA ，∵∠APC =∠B +∠BAP ，∴∠B =∠PAB =50°，∵∠BAC =180°-50°-50°=80°，∴∠PAC =30°故答案为30°．（2）如图3中，作∠BAC 的平分线AP 交BC 于P ，作PD ∥AB 交AC 于D ，∴∠BAP =∠PAD =∠DPA ，∠CPD =∠B ，∵∠CAB =2∠C ，∴∠PAD =∠C ，∴DP =DA ，∴△APD 是等腰三角形且与△APB 与△CDP 相似．（3）如图3′中，当DA =DP 时，设∠APD =∠DAP =x ，①若∠BPD =∠CAP =90°-x ，∠BDP =∠CPA =2x ，∴90°-x +2x +x =180°，∴x =45°，∴三角形都是等腰直角三角形，∴AD =2，②若∠PDB =∠CAP 时，设∠APD =∠DAP =x ，得到∠PDB =∠CAP =2x ，易知x =30°，设AD =a ，则AP ，∵△BPD ∽△CPA ，∴BD PD AC PA =，即44a -=a 如图4中，当PA =PD 时，易知∠PDB 是钝角，∠CAP 是锐角，∴∠PDB=∠CPA，则△BPD≌△CPA，设AD=a，则BD=4-a，BP=BC-CP=BC-BD（2-a）=-4+a，AC=4，∴a=4，解得：a=8-如图5中，当AP=AD时，设∠APD=∠ADP=x，则∠DAP=180°-2x，易知∠PDB为钝角，∠CAP为锐角，∴∠PDB=∠CPA=180°-x，∠CAP=90°-∠DAP=90°-（180°-2x）=2x-90°，在△APC中，2x-90°+180°-x+45°=180°，解得x=45°，不可能成立．综上所述．AD的长为28-．【点睛】本题考查相似三角形综合题、等腰直角三角形的性质、角平分线的定义、相似三角形的判定和性质等知识，解题的关键是理解题意，学会用构建方程的思想思考问题，属于中考压轴题．15．（2022•静安区期末）如图1，四边形ABCD中，∠BAD的平分线AE交边BC于点E，已知AB＝9，AE＝6，AE2＝AB•AD，且DC∥AE．（1）求证：DE2＝AE•DC；（2）如果BE＝9，求四边形ABCD的面积；（3）如图2，延长AD、BC交于点F，设BE＝x，EF＝y，求y关于x的函数解析式，并写出定义域．【分析】（1）先证明△ABE∽△AED，可得∠AEB＝∠ADE，再由平行线性质可推出∠ADE＝∠DCE，进而证得△ADE∽△ECD，根据相似三角形性质可证得结论；（2）如图2，过点B作BG⊥AE，运用等腰三角形性质可得G为AE的中点，进而可证得△ADE≌△ECD（SAS），再求得S△ABE＝×AE×BG＝18，根据△ABE∽△AED 且相似比为3：2，可求得S△AED＝S△CDE＝8，由S＝S△ABE+S△AED+S△CDE可求得答案；（3）四边形ABCD由△ABE∽△AED，可求得：DE＝x，进而得出DC＝x2，再利用△ADE∽△ECD，可得：CE＝x，再利用DC∥AE，可得△AEF∽△DCF，进而求得：CF＝EF，再结合题意得出答案．【解答】（1）证明：如图1，∵AE平分∠BAD，∴∠BAE＝∠DAE，∵AE2＝AB•AD，∴＝，∴△ABE∽△AED，∴∠AEB＝∠ADE，∵DC∥AE，∴∠AEB＝∠DCE，∠AED＝∠CDE，∴∠ADE＝∠DCE，∴△ADE∽△ECD，∴＝，∴DE2＝AE•DC；（2）解：如图2，过点B作BG⊥AE，∵BE＝9＝AB，∴△ABE是等腰三角形，∴G为AE的中点，由（1）可得△ADE、△ECD也是等腰三角形，∵AE2＝AB•AD，AB＝BE＝9，AE＝6，∴AD＝4，DE＝6，CE＝4，AG＝3，∴△ADE≌△ECD（SAS），在Rt△ABG中，BG＝＝＝6，∴S△ABE＝×AE×BG＝×6×6＝18，∵△ABE∽△AED且相似比为3：2，∴S△ABE：S△AED＝9：4，∴S△AED＝S△CDE＝8，∴S四边形ABCD＝S△ABE+S△AED+S△CDE＝18+8+8＝34；（3）解：如图3，由（1）知：△ABE∽△AED，∴＝，∵BE＝x，AB＝9，AE＝6，AE2＝AB•AD，AD＝4，∴＝，∴DE＝x，由（1）知：DE2＝AE•DC，∴DC＝x2，∵△ADE∽△ECD，∴＝＝，∴CE＝x，∵DC∥AE，∴△AEF∽△DCF，∴＝＝，∴CF＝EF，∴＝＝＝，∴y＝EF＝CE＝×x＝，∵即，∴3＜x＜9，∴y关于x的函数解析式为y＝，定义域为3＜x＜9．【点评】本题是相似三角形综合题，考查了角平分线定义，平行线的性质，勾股定理，相似三角形的判定和性质，等腰三角形的性质，三角形面积等知识，熟练掌握相似三角形的判定和性质是解题关键．16．（2022·安徽·校联考三模）在ABC V 中，2ABC ACB Ð=Ð，BD 平分ABC Ð．（1）如图1，若3AB =，5AC =，求AD 的长．（2）如图2，过A 分别作AE AC ^交BC 于E ，AF BD ^于F ．①求证：ABC EAF Ð=Ð；②求BFAC的值．(1)求证：ABE CAD △△≌；(2)求证：AC FB ∥；(3)若点D ，E ，F 在同一条直线上，如图2，求A BB C【答案】(1)见解析(2)见解析(3)2是中位线，则EG CB ∥，加上第二小题结论就能得到四边形BCEF 是平行四边形，那么BC AD =，然后通过三角形外角的性质，可以证得ADE ACD Ð=Ð，就能证ACD V 和ADE V 是一组子母型相似，然后根据相似比可得最终答案．【详解】（1）解：Q 将ACD V 绕点C 逆时针旋转得到FCE △，FCE ACD \△≌△，CE CD \=，2AC CD =Q ，2AC CE \=，2AE AC CE CE CE CE CD \=-=-==，DC ABQ ∥DCA EAB \Ð=Ð，在ABE V 和CAD V 中，AE CD EAB DCA AB CA =ìïÐ=Ðíï=îQ ，()SAS ABE CAD \△≌△．（2）解：由（1）得BE AD =，ABE CAD Ð=Ð，CEF CDA Q △≌△，FE AD =∴，EFC DAC Ð=Ð，BE FE \=，EFC EBA Ð=Ð，EFB EBF \Ð=Ð，OFB EFB EFC Ð=Ð-ÐQ ，OBF EBF EBA Ð=Ð-Ð，OFB OBF \Ð=Ð，ECF DCA Ð=ÐQ ，OAC OCA \Ð=Ð，180OCA OAC AOC Ð+Ð+Ð=°Q ，180OBF OFB BOF Ð+Ð+Ð=°，又AOC BOF Ð=Ð，OCA OAC OBF OFB \Ð+Ð=Ð+Ð，即22CAO FOB Ð=Ð，（1）求证：2=×；AE FE BEÐ的大小；（2）求AFC。

相似的共边共角模型一、 共边共角模型 已知：∠1=∠2 结论：△ACD ∽△ABC 模型分析上图中，不仅要熟悉模型，还要熟记模型的结论，有时候题目中会给出三角形边的乘积或比例关系，要能快速判断题中的相似三角形，模型中由△ACD ∽△ABC ，进而可以得到2AC AD AC =。

例1：如图，D 是△ABC 边BC 上的一点，AB =4， AD =2，∠DAC =∠B ，如果△ABD 的面积为15，那么△ACD 的面积为 。

例2：如图，在Rt △ABC 中，∠BAC -90°，AD ⊥BC 于D 。

（1）图中有多少对相似三角形？写出来； （2）求证：2AC AD AC =精练1．如图所示，能判定△ABC ∽△DAC 的有 ； ①∠B =∠DAC ；②∠BAC =∠ADC ； ③2AC DC BC =；④2AD BD BC =。

精练2．如图①，Rt △ABC 中，∠ACB -90°，CD ⊥AB ，我们可以利用△ABC ∽△ACD 证明2AC AD AB =，这个结论我们称之为射影定理，结论运用：如图②，正方形ABCD 的边长为6，点O 是对角线AC 、BD 的交点，点E 在CD 上，过点C 作CE ⊥BE ，垂足为F ，连接OF 。

（1）试利用射影定理证明△BOF ∽△BED ； （2）若DE =2CE ，求OF 的长。

DBCADBCADBCA2图FABDC图1DBCAOE 21DBCA精练3．已知△AMN 是等边三角形，∠BAC =120°。

求证： （1）2AB BM BC =； （2）2AC CN CB =； （3）2MN BM NC =。

精练4．如图，AB 是半圆O 的直径，C 是半圆上的一点，过C 作CD ⊥AB 于D ，AC =AD ：DB =4：1。

求CD 的长。

BCAM N。

相似三角形经典的基本图形总结(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（相似三角形经典的基本图形总结(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为相似三角形经典的基本图形总结(word版可编辑修改)的全部内容。

相似中的基本图形练习相似三角形是初中数学中重要的内容，应用广泛，可以证明线段的比例式；也可证明线段相等、平行、垂直等；还可计算线段的长、比值，图形面积及比值。

而识别（或构造）A字型、X字型、母子相似型、旋转型、一线三角形等基本图形是解证题的关键。

1．A字型及变形△ABC 中， AD=2，BD=3，AE=1 （1）如图1，若DE∥BC ，求CE的长（2)如图2，若∠ADE=∠ACB ,求CE的长2。

X字型及变形(1)如图1，AB∥CD,求证：AO:DO=BO：CO（2）如图2，若∠A=∠C ，求证：AO×DO=BO×CO3。

母子相似型及变形（1）如右图，在△ABC中， AD把△ABC分成两个三角形△BCD和△CAD,当∠ACD=∠B时,说明△CAD与△ABC相似.说明：由于小三角形寓于大三角形中，恰似子依母怀，故被称为“母子三角形"(2）如图, Rt △ABC 中，CD⊥AB，求证：AC²=ADxAB，CD²=ADxBD,4。

旋转型如图，若∠ADE=∠B,∠BAD=∠CAE，说明△ADE与△ABC相似A D BABCDE5。

一线三等角型（1）在矩形ABCD 中，AB=6，AD=12,点E 在AD 边上，且AE=8,EF ⊥BE 交CD 于△ABE ∽△DEF ；求EF 的长（2）等边△ABC 的边长为3，P 为BC 上一点，且BP=1，D 为AC 上一点,若∠CD 的长？练习题1、如图1，在△ABC 中，中线BE 、CD 相交于点G ，则BCDE = ；2、如图2，在△ABC 中， ∠B=∠AED ，AB=5,AD=3，3、如图3，△ABC 中,M N 在BC 上，BC=2AB,∠BMN= ∽△ ，相似比为 ，NCBN= ； 5、如图5，在△ABC 中，BC=12cm,点D 、F 是AB 的三等分点，点E 、G 是AC 的三等分点，则DE+FG+BC=二、选择题6、如图６,在△ABC 中，高BD 、CE 交于点O ，下列结论错误的是( )A 、CO ·CE=CD ·CAB 、OE ·OC=OD ·OBC 、AD ·AC=AE ·AB D 、CO ·DO=BO ·EO7、如图７,D 、E 分别是△ABC 的边AB 、AC 上的点， ADBD =CEAE =3，且∠AED=∠B,DE=5，求BC 长A BCD E G图1图2ABCDEACCP BCA BCDF图5GE C11。