当前位置：文档之家 › 第六章 光学系统的像差

第六章 光学系统的像差

  • 格式：ppt
  • 大小：708.01 KB
  • 文档页数：80

下载文档原格式

  / 80

合集下载

工程光学讲稿像差

工程光学讲稿像差

n
n'( >n)
UA O A'
物点位于球面旳球心处，即 L=r此时物点
发出旳全部光线将沿球面旳法线方向入射
，即入射角I=0根据折射定律，折射角也
C
-U
A,A'
I'=0,光线无偏折地经过球面，像点也将位
于球心处，即L'=r。
(3) sinI’－sinU＝0，即I’＝U，因为
L0
sin I' n sin I / n' n(L r)sinU / n'r
§6－2 轴上点旳球差
一、 球差定义及表达措施
1、轴向球差
由实际光线旳光路计算公式知，当物距L为定值时，像距L’与入射高 度h1及孔径角U有关，伴随孔径角旳不同，像距L‘是变化旳，即如图所示：
轴上点A点发出旳光束，对于光轴附近旳光用近轴光路计算公式，像点为 A0’（看作高斯像点），对于实际光线采用实际光计算公式，成像于A’1 （实际像）。
(sin I (L-r)sinU r)
故可得： L （n Ln'） rn/nnn ' r
同I '理，U由sin I sUinU' '可得出
L ' 0A'
L' (n n')r / n'
I
-U AC
n
-I' n'( <n)
由上式拟定得共轭点，不论孔径角U多大，均不产生球差。由上式也可 得出，nL＝n’L’ ，则垂轴放大率β＝nL’/n’L=(n/n’)2
单色像差——光学系统对单色光成像时所产生旳像差。 几何像差： 球差、彗差、像散、场曲、畸变 。
色差——不同波长成像旳位置及大小都有所不同。

第六章像差理论

第六章像差理论

轴外点发出充满入瞳的一束光，这束光以通过入瞳中心的
主光线为对称中心，其中包含主光线和光轴的平面称为子
午面。过主光线且垂直于子午面的平面为弧矢面。显然子
午面是光束的对称面。
9
对子午面的情况：主光线Z和一对上下光线a、b，折射前， 上下光线与主光线对称，折射后，上下光线对不再对称于主 光线，它们的交点偏离了主光线。
14
弧矢 子午像点和弧矢像点 像面 都位于主光线上，通
子午 常可将子午像距和弧 像面 矢像距投影到光轴上，
像平 则像散表示为：
面
主光 线
xts lt ls
15
像散的存在使轴外物点的成像在子午方向和弧矢方向各 有不同的聚焦位置。子午方向的光线聚焦成垂直于子午 面的短焦线T′，而弧矢方向的光线聚焦成子午面内的短 焦线S′，两焦线之间是一系列由线到椭圆到圆再到椭圆 再到线的弥散斑变化。 因此，接收器在像方找不到同时能使各个方向的线条都 清晰的像面位置。
xt lt l

xs

ls

l
有像散必然有场曲，但如果没有像散存在，像面弯曲现
象也会因球面光学系统的本身特性而存在。
球面 物体
折射 球面
理想像 平面
17
根据物像同向移动的原则，B的像点进一步偏离理想像平面 P′，这种偏离随视场的大小而变化，使得垂直于光轴的平面 物体经球面成像后变得 弯曲，这种弯曲还没有考虑像散的 影响，把像散为0时的像面弯曲称为匹兹伐场曲。
Lm A1hm2 A2hm4 0 A1 A2hm2
L
h

2A1h 4A2h3
0
h 0.707hm
此时，在0.707孔径处的光线具有最大剩余球差。校正球

第六章 光线的光路计算及像差理论

第六章 光线的光路计算及像差理论
a ' z a a
下光线tgUb ( y h)
y ( L l )tgU
' z '
' z ' b
y ( L l )tgU
' b ' b '
3.折射平面和反射面的光路计算 折射平面远轴光线的光路计算公式： I U

sin I n sin I
'
n
'
U ' I ' L' LtgU tgU '
' 1 ' 2
' k 1
d k 1
校对公式：h lu l 'u '，J n 'u ' y ' nuy
' 求焦距公式：令1 , u1 , f ' h1 / uk l
轴外点近轴光线光路计算 （第二近轴光线光路计 算）：求出理想像高。

初始数据：l z , u z y /(l z l1 ) 像高数据：y (l l )u
1
n
作业
1，2，11，12，17
路计算 2.轴外点沿主光线的细光束光路计算 3.子午面的空间光线光路计算
二、子午面内的光线光路计算： 1.近轴光线光路计算：求出理想像的位置
和大小

近轴光线光路计算
（第一近轴光线光路计算）：求出理想像的位置
l r i u r n i' i n' u' u i i' i' l ' r (1 ) u'
第六章 光线的光路计算 及像差理论
实际光学系统与理想系统之间存在差异；实际像和 理想像之间的差异称为像差。

光学系统的像差

光学系统的像差

25
位置色差是描述2种色光对轴上物点成像 位置差异的色差。
26
正透镜位置色差图示
白光 A
C
F AC′
AF′
LF LC
-LFC
27
P
径轴 光上 线物 不点 聚发 焦出 于的 一大 点孔
28
负透镜位置色差图示
A
LFC -LF -LC
-L
29
因色差的存在，轴上点成像是一个弥散斑 ， 在a点和在c点看到的弥散斑颜色有何不同？
B
17
弧矢彗差：弧矢面上前、后光线的交点BS′到主 光线在垂直光轴方向的偏离，称为弧矢彗差，用
符号KS′表示。
18
19
畸变的产生
对于一般实际光学系统来说，只有在近 轴区垂轴放大率才是常数。当视场增大时， 像的垂轴放大率便会随视场变化而异，这将 会使像相对于原物失去相似性。这种使像变 形的成像缺陷就称为畸变。
33
上排为位置色差，下排为球差，两者均为轴上像差
34
35
倍率色差
此是一种因不同色光成像的高度（也即 倍率）不同而造成的像大小差异的色差。
它是以两种色光（此即F光和C光）的 主光线在高斯像面上的交点高度之差来度量， 以符号YFC′表示之。
36
倍率色差图示
入瞳 A
-YFC
BC′ C
F
BF′ YF YC
41
像散和场曲
轴外物点发出的同心 光束，由于此斜向细 光束的子午面和弧矢 面相对折射球面的位 置不同，使子午和弧 矢面在球面上的截线 曲率不同。使水平方 向和竖直方向的光线 的聚焦点在不同平面 上
42
（2）像散（轴外点细光束）
TS
像 面
物

工程光学 第六章 光线的光路计算及像差理论

工程光学 第六章 光线的光路计算及像差理论
f'h1/u'k
第二节 光线的光路计算
2、轴外点近轴光线 (又称第二近轴光线) ➢是对轴外点而言的， ➢一般要对五个视场： 0.3, 0.5, 0.707，0.85, 1 的物点
分别进行近轴光线光路计算，以求出不同视场的主 光线与理想像面的交点高度，即理想像高y’k。
第二节 光线的光路计算
(二)远轴光线的光路计算 1、轴上点远轴光线 ➢ 轴上点远轴光线的光路计算的初始数据是L1，
第一节 概 述
一、基本概念
除平面反射镜成像之外，没有像差的光学系统是不 存在的。
实践表明: 完全消除像差也是不可能的，且没有必要的。
第一节 概 述
二、像差计算的谱线选择
计算和校正像差时的谱线选择主要取决于光能接收 器的光谱特性。
基本原则是： ➢ 对光能接收器的最灵敏的谱线校正单色像差, ➢ 对接收器所能接收的波段范围两边缘附近的谱
➢同一光学介质对不同的色光有不同的折射率 ➢白光进入光学系统后，由于折射率不同而有不同的
光程， ➢这样就导致了不同色光成像的大小和位置也不相同
第一节 概 述
一、基本概念
(5)这种不同色光的成像差异称为色差。
色差有两种：位置色差、倍率色差
第一节 概 述
一、基本概念
➢以上讨论是基于几何光学的， ➢上述七种像差称为几何像差。
第一节 概 述
二、像差计算的谱线选择
1、目视光学系统
目视光学系统的接收器是人的眼晴。只对波长在 380—760nm范围内的波段有响应，其中最灵敏的 波长555nm，
目视光学系统：
➢一般选择靠近此灵敏波长的D光(589.3nm)或e光 (546.1nm)校正单色像差。 因e光比D光更接近于 555nm，故用e光校正单色像差更为合适，

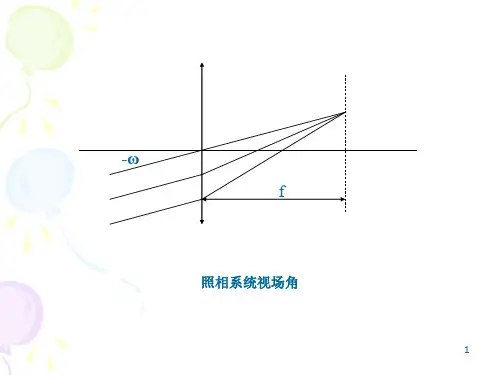
几何光学-第六章-像差理论

几何光学-第六章-像差理论
2、通常情况下，不能以一定宽度的光束对一定大小的物体成完善像。
成像特点： 物点——弥散斑
计算：实际光线计算 追迹成像的位置、大小与理想像的偏离——像差
小结：几何像差
像差类型 轴 单色 球差 上 色球差 物 复色 位置（轴向）色差 点 轴 外 单色 场曲 物 畸变 点 复色 倍率色差 影响因素 孔径 孔径、波长 在高斯像面上 接收到的像 单色弥散圆斑 彩色弥散圆斑
1 1 1
2 2 2
1
2
例：远轴物点发出的同心细光束，经过有像散的光学系统， 同心性会受到破坏，垂直于主轴的光屏在沿轴不同位置时， 所接收到的成像光束截面形状会发生很大的变化。
像散差
子午 焦线
明晰 圆
弧矢 焦线
3、像散特征：一个物点有子午焦线和弧矢焦线同时出现。
物点离轴越远，像散差越显著。
5、像散的物理意义
波长 孔径、视场 视场
大物面 波长
彗差（正弦差） 细光束像散
形状复杂的 弥散斑
作业
1、简述球差的产生机制、表现形式和消除方法。 2、简述慧差的形成机理和影响。 3、简述像散的机制、特征和影响。 4、简述场曲的形成机制和影响。 5、简述畸变的形成机制和影响。 6、简述位置色差及倍率色差的形成机制和影响。
b1 c1
★ 波面的中心光线： b
F 2
2
F 2 F1
a1
b2
a2
a3 b3
c2
c3
F1
F1
F2
F 2
F1
——光束在相互垂直的两截面内， 各有不同的曲率中心。 ★ 焦线：光束曲率中心的轨迹 两条相互垂直的短线 F F F 和 F F F 。 ★ 像散差：沿中心光线上两焦线之间的距离 F F 。

(工程光学教学课件)第6章 光线的光路计算及像差理论

(工程光学教学课件)第6章 光线的光路计算及像差理论

L'
n n' n'
r
如下图所示
该对无球差共扼点位置间的关系
n n′
-I A′ A C
I
A C A′ n n′
n'L' nL
U ' I, U I'
ssiiU nU n' ssiinInI' nn' L L'
即这对共扼点不管孔径角U多大，比值 sU i'n /sU in L /L ' 始终保持常数，故不产生生球差，这一对共扼点称为不晕点(或 齐明点)。
1nn' ssiinU nU' 1LLl'z'
当物体位于无限远时：
h1 1 L'
f'sinU' L'lz'
4.正弦差的定义
轴上点和近轴点不满足等晕成像引起的成像不对称性。 用OSC’表征。 当物体位于有限远时：
1nsiU n L' OS'C n'siU n'Llz' 1
当物体位于无限远时：
OS'Cf'sh1iU n'L' Ll'z' 1
补充：五、光学设计的一般过程和内容 (了解)
(1) 成像要求：基本类型，视场，观测方式，景深，渐晕， 分辨率，仪器尺寸，其它要求等；
(2) 建立理想 基本光组数量，焦距，成像光路，物像共轭距、 系统模型：物像四要素，反射棱镜(用平行平板表示)等；
(3) 构造基本 按最低数量配置透镜，初步确定透镜的材料、 光学系统：形状、孔径、曲率半径等参数，配置必要光阑， 确定反射棱镜的形状和大小，其它器件等；
称球差。它由孔径引起。 L' L' l'

工程光学第六章像差理论解读

工程光学第六章像差理论解读

LF 0.707h LD 0.707h LC 0.707h LD 0.707h LFCD
20
二级 光谱
并称两种波长的球差之差称为 色球差，表示为：
LF LC LFC
lF LC lC LF lFC LFC
为此作一B和球心C的辅助轴，则B点是辅助光轴上的一点，则三 条光线a、b、z对辅助轴相当于三条不同孔径角的轴上入射光线， 则它们在辅助光轴上存在球差且不相等。三条光线不能交于一点， 这样使得出射光线a′、b′不再关于主光轴z′对称。 8
则上下光线对的交点到主光线的垂直距离称为子午彗差。 如用个光线在像面上的交点值来表示，则子午彗差为： 1 KT Ya Yb Yz 2 对弧矢面的情况：弧矢光束中的前后光线c、d入射前对称 于主光线，由于弧矢光线对称子午面，它们折射后仍然交 于子午面内的同一点。但它们的折射情况与主光线不同， 因此并没有交于主光线上。这样出射光线对不再关于主光 线对称，其交点到主光线的垂直距离称为弧矢彗差。
B点的 理想 像点
B点的 实际 像点
16
可见，轴外点B的实际像点偏离了理想像点，产生畸变； 而轴上点A的实际像点与理想像点重合，因此轴上点不存 在畸变。 畸变的度量有： ①绝对畸变：即主光线像点的高度与理想像点的高度之差。
y y z y
z
实际 像高
理想 像高
②相对畸变：即像对于像高的畸变，常用百分比表示。
xt lt l ls l xs
有像散必然有场曲，但如果没有像散存在，像面弯曲现 象也会因球面光学系统的本身特性而存在。
球面 物体
折射 球面
理想像 平面14源自根据物像同向移动的原则，B的像点进一步偏离理想像平面 P′，这种偏离随视场的大小而变化，使得垂直于光轴的平面 物体经球面成像后变得 弯曲，这种弯曲还没有考虑像散的 影响，把像散为0时的像面弯曲称为匹兹伐场曲。

第6章 光线的光路计算及像差理论

第6章 光线的光路计算及像差理论

主光线折射
想一想：你能在图中找出对应光线或平面吗？ 子午面既是光束的对称面，又是系统的对称 面，位于该平面的子午光束通过系统后永远位在同 一平面内，因此计算子午面内光线的光路，是一个 平面的三角、几何问题，可以在一个平面图形表示 出光束的结构。 弧矢平面随主光线折射而改变。
一、轴外像差概述
如果没有像差，则所有光线对(上下、前后) 都 应相交在理想像平面上的同一点。 由于像差的存在，所有光线对(上下、前后)通过 系统后的交点，既不在主光线上，也不在理想像平面 上。
1、目视光学系统：一般选择D光或e光校正单色像 差，对C、F光校正色差。 2、普通照相系统：一般对F光校正单色像差，对D、 G校正色差。 3 、近红外和近紫外光学系统：一般对 C光校正单 色像差，对d、A校正色差。, 4、对特殊光学系统：只对使用波长校正单色像差。
第二节:光线的光路计算
光线光路计算是几何光学研究光学系统成像的 基本方法，也是进行光学设计的基本问题之一。 在光路计算中，根据任务的不同可分为： （ A ）子午光线光路计算。它又包括近轴光路计算 和非近轴光路计算； （B）轴外点细光束的子午焦点和弧矢焦点的计算； （C）空间光线的计算。 对于第一种光路计算任何光学系统设计时都要进 行。 一. 子午面内的光线光路计算 二. 沿轴外点主光线细光束的光路计算 三. 计算举例
轴外点也有球差，宽光束(上下光线)交点(像点) 与细光束(上下光线)像点沿轴距离——子午轴外球差。 前后光线交点(像点)与细光束(前后光线)像点的 就是弧矢轴外球差。
上下、前后光线交点的沿轴距离：宽光束像散X； 细光束像散x.
上下、前后光线交点的沿轴距离：宽光束像散X； 细光束像散x.
② r >0，n>n (或r <0，n<n )的面对光束起会聚作用， 称会聚面； r >0，n<n（或r <0，n>n）的面对光束起发散作 用，称发散面；

几何光学 第六章 像差理论

几何光学 第六章 像差理论
不产生球差的共轭点位置。 ★ 物、像均位于球面顶点： L 0, 1 L0 ★ 物、像位于球面的曲率中心： sin I sin I 0
I I 0
★ 物、像位置： I U
L L r
L (n n)r / n L (n n)r / n
波长 孔径、视场 视场
大物面 波长
彗差（正弦差） 细光束像散
形状复杂的 弥散斑
作业
1、简述球差的产生机制、表现形式和消除方法。 2、简述慧差的形成机理和影响。 3、简述像散的机制、特征和影响。 4、简述场曲的形成机制和影响。 5、简述畸变的形成机制和影响。 6、简述位置色差及倍率色差的形成机制和影响。
4、消除球差的方法
（1）加光阑，选择近轴光束； （2）正、负透镜组合进行校正； （3）采用非球面透镜。
5、小结
轴上物点 1）像点位置的轴向偏离：球差
宽光束(不同孔径角) 2）高斯像面上的弥散圆斑：垂轴球差
**问题：
（1）轴外物点是否有类似球差的现象？ （2）轴外物点发出的宽光束，其对称轴是什么？
三、彗形像差（Coma，Comatic Aberration）
3、物理意义
★ 彗差：轴外像差（孔径、视场的函数）
——大视场（稍远轴物）宽光束成像的不对称。 ★ 正弦差：小视场（近轴物）宽光束成像的不对称。
4、影响：破坏轴外视场成像的清晰度。 **问题：
宽光束的原因造成了球差和彗差，如取无限细光束， 是否就可以避免像差？
四、像散（Astigmatism）
1、与主轴成较大倾斜角的同心光束： 即使是细光束，出射光束也难以保持仍为同心。 2、基本概念：非球面波与象散光束 垂直于波面元，彼此既不相平行也不交于一点的 非对称性光束，称为像散光束。

工程光学第六章像差理论重点讲解

工程光学第六章像差理论重点讲解

校对公式：
h lu lu nuy nuy J
最后可计算出像点位置和系统各基点位置。
焦点位置及焦距计算：l1 , u1 0
f ' h1 / u'k
2、轴外物点近轴光线光路计算（第二近轴光线）
仍用近轴光线光路计算公式和校对公式,所有量均注以下标z.
已知：物方物位、入瞳位置和物高，即 l, lz , uz 。 求解：像方物位、出瞳位置和像高，即 l, lz , uz 。
i
l
r
r
u（当l1
时， u1
0，i1
h1
/
r1）
i' n i
n'
u' u i i'
l' r(1 i' )
u'
l' n'lr
n'l n(l r)
第二节 光线的光路计算
对于有k个面的折射系统，需利用根据过渡公式：
过渡公式：
lk lk1 dk 1 uk uk 1 nk nk 1
对于小视场的光学系统，例如望远物镜和显微物镜等，只 要求校正与孔径有关的像差，所以只需计算上述第一种光线。 对大孔径、大视场的光学系统，如照相物镜等，要求校正所 有像差，所以需要计算上述三种光线。
第二节 光线的光路计算
由已知条件：
光学系统的结构参数（r,d,n）
物体的位置和大小 入瞳的位置和大小
解决问题：
第一节 概述
像差校正：
在实际光学系统中，各种像差是同时存在的，像差 影响光学系统成像的清晰度、相似性和色彩逼真度等 ，就降低了成像质量。故像差的大小反映了光学系统 质量的优劣。
除了平面镜成像以外，没有像差的光学系统是不 存在的。完全消除像、色差是不可能的，针对光学系 统的不同用途，只要把像、色差降低在某范围内，使 光接收器不能分辨，或者说这种差别只要能骗过光接 收器，就可以认为是理想的。

(word完整版)第六章 像差计算

(word完整版)第六章 像差计算

第六章像差计算6。

1 光学系统的像差这里将提供像差的数值计算。

掌握各种像差的基本概念．特别是初级像差。

以及各种表面和薄透镜的三级像差贡献。

光学计算通常要求6位有效数字的精度，这取决于光学系统的复杂程度、仪器精度和应用的领域。

三角函数应在小数点后面取6位数，这相当于0.2弧秒。

这样的精度基本上满足了绝大多数使用要求。

当然，结构尺寸较大的衍射极限光学系统要求的精度比这还要向些。

光学计算所花费的时间明显地取决于设计者的技巧和所使用的计算设备的先进程度.计算技术发展到今天，就是使用普通的个人计算机,光学计算所需的时间也已经很少了。

但要对一个复杂的系统进行优化设计，特别是全局优化设计时．还是要花费一定的时间的。

关于如何进行光学设计，一直有两种观点。

一种观点主张以像差理论为基础,根据对光学系统的质量要求,用像差表达式，特别是用三级像差表达式来求解光学系统的初始结构，然后计算光线并求出像差，对其结果进行分析。

如果不尽人意,那么就要在像差理论的指导下，利用校正像差的手段（弯曲半径,更换玻璃、改变光焦度分配等)，进行像差平衡，直到获得满意的结果。

如果最后得不到满意的结果，那么就要重新利用像差理论求解初始结构,而后再重复上述的过程，直到取得满意的结果。

另一种观点是从现存的光学系统的结构中找寻适合于使用要求的结构,这可从专利或文献中查找，然后计算光线，分析像差，采用弯曲半径，增加或减少透镜个数等校正像差的手段，消除和平衡像差，直到获得满意的结果。

对于常规物镜,如Cooke三片，双高斯、匹兹瓦尔物镜等．常采用这种方法。

这种方法需要计算大量的光线(计算机发展到今天。

这已不成问题）,同时需要光学设计者有较丰富的设计经历和经验．以便对设计结果进行评价。

通常我们可以把二者结合起来,以像差理论为指导，进行像差平衡。

特别是计算机发展到今天,光学计算已经不是干扰光学设计者的问题了.对于常规镜头,通常不再需要像以前那样从求解初始结构开始,而是根据技术指标和使用要求、从光学系统数据库或专利目录中找出合适的结构，然后进行计算和分析。

像差理论

像差理论

70
-0.85
-0.68
在保证光焦度不变的情况下，可以通过增加透镜的 折射率来增大球面的曲率半径，因为选择高折射率 的材料有利于减小球差。
第一节 轴上点球差
1 2 在材料选定后，要保证透镜的光焦度， 2 也随之变 必须为定值。保持该定值，如果改变 1 ， 化，使得透镜的形状发生改变。或者说，同一光焦度 的透镜可以有不同的形状。这种保持焦距不变而改变 透镜形状的做法，称为透镜弯曲。 以物体在无穷远为例，图6-9给出了透镜不同形状下的 球差变化曲线。可以看出，无论是正透镜还是负透镜， 都存在一个最小球差的形状，称为透镜最优形式。
K S ' Ya 'YZ ' Yb 'YZ '
（6-8）
式中各符号的意义与式（6-7）类似。
第二节 慧差
慧差是轴外物点以宽光束成像的一种失对称的垂轴像差，除了 子午和弧矢两个截面外，其它截面也都有不同形式的失对称。 如果入瞳为一圆环，轴外点进入系统的光线就是以物点为顶点、 以主光线为对称中心的圆锥面光束，不同的孔径对应于不同大 小的光锥。此光束经系统后，由于存在慧差，不复为对称于主 光线的圆锥面光束，也不再会聚于一点，它与高斯像面相交成 一封闭的复杂曲线，曲线的形状对称于子午面。光锥角度越大， 失对称的程度也越大。整个入瞳可以看成由无数个大小不等的 圆环组成，由轴外物点发出的所有通过这些圆环的圆锥面光束， 经系统后在高斯像面上截得大小不等、形状不一、并在垂轴方 向上相互错开的封闭曲线，最终叠加成一个形状复杂、对称于 子午面的弥散斑。
第二节 慧差
再看弧矢面的情况，图6-13所示的是物点B以弧矢光线 成像的立体图，弧矢面内有一对前、后光线c、d，它 们对称于主光线，因此也对称于子午面，因此，成像 后的交点也必然在子午面内。这对光线在入射前虽然 对称于主光线，但是它们的折射情况与主光线不同。

工程光学第6章 像差概论

工程光学第6章 像差概论
17
18
校正 • 光阑位置 • 同心原则 • 双分离透镜
19
§6.4 细光束场曲
一、场曲与轴外球差
子午像面：各视场的子午像点构成的像面。 弧矢像面：各视场的弧矢像点构成的像面。
像散和场曲
视场中心（轴上像点）：细光束理想成像，像散为0。 即子午像面、弧矢像面重合且与理想像面相切。
细光束的子午场曲和弧矢场曲计算公式：
• 色差分为位置色差和倍率色差两种。前者是由于不同波 长的光线会聚点不同而产生彩色弥散现象，后者是由于 镜头对不同波长的光的放大率不同而引起的。
31
一、位置色差 1.光学现象及数学表达式
2.
LF C LF LC
lF ClF lC
12 3
C D F
32
• 色差在近轴区也存在，所以它比球差更严 重地影响光学系统的成像质量。
轴上点球差
• 共轴球面系统：单透镜不能校球差，需正 负透镜组合。
• 齐明透镜 • 减小光阑直径
8
§6.2 彗差
子午面：光轴和主光线决定的面； 弧矢面：过主光线且与子午面垂直。
9
一、光学现象及定量表示： 1、光学现象
轴外物点在理想像面上形成的像点如同彗星状的光斑， 靠近主光线的细光束交于主光线形成一亮点，而远离主光线 的不同孔径的光线束形成的像点是远离主光线的不同圆环。
36
§6.7 像差综述
• 任何光学系统都有一定的孔径和视场，所 谓某种像差的校正，也仅是对一个孔径带 或一个视场点进行校正，如对轴上点球差 是对边缘光线进行校正，而对色差是对 0.707带光进行校正。
• 所谓像差校正也是将像差校正到相应的像 差容限内，而不可能使其都为零。
37
• 一般来说，七种像差中，球差、位置色差为轴上点 像差，其余为轴外点像差；球差、彗差、位置色差 属于宽光束像差，像散、场曲、畸变、倍率色差属 细光束像差。

第六章.像差(工程光学)第二讲

第六章.像差(工程光学)第二讲

I
E I’ h n’ U’ C B’ r
4
△A’CE中，正弦定理有：
sin U sin I ' r L r
' '
B y -U A
n O
A’ -y’

L r sin I r sin U '
' '
ห้องสมุดไป่ตู้
-L
L’
5
由 将
3
、 4
L r sin I sin U ' 可以推出： L' r sin I ' sin U
y L r ' ' y L r
' '
y Lr ' y' L r
sin I n' ' sin I n
根据折射定律有： n sin I n sin I

sin I sin U 3 △ACE中，正弦定理有： L r r

Lr sin I r sin U
初级场曲 二级场曲
三级场曲
6、场曲的分布 初级子午场曲和弧矢场曲的分布式分别为： k 1 xt' ' '2 (3S III S IV ) 2nk uk 1 k 1 初 级 像 散 x' ( S III S IV ) s ' ' 2 分布系数 2nk uk 1
（6-46） （6-47） （6-48） （6-49）
对于垂直于光轴平面内的轴上点和轴外点（小视场），理想 成像的条件是正弦条件，即 当物体位于有限远时： 当物体位于无限远时：
nysinU n' y'sinU '

光学系统像差

光学系统像差

手术方法
• 1.
波前相差数据的选择：波前检查数据的是否准确，直接影响手术效果，因此，正确 的选择波前检查数据至关重要。一般情况下，每只眼应进行3-5次检查，如果重复性很 高，可被接受。否则，应重复检查，直到达到满意效果。在比较各次检查结果时，尤 其应注意比较视觉影响最大的相差成分，如慧差、球差、等如果可能的话，最好能检 查每次检查的原始图象。 2. 切削中心确定：传统的LASIK对偏中心有一定容忍度，一般来说，偏中心切削小于 0.5mm则不会明显影响术后视力（但会引起慧差增加，视觉质量下降）但波前像差引 导的个体化切削则对切削区中心的准确性有很高的要求。有研究报道，偏中心0.1 mm 即可对高阶像差的矫正产生影响。临床上尚无理想的的定位方法，（有十字、瞳孔中 心、虹膜定位）尽管存在误差，目前仍采用术中目测定位、对准瞳孔中心的办法，值 得注意是许多激光系统虽可以自动确定瞳孔中心，往往由于前房深度、红外照明情况、 图象对比度等差异而存在误差。因此术中应于纠正。此外，多数情况下波前相差是术 前散瞳下检查，而手术在自然情况下，瞳孔中心往往不一致，60%散瞳前后差0.1mm 在这种情况下则需做出相应调整。 3. 参考标记：术前标记3、9点位。术中/根据显微镜的刻度作出调整，某些虹膜识别 技术，减少眼球旋转的影响。 4. 手术参数的调整：与传统方法不同也需要参数调整，在调整参数前，应对环境（湿 度）角膜刀、角膜床暴露时间、等影响因素尽量控制一致。
像差表示方法
波前可以被分解为基本的形状 (Zernike 多项式)
Renzo Mattioli, PhD
临床应用
• 1.总体高阶像差大，6mm瞳孔时，总体高 阶像差的RMS值超过0.2um • 2.以前因屈光手术不理想造成的显著的球 差和慧差增加者 • 3.暗光下具有ቤተ መጻሕፍቲ ባይዱ瞳孔的年轻人和需要夜间 开车的人。

第六章 像差校正与平衡

第六章 像差校正与平衡
即
边光环带的F、C波面相交，但F、C光由于球差存在，在 其它环带波面不相交，称球色差。
28
几何色差与波色差的关系 一般光学系统： ，校正色差要求：
此时：
当0.707环带
即：对0.707环带消几何色差时， 正好使边缘带的波色差为零。
29
6.3 光学系统的像差容限
球差的像差容限

① 当系统仅有初级球差，其产生的最大波像差由下式决定
以相对高度u’=h/hm表示：
15
1.当仅有初级球差时：
以波长为单位时，
边缘处波像差最大。移动接收面，以接收面为基准，则球差将 改变，波像差曲线随之改变。称为离焦。
离焦为
最大剩余球差
初级球差曲线
初级球差对应的 波像差曲线
以最佳焦点为参考点 时的波像差曲线
最佳焦点：球差曲线 中新选的纵坐标轴位 置应使曲线对其所围 成的面积为最小。

1
CIIC hp hC 0
♣ 光阑位于物镜本身处的双胶合物镜，不管镜头如何“弯曲”， 总不能消除像散和场曲，这是限制普通望远物镜视场不能增 6 大的主要像差。
6.1 像差校正方法

像差校正的基本方法：代数法、实验法和像差自动校正法。

① 代数法 假定结构参数变化不大时，高级像差和透镜厚度影响很小，认为 基本不变，主要是初级像差的改变。先求出希望达到的像差目标 值和由光路计算所得到的像差值之差，用∆δG’k表示。然后对初 代数法相当于重新计算初始结构，工作量大， 级像差普遍表示式进行微分，用有限增量代替微分，可得 适合视场和孔径较小的光学系统，如双胶合、 双分离、密接三透镜系统的像差校正。
II i
第i组 l lp
光阑
第i+1组

光学系统的像差.

光学系统的像差.
第六章 光学系统的像差
•概述 •球差 •慧差 •象散 •场曲 •畸变 •色差
概述 像差的概念
• 实际光学系统只有在近轴区才具有同理想光学系统 相同的性质。但实际系统的孔径和视场都有一定的 大小，不能对物体成完善像
• 描述实际成像与理想成像的差异称为像差，像差用 几何量描述的称几何像差。
• 光学系统的像差计算需要进行实际光路计算
其中F谱线和C谱线在像方光轴有交点，它们的像方截距二 者之差称为该孔径的位置色差
• 近轴区域的位置色差L'FC L'F L'C
• 特别指出，以复色光成l像'FC的物l体'F 即l'使C 在近轴区域也存在色差
• 见附图
位置色差的形成
色差曲线
1 0.85 0.707
h hm DC
0.5
F L'FCD
y / ym
O x't , x's
O x't , x's
场曲的影响
场曲的校正
• 正负透镜组合 • 厚透镜
第五节 像面畸变
• 畸变的定义 • 畸变的形成 • 畸变的度量 • 畸变的影响 • 畸变的校正
畸变的定义
• 理想光学系统物像共轭面上的垂轴放大率为常数， 所以像与物相似
• 实际光学系统的一对共轭面上的放大率并不是常数， 随视场的增大而变化
L'0 0
1
2
3
1
-5
球差随负透镜形状而变的曲线
L' 5
0
-3
-2
-1
1
透镜球差的校正方案
• 对于单透镜而言，减小球差的方法有两种， 一是选择材料，二是透镜弯曲
• 采用正负透镜的组合，最简单的形式有双胶 合透镜和双分离透镜
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Lr
物体位于球心处
-U C
A,A'
物点位于顶点处
n
A U
O A'
n' (>n)
物点位于齐明点处
-I'
I
-U
A'
A
C
n
n' (<n)
正、负齐明透镜
A'
A,C1 C2
C2
C1, A A'
球差随正透镜形状而变的曲线
L'0
1
2
3
1
0
-5
球差随负透镜形状而变的曲线
L' 5
0
-3
-2
-1
1
第五节 像面畸变
• 畸变的定义 • 畸变的形成 • 畸变的度量 • 畸变的影响 • 畸变的校正
畸变的定义
• 理想光学系统物像共轭面上的垂轴放大 率为常数，所以像与物相似
• 实际光学系统的一对共轭面上的放大率 并不是常数，随视场的增大而变化
• 像对于物的变形像差称为畸变
畸变的形成
• 见附图
畸变的度量
• 平面物体成弯曲像面的成像缺陷称 为场曲像差
场曲的形成
• 见附图
场曲的度量
子午场曲 xt ' lt 'l'
子午场曲
弧矢场曲 xs ' ls 'l'
场曲曲线
t' s' p
y / ym
p s' t'
y / ym
O x't , x's
O x't , x's
场曲的影响
场曲的校正
• 正负透镜组合 • 厚透镜
入射光瞳
A 光轴
B
O
折射面
像散的形成
入射光瞳
A 光轴
B
d0 O c0
折射面
像散的形成
图中A为轴上 点，B为轴外 点
入射光瞳
A 光轴
B
d0 O c0
b0
折射面
像散的形成
d
Z
c
入射光瞳
A 光轴
B
d0 O c0
b0
折射面
像散的形成
入射光瞳
A 光轴
B
d
Z
c
b
d0 O c0
b0
图3-5
折射面
象散
球差的影响
• 整个孔径光束的垂轴球差在像面上 形成了一个对称于光轴的圆形弥散 斑，严重时使轴上点成像变得模糊 不清。
球差的校正
• 单个球面不产生球差的三个位置 • 齐名透镜 • 单透镜的球差 • 正负透镜的组合
不产生球差的三个不晕点
1。物点位于球面的球心处。 2。物点位于球面顶点。 3。物点位于齐明点处。
l'
图5.1
球差的形成
A
-U
U'
-l
l'
图
图5.1
球差的度量 L' L'l'
T'
A
-U
返回
-l
图5.1
U'
L'
-L'
l'
球差曲线（1）
h hm
1 0.707
L' a)
h hm
1
0.707
L' b)
球差校正不足和球差过校正
球差曲线（2）
h
h
O L'
球差过校正
O L'
球差校正不足
子午面和弧矢面
入瞳
A
z 子午面弧矢面 B
慧差的形成
入瞳
a z b
B
高斯像面
慧差的形成
入瞳
a z b
B
高斯像面
慧差的形成
入瞳
a
z b B
b' c
子午慧差
KT
'
1 2
(Ya 'Yb ' )
Yz '
入瞳
-K't a'
z'
a
b'
z
c
b
B
高斯像面
B' t
Y' b Y'z
Y' a
弧矢慧差
Ks ' Yc 'Yz ' Yd 'Yz '
第六章 光学系统的像差
概述 像差的概念
• 实际光学系统只有在近轴区才具有同理想 光学系统相同的性质。但实际系统的孔径 和视场都有一定的大小，不能对物体成完 善像
• 描述实际成像与理想成像的差异称为像差， 像差用几何量描述的称几何像差。
• 光学系统的像差计算需要进行实际光路计 算
返回
光路计算简述
• 物体可用子午面内的直线描述 • 子午面内的直线可用若干个物点描述 • 每个物点发出若干条光线 • 光线在入瞳面上的分布 • 光线的计算公式
像散的定义
• 当轴外物点发出的一束很细的光 束通过入瞳时，因轴外子午与弧 矢光线不对称，使得子午像点与 弧矢像点不重合。即一个物点的 成像将被聚焦为子午和弧矢两个 焦线，这种像差称为像散。
像散的形成
• 轴外细光束 • 见附图 • 像散视图
像散的度量
xts ' lt 'ls '
返回
像散的形成
第六节 色差
起的像散要小
像散光束的应用
• 人眼的散光及其校正 • 宽银幕放映镜头 • 半导体激光束的准直
第四节 轴外细光束场曲
• 场曲的定义 • 场曲的形成 • 场曲的度量 • 场曲的影响 • 场曲的校正
场曲的定义
• 理想光学系统对垂轴的平面物体成 垂轴的平面像
• 实际光学系统对平面物体所成的像 不在一个平面内
Y' z
d z
B
入瞳 c
B'z -K's
B' c
d'
B' d B' s
z' c'
高斯 像面
图5.4
Y'z Y'z Y' z
慧差的影响
B' z
返回
慧差的校正
• 当光阑位于球心时，不产生慧差 • 改变光阑位置时慧差发生改变 • 对称结构慧差自动消除
第三节 轴外细光束像散
• 像散的定义 • 像散的形成 • 像散的度量 • 像散的影响 • 像散的校正
• 绝对畸变
Y 'Z Y 'Z y'
• 相对畸变 q Y 'Z y' 100% y'
畸变的影响
畸变反映的是主光变形。
a)
b)
c)
畸变的校正
• 将孔径光阑设在球心处，不产生畸变 • 单个薄透镜或薄透镜组，当孔径光阑与
之重合不产生畸变 • 结构完全对称的光学系统畸变自动消除
透镜球差的校正方案
• 对于单透镜而言，减小球差的方法 有两种，一是选择材料，二是透镜 弯曲
• 采用正负透镜的组合，最简单的形 式有双胶合透镜和双分离透镜
第二节 轴外点慧差
• 慧差的定义 • 慧差的形成 • 慧差的度量 • 慧差的影响 • 慧差的校正
慧差的定义
• 当物点位于光轴外时，物点 偏离了球面系统的对称轴位 置，轴外点的宽光束将会产 生一种失对称的像差, 这种像 差称为慧差。
A
P
z
B
O 光学系统
象散
A
P
z
B
O 光学系统
象散
2
A
P
z
B
O 光学系统
象散
23
A
P
z
B
O 光学系统
象散
23
A
P
z
B
O 光学系统
象散
23
5
A
P
z
B
O 光学系统
象散
23
56
A
P
z
B
O 光学系统
象散
23
56
A
P
z
B
O 光学系统
像散的影响
物 1
子午像
弧矢像
2
3
像散的校正
• 光阑位于球心不产生像散 • 改变光阑位置像散将发生改变 • 球面弯向光阑，比球心背向光阑引
近轴光线 子午面内的实际光线 轴外细光束光线 空间光线
第一节 轴上点球差
1。球差的定义 2。球差的形成 3。 球差的度量 4。球差的影响 5。球差的校正
球差的定义
轴上物点的物距L确定时，其 像点位置L’是孔径角U（或h）的 函数，实际像点与理想像点的位 置之差称为轴上点球差。
返回
球差的形成
A
-l