211点、直线、平面之间的位置关系.docx

高中数学必修《点直线平面之间的位置关系》知识点高中数学必修的《点直线平面之间的位置关系》是一个重要的几何知识点，主要涉及直线与平面、点与直线、点与平面之间的位置关系。

这个知识点对于理解几何图形的形状和性质具有重要作用，也为后续的三角函数、向量等知识打下基础。

下面将详细介绍该知识点的内容。

一、直线与平面的位置关系1.平面方程：平面的一般方程为Ax+By+Cz+D=0，其中A、B、C为不能同时为0的实数，A、B、C为平面的法向量，D为常数项。

2.直线与平面的位置关系：(1)直线与平面相交：直线与平面相交可以有一个交点，也可以有无穷多个交点。

(2)直线含于平面：如果直线的所有点都在平面上，则直线被称为含于平面。

(3)直线与平面平行：如果直线与平面的交点集为空集，则直线与平面平行。

(4)直线与平面垂直：如果直线与平面的任意一条直线都垂直，则直线与平面垂直。

二、点与直线的位置关系1.点与直线的距离：点P(x0,y0)到直线Ax+By+C=0的距离公式为d=，Ax0+By0+C，/√(A^2+B^2)。

2.点到线段的距离：点P到线段AB的距离：(1)如果P在AB的延长线上，则距离为AP或BP的长度。

(2)如果P在线段AB的两边，则距离为点P到线段AB所在直线的距离。

(3)如果P在线段AB上，则距离为0。

三、点与平面的位置关系1.点在平面上：点P(x0,y0,z0)在平面Ax+By+Cz+D=0上的充要条件是Ax0+By0+Cz0+D=0。

2.点到平面的距离：点P到平面Ax+By+Cz+D=0的距离公式为d=，Ax0+By0+Cz0+D，/√(A^2+B^2+C^2)。

3.点关于平面的对称点：点P(x0,y0,z0)关于平面Ax+By+Cz+D=0的对称点的坐标为：(x',y',z')=(x0-2*Ax0/（A^2+B^2+C^2）,y0-2*By0/（A^2+B^2+C^2）,z0-2*Cz0/（A^2+B^2+C^2）)。

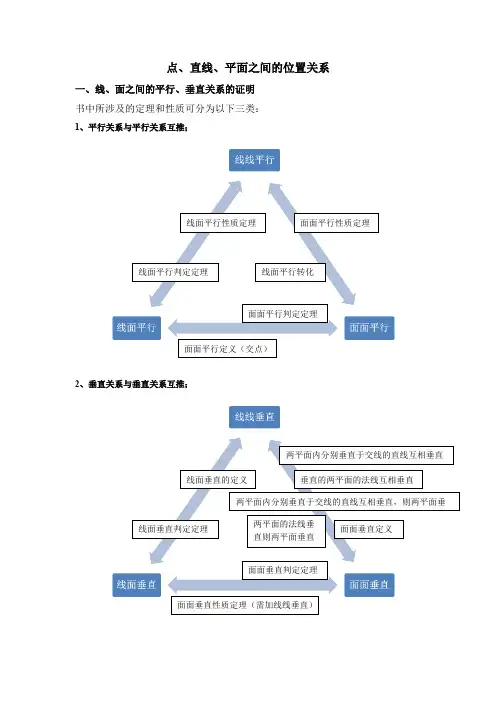
点、直线、平面之间的位置关系一、线、面之间的平行、垂直关系的证明书中所涉及的定理和性质可分为以下三类：1、平行关系与平行关系互推；2、垂直关系与垂直关系互推；线面垂直判定定理线面垂直的定义两平面的法线垂直则两平面垂直面面垂直判定定理线面平行判定定理线面平行性质定理线面平行转化面面平行判定定理面面平行性质定理3、平行关系与垂直关系互推。

以线或面为元素，互推的本质是以某一元素为中介，通过另外两元素与中介元素的垂直或平行关系，推导出该两元素的关系，总共有21种情况，能得出结论的有以下9种情况。

线线平行传递性：；b c c a b a //////⇒⎭⎬⎫面面平行传递性：；γαβγβα//////⇒⎭⎬⎫线面垂直、线面垂直线面平行：；⇒ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥线面垂直线线平行（线面垂直性质定理）：；⇒b a b a //⇒⎭⎬⎫⊥⊥αα线面垂直面面平行：；⇒βαβα//⇒⎭⎬⎫⊥⊥a a 线面垂直、面面平行线面垂直：；⇒βαβα⊥⇒⎭⎬⎫⊥a a //线线平行、线面垂直线面垂直：；⇒αα⊥⇒⎭⎬⎫⊥b a b a //线面垂直、线面平行面面垂直：。

⇒βααβ⊥⇒⎭⎬⎫⊥a a //备注：另外证明平行关系时可以从最基本的定义交点入手，证明垂直关系时可以从最基本的定义角度入手。

符号化语言一览表①线面平行；；；ααα////a a b b a ⇒⎪⎭⎪⎬⎫⊄⊂αββα////a a ⇒⎭⎬⎫⊂ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥②线线平行:；；；；////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ b a b a //⇒⎭⎬⎫⊥⊥αα////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭b c c a b a //////⇒⎭⎬⎫③面面平行:；；；,////,//a b a b O a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭βαβα//⇒⎭⎬⎫⊥⊥a a γαβγβα//////⇒⎭⎬⎫④线线垂直:；b a b a ⊥⇒⎭⎬⎫⊂⊥αα⑤线面垂直:；；,,a b a b O l l a l b ααα⊂⊂⎫⎪=⇒⊥⎬⎪⊥⊥⎭,l a a a l αβαββα⊥⎫⎪=⇒⊥⎬⎪⊂⊥⎭ ；；βαβα⊥⇒⎭⎬⎫⊥a a //αα⊥⇒⎭⎬⎫⊥b a b a //⑥面面垂直：二面角900; ；；βααβ⊥⇒⎭⎬⎫⊥⊂a a βααβ⊥⇒⎭⎬⎫⊥a a //二、立体几何中的重要方法1、求角：（步骤-------Ⅰ找或作角；Ⅱ求角）⑴异面直线所成角的求法：①平移法：平移直线，构造三角形；②补形法：补成正方体、平行六面体、长方体等，发现两条异面直线间的关系．注：还可用向量法，转化为两直线方向向量的夹角．⑵直线与平面所成的角：①直接法（利用线面角定义）；②先求斜线上的点到平面距离h ，与斜线段长度作比，得sin ；③三线三角公式．θ12cos cos cos θθθ=注：还可用向量法，转化为直线的方向向量与平面法向量的夹角．⑶二面角的求法：①定义法：在二面角的棱上取一点（特殊点），作出平面角，再求解；②垂面法：作面与二面角的棱垂直； ③投影法（三垂线定理）；④面积摄影法．注：对于没有给出棱的二面角，应先作出棱，然后再选用上述方法；还可用向量法，转化为两个班平面法向量的夹角．2、求距离：（步骤-------Ⅰ找或作垂线段；Ⅱ求距离）⑴两异面直线间的距离：一般先作出公垂线段，再进行计算；或转化为线面距离、点面距离；⑵点到直线的距离：一般用三垂线定理作出垂线段，再求解；⑶点到平面的距离：①垂面法：借助面面垂直的性质作垂线段（确定已知面的垂面是关键），再求解；②等体积法；还可用向量法：．||n d =3、证明平行、垂直的理论途径：①证明直线与直线的平行的思考途径：（1）转化为判定共面二直线无交点（定义）；（2）转化为两直线同与第三条直线平行；（3）转化为线面平行；（4）转化为线面垂直；（5）转化为面面平行．②证明直线与平面的平行的思考途径：（1）转化为直线与平面无公共点（定义）；（2）转化为线线平行；（3）转化为面面平行．③证明平面与平面平行的思考途径：（1）转化为判定两平面无公共点（定义）；（2）转化为线面平行；（3）转化为线面垂直．④证明直线与直线的垂直的思考途径：（1）转化为相交垂直；（2）转化为线面垂直．⑤证明直线与平面垂直的思考途径：（1）转化为该直线与平面内任一直线垂直（定义）；（2）转化为该直线与平面内相交的两条直线垂直；（3）转化为该直线与平面的一条垂线平行；（4）转化为该直线垂直于另一个平行平面；（5）转化为该直线与两个垂直平面交线垂直．⑥证明平面与平面的垂直的思考途径：（1）转化为判断二面角是直二面角；（2）转化为线面垂直．。

的位置关系-@>% )一平面1.平面的概念平面是一个只描述而不加定义的最基本的原始概念,常见的桌面㊁黑板面㊁海面都给我们以平面的形象.立体几何里所说的平面就是从这样一些物体中抽象出来的.但是几何里所说的平面是无限延展的.2.平面的基本性质三个公理及公理2的三个推论如下:公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内.公理2:经过不在同一条直线上的三点有且只有一个平面.推论1:经过一条直线和直线外的一点有且只有一个平面.推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面.公理3:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.二空间两条直线的位置关系1.空间两条直线的位置关系(1)相交直线:在同一平面内,有且仅有一个公共点.(2)平行直线:在同一平面内,没有公共点.(3)异面直线:不同在任何一个平面内,没有公共点.(4)异面直线所成的角:如图51所示,直线a ,b是异面直线,经过空间一点O ,分别引直线a 'ʊa ㊁b 'ʊb ,相交直线a ',b '所成的锐角(或直角)叫作异面直线a ,b 所成的角.如果两条异面直线所成的角是直角,则称这两条异面直线互相垂直.abαabαOOaa b图512.平行公理与等角定理(1)平行公理(公理4):平行于同一直线的两条直线相互平行.(2)等角定理:空间中如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.三直线和平面、平面和平面的位置关系1.一条直线和一个平面的位置关系有且只有以下三种：(1)直线在平面内 有无数个公共点;(2)直线和平面相交 有且只有一个公共点;(3)直线和平面平行 没有公共点.2.两个平面的位置关系只有两种(1)平行 没有公共点;(2)相交 有一条公共直线.四直线和平面平行的判定与性质1.直线和平面平行的判定定理(1)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)判定定理的符号表示:a⊄α}⇒aʊαb⊂αaʊb2.直线和平面平行的性质定理(1)性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和两平面的交线平行.(2)性质定理的符号表示aʊαa⊂βαɘβ=b}⇒aʊb五平面与平面平行的判定与性质1.平面与平面平行的判定定理(1)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.(2)判定定理的符号表示:a⊂αb⊂αaɘb=A aʊβbʊβüþýïïïïïï⇒αʊβ2.平面与平面平行的性质定理(1)性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.(2)性质定理的符号表示:αʊβγɘα=a γɘβ=b }⇒a ʊb 六直线和平面垂直的判定与性质1.直线和平面垂直的定义如果一条直线l 和一个平面α内的任意一条直线都垂直,我们就说直线l 和平面α互相垂直,记作l ʅα,直线l 叫作平面α的垂线,平面α叫作直线l 的垂面.2.直线和平面垂直的判定(1)直线和平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与这个平面垂直.判定定理的符号表示:a ⊂αb ⊂αa ɘb =P l ʅal ʅbüþýïïïïïï⇒l ʅα(2)如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,即a ʊba ʅα}⇒b ʅα3.直线和平面垂直的性质(1)直线和平面垂直的性质定理:垂直于同一个平面的两条直线平行.性质定理的符号表示:a ʅαb ʅα}⇒a ʊb(2)如果一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意一条直线.(3)过一点有且只有一条直线和已知平面垂直;过一点有且只有一个平面和已知直线垂直.(4)如果一条直线与两个平面都垂直,那么这两个平面平行.七平面与平面垂直的判定与性质1.两个平面垂直的定义(1)二面角:从一条直线出发的两个半平面所形成的空间图形叫作二面角.这条直线叫作二面角的棱,两个半平面叫作二面角的面.(2)二面角的平面角:在二面角α-l -β的棱l 上任取一点O ,以O 为垂足,在两个半平面内分别作垂直于棱的射线O A 和O B ,则射线O A 和O B 所成的角øA O B叫作二面角α-l -β的平面角.(3)直二面角:平面角是直角的二面角叫作直二面角(4)两个平面垂直的定义:两个平面相交,如果它们所成的二面角是直二面角,那么就说这两个平面互相垂直.2.两个平面垂直的判定定理(1)判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.(2)判定定理的符号表示:a ⊂αa ʅβ}⇒αʅβ3.两个平面垂直的性质定理(1)性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.(2)性质定理的符号表示:αʅβ,αɘβ=l b ⊂α,b ʅl}⇒b ʅβ。

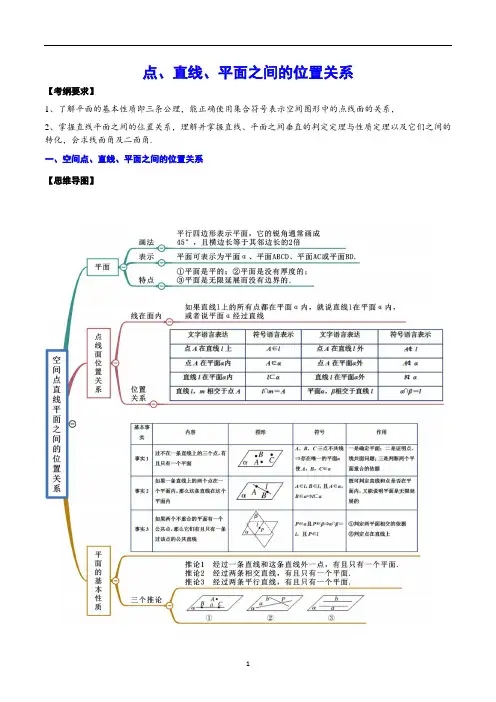
点、直线、平面之间的位置关系【考纲要求】1、了解平面的基本性质即三条公理，能正确使用集合符号表示空间图形中的点线面的关系，2、掌握直线平面之间的位置关系，理解并掌握直线、平面之间垂直的判定定理与性质定理以及它们之间的转化，会求线面角及二面角.一、空间点、直线、平面之间的位置关系【思维导图】一、平面的基本性质(1)基本事实1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内(即直线在平面内)．(2)基本事实2：经过不在同一条直线上的三点，有且只有一个平面(即可以确定一个平面)．(3)基本事实3：如果两个不重合的平面有一个公共点，那么它们有且只有一条通过这个点的公共直线．推论1：经过一条直线和这条直线外一点，有且只有一个平面．推论2：经过两条相交直线，有且只有一个平面．推论3：经过两条平行直线，有且只有一个平面． 二、空间两直线的位置关系 1.位置关系的分类⎩⎨⎧共面直线⎩⎪⎨⎪⎧相交直线平行直线异面直线：不同在任何一个平面内，没有公共点2.等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补． 三、异面直线所成的角 1.异面直线所成的角①定义：设a ，b 是两条异面直线，经过空间任一点O 作直线a ′∥a ，b ′∥b ，把a ′与b ′所成的锐角或直角叫作异面直线a ，b 所成的角(或夹角)． ②范围：.2.异面直线的判定方法：判定定理：平面外一点A 与平面内一点B 的连线和平面内不经过该点的直线是异面直线；反证法：证明两线不可能平行、相交或证明两线不可能共面，从而可得两线异面． 四、空间中直线与平面、平面与平面的位置关系(1)直线与平面的位置关系有三种情况：在平面内---有无数个公共点；相交---有且只有一个公共点；平行---没有公共点．后两种情况直线不在平面内，也称直线在平面外.(2)平面与平面的位置关系有两种情况：平行---没有公共点；相交---有一条公共直线． 二、直线、平面平行的判定及性质 【思维导图】]2,0(π【考点总结】一、空间平行关系1.直线与平面平行的判定与性质判定性质定义定理图形条件 a ∩α＝∅ a ⊂α，b ⊄α，a ∥b a ∥α a ∥α，a ⊂β，α∩β＝b 结论a ∥αb ∥αa ∩α＝∅a ∥b2. 面面平行的判定与性质判定性质定义定理图形条件 α∩β＝∅ a ⊂β，b ⊂β，a ∩b ＝P ， a ∥α，b ∥α α∥β，α∩γ＝a ， β∩γ＝b α∥β，a ⊂β 结论α∥βα∥βa ∥ba ∥α3.利用线面平行的定义，一般用反证法；利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)； 利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)． 二、平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a ⊥α，a ⊥β，则α∥β. (2)垂直于同一个平面的两条直线平行，即若a ⊥α，b ⊥α，则a ∥b. (3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ. 三、直线、平面垂直的判定及性质 【思维导图】【考点总结】一、直线与平面垂直(1)定义：如果直线l与平面α内的任意一条直线都垂直，则直线l与平面α垂直．(2)判定定理与性质定理文字语言图形语言 符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎪⎬⎪⎫a ，b ⊂αa ∩b ＝Ol ⊥a l ⊥b⇒l ⊥α 性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b (1)平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角． (2)当直线与平面垂直和平行(或直线在平面内)时，规定直线和平面所成的角分别为90°和0°. (3)范围：[0,]2π.三、二面角的有关概念(1)二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．(2)二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角． (3)范围：[0，π]． 四、平面与平面垂直(1)定义：如果两个平面所成的二面角是直二面角，就说这两个平面互相垂直． (2)判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直⎭⎪⎬⎪⎫l ⊥αl ⊂β⇒α⊥β 性质定理 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直⎭⎪⎬⎪⎫α⊥βl ⊂βα∩β＝a l ⊥a ⇒l ⊥α(1)若一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意直线. (2)若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面． (3)垂直于同一条直线的两个平面平行．(4)一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直． (5)两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．【题型汇编】题型一：空间点、直线、平面之间的位置关系 题型二：直线、平面平行的判定和性质 题型三：直线、平面垂直的判定和性质 【题型讲解】题型一：空间点、直线、平面之间的位置关系 一、单选题1．（2022·上海长宁·二模）如图，已知A B C D E F 、、、、、分别是正方体所在棱的中点，则下列直线中与直线EF 相交的是（ ）．A ．直线AB B ．直线BC C ．直线CD D ．直线DA ．【答案】A 【解析】 【分析】通过空间想象直接可得. 【详解】 如图，易知,AFHG HG BE ，所以AF BE ∥，且12AF BE =， 所以ABEF 为梯形，故AB 与EF 相交，A 正确； 因为,,BCMH MH NL NL EF ，所以BC EF ∥，故B 错误；因为平面CDH 平面EFNL ，CD ⊂平面CDH ，EF ⊂平面EFNL ， 所以直线CD 与直线EF 无公共点，故C 错误； 因为AD ⊂平面ADF ，EF 平面ADF F =，故AD 与EF 异面，D 错误.故选：A2．（2022·江西萍乡·三模（理））如图，直三棱柱111ABC A B C -中，AC BC ⊥，若11AA AC BC ===，则异面直线1,A C AB 所成角的大小是（ ）A ．6πB ．π4C ．π3D ．π2【答案】C 【解析】 【分析】连接1B C ，则11B AC ∠即为异面直线1,A C AB 所成角，再分别求出11B A C 的边长即可求出11B AC ∠，得到答案 【详解】如图所示，连接1B C11A B AB // ,11B A C ∴∠即为异面直线1,A C AB 所成角11AA AC BC ===，112,2AC BC ∴又AC BC ⊥，112AB A B ∴==在11B A C 中，11112A B AC BC === 11B A C ∴是正三角形11π3B AC ∴∠= 故选：C3．（2022·安徽·蚌埠二中模拟预测（理））正方体1111ABCD A B C D -中，点M 在棱1DD 上，过点C 作平面1BMC 的平行平面α，记平面α与平面11BCC B 的交线为l ，则1A C 与l 所成角的大小为（ ）A ．6πB ．4πC ．3πD ．2π 【答案】D【解析】【分析】根据题意可知平面α与平面11BCC B 的交线为l ，与平面1BMC 与平面11BCC B 的交线平行，即求解平面1BMC 与平面11BCC B 的交线与1A C 所成角的大小即可.【详解】因为平面1//BMC 平面α，平面1BMC ⋂平面111BCC B BC =，平面α平面11BCC B l =，则1BC l ∥； 在正方体中，易证1BC ⊥平面11A B CD ，故11BC A C ，所以1A C l ⊥，即1A C 与l 所成角的大小为2π. 故选:D .4．（2022·陕西·西北工业大学附属中学二模（理））如图，在长方体ABCD A B C D ''''-中，22AB AA AD '==，M 、N 分别是A B ''、D C ''的中点.则直线CN 与DM 是（ ）A ．相互垂直的相交直线B ．相互垂直的异面直线C ．相互不垂直的异面直线D ．夹角为60°的异面直线【答案】B【解析】【分析】连接,,,BM MN BD MD '，可证直线CN 与DM 为异面直线，并可求其所成的角.【详解】设222AB AA AD a '===，连接,,,BM MN BD MD '，因为NC ⊂平面CC D D ''，MD ⋂平面CC D D D ''=，D NC ∉，故直线CN 与DM 异面直线.在矩形A B C D ''''中，因为,M N 为所在棱的中点，故//,=MN B C MN B C ''''，而//,BC B C BC B C ''''=，故//,BC MN MN BC =，故四边形BCNM 为平行四边形，故//CN BM ，所以BMD ∠或其补角为异面直线CN 与DM 所成的角，在BMD 中，222,5,23BM a BD a MD a a a =+=，故222BD BM MD =+，故90BMD ∠=︒，故选：B5．（2022·上海黄浦·二模）如图，已知P 、Q 、R 分别是正方体1111ABCD A B C D -的棱AB 、BC 和11C D 的中点，由点P 、Q 、R 确定的平面β截该正方体所得截面为（ ）．A ．三角形B ．四边形C ．五边形D ．六边形【答案】D【解析】【分析】分别取1111、、A D A A CC 的中点F 、E 、M ，连接、、、、、RF FE EP PQ QM MR ，由正方体性质可得答案.【详解】如图，分别取1111、、A D A A CC 的中点F 、E 、M ，连接、、、、、RF FE EP PQ QM MR ，由正方体性质//RF PQ ，所以、、、∈R F P Q 平面α，且////RF PQ MN ，又、、QF RP EM 交于同一点O ，所以、∈E M 平面α，所以点P 、Q 、R 确定的平面β即为六边形RFEPQM 故选：D ．6．（2022·北京东城·三模）如图，在正方体1111ABCD A B C D -中，E ，F 分别为CC 1，D 1C 1的中点，则下列直线中与直线BE 相交的是（ ）A ．直线1A FB ．直线1ADC ．直线11CD D ．直线1AA【答案】A【解析】【分析】 利用正方体的性质可得111//,2EF A B EF A B =，进而可判断A ，根据经过平面外一点和平面内一点的直线和平面内不经过该点的直线为异面直线可判断BCD.【详解】连接11,,EF CD A B ，则111//,2EF CD EF CD =，由1111//,A D BC A D BC =，可得四边形11A D CB 为平行四边形，∴11//A B CD ，11A B CD =，所以111//,2EF A B EF A B =，即四边形1EFBA 为梯形， 故直线1A F 与直线BE 相交，直线1AD 与直线BE 为异面直线，直线11C D 与直线BE 为异面直线，直线1AA 与直线BE 为异面直线. 故选：A.二、多选题1．（2022·重庆·三模）如图，在正方体1111ABCD A B C D -中，O 为正方形ABCD 的中心，当点P 在线段1BC 上（不包含端点）运动时，下列直线中一定与直线OP 异面的是（ ）A ．1ABB ．1AC C ．1A AD ．1AD【答案】BCD【解析】【分析】 对于A ，当P 为1BC 的中点时，1//OP AB ，故A 不正确；对于BCD ，根据异面直线的判定定理可知都正确.【详解】对于A ，当P 为1BC 的中点时，11////OP DC AB ，故A 不正确；对于B ，因为1AC ⊂平面11AAC C ，O ∈平面11AAC C ，O ∉1A C ，P ∉平面11AAC C ，所以直线1A C 与直线OP 一定 是异面直线，故B 正确；对于C ，因为1A A ⊂平面11AAC C ，O ∈平面11AAC C ，O ∉1A A ，P ∉平面11AAC C ，所以直线1A A 与直线OP 一定 是异面直线，故C 正确；对于D ，因为1AD ⊂平面1AD C ，O ∈平面1AD C ，O ∉1AD ，P ∉平面1AD C ，所以直线1AD 与直线OP 一定 是异面直线，故C 正确；故选：BCD题型二：直线、平面平行的判定和性质一、单选题1．（2022·山西·一模（文））如图，正方体1111ABCD A B C D -中，若E ，F ，G 分别是棱AD ，1C C ，11B C 的中点，则下列结论中正确的是（ ）A ．BE ⊥平面DFGB ．1//A E 平面DFGC ．//CE 平面DFGD ．平面1//A EB 平面DFG【答案】C【解析】【分析】根据线面位置关系分别判断.【详解】 由1111ABCD A B C D -为正方体，且F ，G 分别是棱1C C ，11B C 的中点，则1//FG A D ，则平面DFG 即为平面1A DFG ，A 选项，如图连接1D G ，由正方体可知1//D G BE ，又11D G AG ⊥不成立，所以1BE A G ⊥不成立，即A 选项错误；B 选项，由1A E 平面11A DFG A =，故1A E 与平面1A DFG 不平行，B 选项错误；C 选项，连接CE ，则1//CE A G ，又1AG ⊂平面1A DFG ，CE ⊄1A DFG ，所以//CE 平面1A DFG ，C 选项正确；D 选项，平面1A EB 与平面1A DFG 有公共点1A ，故D 选项错误；故选：C.2．（2022·浙江杭州·二模）设,αβ为两个不同的平面，则α∥β的充要条件是（ ） A ．α内有无数条直线与β平行B ．,αβ垂直于同一平面C ．,αβ平行于同一条直线D ．α内的任何直线都与β平行【答案】D【解析】【分析】根据面面平行、相交的知识确定正确选项.【详解】A 选项，α内有无数条直线与β平行，α与β可能相交，A 选项错误.B 选项，,αβ垂直于同一平面，α与β可能相交，B 选项错误.C 选项，,αβ平行于同一条直线，α与β可能相交，C 选项错误.D 选项，α内的任何直线都与β平行，则//αβ，D 选项正确.故选：D3．（2022·安徽马鞍山·三模（理））设α，β，γ是互不重合的平面，m ，n 是互不重合的直线，给出下面四个命题：①若αγ⊥，βγ⊥，则αβ∥；②若m α⊥，m β⊥，则αβ∥；③若m α∥，n α⊥，则m n ∥；④若αβ⊥，a m β⋂=，n m ⊥，则n β⊥．其中所有正确命题的序号是（ ）A ．①②B ．②C ．④D ．②③【答案】B【解析】【分析】对①，α与β需考虑平行与相交两种情况；对②，线面垂直证面面平行；对③，线面平行得线线平行，线面垂直得线线垂直；对④，不符合面面垂直证线面垂直的条件【详解】对①，若αγ⊥，βγ⊥，则αβ∥或α与β相交，故①错；对②，若m α⊥，m β⊥，则αβ∥，②对；对③，若m α∥，n α⊥，则m n ⊥，③错；对④，若αβ⊥，a m β⋂=，n m ⊥，则n 不一定垂直β，④错故选：B4．（2022·上海奉贤·二模）如图，在直三棱柱111ABC A B C -中，点E ，F 分别是棱11A C ，BC 的中点，则下列结论中不正确的是（ ）A ．1CC ∥平面11A ABBB ．AF ∥平面111A BC C ．EF ∥平面11A ABBD ．AE ∥平面11B BCC【答案】D【解析】【分析】 由线面平行的判定定理，面面平行的性质定理依次判断各选项即可得出结果.【详解】在直三棱柱111ABC A B C -中，因为1CC ∥1AA ,1CC ⊄平面11A ABB ,1AA ⊂平面11A ABB ,所以1CC ∥平面11A ABB ，A 正确； 因为平面ABC //平面111A B C ，AF ⊂平面ABC ，所以AF ∥平面111A B C ，B 正确； 取AB 中点G ,连接1,A G GF ,因为点G ，F 分别是棱AB ，BC 的中点，所以12//GF AC ,且11//2A E AC ,所以1//GF A E ，四边形1GFEA 为平行四边形，所以EF ∥1A G ,EF ⊄平面11A ABB ，1AG ⊂平面11A ABB ,所以EF ∥平面11A ABB ,C 正确；取AC 中点H ,连接1C H ,可证得四边形1AHC E 为平行四边形，所以EA ∥1C H ,1C H 与平面11C CBB 相交,所以AE 与平面11C CBB 相交,D 不正确；故选:D.5．（2022·广东·普宁市华侨中学二模）如图，在四面体ABCD 中，若截面PQMN 是正方形且//PQ AC ，则在下列说法中，错误的为（ ）A ．AC BD ⊥B ．//AC 截面PQMN C ．AC BD =D ．异面直线PM 与BD 所成的角为45°【答案】C【解析】【分析】 A 由题设易得//QM BD ，根据平行线的性质可证AC BD ⊥；B 由线面平行的判定可证//AC 截面PQMN ；C ：,P Q 为特殊位置的点时成立；D 将异面直线平移到截面上即可知夹角大小.【详解】A ：由题设，易知//QM BD ，又PQ QM ⊥，//PQ AC ，即有AC BD ⊥，正确；B ：由//PQ AC ，PQ ⊂截面PQMN ，AC ⊄截面PQMN ，则//AC 截面PQMN ，正确； C ：仅当,P Q 为中点时AC BD =，故错误；D ：由A 知：异面直线PM 与BD 所成的角为4PMQ π∠=，正确.故选：C二、多选题1．（2022·河北邯郸·一模）如图，在空间四边形ABCD 中，E ，F 分别为AB ，AD 的中点，G ，H 分别在BC ，CD 上，且::1:2BG GC DH HC ==，则（ ）A ．BD ∥平面EGHFB ．FH ∥平面ABC C ．AC ∥平面EGHFD ．直线GE ，HF ，AC 交于一点【答案】AD【解析】【分析】 由条件可得GH BD ∥，FH 与AC 为相交直线，即可判断ABC ，EG 与FH 必相交，设交点为M ，然后可证明M AC ∈，即可判断D 正确.【详解】因为::BG GC DH HC =，所以GH BD ∥.又E ，F 分别为AB ，AD 的中点，所以EF BD ∥，且12EF BD =，则EF GH ∥. 易知BD ∥平面EGHF ，FH 与AC 为相交直线，即A 正确，B ，C 错误.因为EFHG 为梯形，所以EG 与FH 必相交，设交点为M ，所以EG ⊂平面ABC ，FH ⊂平面ACD ，则M 是平面ABC 与平面ACD 的一个交点，所以M AC ∈，即直线GE ，HF ，AC 交于一点，即D 正确.故选：AD2．（2022·辽宁葫芦岛·一模）如图所示，点A ，B ，C ，M ，N 为正方体的顶点或所在棱的中点，则下列满足//MN 平面ABC 的是（ ）A ．B ．C ．D ．【答案】BC【解析】【分析】根据线面平行的判定定理或面面平行的性质定理，即可得解．【详解】解：对于A ，如图所示，点E ，F 为正方体的两个顶点，则////MN EF AC ，所以N 、M 、C 、A 四点共面，同理可证//AM BC ，即B 、C 、M 、A 四点共面，MN ∴⊂平面ABC ，故A 错误；对于B ，如图所示，D 为正方体的一个顶点，则//AC MD ，//BC ND ，AC ⊂平面ABC ，DM ⊄平面ABC ，所以//DM 平面ABC ，同理可证//DN 平面ABC又MD ND D =，MD 、ND ⊂平面DMN ，∴平面//ABC 平面DMN ，又MN ⊂平面DMN ，//MN ∴平面ABC ，故B 正确；选项C ，如图所示，G 为正方体的一个顶点，则平面//ABC 平面GMN ，MN ⊂平面GMN ，//MN ∴平面ABC ，故C 正确；对于D ，连接CN ，则//AB CN ，A ∴，B ，C ，N 四点共面，MN ∴平面ABC N =，与//MN 平面ABC 相矛盾，故D 错误．故选：BC ． 题型三：直线、平面垂直的判定和性质 一、单选题1．（2022·四川·石室中学三模（文））已知直线l 和平面α，β满足l α⊄，l β⊄.在l β，l a ⊥，αβ⊥这三个关系中，以其中两个作为条件，余下一个作为结论所构成的命题中，真命题的个数是（ ） A ．0B ．1C ．2D ．3【答案】C【解析】【分析】将l β，l a ⊥，αβ⊥三个关系分别以其中两个作为条件，余下一个作为结论判断命题的正误即可.【详解】当l β且l α⊥时，αβ⊥成立；当l β且αβ⊥时，l α⊥不一定成立；当l α⊥且αβ⊥时，结合l β⊄，得l β成立.故选：C.2．（2022·山西晋中·一模（文））如图所示，圆柱的轴截面是正方形ABCD ，母线4BC =，若点E 是母线BC 的中点，F 是AB 的中点，则下列说法正确的是（ ）A ．EF AC ∥B ．点F 到平面ABCD 的距离为2C ．BF ⊥ACD ．BF 与平面ABCD 所成的角的大小为3π 【答案】B【解析】【分析】 证得OE AC ∥，即可判断A 选项；证得OF ⊥平面ABCD ，即可判断B 选项；证得∠ABF 是BF 与平面ABCD 所成的角，并求出角度，即可判断D 选项；由BF 与AB 不垂直，即可判断D 选项．【详解】如图所示，设O 是AB 的中点，连接OE ，OF ，在正方形ABCD 中，4BC =，可得2OB =，在△ABC 中，可得OE AC ∥，则EF 与AC 不平行，选项A 错误；因为F 是AB 的中点，所以OF ⊥平面ABCD ，所以点F 到平面ABCD 的距离为2，选项B 正确；∠ABF 是BF 与平面ABCD 所成的角，因为OF ⊥OB ，且OF =OB ，∠ABF =4π，选项D 错误； BF 与AB 不垂直，因此也推不出BF ⊥AC ，选项C 错误．故选：B.3．（2022·山东潍坊·三模）我国古代数学名著《九章算术》中给出了很多立体几何的结论，其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥．若一个“鳖臑”的所有顶点都在球O 的球面上，且该“鳖臑”的高为2，底面是腰长为2的等腰直角三角形．则球O 的表面积为（ ）A ．12πB ．43πC ．6πD ．26π【答案】A【解析】【分析】作出图形，设在三棱锥A BCD -中，AB ⊥平面BCD ，BC CD ⊥且2BC CD ==，2AB =，证明出该三棱锥的四个面均为直角三角形，求出该三棱锥的外接球半径，结合球体表面积公式可得结果.【详解】如下图所示：在三棱锥A BCD -中，AB ⊥平面BCD ，BC CD ⊥且2BC CD ==，2AB =，因为AB ⊥平面BCD ，BC 、BD 、CD ⊂平面BCD ，则AB BC ⊥，AB BD ⊥，CD AB ⊥，CD BC ⊥，AB BC B ⋂=，CD 平面ABC ，AC ⊂平面ABC ，AC CD ∴⊥，所以，三棱锥A BCD -的四个面都是直角三角形，且2222BD BC CD +2223AD AB BD =+=设线段AD 的中点为O ，则12OB OC AD OA OD ====， 所以，点O 为三棱锥A BCD -的外接球球心，设球O 的半径为R ，则132R AD ==O 的表面积为2412R ππ=. 故选：A.4．（2022·新疆克拉玛依·三模（理））如图，正方体1111ABCD A B C D -的棱长为1，点P 是11B CD 内部（不包括边界）的动点，若BD AP ⊥，则线段AP 长度的取值不可能为（ ）A 5B 23C 6D 35 【答案】A【解析】【分析】根据点P 是11B CD 内部（不包括边界）的动点且BD AP ⊥，确定点P 的轨迹，然后求出线段AP 长度的取值范围即可.【详解】如图，连接11A C 交11B D 于点O ，连接OC由正方体1111ABCD A B C D -知BD ⊥平面11AAC C又因为点P 是11B CD 内部（不包括边界）的动点，所以点P 的轨迹为线段OC （不含端点）， 又因为6OA =2AC =A 到OC 23， 所以线段AP 长度的取值范围是332⎡⎢⎣. 所以线段AP 5. 故选：A.5．（2022·北京·北师大二附中三模）如图，棱长为1的正方体1111ABCD A B C D -中，P 为线段1A B 上的动点（不含端点），则下列结论正确的个数是（ ）①平面11D A P ⊥平面1A AP②1APD ∠的取值范围是0,2π⎛⎤ ⎥⎝⎦③三棱锥11B D PC -的体积为定值④11DC D P ⊥A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据线面位置关系进行判断．判断①，举反例判断②，利用体积公式，判断③，利用垂直关系的转化判断④.【详解】∵11D A ⊥平面1AA P ，∴平面11D A P ⊥平面1A AP ，①正确；若P 是1A B 上靠近1A 的一个四等分点，22129148D P ⎛=+= ⎝⎭，此时222111152cos 458AP AA A P AA A P =+-⨯⨯=，22211D P AP AD +<，此时1D PA ∠为钝角，②错；由于1//BP CD ，则//BP 平面11B D C ，因此11P B D C -的底面是确定的，高也是定值，其体积为定值，③正确；而11⊥D C DC ，11//D C A B ，所以11DC A B ⊥，且111DC A D ⊥,1111A B A D A =，所以1DC ⊥平面11A PD ,1D P ⊂平面11A PD ，因此11DC D P ⊥，④正确．故选：C ．二、多选题1．（2022·广东惠州·二模）已知正四棱台1111ABCD A B C D -的上下底面边长分别为4，62，E 是11A B 的中点，则（ ）A ．正四棱台1111ABCD ABCD -522 B ．平面1BC D ⊥平面11AAC CC ．AE ∥平面1BC DD ．正四棱台1111ABCD A B C D -的外接球的表面积为104π【答案】BCD 【解析】【分析】A.由题意，利用棱台体积公式求解；B.利用线面垂直和面面垂直的判定定理判断；C.取11D A 的中点F ，连接,AF EF ，且11EF AC G ⋂=，连接AG ，易知四边形12C GAO 是平行四边形，得到12//AG C O ，再由11//EF B D ，利用面面平行的判定定理判断； D. 由球心O 在12O O 上，分外接球的球心O 在正四棱台的内部和外部判断.【详解】如图所示：连接,AC BD 交于点2O ，连接1111,AC B D 交于点1O ，A.正四棱台1111ABCD A B C D -的体积为()()11221176216163636233==+⨯=V S S S S h B.易知12,BD AC BD O O ⊥⊥，又122AC O O O ⋂=，则BD ⊥平面11AAC C ，又BD ⊂平面1BC D ，所以平面1BC D ⊥平面11AAC C ，故正确；C.如图所示：取11D A 的中点F ，连接,AF EF ，且11EF AC G ⋂=，连接AG ，易知2//CG AO ，232CG AO == 所以四边形12C GAO 是平行四边形，则12//AG C O ，又AG ⊄平面1BC D ，12⊂C O 平面1BC D ，则//AG 平面1BC D ，又11//EF B D ，EF ⊄平面1BC D ，11B D ⊂平面1BC D ，则//EF 平面1BC D ，又EF AG G ⋂=，所以平面//AEF 平面1BC D ，则AE ∥平面1BC D ，故正确；D. 如图所示：若外接球的球心O 在正四棱台的内部，则O 在12O O 上， 因为122OO 4，6， 则111121122,3222D O B D DO BD ==== 222221112D O D O DO DO O O -+-=， 228182--R R则若外接球的球心O 在正四棱台的外部，如图所示：228182--=R R 226=R ，所以外接球的表面积为24104ππ=R ，故正确；故选：BCD2．（2022·广东佛山·三模）如图，若正方体的棱长为2，点M 是正方体1111ABCD A B C D -在侧面11BCC B 上的一个动点（含边界），点P 是1AA 的中点，则下列结论正确的是（ ）A ．三棱锥1P DD M -的体积为定值B ．若5PM =，则点M 在侧面11BCC B 运动路径的长度为2πC ．若1D M DP ⊥，则1A M 的最大值为2D ．若1D M DP ⊥，则1A M 65 【答案】AD【解析】【分析】对于A ，三棱锥1P DD M -的体积11P DD M M PDD V V --=，由已知得三角形PDD 1的面积是定值，且点M 到面PDD 1的距离是正方体的棱长，由此可判断；对于B ，过点P 作1PQ BB ⊥，由已知有点M 的轨迹是以Q 为圆心，1为半径的半圆弧，根据圆的周长公式计算可判断；对于C 、D ，过点P 作1PQ BB ⊥，则点Q 是1BB 的中点，连接QC ，取BC 的中点N ，连接NC 1，A 1N ，A 1C 1，由线面垂直的判定和性质得点M 的轨迹是线段1C N ，解11A C M ，可求得1A M 的最大值和最小值，由此可判断C 、D 选项.【详解】解：对于A ，三棱锥1P DD M -的体积11P DD M M PDD V V --=，而因为点P 为1AA 的中点，所以三角形PDD 1的面积是定值，且点M 到面PDD 1的距离是正方体的棱长， 所以三棱锥的体积是定值，故A 正确；对于B ，过点P 作1PQ BB ⊥，则由正方体的性质得PQ ⊥平面11BB C C ，所以PQ MQ ⊥， 又5PM 2，所以()2222521MQ PM PQ =--，所以点M 的轨迹是以Q 为圆心，1为半径的半圆弧， 所以点M 在侧面11BCC B 运动路径的长度为22ππ=，故B 不正确；对于C 、D ，过点P 作1PQ BB ⊥，则点Q 是1BB 的中点，连接QC ，取BC 的中点N ，连接NC 1，A 1N ，A 1C 1， 则//QC PD ，1C N QC ⊥，因为1D M DP ⊥，所以1D M QC ⊥，11D C ⊥平面11BB C C ，所以11D C QC ⊥， 又1111D C D M D =，所以QC ⊥平面11D C M ，所以1QC C M ⊥，所以点M 的轨迹是线段1C N ， 在11A C M 中，221111225AC C N NC CC ==+，22211+3A N AA AB BN =+， 所以1A M 的最大值为3，故C 不正确；在11A C M 中，22235225cos 235N +-∠=⨯⨯25sin N ∠= 所以点A1到C1N 有距离为12565sin 3d A N N =⋅∠==， 所以1A M 65D 正确， 故选：AD.。

点、直线、平面之间的位置关系知识点总结立体几何知识点总结1.直线在平面内的判定1利用公理1：一直线上不重合的两点在平面内;则这条直线在平面内.2若两个平面互相垂直;则经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内;即若α⊥β;A∈α;AB⊥β;则ABα.3过一点和一条已知直线垂直的所有直线;都在过此点而垂直于已知直线的平面内;即若A∈a;a⊥b;A∈α;b⊥α;则aα.4过平面外一点和该平面平行的直线;都在过此点而与该平面平行的平面内;即若Pα;P∈β;β∥α;P∈a;a∥α;则aβ.5如果一条直线与一个平面平行;那么过这个平面内一点与这条直线平行的直线必在这个平面内;即若a∥α;A∈α;A∈b;b∥a;则bα.2.存在性和唯一性定理1过直线外一点与这条直线平行的直线有且只有一条；2过一点与已知平面垂直的直线有且只有一条；3过平面外一点与这个平面平行的平面有且只有一个；4与两条异面直线都垂直相交的直线有且只有一条；5过一点与已知直线垂直的平面有且只有一个；6过平面的一条斜线且与该平面垂直的平面有且只有一个；7过两条异面直线中的一条而与另一条平行的平面有且只有一个；8过两条互相垂直的异面直线中的一条而与另一条垂直的平面有且只有一个.3.射影及有关性质1点在平面上的射影自一点向平面引垂线;垂足叫做这点在这个平面上的射影;点的射影还是点.2直线在平面上的射影自直线上的两个点向平面引垂线;过两垂足的直线叫做直线在这平面上的射影.和射影面垂直的直线的射影是一个点；不与射影面垂直的直线的射影是一条直线.3图形在平面上的射影一个平面图形上所有的点在一个平面上的射影的集合叫做这个平面图形在该平面上的射影.当图形所在平面与射影面垂直时;射影是一条线段；当图形所在平面不与射影面垂直时;射影仍是一个图形.4射影的有关性质从平面外一点向这个平面所引的垂线段和斜线段中：i射影相等的两条斜线段相等;射影较长的斜线段也较长；ii相等的斜线段的射影相等;较长的斜线段的射影也较长；iii垂线段比任何一条斜线段都短.4.空间中的各种角等角定理及其推论定理若一个角的两边和另一个角的两边分别平行;并且方向相同;则这两个角相等.推论若两条相交直线和另两条相交直线分别平行;则这两组直线所成的锐角或直角相等.异面直线所成的角1定义：a、b是两条异面直线;经过空间任意一点O;分别引直线a′∥a;b′∥b;则a′和b′所成的锐角或直角叫做异面直线a和b所成的角.2取值范围：0°＜θ≤90°.3求解方法①根据定义;通过平移;找到异面直线所成的角θ；②解含有θ的三角形;求出角θ的大小.5.直线和平面所成的角1定义和平面所成的角有三种：i垂线面所成的角的一条斜线和它在平面上的射影所成的锐角;叫做这条直线和这个平面所成的角.ii垂线与平面所成的角直线垂直于平面;则它们所成的角是直角.iii一条直线和平面平行;或在平面内;则它们所成的角是0°的角.2取值范围0°≤θ≤90°3求解方法①作出斜线在平面上的射影;找到斜线与平面所成的角θ.②解含θ的三角形;求出其大小.③最小角定理斜线和平面所成的角;是这条斜线和平面内经过斜足的直线所成的一切角中最小的角;亦可说;斜线和平面所成的角不大于斜线与平面内任何直线所成的角.6.二面角及二面角的平面角1半平面直线把平面分成两个部分;每一部分都叫做半平面.2二面角条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱;这两个平面叫做二面角的面;即二面角由半平面一棱一半平面组成.若两个平面相交;则以两个平面的交线为棱形成四个二面角.二面角的大小用它的平面角来度量;通常认为二面角的平面角θ的取值范围是0°＜θ≤180°3二面角的平面角①以二面角棱上任意一点为端点;分别在两个面内作垂直于棱的射线;这两条射线所组成的角叫做二面角的平面角.如图;∠PCD是二面角α-AB-β的平面角.平面角∠PCD的大小与顶点C在棱AB上的位置无关.②二面角的平面角具有下列性质：i二面角的棱垂直于它的平面角所在的平面;即AB⊥平面PCD.ii从二面角的平面角的一边上任意一点异于角的顶点作另一面的垂线;垂足必在平面角的另一边或其反向延长线上.iii二面角的平面角所在的平面与二面角的两个面都垂直;即平面PCD⊥α;平面PCD⊥β.③找或作二面角的平面角的主要方法.i定义法ii垂面法iii三垂线法Ⅳ根据特殊图形的性质4求二面角大小的常见方法①先找或作出二面角的平面角θ;再通过解三角形求得θ的值.②利用面积射影定理S′=S·cosα其中S为二面角一个面内平面图形的面积;S′是这个平面图形在另一个面上的射影图形的面积;α为二面角的大小.③利用异面直线上两点间的距离公式求二面角的大小.7.空间的各种距离点到平面的距离1定义面外一点引一个平面的垂线;这个点和垂足间的距离叫做这个点到这个平面的距离.2求点面距离常用的方法：1直接利用定义求①找到或作出表示距离的线段；②抓住线段所求距离所在三角形解之.2利用两平面互相垂直的性质.即如果已知点在已知平面的垂面上;则已知点到两平面交线的距离就是所求的点面距离.3体积法其步骤是：①在平面内选取适当三点;和已知点构成三棱锥；②求出此三棱锥的体积V和所取三点构成三角形的面积S；③由V=S·h;求出h即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.4转化法将点到平面的距离转化为平行直线与平面的距离来求.8.直线和平面的距离1定义一条直线和一个平面平行;这条直线上任意一点到平面的距离;叫做这条直线和平面的距离.2求线面距离常用的方法①直接利用定义求证或连或作某线段为距离;然后通过解三角形计算之.②将线面距离转化为点面距离;然后运用解三角形或体积法求解之.③作辅助垂直平面;把求线面距离转化为求点线距离.9.平行平面的距离1定义个平行平面同时垂直的直线;叫做这两个平行平面的公垂线.公垂线夹在两个平行平面间的部分;叫做这两个平行平面的公垂线段.两个平行平面的公垂线段的长度叫做这两个平行平面的距离.2求平行平面距离常用的方法①直接利用定义求证或连或作某线段为距离;然后通过解三角形计算之.②把面面平行距离转化为线面平行距离;再转化为线线平行距离;最后转化为点线面距离;通过解三角形或体积法求解之.10.异面直线的距离1定义条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公垂线在这两条异面直线间的线段的长度;叫做两条异面直线的距离.任何两条确定的异面直线都存在唯一的公垂线段.2求两条异面直线的距离常用的方法①定义法题目所给的条件;找出或作出两条异面直线的公垂线段;再根据有关定理、性质求出公垂线段的长.此法一般多用于两异面直线互相垂直的情形.②转化法为以下两种形式：线面距离面面距离③等体积法④最值法⑤射影法⑥公式法。

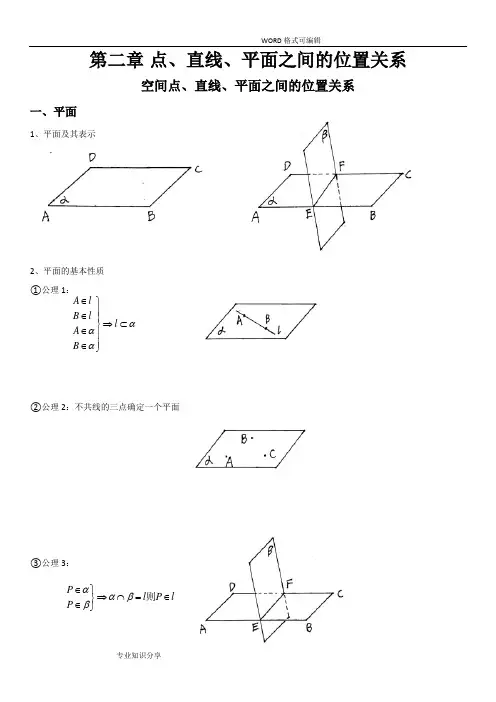
第二章 点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系一、平面1、平面及其表示2、平面的基本性质 ①公理1：②公理2：不共线的三点确定一个平面③公理3：A lB l l A B ααα∈⎫⎪∈⎪⇒⊂⎬∈⎪⎪∈⎭P l P l P ααββ∈⎫⇒⋂=∈⎬∈⎭则二、点与面、直线位置关系1、点与平面有2种位置关系2、点与直线有2种位置关系三、空间中直线与直线之间的位置关系1、异面直线2、直线与直线的位置关系⎧⎧⎨⎪⎨⎩⎪⎩相交共面平行异面3、公理4和定理 公理4：12A B αα∈⎧⎨∉⎩、、12A lB l∈⎧⎨∉⎩、、131223l l l l l l ⎫⇒⎬⎭定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补。

4、求异面直线所成角的步骤： ①作：作平行线得到相交直线；②证：证明作出的角即为所求的异面直线所成的角； ③构造三角形求出该角。

提示：1、作平行线常见方法有：直接平移，中位线，平行四边形。

2、异面直线所的角的范围是 。

四、空间中直线与平面之间的位置关系位置关系公共点有无数个公共点有且只有一个公共点没有公共点符号表示图形表示五、空间中平面与平面之间的位置关系位置关系 两个平面平行 两个平面相交 公共点 没有公共点有一条公共直线符号表示αβa αβ=(000,90⎤⎦a α直线与平面平行a α直线与平面相交a 直线在平面内a α⊂a αa Aα=图形表示直线、平面平行的判定及其性质一、线面平行1、判定：（线线平行，则线面平行）2、性质：（线面平行，则线线平行）二、面面平行1、判定：（线面平行，则面面平行）b a b b a ααα⊄⎫⎪⊂⇒⎬⎪⎭a a ab b αβαβ⎫⎪⊂⇒⎬⎪⋂=⎭a b a b P a b βββααα⊂⎫⎪⊂⎪⎪⋂=⇒⎬⎪⎪⎪⎭2、性质1：（面面平行，则线面平行） 性质2：m m αββα⎫⇒⎬⊂⎭（面面平行，则线面平行）说明（1）判定直线与平面平行的方法：①利用定义：证明直线与平面无公共点。

点直线平面之间的位置关系以点、直线和平面之间的位置关系为题，我们来探讨一下它们之间的联系和特性。

一、点与直线的位置关系：1. 在一个平面上，点与直线可以有三种位置关系：点在直线上、点在直线外、点在直线内。

- 当一个点在直线上时，我们说该点与直线重合。

- 当一个点在直线外时，我们说该点与直线相离。

- 当一个点在直线内时，我们说该点与直线相交。

2. 判断点与直线的位置关系有多种方法：- 使用坐标系：设直线方程为 Ax + By + C = 0，点的坐标为 (x0, y0)，将点的坐标代入直线方程，若等式成立，则点在直线上，否则点在直线外。

- 使用向量：设直线上两点的坐标分别为 (x1, y1) 和 (x2, y2)，点的坐标为 (x0, y0)，计算向量 (x0 - x1, y0 - y1) 和 (x2 - x1, y2 - y1) 的叉积，若叉积为0，则点在直线上，否则点在直线外。

3. 点到直线的距离：- 设点的坐标为 (x0, y0)，直线的方程为 Ax + By + C = 0，点到直线的距离为d。

可以使用以下公式计算点到直线的距离：d = |Ax0 + By0 + C| / √(A^2 + B^2)。

二、点与平面的位置关系：1. 在三维空间中，点与平面可以有四种位置关系：点在平面上、点在平面外、点在平面内、点在平面上方或下方。

- 当一个点在平面上时，我们说该点与平面重合。

- 当一个点在平面外时，我们说该点与平面相离。

- 当一个点在平面内时，我们说该点与平面相交。

- 当一个点在平面上方或下方时，我们说该点与平面平行。

2. 判断点与平面的位置关系有多种方法：- 使用平面方程：设平面方程为 Ax + By + Cz + D = 0，点的坐标为 (x0, y0, z0)，将点的坐标代入平面方程，若等式成立，则点在平面上，否则点在平面外。

- 使用向量：设平面上三点的坐标分别为 (x1, y1, z1)，(x2, y2, z2) 和 (x3, y3, z3)，点的坐标为 (x0, y0, z0)，计算向量 (x0 - x1, y0 - y1, z0 - z1) 与向量 (x2 - x1, y2 - y1, z2 - z1) 的点积和向量 (x0 - x1, y0 - y1, z0 - z1) 与向量 (x3 - x1, y3 - y1, z3 - z1) 的点积，若两个点积均为0，则点在平面上，否则点在平面外。