金堂中学高三适应性考试(文科)答案

四川省成都高中2024年高考适应性考试语文试卷注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

1、阅读下面的文字，完成下列小题。

近日，《中华人民共和国民法典(草案)》首次亮相。

这是我国法治进程中的一件大事，也是国家治理现代化进程中的一件大事。

法治，是治国理政的基本方式，是国家治理体系和治理能力的重要依托。

国家治理要达成现代化的转向，依法治理是不可或缺的一个重要方面。

其中，被称为“社会生活百科全书”的民法典就扮演了重要的角色。

这一角色意义，不仅在于民法典构建了内容集中、体系分明、价值统一的统一法典，更在于民法典契合了中国推进国家治理体系和治理能力现代化的时代命题。

一方面，民法典在国家治理体系中位置重要。

国家治理体系的现代化，离不开法律制度、法律体系以及法治体系的现代化。

作为保障个人权益的最重要法律之一，民法典事关每一个社会个体的方方面面，它以对人的保护为核心，以权利为本位，系统全面地规定了自然人、法人、非法人组织在民事活动中享有的各种人身、财产权益。

民法是万法之母。

孟德斯鸠在《论法的精神》中说，“在民法慈母般的眼里，每一个人就是整个国家”，其重要性可见一斑。

新中国成立以来，我国民事立法不断进步，但是民法体系仍有待完善。

与单行法不同，民法典全面规范民事关系，具有系统性、层次性、科学性的特点，集中体现民法的价值、理念和原则，是民事司法的基本依据和行为准则。

在这个意义上，制定、颁布和实施民法典，是中国法治健全完善的重要标识，更是我国国家治理体系的制度布局。

另一方面，民法典与国家治理能力密切相关。

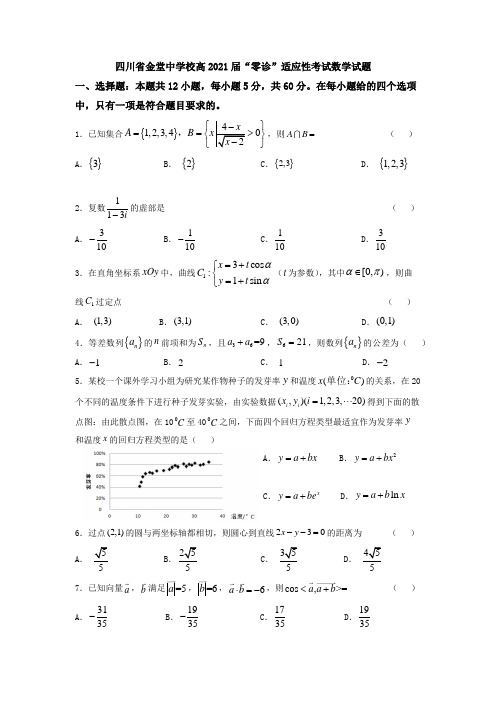
四川省金堂中学校高2021届“零诊”适应性考试数学试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给的四个选项中，只有一项是符合题目要求的。

1．已知集合{}41,2,3,402xA B xx ⎧⎫-==>⎨⎬-⎩⎭，，则A B = （ ） A ．{}3 B ． {}2 C ．{}2,3 D ． {}1,2,32．复数113i-的虚部是 （ ） A ．310-B ．110-C ．110 D ．3103．在直角坐标系xOy 中，曲线13cos :1sin x t C y t αα=+⎧⎨=+⎩（t 为参数），其中[0,)απ∈，则曲线1C 过定点 （ ） A ． (1,3)B ．(3,1)C ． (3,0)D ．(0,1)4．等差数列{}n a 的n 前项和为n S ，且36=9a a +，621S =，则数列{}n a 的公差为（ ） A ．1-B ．2C ． 1D ．2-5．某校一个课外学习小组为研究某作物种子的发芽率y 和温度0()x C 单位：的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据(,)(1,2,3,20)i i x y i =⋅⋅⋅得到下面的散点图：由此散点图，在100C 至400C 之间，下面四个回归方程类型最适宜作为发芽率y 和温度x 的回归方程类型的是（ ）A ．y a bx =+B ．2y a bx =+C ．xy a be =+D ．ln y a b x =+6．过点(2,1)的圆与两坐标轴都相切，则圆心到直线230x y --=的距离为 （ ） A ．55B ．255C ．355 D ． 4557．已知向量a ，b 满足=5a ，=6b ，6a b ⋅=-，则cos ,>=a a b <+ （ ） A ．3135-B ．1935-C ．1735 D ．19358．在ABC ∆中，若()(sin sin )(sin sin )a b A B c c B +-=+，则A ∠= （ ） A ．23π B ．3π C ．56π D ．6π 9．执行如图所示的程序框图，如果输入的0,0k a ==，则输出的k 的值等于（ ） A. 2 B. 3C. 4D. 510．已知双曲线C ：22221(0,0)a b a bx y -=>>的左，右焦点分别为12F F ，，离心率为5，P 是C 上的一点，且12F P F P ⊥，若12PF F ∆的面积为4，则a = （ ）A ． 1B ． 2C ．4D ．811．已知5458<，45138<，设5813log 3log 5log 8a b b ===，，，则 （ ） A. a b c << B. b a c << C. b c a << D. c a b <<12．已知函数()f x 对x R ∀∈均满足()()f x f x -=，(2)()f x f x -=，且当01x ≤≤时，()2=f x x ，如果函数()()()g x f x x m =-+有两个零点，则实数m 的值为 （ ）A ．2()k k Z ∈B ． 122()4k k k Z +∈或 C ． 0 D ．122()4k k k Z -∈或 二、填空题：本题共4小题，每小题5分，共20分。

高中数学学习材料马鸣风萧萧*整理制作金堂中学2015年高三适应性考试（文科）答案1、已知集合{}1==x x M ，{}x x x N ==2，则=⋃N M （D ）（A ）{}1 （B ） {}1,1- （C ） {}1,0 （D ）{}1,0,1-2、复数2(1)1i i+-＝( B )A. 1i +B. 1i -+C. 1i --D. 1i -3、已知平面γβα,,，直线c b a ,,，则下列命题正确的是（C ） （A ）若,,γβγα⊥⊥则βα//；（B ）若,,c b c a ⊥⊥则b a //； （C ）若,,αα⊥⊥b a 则b a //； （D ）若,//,//ααb a 则b a //．4、如图所示，某几何体的三视图相同，均为圆周的41，则该几何体的表面积为（B ）（A ）π43 （Ｂ）π45（Ｃ）π （Ｄ） π2 5、执行右图的程序框图，则输出的结果为 （ C ）（A ）66（Ｂ）64（Ｃ）62（Ｄ）606、设y x ,满足约束条件⎩⎨⎧≤-≤-≤≤0131y x x ，则y x z -=2的最大值为(A )（A ）3 （B ）2 （C ）1 （D ）01 17、设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若bcosC+ccosB=asinA ，则△ABC 的形状为（D ） A ． 等腰三角形B ． 锐角三角形C ． 钝角三角形D ． 直角三角形8、已知直线21//l l ，A 是21,l l 之间的一定点，并且A 点到21,l l 的距离分别为3,2，B 是直线2l 上一动点，作AB AC ⊥，且使AC 与直线1l 交于点C ，则ABC ∆面积的最小值为(C )（A ）2 （B ）3 （C ）6 （D ）49、已知21,F F 分别是双曲线1:2222=-by a x C 的左，右焦点，若2F 关于渐近线的对称点恰落在以1F 为圆心，1OF 为半径的圆上，则双曲线C 的离心率为(D ) （A ）3 （Ｂ）3 （Ｃ）2 （Ｄ）210．已知函数),0()0,()(+∞⋃-∞是定义在x f 上的偶函数，当0>x 时，1)(4)(2),2(21,20,12)(|1|-=⎪⎩⎪⎨⎧>-≤<-=-x f x g x x f x x f x 则函数的零点个数为 ( D )A ．4B ．6C ．8D ．10第二部分 （非选择题 共100分）注意事项：必须使用0.5毫米黑色签字笔在答题卡上题目所指示的答题区域内作答。

四川金堂中学2020年高考语文模拟试题命题人童华池第I卷(选择题共30分)一、（12分，每小题3分）1．下列各组词语中，有两个错别字的一组是A．标识不径而走宣泄蛛丝蚂迹B．松弛食不裹腹追溯不落窠臼C．精萃美仑美奂即使矫揉造作D．重叠天翻地覆痉挛再接再厉2．下列各句中，加点的成语使用恰当的一句是A．随着十月销量数据的出炉，作为影响汽车厂商一年业绩完成情况的最关键的两个月，“金九银十”的销售大战终于落下帷幕。

与往年相比，今年“金九银十”的含金量似乎有所下降，九月车市整体温和增长，十月的表现也不瘟不火。

B．冯小刚刚走，张艺谋要来——《夜宴》刚刚吃过，《黄金甲》呼之欲出。

C．目前，行政体制改革要按照法治的要求积极推进政府转型。

第一，从全能型政府转变为有限型政府。

即要求政府从无所不为转变为有所为、有所不为。

D．是什么力量，使一个农民的儿子取得丰硕的学术成果，成为名闻遐迩、卓尔不群的国学大师？又是什么力量，使一个留学德国十载的学者，没沾染上一点洋味而终生保持着一种朴厚的农民气象？3．下列各句中，没有语病的一句是A．枭龙战斗机的研制走过了一条从观念、管理与技术上的单个原始创新到整个项目上的集成创新的过程。

B．实际上，许多环境污染事故没有得到有效遏制，与其说是被法律遗忘的角落，不如说是有法不依、执法不严。

C．20年前，丁晓兵是赴汤蹈火的英雄；20年后，他是感动中国的榜样。

在他的身上，我们看到了“钢铁般的意志”，这是支撑人生的钢梁，是成就英雄的法宝。

D．如果你的衣柜里有闲置的孕妇装、小玩具、小睡床、小衣服等，请将它们变成一份爱心送给需要它的新主人。

4．填入下面横线处的句子，与上下文衔接最恰当的一组是２００６年在科学发展观的指导下，我国加强和改善宏观调控，推进改革开放，，，，国民经济呈现出、、的态势，实现了“十一五”良好开局。

①发展势头进一步趋好②发展环境进一步优化③发展条件进一步改善④物价水平较低⑤增长速度较快⑥经济效益较好A．①③②④⑥⑤B．③①②⑤⑥④C．①②③⑤⑥④D．②①③④⑤⑥二、（9分，每小题3分）阅读下面的文字，完成5～7题。

四川省成都市四川金堂中学2018-2019学年高三数学文模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若正数m，n满足，则的最小值为（）A. B. C. D. 3参考答案：A【分析】由，利用基本不等式，即可求解，得到答案. 【详解】由题意，因为，则，当且仅当，即时等号成立，所以的最小值为，故选A.【点睛】本题主要考查了利用基本不等式求最小值问题，其中解答中合理构造，利用基本不是准确运算是解答的关键，着重考查了推理与运算能力，属于基础题.2. 已知函数y＝f（x）是偶函数，且函数y＝f（x－2）在[0,2]上是单调减函数，则 A．f（－1）<f（2）<f（0） B．f（－1）<f（0）<f（2）C．f（0）<f（－1）<f（2） D．f（2）<f（－1）<f（0）参考答案：C3. 一个棱锥的三视图如下图，则该棱锥的体积为（）A．28 B．24 C．72 D．36参考答案：B4. 已知p：|x﹣1|＜2，q：f（x）=的最小值为2，则p是q的（）A．充分而不必要条件B．充要条件C．必要而不充分条件D．既不充分也不必要条件参考答案：D【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分必要条件的定义以及集合的包含关系判断即可．【解答】解：由|x﹣1|＜2，解得：﹣1＜x＜3，故p：﹣1＜x＜3；f（x）==x+的最小值为2，得x＞0，故q：x＞0，故p是q的既不充分也不必要条件，故选：D．5. 三角形ABC中，A，B，C的对边分别为a,b,c,已知下列条件：①b=3,c=4,; ②a=5,b=8,;③c=6,b=,; ④c=9,b=12,其中满足上述条件的三角形有两解的是：（）A.①②B.①④C.①②③D.③④参考答案：A略6. 若实数x，y满足约束条件，则的最大值是（）A. －1B. 1C. 10D. 12参考答案：C【分析】本题是简单线性规划问题的基本题型，根据“画、移、解”等步骤可得解.题目难度不大题，注重了基础知识、基本技能的考查.【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以为顶点的三角形区域（包含边界），由图易得当目标函数经过平面区域的点时，取最大值.【点睛】解答此类问题，要求作图要准确，观察要仔细.往往由于由于作图欠准确而影响答案的准确程度，也有可能在解方程组的过程中出错.7. 现有四个函数①y=x·sin x，②y=x·cos x，③y=x·|cos x|，④y=x·2x的部分图象如下，但顺序被打乱，则按照图象从左到名，对应的函数序号正确的一组是(A) ①④②③(B)①④③②(C) ④①②③(D) ③④②①参考答案：A略8. 某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98)，[98，100)，[100，102)，[102，104)，[l04，l06]．已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于102克的产品的个数是A．90 B．75 C．60 D．45参考答案：C9. 若恒成立，其中（）A. B． C． D.参考答案：A10. 则( )(A) (B) (C) (D)参考答案：D略二、填空题:本大题共7小题,每小题4分,共28分11. 如图，椭圆中，F1、F-2分别是椭圆的左、右焦点，A、B分别是椭圆的左、右顶点，C是椭圆上的顶点，若∠CF1B=60°，，则椭圆的离心率e= 。

成都市重点中学高2023届高考适应性模拟检测试题（二）语文注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1-3题。

近来接连出现的爆款文化创新节目，无不证明了艺术创作“古为今用、推陈出新”具有令观众惊艳的力量。

屡屡对这些节目赞美、惊叹的同时，我们也不禁思考，这类既叫好又叫座的文化创新类节目是如何炼成的？河南卫视推出的《唐宫夜宴》《天地之中》《祈》等致力于激活优秀传统文化基因、依托现代技术、精心制作的节目对此做了很好的诠释。

追溯历史，破解传统密码。

与众多新兴媒体及其文化产物不同，传统文化创新节目与生俱来裹挟着厚重的历史感和历经岁月沉淀的独特“包浆”韵味，这使它在文化节目存在形式同质化、制作浅表化等问题的当下依然具有先天的吸引力。

而如何从卷帙浩繁的历史典籍中攫取“文化亮点”并提炼出新奇创意，是制作文化创新类节目面临的首要问题。

河南卫视在这方面可谓别出心裁，表现不俗。

端午节目开场舞《祈》以洛神、飞天为原型，采用真人水中起舞的形式再现曹子建笔下“髣髴兮若轻云之蔽月，飘飖兮苦流风之回雪”的曼妙，舞出文化的“回归”；《丽人行》借老杜诗名，给每位演员画上花钿、斜红、面靥齐全的唐朝妆容，以重现“云想衣裳花想容”的大唐盛世……显然，在深入挖掘传统题材的基础上，选取最能触发受众民族自豪感、最能唤起受众文化认同和民族自信的文化元素，是这类文化创新节目频频“出圈”的关键所在。

以文驭娱，依托现代技术。

任何一种传统艺术的重新演绎都离不开现代元素的融入。

《离骚》曰：“纷吾既有此内美兮，又重之以修能。

”如果说传统文化元素的挖掘赋予文化创新节目以“内美”，那么现代化科技手段则起到了“修能”之用。

成都高2023届高考适应性考试（一）语文（答案在最后）（全卷满分150分，考试时间150分钟）注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在本试卷和答题卡相应位置上。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答。

答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

景观社会理论的提出人居伊·德波认为，在景观社会中，人类生存和生活的本质被“异化”为符号和表征。

尤其是人类社会步入后现代社会之后，伴随不确定性与多样性的加深，相对原有社会生活来说，也需要与后现代性相适应的符号和表征体系。

由于急剧的社会变迁以及与之相伴的社会结构改变，新的表征体系建构在原有符号表征体系的崩溃以及主体性消解的基础之上。

符号的“异化”不仅受到社会结构的约束，形成与之“共变”的过程关系，而网络造词同样是一种社会“异化”的表征，这一过程作用于社会个体和群体的心理状态，其直接的结果就是影响和改变原有的社会心态秩序。

社会心态，在一定程度上依存于一个作为载体的“心理群体”之上，表现出特定的集体氛围和共同情绪。

这一概念与精神分析学家弗洛姆提出的社会性格的概念含义接近，主要被用来描述一个社会或群体基于生活方式、内在期待、社会适应而形成的共同性格结构。

国内关于社会心态的研究不在少数，研究者普遍认为该概念指的是具有普遍性的社会心理状态，是广泛存在于社会群体中的、具有共性的社会心理反应和心理态势。

在哲学和文化研究领域，社会心态被细化为心理取向、精神支柱和社会理智。

贵阳2022届高考适应性月考卷（六）文科综合参考答案一、选择题（本大题共35小题，每小题4分，共140分）题号 1 2 3 4 5 6 7 8 9 10 11 12答案 A C D A B D B C C A D D题号13 14 15 16 17 18 19 20 21 22 23 24答案 A C C D B B D B A C B A题号25 26 27 28 29 30 31 32 33 34 35答案 C B D C C D D B C B A【解析】1．据图1可知，该岛是距离托马斯·奥尼尔隧道和泰德·威廉姆斯隧道较近的海上垃圾填埋场，故选A。

废料堆放不管距离陆地远近，环境污染都较大，离城市远，污染危害小；波士顿位于美国东海岸，为暖流流经，填埋水平、自净能力不是废料堆放地选址的主要因素，B、C、D错误。

故选A。

2．据材料“岛上的垃圾和渗滤液造成的污染不断加剧”可知，该岛覆盖表层土壤的主要目的是覆盖和保护垃圾场密封层，C正确。

覆盖表层土壤，人工养护的成本较高，但无法抵御地震海啸，也无法支持高大乔木的生长，A、B、D错误。

故选C。

3．该岛改造的短期内，减少陡坡数量、设置蜿蜒的道路减缓地表径流的流速，修建大型防浪堤能有效削减流水冲刷，但种植乡土树种的效果要过一段时间才能表现出来，短期内因种树扰动地表覆盖，反而可能加剧流水侵蚀，故①错误，故选D。

4．读表可知，北冰洋的降水量和蒸发量均较小，北冰洋纬度高，蒸发量小，A正确。

对流雨多出现在热带地区或夏季，盛行西风的影响范围不包括北冰洋，北大西洋暖流对降水的影响较小，B、C、D错误。

故选A。

5．考查区域地理，尼罗河注入地中海，流经热带荒漠，径流量有限；亚马孙河、刚果河、密西西比河均是流域面积广、流量大的注入大西洋的河流，故选B。

6．根据材料“山体由花岗岩组成、周边的高原面则以砂岩为主”可以推测形成年保玉则峰的地质作用主要有地壳运动、岩浆活动和冰川作用。

2021年四川省高考数学适应性试卷〔文科〕一、选择题：本大题共10个小题，每题5分，共50分.在每题给出的四个选项中，只有一项为哪一项符合题目要求的.1．集合M，N满足M∪N={1，2，3}，M∩N={a}，那么〔〕A．a=1B．a=2C．a=3D．a∈M∪N2axb012〕，那么ab的值为〔〕2．假设不等式x++＜的解集为〔﹣，A．﹣1B．1C．﹣2D．23z=，那么|z|=〔〕．复数A．1B．C．2D．4．假设“?x∈[﹣1，m]〔m＞﹣1〕，|x|﹣1＞0〞是假命题，那么实数m的取值范围是〔〕A ．〔﹣11B11C1∞D．[01，〕．〔﹣，]．[，+〕，]5．=〔2，1〕，=〔3，λ〕．假设〔2〕∥，那么λ的值为〔〕A．B．C．3D．﹣1或36．执行如下图的程序框图，输出的结果是〔〕A．﹣2B．C．D．37sin=，sin〔α+β〕=，那么cos2〕．α、β为锐角，假设αβ的值为〔A．B．C．或D．8．P，Q，R是圆x2+y2﹣2x﹣8=0上不同三点，它们到直线l：x+y+7=0的距离分别为x1，x2，x3，假设x1，x2，x3成等差数列，那么公差的最大值为〔〕A．1B．2C．3D．49．设P 是左、右顶点分别为A，B的双曲线x2﹣y2=1上的点，假设直线PA的倾斜角为，那么直线PB的倾斜角是〔〕A．B．C．D．10．设0＜a＜1，函数f〔x〕=，假设存在实数b使函数g〔x〕=f〔x〕﹣b有两个零点，那么a的取值范围是〔〕A．B．C．〔0，1〕D．第1页〔共17页〕二、填空题〔每题 5分，总分值 25分，将答案填在答题纸上〕11．假设抛物线 y =ax 2的焦点F 的坐标为〔0，﹣1〕，那么实数 a 的值为_______．12．某几何体的三视图如下图， 其中左视图为半圆， 那么主视图中 α角的正切值为_______．13 f x 〕 =x + 在[ 1 3 2 ，那么正数 k的最大值与最小值之和为．假设函数 〔 ，]上的最小值为 _______．2ax1 214a在区间[16fx=﹣ x++在区间〔，+∞〕上是单调．当实数，]随机取值时，函数〔 〕减函数的概率是_______．15．实数a ，b 满足：5﹣a ≤3b ≤12﹣3a ，e b≤a ，那么 的取值范围为_______．三、解答题〔本大题共 6小题，共 75分.解容许写出文字说明、证明过程或演算步骤.〕 16．为了解学生寒假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表： 本数人数 012345 性别男生 0 1 4 3 2 2女生1331〔I 〕分别计算男生、女生阅读名著本数的平均值 x 1，x 2和方差 ，；II 〕从阅读4本名著的学生中选两名学生在全校交流读后心得，求选出的两名学生恰好是一男一女的概率．17．数列{a n }的前n 项和S n =k?3n﹣m ，且a 1=3，a 3=27．I 〕求证：数列{a n }是等比数列；II 〕假设a n b n =log 3a n+1，求数列{b n }的前n 项和T n ．18．在斜三棱柱 A BC ﹣A 1B 1C 1中，底面ABC 是正三角形，E 是AB 中点，A 1E ⊥平面ABC ．〔I 〕证明：BC 1∥平面A 1EC ；〔II 〕假设A 1A ⊥A 1B ，且AB=2，求三棱锥B 1﹣ACA 1的体积．第2页〔共17页〕19．如图ABCD 是平面四边形，∠ ADB=∠BCD=90°，AB=4，BD=2．〔Ⅰ〕假设BC=1，求AC 的长；〔Ⅱ〕假设∠ACD=30°，求tan ∠BDC 的值．20．圆锥曲线 E ：．〔I 〕求曲线E 的离心率及标准方程；〔II 〕设M 〔x 0，y 0〕是曲线 E 上的任意一点，过原点作⊙M ：〔x ﹣x 0〕2+〔y ﹣y 0〕2=8的 两条切线，分别交曲线 E 于点 P 、Q ．① 假设直线OPOQ 的斜率存在分别为 k ，k ，求证：kk=﹣； ， 1 2 12 ②试问OP 2+OQ 2是否为定值．假设是求出这个定值，假设不是请说明理由． x21．设函数 f 〔x 〕=e ，g 〔x 〕=kx+1． I 〕求函数y=f 〔x 〕﹣〔x+1〕的最小值；II 〕证明：当k ＞1时，存在x 0＞0，使对于任意x ∈〔0，x 0〕都有f 〔x 〕＜g 〔x 〕；〔III 〕假设对于任意 x ∈〔0，+∞〕，|f 〔x 〕﹣g 〔x 〕|＞x 恒成立，求实数 k 的取值范围．第3页〔共17页〕2021年四川省高考数学适应性试卷〔文科〕参考答案与试题解析一、选择题：本大题共10个小题，每题5分，共50分.在每题给出的四个选项中，只有一项为哪一项符合题目要求的. 1．集合M，N满足M∪N={1，2，3}，M∩N={a}，那么〔〕A．a=1 B．a=2 C．a=3D．a∈M∪N【考点】交集及其运算；并集及其运算．【分析】根据集合关系进行判断即可．【解答】解：∵M∪N={1，2，3}，M∩N={a}，a=1，或a=2或a=3，即a∈M∪N，应选：D．2．假设不等式x 2+ax+b＜0的解集为〔﹣1，2〕，那么ab的值为〔〕A．﹣1B．1C．﹣2D．2【考点】一元二次不等式的解法．【分析】根据一元二次不等式与对应方程之间的关系，利用根与系数的关系求出a、b的值，再计算ab的值．【解答】解：不等式x 2+ax+b＜0的解集为〔﹣1，2〕，所以方程x2axb=0的实数根为﹣1和2 ++，所以，解得a=﹣1，b=﹣2，所以ab=﹣1×〔﹣2〕=2．应选：D．3z=，那么|z=〔〕．复数|A．1B．C．2D．【考点】复数代数形式的乘除运算．【分析】根据复数的运算性质化简z，从而求出z的模即可．【解答】解：z===i，那么|z|=1，应选：A．4．假设“?x∈[﹣1，m]〔m＞﹣1〕，|x|﹣1＞0〞是假命题，那么实数m的取值范围是〔〕A ．〔﹣11B11C1∞D．[01，〕．〔﹣，]．[，+〕，]【考点】特称命题．【分析】由|x|﹣1＞0，解得x＞1或x＜﹣1．由“?x∈[﹣1，m]〔m＞﹣1〕，|x|﹣1＞0，可得m＞1．利用“?x∈[﹣1，m]〔m＞﹣1〕，|x|﹣1＞0〞是假命题，即可得出．第4页〔共17页〕【解答】解：由|x|﹣1＞0，解得x＞1或x＜﹣1．∵“?x∈[﹣1，m]〔m＞﹣1〕，|x|﹣1＞0，∴m＞1．∵“?x∈[﹣1，m]〔m＞﹣1〕，|x|﹣1＞0〞是假命题，∴﹣1＜m≤1．应选：B．5．=〔2，1〕，=〔3，λ〕．假设〔2〕∥，那么λ的值为〔〕A．B．C．3D．﹣1或3【考点】平面向量共线〔平行〕的坐标表示．【分析】求出向量2，利用向量共线列出方程，求解即可．【解答】解：=〔2，1〕，=〔3，λ〕．=〔1，2﹣λ〕．〔2〕∥，可得：3〔2﹣λ〕=λ，∴λ=．应选：A．6．执行如下图的程序框图，输出的结果是〔〕A．﹣2 B．C．D．3【考点】程序框图．【分析】根据程序框图，依次计算运行的结果，观察规律可得当a=，k=4时，满足条件k4，退出循环，输出a的值为．【解答】解：模拟执行程序，可得a= ，k=0执行循环体，a=3，k=1不满足条件k≥100，执行循环体，a=﹣2，k=2不满足条件k≥100，执行循环体，a=﹣，k=3第5页〔共17页〕不满足条件k≥100，执行循环体，a=，k=4此时，满足条件k≥4，退出循环，输出a的值为．应选：C．7．α、β为锐角，假设sinα=，sin〔α+β〕=，那么cos2β的值为〔〕A．B．C．或D．【考点】两角和与差的余弦函数．【分析】利用同角三角函数的根本关系求得cosα的值，由题意求得范围π＞α+β＞，从而可求cosαβcosβcos2β的值．〔+〕的值，进而可求的值，再利用二倍角的余弦公式求得αβsinα=sinαβ=，【解答】解：、都是锐角，且，〔+〕∴cosα==，cos〔α+β〕==±，sin〔α+β〕=sinαcosβ+cosαsinβ=〔2cosβ+sinβ〕=，2cosβ+sinβ=，①∵cosα=，α＞，∵＞sin〔α+β〕=＞，∴π＞α+β＞，cos〔α+β〕=﹣，cosαcosβ﹣sinαsinβ=﹣，cosβ﹣2sinβ〕=﹣，∴cosβ﹣2sinβ=﹣，②解①②，得cosβ=，cos2β=2cos 2β﹣1=﹣．应选：A．2y22x﹣8=0上不同三点，它们到直线l x+y7=0的距离分别8．P，Q，R是圆x+﹣：+为x1，x2，x3，假设x1，x2，x3成等差数列，那么公差的最大值为〔〕第6页〔共17页〕A ．1B ．2C ．3D ．4【考点】直线与圆的位置关系．【分析】求出圆心到直线的距离，判断直线与圆的位置关系，继而得出圆上的点到直线的距离的最大值和最小值，那么距离最值的差的一半为最大公差．【解答】解：圆的圆心为〔 1，0〕，半径r=3，圆心到直线 l 的距离d= = =4，所以直线 l 与圆相离．∴圆上的点到直线 l 的距离的最小值为 d ﹣r=1，最大值为 d+r=7．∴当x 1=1，x 3=7时，等差数列的公差取得最大值 =3．应选C ．9．设P 是左、右顶点分别为 A ，B 的双曲线x 2﹣y 2=1上的点，假设直线 PA 的倾斜角为 ，那么直线PB 的倾斜角是〔 〕A ．B ．C ．D ．【考点】双曲线的简单性质．【分析】设P 〔m ，n 〕，那么m 2﹣n 2=1，求得A ，B 的坐标，运用两点的直线的斜率公式，计算可得k PA ?k PB =1，再由倾斜角与斜率的关系，即可得到所求．22【解答】解：设P 〔m ，n 〕，那么m ﹣n=1，由题意可得A 〔﹣1，0〕，B 〔1，0〕，即有k PA ?k PB = ? == =1，由直线PA 的倾斜角为 ，可得k PA =tan =﹣， 即有k PB =﹣，可得直线PB 的倾斜角是．应选：C ．10．设0＜a ＜1，函数 f 〔x 〕= ，假设存在实数 b 使函数g 〔x 〕=f〔x 〕﹣b 有两个零点，那么 a 的取值范围是〔 〕A ．B ．C ．〔0，1〕D ．∴ 【考点】函数零点的判定定理．【分析】由g 〔x 〕=f 〔x 〕﹣b 有两个零点可得 f 〔x 〕=b 有两个零点，即y=f 〔x 〕与y=b的图象有两个交点，那么利用 a= 时，8a 3=1，可求a 的范围．【解答】解：∵g 〔x 〕=f 〔x 〕﹣b 有两个零点f 〔x 〕=b 有两个零点，即y=f 〔x 〕与y=b 的图象有两个交点，由于y=cos πx 在〔0，a]递减，y=8x 3在〔a ，1]递增，第7页〔共17页〕a= 时，8a 3=1．∵存在实数 b 使函数g 〔x 〕=f 〔x 〕﹣b 有两个零点，0＜a ＜ 应选：B ．二、填空题〔每题 5分，总分值 25分，将答案填在答题纸上〕11．假设抛物线 y =ax 2的焦点F 的坐标为〔0，﹣1〕，那么实数 a 的值为 ．【考点】抛物线的简单性质．【分析】先把抛物线方程整理成标准方程，进而根据抛物线的焦点坐标，可得 a 的值．【解答】解：抛物线 y=ax 2的标准方程为 x 2= y ， ∵抛物线 y=ax 2的焦点坐标为〔 0，﹣1〕，∴ =﹣1，∴a=故答案为： ．12．某几何体的三视图如下图，其中左视图为半圆，那么主视图中α角的正切值为．【考点】由三视图求面积、体积．【分析】由三视图可知：该几何体为圆锥的一半．可得母线长 l=3，底面半径 r=1，圆锥的高h= ，利用直角三角形的边角关系即可得出．【解答】解：由三视图可知：该几何体为圆锥的一半．∵母线长 l=3，底面半径 r=1．∴圆锥的高 h= =2 ．∴tan α= = ．故答案为：．第8页〔共17页〕13 fx=x 在[ 1 3 上的最小值为 2 ，那么正数 k 的最大值与最小值之和为 10． ．假设函数〔〕+ ，] 【考点】根本不等式．【分析】运用根本不等式可得 f x 〕≥ 2 ，由等号成立的条件可得 ∈[ 1 3〔 ，]，继而求出k 的最大值与最小值．【解答】解：由题意得：x ＞0， ∴f 〔x 〕=x+ ≥2 ，∵函数f 〔x 〕=x+ 在[1，3]上的最小值为 2 ，当x=时，函数f 〔x 〕取得最小值2，∴∈[1，3]，∴k 的最小值为1，最大值为9．∴正数k 的最大值与最小值之和为 10．故答案为：10．14．当实数a 在区间[1，6]随机取值时，函数f 〔x 〕=﹣x 2+ax+1在区间〔2，+∞〕上是单调减函数的概率是．【考点】几何概型．【分析】由题意，此题属于几何概型的概率求法， 由此只要求出所有事件的区域长度以及满足条件的a 的范围对应的区域长度，利用几何概型概率公式可求．【解答】解：∵函数 f x 〕 = ﹣ x 2ax1 2 ∞〕上是单调减函数，〔 ++在区间〔 ，+∴ ≤2， a ≤4，∵1≤a ≤6，1≤a ≤4，长度为3，∵1≤a ≤6，长度为5∴函数 f 〔x = ﹣ x 2 ax1 在区间〔 2 ∞ 〕 + + ，+ 〕上是单调减函数的概率是．故答案为： ．15．实数a ，b 满足：5﹣a ≤3b ≤12 ba的取值范围为[，]．﹣3a ，e ≤，那么【考点】不等式的根本性质．【分析】作出不等式组表示的平面区域，那么表示与原点的连线的斜率额取值范围．【解答】解：∵e b≤a ， b ≤lna5﹣a ≤3b ≤12﹣3a ，画出如下图的可行域，第9页〔共17页〕由，解得a=，b=，即A〔，〕，=设b=lna，∴b′=，当b=1时，此时斜线的斜率最大，即为=k=，综上所述，的取值范围为，故答案为：[，]．三、解答题〔本大题共6小题，共75分.解容许写出文字说明、证明过程或演算步骤.〕16．为了解学生寒假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表：本数人数012345性别男生014322女生001331（〔I〕分别计算男生、女生阅读名著本数的平均值x1，x2和方差，；II〕从阅读4本名著的学生中选两名学生在全校交流读后心得，求选出的两名学生恰好是一男一女的概率．第10页〔共17页〕【考点】极差、方差与标准差；众数、中位数、平均数；列举法计算根本领件数及事件发生的概率．【分析】〔Ⅰ〕利用公式分别求出男生、女生阅读名著本数的平均数与方差即可；〔Ⅱ〕利用列举法计算根本领件数，即可求出对应的概率值．【解答】解：〔Ⅰ〕全班有 12个男生8个女生，∴男生阅读名著本数的平均值 x 1= =3，女生阅读名著本数的平均值x 2=，∴，；〔II 〕阅读4本名著的学生共有 5人，其中两名男生，三名女生，设两名男生分别为A 1，A 2，三名女生分别为B 1，B 2，B 3，从这5人中任选两人的选法有：1A 2，A 1B 1，A 1B 2，A 1B 3，A 2B 1，A 2B 2，A 2B 3，B 1B 2，B 1B 3，B 2B 3共10种，其中一男一女的选法有：1B 1，A 1B 2，A 1B 3，A 2B 1，A 2B 2，A 2B 3共6种，所以从这 5人中选出的两人是一男一女的概率为．17．数列{a n }的前n 项和S n =k?3n﹣m ，且a 1=3，a 3=27．I 〕求证：数列{a n }是等比数列；II 〕假设a n b n =log 3a n+1，求数列{b n }的前n 项和T n ． 【考点】数列的求和；等比关系确实定．【分析】〔I 〕利用递推关系与等比数列的定义即可证明． II 〕利用“错位相减法〞、等比数列的求和公式即可得出．【解答】〔I 〕证明：∵ ，∴S 1=a 1=3k ﹣m=3，a 3=S 3﹣S 2=18k=27，解得．那么当n ≥2时，，又a 1=3，∴?n ∈N *，．那么 为常数，故由等比数列的定义可知，数列 {a n }是等比数列．〔II 〕解：∵a n b n =log 3a n+1，∴ ． 那么，第11页〔共17页〕∴，那么 ，即〔n ∈N *〕．18．在斜三棱柱A BC ﹣A 1B 1C 1中，底面ABC 是正三角形，E 是AB 中点，A 1E ⊥平面ABC ．〔I 〕证明：BC 1∥平面A 1EC ；〔II 〕假设A 1A ⊥A 1B ，且AB=2，求三棱锥B 1﹣ACA 1的体积．【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定．【分析】〔Ⅰ〕根据线面平行的判定定理进行证明即可． 〔Ⅱ〕根据三棱锥的体积公式求出相应的底面积和高即可．【解答】解：〔I 〕证明：设AC 1与A 1C 交于F 点，连接EF ，∵E ，F 分别是线段 AB ，AC 1的中点，∴ E F ∥BC 1，又EF?平面A 1EC ，BC 1?平面A 1EC 故BC 1∥平面A 1EC〔II 〕由易得BB 1∥平面ACA 1∴点B 到平面ACA 1的距离等于点B 1到平面ACA 1的距离．那么三棱锥B 1﹣ACA 1的体积等于三棱锥 B ﹣ACA 1的体积． 而三棱锥B ﹣ACA 1的体积又等于三棱锥 A 1﹣ABC 的体积，由易得正三角形ABC 的面积为，∵A 1E ⊥平面ABC ，且易得A 1E=1，∴三棱锥A 1﹣ABC 的体积．故三棱锥B 1﹣ACA 1的体积为．第12页〔共17页〕19．如图ABCD是平面四边形，∠ADB=∠BCD=90°，AB=4，BD=2．〔Ⅰ〕假设BC=1，求AC的长；〔Ⅱ〕假设∠ACD=30°，求tan∠BDC的值．【考点】正弦定理；余弦定理．【分析】〔I〕设∠ABD=α，∠CBD=β．在Rt△ABD中，cosα=，可得α．在Rt△CBD 中，cosβ=，可得β．在△ABC中，利用余弦定理即可得出．〔II〕设∠BDC=θ，在△ACD中，由正弦定理可得：=，化为AC=cosθ．同理在△ABC中，利用正弦定理可得：AC=cos〔60°﹣θ〕，化简解出即可得出．【解答】解：〔I〕设∠ABD=α，∠CBD=β．在Rt△ABD中，cosα===，∴α=．在Rt△CBD中，cosβ==，∴β=．αβ=．∴+在△ABC中，AC 2==21．∴AC=．〔II〕设∠BDC=θ，在△ACD中，=，化为AC=cosθ．第13页〔共17页〕在△ABC 中， = ，化为：AC= cos 〔60°﹣θ〕，cos θ═cos 〔60°﹣θ〕，化为：3cos θ=2cos 〔60°﹣θ〕，3cos θ=cos θ+sin θ，tan θ=．20．圆锥曲线 E ：．〔I 〕求曲线E 的离心率及标准方程；M ：〔x ﹣x 0〕2+〔y ﹣y 0〕2=8的 〔II 〕设M 〔x 0，y 0〕是曲线 E 上的任意一点，过原点作⊙两条切线，分别交曲线 E 于点 P 、Q ．①假设直线 OPOQ 的斜率存在分别为 k ，k ，求证：kk=﹣； ， 1 2 12②试问OP 2+OQ 2是否为定值．假设是求出这个定值，假设不是请说明理由．【考点】椭圆的简单性质．【分析】〔I 〕由椭圆定义可知，曲线E 是以和为焦点，长轴长为的椭圆，即可得出．〔II 〕〕① 假设过原点与⊙M 相切的直线斜率存在设为k ，那么切线方程为y=kx ，可得，整理得．由题设可知k 1，k 2是以上关于k 的一元二次方程的两个实根，利用根与系数的关系即可得出． ②设P 〔x 1，y 1〕，Q 〔x 2，y 2〕．当直线OP ，OQ 的斜率存在时，由 ①易得 ，，利用两点之间的距离、根与系数的关系即可得出．当直线 OP ，OQ 的斜率不存在时直接验证即可得出．【解答】解：〔I 〕由椭圆定义可知，曲线 E 是以 和 为焦点，长轴 长为 的椭圆，设椭圆的半长轴长、半短轴长、半焦距分别为 a 、b 、c ．∴ ， ，那么，第14页〔共17页〕∴椭圆的离心率 ，E 的标准方程为 ．〔II 〕①证明：假设过原点与⊙ M 相切的直线斜率存在设为 k ，那么切线方程为 y=kx ，∴ ，整理得 ． 由题设可知k 1，k 2是以上关于 k 的一元二次方程的两个实根，∴，即 ．②设P 〔x 1，y 1〕，Q 〔x 2，y 2〕． 当直线 OP ，OQ 的斜率存在时，由①易得 ， ，而== ==当直线 OP 或OQ 的斜率不存在时，圆 M 与y 轴相切，且圆 M 也与x 轴相切 P ，Q 是椭 圆E 的两个顶点，∴OP 2+OQ 2=a 2+b 2=36． 综上所述：OP 2+OQ 2为定值36．21．设函数 f 〔x 〕=e x ，g 〔x 〕=kx+1． I 〕求函数y=f 〔x 〕﹣〔x+1〕的最小值；II 〕证明：当k ＞1时，存在x 0＞0，使对于任意x ∈〔0，x 0〕都有f 〔x 〕＜g 〔x 〕；〔III 〕假设对于任意 x ∈〔0，+∞〕，|f 〔x 〕﹣g 〔x 〕|＞x 恒成立，求实数 k 的取值范围．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】〔Ⅰ〕求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的最小值即可；〔Ⅱ〕设h 〔x 〕=f 〔x 〕﹣g 〔x 〕，求出函数的导数，得到函数的单调性，从而证出结论；〔Ⅲ〕①当k ＞1时，求出h 〔x 〕的单调区间，得到函数的最小值，证出结论成立； ②当xk1 x1 x 0 k ≤1时，问题等价于f 〔x 〕﹣g 〔x 〕＞x ，设φ〔x 〕=e ﹣〔+ 〕﹣ 〔 ＞〕， 根据函数的单调性证明即可． xx【解答】解：〔I 〕由 y=e ﹣x ﹣1，∴y'=e ﹣1，第15页〔共17页〕∴函数y=e x﹣x ﹣1在〔﹣∞，0〕上递减，在〔0，+∞〕上递增，那么当x=0时，y 有最小值为0证明：〔II 〕设h 〔x 〕=f 〔x 〕﹣g 〔x 〕，即h 〔x 〕=e x﹣kx ﹣1，h'〔x 〕=e x﹣k ，设h'〔x 〕=0，得x=lnk 〔k ＞1〕，∵k ＞1，∴当x ∈〔0，lnk 〕时，h'〔x 〕＜0，即h 〔x 〕在〔0，lnk 〕上单调递减，而h 〔0〕=0，且h 〔x 〕是R 上的连续函数， h 〔x 〕＜0在〔0，lnk 〕上恒成立，即f 〔x 〕＜g 〔x 〕在〔0，lnk 〕上恒成立，∴取0＜x 0≤lnk ，那么对任意x ∈〔0，x 0〕都有f 〔x 〕＜g 〔x 〕解：〔III 〕由〔I 〕知e x ≥x+1即有e x ﹣1≥x ，∴当x ＞0时有lnx ≤x ﹣1〔仅当x=1时取“=〞〕 〔*〕①当k ＞1时，设h 〔x 〕=f 〔x 〕﹣g 〔x 〕=e x﹣〔kx+1〕〔x ＞0〕， h'〔x 〕=e x﹣k令h'〔x 〕＞0得x ＞lnk ，令h'〔x 〕＜0得0＜x ＜lnk ，∴h 〔x 〕在〔0，lnk 〕上递减，在〔lnk ，+∞〕上递增，∴h 〔x 〕min =h 〔lnk 〕=k ﹣klnk ﹣1，由〔*〕式知得k ﹣klnk ﹣1＜0，又=k 3﹣3klnk ﹣1＞k 3﹣3k 〔k ﹣1〕﹣1=k 3﹣ 3k 2 3k 1= k 1 3 0 ，+ ﹣ 〔 ﹣〕＞∴函数y=h 〔x 〕在〔lnk ，3lnk 〕上有唯一零点设为x k ，此时h 〔x k 〕=0，显然h 〔x k 〕＜x k ，即|f 〔x 〕﹣g 〔x 〕|＞x 对任意x ∈〔0，+∞〕不能恒成立，② 当 k ≤ 1 时，对任意数 x0 ∞∈〔，+ 〕，xkx1=e x ﹣〔 x1 〕﹣〔 k 1 x ≥﹣〔 k 1x 0 ，f 〔x 〕﹣g 〔x 〕=e ﹣〔 + 〕+ ﹣ 〕 ﹣〕 ≥ |f 〔x 〕﹣g 〔x 〕|＞x 等价于f 〔x 〕﹣g 〔x 〕＞x ，即e x﹣〔k+1〕x﹣1＞0，设φ〔x 〕=e x ﹣〔k+1〕x ﹣1〔x ＞0〕，那么φ'〔x 〕=e x﹣〔k+1〕，假设k ≤0，那么k+1≤1，∴e x﹣〔k+1〕＞0，那么φ〔x 〕在〔0，+∞〕上递增，注意到φ〔0〕=0，∴φ〔x 〕＞φ〔0〕=0，即|f 〔x 〕﹣g 〔x 〕|＞x 对任意x ∈〔0，+∞〕恒成立，假设0＜k ≤1，令φ'〔x 〕＞0得x ＞ln 〔k+1〕，令φ'〔x 〕＜0，得0＜x ＜ln 〔k+1〕，φ〔x 〕在〔0，ln 〔k+1〕〕上递减，在〔ln 〔k+1〕，+∞〕上递增，∴当x ∈〔0，ln 〔k+1〕〕时，φ〔x 〕＜φ〔0〕=0，即|f 〔x 〕﹣g 〔x 〕|＞x 对于任意x ∈〔0，ln 〔k+1〕〕不成立，那么|f 〔x 〕﹣g 〔x 〕|＞x 对任意x ∈〔0，+∞〕不能恒成立，综合①②可得，满足条件的k 的取值范围为〔﹣∞，0]第16页〔共17页〕2021年9月8日第17页〔共17页〕。