课外资料:无理数趣谈
- 格式:doc
- 大小:30.00 KB
- 文档页数:4
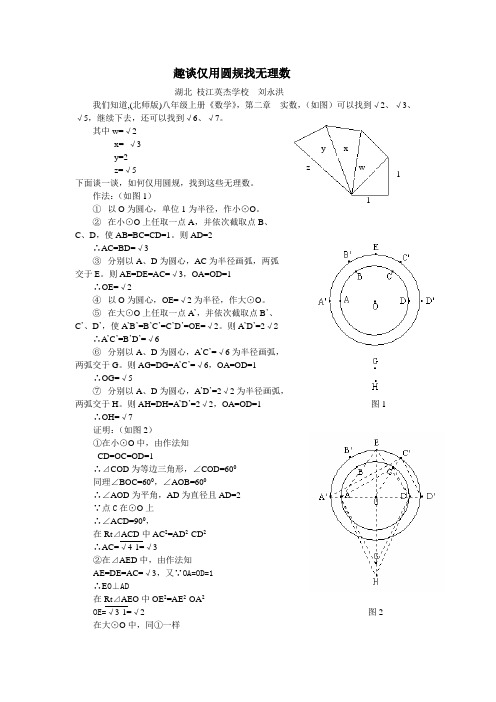
趣谈仅用圆规找无理数湖北 枝江英杰学校 刘永洪我们知道,(北师版)八年级上册《数学》,第二章 实数,(如图)可以找到√2、√3、 √5,继续下去,还可以找到√6、√7。
其中w=√2x= √3 y=2z=√5下面谈一谈,如何仅用圆规,找到这些无理数。
作法:(如图1)① 以O 为圆心,单位1为半径,作小⊙O 。
② 在小⊙O 上任取一点A ,并依次截取点B 、C 、D ,使AB=BC=CD=1。
则AD=2∴AC=BD=√3③ 分别以A 、D 为圆心,AC 为半径画弧,两弧交于E 。
则AE=DE=AC=√3,OA=OD=1∴OE=√2④ 以O 为圆心,OE=√2为半径,作大⊙O 。
⑤ 在大⊙O 上任取一点A ’,并依次截取点B ’、C ’、D ’,使A ’B ’=B ’C ’=C ’D ’=OE=√2。
则A ’D ’=2√2∴A ’C ’=B ’D ’=√6⑥ 分别以A 、D 为圆心,A ’C ’=√6为半径画弧,两弧交于G 。
则AG=DG=A ’C ’=√6,OA=OD=1∴OG=√5⑦ 分别以A 、D 为圆心,A ’D ’=2√2为半径画弧,两弧交于H 。
则AH=DH=A ’D ’=2√2,OA=OD=1图1 ∴OH=√7证明:(如图2)①在小⊙O 中,由作法知CD=OC=OD=1∴⊿COD 为等边三角形,∠COD=600同理∠BOC=600,∠AOB=600∴∠AOD 为平角,AD 为直径且AD=2∵点C 在⊙O 上∴∠ACD=900,在Rt ⊿ACD 中AC 2=AD 2-CD 2∴AC=√4-1=√3②在⊿AED 中,由作法知AE=DE=AC=√3,又∵OA=OD=1∴E O ⊥AD在Rt ⊿AEO 中OE 2=AE 2-OA 2OE=√3-1=√2图2 在大⊙O 中,同①一样 1 1 wy z xOE=OA’=OD’=C’D’=√2, ∴A’D’=2√2在Rt⊿A’C’D’中,A’C’2=A’D’2-C’D’2∴A’C’=√8-2=√6同②一样,在Rt⊿AGO中,OG2=AG2-OA2∴OG=√6-1=√5在Rt⊿AGO中OH2=AH2-OA2∴OH=√8-1=√7就这样通过圆、等腰三角形、直角三角形知识的综合运用,便能达到目的。

无理数的产生与发展300字
无理数是指不能用两个整数的比值来表示的数,例如π和√2。
无理数的产生与发展源自古希腊时期的一个有趣的数学发现。
据说,古希腊的毕达哥拉斯学派发现了一个无法用整数比值表示的数,即
√2。
这个发现震惊了数学界,因为毕达哥拉斯学派坚信一切可以用
整数比值表示。
这一发现导致了无理数的概念的诞生。
随着数学的发展,人们发现了更多的无理数,比如圆周率π。
在17世纪,数学家们开始研究无理数的性质和行为。
他们发现了一
些无理数的重要性质,比如无理数的无限不循环小数表示法。
这些
发现为数学的发展开辟了新的领域。
无理数的产生与发展也推动了数学工具和方法的进步。
为了处
理无理数,数学家们发明了新的符号和计算方法。
无理数的产生也
催生了现代分析学和数学分析领域的发展。
今天,无理数在数学和科学中扮演着重要的角色。
它们被广泛
应用于物理学、工程学、计算机科学等领域。
无理数的产生与发展
不仅丰富了数学理论,也为人类的科学和技术进步做出了贡献。
总的来说,无理数的产生与发展是数学史上的一大里程碑。
它们的发现不仅丰富了数学理论,也推动了科学技术的发展。
无理数的产生与发展是数学史上的一大成就,也是人类智慧的结晶。

奥数大揭秘数学中的奇奇怪怪奥数大揭秘——数学中的奇奇怪怪数学作为一门学科,给很多人带来了困惑和恐惧感。
但是,对于那些热爱数学的人来说,它却是一本充满了奇奇怪怪的魔法书。
在这篇文章中,我们将揭示数学世界中的一些奇奇怪怪的现象,希望能够让更多的人对数学有更深入的理解。
一、无理数的神秘符号无理数是数学中的一种特殊存在。
它们无法用两个整数的比例表示,也无法用有限位数的小数来表示。
最经典的无理数就是圆周率π,它是一个无限不循环的小数。
除了π,开根号2、黄金分割比例等也是无理数。
这些无理数在数学中有着重要的地位,但是它们的神秘之处在于永远无法被准确表示出来。
二、费马大定理的故事费马大定理是数学史上一个备受争议的问题。
这个问题最早由费马提出,他在边写边证明的过程中写下了“我有一种非常精妙的证明方法,但是此处无法写下”这句话,从而引发了无数数学家的寻找。
直到1994年,英国数学家安德鲁·怀尔斯真正给出了费马大定理的证明,这个问题才得以解决。
费马大定理的故事向我们诉说了数学中的创造力和耐心。
三、复数的双重性质复数在数学中是一种特殊的存在。
它由实数和虚数(虚数单位i)构成,虚数在实际生活中似乎没有太多实际意义。
然而,在数学中,虚数的引入却使得一些本来难以解决的问题有了解决的方法。
例如,复数可以用来解决二次方程的问题,也可以用来描述电路中的交流电信号。
复数的双重性质给我们展示了数学中的奇妙魅力。
四、无限级数的奥妙无限级数是一种数学中常见的概念。
它由无穷多个数相加或相乘而成,最经典的例子就是等比数列之和。
但是,无限级数的奥妙在于它们有时会收敛,有时会发散。
对于一个收敛的无限级数,我们可以得到一个确定的值;而对于一个发散的无限级数,我们则无法得到一个确定的值。
这种奇怪的现象在数学中一直是一个重要的研究课题。
五、图论中的世界图论是数学中的一个分支,研究的对象是图。
图是由节点和边组成的一种结构,它可以用来描述现实世界中的一些关系。

与无理数有关的故事
与无理数有关的故事
2500多年前,古希腊有一位伟大的数学家——毕达哥拉斯。
他创立了古希腊数学的“毕达哥拉斯学派”,在数学发展史上留下了光辉的一页。
历史上首先发现无理数的著名数学家希巴斯,就是毕达哥拉斯的一位学生,他也是毕达哥拉斯学派中最杰出的代表人物之一。
在数学史上,毕达哥拉斯最伟大的贡献就是发现了“勾股定理”。
所以直到现在,西方人仍然称勾股定理为“毕达哥拉斯定理”。
据传说,当勾股定理被发现之后,毕达哥拉斯学派的成员们曾经杀了99头牛来大摆筵席,以示庆贺。
其后不久,希巴斯通过勾股定理,发现边长为1的正方形,其对角线长度并不是有理数。
这下可惹祸了。
因为毕达哥拉斯一向认为“万物兼数”,而他所说的“数”,仅仅是整数与整数之比,也就是现代意义上的“有理数”(整数和分数的统称)。
也就是说,他认为除了有理数以外,不可能存在另类的数。
当希巴斯提出他的发现之后,毕达哥拉斯大吃一惊,原来世界上真的有“另类数”存在。
毕达哥拉斯是一个很重面子的人,他无法承受自己的理论将被推翻,于是他下令:“关于另类数的问题,只能在学派内部研究,一律不得外传,违者必究。
”
可是希巴斯出于对科学的尊重,并没有根据老师的指令严守秘密,而是把他的发现公之于众了。
这一举动,令毕达哥拉斯怒不可遏,他下令严惩希巴斯。
最后,希巴斯被毕达哥拉斯学派的人掷进了大海。

引起数学危机的无理数无理数,顾名思义,与有理数相对。
那么它就是不能表示为整数或两整数之比的实数,比如等等。
如果不作数学计算,在实际生活中,我们是不会碰到这些数的。
无论是度量长度,重量,还是计时。
第一个被发现的无理数,当时,毕达哥拉斯学派的一个名叫希帕索斯的学生,在研究1和2的比例中项时(若1:X=X:2,那么X叫1和2的比例中项),怎么也想不出这个比例中项值。
后来,他画一边长为1的正方形,设对角线为X,于是。
他想,X代表对角线长,而,那么X必定是确定的数。
但它是整数还是分数呢?显然,2是1和4之间的数,因而X应是1和2之间的数,因而不是整数.那么X会不会是分数呢?毕达哥拉斯学派用归谬法证明了,这个数不是有理数,它就是无理数.无理数的发现,对以整数为基础的毕氏哲学,是一次致命的打击,以至于有一段时间,他们费了很大的精力,将此事保密,不准外传,并且将希帕索斯本人也扔到大海中淹死了.但是,人们很快发现了等更多的无理数,随着时间的推移,无理数的存在已成为人所共知的事实。
无理数的发现,是毕氏学派最伟大成就之一,也是数学史上的重要里程碑。
尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be someunsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Partof the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

“无理数”的由来
“无理数”的概念最早出现在古希腊数学中。
在公元前5世纪,古
希腊数学家毕达哥拉斯创立了著名的毕达哥拉斯学派,该学派提
出了“一切可以表示为两个整数之比的数称为有理数”的思想。
然而,毕达哥拉斯学派追求数学的完美和对整数有严格的崇拜,因
此对于无法用两个整数之比来表示的数,他们认为是不合逻辑的,甚至是“无理”的。
然而,毕达哥拉斯学派的成员之一海伦(Hippasus)做了一个重要的发现,即勾股定理中的两条腿长度和斜边长度的关系无法用有
理数来表示。
具体而言,当直角三角形的两条腿长度为1时,斜
边长度不能用有理数来表示,这就意味着根号2是一个无理数。
这个发现打破了毕达哥拉斯学派的理论基础,因为根号2无法用
两个整数之比来表示,被他们认为是“无理”的。
这引起了毕达哥
拉斯学派内部的争议,因为这与他们追求完美数学和整数的思想
相悖。
为了保护自己的学派和思想,毕达哥拉斯学派决定对此事保密,
但海伦却违背了誓言将这个发现传播出去。
这引起了学派内部的
愤怒,据说他们甚至将海伦推下海中溺死,这在一定程度上也反
映了无理数这一概念的由来。
从此以后,人们开始接受和研究无理数,并逐渐认识到数学中不
仅仅有有理数,还有无限不循环小数,例如自然常数e和圆周率π等。
通过无理数的研究,人们逐渐开拓了数学的新领域,推动了
数学的发展。
无理数知识点
嘿,朋友们!今天咱们来聊聊无理数这个超有意思的知识点呀!
啥是无理数呢?简单来说,就是那些无限不循环小数呗!比如说圆周率π呀,它就是个典型的无理数呢!就好像你在一个超级大的圆形操场上跑步,你永远也跑不到尽头,这就是无理数的奇妙之处呀!想想看,是不是很神奇呢?
无理数和有理数可不一样哦!有理数咱们都熟悉呀,像整数啦、分数啦,但无理数可就特别啦!比如说根号 2 呀,你怎么算都算不出它到底是个啥精确的数值。
哎呀,这就像是一场永远没有终点的探索之旅呢!
再想想,如果你有一把永远也量不完长度的尺子,那上面的刻度可能就是无理数在和你开玩笑呢!生活中很多地方都会碰到无理数哦!
记住无理数这个特殊的小伙伴,会让我们对数学的世界有更深刻的认识呢!可别小瞧了它们哟!
怎么样,是不是对无理数更感兴趣啦?。
初中数学复习探索无理数的神秘世界数学中的无理数是我们一直在学习的一个重要概念。
无理数是指不能表示为两个整数的比值的实数,它们的小数部分是无限不循环的。
无理数的一大特点就是它们的数值无穷无尽,让我们无法准确地表示出它们的值。
本文将带你进一步探索无理数的神秘世界。
一、无理数的发现众所周知,数学是由人们不断探索与发现而形成的。
在古代,人们发现了一些无法用有理数表示的长度,比如直角三角形的斜边和正方形的对角线。
他们尝试用整数或有理数去表示这些长度,但发现无论怎样都无法得到一个准确的结果。
这些无法用有理数表示的长度被称为无理数。
二、无理数的性质无理数与有理数相比,有一些独特的性质。
首先,无理数是无限不循环的小数,例如π和√2。
这意味着无理数的小数部分没有重复的模式,它们的数字是无穷无尽的。
其次,无理数之间的运算也非常复杂。
当我们将一个有理数与一个无理数相加、相乘或做其他运算时,得到的结果一定是无理数。
三、无理数的表示方法虽然无理数无法用有理数表示,但我们可以使用其他形式来表示它们。
其中一种常见的表示方法是用根号符号表示,例如√2、√3等。
另外,我们还可以用近似值来表示无理数,例如用小数表示的π近似值3.14159。
虽然这些近似值并不准确,但我们可以逐渐增加小数的位数,使得表示更加精确。
四、无理数的应用领域无理数在现实生活中有着广泛的应用领域,尤其在几何和物理学中。
在几何学中,无理数用于描述圆周率π的性质,以及在建筑、绘画等领域中的准确测量。
在物理学中,无理数被用于表示自然界中的各种现象,比如电磁波的频率、物体的质量等。
无理数的应用不仅帮助我们更好地理解自然世界,也推动了科学的发展。
五、无理数的挑战尽管我们已经了解了一些关于无理数的知识,但无理数仍然是一个充满挑战的概念。
无理数的无穷性使得我们永远无法准确地表示出它们的数值。
数学家们一直致力于研究无理数的性质,并寻找更好的表示方法和计算方法。
无论是现今的高速计算机还是未来的技术发展,都有可能为我们解决无理数的难题提供新的思路与方法。
无理数发展简史简介:无理数是指不能用两个整数的比值来表示的数,它是一类无限不循环小数。
无理数的发展历史可以追溯到古希腊时期,经过了数学家们的不断探索和发现,逐渐揭开了无理数的神秘面纱。
本文将为您详细介绍无理数的发展简史。
1. 古希腊时期在古希腊时期,数学家毕达哥拉斯提出了著名的毕达哥拉斯定理,即直角三角形的斜边长的平方等于两直角边长的平方和。
然而,毕达哥拉斯发现了一种无法用两个整数的比值来表示的数,即根号2。
这个发现打破了古希腊人认为所有数都可以用有理数表示的观念,从而引发了对无理数的研究。
2. 欧几里得与连分数在欧几里得的《几何原本》中,他对无理数进行了更加深入的研究。
他提出了连分数的概念,将无理数表示为一个整数与一个无限循环的分数序列的和。
这种表示方法在无理数的研究中起到了重要的作用,为后来数学家们的研究提供了思路。
3. 无理数的发现与证明在17世纪,数学家笛卡尔和费马等人对无理数进行了更加系统的研究。
笛卡尔提出了坐标系的概念,为无理数的研究提供了新的工具。
费马则发现了一种新的无理数,即费马数。
他认为这个数不能表示为两个整数的比值,但直到后来才被证明为无理数。
4. 无理数的性质研究在18世纪,数学家们对无理数的性质进行了更加深入的研究。
欧拉提出了著名的欧拉公式,将无理数与三角函数联系在一起,为无理数的研究提供了新的视角。
拉格朗日则提出了代数数的概念,即满足代数方程的实数,这也是无理数的一种重要分类。
5. 康托尔与集合论在19世纪末,数学家康托尔提出了集合论的概念,为无理数的研究提供了新的工具。
他证明了无理数的集合比有理数的集合更为庞大,并提出了不同无理数集合的无穷性和不可数性的概念。
这一发现引发了对无理数集合的进一步研究。
6. 无理数的应用随着科学技术的发展,无理数在实际应用中发挥着重要的作用。
例如,在物理学中,无理数被用来描述自然界中的各种现象,如波动、震动等。
在金融领域,无理数被用来进行金融建模和风险评估等方面的计算。
引入无理数概念的数学探索在数学领域中,有理数一直以来都是我们熟知的概念,无论是整数、分数还是小数,都可以归类为有理数。
然而,人们逐渐发现有些数无法用两个整数的比值来表示,这些神秘的数被称为无理数。
本文将探索无理数的引入及其在数学中的应用。
一、无理数的引入无理数最早由古希腊数学家毕达哥拉斯在公元前5世纪提出。
当时,他们发现无法用有限的小数或分数来准确表示某些长度、面积或体积,这些不可表示为有理数的数被称为无理数。
二、无理数的定义与性质无理数并不是简单地用分数表示,而是用无限不循环小数来表示。
无理数中最著名的代表是π(圆周率)和√2(根号2)。
这两个数是无限不循环的小数,无法准确表示为有理数。
值得一提的是,无理数是无限不循环小数的一种特殊形式。
三、无理数在几何中的应用无理数在几何中起到了重要的作用。
以√2为例,我们知道正方形的对角线和边长之间的关系为√2倍。
这一关系使得以边长为有理数的正方形,其对角线的长度成为无理数,且无法用有限的小数或分数表示。
另外,无理数也有着广泛的应用,例如在测量中的误差分析、三角函数等领域。
四、无理数与实数的关系无理数是实数的一部分,实数包括有理数和无理数。
实数的定义是包含所有有理数和无理数的数集。
有理数和无理数都是构成实数集的重要组成部分。
五、无理数的证明无理数的证明是数学中的一个重要问题。
盖尔丹·哥尔丹(Georg Cantor)通过构造一种集合,使得该集合中元素的数量无限且无理数构成,从而证明无理数的存在。
这一证明方法奠定了无理数的数学地位,深刻影响着数学研究与应用。
结论无理数的引入为数学领域带来了新的发展方向,打破了人们对数的认知局限。
无理数的定义、性质以及在几何和实数中的应用,都为我们提供了更广阔的数学思维空间。
无理数的研究不仅深化了数学理论,也对其他科学领域的发展起到了积极的推动作用。
通过对无理数概念的数学探索,我们可以更好地理解数学的奥秘,拓展数学的应用领域,促进科学技术的不断发展。
无理数趣谈
无理数是实数中不能精确地表示为两个整数之比的数,即无限不循环小数。
如圆周率、2的平方根等。
实数(real munber)分为有理数和无理数(irrational number)。
无理数与有理数的区别:
1、把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,
比如4=4.0, 4/5=0.8, 1/3=0.33333……而无理数只能写成无限不循环小数,
比如=1.414213562……根据这一点,人们把无理数定义为无限不循环小数.
2、所有的有理数都可以写成两个整数之比;而无理数不能。
根据这一点,有人建议给无理数摘掉“无理”的帽子,把有理数改叫为“比数”,把无理数改叫为“非比数”。
本来嘛,无理数并不是不讲道理,只是人们最初对它不太了解罢了。
利用有理数和无理数的主要区别,可以证明√2是无理数。
不是无理数,而是有理数。
是有理数,它必然可以写成两个整数之比的形式:
=p/q
又由于p和q没有公因数可以约去,所以可以认为p/q 为既约分数,即最简分数形式。
把=p/q 两边平方
得2=(p^2)/(q^2)
即2(q^2)=p^2
由于2q^2是偶数,p 必定为偶数,设p=2m
由2(q^2)=4(m^2)
得q^2=2m^2
同理q必然也为偶数,设q=2n
既然p和q都是偶数,他们必定有公因数2,这与前面假设p/q是既约分数矛盾。
这个矛盾是有假设√2是有理数引起的。
因此√2是无理数。
由来:
毕达哥拉斯(Pythagqras,约公元前885年至公元前400年间),从小就很聪明,一次他背着柴禾从街上走过,一位长者见他捆柴的方法与别人不同,便说:“这孩子有数学奇才,将来会成为一个大学者。
”他闻听此言,便摔掉柴禾南渡地中海到泰勒斯门下去求学。
毕达哥拉斯本来就极聪明,经泰勒一指点,许多数学难题在他的手下便迎刃而解。
其中,他证明了三角形的内角和等于180度;能算出你若要用瓷砖铺地,则只有用正三角、正四角、正六角三种正多角砖才能刚好将地铺满,还证明了世界上只有五种正多面体,即:正4、6、8、12、20面体。
他还发现了奇数、偶数、三角数、四角数、完全数、友数,直到毕达哥拉斯数。
然而他最伟大的成就是发现了后来以他的名字命名的毕达哥拉斯定理(勾股弦定理),即:直角三角形两直角边为边长的正方形的面积之和等于以斜边为边长的正方形的面积。
据说,这是当时毕达哥拉斯在寺庙里见工匠们用方砖铺地,经常要计算面积,于是便发明了此法。
毕达哥拉斯将数学知识运用得纯熟之后,觉得不能只满足于用来算题解题,于是他试着从数学领域扩大到哲学,用数的观点去解释一下世界。
经过一番刻苦实践,他提出“凡物皆数”的观点,数的元素就是万物的元素,世界是由数组成的,世界上的一切没有不可以用数来表示的,数本身就是世界的秩序。
毕达哥拉斯还在自己的周围建立了一个青年兄弟会。
在他死后大约200年,他的门徒们把这种理论加以研究发展,形成了一个强大的毕达哥拉斯学派。
一天,学派的成员们刚开完一个学术讨论会,正坐着游船出来领略山水风光,以驱散一天的疲劳。
这天,风和日丽,海风轻轻的吹,荡起层层波浪,大家心里很高兴。
一个满脸胡子的学者看着辽阔的海面兴奋地说:“毕达哥拉斯先生的理论一点都不错。
你们看这海浪一层一层,波峰浪谷,就好像奇数、偶数相间一样。
世界就是数字的秩序。
”“是的,是的。
”这时一个正在摇桨的大个子插进来说:“就说这小船和大海吧。
用小船去量海水,肯定能得出一个精确的数字。
一切事物之间都是可以用数字互相表示的。
”
“我看不一定。
”这时船尾的一个学者突然提问了,他沉静地说:“要是量
到最后,不是整数呢?”
“那就是小数。
”“要是小数既除不尽,又不能循环呢?”
“不可能,世界上的一切东西,都可以相互用数字直接准确地表达出来。
”
这时,那个学者以一种不想再争辩的口气冷静地说:“并不是世界上一切事物都可以用我们现在知道的数来互相表示,就以毕达哥拉斯先生研究最多的直角三角形来说吧,假如是等腰直角三角形,你就无法用一个直角边准确地量出斜边来。
”
这个提问的学者叫希帕索斯(Hippasus),他在毕达哥拉斯学派中是一个聪明、好学、有独立思考能力的青年数学家。
今天要不是因为争论,还不想发表自己这个新见解呢。
那个摇桨的大个子一听这话就停下手来大叫着:“不可能,先生的理论置之四海皆准。
”希帕索斯眨了眨聪明的大眼,伸出两手,用两个虎口比成一个等腰直角三角形说:
“如果直边是3,斜边是几?”
“4。
”
“再准确些?”
“4.2。
”
“再准确些?”
“4.24。
”
“再准确些呢?”
大个子的脸涨得绯红,一时答不上来。
希帕索斯说:“你就再往后数上10位、20位也不能算是最精确的。
我演算了很多次,任何等腰直角三角形的一边与余边,都不能用一个精确的数字表示出来。
”这话像一声晴天霹雳,全船立即响起一阵怒吼:“你敢违背毕达哥拉斯先生的理论,敢破坏我们学派的信条!敢不相信数字就是世界!”希帕索斯这时十分冷静,他说:“我这是个新的发现,就是毕达哥拉斯先生在世也会奖赏我的。
你们可以随时去验证。
”可是人们不听他的解释,愤怒地喊着:“叛逆!先生的不肖门徒。
”“打死他!批死他!”大胡子冲上来,当胸给了他一拳。
希帕索斯抗议着:“你们无视科学,你们竟这样无理!”“捍卫学派的信条永远有理。
”这时大个子也冲了过来,猛地将他抱起:“我们给你一个最高的奖赏吧!”说着就把希帕索斯扔进了海里。
蓝色的海水很
快淹没了他的躯体,再也没有出来。
这时,天空飘过几朵白云,海面掠过几只水鸟,一场风波过后,这地中海海滨又显得那样宁静了。
一位很有才华的数学家就这样被奴隶专制制度的学阀们毁灭了。
但是这倒真使人们看清了希帕索斯的思想价值。
这次事件后,毕达哥拉斯学派的成员们确实发现不但等腰直角三角形的直角边无法去量准斜边,而且圆的直径也无法去量尽圆周,那个数字是3.1415926535897932384626……更是永远也无法精确。
慢慢地,他们感觉后悔了,后悔杀死希帕索斯的无理行动。
他们渐渐明白了,明白了直觉并不是绝对可靠的,有的东西必须靠科学的证明;他们明白了,过去他们所认识的数字“0”,自然数等有理数之外,还有一些无限的不能循环的小数,这确实是一种新发现的数——应该叫它“无理数”。
这个名字反映了数学的本来面貌,但也真实的记录了毕达哥拉斯学派中学阀的蛮横无理。
由无理数引发的数学危机一直延续到19世纪。
1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数,并把实数理论建立在严格的科学基础上,从而结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机。