中学物理竞赛讲义动能定理

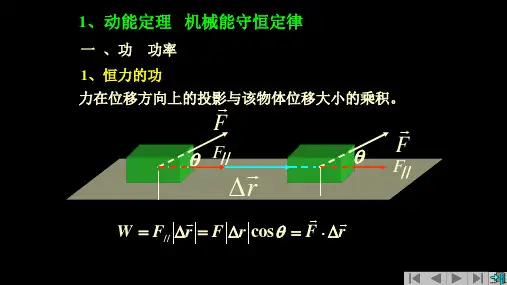
《动能定理的应用》讲义一、什么是动能定理在物理学中，动能定理是一个非常重要的概念。

动能定理表述为：合外力对物体所做的功等于物体动能的变化量。

动能是物体由于运动而具有的能量。

其表达式为$E_{k} ＝＼frac{1}｛2}mv^2$，其中$m$是物体的质量，＄v$是物体的速度。

那么动能定理具体怎么理解呢？我们可以想象一个物体在力的作用下运动。

力对物体做功，会使物体的速度发生变化，从而导致动能的改变。

而动能定理就是描述这个做功与动能变化之间的定量关系。

二、动能定理的表达式动能定理的表达式为：＄W_{合} ＝＼Delta E_{k}＄，其中$W_{合}＄表示合外力做的功，＄＼Delta E_{k}＄表示动能的变化量。

如果物体受到多个力的作用，那么合外力做的功就是这些力做功的代数和。

例如，一个物体受到力$F_1$、＄F_2$、＄F_3$……的作用，它们分别做的功为$W_1$、＄W_2$、＄W_3$……，则合外力做的功$W_{合} ＝ W_1 ＋ W_2 ＋ W_3 ＋＼cdots$。

动能的变化量$＼Delta E_{k} ＝ E_{k2} E_{k1}＄，其中$E_{k2}＄表示末动能，＄E_{k1}＄表示初动能。

三、动能定理的应用场景1、求变力做功在很多情况下，物体所受的力是变化的，直接求力做的功比较困难。

这时利用动能定理就可以通过计算动能的变化来间接求出变力做的功。

例如，一个小球在一根弹簧的作用下运动。

弹簧的弹力是一个变力，我们无法直接计算弹力做的功。

但是，我们可以通过测量小球的初末速度，计算出动能的变化，从而得出弹力做的功。

2、解决多过程问题当物体经历多个运动过程时，每个过程可能受力情况不同。

如果分别对每个过程用牛顿运动定律和运动学公式来求解，会非常复杂。

而动能定理可以将整个过程作为一个整体来考虑，大大简化了计算。

比如，一个物体先在粗糙水平面上匀加速运动一段距离，然后进入光滑斜面继续运动。

我们可以用动能定理直接求出整个过程中合外力做的功，从而得出物体动能的变化。

《动能定理的应用》讲义一、动能定理的基本概念在物理学中，动能定理描述了合外力对物体做功与物体动能变化之间的关系。

动能是物体由于运动而具有的能量，其表达式为$E_{k} ＝＼frac{1}｛2}mv^2$，其中$m$是物体的质量，＄v$是物体的速度。

动能定理指出：合外力对物体所做的功等于物体动能的变化量，即$W ＝＼Delta E_{k}＄。

这里的$W$表示合外力做的功，＄＼DeltaE_{k}＄表示动能的变化量。

理解动能定理的关键在于认识到做功是能量转化的过程。

当合外力对物体做功时，其他形式的能量会转化为物体的动能；反之，当物体克服合外力做功时，物体的动能会转化为其他形式的能量。

二、动能定理的表达式动能定理的数学表达式为：＄W_{合} ＝ E_{k2} E_{k1}＄其中，＄W_{合}＄是合外力对物体所做的功，＄E_{k2}＄是物体末状态的动能，＄E_{k1}＄是物体初状态的动能。

如果合外力是恒力，可以直接用公式$W_{合} ＝ F ＼cdot s ＼cdot ＼cos\theta$来计算合外力做的功，其中$F$是合外力的大小，＄s$是物体在合外力方向上的位移，＄＼theta$是合外力与位移方向的夹角。

如果合外力是变力，我们通常需要通过积分或者分段计算的方法来确定合外力做的功。

三、动能定理的应用场景1、求解物体的速度当已知物体所受合外力做功以及物体的初速度或初动能时，可以利用动能定理求出物体的末速度。

例如，一个质量为$m$的物体，在水平方向受到一个恒力$F$的作用，经过位移$s$后，速度从$v_1$增加到$v_2$。

根据动能定理，＄Fs ＝＼frac{1}｛2}mv_2^2 ＼frac{1}｛2}mv_1^2$，通过这个式子可以求出$v_2$。

2、求解物体所受的合外力如果已知物体的运动情况以及动能的变化，就可以通过动能定理计算出合外力。

比如，一个物体从高处自由下落，下落高度为$h$，已知物体的质量$m$和落地时的速度$v$。

4.2动能定理一、单个质点的动能定理例1、设物体的质量为m ，在与运动方向相同的恒定外力F （F 未知）的作用下，在光滑水平面上发生一段位移l ，速度由v 1增加到v 2，如图所示。

试用牛顿运动定律和运动学公式，推导出力F 对物体做功的表达式（与速度的关系）。

22211122W mv mv =- 功是能量转化的量度，上式右边可以看成是能量的变化（末状态的能量减初状态的能量）。

由于和速度有关，将其定义为动能。

1、动能212K E mv = 2、动能定理：合外力所做的功等于物体动能的变化量。

22211122k W E mv mv =∆=-合 3、动能定理的优越性：(1)适用于恒力做功，也适用于变力做功。

(2)适用于直线运动，也适用于曲线运动。

(3)适用于单一过程，也适用于全过程（复杂运动）。

*(4)机械能守恒定律是有适用条件的，而动能定理是普遍适用的。

例2、两个质量均为m 的小球．用长为2L 的轻绳连接起来，置于光滑水平面上，绳恰好处于伸直状态．如图所示．今用一个恒力F 作用在绳的中点，F 的方向水平且垂直于绳的初始长度方向．原为静止的两个小球因此运动．求：（1）在两个小球第一次相碰前的瞬间,小球在垂直于F 作用线方向上的分速度为多大?（2）若干次碰撞后，两球处于接触状态一起运动，求因碰撞损失的总能量。

二、质点系统的动能定理质点系的动能增量等于作用于质点系所有外力和内力做功的代数和。

k E W W ∆=+∑∑外内注意：系统牛顿第二定律：F =ma ，不需要考虑内力。

但是，系统动能定理，不仅需要考虑外力做功，还要考虑内力做功例3、速度为v 1的子弹射入静止在光滑桌面上的木块，子弹受到的阻力为f ，子弹未从木块中射出，子弹和木块以共同的速度v 2在桌面上运动。

子弹射入木块的深度为d ，求木块和子弹构成的系统动能的减少量。

三、非惯性系中的系统动能定理质点系的动能增量等于作用于质点系所有外力和内力做功以及惯性力做功的代数和。

《动能定理的应用》讲义一、动能定理的基本概念在物理学中，动能定理描述了力对物体做功与物体动能变化之间的关系。

动能定理的表达式为：合外力对物体所做的功等于物体动能的变化量。

动能是物体由于运动而具有的能量，其表达式为$E_k ＝＼frac{1}｛2}mv^2$，其中$m$是物体的质量，＄v$是物体的速度。

当一个力作用在物体上，并使物体在力的方向上发生了位移，我们就说这个力对物体做了功。

功的表达式为$W ＝ Fs\cos\theta$，其中$F$是力的大小，＄s$是位移的大小，＄＼theta$是力与位移之间的夹角。

二、动能定理的推导假设一个质量为$m$的物体，在恒力$F$的作用下，沿直线从位置$A$运动到位置$B$，其位移为$s$，初速度为$v_1$，末速度为$v_2$。

根据牛顿第二定律$F ＝ ma$，其中$a$是加速度。

又因为运动学公式$v_2^2 v_1^2 ＝ 2as$，可得$a ＝＼frac{v_2^2 v_1^2}｛2s}＄。

将$a$代入$F ＝ ma$，得到$F ＝ m\frac{v_2^2 v_1^2}｛2s}＄。

力$F$所做的功$W ＝ Fs ＝ m\frac{v_2^2 v_1^2}｛2}＄。

而物体的初动能$E_{k1} ＝＼frac{1}｛2}mv_1^2$，末动能$E_{k2} ＝＼frac{1}｛2}mv_2^2$。

所以力$F$所做的功等于物体末动能减去初动能，即$W ＝ E_{k2}E_{k1}＄，这就是动能定理。

三、动能定理的应用场景1、单一物体的直线运动在这种情况下，我们可以直接分析物体所受的力，并计算每个力所做的功，然后根据动能定理求出物体的末速度或位移等物理量。

例如，一个质量为$2kg$的物体在水平面上受到一个水平向右的恒力$F ＝10N$，物体运动了$5m$，初速度为$2m/s$，求物体的末速度。

首先分析力做功，水平力$F$做功$W_F ＝ Fs ＝ 10×5 ＝ 50J$，摩擦力做功为$0$（假设水平面无摩擦）。

《动能定理的应用》讲义一、什么是动能定理动能定理是物理学中一个非常重要的定理，它描述了力对物体做功与物体动能变化之间的关系。

动能，简单来说，就是物体由于运动而具有的能量。

一个物体的动能大小等于其质量与速度平方乘积的一半，即$E_k ＝＼frac{1}｛2}mv^2$，其中$m$是物体的质量，＄v$是物体的速度。

而动能定理指出：合外力对物体所做的功等于物体动能的变化量。

用公式表示就是$W ＝＼Delta E_k$，其中$W$是合外力做的功，＄＼Delta E_k$是动能的变化量。

二、动能定理的推导为了更好地理解动能定理，我们来简单推导一下。

假设一个质量为$m$的物体，在恒力$F$的作用下，沿着直线从位置$x_1$运动到位置$x_2$，力的方向与位移方向相同，加速度为$a$。

根据牛顿第二定律$F ＝ ma$，又因为匀变速直线运动的位移公式$x ＝ v_0t ＋＼frac{1}｛2}at^2$，速度公式$v ＝ v_0 ＋ at$。

我们对位移公式进行变形可得：＄t ＝＼frac{v v_0}｛a}＄，将其代入位移公式可得：＄x ＝＼frac{v^2 v_0^2}｛2a}＄。

力$F$做的功$W ＝ Fx ＝ ma ＼times ＼frac{v^2 v_0^2}｛2a} ＝＼frac{1}｛2}mv^2 ＼frac{1}｛2}mv_0^2$。

这正好就是物体末动能与初动能的差值，也就是动能的变化量$＼Delta E_k$。

三、动能定理的应用场景1、求物体的速度当已知物体所受的合力做功以及物体的初动能时，可以通过动能定理求出物体的末速度。

例如，一个质量为$2kg$的物体，在水平方向受到一个大小为$10N$的恒力作用，力的方向与运动方向相同，物体在力的作用下移动了$5m$，初始速度为$2m/s$。

则合力做功$W ＝ Fs ＝ 10×5 ＝ 50J$，根据动能定理$W ＝＼Delta E_k ＝＼frac{1}｛2}mv^2 ＼frac{1}｛2}mv_0^2$，可得$50 ＝＼frac{1}｛2}×2×v^2 ＼frac{1}｛2}×2×2^2$，解得$v ＝ 6m/s$。

《动能和动能定理》讲义一、引入在我们的日常生活中，运动的物体随处可见。

比如飞驰的汽车、投掷出去的铅球、飞行中的子弹等等。

当这些物体运动时，它们似乎具有一种能够对外做功的能力。

那么，这种能力究竟是如何描述和衡量的呢？这就引出了我们今天要探讨的主题——动能和动能定理。

二、什么是动能简单来说，动能就是物体由于运动而具有的能量。

想象一下，一辆快速行驶的汽车和一辆缓慢行驶的汽车，哪一辆具有更大的“冲击力”或者说能够做更多的功呢？显然是快速行驶的那一辆。

这是因为它的运动速度更快，所以具有更大的动能。

动能的大小与物体的质量和速度有关。

其表达式为：＄E_k ＝＼frac{1}｛2}mv^2$ ，其中＄E_k$ 表示动能，＄m$ 表示物体的质量，＄v$ 表示物体的速度。

从这个表达式中，我们可以看出以下几点：1、动能与物体的质量成正比。

质量越大的物体，在相同速度下具有的动能就越大。

比如一辆大卡车和一辆小汽车以相同的速度行驶，大卡车具有更大的动能。

2、动能与速度的平方成正比。

这意味着速度对动能的影响更为显著。

速度增加一倍，动能将增加到原来的四倍。

所以，即使物体的质量较小，但如果速度足够快，也能具有较大的动能。

例如，一颗子弹虽然质量很小，但由于其高速飞行，具有很大的动能，可以造成巨大的杀伤力。

三、动能定理有了对动能的理解，接下来我们来学习动能定理。

动能定理表述为：合外力对物体所做的功等于物体动能的变化量。

用数学表达式可以写成：＄W ＝＼Delta E_k$ ，其中＄W$ 表示合外力对物体做的功，＄＼Delta E_k$ 表示动能的变化量。

假如一个物体在初始时刻的动能为＄E_{k1}＄，经过一段时间，在外力的作用下，其动能变为＄E_{k2}＄，那么动能的变化量＄＼Delta E_k ＝ E_{k2} E_{k1}＄。

为了更好地理解动能定理，我们来看几个例子。

例 1：一个质量为＄m$ 的物体在光滑水平面上，受到一个水平恒力＄F$ 的作用，从静止开始运动，经过一段距离＄s$ 后，速度达到＄v$ 。

《动能定理的应用》讲义一、什么是动能定理在物理学中，动能定理描述了力对物体做功与物体动能变化之间的关系。

动能定理的表达式为：合外力对物体所做的功等于物体动能的变化量。

即：＄W_{合} ＝＼Delta E_{k}＄，其中＄W_{合}＄表示合外力做的功，＄＼Delta E_{k}＄表示动能的变化量。

动能的表达式为＄E_{k} ＝＼frac{1}｛2}mv^｛2}＄，其中＄m$ 是物体的质量，＄v$ 是物体的速度。

二、动能定理的理解1、做功的过程就是能量转化的过程合外力做功，意味着其他形式的能量转化为物体的动能；反之，物体克服合外力做功，物体的动能转化为其他形式的能量。

2、合外力做功的计算合外力做功等于各个力做功的代数和。

要注意功的正负，正功表示能量的输入，负功表示能量的输出。

3、动能的变化动能的变化量只与合外力做功有关，与中间过程无关。

三、动能定理的应用场景1、求物体的速度当已知合外力做功以及物体的质量时，可以通过动能定理求出物体的末速度。

例如：一个质量为＄m$ 的物体，在水平恒力＄F$ 的作用下，沿水平方向移动了距离＄s$ ，已知力＄F$ 与位移方向相同，求物体的末速度＄v$ 。

合外力做功＄W ＝ Fs$ ，根据动能定理＄Fs ＝＼frac{1}｛2}mv^｛2} 0$ ，可解得＄v ＝＼sqrt{＼frac{2Fs}｛m}｝＄。

2、求合外力做功已知物体的质量、初速度和末速度，可以通过动能定理求出合外力做功。

比如：一物体质量为＄m$ ，初速度为＄v_{1}＄，末速度为＄v_{2}＄，求合外力做功＄W_{合}＄。

由动能定理可得：＄W_{合} ＝＼frac{1}｛2}mv_{2}＾｛2} ＼frac{1}｛2}mv_{1}＾｛2}＄。

3、求变力做功当力是变力时，使用牛顿运动定律和运动学公式往往很难求解，但动能定理可以发挥作用。

假设一个物体在一粗糙水平面上运动，受到一个与位移大小成正比的阻力＄F ＝ kx$ ，物体从位置＄x_{1}＄运动到＄x_{2}＄，求阻力做功。

《动能定理的应用》讲义一、什么是动能定理在开始探讨动能定理的应用之前，咱们得先明白动能定理到底是啥。

简单来说，动能定理描述的是合外力对物体所做的功等于物体动能的变化量。

用数学表达式来写就是：W 合＝ΔEk ，其中 W 合表示合外力做的功，ΔEk 表示动能的变化量。

动能 Ek ＝ 1/2 mv²，这里的 m 是物体的质量，v 是物体的速度。

那动能定理有啥用呢？它可是解决力学问题的一把利器，能让咱们更轻松地分析物体的运动情况，求出各种力的作用效果以及物体的速度、位移等重要物理量。

二、动能定理的推导为了更好地理解动能定理，咱们来推导一下。

假设一个物体质量为 m ，在恒力 F 的作用下，沿着直线运动了一段位移 s ，力 F 与位移 s 的夹角为θ 。

根据功的定义，力 F 做的功 W ＝Fscosθ 。

再根据牛顿第二定律 F ＝ ma （其中 a 是加速度），可得 a ＝ F/m 。

又因为匀变速直线运动的位移公式 s ＝ v₀t ＋ 1/2 at²（这里 v₀是初速度），而 t ＝（v v₀) ／ a （v 是末速度），把 t 代入位移公式可得：s ＝（v² v₀²) ／ 2a将 F ＝ ma 和 s ＝（v² v₀²) ／ 2a 代入功的表达式 W ＝Fscosθ ，得到：W ＝ ma ×（v² v₀²) ／2a × cosθ ＝ 1/2 mv² 1/2 mv₀²这就是动能定理的表达式啦，是不是挺神奇的？三、动能定理的应用场景接下来咱们看看动能定理都能在哪些地方大显身手。

1、求变力做功当力的大小或方向在运动过程中发生变化时，直接用恒力做功的公式就不好使了。

这时候动能定理就能派上用场，通过计算物体动能的变化来间接求出变力做的功。

比如，一个小球在一根弯曲的光滑轨道上运动，轨道对小球的支持力是变力，但我们可以通过小球初末状态的动能变化来求出支持力做的功。

4．5 动能 动能定理
4．5．1． 质点动能定理
质量m 的质点以速度v 运动时，它所具有动能k
E 为： 2
21mv E k =
动能是质点动力学状态量,当质点动能发生变化时，是由于外力对质点做了功，其关系是：
W 外=21K K K E E E -=∆
上式表明外力对质点所做功，等于质点动能的变化,这就是质点动能定理.
4．5．2．质点系动能定理
若质点系由n 个质点组成，质点系中任一质点都会受到来自于系统以外的作用力（外力）和系统内其它质点对它作用力(内力），在质点运动时，这些力都将做功。

设质点系由N 个质点组成，选取适当的惯性系，对其中第i 个质点用质点动能定理
i W 外+i W 内=21222121i i i i v m v m - 对所有n 个质点的动能定理求和就有
∑i W 外+∑i W 内=21222121i i i i v m v m ∑-∑
若用W 外、W 内、2K E 、1K E 分别表示∑i W 外、∑i W 内、222
1i i v m ∑、2121i i v m ∑
则上式可写成
W外+ W内=2K E-1K E
由此可见，对于质点系，外力做的功与内力做的功之和等于质点系动能的增量，这就是质点系动能定理.和质点动能定理一样，质点系动能定理只适用于惯性系,但质点系动能定理中的W内一项却是和所选的参照系无关的，因为内力做的功取决于相对位移，而相对位移和所选的参照系是无关的。

这一点有时在解题时十分有效。

1、动能定理应用的基本步骤应用动能定理涉及一个过程，两个状态．所谓一个过程是指做功过程，应明确该过程各外力所做的总功；两个状态是指初末两个状态的动能．动能定理应用的基本步骤是：①选取研究对象，明确并分析运动过程．②分析受力及各力做功的情况，受哪些力？每个力是否做功？在哪段位移过程中做功？正功？负功？做多少功？求出代数和．③明确过程始末状态的动能E k1及E K2④列方程W=E K2一E k1，必要时注意分析题目的潜在条件，补充方程进行求解．2、应用动能定理的优越性(1)由于动能定理反映的是物体两个状态的动能变化与其合力所做功的量值关系，所以对由初始状态到终止状态这一过程中物体运动性质、运动轨迹、做功的力是恒力还是变力等诸多问题不必加以追究，就是说应用动能定理不受这些问题的限制．(2)一般来说，用牛顿第二定律和运动学知识求解的问题，用动能定理也可以求解，而且往往用动能定理求解简捷．可是，有些用动能定理能够求解的问题，应用牛顿第二定律和运动学知识却无法求解．可以说，熟练地应用动能定理求解问题，是一种高层次的思维和方法，应该增强用动能定理解题的主动意识．(3)用动能定理可求变力所做的功．在某些问题中，由于力F的大小、方向的变化，不能直接用W=Fscosα求出变力做功的值，但可由动能定理求解．一、整过程运用动能定理（一）水平面问题1、一物体质量为2kg，以4m/s的速度在光滑水平面上向左滑行。

从某时刻起作用一向右的水平力，经过一段时间后，滑块的速度方向变为水平向右，大小为4m/s，在这段时间内，水平力做功为（）A. 0B. 8JC. 16JD. 32J2、一个物体静止在不光滑的水平面上，已知m=1kg，u=0.1，现用水平外力F=2N，拉其运动5m后立即撤去水平外力F，求其还能滑m（g取2/10s m）3、总质量为M 的列车，沿水平直线轨道匀速前进，其末节车厢质量为m ，中途脱节，司机发觉时，机车已行驶L 的距离，于是立即关闭油门，除去牵引力，如图所示。

动能定理 一、单个质点的动能定理 例1、设物体的质量为m ，在与运动方向相同的恒定外力F （F 未知）的作用下，在光滑水平面上发生一段位移l ，速度由v 1增加到v 2，如图所示。

试用牛顿运动定律和运动学公式，推导出力F 对物体做功的表达式（与速度的关系）。

22211122W mv mv =- 功是能量转化的量度，上式右边可以看成是能量的变化（末状态的能量减初状态的能量）。

由于和速度有关，将其定义为动能。

1、动能212K E mv = 2、动能定理：合外力所做的功等于物体动能的变化量。

22211122k W E mv mv =∆=-合 3、动能定理的优越性：(1)适用于恒力做功，也适用于变力做功。

(2)适用于直线运动，也适用于曲线运动。

(3)适用于单一过程，也适用于全过程（复杂运动）。

*(4)机械能守恒定律是有适用条件的，而动能定理是普遍适用的。

例2、两个质量均为m 的小球．用长为2L 的轻绳连接起来，置于光滑水平面上，绳恰好处于伸直状态．如图所示．今用一个恒力F 作用在绳的中点，F 的方向水平且垂直于绳的初始长度方向．原为静止的两个小球因此运动．求：（1）在两个小球第一次相碰前的瞬间,小球在垂直于F 作用线方向上的分速度为多大?（2）若干次碰撞后，两球处于接触状态一起运动，求因碰撞损失的总能量。

二、质点系统的动能定理质点系的动能增量等于作用于质点系所有外力和内力做功的代数和。

k E W W ∆=+∑∑外内注意：系统牛顿第二定律：F =ma ，不需要考虑内力。

但是，系统动能定理，不仅需要考虑外力做功，还要考虑内力做功例3、速度为v 1的子弹射入静止在光滑桌面上的木块，子弹受到的阻力为f ，子弹未从木块中射出，子弹和木块以共同的速度v 2在桌面上运动。

子弹射入木块的深度为d ，求木块和子弹构成的系统动能的减少量。

三、非惯性系中的系统动能定理质点系的动能增量等于作用于质点系所有外力和内力做功以及惯性力做功的代数和。