2 列联表分析(Crosstabs)
- 格式:pdf
- 大小:264.86 KB
- 文档页数:5


用iReport制作交叉表(CrossTabs) 立方开源商业智能一个CrossTabs是一种在设计的时候既不确定行数和也不确定列数的一种表格,在运行环境下它会像下面显示的不同年份的一个销售报表一样。
CrossTabs在jasperresports中从1.1.0版本时开始提供,同时iReport也从1.1.0开始支持CrossTabs。
Jasperreports的CrossTabs工具允许对行和列的数据进行分组、汇总和自定义每一个cell里的内容。
填充CrossTab的数据可以来自主报表里的dataset或来自subDataset。
使用iReport里提供的向导我们可以简单快速的创建功能强大的交叉报表组件。
一个CrossTabs本质上是一个表格,行和列的数量取决于填充这个表格的数据。
行和列也可以在groups里做聚合操作。
对于每一个行或列的group我们都可以得到一个细节信息和一个可选的行列数据的汇总。
16.1 交叉表向导 (Crosstab wizard)为了说明怎么让一个crosstab工作起来,我们将使用向导创建一个crosstab,当我们在工具条里选择crosstab元素并将其添加到报表中时crosstab的向导会自动启动。
还是以DoradoSample里提供的hsql数据里的employee报为例,我们使用包含下面查询语句的空报表开始:Select * from employee我们把crosstab放在报表的底部:summary band图16.1在第一步里我们需要选择一个dataset来填充crosstab,我们这里使用主报表里提供的dataset,点击下一步继续。
图16.2在第二步里我们需要定义至少一个行分组.我们这里选择对所有记录使用DEPT_ID进行分组。
这样就意味着crosstab的每一行将会采用一个明确的部门编号,这样JasperReports将会使用部门编号对数据集里的数据进行重新整理计算。

2 列联表分析(Crosstabs)列联表是指两个或多个分类变量各水平的频数分布表,又称频数交叉表。
SPSS的Crosstabs过程,为二维或高维列联表分析提供了22种检验和相关性度量方法。
其中卡方检验是分析列联表资料常用的假设检验方法。
例子:山东烟台地区病虫测报站预测一代玉米螟卵高峰期。
预报发生期y为3级(1级为6月20日前,2级为6月21-25日,3级为6月25日后);预报因子5月份平均气温x1(℃)分为3级(1级为16.5℃以下,2级为16.6-17.8℃,3级为17.8℃以上),6月上旬平均气温x2(℃)分为3级(1级为20℃以下,2级为20.1-21.5℃,3级为21.5℃以上),6月上旬降雨量x3(mm)分为3级(1级为15mm以下,2级为15.1-30mm,3级为30mm以上),6月中旬降雨量x4(mm)分为3级(1级为29mm以下,2级为29.1-36mm,3级为36mm以上)。
数据如下表。
山东烟台历年观测数据分级表()注:摘自《农业病虫统计测报》 131页。
1) 输入分析数据在数据编辑器窗口打开“”数据文件。
数据文件中变量格式如下:2)调用分析过程在菜单选中“Analyze-Descriptive- Crosstabs”命令,弹出列联表分析对话框,如下图3)设置分析变量选择行变量:将“五月气温[x1],六月上气温[x2],六月上降雨[x3],六月中降雨[x4]”变量选入“Rows:”行变量框中。
选择列变量:将“玉米螟卵高峰发生期[y]”变量选入“Columns:”列变量框中。
4)输出条形图和频数分布表Display clustered bar charts: 选中显示复式条形图。
Suppress table: 选中则不输出多维频数分布表。
5)统计量输出点击“Statistics”按钮,弹出统计分析对话框(如下图)。
Chi-Square: 卡方检验。
选中可以输出皮尔森卡方检验(Pearson)、似然比卡方检验(Likelihood-ratio)、连续性校正卡方检验(Continuity Correction)及Fisher精确概率检验(Fisher’s Exact test)的结果。




描述性统计分析(Descriptive Statistics)统计分析往往是从了解数据的基本特征开始的。
描述数据分布特征的统计量可分为两类:一类表示数量的中心位置,另一类表示数量的变异程度(或称离散程度)。
两者相互补充,共同反映数据的全貌。
这些内容可以通过SPSS中的“Descriptive Statistics”菜单中的过程来完成。
1 频数分析 (Descriptive Statistics - Frequencies)频数分布分析主要通过频数分布表、条形图和直方图,以及集中趋势和离散趋势的各种统计量来描述数据的分布特征。
下面我们通过例子来学习单变量频数分析操作。
1) 输入分析数据在数据编辑器窗口打开“data1-2.sav”数据文件。
2)调用分析过程在主菜单栏单击“Analyze”,在出现的下拉菜单里移动鼠标至“Descriptive Statistics”项上,在出现的次菜单里单击“Frequencies”项,打开如图3-4所示的对话框。
图3-4 “Frequencies” 对话框3)设置分析变量从左则的源变量框里选择一个和多个变量进入“Variable(s):”框里。
在这里我们选“三化螟蚁螟 [虫口数]”变量进入“Variable(s):”框。
4)输出频数分布表Display frequency tables,选中显示。
5)设置输出的统计量单击“Statistics”按钮,打开图3-5所示的对话框,该对话框用于选择统计量:图3-5 “Statistics”对话框① 选择百分位显示“Percentiles Values”栏:Quartiles:四分位数,显示25%、50%和75%的百分位数。
Cut points for 10 equal groups:将数据平分为输入的10个等份。
Percentile(s)::用户自定义百分位数,输入值0—100之间。
选中此项后,可以利用“Add”、“Change”和“Remove”按钮设置多个百分位数。

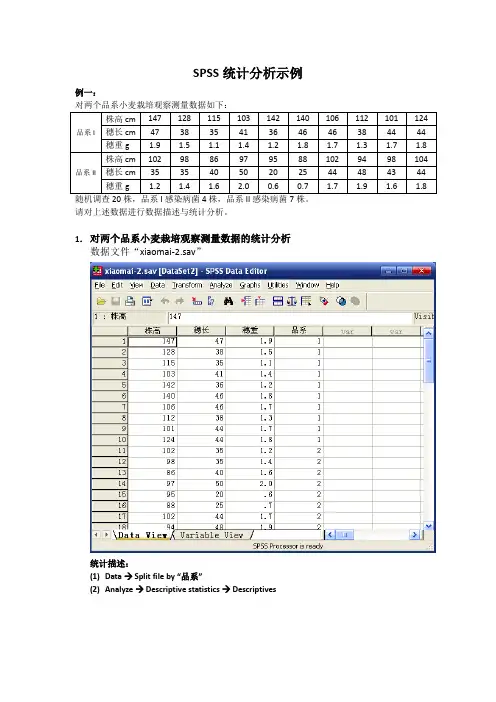
SPSS统计分析示例例一:对两个品系小麦栽培观察测量数据如下:随机调查20株,品系I感染病菌4株,品系II感染病菌7株。
请对上述数据进行数据描述与统计分析。
1.对两个品系小麦栽培观察测量数据的统计分析数据文件“xiaomai-2.sav”统计描述:(1)Data →Split file by “品系”(2)Analyze → Descriptive statistics → Descriptives分别对品系I、II的统计描述:绘图(bar chart with error-bar):Graphs → Interactive →Bar…对两个品系株高、穗长和穗重进行平均值t 检验:Analyze →Compare Means → Independent-samples T test…按品系不同分组’Grouping’,分别比较株高、穗长、穗重SPSS输出:汇总表:品系I 品系II t 株高cm(M±SD) 121.80±16.98 96.40±5.89 4.468**穗长cm(M±SD) 41.50±4.48 38.40±9.74 0.914穗重g (M±SD) 1.54±0.28 1.45±0.48 0.511**:P<0.01从t检验的结果看:(1)株高数据不满足方差齐性,用近似t检验,t=4.468 (df=11.136), 双侧检验P=0.001<<0.01,两品系的株高具有极显著差异,品系I株高显著大于品系II(2)穗长数据不满足方差齐性,用近似t检验,t=0.914 (df=12.640), 双侧检验P=0.378>0.05,两品系的穗长无显著差异(3)穗重数据满足方差齐性,用t检验,t=0.511 (df=18), 双侧检验P=0.615>0.05,两品系的穗重无显著差异对株高、穗重、穗长两两间做相关、回归分析:Analyze →Correlate →Bivariate…(1)穗长、穗重(n=20)穗长、穗重相关关系极显著(相关系数r=0.972,P<<0.01)建立直线回归方程并作图:Graphs → Interactive →Scatterplot…结果输出:穗重(g)(2)穗长、株高(n=20)穗长、株高之间无显著相关(相关系数=0.238,P=0.312>0.05)(3)穗重、株高(n=20)穗重、株高之间无显著相关(相关系数=0.219,P=0.354>0.05)随机调查20株,品系I感染病菌4株,品系II感染病菌7株。


1、crosstabs列联分析——相关分析在问卷调查、产品检验、医学统计等领域,长需对问题按两个或多个不同的特征进行分类,然后对样本进行交叉汇总后就得到了各种各样的列联表。
一般对列联表的统计分析只着重于分类特征之间是否相互依赖,或者说相互独立,此时可借助卡方检验,也可计算相关系数做相关分析,还可根据不同数据类型给出相应的关联系数。
卡方检验是统计判断是否相互依赖,计算相关系数和关联系数是判断和衡量相关或依赖关系的倾向和程度。
不同数据类型间的相关系数或关联系数合理选择列于下表:关于卡方检验、相关系数或关联系数的细节介绍可参考:列联表分析及在SPSS中的实现pdf文件和相关分析案例PPT文件。
SPSS中Crosstabs工具执行列联分析,其选项中Statistics如下图所示:上图指出:名义变量间、顺序变量间、名义变量和区间变量间可选的关联系数,可参考上面表理解。
对上图,Spss的帮助文件解释如下:Chi-square. 对2x2的列联表, 选Chi-square 来计算 Pearson 卡方值, 似然比卡方值, Fisher's 精确检验, and Yates' 修正后卡方值 (连续修正). 对 2 x 2 列联表, 当表中有一个单元格的期望频率少于5时,进行Fisher's 修正检验,其他情况计算 Yates' 修正卡方值。
对那些有任意数目的行和列的表,选择 Chi-square 计算 Pearson 卡方值和似然比卡方值。
当表的变量是数量型的, Chi-square 执行线线关联检验。
.Correlations. 当表的行列中的值都是可排序的, Correlations 计算 Spearman's 修正系数, rho (仅对数字数据). Spearman's rho 是变量秩序间的关联测度. 当变量都是数量型的, Correlations 计算Pearson 相关系数, r, 测度变量间线性相关系数。
第六讲交叉汇总与关联分析(Crosstabs的应用)主要用于研究两个变量之间是相互独立还是存在某种关系,有没有关系,关系程度怎么样。
最适合于分析两个定类变量之间的关系,但是通过对变量的处理,也可以适合于分析测量层次更高级别的变量。
一、变量及其测量层次变量:被操作化了的概念,是可以直接观察的,在经验研究中,在不同的状态下有不同的属性,科学研究一定要使用变量的语言,一定要有操作化。
变量从它测量的层次上看,可以区分为四种类型:定类变量(Nominal ):区分现象、事物的不同性质,而不能从规模大小等方面进行区分,=≠性别(男,女)收入(有收入,无收入)、民族等定序变量(Ordial):当变量不仅区分了对象的属性、特征,还区分出大小、强弱、高低次序时,就是定序变量。
=≠< >如社会地位、文化水平、社会态度、收入等定距变量(Interval):除了类别、次序属性以外,取值之间的距离还可以用标准化的距离去测量,可以进行加减的运算。
年龄定比变量(Ratio):除了以上三类变量提到的属性,定比变量取值可以构成一个有意义的比率。
如智商。
各个变量之间的关系及其测量:定类——定类——列联表、交互分析定序——定序——等级分析定距——定距——回归与相关(简单与多元)定类——定距——方差分析定类——定序——非参数检验二、交叉汇总表的一般形式及其特点的上面,因变量放在表的旁边条件分布:将其中一个变量控制起来,再看另外一个变量的分布,可以得到条件分布,如可以对自变量的同一取值作条件分布,进行分析。
三、如何获得交叉汇总表Analyze-----Descriptives----Crosstabs----出现对话框:●ROWS这个框中的变量作为交互表中的行变量(一般放因变量Y,y1, y2,y3--)●Column框,这个框中的变量作为交互表中的列变量(一般放自变量X,x1,x2,x3…)●Layer框:框中的变量作为控制变量,决定交互表的层,可以多个控制变量。
第七章列联表分析7.1 列联表(Crossta bs)分析的过程7.2 列联表的实例分析7.1 列联表 (Crossta bs) 分析的过程列联表分析的过程是对两个变量之间关系的分析方法。
被分析的变量可以是定类变量也可以是定序变量。
系统是通过生成列联表对两个变量进行列联表分析的。
列联表分析的功能可以通过下述操作来实现。
图7-1 列联表分析对话框1.打开列联表分析对话框执行下述操作:Analyze→Descrip tive→Crossta bs 打开Cross tabs 对话框如图7-1 所示。
2.确定列联分析的变量从左侧的源变量窗口中选择两个定类变量或定序变量分别进入Row(s)(行)窗口和Colu mn(s)(列)窗口。
进入Row(s)窗口的变量的取值将作为行的标志输出,而进入Colu mn(s)窗口的变量的取值将作为列的标志输出。
Display cluster ed bar charts是在输出结果中显示聚类条图。
Suppres s table 是隐藏表格,如果选择此项,将不输出R×C 列联表。
3.选择统计分析内容单击stati stics按钮,打开stati stics对话框,如图7-2 所示。
图7-2statis tics 对话框下面介绍该对话框中的选项和选项栏的内容:(1)Chi-square是卡方(X2)值选项,用以检验行变量和列变量之间是否独立。
适用于定类变量和定序变量。
(2)Correla tions是皮尔逊(Pearson)相关系数r 的选项。
用以测量变量之间的线性相关。
适用于定序或数值变量(定距以上变量)。
(3)Nominal是定类变量选项栏。
选项栏中的各项是当分析的两个变量都为定类变量时可以选择的参数。
1)Conting ency coeffic ient:列联相关的C系数,由卡方系数修正而得。