6.3利用不变量化简二次曲面方程

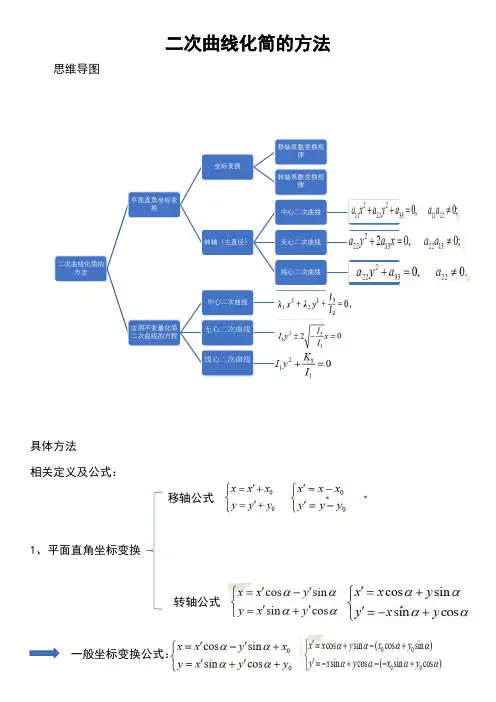
目录摘要 (2)关键词 (2)1引言 (2)2预备知识 (2)3二次曲线的分类 (4)4二次曲线方程的化简 (4)4.1中心二次曲线方程的化简 (4)4.2无心二次曲线方程的化简 (7)4.3线心二次曲线方程的化简 (10)参考文献 (12)英文题目 (12)英文摘要 (12)英文关键词 (12)二次曲线方程的化简与作图曾XX 2008111XXXX数学科学学院数学与应用数学专业 2008级汉班指导老师李XX摘要：二次曲线方程的化简是解析几何中的重难点之一，本文简单介绍了二次曲线方程的分类，将其分为中心、无心、线心曲线三类，并运用待定系数法与配方法相结合的方法，详细介绍了这三类曲线方程的化简，并举例进行了说明.关键词：二次曲线、方程、待定系数、化简1引言我们知道，在不同的坐标系下，同一点有不同的坐标，因而同一图形有不同的方程，方程的形式越简单，它的图形的几何性质就越明显.对于给定的图形，我们就需要选取合适的坐标系，使它的方程更简单，这就涉及到方程的化简问题.二次曲线方程的化简与作图是大学空间解析几何的重点内容之一，它也是解析几何中的一个难点.如何把二次方程代表的曲线化简并作图，以便更容易看出方程所代表的二次曲线的类型，确定曲线的性质、形状以及在坐标中的位置，这具有重要的意义。

纵观有关资料对此问题的研究与讨论，给出了以下几种二次曲线方程化简的方法：坐标变化法、主直径法、不变量与半变量法、参数法、配方法、正交配方法、因式分解法等，这些方法各有优劣。

本文经过深入分析有关二次曲线方程化简的知识，在已知二次曲线分类的基础上，通过对二次曲线化简后所得方程以及其图形形状的探索，运用待定系数法与配方法、因式分解法相结合的方法求出二次曲线方程化简过程中所要知道的未知量，从而求出简化方程，为学习二次曲线方程的化简提供了一定的指导.2预备知识定义1 在平面直角坐标系中，由二元二次方程221112221323332220a x a xy a y a x a y a +++++= (2221112220a a a ++≠) （1） 表示的曲线称为二次曲线.为了方便起见，引进下面一些记号：22111222132333(,)222F x y a x a xy a y a x a y a =+++++；1111213(,)F x y a x a y a =++； 2122223(,)F x y a x a y a =++； 3132333(,)F x y a x a y a =++；11122I a a =+；1112221122121222a a I a a a a a ==-； 1112133122223132333a a a I a a a a a a =. 定义2 把一个点对于某一坐标系的坐标变换为同一个点对于另外一个坐标系的坐标，这种变换称为坐标变换.设在直角坐标系xoy 里给定了两条互相垂直的直线1111:0l A x B y C ++=，2222:0l A x B y C ++=如果取直线1l 为新坐标的横轴''o x ，而直线2l 为纵轴''o y ，并设平面上任意点p 的旧坐标与新坐标分别是(,)x y 与''(,)x y ，则由点到直线的距离公式我们有''x y ⎧=⎪⎪⎨⎪=⎪⎩去掉绝对值便有''x y ⎧=⎪⎪⎨⎪=⎪⎩ (2)其中正负号的选取要使'x 中的x 与'y 中的y 的系数同号.3二次曲线的分类4二次曲线方程的化简4.1中心二次曲线方程的化简对于中心二次曲线方程的化简，实质上是把坐标轴变换到与二次曲线的对称轴（即主直径）重合的位置，坐标原点与曲线中心重合，因此，对中心二次曲线方程的化简，只要先求出曲线的两条互相垂直的主直径，然后以它们作为新坐标轴，作坐标变换即可化为最简单的形式.设中心二次曲线两条互相垂直的主直径分别a kx y +=与b x k y +-=1，则以主直径为新的x 轴、y 轴可以将原方程化0)1()(22=+-++--C b x ky B a kx y A的形式，这里理论上是可以求出待定系数的，但是比较麻烦，因此我们不妨从主直径入手，先求出主直径的方程，从而得出简化方程.二次曲线的特征方程为0-212=+I I λλ，其特征根为2422112,1I I I -±=λ，如果判别式04)(421222211221=+-=-=∆a a a I I ，那么2211a a =，012=a ，这时的中心曲线为圆（包括点圆、虚圆），它的特征根为一对二重根，)0(2211≠==a a λ，任何方向都是圆的渐进主方向，从而通过圆心的任何直线都是圆的主直径.如果特征方程的判别式04)(421222211221>+-=-=∆a a a I I ，那么特征根为两不等的非零实根1λ、2λ，则由特征根1λ与2λ确定的主方向分别为122211111211:)()(::a a a a Y X -=-=λλ， （3）122221121222:)()(::a a a a Y X -=-=λλ， （4） 从而曲线的主直径为0),(),(2111=+y x F Y y x F X 与0),(),(2212=+y x F Y y x F X ，从而我们可以将方程（1）化为0)],(),([)],(),([2221222111=++++C y x F Y y x F X B y x F Y y x F X A （5） 把他与方程（1）的系数作比较，从而可以求出待定系数C B A ，，的值.现在我们把直线0),(),(2111=+y x F Y y x F X 作为新坐标的x 轴，把直线0),(),(2212=+y x F Y y x F X 作为新坐标的y 轴，这里需要注意，一般我们常将斜率大于0的主直径作为新坐标的x 轴，以确保在旋转变换时，其转角θ为锐角.假设两主直径方程中，y x 、的系数分别为11B A 、与22B A 、，作变换⎪⎪⎩⎪⎪⎨⎧++=++=，，)],(),([1)],(),([121112121'22122222'y x F Y y x F X B A y y x F Y y x F X B A x （6）则二次曲线方程（1）可以化为0)()(2'21212'2222=++++C y B A B x B A A做适当变换即可得到下列五种曲线中的一种形式：[1]12222=+b y a x (椭圆)；[2] 12222-=+by a x （虚椭圆）；[3] 12222=-by a x （双曲线）；[4] 02222=+by a x （点或者相交于实点的共轭虚直线）；[5] 02222=-by a x （两相交直线）.例1 化简二次曲线方程01616854822=--+++y x y xy x ，并作出它的图形.解 因为0365228135821≠===+=I I ，，所以曲线为中心二次曲线，曲线的特征方程是03613-2=+λλ，解得两特征根为，，942,1==λλ因而由公式（3）与（4）知，曲线的两个主方向为）（2-:1)84(:2:11=-=Y X 1:28-9:2:22==）（Y X曲线的两主直径为0)852(2428=-+-++y x y x ）（与 0)852()428(2=-++++y x y x ， 即 052=+-y x 与02=+y x .设原方程可以化为0)2()52(22=++++-C y x B y x A ，与原方程系数比较可得365954-===C B A ，，，由（6），作变换⎪⎪⎩⎪⎪⎨⎧+-=+=),52(51-),2(51''y x y y x x 则原方程可化为036942'2'=-+x y ，化为标准方程得1942'2'=+y x ， 这是椭圆，图形如图一所示4.2无心二次曲线方程的化简由二次曲线的分类我们知道无心二次曲线可以化为02''132''22=+x a y a 的形式，设对任意给定的无心二次曲线方程可以表示为：0)()(2=+-+++b y kx B a ky x A的形式，展开得0)()2()2(22222=++-+++++bB A a y B aAk x Bk aA y Ak Akxy Ax ，将其待定系数与方程（1）对比，我们可得：⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=-=+==,,22,22,22,33223131211a bB A a a B aAk a Bk aA a kA a A 解之得⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧=+-+-+=+-=++==,,))((2)()(,2,,112122112311131211223121311112212211332122112311131211212211231213111112a A a a a a a a a a a a a a a a a b a a a a a a a B a a a a a a a a a k （7） 现在我们分别把直线0=++a ky x 与直线0=+-b y kx 作为新坐标的x 轴、y 轴，同样的，一般我们常将斜率大于0的直线作为新坐标的x 轴，以确保'x 轴与x 轴的夹角为锐角。

应用不变量简化二次曲面的方程一f删No,:9|西北轻工业学院Dec.1995 JOURNALOFNORTHWESTINSTITUTEOFLIGHTR4DUSTRYV o1.13 应用不变量简化二次曲面的方程张慧(敦学教研室)摘要末文研究了R’空间(欧氏空间)二次曲面在坐标变换下的不变量.应用不变量简化了R空间二次.盐面的一般方程.谈法简单,出结果快,容易掌握. 关键词:三连堕鱼;丕童量;垩皇兰;堑堑翌参;特征根中圈法分类号:O182.11前言应用不变量来简化二次曲面的方程在三维空间已经有了—套完整的理论.而四维以上空间都是抽象空间,那套理论是否还适用就有待于进一步研究.本文利用线性代数理论研究了R’空间二次曲面在坐标变换下的不变量,并利用这些不变量将二次曲面的—般方程化成标准形.2二次曲面在坐{岳}变换下的不变量与半不变量这里的坐标变换指的是广义的平移+旋转.在R空间,二次曲面的—般方程是:口】】}+】12+2a1ts+2d】1.+2aI】+船l+嚣2a+2az?+2a22+口ai+2a”￡.+2as+口.{+.+a=0(1)其中a,,J=l,2,3.4,5是实数.引进一些记号:0l,z2,z3,’)三a】li+2a11z:-t-2aII￡3-t-2a1】.+2a15z】+≈￡l+2d22z5+2a:..+2a25z2+as3i+2a”3.+2a3s+a|.z}2a4’+口昨10I’2,¨?)三1l+口】:+1s+14+d】5收稿日期,1g95—08一l.第d期张慧;应用不变量简化二伏曲面的方程?93? F20l,02,3,’)三dll+.22+.嚣I+.24+d25F3l,2,I,’)兰Ⅱl+.22+.”I+a34:r4+d惦F’l,2,03,4)三nll+.2z+a34Z$+d”4+d.5F50I’2,.a,￡4)兰n1l+a25xz+a~zs+a45x+.B50l,￡2,3,￡’)兰dll}+ll2+l!Z3+ll~+anzi+2s3+22￡’+d3a￡;+34+d_id1ldl2dI3d】2d22d2315d∞n”d1’d”d34:A=dlldl2d15dl’dm5dI2d22d2ad24d25al3d豁口”d3_d35_d2’ad”d45【.’..”【...a.a55f表示Ial的所有m阶主子式之和,m一1,2,3,4即f1=dl】+.匏+.33+a4413z++K5=dlldI2dI3dl1d12d1.dI2d黯d荔口l2d拦dd2ad3IdI4d2d●’d1lⅡl2dt5 d12ad15da$5d22d嚣d25 d2sd33d35 d25d35dfi$ d1ld”dI5d1zd跎拈013%dnld35++++4d筠d55d拄d笛d2’dl1dIIdI4dndaI“dl3d3ada4d2’da_ d”dI_dsd”dIl13”l5 dI3d3,ddI5da5d晒d2zd2●d25 d2’d”d拍d25d45a55 +++d22d鹞a24 d23d黯a”d”d|’a”dz6d35a’5 dIldI’dlEa拍a3Id3sd25d35d45d$fidI_dd3’a44dI5d15d|5d55d35d5d55口嚣口口+口口L’口口+ n”¨¨口口口口un罅”口口口口吐”口口口a ll2Z口口口口11+如口口口口+v’r口口;穹口口+Ⅱ●口口dll卜;■】5d口口==,?94?西北轻工业学院第l3卷先证明在移轴下,+口1]4l24H口l6口4224244z54l4424口”口4l54口45 口+口ll 口】3 4lt4l5 口】3 口”4”43’口】’4s’4”4”口15 435 4’4陆rz,f3,f?,不变,而K,K,K—般是要改变的】=Yl-+-口2+b3-+-cY?+d其中a,b,c,d为实常数将F(-’I2)写成矩阵形式0l,z,s,?)一0】:3.1)A故F(l+4,+6,3+c,y4+)(】+口2+63+cy.+d1)=(ly03’0)+(ly:3’0)Y1s1l+Y2+6Y3+.y?+d1+bcd1)+(4cd1)口1]4】2口13口¨】(口,b,c,) 4】2a22口232,6,c,d)4】s器33s’F3(4,b,c,d)aH4z4¨Ⅱ44F’(4,b,c,d)F】23.(目,b,c,d)l2aY?1lz3?ljSJl(2)(3)(4)其中F一F.0,bd)m一1,2,3,4可见通过移轴(2),二次曲面的方程二次项系数不变,丽f,f,f,,只与二次项系数有0口6C1第4期张慧:应用不变量简化=歇曲面的方程?95?关,所以移轴后有,一,m=l,2,3,4口11Ⅱ】2Ⅱ222ⅡL323Ⅱt’Ⅱz’tF2口】3口”口25口2’Ⅱ33Ⅱ3IⅡ”Ⅱ44F3F.61L口十口】十Ⅱ1sc++ⅡI6Ⅱt2a十口226+23c+Ⅱ+嚣Ⅱt十z36+33C十3十35口1+a24b+3’c十口.+’5(口,b,c,d)ⅡI3口】4口15口23Ⅱ2●口2.5口53Ⅱ”Ⅱ35Ⅱ”Ⅱ4’口46aIF5(口,b,c,d)即移轴后Js也不变.通过移轴还知二次曲面方程一次项的系数一般要改变,而,,.都与一次项系数有关,所以K,K,K—般是要改变的.由(4)知,只要适当选取a扣,c,,方可消去方程(4)中的一次项.事实上,令只要该方程组系数矩阵的秩与增广矩阵的秩相等,(这里不讨论两秩不相等的情况),方程组有解,可选其中一组作为(,6).此时方程化为dt1{+2aI2l2+2aI蚶】3十2aI’II十口啦f;+哪r23十z’+口33;+砖.十j+z2,3,)=(j231)口口j23‘lO口一():)=(叩.)一因为p-L’P与’相似,根据定理:相似矩阵有相同的特征多项式从而有相同的特征根,知P』4.P与’有相同的特征多项式和特征根.l一l=一,j十,z一,3+,I加一PAP;=一』十,一,十,辑1aI1:l1i2一i2l3一I3,t.一I|,5一{口』4口l—l0llAli口l—l口～llll口l={』4}:可见,在转轴下,|,,,』3,一,,s都不变.不g两个四次多项式对应系数应相等.计算这些系数便可得=,:z,一,这表明在转轴下,,都不变第4期张慧应用不变量简化二狄曲面的方程?97?我们称,,,,,,j,』为上述变换下的不变量,称K,Kz,K,为上述变换下的半不变量.3二次曲面的分类二次曲面(1)通过坐标变换可以化为下面三种类型(I)1i+口{+口;+口?i+口,55=001口≠0) (I)口l{+口l+口-…22a?=001口5≠0) (Ⅲ)其它,(由于篇幅限制,不予讨论) 4应用不变量简i~-T-次曲面的方程(1)对于(I),因为,=口lld22口弛d44=口11a口a口?≠0所以原方程,.≠0.由此可得:当二次曲面(1)的14≠0时,方程可化为(1).此时,,1=,=口1+口+口+口44』2=,一1口,J-口3+口口?+口1口+口1d+口4,3=,一口l口+口口3d’+口】口3口44+口la?二次曲面(1)的特征方程是:一I1+I2好一f+ll=0将(7),(8),(9)代E方程解得一口ll=口,=口,=‘因为』5=,=口1口44U=,=,所以口55=15/l于是(,)可写成:,.…+i+;十{+=0‘‘其中,,,丑为二次曲面(1)的四个特征根.(2)对于(I),因为,.=,5口100000口00000口000000口,.50000=一口5d1口一艘,33≠0(7)(8)(9)0≠11,”●叫和4,13411?98?西北轻工业学院第l3卷所以原的.=0,,,≠0,,≠0.由此可得,当二次曲面(1)的,.一0,,.≠0,,s≠0时,方程可化为(Ⅱ).此时,J一,=d+d+d,2=,:d】d+d0+d1d13:,:口】d2d二次曲面(1)的特征方程是:一0l+2+d)+(d1”+d2d3+d1d3)一d】d2Ⅱ3=0一d】,:d,A=a,丑=0因为,5一,:一dld=--13as所以n一土于是(I)可写成:1+2十3+2z’一1—0化成标准形式.解二次曲面的矩阵与(r,z,rs,z)的矩阵分别是: 0ll—l1l0一ll11——1011——111011lll1—3≠O01l—l—l11—1一ll0l10+II+II+II+I:I一一sr,V0—0l1.十卜010+0ll=第d期张慧:应用不变量简化二次曲面的方程?9g? 0一l11l0+—045.}=315}【1』1【0j卜【_l口t9O—ll0ll400O5=l0336O005—2l3O360一一,V?1O0?西北轻工业学院第l3卷参考文献1江苏师范学院数学系编.解析几何.北京:高等教育出版社,19952北京大学数学力学系代数小组编.高等代数.北京:人民教育出版社,19783高立芳.东北电力学院,1993,2 APPLICATIONOFFIXEDQUANTITIESTOTRANSFORM QUADRATICSURFACEEQUATIONSINT0 STANDARDEQUATIONSABs1’RACJInthispaper.thefixedquantitesofquadiaticsurfaceinfour—dimensionalspace asllldie0underthecoordinatetrantformationApplicationoffixedquantitiestotr ans—frIT1.lJadraticsHrfaceequationsintostandardequations-Theexpressiongive nissimpleaadacceptable.Keywords:quadralicsurface;fixedquantity{orthogonaltransfor--mation;cha ract.,tiemljltinomia1.,characteristlevalue。

第六章 二次曲面的一般理论教学目的: 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面奇向、主径面与主方向等重要概念,从不同角度对二次曲面进行了分类.研究了二次曲面的几何性质,并通过坐标变换和不变量、半不变量两种形式,化二次曲面的一般方程为规范方程,对二次曲面进行了分类和判定,是二次曲面理论的推广和扩充.教学重难点: 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为规范方程,既是重点又是难点. 基本概念二次曲面: 在空间,由三元二次方程022222244342414231312233222211=+++++++++a z a y a x a yz a xz a xy a z a y a x a （1）所表示的曲面.虚元素:空间中，有序三复数组),,(z y x 叫做空间复点的坐标，如果三坐标全是实数，那么它对应的点是实点，否则叫做虚点二次曲面的一些记号≡),,(z y x F 44342414231312233222211222222a z a y a x a yz a xz a xy a z a y a x a +++++++++ 141312111),,(a z a y a x a z y x F +++≡242323122),,(a z a y a x a z y x F +++≡ 343323133),,(a z a y a x a z y x F +++≡ 443424144),,(a z a y a x a z y x F +++≡yz a xz a xy a z a y a x a z y x 231312233222211222),,(+++++≡Φz a y a x a z y x 1312111),,(++≡Φ z a y a x a z y x 2322122),,(++≡Φz a y a x a z y x 3323133),,(++≡Φ z a y a x a z y x 3424144),,(++≡Φ即有恒等式成立: ≡),,(z y x F ),,(),,(),,(),,(4321z y x F z y x zF z y x yF z y x xF +++),,(),,(),,(),,(321z y x z z y x y z y x x z y x Φ+Φ+Φ≡Φ二次曲面),,(z y x F 的系数矩阵: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=44342414343323132423221214131211a a a a a a a a a a a a a a a a A 而由),,(z y x Φ的系数矩阵为 ⎪⎪⎪⎭⎫ ⎝⎛=*332313232212131211a a a a a a a a a A 二次曲面（1）的矩阵A 的第一，第二，第三，与第四行的元素分别是),,(1z y x F ，),,(2z y x F ，),,(3z y x F ，),,(4z y x F 的系数。

应用不变量化简四维欧式空间中二次曲面的方程刘坤; 任润润; 任晓娜【期刊名称】《《陇东学院学报》》【年(卷),期】2019(030)002【总页数】6页(P1-6)【关键词】二次曲面方程; 不变量; 半不变量; 化简【作者】刘坤; 任润润; 任晓娜【作者单位】陇东学院数学与统计学院甘肃庆阳 745000; 西北师范大学教育学院甘肃兰州 730070【正文语种】中文【中图分类】O182.1众所周知，二次曲线方程和二次曲面方程的化简是解析几何中的主要问题之一，对其已经有了较为系统的研究[1-6]。

借助不变量和半不变量可以简化二次曲面的方程[7-12]，现有教材仅对二维欧式空间中二次曲线和三维欧式空间中二次曲面的不变量和半不变量进行了研究[13-14]。

关于三维以上欧式空间中二次曲面不变量的研究首见于2015年张海芳所写的《R4中二次曲面的不变量》一文[15]；该文给出了四维欧式空间中二次曲面的不变量和半不变量的定义，得到了在四维欧式空间中二次曲面有5个不变量和3个半不变量的重要结果，但应用这些不变量和半不变量来简化四维欧式空间中二次曲面方程的研究尚未见到。

本文根据不变量和半不变量取值的不同情形对此问题做了一些讨论，得到了四维欧式空间中二次曲面在6种情形下的简化方程的一般形式，并就各种情形给出了算例。

1 定义及相关记号通常，称所表示的曲面为四维欧式空间中的二次曲面方程。

(1)其矩阵的形式为(2)下面给出本文要用到的一些记号：F1(x1,x2,x3,x4)≡a11x1+a12x2+a13x3+a14x4+a15,F2(x1,x2,x3,x4)≡a12x1+a22x2+a23x3+a24x4+a25,F3(x1,x2,x3,x4)≡a13x1+a23x2+a33x3+a34x4+a35,F4(x1,x2,x3,x4)≡a14x1+a24x2+a34x3+a44x4+a45,F5(x1,x2,x3,x4)≡a15x1+a25x2+a35x3+a45x4+a55,Φ1(x1,x2,x3,x4)≡a11x1+a12x2+a13x3+a14x4,Φ2(x1,x2,x3,x4)≡a12x1+a22x2+a23x3+a24x4,Φ3(x1,x2,x3,x4)≡a13x1+a23x2+a33x3+a34x4,Φ4(x1,x2,x3,x4)≡a14x1+a24x2+a34x3+a44x4,Φ5(x1,x2,x3,x4)≡a15x1+a25x2+a35x3+a45x4.显然可得如下两个恒等式F(x1,x2,x3,x4)≡x1F1(x1,x2,x3,x4)+x2F2(x1,x2,x3,x4)+x3F3(x1,x2,x3,x4)+x4F4(x1,x2,x3,x4)+F5(x1,x2,x3,x4),Φ(x1,x2,x3,x4)≡x1Φ1(x1,x2,x3,x4)+x2Φ2(x1,x2,x3,x4)+x3Φ3(x1,x2,x3,x4)+x4Φ4(x1,x2,x3,x4)，一般地,称F(x1,x2,x3,x4)的系数排成的矩阵为二次曲面(1)的矩阵(或称为F(x1,x2,x3,x4)的矩阵),而由Φ(x1,x2,x3,x4)的系数所排成的矩阵A*称为Φ(x1,x2,x3,x4)的矩阵。

二次曲面参数方程
二次曲面是由二次方程定义的曲面，它通常可以用参数方程来表示。

以下是几个常见的二次曲面的参数方程：
椭球面：x = a * cos(u) * sin(v) y = b * sin(u) * sin(v) z = c * cos(v)
其中，u和v是参数，a、b、c分别是x、y、z轴上的半轴长度。

长方体面：x = a * cos(u) y = b * sin(u) z = c * sin(v)
其中，u和v是参数，a、b、c分别是x、y、z轴上的长度。

双曲面：x = a * cosh(u) * cos(v) y = b * cosh(u) * sin(v) z = c * sinh(u)
其中，u和v是参数，a、b、c分别是x、y、z轴上的缩放因子。

抛物面：x = u y = v z = au^2 + bv^2
其中，u和v是参数，a、b是曲面的形状参数。

这只是一些常见的二次曲面的参数方程示例，实际上还有许多其他类型的二次曲面。

通过选择不同的参数和形式，可以生成各种不同形状的二次曲面。

第六章-二次曲面的一般理论-CAL-FENGHAI.-(YICAI)-Company One1第六章 二次曲面的一般理论教学目的: 本章讨论了一般二次曲面的渐近方向、中心、切线、切平面、径面奇向、主径面与主方向等重要概念,从不同角度对二次曲面进行了分类.研究了二次曲面的几何性质,并通过坐标变换和不变量、半不变量两种形式,化二次曲面的一般方程为规范方程,对二次曲面进行了分类和判定,是二次曲面理论的推广和扩充.教学重难点: 通过坐标变换和运用不变量、半不变量化二次曲面的一般方程为规范方程,既是重点又是难点. 基本概念二次曲面: 在空间,由三元二次方程022222244342414231312233222211=+++++++++a z a y a x a yz a xz a xy a z a y a x a（1） 所表示的曲面.虚元素:空间中，有序三复数组),,(z y x 叫做空间复点的坐标，如果三坐标全是实数，那么它对应的点是实点，否则叫做虚点二次曲面的一些记号≡),,(z y x F 44342414231312233222211222222a z a y a x a yz a xz a xy a z a y a x a +++++++++ 141312111),,(a z a y a x a z y x F +++≡242323122),,(a z a y a x a z y x F +++≡ 343323133),,(a z a y a x a z y x F +++≡ 443424144),,(a z a y a x a z y x F +++≡yz a xz a xy a z a y a x a z y x 231312233222211222),,(+++++≡Φz a y a x a z y x 1312111),,(++≡Φ z a y a x a z y x 2322122),,(++≡Φz a y a x a z y x 3323133),,(++≡Φ z a y a x a z y x 3424144),,(++≡Φ即有恒等式成立: ≡),,(z y x F ),,(),,(),,(),,(4321z y x F z y x zF z y x yF z y x xF +++),,(),,(),,(),,(321z y x z z y x y z y x x z y x Φ+Φ+Φ≡Φ二次曲面),,(z y x F 的系数矩阵: ⎪⎪⎪⎪⎪⎭⎫⎝⎛=44342414343323132423221214131211a a a a a a a a a a a a a a a a A 而由),,(z y x Φ的系数矩阵为 ⎪⎪⎪⎭⎫ ⎝⎛=*332313232212131211a a a a a a a a a A 二次曲面（1）的矩阵A 的第一，第二，第三，与第四行的元素分别是),,(1z y x F ，),,(2z y x F ，),,(3z y x F ，),,(4z y x F 的系数。

二次曲线方程是一种数学形式，用来表达一条曲线的几何特征的方程。

它是一元二次方程的一般形式，其关键是表示二维坐标系中的曲线。

一般来说，二次曲线方程可以表示为 y = ax² + bx + c，其中，a, b, c 为
任一实数。

了解了这样一个形式，我们可以计算它在x轴上的拐点，
可以利用求根公式求出这样一个方程的拐点，其根是：
x1 = [-b + √(b² - 4ac) ] / 2a
x2 = [-b - √(b² - 4ac) ] / 2a
这样我们就可以以a,b,c为参数，来写出一个二次曲线的方程表达式。

需要注意的是，当参数a的值为0的时候，方程实际上就是一个一次函数，不再是二次函数了。

二次曲线方程的化简对数学中一些概念的理解非常重要，例如，曲线
的极值，切线斜率，矩形轴对称，椭圆形等等。

其实，二次曲线方程化简的技巧可以分为三种：平移法、标准形式化
简法和具体数值求解法。

（1）平移法：将原始方程中的每一项的常数项“平移”到右边，令原始方程的左边变为0，从而表达出一个标准的二次曲线方程。

（2）标准形式化简法：把方程中的变量变为标准形式，这样只要把变量重新合并就可以得到一个标准的二次曲线方程。

（3）具体数值求解法：意味着直接利用求根公式计算出二次曲线方程
的解。

总的来说，二次曲线方程的化简是一个非常重要的数学知识点，对于理解数学形状的概念有很大的帮助。

要想掌握其中的知识，需要深入研究，努力理解，并在此基础上不断练习。