当前位置：文档之家 › 常用的二次曲面方程及其图形

常用的二次曲面方程及其图形

  • 格式：pdf
  • 大小：158.60 KB
  • 文档页数：9

下载文档原格式

  / 9

合集下载

第七章第5节几种常见的二次曲面

第七章第5节几种常见的二次曲面
所求方程为
x x 0 2 y y 0 2 z z 0 2 R 2
特殊地：球心在原点时方程为
x2y2z2R2 4
例 2求 与 原 点 O 及 M 0 ( 2 ,3 ,4 )的 距 离 之 比 为 1 :2 的 点 的 全 体 所 组 成 的 曲 面 方 程 .
与平面 z z1 (|z1|c)的交线为圆.
24
截面上圆的方程
x2

y2

a2 c2
(c2

z12).
z z1
(2 ) abc,
x2 a2
ay22
az22
1
球面
方程可写为 x2y2z2a2.
25
（二）抛物面
x2 y2 z （ p与 q同号） 2 p 2q
cz22
1
双叶双曲面
o
y
x
37
五、小结
曲面方程的概念 F (x ,y,z)0 . 旋转曲面的概念及求法. 柱面的概念(母线、准线). 椭球面、抛物面、双曲面、截痕法.
（熟知这几个常见曲面的特性）
38
习题 75 P235
A组
1(1)2,， 3(2)4 ()， 4,5
39
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形？
20
四、二次曲面
曲面方程: F(x,y,z)0
二次曲面： 三元二次方程所表示的曲面称之．
如 x2(y1)2z21
相应地平面被称为一次曲面．
如2xy3z0
讨论二次曲面方法:截痕法： 特殊的二次曲面．
21
（一）椭球面
x2 y2 z2 a2 b2 c2 1
椭球面与

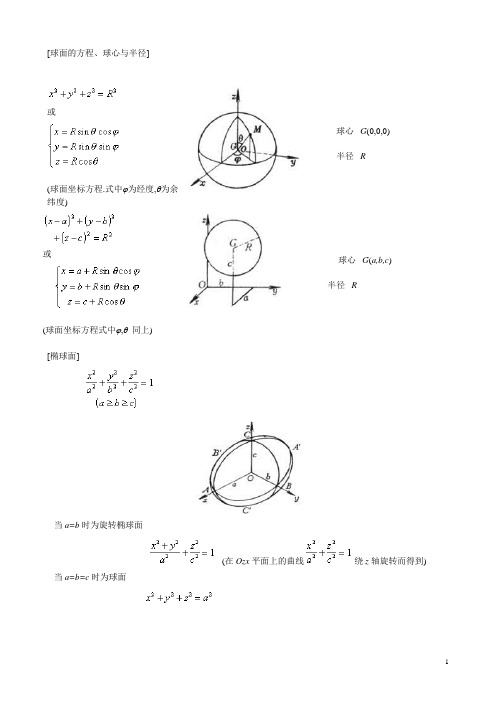
高等数学二次曲面图

高等数学二次曲面图

[球面的方程、球心与半径]
[椭球面]
当a=b 时为旋转椭球面
(在Ozx 平面上的曲线 绕z 轴旋转而得到)
当a=b=c 时为球面
或
(球面坐标方程.式中ϕ为经度,θ为余纬度)
球心 G (0,0,0) 半径 R
或
(球面坐标方程式中ϕ,θ 同上)
球心 G (a,b,c ) 半径 R
[单叶双曲面]
[双叶双曲面]
当a=b时,为[旋转双曲面] (在Oxz平面上的曲线绕z轴旋转而得到) [椭圆抛物面]
当a=b时,为旋转抛物面
(在Ozx平面上的曲线绕z轴旋转而得到) [双曲抛物面]
[椭圆锥面]
当a=b时, 为圆锥面(在Oxz平面上的直线绕z轴旋转而得到)
[椭圆柱面]
当a=b时,为圆柱面[双曲柱面]
[抛物柱面]。

二次曲面方程

二次曲面方程

二次曲面方程一、引言二次曲面方程是数学中非常重要的一类曲面方程。

它们具有丰富的几何性质和广泛的应用领域，如物理学、工程学和计算机科学等。

本文将从二次曲面的定义和性质、几何图形以及实际应用三个方面，生动全面地介绍二次曲面方程。

二、定义和性质二次曲面是由二次方程表示的曲面。

一般地，二次曲面方程可以写成Ax² + By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0的形式。

其中A、B、C不全为零，D、E、F、G、H、I、J是常数。

这种方程描述了空间中的一个曲面，其形状和性质与方程的系数有关。

对于二次曲面方程，有一系列重要的性质。

首先，二次曲面在三维空间中通常表示一个曲面，形状可以是椭圆、双曲线或抛物面。

其次，二次曲面可能有中心或焦点等特殊点，这些点对于曲面的性质和几何特征具有重要意义。

最后，通过调整方程的系数，可以改变二次曲面的形状和方向，从而产生不同的几何图形。

三、几何图形根据二次曲面方程的不同形式，我们可以了解到不同的几何图形。

首先是椭球面，当A、B、C都为正数时，方程描述了一个椭球体。

椭球体在三维空间中呈现出类似于地球的形状，可以用来表示行星、人工卫星等球状物体。

其次是双曲面，当A、B、C中有一个为负数时，方程描述了一个双曲体。

双曲体的形状类似于双曲线，可以用来表示一些物理现象，如电场分布和透镜等。

最后是抛物面，当A或B为零，且C不为零时，方程描述了一个抛物体。

抛物体可以用来描述抛物运动，也可以用于建模天文、航空等领域的问题。

四、实际应用二次曲面方程在现实生活中有广泛的应用。

首先，它们在物理学中发挥着重要作用。

例如，抛物面方程可以用来描述物体的运动轨迹，从而对物体的运动进行预测和分析。

其次，二次曲面方程在工程学中也有重要应用。

通过使用椭球面方程，工程师可以设计出符合实际需求的复杂三维结构，如建筑物、车辆和飞机等。

此外，二次曲面方程还在计算机科学领域得到了广泛应用。

二次曲面

二次曲面

u,v 为参数，且不全为0.
（1）对于单叶双曲面S上的每一点，两类直母线中各有一条直 母线经过它。 （2）单叶双曲面S上异族的两个直母线一定共面，同族的两个 直母线一定异面。
可以看出下面两直线在S上。
x z y x z y u v 1 0 u a c v 1 b 0, a c b I2 : I1 : v x z u 1 y 0 y x z v u 1 0 a c b a c b
当 | h | b时， 截线为双曲线 实轴//z轴 c 2 实半轴： b h 2 b 虚轴//x轴 a 2 虚半轴： b h 2 b
用平行与坐标面的平面y h来截割双曲面： x2 z 2 h2 2 2 1 2 截口方程为：a c b ; y h
当 | h | b时， 截线为两条直线 x z 0 a c y b x z 0 或a c y b
二次曲面
一个仿射坐标系中, x,y,z的一个二次方程的图 形成为二次曲面.
二次方程的一般形式:F ( x, y, z ) 0 F ( x, y, z ) a11 x a22 y a33 z 2a12 xy 2a23 yz 2a13 xz 2b1 x 2b2 y 2b3 z c
u,v 为参数，且不全为0.
三、性质： 1. 单叶双曲面上异族的任意两条直母 线必共面, 而双曲抛物面上异族的任意 两条直母线必相交. 2. 单叶双曲面或双曲抛物面上同族的 任意两条直母线总是异面直线, 而且双 曲抛物面同族的全体直母线平行于同一 平面. 3. 对于单叶双曲面和双曲抛物面上的 每一点, 两族直母线中各有一条通过这 一点.

高等数学常用二次曲面图形.ppt

高等数学常用二次曲面图形.ppt

围成的图形如下：
y 0,
y2
12024/9/27
图30：由 z x2 y2 , z x2 y2 围成的图形如下：
z x2 y2 , z x2 y2
22024/9/27
图31：由 z x2 y2 , x2 y2 1, z 0
围成的图形：
图32： 32024/9/27
图14：函数 函
z
1 ey
cos x yey
有无穷多个
极大值，但无极小值。
z 1 ey cos x yey
图15： 62024/9/27
抛物面 z x2 y2 被平面 x y z 1
截成一椭圆。
图16： 72024/9/27
椭球面
x2 a2
y2 b2
z2 c2
1 在
点
3 a, 3
x2 y2 2x
02024/9/27
图39：由曲面 z x2 y2 和平面
z 0, x 1, y 1 围成图形如下：
z 0, x 1, y 1
12024/9/27
图40：双曲抛物面 z xy 被柱面 x2 y2 1
所截得的图形如下：
x2 y2 1
图41： 22024/9/27
62024/9/27
图1（2）：x2 y2 z2 4, x2 y2 2x
的图形在第一卦限部分如下：
x2 y2 z2 4, x2 y2 2x
图2： 72024/9/27
（2）、曲线
xyz 1
y
21
处的切线
图3： 82024/9/27
（3） 曲线
2x2 y2 z2 16
图46：曲线 x2 y2 z2 1 y z 0
的图形如下：

二次曲面的标准方程

二次曲面的标准方程

二次曲面的标准方程
二次曲面的标准方程是：x²+y²+z²=R²。

其中，R是球的半径，(x,y,z)表示空间中任意一点的位置。

如果二次曲面在三个坐标面上的截距都是圆，并且圆心都在原点，则它的方程为：x²+y²+z²=R²。

其中，R是球的半径。

如果二次曲面在xoy平面上的截距是一个圆，并且圆心在原点，则它的方程为：(x²+y²)=R²。

如果二次曲面在xoz平面上的截距是一个圆，并且圆心在原点，则它的方程为：(x²+z²)=R²。

如果二次曲面在yoz平面上的截距是一个圆，并且圆心在原点，则它的方程为：(y²+z²)=R²。

总之，二次曲面的标准方程可以根据不同的条件选择不同的形式，但它们都涉及到三个坐标轴和球心在原点的球面。

常见的二次曲面


(1)
所确定的曲面称为椭球面.
用Oxy坐标平面(即z=0)截所给曲面，截痕为椭圆
x2 y2 2 2 1, a b z 0.
用平行于Oxy坐标平面的平面z=h截所给曲面，截
痕为椭圆
x2 y2 h2 2 2 1 2 , a b c z h.
x y 当h=±c时，截痕为 2 2 0，即截痕缩为一 a b 点.当|h|>c时，截痕为虚椭圆，说明椭球面与平面
用Oyz坐标面截所给曲面，截痕方程为
y2 z2 2 2 1, b c x 0.
无图形.
用平面x=h截所给曲面，其截痕方程为
y 2 z 2 h2 2 2 2 1, b c a x h.
b 2 当|h|>a时，其图形为椭圆，半轴分别为 h a2 a c 2 2 和 h a ； a
方程
x2 y2 z ( p, q同号) 2 p 2q
(5)
所确定的曲面为椭圆抛物面. 若p>0，q>0.利用截痕法可作出其图形.
六、双曲抛物面
x2 y2 z ( p, q同号) 方程 2 p 2q
确定的曲面为双曲抛物面.
(6)
设p>0，q>0.
用Oxy坐标面截所给曲面，截痕为两条直线
由方程
x2 y2 z 2 2 2 1 2 a b c
(3)
所确定的曲面称为双叶双曲面.
用Oxy坐标面截所给曲面，得截痕为双曲线
x2 y2 2 2 1, a b z 0.
用平面z=h截所给曲面，得截痕为双曲线
x2 y2 Βιβλιοθήκη 2 2 2 1 2 , a b c z h.

二次曲面

二次曲面是由三元二次方程F(x, y, z) = 0所表示的空间曲面。其中，常见的九种类型包括：椭球面、抛物面（分为椭圆抛物面和双曲抛物面）、双曲面（分为单叶双曲面和双叶双曲面）、椭圆锥面和柱面（包括椭圆柱面、双曲柱面和抛物柱面）。椭球面可以通过将xoy面上的椭圆绕x轴旋转并沿z轴方向伸缩得到。抛物面则是由平面上的抛物线绕轴旋转并伸缩变形而并伸缩变形得到。椭圆锥面是圆锥面在某一轴向上伸缩变形的结果。柱面则是母线平行于某一轴的平面曲线沿该轴移动所形成的曲面。这些二次曲面的形状和特性可以通过截痕法和伸缩变形法来研究和理解。每种曲面都有其特定的方程形式，这些方程描述了曲面上点的坐标之间的关系，从而定义了曲面的几何形状。

1曲面方程(轨迹)2曲面形状


x
x 2y z 0
（1）消去z 得投影
x2 5 y2 4xy x 0
,
z 0
（2）消去y 得投影
x2 5z2 2xz 4x 0
,
y 0
（3）消去x
得投影
y2
z2
2
y
z
0 .
x 0
x2 y2 z2 1
例6
求曲线
z
1 2
在坐标面上的投影.
解 （1）消去变量z后得
x2 y2 3, 4
五、空间曲线及其方程
1、空间曲线的一般方程
F(x, y,z) 0 G( x, y, z) 0
z
例1
x2 y2 1
表示怎样的曲线？ S1
2x 3 y 3z 6
S2
交线为椭圆.
C
o
y
x
2、空间曲线的参数方程
x x(t)
y
y(t )
空间曲线的参数方程
z z(t)
当给定t t1 时，就得到曲线上的一个点 ( x1 , y1 , z1 )，随着参数的变化可得到曲线上的全
而：z
x2 a2
y2 b2
椭圆抛物面（图7-25）
xo
y
圆锥面：
z a x2 y2
zz
或z2 a（2 x2 y2）
yoz面上直线 z ay 绕z轴旋转 o
x
y
z ay
y2 z2 （例 7.6.4）椭圆 a 2 c2 1绕 y 轴和 z 轴；
x 0
绕 y 轴旋转
y2 x2 z2 a2 c2 1
F(x, y,z) 0 G( x, y, z) 0
x x(t)
y
y(t )

高数-附-2 二次曲面



1
与xoy平面平行的平面 z=z1 的交线为

x2 a2

y2 b2
1
z12 c2
z z1 为椭圆.
与yoz平面的交线

y2 b2

z2 c2

1
双曲线.
x 0
x0
x2 a2

y2 b2

z2 c2

1
与yoz平面平行平面的交线

y2 b2

z2 c2
（二）抛物面
(1) x2 y2 z（ p 与 q 同号）
2 p 2q
椭圆抛物面
椭圆抛物面的图形如下：
z z
o x
y
p 0, q 0
xo y
p 0, q 0
用截痕法讨论：设 p 0, q 0
z
（1）用坐标面 xoy(z=0) 与曲面
相截, 截得一点，即坐标原点O.
原点也叫椭圆抛物面的顶点.
与平面 z=z1 ( z1>0 ) 的交线为:
xo y
x2

2
pz1

y2 2qz1

1
当 z1变动时，这种椭 圆的中心都在 z 轴上.
z z1 为椭圆.
与平面 z z1 (z1 0)不相交.
（2）用坐标面 xoz ( y 0)与曲面相截
截得
x2

2
pz
为抛物线
z
z12
)

b2 c2
y2 (c2

z12 )
为椭
1
z z1 | z1 | c
圆
同理与平面 x x1 和 y y1 的交线也是椭圆.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

这些交线都是椭圆。
3） 再看这个曲面平行于 xoy 的平面 z= z1 ( z1 c )的交线
x 2 y 2 z12 1 a2 b2 c2
a2 c2
x2 (c2
z
2 1
)
b2 c2
y2 (c2
z12 )
1
z= z 1
4） 如果 a=b,那么方程变为：
x2 a2
y2 a2
z2 c2
1
x2 y2 a2
4、 双曲面
方程为： 单叶双曲面
x2 a2
y2 b2
z2 c2
1
1） 当 z=0 时，为过原点的圆，圆点在原点上。
x2 y2 1 a2 b2
2） 当用平行与 z=0 的平面 z= z1 截双曲面时，
x2 y2 z2 1 a2 b2 c2
Z= z1
x 2 y 2 1 z12
a2 b2
c2
-------------椭圆
3） 当 y=0 时，在 xoz 平面上为一双曲线
x2 z2 1 a2 c2
4） 当用平行 y=0 的平面 y= y1（ y1 ≠±b）截得曲面为中心在 y 轴上的双曲线
x2 a2
z2 c2
1
y12 b2
双曲线知识回顾：
双曲线定义 图形
m MF1 MF2 2a2a F1F2
常用的二次曲面方程及其图形
旋转曲面：L 是 XOZ 平面内的一个曲面
p0
P
f (x, z) 0
y0
其方程是：
得到旋转面的方程为： f ( x2 y2 , z) 0
柱面： 是空间的一个曲线，直线 L 沿着 平行移动 所形成的曲面，叫做柱面， 称作柱面的准线，L 称作柱面的母线。
若准线的方程为 f ( x , y ) 0
a2
z2 c2
1Leabharlann 2、 抛物面方程为：
x 2 y 2 z （p 与 q 同号） 2 p 2q
取 p>0,q>0
1） 当 z=0 时，截得为原点 O,原点叫做抛物面的顶点
z= z 2） 当
1 平面截得曲面为圆点在 z 轴上的圆。
x2 y2 z 2 p 2q
z= z 1
x2 y2 1 2 pz 1 2 qz 1
3） 当 y=0 时，截得的为 xoz 平面上的抛物线 x2 2 pz
y 4） 当 y= 1 平面截得曲面为平行 xoz 平面的抛物线
x2 y2 z 2 p 2q
y= y1
x2 2 p(z y12 ) 2q
5） 当 p=q 时，
x 2 y 2 z 表 示 xoz 平 面 上 的 抛 物 线 2p 2p
2） 旋转，根据旋转曲面与平面方程（母线）的关系，列 出空间旋转曲面等式
3） 当 z 0 =z，带入平面曲线方程。
M0 (x0,0, z0 )
M(x,y,z)
x02 z02 1
a2
c2
x2 y 2 x0
x2 y2 带入平面曲线方程： a 2
z02 c2
1
x2 y2
当 z 0 =z 时，得到：
z2 c2
1
根据旋转曲面的知识：
-----------------------（2）
（2）式表示在 xoz 平面上的椭圆
x2 a2
z2 c2
1 围绕 z 轴的而行程的
旋转曲面，它与一般椭圆球不同之处在于，其用 z= z1 平面截得的平面为一个
圆点在 z 轴上的圆。
具体步骤：
1） 列出平面曲线（母线）方程，比如 f (x0, y0) 0
z0
当 母 线 方 向 向 量 是 {l , m, n} 时 ， 柱 面 方 程 是
f (x l z, y m z) 0
n
n
x f (t)
若准线的方程是： : y h ( t ) ，母线的方向向量为
z g (t)
x f (t) lu {l , m, n}时，柱面方程是： : y h ( t ) m u
x 2 2 pz 围绕 z 轴而称的旋转曲面。
具体步骤：
M 1 (x1 ,0, z1 )
M (x, y, z)
1） x12 2 pz1
2）
x 2 y 2 x1
x 2 y 2 2 pz1
3) z1 =z 时，得到：
x2 y2 z 2p 2p
3、 双曲抛物面（鞍型曲面）
方程为：
x 2 y 2 z （p 与 q 同号） 2 p 2q
z g (t) nu
1、 椭圆球
x2 方程为： a 2
y2 b2
z2 c2
1
曲线为：
-------------------（1）
1）
由方程（1）可知
x2 a2
1，
y2 b2
1
，
z c
2 2
1，
2） 其与三个坐标平面的交线为：
x2 a2
y2 b2
1
z=0
x2 a2
z2 c2
1
y =0
y2 z2 1 b2 c2 x=0
( F1、F2 为定点， 为a常数)
标准方程
焦点坐标
a,b,c
x2 y2 1a 0，b 0
a2 b2
F1 c，0 F2 c，0
y2 a2
x2 b2
1a
0，b 0
F10， c F2 0，c
c2 a2 b2 c a 0，c b 0
双叶双曲面
x2 a2
y2 b2
z2 c2
1