三维数据结构

三维数据结构及其分类姓名：班级：学号：日期：三维数据结构及其分类一、引言随着GIS理论的日趋成熟及其应用的不断拓展，其许多商业化的GIS软件的功能也逐渐完善。

但是绝大多数的商品化GIS软件包还只是在二维平面基础上对现实世界的实体及实体之间的关系的模拟和处理，而我们生活在三维的世界里，所涉及到的有关气象、水文、采矿、灾害、污染等方面的自然现象都是三维的，显然当我们仅仅用二维的方法和思路解释和处理三维问题时，就不能够精确地或正确地反映、存储、分析、处理和显示地理空间信息。

因此，为更逼真精确地描述现实三维世界，探讨和研究三维数据结构显得尤为重要。

二、三维数据结构数据结构是即数据的逻辑结构形式，我们所熟悉的是二维数据结构，从类别上分，二维数据结构包括矢量数据结构、栅格数据结构、矢量-栅格一体化数据结构等，这主要是依据其数据模型进行分类的，即栅格数据模型、矢量数据模型、面向对象数据模型等，这与我们通常先建立数据模型，再依据数据模型选用合适的数据结构对数据进行组织的思路是一致的。

通常我们所说的三维景观可视化和已经具有的2.5维表面建模都还不是真正意义上的三维，比如利用DEM数据建立的三维景观模型可视化，或者利用多属性的实体的某一属性作为第三维对平面图形进行三维显示等。

如利用v = f(x,y)表达一个二维系统，(x,y)是二维平面坐标，v是对应点的属性值，当v表示高程时，就可以表示数字高程模型。

但这里v受x,y变化的影响；而真正意义上的三维数据模型中，三维变量之间应是相互独立的。

也就是说，对于一个真正的三维数据模型，可以用V = f(x,y,z)来描述，其中z是自变量，不受x，y变化的影响，即(x,y,z)是在三维空间连续变化的。

总的来说，即是与二维相比，三维多出了一维，但仍然可以将二维的观点引入对三维的研究之中。

三维空间数据模型是人们对客观世界的理解和抽象，是建立三维空间数据库的理论基础。

三维空间数据结构是三维空间数据模型的具体实现，是客观对象在计算机中的底层表达，是对客观对象进行可视表现的基础。

超图三维数据格式解析之前有讲过Cesium的三维数据格式：3dtiles。

超图的三维数据格式和它有什么不同呢？它⽐3dtiles好在哪⾥？空间三维模型数据格式规定了三维地理空间数据格式的逻辑结构及存储格式要求。

该标准适⽤于⽹络环境和离线环境下海量、多源三维地理空间数据的数据传输、交换和⾼性能可视化，以及满⾜不同终端(移动设备、浏览器、桌⾯电脑)上的三维地理信息系统相关应⽤。

该标准定义的S3M数据格式具备以下技术特点和优势：1、⽀持表达多源地理空间数据：倾斜摄影模型、BIM、⼈⼯建模、激光点云、⽮量、地下管线等多源数据。

2、具备海量数据⾼效绘制的能⼒：⽀持LOD、批次绘制、实例化等，提升渲染性能。

3、具备单体化选择和查询能⼒：⽀持⾼效选择、⽀持批量修改对象颜⾊、批量修改对象可见性。

4、简洁易读：格式简洁，易解析，适⽤于WebGL等轻量级客户端。

5、⾼效传输：数据紧凑，以⼆进制形式保存，占⽤空间⼩，传输性能⾼。

6、快速载⼊显卡：数据结构尽可能跟OpenGL接⼝保持⼀致，减少加载时间，⾼性能，低消耗。

7、跨终端：独⽴于任何终端，适⽤于PC端、Web端、移动端，具有较好的兼容性。

8、扩展性好：⽀持扩展，允许增加⼀些多⽤途扩展或特定⼚商的扩展。

9、完善的⼯具⽀撑：提供开源免费的S3M数据解析和转换⼯具，⽀持3D-Tiles、OSGB等格式与S3M格式相互转换。

(开源地址：。

)10、完善的配套设施：完整的解决⽅案，成熟的可⾏性，强⼤的实⽤性。

基于S3M形成了完整的B/S及C/S架构的三维GIS应⽤解决⽅案，从数据⽣成、服务器端发布到多种客户端加载应⽤等多个环节解决⽤户实际问题。

⽬录前⾔Ⅲ …………………………………………………………………………………………………………引⾔Ⅳ …………………………………………………………………………………………………………１范围１ ………………………………………………………………………………………………………２规范性引⽤⽂件１ …………………………………………………………………………………………３术语和定义１ ………………………………………………………………………………………………４符号和缩略语２ ……………………………………………………………………………………………４．１缩略语２ ………………………………………………………………………………………………４．２ＵＭＬ图⽰符号２ ………………………………………………………………………………………４．３ＵＭＬ多样性描述３ ……………………………………………………………………………………５基本规定３ …………………………………………………………………………………………………５．１基本数据类型３ ………………………………………………………………………………………５．２字符串类型４ …………………………………………………………………………………………５．３ｊｓｏｎ格式存储４ ………………………………………………………………………………………６组织结构４ …………………………………………………………………………………………………６．１⽂件组织４ ……………………………………………………………………………………………６．２树形结构描述５ ………………………………………………………………………………………７存储格式５ …………………………………………………………………………………………………７．１描述⽂件５ ……………………………………………………………………………………………７．２数据⽂件８ ……………………………………………………………………………………………７．３索引树⽂件２１ …………………………………………………………………………………………７．４属性⽂件２２ ……………………………………………………………………………………………附录Ａ（资料性附录）数据⽰例２５ …………………………………………………………………………参考⽂献３２ ……………………………………………………………………………………………………前⾔我们现在还需要多⼀种三维数据格式吗？似乎数据格式已经够多了够⽤了。

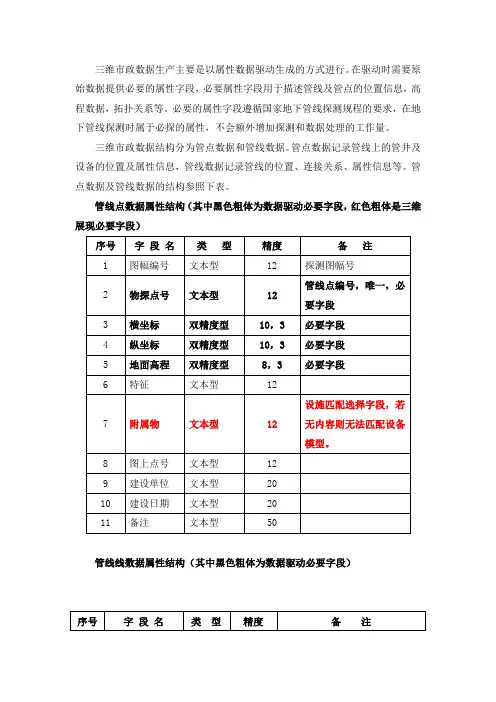
三维市政数据生产主要是以属性数据驱动生成的方式进行。

在驱动时需要原始数据提供必要的属性字段，必要属性字段用于描述管线及管点的位置信息，高程数据，拓扑关系等。

必要的属性字段遵循国家地下管线探测规程的要求，在地下管线探测时属于必探的属性，不会额外增加探测和数据处理的工作量。

三维市政数据结构分为管点数据和管线数据。

管点数据记录管线上的管井及设备的位置及属性信息，管线数据记录管线的位置、连接关系、属性信息等。

管点数据及管线数据的结构参照下表。

管线点数据属性结构（其中黑色粗体为数据驱动必要字段，红色粗体是三维展现必要字段）管线线数据属性结构（其中黑色粗体为数据驱动必要字段）支持GIS数据（shp），AutoCAD数据，外业探测表格数据等多种类型的数据驱动，只要数据属性内容满足以上的数据要求，就可以实现三维管线的数据驱动生成。

针对AutoCAD数据，必须满足一定的图形和标注的要求。

规定：AutoCAD数据的标注格式，用户可以将在AutoCAD中将标准属性字段以块的形式插入到数据中，与相关的管点或管线进行对应。

系统在导入AutoCAD数据时，可自动提取相关的属性内容录入到属性表格中，实现AutoCAD数据的驱动。

AutoCAD数据的相关标注如下图形标准：1、管线与管点数据的图层分离，管点是单独图层，管线是单独图层2、管线与管点连接，两管点之间的管线应为一条完整的线。

一条管线不可以通过多个管点。

3、管线必须通过管点的中心标注内容1、管点与管线的属性采用块标注的方式标注在图上。

管点块标注的中心与管点所在位置的中心重合。

管线的标注应尽量的靠近管线。

2、管点的标注内容参照前文的管线点属性结构，应标注必要字段。

最少需要标注管点编号、地面高程、特征或附属物。

3、管线标注内容参照前文的管线属性结构，应标注必要字段。

最少需要标注起点高程、终点高程、起点埋深、终点埋深、管径。

4、管点标注与管线标注图层分离。

管点标注为单独图层，管线标注为单独图层。

3.平时作业完成三维实体模型中B_Rep或CSG表示法的一种C/C++语言的数据结构定义。

物体的CSG树表示物体的体素构造表示法（Constructive Solid Geometry, CSG）是用两个物体间的并、交、差正则集合运算操作生成一个新的物体的方法。

CSG表示法：先定义一些形状比较简单的常用体素，如方块、圆柱、圆锥、球、棱柱等。

然后用集合运算并、交、差把体素修改成复杂形状的形体。

早期的CSG 模型仅使用代数方程及半空间的概念，体素只支持多面体与二次曲面体，而不支持表面含有自由曲面的实体。

整个模型是棵树结构，最终形体的表面交线与有效区域没有显式给出，不能直接用于NC加工与有限元分析等后继处理。

集合运算构造实体的过程可用二叉树结构表示，称该二叉树为CSG树。

树的叶节点表示体素或带有几何变换参数的体素，非叶节点表示施加于其子节点的正则集合算子，或称布尔算子。

树的根节点表示集合运算的最终结果，也即希望得到的实体。

边界表示法边界表示法（Brep-Boundary Representation）通过描述物体的边界来表示一个物体。

所谓的边界是指物体的内部点与外部点的分界面，定义了物体的边界，该物体也就被唯一地定义了。

如下图：边界表示法一个重要的特点是：描述物体的信息包括几何信息与拓扑信息两个方面。

几何信息是指物体在欧氏空间中的位置、形状和大小；而拓扑信息是指拓扑元素（顶点、边和表面）的数量及其相互间的连接关系。

拓扑信息构成物体的“骨架”，而几何信息则犹如附着在这一“骨架”上的“肌肉”。

几何信息有面（face）、环（loop）、边（edge）和点（vertex），拓扑信息有模型（model）、区域（region）、外壳（shell）、面引用（face use）、环引用（loop use）、边引用（edge use）和点引用（vertex use）。

如下图是用辐射边数据结构表示的一个形体模型，注意其中实体、面、线是用统一的数据结构表示的。

地质三维数据结构模型
地质三维数据结构模型是将地质数据以三维形式进行表示和存储的模型。

它通过使用空间坐标和属性信息，以及各种先进的计算和可视化技术，将地质对象的空间分布、几何形状和属性特征进行描述和呈现。

以下是几种常见的地质三维数据结构模型：
1.点云模型：点云模型使用大量的点来描述地质对象的空间位置，在每个点上附加了属性信息。

这种模型通常用于地质勘探、地形测绘和三维扫描等应用，如激光雷达扫描得到的地形数据。

2.三角网格模型：三角网格模型使用一系列相连接的三角形来近似地表面或地质对象的几何形状。

每个三角形都有顶点和属性信息，可以包括地层分布、岩性、地球化学特征等。

这种模型常用于地质建模和地质工程分析。

3. 体素模型：体素模型将空间划分为一系列相等大小的立方体单元（体素），每个体素都有一组属性信息，如密度、属性、岩石类型等。

这种模型主要用于岩石物性模拟、地下水模拟和地震模拟等领域。

4. 网格模型：网格模型将地质对象分割为规则或不规则的网格单元，每个单元都带有属性信息，如物性参数、岩性等。

这种模型常用于地下水流动模拟、矿产资源评估和地质灾害分析等应用。

5. 分层模型：分层模型根据地质体的内部结构和层序关系来描述地层的连续性。

它可以用来表示地层的分布、变形和岩性等信息，用于石油勘探、地层建模和地质演化研究等领域。

这些地质三维数据结构模型能够更好地支持地质数据的可视化、分析和预测，为地质学研究、资源开发和环境保护等提供有力的工具和方法。

三维CAD数据结构分析一、前言加强市场推广和服务是提高客户满意度的重要手段。

在三维CAD领域，通过市场调研和分析、品牌建设和宣传、客户关系管理、产品质量和技术支持等方面的努力，可以帮助企业增强市场竞争力，提高客户满意度，实现长期的可持续发展。

当前，新兴技术如虚拟现实、增强现实和人工智能等已经开始在设计领域中得到广泛应用。

这些新兴技术的渗透也会对三维CAD市场带来挑战。

工程师需要不断学习和掌握这些新技术，才能更好地应对日益复杂的设计需求。

云计算技术将在三维CAD中得到广泛应用。

设计师可以通过云平台存储和共享大量的设计数据，实现多人协同设计。

云计算的使用将极大地提高团队协作的效率，减少数据传输和存储的成本。

目前，三维CAD被广泛应用于汽车、航空航天、建筑、机械等行业。

其中，汽车、航空航天和建筑业是三维CAD市场的主要消费者，这些行业需要高效准确的设计和制造工具来提高生产效率和产品质量。

自20世纪80年代三维CAD技术问世以来，其市场规模一直呈现稳步增长的趋势。

其中，北美地区和欧洲地区是三维CAD市场的主要消费地区，占据了全球三维CAD市场的60%份额。

而亚太地区的三维CAD市场正在快速崛起，预计未来几年将成为三维CAD市场的重要增长点。

声明：本文内容信息来源于公开渠道，对文中内容的准确性、完整性、及时性或可靠性不作任何保证。

本文内容仅供参考与学习交流使用，不构成相关领域的建议和依据。

二、三维CAD数据结构三维计算机辅助设计（3DCAD）是一种利用计算机技术来创建、修改和分析三维模型的过程。

在三维CAD中，数据结构是非常重要的，它决定了如何表示和组织三维模型的信息。

三维CAD数据结构包括几何数据结构、拓扑数据结构和属性数据结构。

（一）几何数据结构1、点（Point）:点是最基本的几何元素，用于定义三维空间中的位置。

每个点由其坐标值确定，通常表示为（x,y,z）o在三维CAD中，点被广泛用于构建其他几何实体。

地理信息系统课程重点复习提纲一、填空：1、GIS 的英文全称：geographic information systems2、在GIS中计算机硬件包括：中央处理器、存储器、外部储存介质、输入输出设备、网络传输设备3、GIS中的计算机软件包括：系统软件、GIS专业软件4、空间信息的基本特征：空间位置特征、属性特征、时态特征5、专题地图内容表示方法：符号法、等值线法、质底法和范围法、基于统计资料的方法P236二、解释概念1、信息：是向人们或机器提供关于现实世界新的事实的知识，是数据、消息中所包含的意义，它不随载体的物理设备形式的改变而改变。

特点：客观性、实用性、传输性、共享性。

2、数据结构：（P38）具体指同一类数据元素中各元素之间的相互关系，包括三个组成成分：数据的逻辑结构，数据的存储结构和数据的运算。

3、数字高程模型：（P170）（Digital elevation model，简称DEM）：是以（x,y）为自变量的高程z数据的有序集合。

常用的DEM有两种形式：一种称为高程矩阵，高程数据布满覆盖整个区域的方格网的网格，相当于高程的栅格数据；一种称为DEM的高程数据布满覆盖整个区域的三角网网点，实际上就是TIN数据。

4、不规则三角网：（P84）（Triangulated irregular network,简称TIN）： TIN由基于离散数据样点直接构造，即直接采用不规则样点构成的三角形作为空间分析的地面单元。

TIN的网眼结构本身适应于数据的实际分布，即在空间数据或事件密度较高的区域，TIN的地面单元即分析单元自然地小而密；反之则变大而疏。

5、数字地形模型：是在一个区域内，以密集的地形模型点的坐标（x，y，z）表达地面形态的有序数值阵列。

（是地形表面形态属性信息的数字表达，是带有空间位置特征和地形属性特征的数字描述。

是描述地面特性的空间分布的有序数值阵列。

）6、空间数据插值：是指通过已知点或分区的数据，推求任意点或分区数据的处理及其方法。

八叉树三维数据结构（一）基本原理用八叉树来表示三维形体，并研究在这种表示下的各种操作及应用是在进入80年代后才比较全面地开展起来的。

这种方法，既可以看成是四叉树方法在三维空间的推广，也可以认为是用三维体素阵列表示形体方法的一种改进。

八叉树的逻辑结构如下：假设要表示的形体V可以放在一个充分大的正方体C内，C的边长为2 n，形体V C，它的八叉树可以用以下的递归方法来定义：八叉树的每个节点与C的一个子立方体对应，树根与C本身相对应，如果V＝C，那么V 的八叉树仅有树根，如果V≠C，则将C等分为八个子立方体，每个子立方体与树根的一个子节点相对应。

只要某个子立方体不是完全空白或完全为V所占据，就要被八等分（图2-5-1），从而对应的节点也就有了八个子节点。

这样的递归判断、分割一直要进行到节点所对应的立方体或是完全空白，或是完全为V占据，或是其大小已是预先定义的体素大小，并且对它与V之交作一定的“舍入”，使体素或认为是空白的，或认为是V占据的。

如此所生成的八叉树上的节点可分为三类：灰节点，它对应的立方体部分地为V所占据；白节点，它所对应的立方体中无V的内容；黑节点，它所对应的立方体全为V所占据。

后两类又称为叶结点。

形体V关于C的八叉树的逻辑结构是这样的：它是一颗树，其上的节点要么是叶节点，要么就是有八个子节点的灰节点。

根节点与C相对应，其它节点与C 的某个子立方体相对应。

因为八叉树的结构与四叉树的结构是如此的相似，所以八叉树的存贮结构方式可以完全沿用四叉树的有关方法。

因而，根据不同的存贮方式，八叉树也可以分别称为常规的、线性的、一对八的八叉树等等。

另外，由于这种方法充分利用了形体在空上的相关性，因此，一般来说，它所占用的存贮空间要比三维体素阵列的少。

但是实际上它还是使用了相当多的存贮，这并不是八叉树的主要优点。

这一方法的主要优点在于可以非常方便地实现有广泛用途的集合运算(例如可以求两个物体的并、交、差等运算)，而这些恰是其它表示方法比较难以处理或者需要耗费许多计算资源的地方。

matlab三维度数组引用Matlab是一种强大的数学计算软件，它可以处理各种类型的数据，包括三维数组。

在Matlab中，三维数组是一种非常有用的数据结构，它可以用来存储和处理三维数据，例如图像、声音和视频等。

三维数组在Matlab中的引用方式与二维数组类似，但需要使用三个索引来引用元素。

三维数组的索引包括行、列和深度，其中深度表示数组中的第三个维度。

在Matlab中，可以使用以下方式创建一个三维数组：A = rand(3,4,2);这个命令将创建一个大小为3x4x2的三维数组A，其中每个元素都是随机生成的。

要引用三维数组中的元素，需要使用三个索引，例如：A(2,3,1)这个命令将返回A数组中第2行、第3列、第1个深度的元素。

在Matlab中，还可以使用冒号运算符来引用三维数组中的一部分元素。

例如，要引用第1个深度的所有元素，可以使用以下命令：A(:,:,1)这个命令将返回A数组中所有行和列的第1个深度的元素。

除了使用冒号运算符，还可以使用逗号运算符来引用三维数组中的一部分元素。

例如，要引用第1个深度的第2列和第3列的所有元素，可以使用以下命令：A(:,2:3,1)这个命令将返回A数组中所有行的第2列和第3列的第1个深度的元素。

在Matlab中，还可以使用一些函数来处理三维数组，例如sum、mean和std等。

这些函数可以对三维数组中的元素进行求和、求平均值和计算标准差等操作。

总之，三维数组是Matlab中非常有用的数据结构，它可以用来存储和处理各种类型的三维数据。

在Matlab中，可以使用索引、冒号运算符和逗号运算符来引用三维数组中的元素，还可以使用各种函数来处理三维数组中的数据。